Zhang Yanyan
Zhang Pan
Li Mingkun
Song Jiazheng1- 1School of Artificial Intelligence, Optics and Electronics, Northwestern Polytechnical University, Xi’an, China
- 2National Time Service Center, Chinese Academy of Sciences, Xi’an, China
- 3Jinan Institute of Quantum Technology, Jinan, Shandong, China
In this research, we demonstrate an optical frequency comb (OFC) based on a figure-9 laser and polarization-maintaining fibers to measure the dispersion of a microcavity. We adopt a multi-branch structure to obtain a broadband spectrum from 1,250 nm to 1,640 nm with 6-dB bandwidth. The single-mode power at each wavelength of the supercontinuum spectra is greater than 300 nJ, which assures the signal-to-noise ratio of the beat notes between the OFC and the diode laser. The frequency stability of the repetition rate is about 7.5 × 10–14 in an integration time of 1 s. This system allows us to extend the measurement bandwidth to 60 THz at the sub-megahertz resolution, which meets the requirements of the microcavity’s higher-order dispersion measurement.
Introduction
Since the first realization of the optical frequency comb (OFC) in 1999, OFCs have produced many unexpected and remarkable developments in many fields, such as frequency synthesis [1], ultrafast science [2], low-noise microwave generation [3], distance measurements [4], and time and frequency measurements [5]. Broadband frequency comb spectroscopy (BFCS) [6–10], which employs the advantage of an OFC to provide an equidistant pulse train composed of the broadband coherent spectrum, has become one of the most important applications and has attracted many scientists. Furthermore, the spectral range is the most important parameter for BFCS. In addition, many other parameters of BFCS should be considered, such as the repetition rate (fr), optical power per comb tooth, frequency stability, and robustness.
Several BFCS methods, such as direct frequency comb spectroscopy (DFCS) [11–14], Michelson-based Fourier transform spectroscopy (MFTS) [15, 16], and dual-comb spectroscopy (DCS) [17–19], have been developed to date. Direct frequency comb spectroscopy was the first spectroscopy experiment based on the OFC. In this scheme, a comb tooth with high intensity should be resonant with a transition, which is an effective tool in simple spectra comprising a narrow transition. The absolute frequency calibration can also be calculated by counting the FCS’s fr and the carrier-envelope offset frequency (fceo) with unprecedented precision. However, a continuous laser, as the transfer laser, has to be phase locked to the OFC or a high-finesse cavity, which makes it challenging to measure the frequency over a large bandwidth within a short time. MFTS, as the most successful broadband spectroscopic technique, can record spectra of the entire spectral spans simultaneously. Owing to the high coherent property of the OFC, MFTS can obtain increased signal-to-noise ratios. The limitations to MFTS involve the resolution thereof being inversely proportional to the moving-arm velocity of the scanning Michelson interferometer, which is usually slow. In addition, dual-comb spectroscopy, which uses two coherent OFCs with slightly different repetition rates Δfr, is a rapid and accurate MFTS approach without a mechanical delay arm. The resolution and the measuring speed of DCS are only determined by the OFCs’ fr and Δfr. To date, dual-comb spectroscopy has been used in many fields such as distance measurement, remote sensing, and atmospheric composition monitoring. However, the major drawback of DCS is the low comb tooth energy, which limits the scope of application. In addition, DCS becomes expensive and bulky due to the OFC requirement. Moreover, to maintain the high coherence between two OFCs, OFCs require a tight phase locked to a narrow-linewidth laser, which is demanding.
Another approach has utilized the idea of calibrating a frequency tunable diode laser with the comb’s mode spacing by calibrating a large tunable CW laser with the OFC [20–22]. The “running” beat notes fBP have been obtained between the OFC and the diode laser at the frequency of f when tuning the CW laser. Calibration markers, which equal f = fceo + nfrep ± fBP, could be obtained by using a narrowband band-pass filter. This approach was first used to measure the higher-order dispersion of the microcavity, owning the capability of rapid data acquisition and measurement of the spectral features smaller than the mode spacing of the comb teeth.
The precision test dispersion of a microcavity is important for the design and manufacturing process. The cavity dispersion can be conveniently characterized by measuring the variation of the free spectral range (FSR) as a function of the wavelength [20]. Additionally, the high resonance relative to the central resonance frequency, which requires broadband dispersion characterization to cover different spectral regions, is directly related to the quadratic and higher-order dispersions of the cavity [23]. Moreover, a high measurement speed is needed for the precise measurement of the temporal and spectral components. Hence, white light sources [24] are a traditional method for measuring dispersion by filtering a narrow bandwidth. Data acquisition requires extended periods to be spent scanning the filter window. Optical frequency combs provide a convenient way to characterize cavity dispersion [25]. The cavity group delay dispersion (GDD) is measured by varying frep. However, high-order transmission peaks are not included in this method, which limit the method to measure the quadratic and higher-order dispersions.
In this study, we demonstrate an OFM based on an all-polarization-maintaining fiber laser with a broad and flat spectrum for the dispersion measurement of a microcavity. We achieve 60 THz spectroscopy by chirped pulse amplification and nonlinear spectral broadening of a highly nonlinear fiber based on an Er-doped comb. The multi-branch architecture is designed to guarantee the power per comb tooth (more than 300 nJ) and the flatness of the spectroscopy. The frequency stability of the repetition rate is about 7.5 × 10–14 in an integration time of 1 s by phase-locking the harmonic frequency.
Experimental results and discussion
The experimental setup is depicted in Figure 1. The frequency comb broadband spectroscopy system is combined with an OFC based on an all-polarization-maintaining Er-doped fiber laser with the NALM technique and eight application branches for spectral broadening.
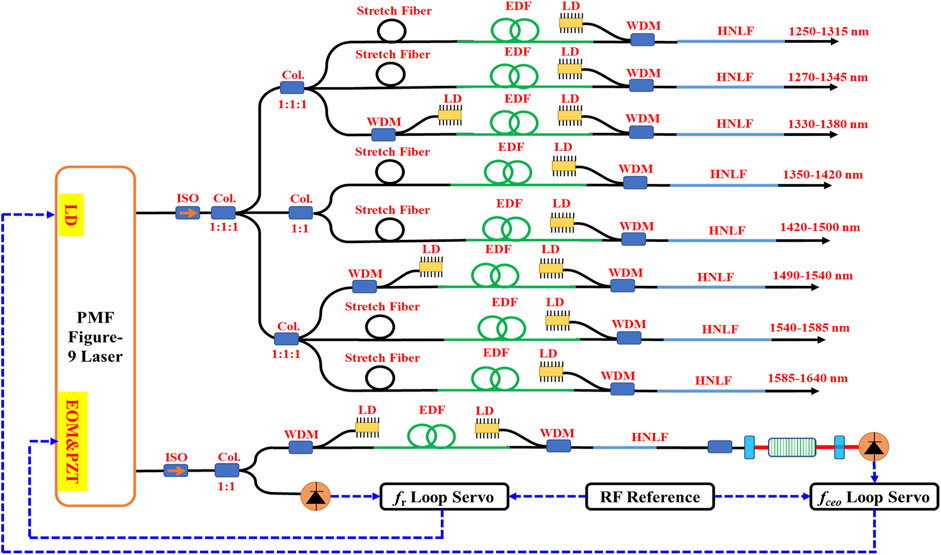
FIGURE 1. Experimental setup of frequency comb broadband spectroscopy. LD: laser diode; ISO: optical isolator; WDM: wavelength division multiplexer; Col: collimator; EDF: Er-doped fiber; HNLF: high nonlinear fiber.
A homemade figure-9 laser has the same structure as [26], composed of a polarization-maintaining fiber loop and a pace linear arm, and a non-reciprocal phase device is installed in the linear arm. By optimizing the dispersion of the laser cavity, the laser can start mode locking automatically. The output powers of output 1 and output 2 are 12 mW and 20 mW, respectively, when the pump power is about 700 mW, as described in [26]. Figure 2A shows the optical spectra of the outputs. The 10-dB bandwidths are about 90 nm and 50 nm for output 1 and output 2, respectively. A lower intrinsic phase noise for fr and the extended spectrum output is expected based on output 1 [26]. The repetition rate of the laser is 200 MHz. An electro-optic modulator (EOM) and a piezo actuator (PZT) are installed in the laser for control of fr. The carrier-envelope offset frequency is controlled by feedbacking the current of the laser diode (LD).
FIGURE 2. (A) Spectra of the laser outputs. (B) rf spectrum of fceo.
The power of 12 mW at the output 1 port is divided into nine branches with couplers, with one branch for fceo detection and the other eight branches for spectral broadening. For the branch for fceo detection, about 1 mW of laser power is pre-chirped before being launched into an Er-doped fiber amplifier (EDFA). Then, the pulses are compressed to 60 fs with a PM 1550 fiber. The compressed pulses are coupled into a HNLF to achieve octave-spanning spectrum broadening. The optical spectrum spans from 1,050 nm to 2,100 nm. An f-to-2f interferometer is used to obtain the fceo signal by doubling the 2,100 nm spectral composition and heterodyning it with the 1,050-nm composition of the laser. Figure 2B shows the radio-frequency spectrum of the detected fceo signal with a 1-GHz wide InGaAs photodetector (PD). The signal-to-noise ratio is more than 40 dB with a resolution bandwidth of 300 kHz, which benefits the robustness of the system.
To reduce the additional phase noise induced by the phase-locking process, we do not stabilize fr directly but rather stabilize its fifth harmonic of the repetition rate (1 GHz) to a 1-GHz reference signal, which is frequency multiplied from 200 MHz. The repetition rate is stabilized with a standard phase-locked loop technique. Two servo actuators are used to guarantee the high bandwidth and a large range of the locking loop. The down-converted frequency of 5fr at 5 MHz is recorded with a counter (Microchip 53100A). Figure 3A shows that the frequency instability of fr is about 7.5 × 10–14 at 1 s with a slope of τ−1/2. Figure 3B shows the phase noise of the 200-MHz reference signal and the additional phase noise of the fr phase-locking loop measured with the Microchip 53100A phase noise analyzer. Using the harmonic phase-locking method, the phase noise of the OFC is suppressed. This result is limited by the noise of the reference signal. The OFC stability can be enhanced by improving the phase noise of the reference signal.
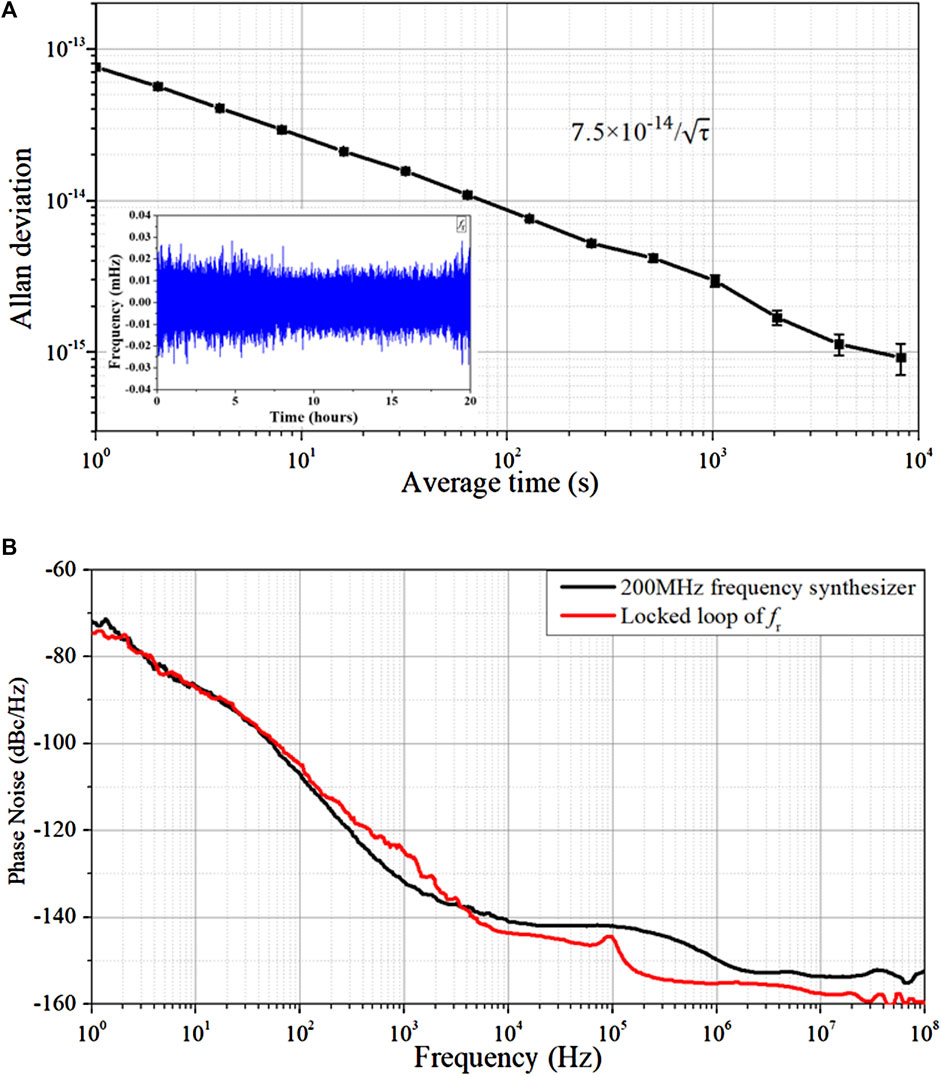
FIGURE 3. (A) Allan deviation of fr. (B) Phase noise of the frequency synthesizer and the additional phase noise of the fr-locked loop.
For the application of the dispersion measurement of a microcavity, the spectrum should cover the wavelength range from 1,260 nm to 1,640 nm, with the power of the comb teeth in this range being over 100 nJ and the flatness being smaller than 10 dB, simultaneously. To meet the application requirements, we expanded the optical spectra with chirped pulse amplification (CPA) technology and a HNLF by dividing the power (about 10 mW) of the OFC into eight branches. This structure is beneficial for both the spectral tailoring and the energy of the comb teeth. All eight application ports mentioned earlier have a similar structure to the fceo detection portion without the f-2f interference. By optimizing HNLF lengths, the parameters of the EDF, and the pumping powers, we obtain the target broadband spectra.
Figure 4 shows the spectra of the eight application ports with the target wavelength range from 1,250 nm to 1,640 nm in the dB scale, which were measured with an optical spectrum analyzer (Yokogawa, AQ6370). To guarantee a high power per comb mode and a relatively flat spectrum in the wide spectral range (about 60 THz), we finely adjust the parameters of the input pulse, HNLF, and pumping power. Moreover, the spectral output from different ports has partial overlaps with each other to improve the robustness.
FIGURE 4. Extended spectrum for the dispersion measurement of a microcavity.
The zero-dispersion wavelength (ZDW) and the dispersion characteristics are the important influencing factors on the energy distribution of the broadband spectrum. For the two ports of 1,250 nm–1,315 nm and 1,270 nm–1,345 nm, we use a PM-HNLF with a ZDW of 1,339 nm and a dispersion slope of 0.026 (ps/nm2)/km at 1,550 nm. Because of the large distance between the signal wavelength (at about 1,550 nm) and the ZDW, the dispersion wave is easy to be produced in the short wavelength. For the port of 1,330 nm–1,380 nm, the efficiency of the spectral transfer is suppressed by the water absorption peak near 1,380 nm. By increasing the input power with two 1-W pump lasers, the power of the signal comb teeth is improved. In addition, the fission solitons produce a continuous shift to the longer wavelength with the effect of the soliton self-frequency shift, which covers the wavelength range of 1,585–1,640 nm. To generate enough spectrum distribution between 1,350 nm and 1,500 nm, we choose the HNLF with the ZDW at 1,525 nm and the dispersion slope of 0.006 (ps/nm2)/km at 1,550 nm. Although the ZDW is close to the input light wavelength (1,550 nm) and the dispersion slope is small, the spectral components around 1,350–1,500 nm are easily obtained. For 1,490–1,585 nm, the negative group velocity dispersion (GVD) is chosen. Because the target spectral region is located near the input spectrum, self-phase modulation (SPM) dominates the fiber-optic nonlinearities, and the wavelength is tunable with the input pulse energy. The flatness of the spectrum in the range of 1,490–1,540 nm is large for the strong self-phase modulation effect, and we use two pump lasers to adjust the detailed parameters of the input pulse to the HNLF.
Low relative intensity noise (RIN) is an important condition for the lasers used for an OFC. The intensity noise of a laser can influence the system performance via the amplitude-to-phase conversion. The amplified spontaneous emission of the amplifier and the pump noise are the main contributions. Figure 5 shows the RIN measurement results of the different output ports of the laser. The RIN of the direct output port of the laser is the lowest. The RIN levels of the 1,490–1,540-nm port and the 1,330–1,380-nm port are higher than those of the other ports because two pump laser drivers are used in each port. In addition, Figure 5 shows the impact of the pump current on the RIN, which is the main factor that influences the RIN of the output ports. Specifically, for the 1,490–1,540-nm port, the forward pump laser current is set to 30 mW, and the RIN is higher than those of the other pump currents.
FIGURE 5. Relative intensity noises of the application ports.
Conclusion
In conclusion, a broad spectrum low-phase noise OFC based on the all-polarization-maintaining Er-doped fiber for the measurement of microcavity dispersion was developed. The fiber-based frequency comb with eight spread spectrum output ports could cover a spectral range of 60 THz at 6-dB flatness. Low-phase stabilization of the comb was obtained by locking the fifth harmonic of fr using a standard phase-locked loop technique. The Allan deviation was about 7.5 × 10–14 at 1 s with a slope of τ−1/2, which could support the sub-megahertz resolution measurement of the microcavity dispersion. Furthermore, some new [26, 27] lasers can use smaller ports to cover the broad spectrum for cascaded laser spectroscopy.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
YZ conceived the study and wrote the manuscript. PZ, ML, FC, and LL were responsible for the experiment setting. ZS was mainly engaged in picture editing and related data processing. All authors have made positive contributions to the work.
Funding
This work was supported by a general program from the National Science Foundation of China (No.61875226).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Fortier TM, Kirchner MS, Quinlan F, Taylor J, Bergquist JC, Rosenband T, et al. Generation of ultrastable microwaves via optical frequency division. Nat Photon (2011) 5:425–9. doi:10.1038/nphoton.2011.121
2. Hassan MT, Luu TT, Moulet A, Raskazovskaya O, Zhokhov P, Garg M, et al. Optical attosecond pulses and tracking the nonlinear response of bound electrons. Nature (2016) 530:66–70. doi:10.1038/nature16528
3. Xie X, Bouchand R, Nicolodi D, Giunta M, Hansel W, Lezius M, et al. Photonic microwave signals with zeptosecond-level absolute timing noise. Nat Photon (2016) 21:44–7. doi:10.1038/NPHOTON.2016.215
4. Baumann E, Giorgetta F, Coddington I, Sinclair L, Knabe K, Swann W, et al. Comb-calibrated frequency-modulated continuous-wave ladar for absolute distance measurements. Opt Lett (2013) 38:2026–8. doi:10.1364/OL.38.002026
5. Pupeza I, Zhang C, Högner M, Ye J. Extreme-ultraviolet frequency combs for precision metrology and attosecond science. Nat Photon (2021) 15:175–86. doi:10.1038/s41566-020-00741-3
6. Rieker GB, Giorgetta FR, Swann WC, Kofler J, Zolot AM, Sinclair LC, et al. Frequency-comb-based remote sensing of greenhouse gases over kilometer air paths. Optica (2014) 1:290–9. doi:10.1364/OPTICA.1.000290
7. Wang Q, Wang Z, Zhang H, Jiang S, Wang Y, Jin W, et al. Dual-comb photothermal spectroscopy. Nat Commun (2022) 13:2181–7. doi:10.1038/s41467-022-29865-6
8. Vicentini E, Wang Z, Gasse K, Hänsch T, Picqué N. Dual-comb hyperspectral digital holography. Nat Photon (2021) 15:890–4. doi:10.1038/s41566-021-00892-x
9. Nr Newbury EB, Coddington I, Giorgetta F, Swann W, Zolot A. Performance of a coherent dual frequency comb spectrometer. Imaging and applied optics technical digest (2011). FthB2.
10. Pinkowski NH, Biswas P, Shao J, Strand C, Hanson RK. Thermometry and speciation for high-temperature and pressure methane pyrolysis using shock tubes and dual-comb spectroscopy. Meas Sci Technol (2021) 32:125502–15. doi:10.1088/1361-6501/ac22ef
11. Picque N, Hansch TW. Frequency comb spectroscopy. Nat Photon (2019) 13:146–57. doi:10.1038/s41566-018-0347-5
12. Cingoz A, Yost DC, Allison TK, Ruehl A, Fermann ME, Hartl I, et al. Direct frequency comb spectroscopy in the extreme ultraviolet. Nature (2012) 482:68–71. doi:10.1038/nature10711
13. Yost DC, Matveev A, Grinin A, Peters E, Maisenbacher L, Beyer A, et al. Spectroscopy of the hydrogen1S−3Stransition with chirped laser pulses. Phys Rev A (Coll Park) (2016) 93:042509. doi:10.1103/PhysRevA.93.042509
14. Solaro C, Meyer S, Fisher K, Depalatis MV, Drewsen M, et al. Direct frequency-comb-driven Raman transitions in the terahertz range. Phys Rev Lett (2018) 120:253601. doi:10.1103/PhysRevLett.120.253601
15. Grifths PR, Haseth JA. Fourier transform infrared spectroscopy. 2nd ed. Hoboken: John Wiley (2007).
16. Spaun B, changala PB, Patterson D, Bjork BJ, Oh H, Doyle JM, et al. Continuous probing of cold complex molecules with infrared frequency comb spectroscopy. Nature (2016) 533:517–20. doi:10.1038/nature17440
17. Okubo S, Iwakuni K, Inaba H, Hosaka K, Onae A, Sasada H, et al. Ultra-broadband dual-comb spectroscopy across 1.0–1.9 μm. Appl Phys Express (2015) 8:082402. doi:10.7567/APEX.8.082402
18. Chen Z, Yan M, Hänsch TW, Picque N. A phase-stable dual-comb interferometer. Nat Commun (2018) 9:3035. doi:10.1038/s41467-018-05509-6
19. Chen Z, Hänsch TW, Picqué N. Mid-infrared feed-forward dual-comb spectroscopy. Proc Natl Acad Sci U S A (2019) 116(9):3454–9. doi:10.1073/pnas.1819082116
20. Delhaye P, Arcizet O, Gorodetsky ML, Holzwarth R, Kippenberg TJ. Frequency comb assisted diode laser spectroscopy for measurement of microcavity dispersion. Nat Photon (2009) 3:529–33. doi:10.1038/NPHOTON.2009.138
21. Giorgetta FR, Coddington I, Baumann E, Swann WC, Newbury NR. Fast high-resolution spectroscopy of dynamic continuous-wave laser sources. Nat Photon (2010) 24:853–7. doi:10.1038/NPHOTON.2010.228
22. Nishiyama A, Matsuba A, Misono M. Precise frequency measurement and characterization of a continuous scanning single-mode laser with an optical frequency comb. Opt Lett (2014) 39:4923–6. doi:10.1364/OL.39.004923
23. Liu J, Brasch V, Pfeiffer MH, Kordts A, An K, Guo H, et al. Frequency-comb-assisted broadband precision spectroscopy with cascaded diode lasers. Opt Lett (2016) 41:3134–7. doi:10.1364/OL.41.003134
24. Anatoliy AS, Enrio R, Andrey BM, Vladimir SI, Lute M. Phase noise of whispering gallery photonic hyper-parametric microwave oscillators. Opt Express (2008) 16:4130–7. doi:10.1364/oe.16.004130
25. Jiang L, Hansuek L, Ki Y, Kerry JV. Sideband Spectrosc dispersion Meas microcavities (2012) 20:26337–44. doi:10.1364/OE.20.026337
26. Zhang P, Zhang YY, Li MK, Rao BJ, Yan LL, Chen FX, et al. All polarization-maintaining Er: Fiber-based optical frequency comb for frequency comparison of optical clocks. Chin Phys B (2022) 31:054210. doi:10.1088/1674-1056/ac40f6
Keywords: optical frequency comb, all-polarization-maintaining, dispersion measurement, microcavity, broad spectral band
Citation: Yanyan Z, Pan Z, Mingkun L, Jiazheng S, Faxi C, Libo L, Xuelong L and Yuanshan L (2022) All-polarization-maintaining fiber optical frequency comb for the dispersion measurement of a microcavity. Front. Phys. 10:1036218. doi: 10.3389/fphy.2022.1036218
Received: 04 September 2022; Accepted: 10 October 2022;
Published: 25 October 2022.
Edited by:
Hainian Han, Institute of Physics (CAS), ChinaReviewed by:
Yanyi Jiang Jiang, East China Normal University, ChinaXiaohui Li, Shaanxi Normal University, China
Copyright © 2022 Yanyan, Pan, Mingkun, Jiazheng, Faxi, Libo, Xuelong and Yuanshan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Li Xuelong, bGlAbndwdS5lZHUuY24=; Liu Yuanshan, bGl1eXVhbnNoYW5AbndwdS5lZHUuY24=