Efficiency of navigation strategies for active particles in rugged landscapes

Optimal navigation in complex environments is a problem with multiple applications ranging from designing efficient search strategies to engineering microscopic cargo delivery. When motion happens in presence of strong external forces, route optimization is particularly important as active particles may encounter trapping regions that would substantially slow down their progress. Here, considering a self-propelled agent moving at a constant speed, we study the efficiency of Zermelo’s classical solution for navigation in a sinusoidal potential landscape. Investigating both cases of motion on the plane and on curved surfaces, we focus on the regime where the external force exceeds self-propulsion in finite regions. There, we show that, despite the fact that most trajectories following the trivial policy of going straight get arrested, the Zermelo policy allows for a comprehensive exploration of the environment. However, our results also indicate an increased sensitivity of the Zermelo strategy to initial conditions, which limits its robustness and long-time efficiency, particularly in presence of fluctuations. These results suggest an interesting trade-off between exploration efficiency and stability for the design of control strategies to be implemented in real systems.

1 Introduction

Determining the optimal way to navigate in a complex environment is a central problem for living organisms constantly searching for food, breeding partners, or escaping predators [1–3]. On the other hand, optimal navigation has important engineering applications such as route planning [4, 5], environment monitoring [6], or due to recent advances in the design of microswimmers [7, 8], even targeted microscopic cargo delivery [9, 10]. Optimal search strategies, for example, often consist of intermittent stochastic processes alternating between ballistic moving and diffusive searching phases [11–13]. Efficiently moving, for example, by minimizing travel time or energy consumption, is thus a crucial aspect of target search optimization. In absence of external influence from the environment, the natural moving strategy is to follow straight trajectories. This trivial straight policy (SP), however, becomes disadvantageous when motion happens on a rugged landscape or in presence of advection by a flow field. Optimizing the motion, moreover, becomes especially important if the external influence of the environment is sufficiently strong to forbid certain routes or induce trapping.

Mathematically, the problem of optimal navigation is addressed by optimal control theory [14–16]. Given a set of deterministic differential equations ruling the dynamics of interest and a cost function to minimize, the optimal strategy is obtained by applying Pontryagin’s maximum principle [17]. The minimal travel time problem with stationary environmental conditions and constant self-propulsion speed, such that the agent navigates adjusting its direction of motion, is known as the Zermelo problem [18]. Its generalization to self-propelled motion on curved manifolds was, moreover, carried out in Ref. [19], where it was shown that the optimal paths correspond to the geodesics of a Randers metric [20–22]. The navigation strategies obtained by solving the Zermelo problem and its generalizations have been mostly theoretically studied for simple configurations and in the regime where the self-propulsion force is always greater than the external force [19, 23–26] (see, however, Ref. [27]).

Here, we revisit the problem of optimal navigation considering self-propelled agents moving in a two-dimensional sinusoidal potential landscape and evaluate the SP and Zermelo policy’s (ZP) ability to efficiently explore space in presence of a strong force field influencing the motion. Given a point-to-point navigation problem, the performance of ZP is usually measured in terms of the travel time taken by the particle with the appropriate initial self-propulsion orientation to reach its assigned target. An alternative—and more general—approach consists of considering a distribution of initial orientations and analyzing the isochrone curves [19], here defined as the set of space points with equal travel time. Indeed, as the isochrones essentially delimit the potentially explored region up to some time, they provide quantitative information on how for uncontrolled initial orientations the optimal trajectories will manage to explore the surrounding space on average.

Performing extensive numerical simulations, our results reveal that, as expected, in a deterministic setting, ZP systematically performs better than SP over all the available parameter space. The differences between the two policies are, moreover, particularly striking in the regime of large external force. Although, in this case, a significant proportion of trajectories following SP get arrested, thus strongly restricting the amount of space that can be visited, ZP manages to sustain ergodic exploration as long as there exist available routes. As our analysis shows, ZP’s good performance stems from its ability to circumvent regions with a strong force field opposing the motion. On the other hand, we also show that in the presence of strong external forces, the dynamics produced by ZP are generally chaotic, which leads to an increased sensitivity to initial conditions and limits its long-time efficiency. When the dynamics are subject to fluctuations, ZP then becomes disadvantageous as it leads most of the trajectories to be deflected toward trapping regions. In contrast, SP exhibits performances that are robust to the presence of fluctuations. Finally, considering a navigation setup on a curved sinusoidal surface, we show that these conclusions remain valid in presence of finite space curvature.

2 Methods

We study the overdamped motion of a self-propelled particle moving on the plane at constant speed v₀ in presence of an externally applied stationary force field f. The position $\mathit{r}=x\widehat{\mathit{x}}+y\widehat{\mathit{y}}$ of the particle thus obeys

$\dot{\mathit{r}}=v_0\widehat{\mathit{e}}\left(\theta \right)+\mu \mathit{f}\left(\mathit{r}\right),(1)$

where μ is mobility—which hereafter we set to unity—and $\widehat{\mathit{e}}(\theta )$ denotes the unit vector oriented along the direction defined by the angle θ. In order to study the efficiency of the navigation protocols under a possibly motion-limiting force field, we, moreover, consider a potential force f(r) = −∇U(r) with

$U\left(\mathit{r}\right)=\frac{u}{4}\left[\sin \left(kx\right)+\sin \left(ky\right)\right],(2)$

where u and k = π/(2ℓ) are parameters that set the strength and periodicity of the potential. The potential U consists of a square lattice of local minima and maxima, and the resulting force field is pictured in Figure 1. Rescaling space and time, respectively, with ℓ and ℓ/v₀, the dynamics of (1) depends on a single control parameter γ ≡ πu/(8v₀) which measures the relative strength of the force with respect to self-propulsion.

FIGURE 1

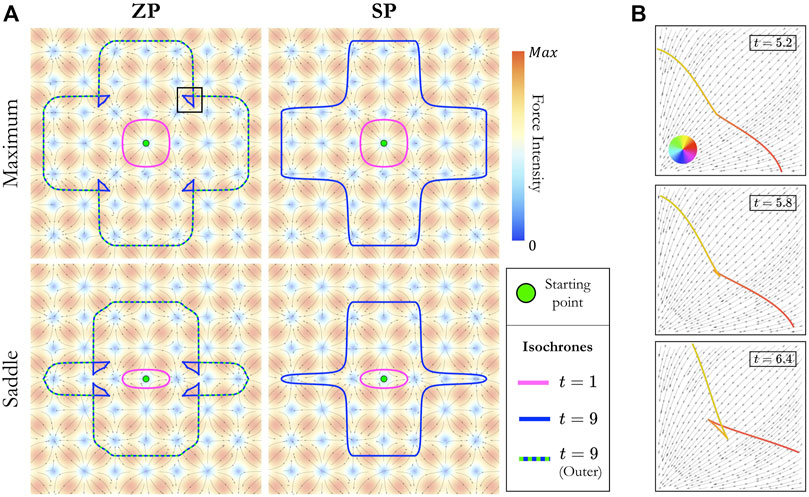
FIGURE 1. Short-time isochrones in the confining regime. (A) Each panel shows two exemplary short-time isochrones at times t = 1 and t = 9 for a relative force strength γ = 0.79. The top and bottom rows correspond, respectively, to a departure point located at a local maximum or a saddle point of the potential (2), leading to different symmetries of the isochrones. Contrary to SP (right column), ZP (left column) exhibits characteristic self-crossings which allow trajectories to circumvent otherwise inaccessible regions of space. In all panels, the color map indicates the intensity of the external force field, and the gray arrows indicate its direction. Panel (B) shows zooms of the region indicated by the black square in (A). These three snapshots at different times show the formation of a self-intersection and two cusps in the ZP isochrone starting from a local maximum. The color code along the curve stands for the initial orientation of the trajectory as indicated by the color wheel.

The value of γ defines several dynamical regimes for the self-propelled motion. Indeed, for $\gamma <1/\sqrt{2}$, the self-propulsion speed overcomes the strength of the external force over all the space, such that the particles can, in principle, travel everywhere without restriction. In the following, we refer to this case as the weak force regime. On the contrary, the condition γ > 1 defines a trapping regime where the self-propelled particles are not able to escape local minima of the potential. Lastly, in the intermediate confining regime $1/\sqrt{2}<\gamma <1$, the strength of the external drive is larger than that of self-propulsion only in disconnected regions between which the particles can travel almost freely.

To fully characterize the dynamics, we must specify an update rule for the self-propulsion orientation θ. The most straightforward choice for such a navigation policy is to pick an orientation θ₀ at time t = 0 and keep it forever. This choice corresponds to the trivial straight policy which we expect to be sub-optimal as for large values of γ, it does not allow the particles to avoid trapping regions of the potential. On the other hand, applying variational calculus in order to minimize the integral cost $T\equiv {\int }_0^t\mathrm{d}{t}^{\prime }$, we obtain the Zermelo policy that corresponds to the following dynamical equation for the orientation [17, 18].

$\dot{\theta }={\sin }^2\theta {\partial }_x{f}_y-{\cos }^2\theta {\partial }_y{f}_x+\sin \theta \cos \theta \left({\partial }_x{f}_x-{\partial }_y{f}_y\right),(3)$

and which ensures minimal travel time as the particles travel across the potential. The extension of ZP to curved geometries via a mapping to Randers spaces is discussed in detail in Section 2.1.

All results presented were obtained from numerical simulations performed by means of a fourth-order Runge–Kutta method with a time step dt = 10⁻³. We checked that decreasing the value of dt did not qualitatively affect the results. For all policies, the isochrones were calculated simulating multiple trajectories with initial orientation θ₀ uniformly distributed on the circle. The corresponding angular resolution δθ₀ was taken between 10⁻⁴ for SP and 10⁻⁶ for ZP. When specified, data fits were performed via the FindFit routine of Mathematica [28].

3 Results

3.1 Isochrones analysis on the plane

In this section, we analyze the performances of ZP and SP for space exploration in the three dynamical regimes defined by the value of the parameter γ.

3.1.1 Short-time behavior of the isochrones

Figure 1A shows typical isochrones obtained in 2D with both ZP and SP. These curves can be viewed as the front of active particles propagating away from the departure point. They correspond to relatively short times as their overall surface extends to only a few periods of potential. Starting from a local maximum of the potential (upper row in Figure 1A), the isochrones are initially isotropic (pink curves) and at later times deform into a cross-like shape (blue curves) due to the local structure of the force field. In contrast, taking a saddle point as the initial condition (lower row in Figure 1A), the isochrones naturally elongate in the directions along which the force points away from the initial position. Although the shapes of the isochrones at later times resemble that of their counterpart originating from the local maximum, they still carry the signature of the initial anisotropy. Figure 1, moreover, shows that, contrary to SP, the ZP isochrones develop self-crossing points in regions of strong and unfavorable force (i.e., pointing towards the departure position). As pictured in Figure 1B, these self-crossings form because trajectories starting with neighboring initial orientations cross each other. As we will discuss, these crossings are essential for ZP to be able to explore regions of space which would be unreachable otherwise.

The rest of this section is devoted to the characterization of the long-time isochrone properties. Despite the quantitative shape differences observed for different starting points, we show in the Supplementary Material that the long-time properties of the isochrones remain qualitatively independent of the starting position. We, therefore, restrict the following analysis to the case where the isochrones are initialized at a local maximum of the potential, corresponding to the upper row of Figure 1A.

3.1.2 Isochrone areas and exploration performances

The first quantity of interest to measure the ability of the policies to efficiently explore the surrounding space is the isochrone area A. Figure 2A shows the scaling of A versus t². In absence of an external drive (γ = 0), SP and ZP are strictly equivalent as the fastest way to travel between two points is to join them via a straight line. Therefore, in this limit, isochrones expand isotropically along all directions and A ∼ t² up to a constant prefactor. This behavior, moreover, remains qualitatively valid throughout the weak force regime as the measured exponent α defined from the long-time scaling A ∼ t^2α takes values close to 1 (Figure 2B). To measure the isochrone anisotropy, we, moreover, define the fractional area ϕ as the ratio between the area A and that of the smallest disk containing the isochrone. For γ = 0, isochrones are perfect circles such that ϕ = 1. Figure 2C shows that for $\gamma <1/\sqrt{2}$ (in the weak force regime), ϕ oscillates due to the local force field structure, but takes a well-defined average value $<1$. This value is systematically larger for ZP than for SP, indicating that isochrones associated with the former are more isotropic (more details in the SM).

FIGURE 2

FIGURE 2. Isochrone area analysis in the 2D periodic potential. (A) Isochrone area as a function of squared time for ZP and SP and two values of the relative force strength γ, respectively, in the weak force and confining regimes. (B) Best fit of the exponent α (defined in the main text) showing different scalings between SP and ZP in the confining regime. (C) Fractional area covered by the isochrones as a function of time; the legend is the same as (A). The insets show the outer boundary of the isochrones (yellow region) enclosed in the corresponding bounding disk (purple) for both policies at t = 20 and γ = 0.79.

For $1/\sqrt{2}<\gamma <1$, the dynamics (1–3) is in the confining regime, meaning that the amplitude of the force field overcomes that of the self-propulsion in certain regions of space. As a consequence, for SP, the exponent α exhibits a sudden decrease from 1 to $\approx \frac{1}{2}$ at $\gamma \approx 1/\sqrt{2}$ (Figure 2B). This behavior is due to the fact that in this regime, only trajectories starting with θ₀ close to a multiple of $\frac{\pi }{2}$ manage to progress away from the departure point after some time, while the others stop as the force created by the potential balances the self-propulsion. Consequently, the isochrones only grow along the horizontal and vertical axis, resulting in an increasingly strong anisotropy (see the inset of Figure 2C). In this context, it is natural to expect that the isochrone area grows linearly in time, resulting in an exponent $\alpha =\frac{1}{2}$. This behavior is reminiscent of that of the initial spreading of the particle distribution in an infinite-horizon Lorentz gas [29]. These observations are, moreover, confirmed by the behavior of the fractional area ϕ which is found to approach zero as ϕ ∼ 1/t. Hence, in confining environments, SP generally allows exploring only a limited portion of the space.

For ZP, on the contrary, the situation is remarkably different. Indeed, in this case, area A keeps growing almost as t², such that the best fits of the exponents α provide values close to 1 even for γ ≳ 0.8 (see Figures 2A,B). Similar to the weak force regime, ZP ϕ oscillates around a well-defined value ≳ 0.8 even when the potential strongly constrains the dynamics (see Figure 2C and SM). The amplitude of fractional area oscillations, moreover, grows with γ as a result of the increasing influence of the potential landscape. Therefore, and contrary to SP, the ZP isochrones manage to entirely explore the space despite the presence of stopping points in the force field (compare, in particular, the two insets of Figure 2C and see the Supplementary Movie S1).

This remarkable feature, however, becomes harder to observe as γ approaches 1. Indeed, as we will describe for ZP, the isochrone boundaries become sharper as γ grows, such that resolving them requires a rapidly increasing resolution. The limit γ → 1 is thus numerically intractable, but we expect the aforementioned conclusions to hold qualitatively until the trapping regime occurs at γ = 1, where the particles cannot travel further than a potential period regardless of the policy employed.

3.1.3 Robustness and sensitivity to initial conditions

Interestingly, ZP manages to sustain ergodic exploration of space even in the presence of a strongly confining force field. As we show now, this feat comes at the price of ZP being much more sensitive to the chosen initial orientation than SP.

Figure 3A shows color maps of the distance reached by trajectories as a function of their initial orientation θ₀ and time. In the weak force regime, isochrones grow nearly isotropically such that the distance reached by a trajectory after a certain time weakly depends on θ₀ (upper row of Figure 3A). On the contrary, in the confining regime, the potential landscape draws escape routes—corresponding to the parameters considered here to θ₀ being a multiple of π—along which the self-propelled particles travel significantly faster (lower row of Figure 3A). Surprisingly, although ZP is globally better at exploring space, its escape routes are substantially narrower than that of SP. Therefore, considering a uniform distribution of initial orientations, ZP counter-intuitively leads to a lower proportion of trajectories that manage to reach a given distance from the departure point than SP.

FIGURE 3

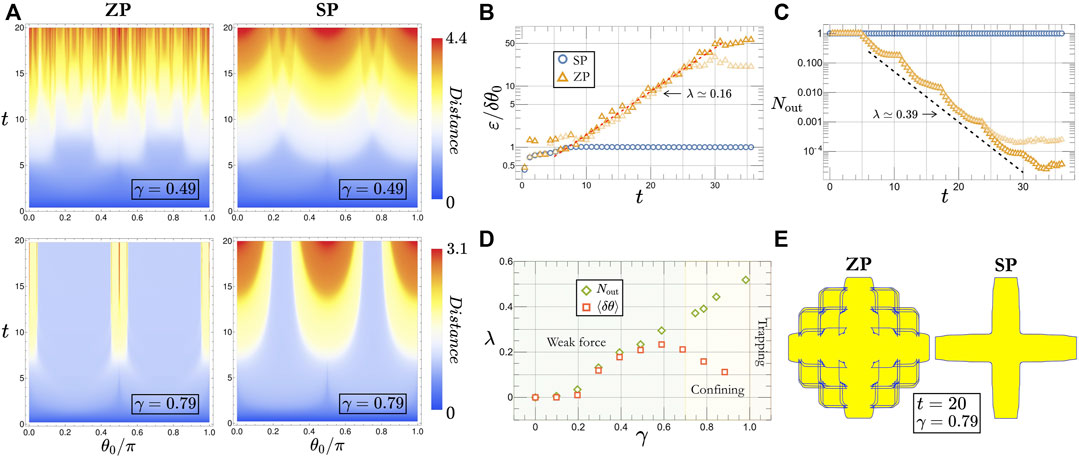
FIGURE 3. Sensitivity of the navigation policies to the initial orientation. (A) Color maps of the distance from the starting point as a function of the initial angle θ₀ and time t for both ZP (left column) and SP (right column) in two different regimes: weak force (γ = 0.49, top row) and confining potential (γ = 0.79, bottom row). (B) Scaling with a time of the mean angular separation ɛ defined in Eq. 4 for SP (blue circles) and ZP (orange triangles) at γ = 0.79. Opaque and semi-transparent symbols, respectively, correspond to an initial orientation resolution of δθ₀ = 10⁻⁶ and δθ₀ = 10⁻⁵. (C) Number of trajectories located on the outer isochrone as a function of time; the legend and parameters are the same as those in (B). (D) Best fits of the two sets of exponents obtained from the exponential scalings of ɛ and N_out [see (B) and (C)] for ZP as a function of γ. (E) Example of long-time isochrones (t = 20) in the confining regime (γ = 0.79) for the two policies. In both cases, the blue curve represents the entire isochrone, while the area highlighted in yellow is the region enclosed by the outer boundary. The complexity of the ZP isochrone is consistent with its larger sensitivity to the initial self-propulsion orientation.

We now quantify the sensitivity to the initial orientation with the mean spatial angular separation

$\epsilon \left(t\right)\equiv {⟨\arccos \left[\frac{\mathit{r}\left(t|{\theta }_0\right)\cdot \mathit{r}\left(t|{\theta }_0+\delta {\theta }_0\right)}{r\left(t|{\theta }_0\right)r\left(t|{\theta }_0+\delta {\theta }_0\right)}\right]⟩}_{{\theta }_0},(4)$

where r(t|θ₀) denotes the position at time t of the particle given the initial orientation θ₀ (taking the departure point for origin), and r(t|θ₀) is the associated distance, while δθ₀ in Eq. 4 corresponds to the angular resolution of θ₀. Figures 3B,D show that for γ ≳ 0.2, the mean separation ɛ(t) grows exponentially at large t for ZP over a time range that increases as δθ₀ → 0. In contrast, for SP, ɛ(t) converges to a finite value, such that over long times, the isochrones take a scale-invariant form. Based on these observations, we may define a generalized Lyapunov exponent λ_ɛ ≡ ln [ɛ(t)]/t from a long-time scaling of ɛ(t). While ${\lambda }_{\epsilon }^{\text{SP}}=0$ over the whole available range of γ, ${\lambda }_{\epsilon }^{\text{ZP}}>0$ for γ ≳ 0.2 indicates that for sufficiently strong forces, the dynamical system formed by Eqs 1–3 is chaotic. Similar chaotic behavior of ZP was actually reported for navigation in turbulent flows [27].

We now build further insight from the analysis of outer isochrones, which we define as the minimal set of points that draw the boundary of the region enclosed by the isochrones (see, e.g., the dashed green lines in Figure 1A). We show in Figure 3C that the number of trajectories N_out(t) remaining on the outer envelope of the isochrones is found to decay exponentially fast in time for ZP while staying constant for SP. The exponential decay of N_out(t) for ZP is explained by the increasing number of self-crossings of the isochrones with time (see Figure 3E) which leads a large part of the trajectories to quit the boundary. We thus define from the long-time regime a second exponent λ_N ≡ − ln [N_out(t)]/t such that, in agreement with the analysis of the angular separation ɛ, ${\lambda }_N^{\text{SP}}=0$ for all values of γ, while ${\lambda }_N^{\text{ZP}}>0$ for γ large enough. As shown in Figure 3D, ${\lambda }_{\epsilon }^{\text{ZP}}\approx {\lambda }_N^{\text{ZP}}$ in the weak force regime, but the exponents depart from each other when approaching the confining regime. Namely, although ${\lambda }_{\epsilon }^{\text{ZP}}$ is maximal at γ ≈ 0.6 and starts to decay when entering the confining regime, ${\lambda }_N^{\text{ZP}}$ increases almost linearly with γ up to the trapping regime at γ = 1. This difference in behaviors is well understood from the fact that the average in Eq. 4 is taken over all trajectories, including those that remain inside of the envelope formed by the outer isochrone, while N_out(t) only gets contributions from the most quickly diverging trajectories.

The multiple crossings observed on the ZP isochrones allow the trajectories to circumvent regions which are inaccessible when approached by facing the external force. Therefore, as long as γ < 1, ZP shall, in principle, ensure total coverage of space despite the presence of strong external force, in contrast with SP for which space exploration becomes quickly limited. However, due to the exponential decrease of the number of trajectories at the isochrones boundaries with time, the maximum area that can be spanned by ZP grows with the total number of trajectories N as A_max ∼ ln²N, which limits the numerical exploration of the long-time regime as γ approaches 1. In practical situations, these results, moreover, suggest that for strong forces, ZP is less reliable than SP, as its sensitivity to initial conditions can easily lead trajectories to depart from the predetermined route, which we now illustrate by including noise in the dynamics.

3.1.4 Effect of fluctuations on the navigation performances

The increased sensitivity of ZP to the initial particle orientation described previously raises the question of the impact of noise on exploration performances. Fluctuations are a particularly important feature of the motion of swimmers evolving at the microscopic scale. They can arise due to thermal noise, but also due to fluctuations in the processes generating self-propulsion. Here, we model such fluctuations as uncorrelated Gaussian white noises affecting the position r and orientation θ of the particle. Details on the implementation of the stochastic dynamics can be found in the SM. Our simulations, moreover, indicate that both sources of noise (translational and rotational) have a similar effect on the dynamics, such that we focus here on rotational noise and denote the corresponding diffusion coefficient D_r.

Considering the weak force regime, we find that the performances of both policies do not change significantly with respect to the noiseless case (data not shown). Conversely, in the confining regime, the presence of rotational noise strongly impairs the ZP's ability to explore the surroundings. This feature is clear from the behavior of the noise-averaged isochrone (Figure 4A) whose area stops growing as soon as trajectories reach the local minima of the potential (see the green curve in Figure 4B). We thus conclude that for large enough γ, the ZP escape routes identified in Figure 3A are unstable, while the potential local minima act as attractors of the dynamics. Trajectories initially on the escape routes, therefore, deviate (on average) because of fluctuations and end up at the potential minima where they get stuck. This effect is, moreover, enhanced by the chaos of the ZP dynamics characterized previously, such that we expect it to be present for arbitrary weak noise. As a consequence, Figure 4C shows that the mean distance reached by ZP trajectories is bounded for all initial orientations, leading to a disappearance of the escape routes. In contrast, we find that the properties of the SP isochrones are barely affected by noise, proving it to be a more robust strategy than ZP in presence of strong external forces.

FIGURE 4

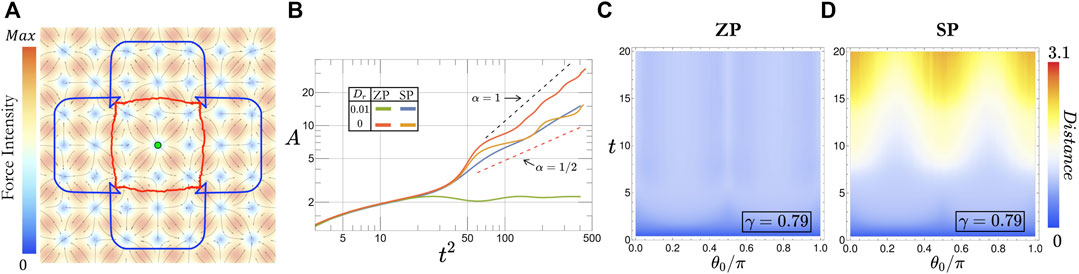
FIGURE 4. (A) Comparison between the noiseless (blue curve) and noise-averaged (red curve) isochrones at time t = 9. Color gradient indicates the intensity of the external force field, and the gray arrows in its direction. (B) Area enclosed by the isochrones as a function of squared time for both ZP and SP with and without rotational noise. (C) Color maps of the average distance from the starting point as a function of the initial orientation θ₀ and time t for both ZP (left column) and SP (right column) in presence of rotational noise. All data shown in (A–C) are averaged over 10² independent trajectories with a resolution δθ₀ = 10⁻². The relative force strength here is set to γ = 0.79 (confining regime) and the rotational diffusion coefficient is equal to D_r = 0.01.

3.2 Navigation on curved surfaces

3.2.1 Optimal trajectories and Randers geodesics

In a number of situations, self-navigating agents move on non-Euclidean spaces including planes above the Earth [30, 31] or migrating cells [32, 33]. As the presence of a nonzero curvature locally leads to a stretching or compressing of distances, one naturally expects it to affect optimal navigation strategies. In this section, building on the results of Ref. [19], we consider the optimal navigation problem on a two-dimensional curved surface in the presence of strong external forces.

Such a surface embedded in a three-dimensional Euclidean space $(\widehat{\mathit{x}},\widehat{\mathit{y}},\widehat{\mathit{z}})$ can be locally described using the Monge representation [34] by a height function z(x, y) such that the position vector on the surface satisfies $\mathit{r}(x,y)=x\widehat{\mathit{x}}+y\widehat{\mathit{y}}+z(x,y)\widehat{\mathit{z}}$. Any vector tangential to the surface can then be expressed in the (nonorthogonal) local basis $({\widehat{\mathit{t}}}_1,{\widehat{\mathit{t}}}_2)$ where [35].

${\widehat{\mathit{t}}}_1=\frac{\widehat{\mathit{x}}+\left({\partial }_{x}z\right)\widehat{\mathit{z}}}{\sqrt{1+{\left({\partial }_{x}z\right)}^2}},{\widehat{\mathit{t}}}_2=\frac{\widehat{\mathit{y}}+\left({\partial }_{y}z\right)\widehat{\mathit{z}}}{\sqrt{1+{\left({\partial }_{y}z\right)}^2}},$

while the metric tensor h(x, y) describing the local geometry of the surface is obtained from this parametrization as

$\mathit{h}\left(x,y\right)=\left(\begin{array}{cc}\hfill 1+{\left({\partial }_{x}z\right)}^2\hfill & \hfill \left({\partial }_{x}z\right)\left({\partial }_{y}z\right)\hfill \\ \hfill \left({\partial }_{x}z\right)\left({\partial }_{y}z\right)\hfill & \hfill 1+{\left({\partial }_{y}z\right)}^2\hfill \end{array}\right).(5)$

The metric tensor is, in particular, useful to work with vectors tangential to the surface whose components are expressed in the Cartesian orthogonal basis $(\widehat{\mathit{x}},\widehat{\mathit{y}})$. Indeed, given two tangential vectors p and q, their scalar product is given by p ⋅q ≡ h_ijp^jqⁱ with i and j = x or y, and where hereafter summation over repeated indices is assumed. In this section, the components of a vector in $(\widehat{\mathit{x}},\widehat{\mathit{y}})$ are expressed using upper indices, while the lower index notation is defined by p_i ≡ h_ijp^j.

Considering the dynamics (1), the optimal navigation policy on curved surface minimizes, as for the motion on the plane, the travel time cost function $T={\int }_0^t\mathrm{d}{t}^{\prime }$. In fact, we show in the SM that this minimization problem can be mapped to finding the geodesics of an asymmetric Finsler-type metric known as Randers metric [20–22] which is described by a Lagrangian $\mathcal{L}$ of the form

$\mathcal{L}\equiv \sqrt{a_{ij}{\dot{r}}^i{\dot{r}}^j}+b_i{\dot{r}}^i,(6)$

where the parameters are defined as

$a_{ij}\equiv \lambda \left(h_{ij}+\lambda f_i{f}_j\right),b_i\equiv -\lambda f_i,{\lambda }^{-1}\equiv v_0^2-f^2,$

with the metric tensor h defined in Eq. 5 and where f² ≡f ⋅f. The mapping, therefore, provides a geometric interpretation of the optimal trajectory, which is obtained by integrating the associated geodesic equation

${\ddot{r}}^k+{\mathrm{\Gamma }}_{ij}^k{\dot{r}}^i{\dot{r}}^j=0,(7)$

where the coefficients ${\mathrm{\Gamma }}_{ij}^k$ are the so-called Christoffel symbols [35] associated with the generalized metric tensor of the Randers space $g_{ij}\equiv \frac{1}{2}\frac{{\partial }^2{\mathcal{L}}^2}{\partial {\dot{r}}^i\partial {\dot{r}}^j}$ (details in the SM). It was initially argued [19, 26] that the validity of the above mapping was limited to the weak force regime (v₀ > f over the whole surface). Under such an assumption, the Randers metric $\mathcal{L}$ is indeed both positively definite and strongly convex. As detailed in the SM, appropriately treating the limit f → v₀, the Lagrangian $\mathcal{L}$ is found to remain positively definite at arbitrary force strength such that it can always be identified as a Randers metric. The weak force constraint can therefore be relaxed and the solution (6,7), which hereafter we refer to as the Randers policy (RP), holds for any dynamical regime. Naturally, in flat spaces, Randers geodesics correspond to the Zermelo trajectories studied in the previous section.

In contrast with the planar case, following natural geodesics on curved surfaces requires for the self-propelled agent to adjust its direction of motion $\widehat{\mathit{e}}(\theta )$. Namely, the policy generalizing SP to curved spaces is based on the parallel transport equation (35).

${\dot{e}}^k+{\gamma }_{ij}^k{\dot{r}}^i{e}^j=0,(8)$

which is to be integrated together with Eq. 1, and where the coefficients ${\gamma }_{ij}^k$ are the Christoffel symbols associated with the metric tensor of the physical space h.

3.2.2 Optimal navigation on a wavy surface

As pictured in Figure 5, we consider a one-dimensional wave-like perturbation of the 2D plane described by the height function z (x, y) = Δ sin (k_wx), where the parameters k_w and Δ set the period and amplitude of the wave (both in units of ℓ). As our numerical results do not show significant variations with k_w (not shown), we set k_w = k so as to match the period of the wave with that of the potential (2).

FIGURE 5

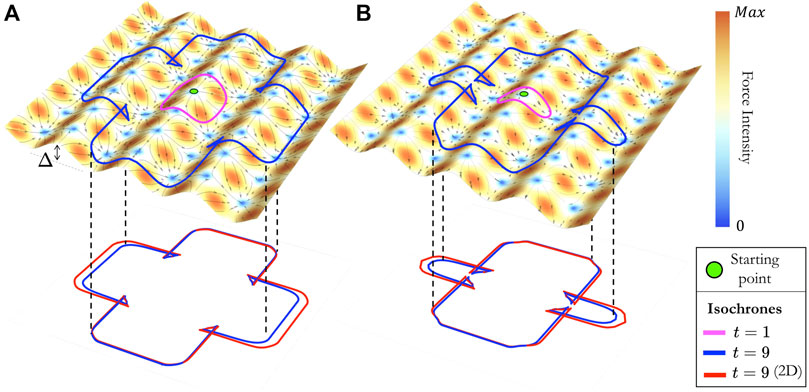
FIGURE 5. Schematic representation of the wavy surface used to study the effect of space curvature on the active particle navigation in the same potential landscape defined by Eq. 2. Two short-time RP isochrones (t = 1 and t = 9 corresponding to the magenta and blue curves, respectively) are shown here for two different starting points (green dots): (A) maximum and (B) saddle point. The relative force strength here is fixed at γ = 0.79, while the wave amplitude is set to Δ = 0.5. The most immediate effect of space curvature is to break the force field spatial symmetry. This is apparent by comparing the 2D projection of the isochrone on the surface with its counterpart obtained from the planar simulations (Δ = 0, red curve). The former is indeed clearly shorter along the direction of the wave. In both panels, the color gradient shows the intensity of the external force field, while the gray arrows indicate its direction.

A feature occurring in presence of nonzero space curvature is that the local force field strength $f=\sqrt{h_{ij}{f}^i{f}^j}$ depends on the properties of the metric h, namely, here $f^2=f^{x^2}[1+k_w^2{\mathrm{\Delta }}^2{\cos }^2(k_{w}x)]+f^{y^2}$. In order to properly distinguish between the effects of the local curvature and that of the force amplitude, in the following, we rescale the force field components in order to keep f independent of k_w and Δ. It is straightforward to show that for a general metric, an appropriate rescaling corresponds to the following transformation to the force field components:

$f^x⟼\frac{1}{\sqrt{h_{xx}}}\left(f^x-f^y\frac{h_{xy}}{\sqrt{h}}\right),f^y⟼f^y\sqrt{\frac{h_{xx}}{h}},$

where h stands as a shorthand notation for det  h. For the following analysis, we, moreover, focus on the most interesting confining regime by fixing γ = 0.79, while the performance of SP and RP will be assessed by varying the wave amplitude Δ.

3.2.3 Properties of the isochrones in the presence of space curvature

Figure 5 shows two short-time isochrones obtained from RP trajectories starting from a local maximum and saddle point of the potential. As shown from their projections on the plane, the shape of the isochrones is not strongly influenced by the presence of finite curvature. The curves are indeed not modified in the direction transverse to that of the surface wave, while they appear compressed along the wave direction. Here, the surface curvature therefore essentially introduces a breaking of the discrete rotational symmetry of the potential. Despite these quantitative differences with the planar case, the qualitative features of the RP isochrones such as the presence of self-intersections are unchanged by the presence of space curvature. As for the planar case, we did not find significant variations in the isochrones properties with the departure point; thus, in the following, we fix it to be a local maximum of the potential.

As shown in Figure 6, the presence of surface oscillations does not qualitatively modify the isochrones properties for RP and SP. Indeed, the exponent α ruling the long-time growth of the isochrone area with time is, in both cases, constant upon varying Δ, and takes values α^RP ≈ 1 and ${\alpha }^{\text{SP}}\approx \frac{1}{2}$ (Figure 6A). Moreover, the fractional area ϕ for RP oscillates around a well-defined value $\approx 0.85$ (Figure 6B), while it decays to zero at long time for SP (not shown). Analogous to the planar case and in contrast with SP, the optimized Randers policy allows the self-propelled particles to make use of the potential landscape in order to visit otherwise inaccessible regions, thus ensuring ergodic spatial exploration even in the presence of potential confinement. As the evaluation of geodesic distance is generally computationally demanding, we characterize the sensitivity of the policies via the scaling of the number of trajectories N_out lying on the outer isochrone. Consistent with the behavior of the isochrone area, our results indicate that N_out decays exponentially with time for RP (Figure 6C) and remains constant for SP. The corresponding exponent λ_N, moreover, varies little with Δ, highlighting the robustness of the isochrone properties with space curvature.

FIGURE 6

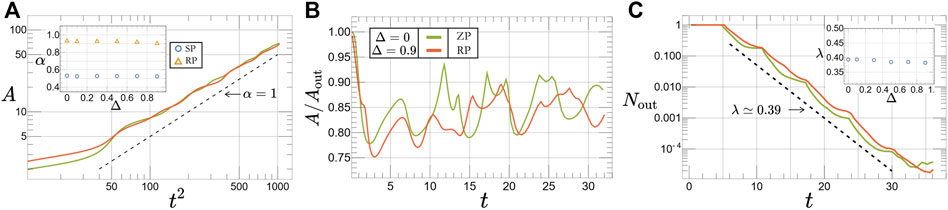
FIGURE 6. Long-time properties of the isochrones in curved space. (A) Area covered by the RP isochrone vs. t² on the oscillating surface with Δ = 0.9 (red curve). The green curve shows the corresponding ZP isochrone at Δ = 0. The inset shows the value of the exponent α defined in the main text as a function of the wave amplitude Δ for both SP and RP. (B) Comparison between the time evolution of the fractional area for RP at Δ = 0.9 and ZP. Both curves oscillate around similar values ≈ .85. (C) Number of trajectories N_out on the outer isochrone for both RP and ZP [legend is the same as (B)]. The inset shows the variation of the associated exponent with Δ. In all panels, the relative force strength is set to γ = 0.79 (confining regime).

4 Discussion

We have shown that the long-time properties of isochrones provide useful information about the efficiency of navigation strategies for exploration. Our results reveal that for deterministic dynamics in the presence of strong motion-limiting force, the travel time minimizing strategies—ZP on the plane and RP in curved space—surprisingly allow for ergodic exploration, contrary to the trivial straight policy for which only a restricted portion of space is visited. Isochrones of ZP and RP are indeed nearly isotropic with a fractional area ϕ ≥ 0.80, while those of SP extend only in specific directions corresponding to escape routes drawn by the force-field landscape.

However, our results also indicate that ZP and RP lead to chaotic dynamics, which manifests as an exponentially fast divergence of trajectories whose number at the isochrone's outer boundaries also decays exponentially. The resulting sensitivity to initial conditions is more pronounced in the confining regime, where it becomes increasingly harder to resolve the isochrones over a long time. This complexity is however necessary to ensure full space coverage, as the only option for the particles to reach certain regions of space—where the external force is too strong—is to circumvent them. More dramatically, ZP was found to be unstable in the presence of fluctuations in the dynamics, as those lead to global trapping of trajectories regardless of the initial condition. If fluctuations cannot be neglected—as is often the case for the motion of microscopic objects—ZP and, by extension, RP are thus poor candidates for optimal navigation in the presence of strong external forces. These results, moreover, counter-intuitively suggest that even though they are designed to maximize the effective speed of the particles, ZP and RP do not always constitute good escape strategies. Indeed, compared to ZP or RP, the trivial SP generally leads to a higher fraction of trajectories reaching a certain distance from the starting point, a difference that is even larger in presence of noise.

Our study demonstrates in particular that the chaos of ZP and RP is closely linked to the presence of isochrone self-crossings that occur in strong force regions. Inhibiting self-crossings, thus, seems crucial in order to improve the stability and robustness of the policies. A possibility could be to include an additional cost in the derivation of ZP which would lead the agents to reorient their self-propulsion when entering strong force regions. It would, moreover, be interesting to compare ZP and RP with reinforcement learning-based approaches [36–39], which have already been shown to outperform ZP in the presence of strong forces [27]. Finally, improvement of ZP and RP could also be achieved by allowing for some degree of variation in the particle's self-propulsion speed. Such a feature indeed would provide the particles with a mechanism to visit otherwise inaccessible regions while inhibiting self-crossings at a minimal energetic cost.

Although all the results presented here were obtained with the sinusoidal potential (2), we expect our main conclusions to hold in more general settings. Indeed, as long as the potential is locally confining—the resulting external force overcomes self-propulsion only in disconnected regions—the ZP isochrones should always exhibit self-crossings. Moreover, in the long-time regime where their area is much larger than the scale associated with the potential, it is natural to expect that the behavior of the isochrones will remain qualitatively independent of the details of the potential. To stress this idea, we provide the SM simulation results obtained with a quasi-periodic potential in the confining regime which show that all scaling laws and measures of chaos reported for the sinusoidal potential remain qualitatively unchanged.

As we considered deterministic dynamics for most of this study, we did not discuss the trapping regime occurring for γ ≥ 1, where the particles must rely on fluctuations to cross the potential barrier. It has been argued that in the presence of confinement induced, for example, by obstacles [40, 41] or high-potential barriers [42, 43], efficient exploration strategies favor diffusive over ballistic motion. However, in all these works, no optimization policy making use of the environmental conditions was considered. In light of the results reported here, notions of stability could be a decisive factor in the design of navigation strategies for ballistic exploration of rugged landscapes in order to ensure reasonable performances.

More generally, our results highlight an emergent trade-off between exploration efficiency and stability, which, depending on the context and the desired task, must be taken into consideration for the design of the corresponding navigation policy.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material: further inquiries can be directed to the corresponding authors.

Author contributions

LP performed the numerical simulations. LP and BM designed the simulation code and analyzed the data. All authors took part in the conception of the research and in the redaction of the manuscript.

Funding

LP is thankful for the funding from the International Max Planck Research School (IMPRS) for the Physics of Biological and Complex Systems. The study has received support from the Max Planck School Matter to Life and the MaxSynBio Consortium, which are jointly funded by the Federal Ministry of Education and Research (BMBF) of Germany, and the Max Planck Society.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1034267/full#supplementary-material.

References

1. David C, Kennedy J, Ludlow A. Finding of a sex pheromone source by gypsy moths released in the field. Nature (1983) 303:804–6. doi:10.1038/303804a0

CrossRef Full Text | Google Scholar

2. Hein AM, Carrara F, Brumley DR, Stocker R, Levin SA. Natural search algorithms as a bridge between organisms, evolution, and ecology. Proc Natl Acad Sci U S A (2016) 113:9413–20. doi:10.1073/pnas.1606195113

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Vidal-Mateo J, Benavent-Corai J, López-López P, García-Ripollés C, Mellone U, De la Puente J, et al. Search foraging strategies of migratory raptors under different environmental conditions. Front Ecol Evol (2022) 10. doi:10.3389/fevo.2022.666238

CrossRef Full Text | Google Scholar

4. Szczerba R, Galkowski P, Glicktein I, Ternullo N. Robust algorithm for real-time route planning. IEEE Trans Aerosp Electron Syst (2000) 36:869–78. doi:10.1109/7.869506

CrossRef Full Text | Google Scholar

5. Panda M, Das B, Subudhi B, Pati BB. A comprehensive review of path planning algorithms for autonomous underwater vehicles. Int J Autom Comput (2020) 17:321–52. doi:10.1007/s11633-019-1204-9

CrossRef Full Text | Google Scholar

6. Trincavelli M, Reggente M, Coradeschi S, Loutfi A, Ishida H, Lilienthal AJ. Towards environmental monitoring with mobile robots. In: 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice (France), 22-26 September 2008 (2008). 2210–5. doi:10.1109/IROS.2008.4650755

CrossRef Full Text | Google Scholar

7. Illien P, Golestanian R, Sen A. ‘fuelled’ motion: Phoretic motility and collective behaviour of active colloids. Chem Soc Rev (2017) 46:5508–18. doi:10.1039/c7cs00087a

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Jiang J, Yang Z, Ferreira A, Zhang L. Control and autonomy of microrobots: Recent progress and perspective. Adv Intell Syst (2022) 4:2100279. doi:10.1002/aisy.202100279

CrossRef Full Text | Google Scholar

9. Park BW, Zhuang J, Yasa O, Sitti M. Multifunctional bacteria-driven microswimmers for targeted active drug delivery. ACS Nano (2017) 11:8910–23. doi:10.1021/acsnano.7b03207

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chamseddine IM, Kokkolaras M. Nanoparticle optimization for enhanced targeted anticancer drug delivery. J Biomech Eng (2018) 140. doi:10.1115/1.4038202

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bell WJ. Searching behaviour: the behavioural ecology of finding resources. Berlin: Springer Science & Business Media (2012).

Google Scholar

12. Bénichou O, Loverdo C, Moreau M, Voituriez R. Intermittent search strategies. Rev Mod Phys (2011) 83:81–129. doi:10.1103/RevModPhys.83.81

CrossRef Full Text | Google Scholar

13. James A, Plank MJ, Edwards AM. Assessing Lévy walks as models of animal foraging. J R Soc Interf (2011) 8:1233–47. doi:10.1098/rsif.2011.0200

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bellman R. The theory of dynamic programming. Bull Amer Math Soc (1954) 60:503–15. doi:10.1090/S0002-9904-1954-09848-8

CrossRef Full Text | Google Scholar

15. Bertsekas DP. Dynamic programming and optimal control. 4th ed., 2. Belmont, MA: Athena scientific (2012).

Google Scholar

16. Yong J, Zhou XY. Stochastic controls: hamiltonian systems and HJB equations, 43. Berlin: Springer Science & Business Media (1999). doi:10.1007/978-1-4612-1466-3

CrossRef Full Text | Google Scholar

17. Pontryagin LS. Mathematical theory of optimal processes. England: Routledge (1987). doi:10.1201/9780203749319

CrossRef Full Text | Google Scholar

18. Zermelo E. Über das navigationsproblem bei ruhender oder veränderlicher windverteilung. Z Angew Math Mech (1931) 11:114–24. doi:10.1002/zamm.19310110205

CrossRef Full Text | Google Scholar

19. Piro L, Tang E, Golestanian R. Optimal navigation strategies for microswimmers on curved manifolds. Phys Rev Res (2021) 3:023125. doi:10.1103/PhysRevResearch.3.023125

CrossRef Full Text | Google Scholar

20. Randers G. On an asymmetrical metric in the four-space of general relativity. Phys Rev (1941) 59:195–9. doi:10.1103/physrev.59.195

CrossRef Full Text | Google Scholar

21. Bao D, Chern SS, Shen Z. An introduction to riemann-finsler geometry. New York, NY: Springer (2000).

Google Scholar

22. Cheng X, Shen Z. Finsler geometry: An approach via Randers spaces. New York, NY: Springer (2012).

Google Scholar

23. Liebchen B, Löwen H. Optimal navigation strategies for active particles. EPL (Europhysics Letters) (2019) 127:34003. doi:10.1209/0295-5075/127/34003

CrossRef Full Text | Google Scholar

24. Daddi-Moussa-Ider A, Löwen H, Liebchen B. Hydrodynamics can determine the optimal route for microswimmer navigation. Commun Phys (2021) 4:15. doi:10.1038/s42005-021-00522-6

CrossRef Full Text | Google Scholar

25. Piro L, Mahault B, Golestanian R. Optimal navigation of microswimmers in complex and noisy environments. New J Phys (2022) 24:093037. doi:10.1088/1367-2630/ac9079

CrossRef Full Text | Google Scholar

26. Bao D, Robles C, Shen Z. Zermelo navigation on Riemannian manifolds. J Differential Geom (2004) 66:377–435. doi:10.4310/jdg/1098137838

CrossRef Full Text | Google Scholar

27. Biferale L, Bonaccorso F, Buzzicotti M, Leoni PCD, Gustavsson K. Zermelo’s problem: Optimal point-to-point navigation in 2d turbulent flows using reinforcement learning. Chaos (2019) 29:103138. doi:10.1063/1.5120370

PubMed Abstract | CrossRef Full Text | Google Scholar

28.Inc WR. Mathematica, version 12.3.1 (2021). Champaign, Illinois: Wolfram Research, Inc

Google Scholar

29. Zarfaty L, Peletskyi A, Fouxon I, Denisov S, Barkai E. Dispersion of particles in an infinite-horizon Lorentz gas. Phys Rev E (2018) 98:010101. doi:10.1103/PhysRevE.98.010101

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Chitsaz H, LaValle S. Time-optimal paths for a dubins airplane proceedings of the 46th IEEE conference on decision and control 2007 CDC (United States: Institute of electrical and electronics engineers inc.). In: Proceedings of the IEEE Conference on Decision and Control; 12-12-2007 14-12-2007 (2007). p. 2379–84. doi:10.1109/CDC.2007.4434966

CrossRef Full Text | Google Scholar

31. Guerrero JA, Bestaoui Y. Uav path planning for structure inspection in windy environments. J Intell Robot Syst (2013) 69:297–311. doi:10.1007/s10846-012-9778-2

CrossRef Full Text | Google Scholar

32. Callens SJ, Uyttendaele RJ, Fratila-Apachitei LE, Zadpoor AA. Substrate curvature as a cue to guide spatiotemporal cell and tissue organization. Biomaterials (2020) 232:119739. doi:10.1016/j.biomaterials.2019.119739

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lin SZ, Li Y, Ji J, Li B, Feng XQ. Collective dynamics of coherent motile cells on curved surfaces. Soft Matter (2020) 16:2941–52. doi:10.1039/C9SM02375E

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Schutz B. Geometrical methods of mathematical Physics. Cambridge: Cambridge University Press (1980).

Google Scholar

35. Deserno M. Notes on differential geometry (2014).

Google Scholar

36. Colabrese S, Gustavsson K, Celani A, Biferale L. Flow navigation by smart microswimmers via reinforcement learning. Phys Rev Lett (2017) 118:158004. doi:10.1103/PhysRevLett.118.158004

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Schneider E, Stark H. Optimal steering of a smart active particle. EPL (Europhysics Letters) (2019) 127:64003. doi:10.1209/0295-5075/127/64003

CrossRef Full Text | Google Scholar

38. Yang Y, Bevan MA, Li B. Efficient navigation of colloidal robots in an unknown environment via deep reinforcement learning. Adv Intell Syst (2020) 2:1900106. doi:10.1002/aisy.201900106

CrossRef Full Text | Google Scholar

39. Muiños-Landin S, Fischer A, Holubec V, Cichos F. Reinforcement learning with artificial microswimmers. Sci Robot (2021) 6:eabd9285. doi:10.1126/scirobotics.abd9285

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Volpe G, Volpe G. The topography of the environment alters the optimal search strategy for active particles. Proc Natl Acad Sci U S A (2017) 114:11350–5. doi:10.1073/pnas.1711371114

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Irani E, Mokhtari Z, Zippelius A. Dynamics of bacteria scanning a porous environment. Phys Rev Lett (2022) 128:144501. doi:10.1103/PhysRevLett.128.144501

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Zanovello L, Caraglio M, Franosch T, Faccioli P. Target search of active agents crossing high energy barriers. Phys Rev Lett (2021) 126:018001. doi:10.1103/PhysRevLett.126.018001

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zanovello L, Faccioli P, Franosch T, Caraglio M. Optimal navigation strategy of active brownian particles in target-search problems. J Chem Phys (2021) 155:084901. doi:10.1063/5.0064007

PubMed Abstract | CrossRef Full Text | Google Scholar