- 1Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Information and Optoelectronic Science and Engineering, South China Normal University, Guangzhou, China
- 2Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, School of Information and Optoelectronic Science and Engineering, South China Normal University, Guangzhou, China
Semi-quantum key distribution is based on the basic principle of quantum mechanics, which allows a classical user and quantum user to use information theory to have a secure shared key. In 2021, our research group proved the first proof-of-principle experimental demonstration of semi-quantum key distribution and verified its feasibility. Due to the limitations of existing science and technology, the experimental system still features a combination of multiphoton signal source and loss in the transmission line. This makes semi-quantum key distribution as susceptible to a photon-number splitting attack as quantum key distribution, leading to limitations of secure transmission distance. It seems that practical single-state semi-quantum key distribution can overcome photon-number splitting attack due to the SIRT bits (also known as the “sifted key”). However, its dual-channel feature still opens up an observation window to Eve. We present two joint photon-number splitting attacks suitable for a single-state semi-quantum key distribution system and show that through the joint photon-number splitting attack, Eve can obtain key information without being detected by Alice or Bob.
1 Introduction
In recent years, with the rapid development of quantum computing, the security of the original classical secure communication has been greatly compromised. Compared with classical communication, whose security depends on the complexity of mathematical computation, quantum communication, whose security is based on quantum theory [1], is not threatened by the quantum computer, which theoretically guarantees the absolute security of the communication. The field of quantum communication includes quantum key distribution (QKD) [2–7], quantum secret sharing (QSS) [8–10], quantum secure direct communication (QSDC) [11–13], quantum teleportation (QT) [14–16], quantum dense coding (QDC) [17–19], and quantum digital signature (QDS) [20]. After more than 30 years of efforts by scientists, QKD, the most mature quantum communication technology, has made breakthrough progress in both theory and experiment and has become an indispensable component in the development of information security field. It is worth mentioning that measurement-device-independent quantum key distribution (MDI-QKD) [21, 22] can be immune to all detector side-channel attacks. Moreover, it can be easily implemented in combination with the matured decoy-state methods under current technology. In 2021, Yi-Peng Chen et al. implemented the double-scanning method into MDI-QKD for the first time and carried out corresponding experimental demonstration [5]. In 2022, Pei Zeng et al. proposed a mode-pairing measurement-device-independent quantum key distribution scheme in which the encoded key bits and bases are determined during data post processing [23].
Based on the consideration of reducing quantum resources in the process of key distribution, the concept of semi-quantum key distribution (SQKD) [24] has been proposed and extended into semi-quantum cryptography, such as semi-quantum secret sharing (SQSS) [25, 26], semi-quantum secure direct communication (SQSDC) [27–29], semi-quantum digital signature (SQDS) [30], semi-quantum private comparison (SQPC) [31–35], and semi-quantum key agreement (SQKA) [36, 37]. In 2007, Boyer et al. proposed the first SQKD protocols: BKM07 [24], which place a further restriction on the classical user. The classical user just can access a segment of the channel, whenever a qubit passes through that segment Bob can either let it go undisturbed (Ctrl) or measure the qubit in the classical basis and resend a fresh qubit (Sift); in 2009, the second SQKD protocol BGKM09 [38] was proposed. This protocol utilized the Permute operation as opposed to the Measure and Resend operations. The same year, Zou et al. proposed five new protocols based on the consideration of whether quantum resources can be further reduced on the part of the two users [39], among which the single-state protocol attracted the most attention. It was show for the first time that fully quantum users can also reduce their resource requirements. In 2014, Reflection-based SQKD was proposed [40], it was similar to B92-protocol, and was shown that a key can be distilled from B’s action. In 2017, Boyer et al. extended the operation of Bob side to cleverly avoid the problem of reproducing new photons, and proposed a mirror protocol [41] that could overcome “tagged” attack. To some extent, this is also a single-state protocol, and only two SQKD experiments have been based on it. Subsequently, other important SQKD protocols have also been proposed, such as the high-efficiency SQKD protocol [42, 43], which can improve efficiency by biasing choices to improve their overall efficiency; the authenticated SQKD protocol [44–47], which does not utilize an authenticated channel (instead relying on a pre-shared key); and the high-dimensional SQKD protocol [48, 49], which has been shown to tolerate high levels of noise as the dimension of the quantum state increases.
The security of idealized SQKD has been reported against individual [50, 51] and very sophisticated collective [40, 52–54] attacks. A lower bound has been derived for the key rate as a function of the noise of the quantum channel in high dimension semi-quantum key distribution [55]. In 2021, our research group performed the first proof-of-principle demonstration [56] of semi-quantum key distribution based on the Mirror protocol, which contributed to the further application of SQKD. The experiments are also based on weak coherent pulses as signal states with a low probability of containing more than one photon. This SQKD experiment, like the QKD experiment, is also based on weak coherent pulses (WCP) as signal states with a low probability of containing more than one photon. Whether the multiphoton problem of such non-ideal light source will lead to security vulnerabilities of the SQKD system is an urgent issue to be discussed. The most powerful tool at the disposition of an eavesdropper, as we know, is the photon-number splitting attack [57–59]. This multiphoton problem in semi-quantum contexts was discussed as early as 2009 [38], but the examination of the protocol against PNS attacks was left to future research. In Gurevich’s experiment [60], some operations in SQKD protocol were realized with the use of a time-coding scheme, and it was mentioned that a pulse power level that is too high, which is a security hole that enables various attacks. In 2018, Chrysoula presented a short discussion [48] of possible attacks and countermeasures for the case of optical implementations. He proposed that while the PNS attack is applicable to most of the protocols that use imperfect photon sources, the above description of its particular implementation is given on the example of a standard QKD one-way scheme, thus, it should be re-examined when applied to different protocols. Some other reports [37, 61–63] have mentioned Bob should set up a photon number splitter (PNS) to protect against a Trojan horse attack. In Ref. [64], the author mentioned that due to the two-way channel and the use of the Measure-Resend operation, Eve is afforded even more attack opportunities, such as the photon-tagging attack and PNS attack, and it is an open question in the semi-quantum case. To our knowledge, we are the first to do further subject research in this issue. We prove that it is useless to implement single-channel PNS attack in SQKD. Does this mean that a single-state SQKD system with multiphoton sources has unconditional security? The answer is no, because due to SQKD’s requirement of a two-way quantum channel, Eve has the opportunity to implement joint PNS attack through the forward channel and reverse channel. Based on this, we propose two kinds of joint PNS attack for a single-state SQKD system, as long as there is loss in the channel, Eve can get the key information. With a large enough loss, Eve can obtain all key information without being detected by Alice and Bob.
The remainder of this study is organized as follows. In Section 2, a brief background on PNS attacks and the SQKD model is provided. In Section 3, two joint PNS attack were designed for single-state SQKD. In Section 4, an evaluation of a joint PNS attack is given, and the conclusion is given in Section 5.
2 Single-channel attack in single-state SQKD
2.1 Review of PNS attack
In a quantum optical implementation, single-photon states are ideally suited for quantum key distribution. However, such states have not been practically implemented for QKD and SQKD. The experiments attenuate the weakly coherent light generated by the laser light source to the order of single photon to replace the single-photon light source. The realistic signal sources with a certain probability of containing multiple photons. For the practical system, consisting of the actual signal source, lossy channel, and threshold detector, Eve can implement PNS attack [57, 58]. In a PNS attack, eavesdropper Eve needs to have three abilities: 1) ability to replace the noisy and lossy transmission line by a superior one, 2) ability to use quantum nondestructive (QND) measurement technology to measure the number of photons contained in the pulse and block or separate the photons without modifying the polarization of the photons, and 3) and possession of a quantum register, can keep photon. When receiving the data regarding the basis, Eve measures her photon and obtains qubit information.
In this study, we assume the model where any non-accessible loss [58] of the quantum channel is considered to be part of detection apparatus, which allows us to conduct our research without loss of generality. Moreover, a PNS attack that keeps the photon number distribution constant in the detector is not considered. When there is available loss in the channel, for the case of a single-photon state, Eve directly blocks the photon. For the multiphoton pulse with the number of photons greater than or equal to 2, Eve extracts a photon from the pulse and puts it into quantum memory, sending the remaining photons to Bob, so that Eve can replace the lossy quantum channel by an ideal one, block a fraction b of the single-photon signals or even use only a multiphoton signal to match the detector’s expectation of non-vacuum pulses. The general process of this protocol is shown in Figure 1.
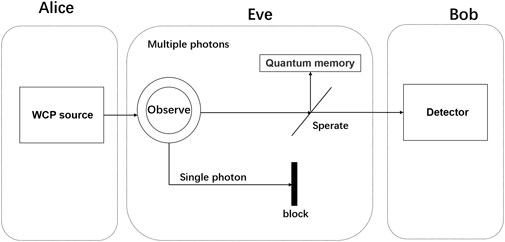
FIGURE 1. Schematic of a PNS attack. Eve learns the number of photons in the pulse through nondestructive measurements. For single photons, Eve blocks them with a certain probability, and she separates one photon from multiphotons.
2.2 Review of single-state SQKD
The quantum communication process of single-state SQKD [39, 65] operates by repeating the following (Alice is a quantum user and Bob is a classical user):
Step 1. Alice prepares a single qubit in the state |+> and sends it to Bob. Alice’s photon source emits signals with a Poisson photon number distribution that has a mean value of ν. The quantum channel is described by a single-photon transmission efficiency η. We can find at Bob’s end of the quantum channel a Poisson photon number distribution with mean photon number
Step 2. Bob will choose to either Measure and Resend or to Reflect the incoming qubit.
a. Bob’s Ctrl operation uses a fully reflective instrument (that is, no optical loss), the average number of photons of the pulse entering the reverse channel after the Ctrl operation is still
b. Bob selects the measurement but gets no information and sends an empty pulse to the reverse channel, which we call Sift-0.
c. Bob subjects the incoming qubit to a Z basis measurement and then resend the result back to A as a Z basis qubit with a Poisson photon number distribution with mean value μ, which we call Sift-1.
Step 3. Alice chooses to measure the returning qubit in the Z or the X basis randomly.
Step 4. Users Alice and Bob disclose their choices. If Bob has chosen Sift-1 and if Alice has chosen to measure in the Z basis, they should share a correlated bit to be used for their raw key. If Bob has chosen Ctrl and if Alice has chosen to measure in the X basis, she should observe outcome |+>, and any other outcome is considered an error.
The general process of this protocol is shown in Figure 2.
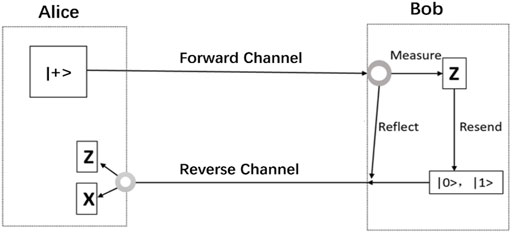
FIGURE 2. The typical setup of a single-state SOKD protocol. Reflect is Ctrl, meaning that Bob reflects the qubit back to Alice undisturbed. Measure and Resend is Sift, meaning that Bob measures it in the Z basis and resends it to Alice in the same state that he found it. For the returned qubit, Alice chooses to measure it on the Z or the X basis randomly.
2.3 Why single-state SQKD can overcome single-channel PNS attack
By implementing the attack procedure described in Section 2.1 in the forward channel, Eve can take away the qubit information in the forward channel, but Eve’s qubit information |+> is not valid information and is public information, so the PNS attack in the forward channel is meaningless.
According to the analysis in 2.2, Ctrl’s bits (Bob has chosen Ctrl and Alice has chosen to measure in the X basis) are not only used as Text bits but are also equivalent to inserts of a Ctrl state pulse into the Sift state pulse and sends it together with the signal state pulse to Bob. We can confirm that there are two kinds of pulses with different average photon number (when
It is worth mentioning that the first proposed SQKD protocol is BKM07. In this article, we call this the four-state protocol. The general process of this protocol is shown in Figure 3 [65]. There are two differences between these two protocols. First, the states sent by Alice are different. In the four-state protocol, Alice prepares and sends one of the four states
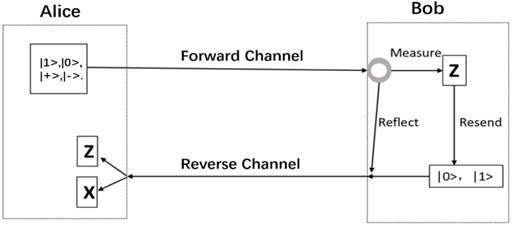
FIGURE 3. The typical setup of a four-state SOKD protocol. The figure is from [61], Alice prepares and sends one of the four states with uniform probability, and Bob chooses either to Measure and Resend or to Reflect the incoming qubit, and Alice measures the returning qubit on the same basis she initially used to prepare it (Z or X).
3 Two joint PNS attack methods for single-state SQKD
Let’s take Eve’s perspective and model the experimental process of single-state SQKD as follows:
Step 1: Alice prepares and sends signals with a Poisson photon number distribution with mean value
Step 2: The quantum channel is described by a single-photon transmission efficiency
Step 3: Bob’s action:
a. Bob has a probability of
b. Bob has a probability of
c. Bob has a probability of
Step 4: The distribution of the pulse reaching Alice’s detector after the loss of reverse channel:
d. Ctrl:
e. Sift-0:
f. Sift-1:
Step 5: The vacuum signals are expected at the entrance to Alice’s apparatus of the lossy channel:
3.1 The first joint PNS attack mode
In the forward channel, Eve blocks single-photon signal with a probability
We model the first joint PNS attack process as follows:
Step 1: Alice prepares and sends signals with a Poisson photon number distribution with mean value
Step 2: Eve replaces the original channel with a lossless channel and blocks single photon with probability
Step 3: Bob’s action.
a. Bob has a probability of
b. Bob has a probability of
c. Bob has a probability of
Step 4: Eve replaces the original channel with a lossless channel and blocks a single photon with probability
d. Ctrl:
e. Sift-0:
f. Sift-1:
Step 5: Vacuum signals are expected at the entrance to Alice’s apparatus of the first joint PNS attack.
First, to remain undetected, Eve adjusts f to match the number of vacuum signals arriving at Bob’s detector of the PNS attack to that of the lossy channel,
Second, to remain undetected, Eve adjusts
It is possible to fulfill this matching condition if
We find, for
We find that all single-photon signals can be blocked if there are exactly as many multiphoton signals leaving the source as non-vacuum signals are arriving at the receiver of Alice and Bob, that is
Assuming that
When
When
Assuming that
When
When
3.2 The second joint PNS attack mode
Eve does not operate the photons in the forward channel and only observes the number of photons in the forward channel pulse. The single photon in the reverse channel (a single photon cannot be distinguished from Ctrl or Sift-1) is blocked with probability
Eve performs nondestructive measurements on the number of photons in the forward and reverse pulses. When the number of photons in the reverse channel of the same pulse is larger than that in the forward channel, Eve can determine that the pulse in this reverse channel is from the Sift-1 operation. The probability of all m-photon pulses for Bob to perform the Sift-1 operation is:
In the reverse channel, the m-photon pulse probability of Sift-1 that Eve can distinguish is:
Then, the probability that the Sift-1 operation m-photon pulse that Eve can distinguish accounted for all the Sift-1 photons is:
In the second joint PNS attack, Eve only operates in reverse channel after Bob’s operation:
g. Ctrl:
h. Sift-0:
i. Sift-1:
Vacuum signals are expected at the entrance to Alice’s apparatus of the second joint PNS attack:
Eve adjusts
As a first step for remaining undetected, we let
Assuming Eve only blocks distinguishable two-photon pulses from Bob’s SIFT-1 operation, combined with the condition that
Substituting
It is possible to fulfill this matching condition if
We find, for
When
When
4 Results of the two joint PNS attack
From the analysis in Section 2, we know that PNS is found in the reverse channel because Eve is unable to distinguish whether the photons in the pulse originate from Ctrl or Sift-1 (the average number of photons is different). It is easy to come up with two possible solutions.
The inspiration of the first attack is that Eve does not distinguish between the pulse after Bob performs Ctrl operation (the average number of photons is
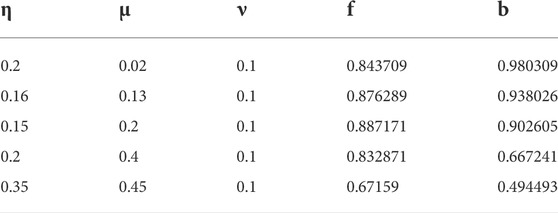
For different values of
For the first joint PNS attack, when
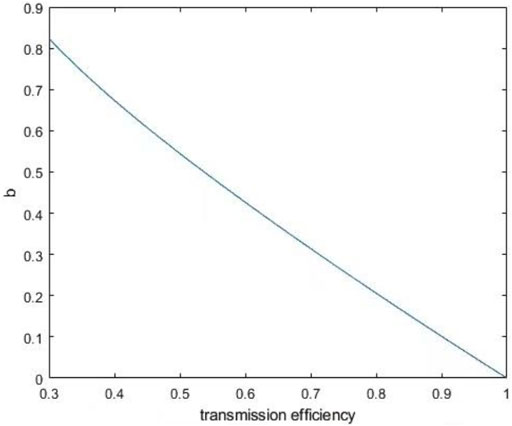
FIGURE 4. When μ = 0.03 and v = 0.01, the relation image between b and ŋ is obtained according to Eq. 15. The stronger the loss in the channel, the higher the value of b (the probability that Eve can block a single photon).
Based on the second idea, the Sift and Ctrl bits are distinguished to carry out PNS attack by the change of photon number in the same pulse in the forward and reverse channels, respectively. We can identify Eve without changing the intercepted pulse under the condition that a quantum nondestructive measurement technique is used to measure whether the pulse contains the number of photons, but only for the same pulse; the reverse channel of the photon number is greater than the former channel of the photon number that we can distinguish. The inspiration of the second attack is that Eve can distinguish between the pulse after Bob performs Ctrl operation (the average number of photons is
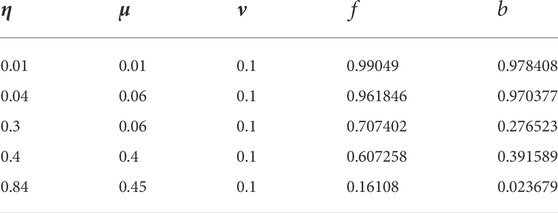
For different values of
For the first joint PNS attack, when
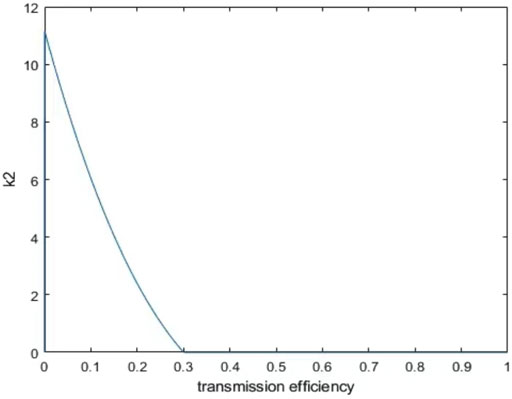
FIGURE 5. When μ = 0.03 and v = 0.01, the relation image between K2 and ŋ is obtained according to Eq. 25. We can see that the stronger the loss in the channel, the higher the value of K2 (the probability that Eve can block a single photon), which is the same as in Figure 4. We can also see that the second method requires more loss.
Here we also discuss the joint PNS attack in four-state SQKD, and the two joint PNS attack methods mentioned above are also applicable to four-state SQKD and other Measure and Resend SQKD. Because both the forward channel and reverse channel of four-state SQKD can leak information, Eve can get more information when implementing joint PNS attack on four-state SQKD compared with single-state SQKD.
5 Conclusion
SQKD was proposed by scientists based on the consideration of reducing quantum resources, and it has shown that even though semi-quantum protocols are limited in their quantum capabilities, they hold similar security properties to that of fully quantum protocols, at least in ideal qubit channels. However, it is not clear whether SQKD has an advantage in practical application scenarios. With the continuous improvement of SQKD experimental implementation, we can gradually clarify the application potential and application value of SQKD in real scenes.
Of course, SQKD also faces the multiphoton problem due to the limitation of experimental conditions. We are the first to consider the multiphoton problem in a single-state SQKD system. Through analysis, we find that the single-state SQKD system can overcome the PNS attack in a one-way channel by making the average photon number of the pulse distribution different. Even so, the SQKD of the actual system is also not secure. We propose two models of joint PNS attack, through which Eve can take away information without being detected.
As a reminder, in the second joint PNS attack, we only blocked off the distinguishable two-photon signal, and we can also block out three photons and even block all distinguishable multiphotons. The probability of blocking off
In this study, we do not consider this type of PNS which can preserve the Poisson photon number distribution of the combination of the signal source and the lossy channel. We will address this issue in future work.
Data availability statement
The original contributions presented in the study are included in the article and in the Supplementary Material. Further inquiries can be directed to the corresponding author.
Author contributions
SM: conceptualization, methodology, investigation, formal analysis, writing—original draft; SD: resources, supervision; QH: resources, supervision; JW: conceptualization, funding acquisition, resources, supervision, writing–review and editing resources, supervision; YY: resources, supervision; ZW: resources, supervision; ZZ: resources, supervision.
Funding
National Science Foundation of China (62071186, 61771205); National Science Foundation of Guangdong Province (2015A030313388).
Acknowledgments
The authors thank the Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials for provision of experimental platform.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bennett CH, Brassard G. Quantum cryptography: Public key distribution and coin tossing. Quan Phys (2020) 560:7–11. doi:10.48550/arXiv.2003.06557
2. Bennett CH. Quantum cryptography using any two nonorthogonal states. Phys Rev Lett (1992) 68:683121–4. doi:10.1103/PhysRevLett.68.3121
3. Bruß D. Optimal eavesdropping in quantum cryptography with six states. Phys Rev Lett (1998) 8114:3018–21. doi:10.1103/PhysRevLett.81.3018
4. Buzek V, Hillery M. Quantum copying: Beyond the no-cloning theorem. Phys Rev A (Coll Park) (1996) 546:1844–52. doi:10.1103/physreva.54.1844
5. Chen Y-P, Liu J-Y, Sun M-S, Zhou X-X, Zhang C-H, Li J, et al. Experimental measurement-device-independent quantum key distribution with the double-scanning method. Opt Lett (2021) 4615:3729–32. doi:10.1364/ol.431061
6. Liu J-Y, Ding H-J, Zhang C-M, Xie S-P, Wang Q. Practical phase-modulation stabilization in quantum key distribution via machine learning. Phys Rev Appl (2019) 121:014059. doi:10.1103/PhysRevApplied.12.014059
7. Zhou X-Y, Zhang C-H, Zhang C-M, Wang Q. Asymmetric sending or not sending twin-field quantum key distribution in practice. Phys Rev A (Coll Park) (2019) 996:062316. doi:10.1103/PhysRevA.99.062316
8. Hillery M, Bužek V, Berthiaume A. Quantum secret sharing. Phys Rev A (Coll Park) (1999) 593:1829–34. doi:10.1103/PhysRevA.59.1829
9. Deng FG, Zhou HY, Long GL. Circular quantum secret sharing. J Phys A: Math Gen (2006) 3945:14089–99. doi:10.1088/0305-4470/39/45/018
10. Wei KJ, Ma HQ, Yang JH. Experimental circular quantum secret sharing over telecom fiber network. Opt Express (2013) 2114:16663–9. doi:10.1364/OE.21.016663
11. Long GL, Liu XS. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys Rev A (Coll Park) (2002) 653:032302. doi:10.1103/PhysRevA.65.032302
12. Zhang W, Ding DS, Sheng YB, Zhou L, Shi BS, Guo GC. Quantum secure direct communication with quantum memory. Phys Rev Lett (2017) 11822:220501. doi:10.1103/PhysRevLett.118.220501
13. Zhu F, Zhang W, Sheng YB, Huang YD. Experimental long-distance quantum secure direct communication. Sci Bull (2017) 6222:1519–24. doi:10.1016/j.scib.2017.10.023
14. Bennett CH, Brassard G, Crepeau C, Jozsa R, Peres A, Wootters WK. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys Rev Lett (1993) 7013:1895–9. doi:10.1103/PhysRevLett.70.1895
15. Bouwmeester D, Pan JW, Mattle K, Eibl M, Weinfurter H, Zeilinger A. Experimental quantum teleportation. Nature (1997) 3906660:575–9. doi:10.1038/37539
16. Furusawa A, Sorensen JL, Braunstein SL, Fuchs CA, Kimble HJ, Polzik ES. Unconditional quantum teleportation. Science (1998) 2825389:706–9. doi:10.1126/science.282.5389.706
17. Bennett CH, Wiesner SJ. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys Rev Lett (1992) 6920:2881–4. doi:10.1103/PhysRevLett.69.2881
18. Mattle K, Weinfurter H, Kwiat PG, Zeilinger A. Dense coding in experimental quantum communication. Phys Rev Lett (1996) 7625:4656–9. doi:10.1103/PhysRevLett.76.4656
19. Chen Y, Liu S, Lou Y, Jing J. Orbital angular momentum multiplexed quantum dense coding. Phys Rev Lett (2021) 1279:093601. doi:10.1103/PhysRevLett.127.093601
20. Zhang C-H, Zhou X-Y, Ding H-J, Zhang C-M, Guo G-C, Wang QJ. Proof-of-principle demonstration of passive decoy-state quantum digital signatures over 200 km. Phys Rev Appl (2018) 103:034033. doi:10.1103/physrevapplied.10.034033
21. Ranu SK, Prabhakar A, Mandayam P. Differential phase encoded measurement-device-independent quantum key distribution. Quan Inf Process (2021) 202:67–37. doi:10.1007/s11128-021-03006-2
22. Tang GZ, Li CY, Wang MJ. Polarization discriminated time‐bin phase‐encoding measurement‐device‐independent quantum key distribution. Quan Eng (2021) 34:e79. doi:10.1002/que2.79
23. Zeng P, Zhou H, Wu W, Ma X. Quantum key distribution surpassing the repeaterless rate-transmittance bound without global phase locking. Quan Physice(2022) 2201:04300. doi:10.48550/arXiv.2201.04300
24. Boyer M, Kenigsberg D, Mor T. Quantum key distribution with classical Bob. Phys Rev Lett (2007) 99:99140501. doi:10.1103/PhysRevLett.99.140501
25. Li Q, Chan WH, Long DY. Semiquantum secret sharing using entangled states. Phys Rev A (Coll Park) (2010) 822:022303. doi:10.1103/PhysRevA.82.022303
26. Wang J, Zhang S, Zhang Q, Tang CJ. Semiquantum secret sharing using two-particle entangled state. Int J Quan Inform (2012) 105:1250050. doi:10.1142/S0219749912500505
27. Zou XF, Qiu DW. Three-step semiquantum secure direct communication protocol. Sci China Phys Mech Astron (2014) 579:1696–702. doi:10.1007/s11433-014-5542-x
28. Zhang MH, Li HF, Xia ZQ, Feng XY, Peng JY. Semiquantum secure direct communication using EPR pairs. Quan Inf Process (2017) 165:117–4. doi:10.1007/s11128-017-1573-3
29. Li-Hua G, Zhen-Yong C, Liang-Chao X, Nan-Run Z. Bi-Directional semi-quantum secure direct communication protocol based on high-dimensional single-particle states (2022). doi:10.7498/aps.71.20211702
30. Xia C, Li H, Hu J. Semi-quantum digital signature protocol based on Einstein–Podolsky–Rosen steering. J Phys A: Math Theor (2022) 5532:325302. doi:10.1088/1751-8121/ac7f6d
31. Thapliyal K, Sharma RD, Pathak A. Orthogonal-state-based and semi-quantum protocols for quantum private comparison in noisy environment. Int J Quan Inform (2018) 165:1850047. doi:10.1142/S0219749918500478
32. Zhou NR, Xu QD, Du NS, Gong LH. Semi-quantum private comparison protocol of size relation with d-dimensional Bell states. Quan Inf Process (2021) 203:124–15. doi:10.1007/s11128-021-03056-6
33. Luo Q-b., Li X-y., Yang G-w., Lin C. A mediated semi-quantum protocol for millionaire problem based on high-dimensional Bell states. Quan Inf Process (2022) 217:257–15. doi:10.1007/s11128-022-03590-x
34. Tian Y, Li J, Ye C, Chen X-B, Li C. W-state-based semi-quantum private comparison. Int J Theor Phys (Dordr) (2022) 612:18–6. doi:10.1007/s10773-022-05005-0
35. Tang Y-H, Jia H-Y, Wu X, Chen H-M, Zhang Y-M. Robust semi-quantum private comparison protocols against collective noises with decoherence-free states. Quan Inf Process (2022) 213:97–24. doi:10.1007/s11128-022-03444-6
36. Xu T-J, Chen Y, Geng M-J, Ye T-Y. Single-state multi-party semiquantum key agreement protocol based on multi-particle GHZ entangled states. Quan Inf Process (2022) 217:266–18. doi:10.1007/s11128-022-03615-5
37. Lili Y, Shibin Z, Yan C, Zhiwei S, Xiangmei L. Mutual weak quantum users key agreement protocol based on semi-honest quantum server. Int J Theor Phys (Dordr) (2022) 617:198–11. doi:10.1007/s10773-022-05161-3
38. Boyer M, Gelles R, Kenigsberg D, Mor T. Semiquantum key distribution. Phys Rev A (Coll Park) (2009) 793:032341. doi:10.1103/PhysRevA.79.032341
39. Zou XF, Qiu DW, Li LZ, Wu LH, Li LJ. Semiquantum-key distribution using less than four quantum states. Phys Rev A (Coll Park) (2009) 795:052312. doi:10.1103/PhysRevA.79.052312
40. Krawec WO. Restricted attacks on semi-quantum key distribution protocols. Quan Inf Process (2014) 1311:2417–36. doi:10.1007/s11128-014-0802-2
41. Boyer M, Katz M, Liss R, Mor T. Experimentally feasible protocol for semiquantum key distribution. Phys Rev A (Coll Park) (2017) 966:062335. doi:10.1103/PhysRevA.96.062335
42. Liu W, Zhou H. A new semi-quantum key distribution protocol with high efficiency. In: Proceeding of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC); October 2018; Chongqing, China. IEEE (2018). p. 2424–7. doi:10.1109/IAEAC.2018.8577673
43. Wang MM, Gong LM, Shao LH. Efficient semiquantum key distribution without entanglement. Quan Inf Process (2019) 189:260–10. doi:10.1007/s11128-019-2378-3
44. Yu KF, Yang CW, Liao CH, Hwang T. Authenticated semi-quantum key distribution protocol using Bell states. Quan Inf Process (2014) 136:1457–65. doi:10.1007/s11128-014-0740-z
45. Li CM, Yu KF, Kao SH, Hwang T. Authenticated semi-quantum key distributions without classical channel. Quan Inf Process (2016) 157:2881–93. doi:10.1007/s11128-016-1307-y
46. Meslouhi A, Hassouni Y. Cryptanalysis on authenticated semi-quantum key distribution protocol using Bell states. Quan Inf Process (2017) 161:18–7. doi:10.1007/s11128-016-1468-8
47. Wang H-W, Tsai C-W, Lin J, Yang C-W. Authenticated semi-quantum key distribution protocol based on W states. sensors (2022) 2213:4998. doi:10.3390/s22134998
48. Vlachou C, Krawec W, Mateus P, Paunkovic N, Souto A. Quantum key distribution with quantum walks. Quan Inf Process (2018) 1711:288–37. doi:10.1007/s11128-018-2055-y
50. Sun ZW, Du RG, Long DY. Quantum key distribution with limited classical Bob. Int J Quan Inform (2013) 111:1350005. doi:10.1142/S0219749913500056
51. Miyadera T. Relation between information and disturbance in quantum key distribution protocol with classical Alice. Int J Quan Inform (2011) 96:1427–35. doi:10.1142/S0219749911008118
52. Krawec WO. Key-rate bound of a semi-quantum protocol using an entropic uncertainty relation. In: Proceeding of the 2018 IEEE International Symposium on Information Theory (ISIT); June 2018; Vail, CO, USA. IEEE (2018). p. 2669–73.
53. Krawec WO. Security proof of a semi-quantum key distribution protocol. In: Proceeding of the 2015 IEEE International Symposium on Information Theory (ISIT); June 2015; Hong Kong, China. IEEE (2015). p. 686–90. doi:10.1109/ISIT.2015.7282542
54. Krawec WO. Quantum key distribution with mismatched measurements over arbitrary channels. Quan Phys (2016) 17:209–241. doi:10.48550/arXiv.1608.07728
55. Hajji H, El Baz M. Mutually unbiased bases in 3 and 4 dimensions semi-quantum key distribution protocol. Phys Lett A (2022) 426:127884. doi:10.1016/j.physleta.2021.127884
56. Han SY, Huang YT, Mi S, Qin XJ, Wang JD, Yu YF, et al. Proof-of-principle demonstration of semi-quantum key distribution based on the Mirror protocol. EPJ Quan Technol (2021) 81:28–10. doi:10.1140/epjqt/s40507-021-00117-8
57. Brassard G, Lutkenhaus N, Mor T, Sanders BC. Limitations on practical quantum cryptography. Phys Rev Lett (2000) 856:1330–3. doi:10.1103/PhysRevLett.85.1330
58. Lütkenhaus N, Jahma M. Quantum key distribution with realistic states: Photon-number statistics in the photon-number splitting attack. New J Phys (2002) 41:344. doi:10.1088/1367-2630/4/1/344
59. Lütkenhaus N. Security against individual attacks for realistic quantum key distribution. Phys Rev A (Coll Park) (2000) 615:052304. doi:10.1103/PhysRevA.61.052304
60. Gurevish P. Experimental quantum key distribution with classical Alice. Mastersthesis (2013). doi:10.3390/e20070536
61. Chen L-Y, Gong L-H, Zhou N-R. Two semi-quantum key distribution protocols with G-like states. Int J Theor Phys (Dordr) (2020) 596:1884–96. doi:10.1007/s10773-020-04456-7
62. Ye T-Y, Li H-K, Hu J-L. Semi-quantum key distribution with single photons in both polarization and spatial-mode degrees of freedom. Int J Theor Phys (Dordr) (2020) 599:2807–15. doi:10.1007/s10773-020-04540-y
63. Zhou Y-H, Qin S-F, Shi W-M, Yang Y-G. Measurement-device-independent continuous variable semi-quantum key distribution protocol. Quan Inf Process (2022) 218:303–21. doi:10.1007/s11128-022-03626-2
64. Guskind J, Krawec WO. Mediated semi-quantum key distribution with improved efficiency. Quan Sci Technol (2022) 73:035019. doi:10.1088/2058-9565/ac7412
Keywords: quantum key distribution, semi-quantum key distribution, practical security, weak coherent pulses, photon-number splitting attack
Citation: Mi S, Dong S, Hou Q, Wang J, Yu Y, Wei Z and Zhang Z (2022) Joint photon-number splitting attack on semi-quantum key distribution. Front. Phys. 10:1029552. doi: 10.3389/fphy.2022.1029552
Received: 27 August 2022; Accepted: 23 September 2022;
Published: 03 November 2022.
Edited by:
Mingxing Luo, Southwest Jiaotong University, ChinaCopyright © 2022 Mi, Dong, Hou, Wang, Yu, Wei and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jindong Wang, V2FuZ2ppbmRvbmdAbS5zY251LmVkdS5jbg==
 Shang Mi
Shang Mi Shuang Dong1
Shuang Dong1 Yafei Yu
Yafei Yu