Study on flow characteristics of natural gas containing CO2 invading wellbore during drilling

He, Haikang; Sun, Baojiang; Sun, Xiaohui; Li, Xuefeng; Shan, Zhengfeng

doi:10.3389/fphy.2022.1028671

ORIGINAL RESEARCH article

Front. Phys., 07 October 2022

Sec. Interdisciplinary Physics

Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1028671

This article is part of the Research Topic Multiphase Flow Behavior in the Deep-Stratum and Deep-Water Wellbores View all 13 articles

Study on flow characteristics of natural gas containing CO₂ invading wellbore during drilling

Haikang He¹

Baojiang Sun¹*

Xiaohui Sun¹

Xuefeng Li¹

Zhengfeng Shan²

¹School of Petroleum Engineering, China University of Petroleum (East China), Qingdao, China
²Drilling Division of China Petroleum Offshore Engineering Co., Ltd., Beijing, China

The dissolution of invaded gas in the drilling fluid during drilling results in an increase in the gas invasion concealment. This is of great significance for the development of acid gas reservoirs to determine the solubility change and multiphase flow law in an annulus after invasion by natural gas with high CO₂ content. In this study, control equations of gas–liquid flow during drilling gas invasion are established considering the influence of gas solubility. For the prediction of gas solubility, the interaction parameters of CH₄ and water in the Peng–Robinson equation of state are optimised to establish a gas solubility prediction model. The solubility of natural gas with high CO₂ content in water and brine solution is measured through phase-equilibrium experiments. The results indicate that the newly optimised solubility model can accurately predict the solubility of CH₄ and CO₂ in water, and the prediction error is within 5%. Moreover, the prediction error for the solubility of CH₄ and CO₂ mixed gas is within 15%. The analysis of gas invasion in example engineering drilling applications reveals that an increase in the CO₂ content in the invaded gas leads to a slow change in the mud-pit increment, and the concealment strengthens as the distance between the gas-migration front and the wellhead increases. Gas solubility has a significant impact on the monitoring of gas invasion in low permeability reservoirs.

1 Introduction

The Liwan 3-1 gas field in China, with CH₄ content exceeding 80% and CO₂ content exceeding 3%, is a type of acidic gas field [1–7]. Romania, Mexico, and Indonesia have gas reservoirs with high CO₂ content, that is, the CO₂ concentration in the reservoir fluid is as high as 86% [8–10], and the CO₂ content in the natural gas produced at the Tugu Barat oilfield in Indonesia is as high as 76 mol% [11]. During the drilling and development of natural gas fields containing CO₂, formation fluid invasion can easily occur. A high amount of invaded gas dissolution in the drilling fluid makes it difficult to monitor the ground and increases the blowout risk. Several studies have focused on the law of gas dissolution in multiphase flow. For example, Yin et al. (2017) established an annular multiphase transient flow model based on gas–liquid two-phase flow and flash theory, considering the dissolution of gas in an oil-based drilling fluid. The dissolution of gas led to a slow change of mud pit, and the mud pit increment associated with the oil-based drilling fluid was smaller than that of the water-based drilling fluid [12]. Sun et al. (2018) considered the phase change and dissolution of the acidic natural mixture in a drilling fluid and proposed a flow-transition criterion for multiphase flow. When the invading gas rises in a vertical wellbore, the gas phase change causes large volume expansion and increases the blowout risk. However, they focused on the gas phase state analysis and did not consider the gas dissolution effect [13]. Xu et al. (2018) used the standing bubble point formula to calculate the solubility of gas in oil. Neglecting the gas dissolution effect, the bottom-hole temperature was overestimated by 3.74°C, and the bottom-hole pressure increased by 2.92 MPa [14].

The O’Bryan formula [15] is widely used to predict the solubility of gas in an oil-based drilling fluid. A water-based drilling fluid system is mainly composed of water and salt; therefore, the solubility of water-based drilling fluids is typically studied using water and salt water. Wiebe and Gaddy (1939), Briones et al. (1987), and Sabirzyanov et al. (2003) conducted a large number of experimental studies on the solubility of CO₂ gas in water [16–18]. It was found that the temperature could be as high as 373.15 K and the pressure could reach 70 MPa. However, studies on the solubility of a mixture of CH₄ and CO₂ in water and salt water remain limited. Dhima (1999) measured the solubility of CO₂ + CH₄ mixture in water at 344.5 K and 10–100 MPa [19]. Subsequently, Qin et al. (2008), Ghafri (2014), and Loring et al. (2017) obtained the vapour–liquid equilibrium data for the CO₂ + CH₄ + H₂O ternary system at 323.15–423.15 K and 1–20 MPa [20–22]. Zirrahi et al. [23] recalculated the mutual parameters between gases in the Peng–Robinson equation of state (PR-EOS) [24] using existing experimental data for mixed gas solubility. The prediction deviation of the solubility of the acidic mixed gas in water was less than 5%; however, the applicability must be evaluated based on the adjustment of the fitting parameters of the experimental data. Ziabakhsh-Ganji and Kooi [25] improved the state equation to establish a gas solubility prediction model. Although the model could accurately predict the solubility of single gas in water and brine, the prediction accuracy of the solubility of mixed gases remains unknown. Li [26] predicted the phase equilibrium of CO₂–CH₄–H₂S–brine using fugacity-fugacity and fugacity-activity models and found that the fugacity-activity model was more accurate in predicting the solubility of CO₂ + CH₄ mixed gas.

Research on the effect of gas dissolution on multiphase flow has focused on oil-based drilling fluids, and water-based drilling fluids have typically been neglected because of the low solubility of gases in water. Furthermore, the accuracy and applicability of existing prediction models are insufficient for determining the water solubility of a mixed gas containing CO₂. Therefore, according to the characteristics of deep-water drilling, a gas–liquid two-phase flow control model incorporating the gas dissolution effect was established in this study. To realise accurate prediction and analysis of gas solubility, the interaction parameters of CH₄ and water in the PR-EOS were optimised to establish a gas solubility prediction model. The finite difference method was used to solve the proposed multiphase flow model. The influence of gas solubility on gas phase flow law during gas invasion was analysed using an example to provide guidance for the control safety of field wells.

2 Gas–liquid control model

2.1 Gas–liquid two-phase flow equation

According to the law of mass conservation, a physical model of continuity, momentum, and energy was established by considering the dissolution of gas in a drilling fluid based on the following assumptions.

1) The flow in the wellbore is one-dimensional.

2) The dissolution of gas in the drilling fluid is completed instantaneously.

3) The compressibility change of drilling fluid is negligible.

4) The influence of rock debris can be neglected.

The continuity equation for the free gas phase can be expressed as follows:

\frac{\partial}{\partial t} (ρ_{g} E_{g} A) + \frac{\partial}{\partial z} (ρ_{g} u_{g} E_{g} A) = q_{g} - m_{g - L} (1)

where m_g-L is the mass transfer rate from gas phase to liquid phase [kg/(m s)], which can be expressed as

\frac{\partial}{\partial t} (ρ_{s g} R_{s m} E_{m} A) + \frac{\partial}{\partial z} (ρ_{s g} R_{s m} u_{m} E_{m} A) = m_{g - L} (2)

The mass conservation of the liquid phase can be expressed as

\frac{\partial}{\partial t} (A ρ_{m} E_{m}) + \frac{\partial}{\partial z} (A ρ_{m} u_{m} E_{m}) = m_{g - L} (3)

Considering the slippage of the gas–liquid phase, the momentum equation of the gas–liquid phase can be expressed as

\begin{array}{l} \frac{\partial}{\partial t} (A ρ_{g} u_{g} E_{g} + A ρ_{m} u_{m} E_{m}) + \frac{\partial}{\partial z} (A ρ_{g} u_{g}^{2} E_{g} + A ρ_{m} u_{m}^{2} E_{m}) \\ = - A g \cos α (ρ_{g} E_{g} + ρ_{m} E_{m}) - \frac{d (A P)}{d z} - A | \frac{d F_{r}}{d z} | \end{array} (4)

Latent heat of phase change exists during the process of gas–liquid phase equilibrium. Considering the existence of heat associated with phase change, the energy equation of the annulus in a wellbore is expressed as follows.

Gas phase:

\frac{\partial}{\partial t} (A ρ_{g} E_{g} C_{p g} T_{a}) + \frac{\partial}{\partial z} (w_{g} C_{p g} T_{a}) = \frac{Q_{A, g} - Q_{D, g}}{d z} (5)

Liquid phase:

\frac{\partial}{\partial t} (A ρ_{m} E_{m} C_{p m} T_{a}) + \frac{\partial}{\partial z} (w_{m} C_{p m} T_{a}) = \frac{Q_{A, m} - Q_{D, m}}{d z} (6)

Phase-change heat:

\frac{\partial}{\partial t} (ρ_{m} E_{m} R_{s m}) (7)

Therefore, the energy equation in the wellbore annulus can be expressed as

\begin{array}{l} \frac{\partial}{\partial t} (A ρ_{g} E_{g} C_{p g} T_{a} + A ρ_{m} E_{m} C_{p m} T_{a}) + \frac{\partial}{\partial z} (w_{g} C_{p g} T_{a} + w_{m} C_{p m} T_{a}) \\ = \frac{Q_{A, g} - Q_{D, g}}{d z} + \frac{Q_{A, m} - Q_{D, m}}{d z} + \frac{\partial}{\partial t} (ρ_{m} E_{m} R_{s m}) \end{array} (8)

2.2 Calculation of frictional pressure drop

2.2.1 Single phase flow

Sun et al. applied the power-law for fluid flow to liquid phase flow [27] to obtain the following equation:

F_{r} = \frac{2 f u_{a m}^{2} ρ_{a m}}{D_{e}} (9)

When Re < 2,000,

f = \frac{8 k}{ρ_{a m} u_{a m}^{2}} {[\frac{8 u_{a m}}{D_{e}} \frac{3 n + 1}{4 n}]}^{n} (10)

When Re > 2,000,

\frac{1}{\sqrt{f}} = \frac{2 k}{n^{0.75}} \log [R e {(\frac{f}{4})}^{1 - \frac{n}{2}}] - \frac{0.2}{n^{1.2}} (11)

2.2.2 Gas–liquid two-phase flow

Bubbly flow:

F_{r} = \frac{2 f u_{a m}^{2} ρ_{a m}}{D_{e}} (12)

Slug and churn flows:

F_{r} = \frac{2 f (1 - E_{g}) u_{a m}^{2} ρ_{a m}}{D_{e}} (13)

\frac{1}{\sqrt{f}} = - 4 \log (\frac{ε_{e}}{3.71} D_{e} - 5.05 \log \frac{A}{R e}) (14)

A = {(\frac{ε_{e}}{2.549 D_{e}})}^{1.11} + {(\frac{7.149}{R e})}^{0.898} (15)

Annular fog flow:

F_{r} = \frac{2 f u_{a m}^{2} ρ_{a m}}{D_{e} E_{g}^{2}} (16)

f = 0.079 [1 + \frac{75 (1 - E_{g})}{R e g^{0.25}}] (17)

2.3 Development of gas inflow model

The occurrence of gas kicks in deep-water drilling wellbores induces multiphase flow in the wellbore as well as gas inflow from the reservoir, which are influenced by each other. For example, when the wellbore pressure is lower than the pore pressure of the open-hole section, a gas surge occurs. Subsequently, once the gas enters the wellbore, the flow rate, gas porosity, and fluid pressure change. The gas inflow can be calculated using the following [28]

Q_{g} = 2 π K \frac{p_{e}^{2} - p^{2}}{μ \ln \frac{2.25 \frac{K}{μ_{g} C_{t}} t}{R_{w}^{2}}} \frac{T z}{P z_{e} T_{e}} ρ_{g} (18)

PR-EOS was used for calculating the physical properties of the fluid components in the wellbore. The auxiliary equations such as velocity and two-phase flow-state discrimination equations were obtained from Gao et al. [29].

3 Gas solubility

3.1 Gas solubility calculation model

The gas–liquid two-phase equilibrium in a closed system can be expressed as follows:

f_{i}^{v} = f_{i}^{l} (19)

f_{i}^{v} = p ϕ_{i}^{v} y_{i} (20)

f_{i}^{l} = p ϕ_{i}^{l} x_{i} (21)

PR-EOS was used for calculating the fugacity coefficients of component i in the gas and liquid phases, and its basic form can be expressed as follows:

P = \frac{R T}{V - b} + \frac{a}{V (V + b) + b (V + b)} (22)

For a single gas, the parameters a and b are

b = 0.0778 \frac{R T_{c}}{P_{c}} (23)

a = a (T_{c}) α (T) (24)

a (T_{c}) = 0.45724 \frac{{(R T_{c})}^{2}}{P_{c}} (25)

α (T) = {[1 + β (1 - \sqrt{\frac{T}{T_{c}}})]}^{2} (26)

β = 0.37464 + 1.54226 ω - 0.26992 ω^{2} (27)

A non-random mixing rule was used for calculating the mixed gas parameters a and b, as follows:

a_{m i x} = \sum_{i} \sum_{j} y_{i} y_{j} {(a_{i} a_{j})}^{0.5} (1 - k_{i j}) (28)

b_{m i x} = \sum_{i} y_{i} b_{i} (29)

where k_ij is the interaction parameter between i and j components, with k_ij = k_ji. For calculating the fugacity coefficients, combined with van der Waals mixing rule [30], the following expression was used:

\ln ϕ_{i} = \frac{b_{i}}{b} (Z - 1) - \ln (Z - B) - \frac{A}{2 \sqrt{2} B} (\frac{2 \sum_{i = 1}^{N} y_{j} a_{i j}}{a} - \frac{b_{j}}{b}) \ln (\frac{Z + (1 + \sqrt{2}) B}{Z + (1 - \sqrt{2}) B}) (30)

The compression factor is calculated as

Z^{3} - (1 - B) Z^{2} + (A - 2 B - 3 B^{2}) Z - (A B - B^{2} - B^{3}) = 0 (31)

where the parameters A and B are functions of temperature and pressure and are expressed as follows:

A = \frac{a P}{{(R T)}^{2}} (32)

B = \frac{b P}{R T} (33)

3.2 Optimization of interaction parameters between methane-water

The binary interaction parameter in PR-EOS reflects the nature of the interaction between two molecules in a mixed system of gas and water and is the key parameter for obtaining an accurate prediction of phase equilibrium using PR-EOS. Interaction parameters are typically determined based on the optimised regression of the experimental data for gas–liquid phase equilibrium. There are several reports on the solubility of CH₄ in water, and the data incorporated in this study are presented in the Appendix. The interaction parameters were calculated at different temperatures and pressures (see Figure 1). Evidently, the interaction parameters increase with an increase in temperature, whereas they exhibit a decreasing trend with an increase in pressure; however, the fluctuation range is not significantly affected by temperature. The interaction parameters were fitted as a function of temperature and pressure, as follows:

\begin{array}{l} k_{C H_{4} - H_{2} O} = - 1.45 + 2.96 \times 10^{- 4} P + 0.00469 T - 1.22 \times 10^{- 6} P^{2} - \\ 2.85 \times 10^{- 6} T^{2} - 8.62 \times 10^{- 7} P T \end{array} (34)

FIGURE 1

FIGURE 1. Variation in the interaction parameters of CH₄ and water with temperature and pressure.

3.2.1 Experimental evaluation of gas solubility

To verify the applicability of the gas solubility prediction model established by optimising the parameters of PR-EOS, the solubility of CO₂, CH₄, and CO₂ + CH₄ mixed gas in water was measured using a phase-equilibrium experimental device. The accuracy of the model prediction was expressed by the average relative deviation percentage ARD%, and average absolute relative deviation AARD%.

A R D % = (\frac{| y_{i}^{\exp} - y_{i}^{p r e d i c t} |}{y_{i}^{\exp}}) \times 100 (35)

A A R D % = \frac{1}{N} \sum (A R D %) (36)

3.2.1.1 Materials

The purity of CO₂ and CH₄ was greater than 99.9%, and the purity of CH₄ in the CO₂ + CH₄ mixed gas was greater than 49.9%. Figure 2 shows the experimental flow diagram. The high-temperature and high-pressure reactor used had a volume of 300 ml, with a maximum pressure and temperature resistance of 60 MPa and 473 K, respectively. A constant-speed and constant-pressure pump (D-250L) was used for pressurisation, with a maximum pressure of 70 MPa.

FIGURE 2

FIGURE 2. Schematic of the experimental flow.

3.2.1.2 Experimental procedure

The operational process for gas solubility measurement is as follows.

1) The experimental device is cleaned and checked for air tightness. Deionized water is used to clean the high-temperature and high-pressure reaction kettle 2–3 times; the intermediate vessel and reaction kettle are connected; the pressure of the reaction kettle is increased to 5 MPa. If the pressure of the reaction kettle and intermediate vessel is stable without fluctuation within 2 h, the sealing of the experimental device is considered adequate. Otherwise, the connection is rechecked.

2) The phase-equilibrium experiment is conducted by pressurising and heating. A vacuum is generated in the reaction kettle using a vacuum pump. Approximately 200 ml of liquid is injected with a constant-speed and constant-pressure pump, and the heating device is turned on to increase the temperature to the pre-set value. The reaction kettle is filled with gas to a certain pre-set pressure through the intermediate vessel to form a gas–liquid mixed state in the kettle. During the pressurisation process, certain temperature fluctuations occur because of the adiabatic condition in the reaction kettle; therefore, the temperature must be stabilised to the pre-set temperature. After stirring for 1–2 h with an electromagnetic stirrer, the pressure change in the kettle is no longer monitored. If the pressure is stable within 2–3 h, the gas–liquid equilibrium is considered stable.

3) The measurement data is recorded, sampled, and analysed. A vacuum pump is used to generate a vacuum in the sampler and extract the liquid in the kettle. A constant-speed and constant-pressure pump is used to inject the liquid into the reaction kettle and maintain a stable pressure in the kettle. A gas meter is used to measure the volume of the precipitated gas. After the gas is collected, the gas and liquid volumes are recorded in real-time. The average value of the three measurements is calculated and chromatographic analysis of the precipitated gas is performed.

4) Steps 2)–3) are repeated to perform the solubility measurements at different pressures and temperatures. After the experiment is completed, the exhaust pipeline is vented.

3.2.1.3 Accuracy verification of experimental methods

To verify that the aforementioned experimental devices and methods can be used for solubility measurements, the measurement results of CO₂ gas at 325.15 K were compared with previously reported experimental data [18, 20, 31], as presented in Table 1. Evidently, the maximum ARD% of our experimental data compared with reported data is 3.54, and the minimum ARD% is 1.55, indicating good accuracy. Therefore, the proposed experimental apparatus and method can be used for gas solubility measurements.

TABLE 1

TABLE 1. Comparison between experimental and previously reported values of CO₂ solubility in water measured at 323.15 K.

3.2.2 Verification of prediction accuracy of gas solubility model

3.2.2.1 Prediction of single-gas solubility model

Solubility of CH₄ and CO₂ in water at 323.15 K was measured using the proposed experimental device. The developed solubility-prediction model was used to predict and analyse the solubility of CO₂ and CH₄ in water, as shown in Figures 3, 4. The experimental data obtained in this study were compared with previously reported data [16–18, 32–35] for model analysis.

FIGURE 3

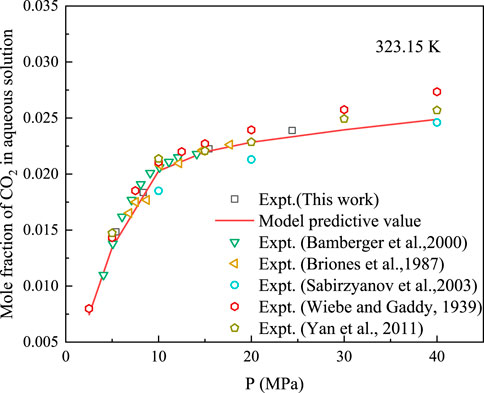
FIGURE 3. Comparison between predicted data of CO₂ solubility model and experimental data at 323.15 K.

FIGURE 4

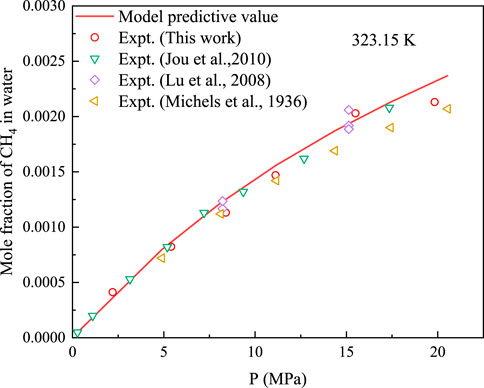
FIGURE 4. Comparison between predicted data of CH₄ solubility model and experimental data at 323.15 K.

At 323.15 K, the AARD% of the model predicted and experimental values for CH₄ was 5.66, and the AARD% for the solubility of CO₂ in water was 3.71. Therefore, the proposed solubility-prediction model can be used to accurately predict the solubility of CH₄ and CO₂.

3.2.2.2 Prediction of mixed gas solubility model

The solubility of the CH₄ + CO₂ mixture in water and 5% NaCl aqueous solution was measured at 302.15 K and 323.15 K. The established solubility model was used to predict the experimental results, as shown in Figure 5. Evidently, the model predicted values are not consistent with the experimental values and a certain deviation exists. For the solubility of the mixture in water, the AARD% of the model predicted and experimental values was 14.80. The AARD% of the mixed gas in 5% NaCl was 14.32, showing a certain deviation. This is because this study only investigated the interaction parameters of CH₄ gas and water. The interaction parameters of CO₂–H₂O are 0.19014, as reported by Ziabakhsh-Ganji and Kooi [25], and the interaction parameters of CO₂–CH₄ are 0.1 [36]. Therefore, the selection of interaction parameters resulted in a lower model predicted value for CO₂.

FIGURE 5

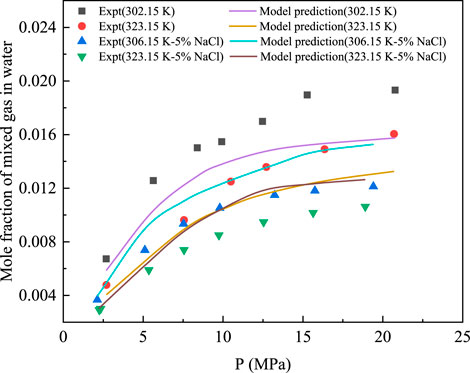
FIGURE 5. Comparison between the predicted data of CH₄ solubility model and the experimental data at 323.15 K.

4 Solution of multiphase flow model

The finite difference method was used to calculate the differences in the proposed multiphase flow model [37]. The basic difference calculation can be expressed as follows:

Y_{j + 1}^{n + 1} - Y_{j}^{n + 1} = \frac{Δ z}{2 Δ t} (X_{j}^{n} + X_{j + 1}^{n} - X_{j}^{n + 1} - X_{j + 1}^{n + 1}) (37)

The discretisation of the differential equation describing the gas phase non-production interval can be expressed as follows:

\begin{array}{l} {(ρ_{g} u_{g} E_{g} A)}_{j + 1}^{n + 1} - {(ρ_{g} u_{g} E_{g} A)}_{j}^{n + 1} \\ = \frac{Δ z}{2 Δ t} [{(ρ_{g} E_{g} A)}_{j}^{n + 1} - {(ρ_{g} E_{g} A)}_{j}^{n} + {(ρ_{g} E_{g} A)}_{j + 1}^{n + 1} - {(ρ_{g} E_{g} A)}_{j + 1}^{n}] \\ - \frac{Δ z}{2} [{(m_{g - l})}_{j}^{n + 1} + {(m_{g - l})}_{j + 1}^{n + 1}] \end{array} (38)

The discretisation of the differential equation of the dissolved phase can be expressed as follows:

\begin{array}{l} {(ρ_{s g} R_{s m} E_{m} A u_{m})}_{j + 1}^{n + 1} - {(ρ_{s g} R_{s m} E_{m} A u_{m})}_{j}^{n + 1} = \frac{Δ z}{2 Δ t} [{(ρ_{s g} R_{s m} E_{m} A)}_{j}^{n} + {(ρ_{s g} R_{s m} E_{m} A)}_{j + 1}^{n} \\ - {(ρ_{s g} R_{s m} E_{m} A)}_{j}^{n + 1} - {(ρ_{s g} R_{s m} E_{m} A)}_{j + 1}^{n + 1}] - \frac{Δ z}{2} [{(m_{g - l})}_{j}^{n + 1} + {(m_{g - l})}_{j + 1}^{n + 1}] \end{array} (39)

The phase discretisation of the drilling fluid differential equation can be expressed as follows:

\begin{array}{l} {(ρ_{m} u_{m} E_{m} A)}_{j + 1}^{n + 1} - {(ρ_{m} u_{m} E_{m} A)}_{j}^{n + 1} \\ = \frac{Δ z}{2 Δ t} [{(ρ_{m} E_{m} A)}_{j}^{n + 1} - {(ρ_{m} E_{m} A)}_{j}^{n} + {(ρ_{m} E_{m} A)}_{j + 1}^{n + 1} - {(ρ_{m} E_{m} A)}_{j + 1}^{n}] \\ + \frac{Δ z}{2} [{(m_{g - l})}_{j}^{n + 1} + {(m_{g - l})}_{j + 1}^{n + 1}] \end{array} (40)

The momentum equation discretisation can be expressed as follows:

\begin{array}{l} {(A P + A F_{r})}_{j + 1}^{n + 1} - {(A P + A F_{r})}_{j}^{n + 1} + {(A E_{g} ρ_{g} u_{g}^{2} + A E_{m} ρ_{m} u_{m}^{2})}_{j + 1}^{n + 1} - {(A E_{g} ρ_{g} u_{g}^{2} + A E_{m} ρ_{m} u_{m}^{2})}_{j}^{n + 1} \\ = \frac{Δ z}{2 Δ t} [{(A E_{g} ρ_{g} u_{g} + A E_{m} ρ_{m} u_{m})}_{j + 1}^{n + 1} - {(A E_{g} ρ_{g} u_{g} + A E_{m} ρ_{m} u_{m})}_{j + 1}^{n} \\ + {(A E_{g} ρ_{g} u_{g} + A E_{m} ρ_{m} u_{m})}_{j + 1}^{n + 1} - {(A E_{g} ρ_{g} u_{g} + A E_{m} ρ_{m} u_{m})}_{j + 1}^{n}] \\ - \frac{Δ z}{2} [(A g \cos α (E_{g} ρ_{g} + E_{m} ρ_{m}))_{j}^{n + 1} - (A g \cos α (E_{g} ρ_{g} + E_{m} ρ_{m}))_{j + 1}^{n + 1}] \end{array} (41)

The flow diagram of the solution process in the proposed model is illustrated in Figure 6. The specific steps of the multiphase flow model are as follows.

1) The bottom-hole pressure $p_{j}^{n (0)}$ at time n is estimated, and the temperature $T_{j}^{n}$ at time n is calculated.

2) The dissolved gas at node j and time n is calculated. The relationship between the calculated gas dissolution and the formation-gas inflow or production is examined, as follows.

① If the calculated gas dissolution is less than the gas inflow, the gas dissolution at the current time is the calculated gas solubility.

② If the calculated gas dissolution is greater than the gas inflow, the gas dissolution at the current time is the inflow of formation gas.

3) According to the calculated temperature and pressure at node j at time n, output of each phase, and dissolved amount of gas, the physical property parameters of each component phase at node j and time n are calculated using the equation of state.

4) The continuity equation is used to calculate the velocity and volume fraction ${E_{i,}}_{j}^{n (0)}$ of each component phase at node j and time n using the known parameters of spatial node j + 1 at time n;

5) The pressure $p_{j + 1}^{n}$ at node j + 1 and time n is estimated, Steps 2)–4) are repeated, and $p_{j + 1}^{n (0)}$ at node j + 1 and time n is calculated using the momentum equation. If $| p_{j + 1}^{n} - p_{j + 1}^{n (0)} | \leq ε$ , the calculation is considered correct. The parameters calculated at node j + 1 and time n are used as the known conditions at time n + 1. Otherwise, the calculation is repeated.

6) Steps 2)–5) are repeated to calculate the wellhead parameters, and the calculated wellhead back pressure is $p_{h}$ . Compared with the measured wellhead back pressure $P_{h}^{0}$ , if $| p_{h} - p_{h}^{o} | \leq ε$ is true, the assumption of bottom-hole pressure $p_{j}^{n}$ at time n is considered correct. Otherwise, Step 2) is repeated and a new value is assigned to bottom-hole pressure $p_{j}^{n (0)}$ at time n.

FIGURE 6

FIGURE 6. Flowchart of multiphase flow model solution.

5 Results and discussion

5.1 Analysis of gas–liquid flow law

A deep-water vertical well in the South China Sea was used as an example to perform a project case analysis. The basic data are listed in Table 2.

TABLE 2

TABLE 2. Specifications of the example well.

Figure 7 shows the deviation between the calculated mud-pit increment and the measured values. It can be observed that the mud-pit increment rapidly changes in the range of 0–210 s. Furthermore, the difference between the calculated curve and the measured points is small, and the error between the predicted and the measured values remains within 15%. In actual engineering projects involving drilling, the measured data fluctuates owing to the influence of tide, instrument error, and typhoon.

FIGURE 7

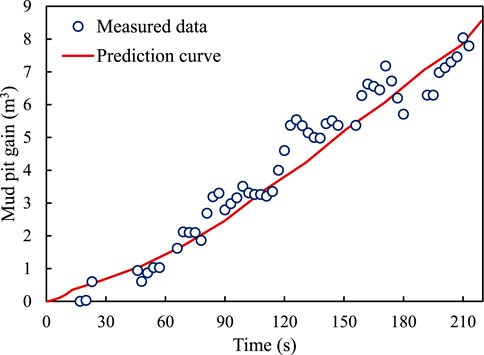
FIGURE 7. Variation in the relationship between mud-pit increment and bottom-hole pressure with invasion time.

Figures 8, 9 show the variation in the relationship between the volume fraction of the free gas and the mass fraction of the dissolved gas with invasion time. As the well depth decreases, both the mass fraction of the dissolved gas and the corresponding free gas integral number gradually decrease. This is because the amount of gas invaded by the formation is limited, and the gas gradually extends to the front. The gas dissolution causes the volume fraction of the gas at the front to decrease. However, when the well depth is fixed, volume fraction of the free gas increases with an increase in invasion time, primarily because the amount of dissolved gas in the drilling fluid reaches the saturated state, and the amount of gas released increases. As is evident from Figure 9, the dissolved gas content in the wellbore has a certain limit and does not increase beyond the liquid saturation value.

FIGURE 8

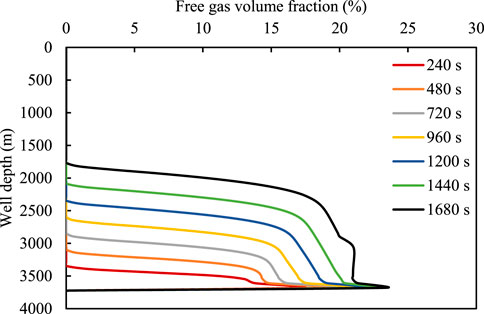
FIGURE 8. Relationship between free gas integral number and well depth for different time durations.

FIGURE 9

FIGURE 9. Relationship between dissolved gas mass fraction and well depth.

5.2 Influence of CO₂ content and reservoir permeability on multiphase flow

The gas–liquid two-phase flow law was simulated and analysed for a reservoir permeability of 10 md, gas invasion time of 1,200 s, and displacement of 36 L/s. Figure 10 shows the variations in the mud-pit increment with gas invasion time under different acid gas contents and permeabilities. If the invaded gas does not contain CO₂, the mud pit changes rapidly and the gas invasion monitoring time is shorter. By contrast, if the invaded gas contains a high concentration of CO₂, the incremental change time of the mud pit increases. If the monitoring value of the mud-pit increment is considered as 10 m³, it can be monitored in 252 s when the gas without CO₂ is dissolved. When 10% CO₂ is present in the invading gas, the monitoring time of gas invasion increases by 10 s. Similarly, the monitoring time of the gas containing 20% CO₂ is increased by 22 s. Therefore, the dissolution of an acid gas causes a certain lag and increased risk in gas invasion monitoring. For the 90% CH₄ + 10% CO₂ intrusive gas, the monitoring time changes in mud pits with different permeabilities. With an increase in invasion time, the mud-pit increment changes rapidly under high permeability. If 5 m³ is used as the monitoring standard, the time required to attain the monitoring value under high permeability is shorter. This is because an increase in gas invasion under high permeability results in an increase in gas content in the wellbore.

FIGURE 10

FIGURE 10. Variation in the mud pit increment with time for different gas types and permeabilities.

Figures 11, 12 show the relationship between the volume fraction of the free gas and the mass fraction of the dissolved gas for different acid gas contents and well depths. Evidently, the number of free gas integrals decreases and the corresponding dissolved gas content increases with an increase in the CO₂ content. This is because an increase in the acid gas content leads to a rapid increase in the amount of dissolved gas in the drilling fluid; consequently, more gas enters the drilling fluid, resulting in a decrease in the number of free gas integrals.

FIGURE 11

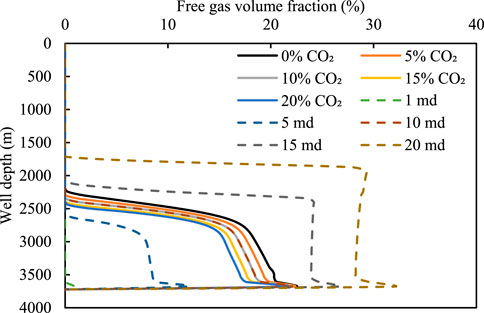
FIGURE 11. Variation in the free gas integral number with well depth for different intrusive gases and permeabilities.

FIGURE 12

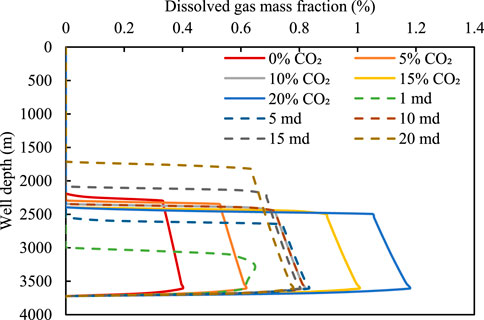
FIGURE 12. Relationship between mass fraction of dissolved gas and well depth for different intrusive gases and permeabilities.

For the 90% CH₄ + 10% CO₂ intrusive gas, the changes in the free gas and dissolved gas under different reservoir permeabilities are examined. Under a low permeability of 1 md, the amount of invading gas is small. Therefore, the gas is completely dissolved in the drilling fluid, causing the integral number of free gas to be 0 (see Figure 11). With an increase in permeability, the amount of invading gas in the wellbore increases, because the solubility of the gas in the drilling fluid is limited. The integral number of free gas increases gradually with an increase in permeability, and the position of the gas movement front is closer to the wellhead. Therefore, the dissolution of gases makes timely detection of gas invasion under low permeability difficult; therefore, the concealment is enhanced.

6 Conclusion

In this study, a multiphase flow model considering gas dissolution was established, and the auxiliary equations of gas solubility were examined based on the dynamic analysis of the migration process of an acid gas invading a wellbore. The main conclusion are as follows.

1) By optimising the interaction parameters of CH₄ and water, a new solubility model was established. The prediction accuracy of CH₄ gas solubility was maintained at 96.4%. However, the prediction error for the mixed gas composed of CO₂ and CH₄ was large, and the accuracy was less than 85%.

2) The higher the CO₂ content in the invading gas, the greater the amount of dissolved gas in the drilling fluid, the lower the volume fraction of the free gas phase in the wellbore, and the farther the gas front was from the wellhead. Furthermore, the dissolution of gas with high CO₂ content caused an increase in the time required for the mud pit increment to reach the warning or critical value.

3) The greater the permeability of the reservoir, the smaller the influence of gas dissolution. For a low permeability reservoir, the influence of gas dissolution plays a key role, resulting in a slow change in the free gas integral number in the wellbore. Moreover, the ground monitoring time was significantly increased, making gas invasion monitoring challenging.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HH: Methodology, Writing—Original draft preparation. BS: Conceptualization, Supervision, Funding acquisition. XS: Validation, Data curation, Funding acquisition. XL: Data curation. ZS: Data curation.

Funding

The author sincerely thanks the Postdoctoral innovative talents support program in China (BX2021374), and the National Natural Science Foundation—Youth Foundation (5210040269) to provide fund support.

Conflict of interest

Author ZS was employed by the company Drilling Division of China Petroleum Offshore Engineering Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Gao G, Gang W, Zhang G, He W, Cui X, Shen H, et al. Physical simulation of gas reservoir formation in the Liwan 3-1 deep-water gas field in the Baiyun sag, Pearl River Mouth Basin. Nat Gas Industry B (2015) 2(1):77–87. doi:10.1016/j.ngib.2015.02.006