Building surrogate models of nuclear density functional theory with Gaussian processes and autoencoders

From the lightest Hydrogen isotopes up to the recently synthesized Oganesson (Z = 118), it is estimated that as many as about 8,000 atomic nuclei could exist in nature. Most of these nuclei are too short-lived to be occurring on Earth, but they play an essential role in astrophysical events such as supernova explosions or neutron star mergers that are presumed to be at the origin of most heavy elements in the Universe. Understanding the structure, reactions, and decays of nuclei across the entire chart of nuclides is an enormous challenge because of the experimental difficulties in measuring properties of interest in such fleeting objects and the theoretical and computational issues of simulating strongly-interacting quantum many-body systems. Nuclear density functional theory (DFT) is a fully microscopic theoretical framework which has the potential of providing such a quantitatively accurate description of nuclear properties for every nucleus in the chart of nuclides. Thanks to high-performance computing facilities, it has already been successfully applied to predict nuclear masses, global patterns of radioactive decay like β or γ decay, and several aspects of the nuclear fission process such as, e.g., spontaneous fission half-lives. Yet, predictive simulations of nuclear spectroscopy—the low-lying excited states and transitions between them—or of nuclear fission, or the quantification of theoretical uncertainties and their propagation to basic or applied nuclear science applications, would require several orders of magnitude more calculations than currently possible. However, most of this computational effort would be spent into generating a suitable basis of DFT wavefunctions. Such a task could potentially be considerably accelerated by borrowing tools from the field of machine learning and artificial intelligence. In this paper, we review different approaches to applying supervised and unsupervised learning techniques to nuclear DFT.

1 Introduction

Predicting all the properties of every atomic nucleus in the nuclear chart, from Hydrogen all the way to superheavy elements, remains a formidable challenge. Density functional theory (DFT) offers a compelling framework to do so, since the computational cost is, in principle, nearly independent of the mass of the system Eschrig [1]. Because of our incomplete knowledge of nuclear forces and of the fact that the nucleus is a self-bound system, the implementation of DFT in nuclei is slightly different from other systems such as atoms or molecules and is often referred to as the energy density functional (EDF) formalism Schunck [2].

Simple single-reference energy density functional (SR-EDF) calculations of atomic nuclei can often be done on a laptop. However, large-scale SR-EDF computations of nuclear properties or higher-fidelity simulations based on the multi-reference (MR-EDF) framework can quickly become very expensive computationally. Examples where such computational load is needed range from microscopic fission theory Schunck and Regnier [3]; Schunck and Robledo [4] to parameter calibration and uncertainty propagation Kejzlar et al. [5]; Schunck et al. [6] to calculations at the scale of the entire chart of nuclides Erler et al. [7]; Ney et al. [8] relevant, e.g., for astrophysical simulations Mumpower et al. [9]. Many of these applications would benefit from a reliable emulator of EDF models.

It may be useful to distinguish two classes of quantities that such emulators should reproduce. What we may call “integral” quantities are quantum-mechanical observables such as, e.g., the energy, radius, or spin of the nucleus, or more complex data such as decay or capture rates. By contrast, we call “differential” quantities the basic degrees of freedom of the theoretical model. In this article, we focus on the Hartree-Fock-Bogoliubov (HFB) theory, which is both the cornerstone of the SR-EDF approach and provides the most common basis of generator states employed in MR-EDF calculations. In the HFB theory, all the degrees of freedom are encapsulated into three equivalent quantities: the quasiparticle spinors, as defined either on some spatial grid or configuration space; the full non-local density matrix ρ(rστ, r′σ′τ′) and pairing tensor κ(rστ, r′σ′τ′), where r refers to spatial coordinates, σ = ±1/2 to the spin projection and τ = ±1/2 to the isopin projection Perlińska et al. [10]; the full non-local HFB mean-field and pairing potentials, often denoted by h (rστ, r′σ′τ′) and Δ(rστ, r′σ′τ′).

Obviously, integral quantities have the clearest physical meaning and can be compared to data immediately. For this reason, they have been the focus of most of the recent efforts in applying techniques of machine learning and artificial intelligence (ML/AI) to low-energy nuclear theory, with applications ranging from mass tables Utama et al. [11]; Utama and Piekarewicz [12,13]; Niu and Liang [14]; Neufcourt et al. [15]; Lovell et al. [16]; Scamps et al. [17]; Mumpower et al. [18], β-decay rates Niu et al. [19], or fission product yields Wang et al. [20]; Lovell et al. [21]. The main limitation of this approach is that it must be repeated for every observable of interest. In addition, incorporating correlations between such observables, for example the fact that β-decay rates are strongly dependent on Q_β-values which are themselves related to nuclear masses, is not easy. This is partly because the behavior of observables such as the total energy or the total spin is often driven by underlying shell effects that can lead to very rapid variations, e.g. at a single-particle crossing. Such effects could be very hard to incorporate accurately in a statistical model of integral quantities.

This problem can in principle be solved by emulating what we called earlier differential quantities. For example, single-particle crossings might be predicted reliably with a good statistical model for the single-particle spinors themselves. In addition, since differential quantities represent, by definition, all the degrees of freedom of the SR-EDF theory, any observable of interest can be computed from them, and the correlations between these observables would be automatically reproduced. In this sense, an emulator of differential quantities is truly an emulator for the entire SR-EDF approach and can be thought of as a variant of intrusive, model-driven, model order reduction techniques discussed in Melendez et al. [22]; Giuliani et al. [23]; Bonilla et al. [24]. In the much simpler case of the Bohr collective Hamiltonian, such a strategy gave promising results Lasseri et al. [25].

The goal of this paper is precisely to explore the feasibility of training statistical models to learn the degrees of freedom of the HFB theory. We have explored two approaches: a simple one based on independent, stationary Gaussian processes and a more advanced one relying on deep neural networks with autoencoders and convolutional layers.

In Section 2, we briefly summarize the nuclear EDF formalism with Skyrme functionals with a focus on the HFB theory preserving axial symmetry. Section 3 presents the results obtained with Gaussian processes. After recalling some general notions about Gaussian processes, we analyze the results of fitting HFB potential across a two-dimensional potential energy surface in ²⁴⁰Pu. Section 4 is devoted to autoencoders. We discuss choices made both for the network architecture and for the training data set. We quantify the performance of autoencoders in reproducing canonical wavefunctions across a potential energy surface in ⁹⁸Zr and analyze the structure of the latent space.

2 Nuclear density functional theory

In very broad terms, the main assumption of density functional theory (DFT) for quantum many-body systems is that the energy of the system of interest can be expressed as a functional of the density of particles Parr and Yang [26]; Dreizler and Gross [27]; Eschrig [1]. Atomic nuclei are a somewhat special case of DFT, since the nuclear Hamiltonian is not known exactly and the nucleus is a self-bound system Engel [28]; Barnea [29]. As a result, the form of the energy density functional (EDF) is often driven by underlying models of nuclear forces, and the EDF is expressed as a function of non-local, symmetry-breaking, intrinsic densities Schunck [2]. In the single-reference EDF (SR-EDF) approach, the many-body nuclear state is approximated by a simple product state of independent particles or quasiparticles, possibly with some constraints reflecting the physics of the problem. We notate |Φ(q)⟩ such as state, with q representing a set of constraints. The multi-reference EDF (MR-EDF) approach builds a better approximation of the exact many-body state by mixing together SR-EDF states.

2.1 Energy functional

The two most basic densities needed to build accurate nuclear EDFs are the one-body density matrix ρ and the pairing tensor κ (and its complex conjugate κ*). The total energy of the nucleus is often written as

$E\left[\rho ,\kappa ,{\kappa }^{*}\right]=E_{\text{nuc}}\left[\rho \right]+E_{\text{Cou}}\left[\rho \right]+E_{\text{pair}}\left[\rho ,\kappa ,{\kappa }^{*}\right],(1)$

where E_nuc [ρ] represents the particle-hole, or mean-field, contribution to the total energy from nuclear forces, E_Cou [ρ] the same contribution from the Coulomb force, and E_pair [ρ, κ, κ*] the particle-particle contribution to the energy¹. In this work, we model the nuclear part of the EDF with a Skyrme-like term

$E_{\text{nuc}}\left[\rho \right]=\sum _{t=\mathrm{0,1}}\int {\mathrm{d}}^3\mathit{r}{\chi }_t\left(\mathit{r}\right),(2)$

which includes the kinetic energy term and reads generically

${\chi }_t\left(\mathit{r}\right)=C_t^{\rho \rho }{\rho }_t^2+C_t^{\rho \tau }{\rho }_t{\tau }_t+C_t^{JJ}{\mathsf{J}}_t^2+C_t^{\rho \mathrm{\Delta }\rho }{\rho }_t\mathrm{\Delta }{\rho }_t+C_t^{\rho \nabla J}{\rho }_t\mathbf{\nabla }\cdot {\mathit{J}}_t.(3)$

In this expression, the index t refers to the isoscalar (t = 0) or isovector (t = 1) channel and the terms $C_t^{u{u}^{\prime }}$ are the coupling constants associated with the energy functional. The particle density ρ_t(r), kinetic energy density τ_t(r), spin-current tensor ${\mathsf{J}}_t(\mathit{r})$, and vector density J_t(r) are all derived from the full one-body, non-local density ρ(rστ, r′σ′τ′) where r are spatial coordinates, σ is the intrinsic spin projection, σ = ±1/2, and τ = ±1/2 is the isospin projection; see Engel et al. [30]; Dobaczewski and Dudek [31]; Bender et al. [32]; Perlińska et al. [10]; Lesinski et al. [33] for their actual definition. Since we do not consider any proton-neutron mixing, all densities are diagonal in isospin space. The two remaining terms in Eq. 1 are treated in exactly the same way as in Schunck et al. [34]. In particular, the pairing energy is derived from a surface-volume density-dependent pairing force

$V^{\left(\tau \right)}\left(\mathit{r},{\mathit{r}}^{\prime }\right)=V_0^{(\tau )}\left[1-\frac{1}{2}\frac{\rho \left(\mathit{r}\right)}{{\rho }_c}\right]\delta \left(\mathit{r}-{\mathit{r}}^{\prime }\right),(4)$

where ρ_c = 0.16 fm⁻³ is the saturation density of nuclear matter.

2.2 Hartree-Fock-Bogoliubov theory

The actual densities in (3) are obtained by solving the Hartree-Fock-Bogoliubov (HFB) equation, which derives from applying a variational principle and imposing that the energy be minimal under variations of the densities Schunck [2]. The HFB equation is most commonly solved in the form of a non-linear eigenvalue problem. The eigenfunctions define the quasiparticle (q.p.) spinors. Without proton-neutron mixing, we can treat neutrons and protons separately. Therefore, for any one type of particles, the HFB equation giving the μ^th eigenstate reads in coordinate space Dobaczewski et al. [35].

$\int {\mathrm{d}}^3{\mathit{r}}^{\prime }\sum _{{\sigma }^{\prime }}\left(\begin{array}{cc}\hfill h\left(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)-\lambda {\delta }_{\sigma {\sigma }^{\prime }}\hfill & \hfill \tilde{h}\left(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)\hfill \\ \hfill {\tilde{h}}^{*}\left(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)\hfill & \hfill -h\left(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)+\lambda {\delta }_{\sigma {\sigma }^{\prime }}\hfill \end{array}\right)\left(\begin{array}{c}\hfill U\left(E_{\mu },{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)\hfill \\ \hfill V\left(E_{\mu },{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)\hfill \end{array}\right)=E_{\mu }\left(\begin{array}{c}\hfill U\left(E_{\mu },\mathit{r}\sigma \right)\hfill \\ \hfill V\left(E_{\mu },\mathit{r}\sigma \right)\hfill \end{array}\right),(5)$

where h (rσ, r′σ′) is the mean field, $\tilde{h}(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime })$ the pairing field² and λ the Fermi energy. Such an eigenvalue problem must be solved for protons and for neutrons.

For the case of Skyrme energy functionals and zero-range pairing functionals, both the mean field h and pairing field $\tilde{h}$ become semi-local functions of r (semi-local refers to the fact that these potentials involve differential operators). We refer to Vautherin and Brink [36]; Engel et al. [30] for an outline of the derivations leading to the expressions of the mean field in the case of Skyrme functionals and to, e.g., Dobaczewski and Dudek [37]; Bender et al. [38]; Hellemans et al. [39]; Ryssens et al. [40] for the expression of the mean field in terms of coupling constants rather than the parameters of the Skyrme potential. In the following, we simply recall the essential formulas needed in the rest of the manuscript.

Expression 5 is written in coordinate space. In configuration space, i.e., when the q.p. spinors are expanded on a suitable basis of the single-particle (s.p.) Hilbert space, the same equation becomes a non-linear eigenvalue problem that can be written as

$\left(\begin{array}{cc}\hfill h-\lambda \hfill & \hfill \tilde{h}\hfill \\ \hfill {\tilde{h}}^{*}\hfill & \hfill -h^{*}+\lambda \hfill \end{array}\right)\left(\begin{array}{cc}\hfill U\hfill & \hfill V^{*}\hfill \\ \hfill V\hfill & \hfill U^{*}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill U\hfill & \hfill V^{*}\hfill \\ \hfill V\hfill & \hfill U^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill -E\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill E\hfill \end{array}\right),(6)$

where h, $\tilde{h}$, U and V are now N_basis × N_basis matrices, with N_basis the number of basis states. Eigenvalues are collected in the diagonal N_basis × N_basis matrix E. The set of all eigenvectors define the Bogoliubov matrix,

$\mathcal{W}=\left(\begin{array}{cc}\hfill U\hfill & \hfill V^{*}\hfill \\ \hfill V\hfill & \hfill U^{*}\hfill \end{array}\right),(7)$

which is unitary: $\mathcal{W}{\mathcal{W}}^{†}={\mathcal{W}}^{†}\mathcal{W}=1$. Details about the HFB theory can be found in the standard references Valatin [41]; Mang [42]; Blaizot and Ripka [43]; Ring and Schuck [44].

2.3 Mean-field and pairing potentials

The mean fields are obtained by functional differentiation of the scalar-isoscalar energy functional (1) with respect to all relevant isoscalar or isovector densities, ρ₀, ρ₁, τ₀, etc. For the case of a standard Skyrme EDF when time-reversal symmetry is conserved, the corresponding mean-field potentials in the isoscalar-isovector representation become semi-local Dobaczewski and Dudek [37,45]; Stoitsov et al. [46]; Hellemans et al. [39].

$h_t\left(\mathit{r}\right)=-\mathbf{\nabla }{M}_t^{\ast }\left(\mathit{r}\right)\mathbf{\nabla }+U_t\left(\mathit{r}\right)+\frac{1}{2i}\sum _{\mu \nu }\left({\nabla }_{\mu }{\sigma }_{\nu }{B}_{t,\mu \nu }\left(\mathit{r}\right)+B_{t,\mu \nu }\left(\mathit{r}\right){\nabla }_{\mu }{\sigma }_{\nu }\right),(8)$

where, as before, t = 0, 1 refers to the isoscalar or isovector channel and the various contributions are.

$M_t\left(\mathit{r}\right)=\frac{{\hslash }^2}{2m}+C_t^{\rho \tau }{\rho }_t,(\mathrm{9a})$

$U_t\left(\mathit{r}\right)=2C_t^{\rho \rho }{\rho }_t+C_t^{\rho \tau }{\tau }_t+2C_t^{\rho \mathrm{\Delta }\rho }\mathrm{\Delta }{\rho }_t+C_t^{\rho \nabla J}\mathbf{\nabla }\cdot {\mathit{J}}_t+U_t^{\left(\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{r}\right)},(\mathrm{9b})$

$B_{t,\mu \nu }\left(\mathit{r}\right)=2C_t^{\rho J}{J}_{t,\mu \nu }-C_t^{\rho \mathrm{\Delta }J}{\nabla }_{\mu }{\rho }_{t,\nu }.(\mathrm{9c})$

In these expressions, μ, ν label spatial coordinates and σ is the vector of Pauli matrices in the chosen coordinate system. For example, in Cartesian coordinates, μ, ν ≡ x, y, z and σ = (σ_x, σ_y, σ_z). The term $U_t^{(\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{r})}$ is the rearrangement potential originating from the density-dependent part of the energy. The resulting isoscalar and isovector mean-field and pairing potentials can then recombined to give the neutron and proton potentials,

$h^{\left(n\right)}=h_0+h_1,h^{\left(p\right)}=h_0-h_1.(10)$

Note that the full proton potential should also contain the contribution from the Coulomb potential.

The pairing field is obtained by functional differentiation of the same energy functional (1), this time with respect to the pairing density. As a result, one can show that it is simply given by

${\tilde{h}}^{\left(\tau \right)}\left(\mathit{r}\right)=V_0^{(\tau )}\left[1-\frac{1}{2}\frac{{\rho }_0\left(\mathit{r}\right)}{{\rho }_c}\right]{\tilde{\rho }}^{\left(\tau \right)}\left(\mathit{r}\right).(11)$

2.4 Collective space

Nuclear fission or nuclear shape coexistence are two prominent examples of large-amplitude collective motion of nuclei Schunck and Regnier [3]; Heyde and Wood [47]. Such phenomena can be accurately described within nuclear DFT by introducing a small-dimensional collective manifold, e.g., associated with the nuclear shape, where we assume the nuclear dynamics is confined Nakatsukasa et al. [48]; Schunck [2]. The generator coordinate method (GCM) and its time-dependent extension (TDGCM) provide quantum-mechanical equations of motion for such collective dynamics Griffin and Wheeler [49]; Wa Wong [50]; Reinhard and Goeke [51]; Bender et al. [32]; Verriere and Regnier [52]. In the GCM, the HFB solutions are generator states, i.e., they serve as a basis in which the nuclear many-body state is expanded. The choice of the collective manifold, that is, of the collective variables, depends on the problem at hand. For shape coexistence or fission, these variables typically correspond to the expectation value of multipole moment operators on the HFB state. A pre-calculated set of HFB states with different values for the collective variables defines a potential energy surface (PES).

In practice, PES are obtained by adding constraints to the solutions of the HFB equation. This is achieved by introducing a set of constraining operators ${\widehat{Q}}_a$ capturing the physics of the problem at hand. The set of all such constraints q ≡ (q₁, …, q_N) defines a point in the PES. In this work, our goal is to design emulators capable of reproducing the HFB solutions at any given point q of a PES. Throughout this article, we consider exclusively two-dimensional collective spaces spanned by the expectation values of the axial quadrupole ${\widehat{Q}}_{20}$ and axial octupole ${\widehat{Q}}_{30}$ moment operators. In the presence of constraints, the mean-field potential in the HFB equation is modified as follows

$h\left(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)-\lambda {\delta }_{\sigma {\sigma }^{\prime }}\to h\left(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime }\right)-\left(\lambda +\sum _a{\lambda }_a{Q}_a\left(\mathit{r}\right)\right){\delta }_{\sigma {\sigma }^{\prime }}.(12)$

As is well known, the Fermi energies play in fact the role of the Lagrange parameters λ_a for the constraints on particle number. When performing calculations with constraints on the octupole moment, it is also important to fix the position of the center of mass. This is typically done by adding a constraint on the dipole moment ${\widehat{Q}}_{10}$. In the following, we note q_λμ the expectation value of the operator ${\widehat{Q}}_{\lambda \mu }$ on the quasiparticle vacuum, $q_{\lambda \mu }=⟨\mathrm{\Phi }(\mathit{q})|{\widehat{Q}}_{\lambda \mu }|\mathrm{\Phi }(\mathit{q})⟩$.

Potential energy surfaces are a very important ingredient in a very popular approximation to the GCM called the Gaussian overlap approximation (GOA) Brink and Weiguny [53]; Onishi and Une [54]; Une et al. [55]. By assuming, among other things, that the overlap between two HFB states with different collective variables q and q′ is approximately Gaussian, the GOA allows turning the integro-differential Hill-Wheeler-Griffin equation of the GCM into a much more tractable Schrödinger-like equation. The time-dependent version of this equation reads as Verriere and Regnier [52].

$i\hslash \frac{\partial }{\partial t}g\left(\mathit{q},t\right)=\left[-\frac{{\hslash }^2}{2}\sum _{\alpha \beta }\frac{\partial }{\partial q_{\alpha }}{B}_{\alpha \beta }\left(\mathit{q}\right)\frac{\partial }{\partial q_{\beta }}+V\left(\mathit{q}\right)\right]g\left(\mathit{q},t\right),(13)$

where the probability to be at point q of the collective space at time t is given by |g (q, t)|², V(q) is the actual PES, typically the HFB energy as a function of the collective variables q (sometimes supplemented by some zero-point energy correction) and B_αβ(q) the collective inertia tensor. In (13), indices α and β run from 1 to the number N_col of collective variables. While the HFB energy often varies smoothly with respect to the collective variables, the collective inertia tensor can exhibit very rapid variations near level crossings.

2.5 Canonical basis

The Bloch-Messiah-Zumino theorem states that the Bogoliubov matrix $\mathcal{W}$ of (7) can be decomposed into a product of three matrices Ring and Schuck [44]; Bloch and Messiah [56]; Zumino [57].

$\mathcal{W}=\mathcal{D}\bar{\mathcal{W}}\mathcal{C}=\left(\begin{array}{cc}\hfill D\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill D^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill \bar{U}\hfill & \hfill \bar{V}\hfill \\ \hfill \bar{V}\hfill & \hfill \bar{U}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill C\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill C^{*}\hfill \end{array}\right),(14)$

where D and C are unitary matrices. The matrices $\bar{U}$ and $\bar{V}$ take the very simple canonical form

$\bar{U}=\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill u_k\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill u_{\bar{k}}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill \end{array}\right),\bar{V}=\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill v_k\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill v_{\bar{k}}\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill \end{array}\right).(15)$

Starting from an arbitrary s.p. basis $(\widehat{c},{\widehat{c}}^{†})$ of the Hilbert space, the transformation characterized by the matrix $\mathcal{D}$ leads to a new basis $(\widehat{a},{\widehat{a}}^{†})$ that diagonalizes the density matrix ρ and puts the pairing tensor κ into the canonical form similar to that of $\bar{V}$. This new basis is called the canonical basis of the HFB theory. Properties of the canonical basis are discussed in details in the literature; see, e.g., Ring and Schuck [44]; Schunck [2]. In the HFB theory, quasiparticles are superpositions of particle operators ${\widehat{a}}^{†}$ and hole operators $\widehat{a}$. Thus, the canonical basis is transformed according to the matrix $\bar{\mathcal{W}}$ to obtain a set of quasiparticle operators $(\widehat{\alpha },{\widehat{\alpha }}^{†})$. There is another transformation of these operators associated with the matrix $\mathcal{C}$. However, the most important property for the purpose of this paper is that physical observables associated with HFB solutions do not depend on that last transformation.

In addition to simplifying the calculation of many-body observables, the canonical basis is also computationally less expensive than the full Bogoliubov basis³. As an illustration, let us take the example of the local density ρ(r). Assuming the s.p. basis $(\widehat{c},{\widehat{c}}^{†})$ is represented by the basis functions ${\{{\psi }_n(\mathit{r},\sigma )\}}_{n\in \mathbb{N}}$, the local density (for isospin τ) is obtained from the matrix of the Bogoliubov transformation by

$\rho \left(\mathit{r}\right)=\sum _{\sigma }\sum _{\mu }\sum _{mn}{V}_{m\mu }^{*}{V}_{n\mu }{\psi }_m\left(\mathit{r},\sigma \right){\psi }_n^{*}\left(\mathit{r},\sigma \right).(16)$

Notwithstanding the constraints imposed by the orthonormality of the q.p. spinors, the number of independent parameters in this expression approximately scales like $2\times N_{\text{basis}}^2\times N_{\text{qp}}\times N_{\mathbf{r}}$, where N_basis is the size of the s.p. basis, N_qp the number of q.p. states μ and N_r the total number of points in the spatial grid r (which depends on the symmetries imposed). In the canonical basis, and assuming that the state ${\widehat{a}}_{\mu }|0\rangle$ is associated with the wavefunction φ_μ(r, σ), the same object is represented by

$\rho \left(\mathit{r}\right)=\sum _{\sigma }\sum _{\mu }{v}_{\mu }^2|{\phi }_{\mu }\left(\mathit{r},\sigma \right){|}^2.(17)$

The number of data points now scales like 2 × N_qp × N_r + N_qp, or about $N_{\text{basis}}^2$ smaller than before. For calculations with N_basis ≈ 1,000 the compression enabled by the canonical basis is of the order of 10⁶.

2.6 Harmonic oscillator basis

All calculations in this article were performed with the HFBTHO code Marević et al. [58]. Recall that HFBTHO works by expanding the solutions on the axially-deformed harmonic oscillator basis Stoitsov et al. [46]. Specifically, the HO basis functions are written

${\psi }_{\mathit{n}}\left(\mathit{r},\sigma \right)={\psi }_{n_r}^{\mathrm{\Lambda }}\left(r\right){\psi }_{n_z}\left(z\right)\frac{e^{i\mathrm{\Lambda }\theta }}{\sqrt{2\pi }}\chi \mathrm{\Sigma }\left(\sigma \right),(18)$

where n ≡ (n_r, n_z, Λ, Ω = Λ ±Σ) are the quantum numbers labeling basis states and.

${\psi }_{n_r}^{\mathrm{\Lambda }}\left(r\right)=N_{n_r}{\beta }_{\perp }\sqrt{2}{\eta }^{|\mathrm{\Lambda }|/2}{e}^{-\eta /2}{L}_{n_r}^{|\mathrm{\Lambda }|}\left(\eta \right),(\mathrm{19a})$

${\psi }_{n_z}\left(z\right)=N_{n_z}\sqrt{{\beta }_z}{e}^{-{\xi }^2/2}{H}_{n_z}\left(\xi \right),(\mathrm{19b})$

With $\eta ={\beta }_{\perp }^2{r}^2$ and ξ = β_zz dimensionless variables, $L_{n_r}^{|\mathrm{\Lambda }|}$ the associated Laguerre polynomials of order n_r and $H_{n_z}$ the Hermite polynomial of order n_z. The oscillator scaling factors β_⊥ and β_z are the inverse of the oscillator lengths, i.e., β_z = 1/b_z.

All integrations are performed by Gauss quadrature, namely Gauss-Hermite for integrations along the ξ-axis of the intrinsic reference frame and Gauss-Laguerre for integrations along the perpendicular direction characterized by the variable η. In the following, we note N_z the number of Gauss-Hermite nodes and N_⊥ the number of Gauss-Laguerre nodes.

3 Supervised learning with Gaussian processes

Gaussian processes (GPs) are a simple yet versatile tool for regression that has found many applications in low-energy nuclear theory over the past few years, from determining the nuclear equation of state Drischler et al. [59], quantifying the error of nuclear cross sections calculations Kravvaris et al. [60]; Acharya and Bacca [61] to modeling of neutron stars Pastore et al. [62]. In the context of nuclear DFT, they were applied to build emulators of χ₂ objective functions in the UNEDF project Kortelainen et al. [63–65]; Higdon et al. [66]; McDonnell et al. [67]; Schunck et al. [6], of nuclear mass models Neufcourt et al. [15,68–70], or of potential energy surfaces in actinides Schunck et al. [34]. In this section, we test the ability of GPs to learn directly the HFB potentials across a large, two-dimensional collective space.

3.1 Gaussian processes

Gaussian processes are commonly thought of as the generalization of normally-distributed random variables (Gaussian distribution) to functions. There exists a considerable field of applications for GPs and we refer to the reference textbook by Rasmussen and Williams for a comprehensive review of the formalism and applications of GPs Rasmussen and Williams [71]. For the purpose of this work, we are only interested in the ability of GPs to be used as a regression analysis tool and we very briefly outline below some of the basic assumptions and formulas.

We assume that we have a dataset of observations ${\{\mathbf{y}=y_i\}}_{i=1,\dots ,n}$ and that these data represent n realizations of

$y=f\left(\mathbf{x}\right)+ϵ,(20)$

where f: x↦f(x) is the unknown function we are seeking to learn from the data. Saying that a function f is a Gaussian process means that every finite collection of function values f = (f (x₁), …, f (x_p)) follows a p-dimensional multivariate normal distribution. In other words, we assume that the unknown function f follows a normal distribution in ‘function space’. This is denoted by

$f\left(\mathbf{x}\right)\sim \mathcal{GP}\left(m\left(\mathbf{x}\right),k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)\right),(21)$

where m: x↦m(x) is the mean function and k: (x, x′)↦k (x, x′) the covariance function, which is nothing but the generalization to functions of the standard deviation,

$k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)=\mathbb{E}\left[\left(f\left(\mathbf{x}\right)-m\left(\mathbf{x}\right)\right)\left(f\left({\mathbf{x}}^{\prime }\right)-m\left({\mathbf{x}}^{\prime }\right)\right)\right].(22)$

Thanks to the properties of Gaussian functions, the mean and covariance functions have analytical expressions as a function of the test data y and covariance k; see Eqs (2.25)-(2.26) in Rasmussen and Williams [71].

The covariance function is the central object in GP regression. It is typically parametrized both with a functional form and with a set of free parameters called hyperparameters. The hyperparameters are determined from the observed data by maximizing the likelihood function. In our tests, the covariance matrix is described by a standard Matérn 5/2 kernel,

$k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)=\left(1+\frac{\sqrt{5}}{\ell }\Vert \mathbf{x}-{\mathbf{x}}^{\prime }\Vert +\frac{5}{3{\ell }^2}\Vert \mathbf{x}-{\mathbf{x}}^{\prime }{\Vert }^2\right)\exp \left(-\frac{\sqrt{5}}{\ell }\Vert \mathbf{x}-{\mathbf{x}}^{\prime }\Vert \right),(23)$

where ℓ is the length-scale that characterizes correlations between values of the data at different locations. The length-scale is a hyper-parameter that is optimized in the training phase of the Gaussian process. In this work, we only considered stationary GPs: the correlation between data points x and x′ only depends on the distance ‖x − x′‖ between these points, not on their actual value.

3.2 Study case

3.2.1 HFB potentials

Section 2.2 showed that the HFB mean-field potential involves several differential operators. When the HFB matrix is constructed by computing expectation values of the HFB potential on basis functions, differentiation is carried over to the basis functions and computed analytically—one of the many advantages of working with the HO basis. In practice, this means that the elements of the HFB matrix are computed by multiplying spatial kernels with different objects representing either the original HO functions or their derivatives. This means that we cannot consider a single emulator for the entire HFB potential. Instead, we have to build several different ones for each of its components: the central potential U (derivative of the EDF with respect to ρ), the r- and z-derivatives of the effective mass M* (derivative with respect to the kinetic density τ), the r- and z-derivatives of the spin-orbit potential W, and the pairing field $\tilde{h}$. There are six such functions for neutrons and another six for protons. We denote this set of twelve functions as ${\{f_i\}}_{i=1,\dots ,12}$.

At any given point q of the collective space, these functions are all local, scalar functions of η and ξ, f_i(q) ≡ f_i: (η, ξ)↦f_i (η, ξ; q) where (η, ξ) are the nodes of the Gauss-Laguerre and Gauss-Hermite quadrature grid. We note generically f_ik(q) the value at point k of the quadrature grid (linearized) of the sample at point q of the function f_i. When fitting Gaussian process to reproduce mean-field and pairing potentials, we consider a quadrature grid of N_z × N_⊥ = 3,200 points. Our goal is thus to build 3,200 different emulators, one for each point k of that grid, for each of the 12 local functions characterizing the mean-field and pairing potentials. This gives a grand total of 38,400 emulators to build. While this number is large, it is still easily manageable on standard computers. It is also several orders of magnitude smaller than emulating the full set of quasiparticle spinors, as we will see in the next section.

In addition, the value of all the Lagrange parameters used to set the constraints must also be included in the list of data points. In our case, we have 5 of them: the two Fermi energies λ_n and λ_p and the three constraints on the value of the dipole, quadrupole and octupole moments, λ₁, λ₂ and λ₃, respectively. Finally, we also fit the expectation value of the three constraints on ${\widehat{Q}}_{10}$, ${\widehat{Q}}_{20}$ and ${\widehat{Q}}_{30}$. We thus have a grand total of 38,408 functions of q to emulate.

3.2.2 Training data and fitting procedure

We show in Figure 1 the potential energy surface that we are trying to reconstruct. This PES is for the ²⁴⁰Pu nucleus and was generated with the SkM* parameterization of the Skyrme energy functional Bartel et al. [72]. The pairing channel is described with the zero-range, density-dependent pairing force of Eq. 4 that has exactly the same characteristics as in Schunck et al. [73].

FIGURE 1

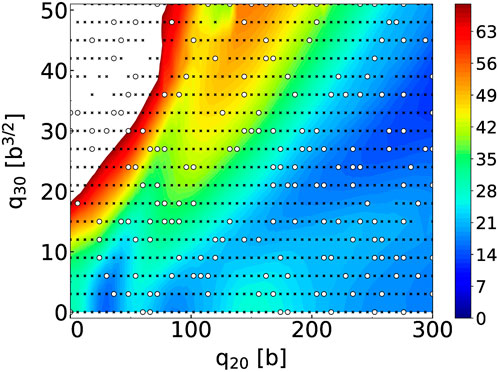
FIGURE 1. Potential energy surface of ²⁴⁰Pu with the SkM* EDF for the grid (q₂₀, q₃₀) ∈ [0 b, 300 b] × [0 b^3/2, 51 b^3/2] with steps δq₂₀ = 6 b and δq₃₀ = 3 b^3/2. The black crosses are the training points, the white circles the validation points. Energies indicated by the color bar are in MeV relatively to −1820 MeV.

We imposed constraints on the axial quadrupole and octupole moments such that: 0 b ≤ q₂₀ ≤ 300 b and 0 b^3/2 ≤ q₃₀ ≤ 51 b^3/2 with steps of δq₂₀ = 6 b and δq₃₀ = 3 b^3/2, respectively. The full PES should thus contain 918 collective points. In practice, we obtained N_p = 887 fully converged solutions. Calculations were performed with the HFBTHO solver by expanding the solutions on the harmonic oscillator basis with N_max = 28 deformed shells and a truncation in the number of states of N_basis = 1,000. At each point of the PES, the frequency ω₀ and deformation β₂ of the HO basis are set according to the empirical formulas given in Schunck et al. [73]. Following standard practice, we divided the full N_p = 887 dataset of points into a training (80% of the points) and validation (20% of the points) set. The selection was done randomly and resulted in N_train = 709 training points and N_valid. = 178 validation points. The training points are marked as small black crosses in Figure 1 while the validation points are marked as larger white circles.

Based on the discussion in Section 3.2.1, we fit a Gaussian process to each of the 38,408 variables needed to characterize completely the HFB matrix. Since we work in a two-dimensional collective space, we have two features and the training data is represented by a two-dimensional array X of dimension (n_samples, n_features) with n_samples = N_p and n_features = 2. The target values Y (= the value at point k on the quadrature grid of any of the functions f_i) are contained in a one-dimensional array of size N_p. Prior to the fit, the data is normalized between 0 and 1. The GP is based on a standard Matérn kernel with ν = 2.5 and length-scale ℓ. In practice, we use different length-scales for the q₂₀ and q₃₀ directions so that ℓ = ℓ is a vector. We initialized these values at the spacing of the grid ℓ = (δq₂₀, δq₃₀). We added a small amount of white noise to the Matérn kernel to account for the global noise level of the data.

3.2.3 Performance

Once the GP has been fitted on the training data, we can estimate its performance on the validation data. For each of the N_valid. = 178 validation points, we used the GP-fitted HFB potentials to perform a single iteration of the HFB self-consistent loop and extract various observables from this single iteration. Figure 2 focuses on the total HFB energy and the zero-point energy correction ɛ₀. Together, these two quantities define the collective potential energy in the collective Hamiltonian (13) of the GCM. The left panel of the figure shows the histogram of the error $\mathrm{\Delta }E=E_{\text{HFB}}^{(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e})}-E_{\text{HFB}}^{(\mathrm{G}\mathrm{P})}$, where $E_{\text{HFB}}^{(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e})}$ is the result from the fully converged HFB solution and $E_{\text{HFB}}^{(\mathrm{G}\mathrm{P})}$ is the value predicted by the Gaussian process. The bin size is 100 keV. Overall, we find that the large majority of the error is within ±200 keV. This is a rather good result considering the span of the PES and the fact that basis truncation errors can easily amount to a few MeV Schunck [74].

FIGURE 2

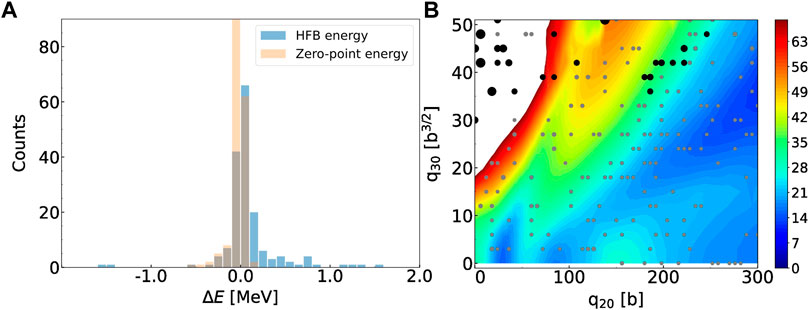
FIGURE 2. (A): Histogram of the error on the GP-predicted total HFB energy and zero-point energy correction across the validation points. Bin size is 100 keV. (B): Size of the error on the GP-predicted total HFB energy across the validation set. Gray circles have an error lower than 500 keV and the size of the markers correspond to energy bins of 100 keV. Black circles have an error greater than 500 keV and are binned by 400 keV units. Energies indicated by the color bar are in MeV relatively to −1820 MeV.

To gain additional insight, we draw in the right panel of Figure 2 each of the validation points with a marker, the size of which is proportional to the error of the prediction. To further distinguish between most points and the few outliers, we show in gray the points for which the absolute value of the error is less than 500 keV and in black the points for which it is greater than 500 keV. For the gray points, we use 5 different marker sizes corresponding to energy bins of 100 keV: the smaller grey symbol corresponds to an error smaller than 100 keV, the larger one between 400 and 500 keV. Similarly, the larger black circles have all an error greater than 500 keV and are ordered by bins of 400 keV (there are only two points for which the error is larger than 4 MeV). Interestingly, most of the larger errors are concentrated in the region of small elongation q₂₀ < 80 b and high asymmetry q₃₀ > 30 b^3/2. This region of the collective space is very high in energy (more than 100 MeV above the ground state) and plays no role in the collective dynamics.

Note that the expectation values of the multipole moments themselves are not reproduced exactly by the GP: strictly speaking, the contour plot in the right panel of Figure 2 is drawn based on the requested values of the constraints, not their actual values as obtained by solving the HFB equation once with the reconstructed potentials. The histogram in the left panel of Figure 3 quantifies this discrepancy. It shows the absolute error $\mathrm{\Delta }{q}_{\lambda \mu }=q_{\lambda \mu }^{(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e})}-q_{\lambda \mu }^{(\mathrm{G}\mathrm{P})}$, where $q_{\lambda \mu }^{(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e})}$ is the result from the fully converged HFB solution and $q_{\lambda \mu }^{(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e})}$ is the value predicted by the Gaussian process. On average, the error remains within ±0.5 b for q₂₀ and ±0.5 b^3/2 for q₃₀, which is significantly smaller than the mesh size.

FIGURE 3

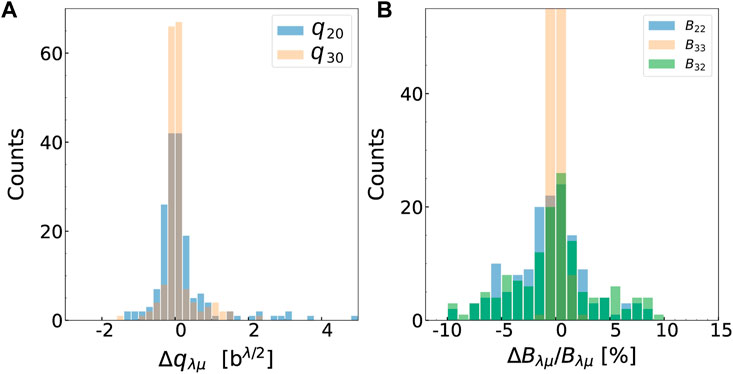
FIGURE 3. (A): Histogram of the error on the GP-predicted values of the multipole moments. The bin size is 0.2 b^λ/2 with λ = 2 (quadrupole moment) or λ = 3 (octupole moment). (B): Histogram of the relative error, in percents, on the GP-predicted values of the components of the collective inertia tensor. The bin size is 1, corresponding to 1% relative errors.

The collective potential energy is only one of the two ingredients used to simulate fission dynamics. As mentioned in Section 2.4, see Eq. 13, the collective inertia tensor is another essential quantity Schunck and Robledo [4]; Schunck and Regnier [3]. In this work, we computed the collective inertia at the perturbative cranking approximation Schunck and Robledo [4]. Since we work in two-dimensional collective spaces, the collective inertia tensor $\mathsf{B}$ has three independent components, hereafter labeled B₂₂, B₃₃ and B₃₂ = B₂₃. Figure 3 shows the relative error on these quantities, defined as $ϵ=(B_{\lambda {\lambda }^{\prime }}^{(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e})}-B_{\lambda {\lambda }^{\prime }}^{(\mathrm{G}\mathrm{P})})/B_{\lambda {\lambda }^{\prime }}^{(\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e})}$. Overall, the error is more spread than for the energy but rarely exceeds five percents⁴.

Both the total energy and the collective mass tensor are computed from the HFB solutions. However, since the GP fit is performed directly on the mean-field and pairing potentials, one can analyze the error on these quantities directly. In Figure 4, we consider two different configurations. The configuration ${\mathcal{C}}_1=(q_{20},q_{30})=(198\mathrm{b},30{\mathrm{b}}^{3/2})$ is very well reproduced by the GP with an error in the HFB energy of 4.4 keV and a relative error on B₂₂ of -0.43% and B₂₂ of -0.84% only. In contrast, the configuration ${\mathcal{C}}_2=(q_{20},q_{30})=(138\mathrm{b},51{\mathrm{b}}^{3/2})$ is one of the worst possible cases, with a total error on the HFB energy of 9.0 MeV and relative errors on B₂₂ of -71.0% and B₂₂ of -13.7%. For each of these two configurations, we look at the central part of the mean-field potential for protons, the term U_p = U₀ − U₁ of (9b). The left side of Figure 4 shows, respectively, the actual value of U_p(r, z) across the quadrature grid (top panel) and the difference between the true value and the GP fit (bottom panel) for the configuration ${\mathcal{C}}_1$. The right side of the figure shows the same quantity for the configuration ${\mathcal{C}}_2$. In all four plots, the energy scale is in MeV; it is identical for the two panels at the top, but it is different for the two at the bottom.

FIGURE 4

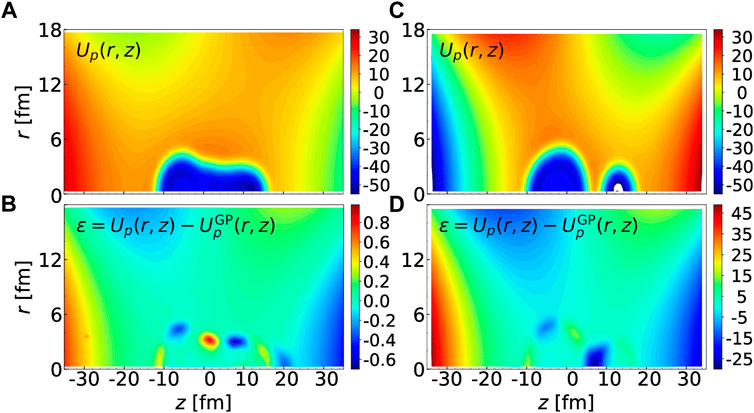
FIGURE 4. (A): Central part of the mean-field potential for protons, U_p(r, z) for the configuration (q₂₀, q₃₀) = (198 b, 30 b^3/2); (B): Error in the GP fit for that same configuration. (C): Central part of the mean-field potential for protons, U_p(r, z) for the configuration (q₂₀, q₃₀) = (138 b, 51 b^3/2); (D): Error in the GP fit for that same configuration. In all figures, the energy given by the error bar is in MeV. Note the much smaller energy scale for the bottom left panel.

We see that for the “good” configuration ${\mathcal{C}}_1$, the error is between −0.6 MeV and 1.0 MeV but is mostly occurring at the surface of the nucleus and at the edges of the domain. Conversely, the “bad” configuration ${\mathcal{C}}_2$ actually corresponds to a scissioned configuration: the mean-field potential (upper right panel) shows two different regions corresponding to fully separated fragments⁵. Such a geometric configuration is very different from the rest of the potential energy surface shown in Figure 1, which contains mostly non-scissioned configurations. As a result, the error in the GP fit is very large in the region between the two fragments since it predicts this configuration to be non-scissioned. Note that in HFBTHO, the representation of the potentials on the quadrature points does not contain the exponential factor $\exp (-{\beta }_z{\xi }^2)\exp (-{\beta }_{\perp }^2{\xi }^2)$ which is factored in the quadrature weights. Therefore, the large errors at the edges of the domain, for z ≈ − 30 fm, z ≈ + 30 fm or r ≈ 18 fm are not significant since they are entirely absorbed by this exponential factor.

Overall, Gaussian processes seem to provide an efficient way to predict HFB solutions across potential energy surfaces. Their primary advantage is that they are very simple to implement, with several popular programming environments offering ready-to-use, full GP packages, and very fast to train (a few minutes at most for a few hundreds of samples). As our examples suggest, GPs are very good at interpolating across a domain where solutions behave smoothly. In the case of PES, this implies that the training data must not contain, e.g., scissioned and non-scissioned configurations. More generally, it should not feature too many discontinuities Dubray and Regnier [75]. When these conditions are met, GPs can be used to quickly and precisely densify a PES, e.g., to obtain more precise fission paths in spontaneous fission half-live calculations Sadhukhan [76].

However, Gaussian processes are intrinsically limited. In our example, we treated the value of each potential at each point of the quadrature mesh as an independent GP. Yet, such data are in reality heavily correlated. To incorporate such correlations requires generalizing from scalar GPs to vector, or multi-output GPs Bruinsma et al. [77]. In our example of nuclear potentials, the output space would be ${\mathbb{R}}^D$ with D ≈ 32,008. An additional difficulty is related to choosing the kernel that is appropriate to describe the correlated data and identifying what the prior distribution should be Álvarez et al. [78]. Yet another deficiency of standard Gaussian processes, especially in contrast to the deep-learning techniques discussed below, is that they are not capable to learn a latent representation of the data. For these reasons, we consider such techniques helpful mostly to densify existing potential energy surfaces.

4 Deep learning with autoencoders

Even though self-consistent potential energy surfaces are key ingredients in the microscopic theory of nuclear fission Bender et al. [79], we must overcome two significant obstacles to generate reliable and complete PES. First, the computational cost of nuclear DFT limits the actual number of single-particle d.o.f. When solving the HFB equation with basis-expansion methods, for example, the basis must be truncated (up to a maximum of about a few thousand states, typically), making the results strongly basis-dependent Schunck [80]; even in mesh-based methods, the size of the box and lattice spacing also induce truncation effects Ryssens et al. [81]; Jin et al. [82]. Most importantly, the number of collective variables that can be included in the PES is also limited: in spontaneous fission calculations, which do not require a description of the PES up to scission, up to N_col = 5 collective variables have been incorporated Sadhukhan [76]; when simulating the PES up to scission, only 2 collective variables are included with only rare attempts to go beyondRegnier et al. [83]; Zhao et al. [84]. As a consequence, the combination of heavily-truncated collective spaces and the adiabatic hypothesis inherent to such approaches leads to missing regions in the PES and spurious connections between distinct channels with unknown effects on physics predictions Dubray and Regnier [75]; Lau et al. [85]. The field of deep learning may offer an appealing solution to this problem by allowing the construction of low-dimensional and continuous surrogate representations of potential energy surfaces. In the following, we test the ability of autoencoders—a particular class of deep neural networks—to generate accurate low-dimensional representations of HFB solutions.

4.1 Network architecture

The term ‘deep learning’ encompasses many different types of mathematical and computational techniques that are almost always tailored to specific applications. In this section, we discuss some of the specific features of the data we seek to encode in a low-dimensional representation, which in turn help constrain the network architecture. The definition of a proper loss function adapted to quantum-mechanical datasets is especially important.

4.1.1 Canonical states

We aim at building a surrogate model for determining canonical wavefunctions as a function of a set of continuous constraints. Canonical states are denoted generically ${\phi }_{\mu }^{(\tau )}(\mathit{r},\sigma )$ with r ≡ (r, z, θ) the cylindrical coordinates and σ = ±1/2 the spin. Fully characterizing an HFB state requires the set of canonical wavefunctions for both neutrons and protons, which are distinguished by their isospin quantum number τ = +1/2 (neutrons) and τ = −1/2 (protons). As mentioned in Section 2, an HFB solution |Φ(q)⟩ is entirely determined up to a global phase by the set of all canonical states ${\{{\phi }_{\mu }^{(\tau )}(\mathit{r},\sigma )\}}_{\mu }$ and their associated occupation amplitudes ${\{v_{\mu }^{(\tau )}\}}_{\mu }$.

In this work, we restrict ourselves to axially-symmetric configurations. In that case, the canonical wavefunctions are eigenstates of the projection of the total angular momentum on the symmetry axis ${\widehat{J}}_{\text{z}}$ with eigenvalue Ω and acquire the same separable structure (18) as the HO basis functions,

${\phi }_{\mu }^{\left(\tau \right)}\left(\mathit{r},\sigma \right)={\phi }_{\mu }^{\left(\tau \right)}\left(r,z,\sigma \right)\frac{e^{i\mathrm{\Lambda }\theta }}{\sqrt{2\pi }},(24)$

where ${\phi }_{\mu }^{(\tau )}(r,z,\sigma )$ is the canonical wavefunction at θ = 0. In this initial work, we only consider even-even nuclear systems and time-reversal symmetric nuclear Hamiltonians. Therefore, Kramer’s degeneracy ensures that paired particles in the canonical basis are time-reversal partners of each other: ${\phi }_{\bar{\mu }}^{(\tau )}(\mathit{r},\sigma )=2\sigma {\phi }_{\mu }^{(\tau )*}(\mathit{r},-\sigma )$. This guarantees that the canonical wavefunction at θ = 0 can be chosen purely real. Incidentally, it also means that we only need to describe one wavefunction per pair of particles. Using these properties, we can completely describe a canonical wavefunction in our model by only predicting a single pair of real-valued functions (one for each spin projection σ).

As shown by Eqs 8, Eqs 9a–9c, all mean-field and pairing potentials are functions of the Skyrme densities. The kinetic energy density τ(r, z), spin-current tensor $\mathsf{J}(r,z)$, and vector density J (r, z) involve derivatives of the quasiparticle spinors or, in the canonical basis, of the canonical wavefunctions on the quadrature grid Stoitsov et al. [46]. We compute these derivatives by first extracting the coefficients ${\alpha }_{\mathit{n}\mu }^{(\tau )}$ of the expansion of the canonical wavefunctions ${\phi }_{\mu }^{(\tau )}(\mathit{r},\sigma )$ in the HO basis

${\phi }_{\mu }^{\left(\tau \right)}\left(\mathit{r},\sigma \right)=\sum _{\mathit{n}}{\alpha }_{\mathit{n}\mu }^{\left(\tau \right)}{\psi }_{\mathit{n}}\left(\mathit{r},\sigma \right)\Rightarrow {\alpha }_{\mathit{n}\mu }^{\left(\tau \right)}=\int {\mathrm{d}}^3\mathit{r}{\psi }_{\mathit{n}}^{*}\left(\mathit{r},\sigma \right){\phi }_{\mu }^{\left(\tau \right)}\left(\mathit{r},\sigma \right),(25)$

using Gauss-Laguerre and Gauss-Hermite quadrature. Since all the derivatives of the HO functions can be computed analytically, the expansion (25) makes it very easy to compute partial derivatives with respect to r or z, for example,

$\frac{\partial {\phi }_{\mu }^{\left(\tau \right)}}{\partial z}\left(\mathit{r},\sigma \right)=\sum _{\mathit{n}}{\alpha }_{\mathit{n}\mu }^{\left(\tau \right)}\frac{\partial {\psi }_{\mathit{n}}}{\partial z}\left(\mathit{r},\sigma \right).(26)$

4.1.2 Structure of the predicted quantity

In the ideal case, the canonical wavefunctions evolve smoothly with the collective variables. The resulting continuity of the many-body state with respect to collective variables is a prerequisite for a rigorous description of the time evolution of fissioning systems, yet it is rarely satisfied in practical calculations. We discuss below the three possible sources of discontinuity of the canonical wavefunctions in potential energy surfaces.

First, the canonical wavefunctions are invariant through a global phase. Since the quantity we want to predict is real, the orbitals can be independently multiplied by an arbitrary sign. Even though this type of discontinuity does not impact the evolution of global observables as a function of deformation, it affects the learning of the model: since we want to obtain continuous functions, a flipping of the sign would be seen by the neural network as a discontinuity in the input data. We address this point through the choice of the loss, as discussed in Section 4.1.3, and through the determination of the training set, as detailed in Section 4.2.

Second, we work within the adiabatic approximation, which consists in building PES by selecting the q.p. vacuum that minimizes the energy at each point. When the number N_col of collective variables of the PES is small, this approximation may lead to discontinuities Dubray and Regnier [75]. These discontinuities correspond to missing regions of the collective space and are related to the inadequate choice of collective variables. Since we want to obtain a continuous description of the fission path, we must give our neural network the ability to choose the relevant degrees of freedom. This could be achieved with autoencoders. Autoencoders are a type of neural networks analogous to the zip/unzip programs. They are widely used and greatly successful for representation learning—the field of Machine Learning that attempts to find a more meaningful representation of complex data Baldi [86]; Burda et al. [87]; Chen et al. [88]; Gong et al. [89]; Bengio et al. [90]; Zhang et al. [91]; Yu et al. [92] and can be viewed as a non-linear generalization of principal component analysis (PCA). As illustrated in Figure 5, an autoencoder Ξ typically consists of two components. The encoder E (T^(φ)) encodes complex and/or high-dimensional data T^(φ) to a typically lower-dimensional representation v^(φ). The latent space is the set of all possible such representations. The decoder D (v^(φ)) takes the low-dimensional representation of the encoder and uncompresses it into a tensor T^(ϕ) as close as possible to T^(φ). Such architectures are trained using a loss function that quantifies the discrepancy between the initial input and the reconstructed output,

${\mathcal{L}}_{\text{rec.}}\left(T^{(\varphi )}\right)=d\left(T^{(\phi )},T^{(\varphi )}\right),(27)$

where d (., .) defines the metric in the space of input data. We discuss the choice of a proper loss in more details in Section 4.1.3.

FIGURE 5

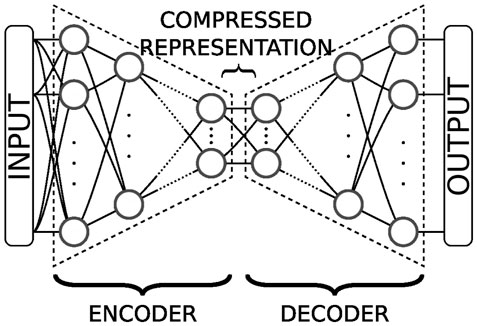
FIGURE 5. An autoencoder is the association of two blocks. The first one, on the left, compresses the input data into a lower-dimensional representation, or code, in the latent space. The second one, on the right, decompresses the code back into the original input.

Third, the evolution of the q.p. wavefunctions as a function of the collective variables q may lead to specific values q_i where the q.p. solutions are degenerate. These degeneracies form a sub-manifold of dimension at most D − 2, where D is the number of collective d.o.f.s. As a consequence, they cannot appear in one-dimensional PES: q.p. solutions with the same symmetry “cannot cross” (the famous no-crossing rule von Neuman and Wigner [93]). In multi-dimensional spaces, this rule does not hold anymore: when following a closed-loop trajectory around such a degeneracy, the sign of the q.p. wavefunctions is flipped, in a similar manner that we flip side when winding around a Moebius strip Teller [94]; Longuet-Higgins et al. [95]; Longuet-Higgins [96]. In the field of quantum chemistry, such degeneracies are referred to as diabolical points or conical intersections Domcke et al. [97]; Larson et al. [98]. The practical consequence of conical intersections for deep learning is that the manifold of all the q.p. wavefunctions cannot be embedded in a D-dimensional latent space. Such singularities can be treated in two ways: (i) by using a latent space of higher dimension than needed or (ii) by implementing specific neural network layers capable of handling such cases. For now, we do not consider these situations.

4.1.3 Loss functions and metrics

As already discussed in Section 4.1.2, autoencoders are trained through the minimization of a loss function that contains a reconstruction term of the form (27). As suggested by its name, this term ensures that the autoencoder can correctly reconstruct the input tensor T^(φ) from its compressed representation. It depends on a definition for the metric d (., .) used to compare the different elements of the input space. Since our canonical wavefunctions φ_μ are expanded on the axial harmonic oscillator basis of Section 2.6, they are discretized on the Gauss quadrature mesh without any loss of information. Therefore, both the input and output tensors of our surrogate model are a rank-3 tensor T^(ϕ) ≡ T^(φ) ≡ T_ijk of dimensions N_⊥× N_z × 2, where i is the index of the Gauss-Laguerre node along the r-axis, j the index of the Gauss-Hermite node along the z-axis, and k the index of the spin component.

A standard loss used with autoencoders is the mean-square-error (MSE). Because of the structure of our input data, see Section 4.1.1, the MSE loss reads in our case

$d_{\text{MSE}}\left(T^{(\phi )},T^{(\varphi )}\right)=\frac{1}{N_{\perp }\times N_z\times 2}\sum _{i=0}^{N_{\perp }-1}\sum _{j=0}^{N_z-1}\sum _{i=0}^1{\left(T_{\mathit{ijk}}^{(\varphi )}-T_{\mathit{ijk}}^{(\phi )}\right)}^2.(28)$

The MSE is very general and can be thought of, quite simply, as the mean squared “distance” between the initial and reconstructed data. However, this generality implies that it does not contain any information about the properties of the data one tries to reconstruct.

Indeed, we can define a metric that is better suited to the physics we aim to describe. Let us recall that our goal is to compute potential energy surfaces that can be used, e.g., for fission simulations. These PES are nothing but generator states for the (TD)GCM mentioned in Section 2.4. The GCM relies on the norm kernel $\mathcal{N}(\mathit{q},{\mathit{q}}^{\prime })$ and the Hamiltonian kernel $\mathcal{H}(\mathit{q},{\mathit{q}}^{\prime })$, which are defined as.

$\mathcal{N}\left(\mathit{q},{\mathit{q}}^{\prime }\right)=⟨\mathrm{\Phi }(\mathit{q})|\mathrm{\Phi }({\mathit{q}}^{\prime })⟩,(29)$

$\mathcal{H}\left(\mathit{q},{\mathit{q}}^{\prime }\right)=⟨\mathrm{\Phi }(\mathit{q})|\widehat{H}|\mathrm{\Phi }({\mathit{q}}^{\prime })⟩.(30)$

Since the norm kernel involves the standard inner product in the many-body space, it represents the topology of that space. Therefore, it should be advantageous to use for the loss a metric induced by the same inner product that defines the norm kernel.

In our case, we want to build an AE where the encoder v^(φ) = E (T^(φ)) compresses the single-particle, canonical orbitals ${\{{\phi }_{\mu }\}}_{\mu }$ associated with |Φ⟩ into a low-dimensional vector v^(φ) and where the decoder T^(ϕ) = D (v^(φ)) is used to compute the set of reconstructed canonical orbitals ${\{{\varphi }_{\mu }\}}_{\mu }$. Most importantly, this reconstruction should be such that the reconstructed many-body state |Ψ⟩ is as close as possible to the original state |Φ⟩. In other words, we need to use a loss that depends on the norm overlap (between many-body states) but since we work with single-particle wavefunctions, we must have a way to relate the norm overlap to these s.p. wavefunctions. This can be achieved with Equations 5.4 and (5.6) of Haider and Gogny [99], which relate the inner product ⟨Φ|Ψ⟩ in the many-body space with the inner product (overlap) ⟨φ_μ|ϕ_ν⟩ between the related canonical orbitals φ_μ and ϕ_ν,

$⟨{\phi }_{\mu }|{\varphi }_{\nu }⟩\equiv {\tau }_{\mu \nu }^{\left(\phi \varphi \right)}=\left\{{\widehat{a}}_{\mu }^{(\phi )†},{\widehat{a}}_{\nu }^{\varphi }\right\}=\sum _{\sigma }\int {\mathrm{d}}^3\mathit{r}{\phi }_{\mu }^{*}\left(\mathit{r},\sigma \right){\varphi }_{\nu }\left(\mathit{r},\sigma \right)(31)$

and with the occupation amplitudes. However, it assumes that the canonical wavefunctions of each many-body state are orthogonal. This property is not guaranteed for our reconstructed canonical wavefunctions. In fact, because of this lack of orthogonality, the reconstructed wavefunctions cannot be interpreted as representing the canonical basis of the Bloch-Messiah-Zumino decomposition of the quasiparticle vacuum and the Haider and Gogny formula cannot be applied ‘as is’. However, we show in Supplementary Appendix S1 that it is possible to find a set of transformations of the reconstructed wavefunctions that allows us to define such as genuine canonical basis.

We want the loss function to depend only on the error associated with the reconstructed orbital ϕ_μ. Therefore, we should in principle consider the many-body state $|{\tilde{\mathrm{\Phi }}}_{\mu }\rangle$ where only the orbital φ_μ is substituted by its reconstruction ϕ_μ. We can then compute the inner product between |Φ⟩ and $|{\tilde{\mathrm{\Phi }}}_{\mu }\rangle$ using Supplementary Appendix S1 and deduce any induced metric f

$d_{\text{exact}}^f\left(T^{\left(\phi \right)},T^{\left(\varphi \right)}\right)=f\left(\frac{⟨\mathrm{\Phi }|{\tilde{\mathrm{\Phi }}}_{\mu }⟩}{\sqrt{⟨{\tilde{\mathrm{\Phi }}}_{\mu }|{\tilde{\mathrm{\Phi }}}_{\mu }⟩}}\right).(32)$

However, computing this metric is too computationally involved to be carried out explicitly for each training data at each epoch. Instead, we keep this metric for comparing a posteriori the performance of our model.

Instead of explicitly determining $d_{\text{exact}}^f(T^{(\phi )},T^{(\varphi )})$, we focus on reproducing canonical orbitals using the metrics of the one-body Hilbert space. In practice we considered the distance noted $d_{◦}^{(0)}$ that is induced by the inner product between normalized functions in the one-body Hilbert space, that is,

$d_{◦}^{\left(0\right)}\left(\phi ,\varphi \right)\equiv \left(\frac{\langle \phi |}{\sqrt{⟨\phi |\phi ⟩}}-\frac{\langle \varphi |}{\sqrt{⟨\varphi |\varphi ⟩}}\right)\left(\frac{|\phi \rangle }{\sqrt{⟨\phi |\phi ⟩}}-\frac{|\varphi \rangle }{\sqrt{⟨\varphi |\varphi ⟩}}\right),(33)$

which is nothing but

$d_{◦}^{\left(0\right)}\left(\phi ,\varphi \right)=\sum _{\sigma }\int {\mathrm{d}}^3\mathit{r}{\left|\phi \left(\mathit{r},\sigma \right)-\varphi \left(\mathit{r},\sigma \right)\right|}^2,(34)$

where the φ(r, σ) and ϕ(r, σ) have been normalized. Since all wavefunctions are discretized on the Gauss quadrature mesh, this distance reads

$d_{◦}^{\left(0\right)}\left(\phi ,\varphi \right)=\sum _{n_{\perp }{n}_z{n}_{\sigma }}{W}_{n_{\perp }{n}_z}{\left|T_{n_{\perp }{n}_z{n}_{\sigma }}^{\left(\phi \right)}-T_{n_{\perp }{n}_z{n}_{\sigma }}^{\left(\varphi \right)}\right|}^2,(35)$

where the weights W are given by

$W_{n_{\perp }{n}_z}=\frac{w_{n_{\perp }}^{\text{GL}}}{2b_{\perp }^2}\times 2\pi \times \frac{w_{n_z}^{\text{GH}}}{b_z}.(36)$

These weights, which depend on the indices n_⊥ and n_z in the summation, are the only difference between the squared distance loss (Eq. 35) and the MSE loss (Eq. 28). Although the distance (Eq. 35) is norm-invariant⁶, it still depends on the global phase of each orbital. We have explored other possible options for the loss based on norm- and phase-invariant distances; see Supplementary Appendix S2 for a list. However, we found in our tests that the distance $d_{◦}^{(0)}$ systematically outperformed the other ones and, for this reason, only show results obtained with this one.

4.1.4 Physics-informed autoencoder

From a mathematical point of view, deep neural networks can be thought of as a series of compositions of functions. Each composition operation defines a new layer in the network. Networks are most often built with alternating linear and nonlinear layers. The linear part is a simple matrix multiplication. Typical examples of nonlinear layers include sigmoid, tanh, Rectified Linear Unit (ReLU) functions. In addition to these linear and nonlinear layers, there could be miscellaneous manipulations of the model for more specific purposes, such as adding batch normalization layers Ioffe and Szegedy [100], applying dropout Srivastava et al. [101] to some linear layers, or skip connection He et al. [102] between layers.

Our data is a smooth function defined over a N_⊥× N_z = 60 × 40 grid and is analogous to a small picture. For this reason, we chose a 2D convolutional network architecture. Convolutional layers are popular for image analysis, because they incorporate the two-dimensional pixel arrangement in the construction of the weights of the network. These two-dimensional weights, or filters, capture local shapes and can model the dependent structure in nearby pixels of image data. Given a 2D m × m input array, a 2D filter F is a n × n matrix, usually with n ≪ m. If we note Iⁿ the space of n × n integer-valued matrices, then the convolutional layer $\mathcal{C}$ is an operation of the $\mathcal{C}:(I^n,I^n)\to \mathbb{N}$ that is applied to all pairs (F, C) where C is any n × n chunk of the input image; see Figure 6 for an example. This way, the resulting output summarizes the strength and location of that particular filter shape within the image. As the model gets trained, the filter parameters are fitted to a shape that is learned to be important in the training data. Convolutional neural network are very effective for image analysis and are currently widely used Krizhevsky et al. [103]; Zeiler and Fergus [104]; Sermanet et al. [105]; Szegedy et al. [106].

FIGURE 6

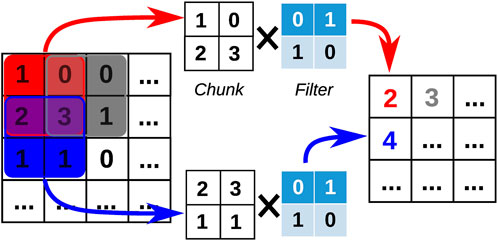
FIGURE 6. Schematic example of a convolutional layer. For any 2 × 2 chunk C of the input image on the left, this convolutional layer performs the point-wise multiplication of C with the filter F followed by the addition of all elements. This compresses the initial chunk of the image into a single integer.

In this work, we used the Resnet 18 model as our encoder and constructed the decoder from a transposed convolution architecture of the Resnet 18. The Resnet 18 model was first introduced by He et al. as a convolutional neural network for image analysis He et al. [102]. It was proposed as a solution to the degradation of performance as the network depth increases. Resnet branches an identity-function addition layer to sub-blocks (some sequential layers of composition) of a given network. While a typical neural network sub-block input and output could be represented by x and f(x), respectively, a Resnet sub-block would output f(x) + x for the same input x, as in Figure 2 of He et al. [102]. This architecture is called ‘skip connection’ and was shown to be helpful for tackling multiple challenges in training deep neural network such as vanishing gradient problem and complex loss function Li et al. [107]; He et al. [102]. Since then, the Resnet architecture has been widely successful, often being used as a baseline for exploring new architectures Zhang et al. [108]; Radosavovic et al. [109] or as the central model for many analyses Cubuk et al. [110]; Yun et al. [111]; Zhang et al. [112]. In a few cases, it was also combined with autoencoders for feature learning from high-dimensional data Wickramasinghe et al. [113].

For the decoder part, we designed a near-mirror image of the encoder using transposed convolution. Transposed convolution is essentially the opposite operation to convolution in terms of input and output dimensions. Here the meaning of transpose refers to the form of the filter matrix when the convolution layer is represented by a 1D vector input obtained from linearizing the 2D input. Note that the mirror-located filters in the decoder are independent parameters and not the actual transposed filter matrix of the encoder. Such a construction ensures symmetrical encoder and decoder models, making the decoder model close to the inverse shape of the encoder model. Figure 7 illustrates the operation: one input value is multiplied by the entire kernel (filter) and is added to the output matrix at its corresponding location. The corresponding output location for each colored input number are color-coded and show how the addition is done.

FIGURE 7

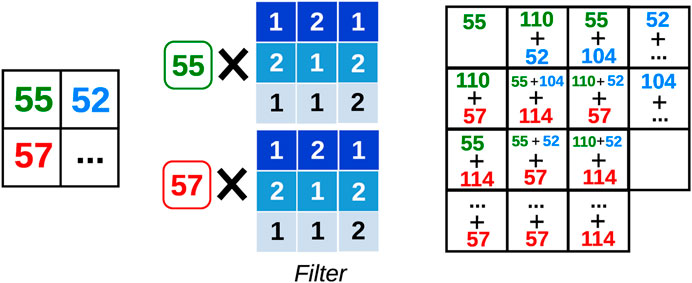
FIGURE 7. Schematic illustration of the 2D-transposed convolution. Each input value, e.g., 55, 57, etc., is multiplied by the entire kernel resulting in a 3 × 3 matrix. These matrices are then added to one another in a sliding and overlapping way.

The first and the last layer of the Resnet architecture are mostly for resizing and were minimally modified from the original Resnet 18 model since the size of our input data is significantly smaller than typical image sizes used for Resnet image classification analyses. We also modified the number of input channels of the first layer of the encoder to be 2 (for each of the spin components of the nuclear wavefunction) instead of the usual number 3 (for the RGB colors of colored images) or 1 (for black-and-white images). The spin components are closely related to each other with covariance structure, similar to how colors interact within an image. Therefore, we treat a pair of spin components as a single sample and treat each component as an input channel. The same applies to the output channel of the decoder.

The full network is represented schematically in Figure 8. Parametric Rectified Linear Unit, or PRELU, layers were added to impose nonlinearity in the model He et al. [114]. PRELU layers are controlled by a single hyperparameter that is trained with the data. Batch normalization is a standardizing layer that is applied to each batch by computing its mean and standard deviation. It is known to accelerate training by helping with optimization steps Ioffe and Szegedy [100]. The average pooling layer (bottom left) averages each local batch of the input and produces a downsized output. The upsampling layer (top right) upsamples the input using a bilinear interpolation.

FIGURE 8

FIGURE 8. Representation of our modified Resnet 18 architecture for the encoder (A) and the decoder (B). Large numbers on the left of each side label the different layers. Numbers such as 64, 128, etc. refer to the size of the filer; see text for a discussion of some of the main layers.

4.2 Training

As mentioned in Section 4.1.4, the loss is the discrepancy between the input of the encoder and the output of the decoder. The minimization of the loss with respect to all the model parameters w, such as the filter parameters, is the training process. We used the standard back-propagation algorithm to efficiently compute the gradient of the loss function with respect to the model parameters. The gradient computation is done with the chain rule, iterating from the last layer in the backward direction. We combined this with the mini-batch gradient descent algorithm: ideally, one would need the entire dataset to estimate the gradient at the current model parameter value. However, with large datasets, this becomes computationally inefficient. Instead we use a random subset of the entire data, called mini-batch, to approximate the gradient, and expedite the convergence of the optimization. For each mini-batch, we update each parameter w by taking small steps of gradient descent, $w_{t+1}=w_t-\alpha \frac{\partial \mathcal{L}}{\partial w_t}$. At step t, or at tth mini-batch, the average loss $\mathcal{L}$ and the gradient with respect to current model parameter w_t are computed. Then α-sized gradient descent step is taken to update the model parameters. Instead of using the current gradient for the update, one can use a weighted average of past gradients. We employed the well-known Adam algorithm, which uses the exponential moving average of current and past gradients Kingma and Ba [115].

Iterating over the entire dataset once, using multiple mini-batches, is called an epoch. Typically a deep neural network needs hundreds to thousands of epochs for the algorithm to converge. Parameters such as the batch size or learning rate, the parameters of the optimizer itself (Adam’s or other), and the number of epochs are hyper-parameters that must be tuned for model fitting. For our training, we used the default initialization method in PyTorch for the model parameters. The linear layers were initialized with a random uniform distribution over [ − 1/k, 1/k], where k is the size of the weight. For example, if there are 2 input channels and 3 × 3 convolution filters are used, k = 2 × 3 × 3. PRELU layers were initialized with their default PyTorch value of 0.25. We proceeded with mini-batches of size 32 with the default β₁ = 0.9, β₂ = 0.999 and ϵ = 10^–8: all these numbers refer to the PyTorch implementation of the Adam’s optimizer. For α, we used 0.001 as starting value and used a learning rate scheduler, which reduces the α value by a factor of 0.5 when there is no improvement in the loss for 15 epochs. After careful observation of the loss curves, we have estimated that at least 1,000 epochs are needed to achieve convergence.

To mitigate the problem of the global phase invariance of the canonical wavefunctions discussed in Section 4.1.2, we doubled the size of the dataset: at each point q of the collective space (=the sample), we added to each canonical wavefunction φ_μ(r, σ) the same function with the opposite sign − φ_μ(r, σ). The resulting dataset was then first split into three components, training, validation and test datasets, which represent 70%, 15%, and 15% of the entire data respectively. Training data is used for minimizing the loss with respect to the model parameters as explained above. Then we choose the model at the epoch that performs the best with the validation dataset as our final model. Finally, the model performance is evaluated using the test data.

4.3 Results

In this section, we summarize some of the preliminary results we have obtained after training several variants of the AE. In Section 4.3.1, we give some details about the training data and the quality of the reconstructed wavefunctions. We discuss some possible tools to analyze the structure of the latent space in Section 4.3.2. In these two sections, we only present results obtained for latent spaces of dimension D = 20. In Section 4.3.3, we use the reconstructed wavefunctions to recalculate HFB observables with the code HFBTHO. We show the results of this physics validation for both D = 20 and D = 10.

4.3.1 Performance of the network

Figure 9 shows the initial potential energy surface in ⁹⁸Zr used in this work. Calculations were performed for the SkM* parametrization of the Skyrme potential with a surface-volume, density-dependent pairing force with $V_0^{(n)}=-199.69$ MeV.fm⁻³, $V_0^{(p)}=-223.59$ MeV.fm⁻³ and an “infinite” pairing cutoff. The basis was identical for all points with oscillator length b₀ = 1.971 fm, deformation β₀ = 0.3 and number of shells N_basis = 20. The PES contains 548 HFB calculations with constraints on the axial quadrupole, $q_{20}=⟨{\widehat{Q}}_{20}⟩$, and axial octupole moment, $q_{30}=⟨{\widehat{Q}}_{30}⟩$. The mesh was: − 12.5 b ≤ q₂₀ ≤ 25.0 b with steps δq₂₀ = 1 b and 0.0 b3/2 ≤ q₃₀ ≤ 3.0 b^3/2 with step δq₃₀ = 0.125 b^3/2. The black dots in Figure 9 indicate the location of the converged solutions. For each solution, the n_p = 60 highest-occupation proton and n_n = 87 highest-occupation neutron canonical wavefunctions were used as training data for the network⁷.

FIGURE 9

FIGURE 9. Potential energy surface of ⁹⁸Zr in the (q₂₀, q₃₀) plane. Converged HFBTHO solutions are represented by black dots. Energies given by the color bar are in MeV relatively to the ground state.

For each of the losses discussed in Supplementary Appendix S2, we trained the AE with the slightly modified Resnet 18 architecture described in Section 4.1.4. It is important to keep in mind that the value of these losses should not be compared with one another. The only rigorous method to compare the performance of both networks would be to compute the many-body norm overlap across all the points in each case—or to perform a posteriori physics validation with the reconstructed data, as will be shown in Section 4.3.3.

To give an idea of the quality of the AE, we show in Figure 10 one example of the original and reconstructed canonical wavefunctions. Specifically, we consider the configuration (q₂₀, q₃₀) = ( − 7.0 b, − 0.25 b^3/2) in the collective space and look at the neutron wavefunction with occupation number $v_{\mu }^2=0.945255$, which is located near the Fermi surface. This example was obtained for an AE trained with the $d_o^{(0)}$ loss and compressed to D = 20. The figure shows, in the left panel, the logarithm of the squared norm of the original wavefunction across the quadrature mesh, $\ln |{\phi }_{\mu }{|}^2\equiv \ln |T_{n_{\perp }{n}_z{n}_{\sigma }}^{({\phi }_{\mu })}{|}^2$, in the middle panel, the same quantity for the reconstructed wavefunction, and in the right panel the logarithm of the absolute value of the difference between the two. On this example, the AE can reconstruct the wavefunction with about 3% error.

FIGURE 10

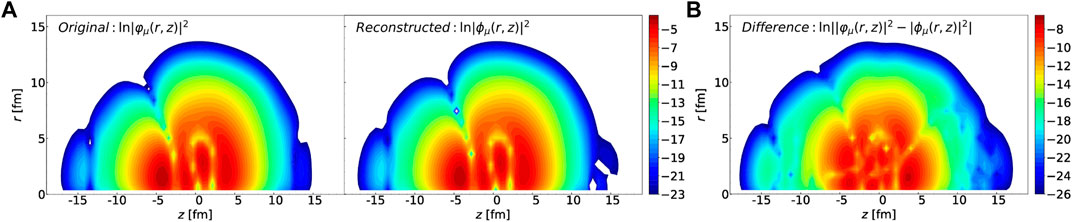
FIGURE 10. (A): Contour plot of the logarithm of the squared norm of the neutron canonical wavefunction with occupation number $v_{\mu }^2=0.945255$ (without the exponential factor). Middle: Same for the reconstructed wavefunction. (B): Logarithm of the difference between the squared norm of the original and reconstructed wavefunctions.

4.3.2 Structure of the latent space

One of the advantages of AEs is the existence of a low-dimensional representation of the data. In principle, any visible structure in this latent space would be the signal that the network has properly learned, or encoded, some dominant features of the dataset. Here, our latent space has dimension D = 20. This means that every canonical wavefunction, which is originally a matrix of size n = N_⊥× N_z, is encoded into a single vector of size D. From a mathematical point of view, the encoder is thus a function

$\begin{array}{cc}\hfill \widehat{E}:{\mathbb{R}}^n& \to {\mathbb{R}}^D\hfill \\ \hfill \phi & ⟼\mathit{v}=\widehat{E}\left(\phi \right)\hfill \end{array}(37)$

Let us consider some (scalar) quantity P associated with the many-body state |Φ(q)⟩ at point q. Such a quantity could be an actual observable such as the total energy but it could also be an auxiliary object such as the expectation value of the multipole moment operators. In fact, P could also be a quantity associated with the individual degrees of freedom at point q, for example the q.p. energies. In general terms, we can think of P as the output value of the function

$\begin{array}{cc}\hfill \widehat{P}:{\mathbb{R}}^n& \to \mathbb{R}\hfill \\ \hfill \phi & ⟼P=\widehat{P}\left(\phi \right)\hfill \end{array}(38)$

For example, if P represents the s.p. canonical energies, then the function $\widehat{P}$ is the one that associates with each canonical wavefunction its s.p. energy. Therefore, for every canonical wavefunction, there is a different value of P. Conversely, if $P=⟨{\widehat{Q}}_{20}⟩$, there is a single value for all the canonical wavefunctions at point q. Since there is a vector in the latent space for each canonical wavefunction, and there is also a value for the quantity P for each such function, we can then define the new function $\widehat{\mathcal{P}}$ acting on vectors of the latent space and defined as

$\begin{array}{cc}\hfill \widehat{\mathcal{P}}:{\mathbb{R}}^D& \to \mathbb{R}\hfill \\ \hfill \mathit{v}& ⟼P=\widehat{\mathcal{P}}\left(\mathit{v}\right)\hfill \end{array}(39)$

and it is straightforward to see that: $\widehat{P}=\widehat{\mathcal{P}}◦\widehat{E}$. Our goal is now to try to analyze where various quantities P are located in the latent space and whether one can identify some specific features of these locations.

Since we have a total of n_t = 147 wavefunctions for each of the N_p = 552 points in the collective space, the encoder yields a set of n_t × N_p vectors of dimension D. This means that, in the latent space, every quantity P above is also represented by a cloud of n_t × N_p such vectors. This is obviously impossible to visualize. For this reason, we introduce the following analysis. First, we perform a linear regression in the D-dimensional latent space of a few select quantities of interest P, that is, we write

$P=\mathit{\alpha }\cdot \mathit{v}+b,(40)$

where α is a D-dimensional vector, v is the vector associated with the quantity P in the latent space and $b\in \mathbb{R}$. The unit vector u = α/‖α‖ can be interpreted as representing the leading direction in the latent space. The quantity u = u ⋅v is a scalar which we obtain easily from the result of the linear regression. We can thus plot the function P: u↦P(u). Examples of such functions are shown in Figure 11. Each point in the figures represents the value $P=\widehat{\mathcal{P}}(\mathit{v})$ of some characteristic quantity at point u = u ⋅v.

FIGURE 11

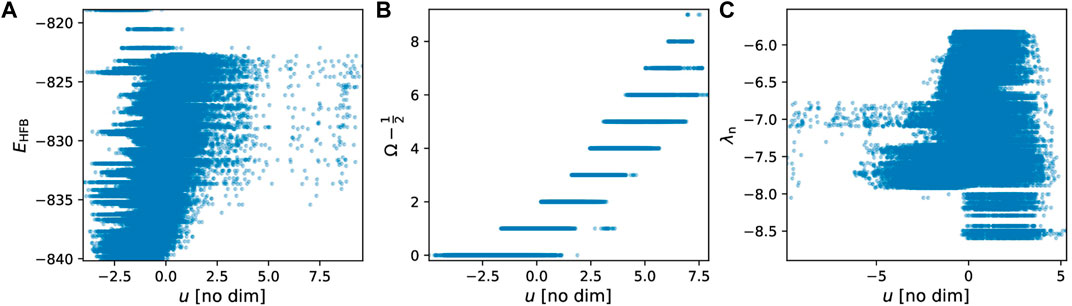
FIGURE 11. One-dimensional projections of the D-dimensional linear fit for the total energy E_HFB (A), the projection Ω of the canonical state (B) and the neutron Fermi energy λ_n (C). Each point represents one of these quantities for a canonical wavefunction μ and a point q in the collective space.

The three cases shown in Figure 11 illustrate that the network has not always identified relevant features. The case of Ω, middle panel, is the cleanest: there is a clear slope as a function of u: if one sets u = 1, for example, then only values of 7/2 ≤ Ω ≤ 15/2 are possible. Conversely, the AE has not really discovered any feature in the neutron Fermi energy (right panel): for any given value of u, there is a large range of possible values of Fermi energies. In the case of the total energy (left panel), the situation is somewhat intermediate: there is a faint slope suggesting a linear dependency of the energy as a function of u.

4.3.3 Physics validation

The results presented in the Section 4.3.1 suggest the AE has the ability to reproduce the canonical wavefunctions with good precision. To test this hypothesis, we recalculated the HFB solution at all the training, validation and testing points by substituting in the HFBTHO binary files the original canonical wavefunctions by the ones reconstructed by the AE. Recall that only the lowest n_t wavefunctions with the largest occupation were encoded in the AE (n_n = 87 for neutrons and n_p = 60 for protons); the remaining ones were unchanged. In practice, their occupation is so small that their contribution to nuclear observables is very small ($<$ 10 keV for the total energy, for example).

Figure 12 shows the error on the potential energy across the (q₂₀, q₃₀) collective space obtained with the reconstructed canonical wavefunctions for latent spaces of dimension D = 20 (left) and D = 10 (right). In each case, we only show results obtained when using the $d_o^{(0)}$ loss, which gives the best results. The black crosses denote the location of all the original points; the white circles show the location of the validation points. Overall, the results are very encouraging. In both cases, most of the error is concentrated near regions of the PES where there are discontinuities (hence, the lack of converged solutions). Everywhere else, the error is small and mostly randomly distributed across the PES, that is, it is not systematically larger at the validation points. As expected, the quality of the reconstruction is a little worse when D = 10: one can notice about a dozen points for which the error is significantly larger, in absolute value. Examples include (q₂₀, q₃₀) = ( − 5.0 b, 1.125 b^3/2) or (q₂₀, q₃₀) = ( + 8.0 b, 2.5 b^3/2) in the validation set, and (q₂₀, q₃₀) = (0.0 b, 1.75 b^3/2) or the region around 1 b ≤ q₂₀ ≤ 4 b and 1.5 b^3/2 ≤ q₃₀ ≤ 2.25 b^3/2 in the training set. These may suggest that for D = 10, the loss may not have fully converged yet. Because of the existence of discontinuities near these points, this could also be the manifestation that our continuous AE cannot build a continuous representation of the data everywhere. However, the fact that an increase of the compression by a factor 2, from D = 20 to D = 10, does not substantially degrade the performance of the AE is very promising.

FIGURE 12

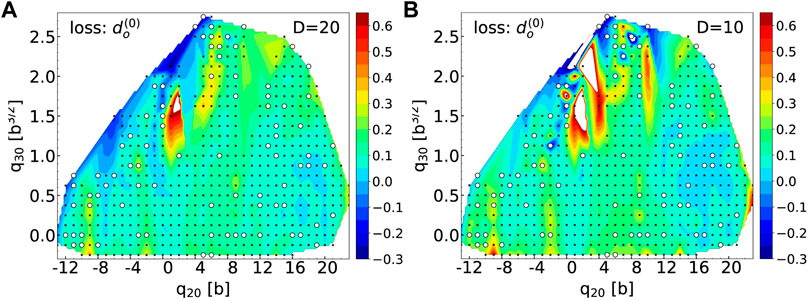
FIGURE 12. (A): Potential energy surface in the (q₂₀, q₃₀) plane for ⁹⁸Zr obtained after replacing the first n_n = 87 and n_p = 60 highest-occupation canonical wavefunctions by their values reconstructed by the AE for a latent space of dimension D = 20. The black dots show the location of the training points only, the white circles the location of the validation points. (B): same figure for a latent space of dimension D = 10. For both figures, energies are given in MeV.

The two histograms in Figure 13 give another measure of the quality of the AE. The histogram in the left shows the distribution of the error on the HFB energy for two sizes of the latent space, D = 20 and D = 10. For the D = 20 case, the mean error is $\overline{\mathrm{\Delta }E}=104$ keV and the standard deviation σ_E = 89 keV. These numbers increase a little bit in the case of D = 10: $\overline{\mathrm{\Delta }E}=122$ keV and σ_E = 153 keV. To better estimate the quality of the AE, we applied the same Gaussian process technique as described in Section 3 to the dataset in ⁹⁸Zr. Since GPs are interpolators and reproduce the training data, we can only test them across the validation set, which, in the case of ⁹⁸Zr contains only 110 configurations. After computing the energy with the HFB potentials obtained from the GP across this set, we obtain: ${\overline{\mathrm{\Delta }E}}^{(\mathrm{G}\mathrm{P})}=-32$ keV and ${\sigma }_E^{(\mathrm{G}\mathrm{P})}=225$ keV. This is comparable to what the AE predicts. As mentioned before, it is important to bear in mind that, for the AE, the points with the higher error ΔE < − 150 keV or ΔE > 250 keV do not correspond to testing points only.

FIGURE 13

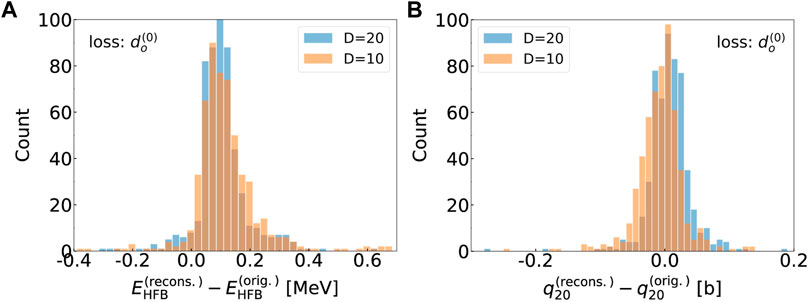
FIGURE 13. (A): Histogram of the difference in total HFB energy between the original HFBTHO calculation and the result obtained by computing the energy in the canonical basis with the reconstructed wavefunctions (see text for details). Calculations were performed both for a D = 20 and D = 10 latent space. (B): Similar histogram for the expectation value of the axial quadrupole moment.

The histogram on the right shows the distribution of the error for q₂₀, in units of b. Here, the mean and standard deviation of the error are: $\overline{\mathrm{\Delta }{q}_{20}}=6.8$ mb and σ_q = 33.0 mb for D = 20, and $\overline{\mathrm{\Delta }{q}_{20}}=-7.4$ mb and σ_q = 48.2 mb for D = 10. For comparison, the results obtained (across the validation set only) with the GP are: $\overline{\mathrm{\Delta }{q}_{20}}=-12.7$ mb and σ_q = 68.3 mb. Once again, the AE performs just as well, if not slightly better, than the GP fit.

5 Conclusion

Nuclear density functional methods are amenable to large-scale calculations of nuclear properties across the entire chart of isotopes relevant for, e.g., nuclear astrophysics simulations or uncertainty quantification. However, such calculations remain computationally expensive and fraught with formal and practical issues associated with self-consistency or reduced collective spaces. In this article, we have analyzed two different techniques to build fast, efficient and accurate surrogate models, or emulators, or DFT objects.

We first showed that Gaussian processes could reproduce reasonably well the values of the mean-field and pairing-field potentials of the HFB theory across a large two-dimensional potential energy surface. The absolute error on the total energy was within ±100 keV and the relative errors on the collective inertia tensor smaller than 5%. However, GPs require the training data to be “smoothly-varying”, i.e., they should not include phenomena such as nuclear scission or, more generally, discontinuities in the PES. It is well known that GPs are not reliable for extrapolation: such a technique can thus be very practical to densify (=interpolate) an existing potential energy surface but must not be applied outside its training range.

Our implementation of standard versions of GPs is fast and simple to use, but it misses many of the correlations that exist between the values of the HFB potentials on the quadrature grid: (i) all components of the full Skyrme mean field (central, spin-orbit, etc.) are in principle related to one another through their common origin in the non-local one-body density matrix; (ii) the correlations between the value of any given potential at point (r, z) and at point (r′, z′) were not taken into account; (iii) the correlations between the variations of the mean fields at different deformations was also neglected. Incorporating all these effects may considerably increase the complexity of the emulator. In such a case, it is more natural to directly use deep-learning techniques. In this work, we reported the first application of autoencoders to emulate the canonical wavefunctions of the HFB theory. Autoencoders are a form of deep neural network that compresses the input data, here the canonical wavefunctions, into a small-dimensional space called the latent representation. The encoder is trained simultaneously with a decoder by enforcing that the training data is left invariant after compression followed by decompression. In practice, the measure of such “invariance” is set by what is called the loss of the network. We discussed possible forms of the loss that are best adapted to learning quantum-mechanical wavefunctions of many-body systems such as nuclei. We showed that such an AE could successfully reduce the data into a space of dimension D = 10 while keeping the total error on the energy lower than ΔE = 150 keV (on average). The analysis of the latent space revealed well-identified structures in a few cases, which suggests the network can learn some of the physics underlying the data. This exploratory study suggests that AE could serve as reliable canonical wavefunctions generators. The next step will involve learning a full sequence of such wavefunctions, i.e., an ordered list, in order to emulate the full HFB many-body state.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MV led the study of autoencoders for canonical wavefunctions: design of the overall architecture of the autoencoders, development of the software stack and analysis of the results. NS led the study of Gaussian process for mean-field potentials—training and validation runs, code development and HFBTHO calculations—and supervised the whole project. IK implemented, tested and trained different architectures of autoencoders and helped with the analysis of the results. PM developed an HFBTHO module to use canonical wavefunctions in HFB calculations. KQ provided technical expertise about Gaussian processes and supervised MN, who implemented and fitted Gaussian processes to mean-field potentials. DR and RL provided technical consulting on deep neural network and the architecture of autoencoders. All authors contributed to the writing of the manuscript, and read and approved the submitted version.

Funding

This work was performed under the auspices of the United States Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. Computing support came from the Lawrence Livermore National Laboratory (LLNL) Institutional Computing Grand Challenge program.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1028370/full#supplementary-material

Footnotes

¹The pairing contribution lumps together terms coming from nuclear forces, Coulomb forces and possibly rearrangement terms.

²Following Dobaczewski et al. [35,117], we employ the ‘russian’ convention where the pairing field is defined from the pairing density $\tilde{\rho }(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime })$ rather than the pairing tensor. The quantity $\tilde{h}$ is related to the more traditional form of the pairing field Δ through: $\tilde{h}(\mathit{r}\sigma ,{\mathit{r}}^{\prime }{\sigma }^{\prime })=-2{\sigma }^{\prime }\mathrm{\Delta }(\mathit{r}\sigma ,{\mathit{r}}^{\prime }-{\sigma }^{\prime })$.

³This statement is obviously not true when solving the HFB equation directly in coordinate space. In the case of the local density discussed here, the expression $\rho (\mathit{r})={\sum }_{\sigma }{\sum }_{\mu }{V}_{\mu }(\mathit{r},\sigma )V_{\mu }^{*}(\mathit{r},\sigma )$ is just as computationally expensive as the canonical basis expression $\rho (\mathit{r})={\sum }_{\sigma }{\sum }_{\mu }{v}_{\mu }^2|{\phi }_{\mu }(\mathit{r},\sigma ){|}^2$.

⁴Note that B₃₂ vanishes for axially-symmetric shapes. As a result, the relative error can be artificially large for values of q₃₀ ≈ 0 b^3/2.

⁵This particular scission configuration corresponds to what is called cluster radioactivity Warda and Robledo [118]; Warda et al. [119]; Matheson et al. [120]. The heavy fragment is much larger than the light one. Here, ⟨A_H⟩ = 205.6, ⟨A_L⟩ = 34.4.

⁶A distance d(u, v) is norm-invariant if for any positive real number α and β, we have d(αu, βv) = d(u, v).

⁷Since time-reversal symmetry is conserved, the Fermi energy is located around states with indices μ_p ≈ 20 and μ_n ≈ 29. Therefore, our choice implies that in our energy window, about 1/3 of all states are below the Fermi level and about 2/3 of them are above it.

References

1. Eschrig R. Fundamentals of density functional theory. Leipzig: Teubner (1996).

Google Scholar

2. Schunck N. IOP expanding physics. Bristol, UK: IOP Publishing (2019).Energy density functional methods for atomic nuclei.

CrossRef Full Text | Google Scholar

3. Schunck N, Regnier D. Theory of nuclear fission. Prog Part Nucl Phys (2022) 125:103963. doi:10.1016/j.ppnp.2022.103963

CrossRef Full Text | Google Scholar

4. Schunck N, Robledo LM. Microscopic theory of nuclear fission: A review. Rep Prog Phys (2016) 79:116301. doi:10.1088/0034-4885/79/11/116301

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kejzlar V, Neufcourt L, Nazarewicz W, Reinhard PG. Statistical aspects of nuclear mass models. J Phys G: Nucl Part Phys (2020) 47:094001. doi:10.1088/1361-6471/ab907c

CrossRef Full Text | Google Scholar

6. Schunck N, O’Neal J, Grosskopf M, Lawrence E, Wild SM. Calibration of energy density functionals with deformed nuclei. J Phys G: Nucl Part Phys (2020) 47:074001. doi:10.1088/1361-6471/ab8745

CrossRef Full Text | Google Scholar

7. Erler J, Birge N, Kortelainen M, Nazarewicz W, Olsen E, Perhac AM, et al. The limits of the nuclear landscape. Nature (2012) 486:509–12. doi:10.1038/nature11188

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ney EM, Engel J, Li T, Schunck N. Global description of β⁻ decay with the axially deformed Skyrme finite-amplitude method: Extension to odd-mass and odd-odd nuclei. Phys Rev C (2020) 102:034326. doi:10.1103/PhysRevC.102.034326

CrossRef Full Text | Google Scholar

9. Mumpower MR, Surman R, McLaughlin GC, Aprahamian A. The impact of individual nuclear properties onr-process nucleosynthesis. Prog Part Nucl Phys (2016) 86:86–126. doi:10.1016/j.ppnp.2015.09.001

CrossRef Full Text | Google Scholar

10. Perlińska E, Rohoziński SG, Dobaczewski J, Nazarewicz W. Local density approximation for proton-neutron pairing correlations: Formalism. Phys Rev C (2004) 69:014316. doi:10.1103/PhysRevC.69.014316

CrossRef Full Text | Google Scholar

11. Utama R, Piekarewicz J, Prosper HB. Nuclear mass predictions for the crustal composition of neutron stars: A bayesian neural network approach. Phys Rev C (2016) 93:014311. doi:10.1103/PhysRevC.93.014311

CrossRef Full Text | Google Scholar

12. Utama R, Piekarewicz J. Refining mass formulas for astrophysical applications: A bayesian neural network approach. Phys Rev C (2017) 96:044308. doi:10.1103/PhysRevC.96.044308

CrossRef Full Text | Google Scholar

13. Utama R, Piekarewicz J. Validating neural-network refinements of nuclear mass models. Phys Rev C (2018) 97:014306. doi:10.1103/PhysRevC.97.014306

CrossRef Full Text | Google Scholar

14. Niu ZM, Liang HZ. Nuclear mass predictions based on Bayesian neural network approach with pairing and shell effects. Phys Lett B (2018) 778:48–53. doi:10.1016/j.physletb.2018.01.002

CrossRef Full Text | Google Scholar

15. Neufcourt L, Cao Y, Nazarewicz W, Olsen E, Viens F. Neutron drip line in the Ca region from bayesian model averaging. Phys Rev Lett (2019) 122:062502. doi:10.1103/PhysRevLett.122.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lovell AE, Mohan AT, Sprouse TM, Mumpower MR. Nuclear masses learned from a probabilistic neural network. Phys Rev C (2022) 106:014305. doi:10.1103/PhysRevC.106.014305

CrossRef Full Text | Google Scholar

17. Scamps G, Goriely S, Olsen E, Bender M, Ryssens W. Skyrme-Hartree-Fock-Bogoliubov mass models on a 3D mesh: Effect of triaxial shape. Eur Phys J A (2021) 57:333. doi:10.1140/epja/s10050-021-00642-1

CrossRef Full Text | Google Scholar

18. Mumpower MR, Sprouse TM, Lovell AE, Mohan AT. Physically interpretable machine learning for nuclear masses. Phys Rev C (2022) 106:L021301. doi:10.1103/PhysRevC.106.L021301

CrossRef Full Text | Google Scholar

19. Niu ZM, Liang HZ, Sun BH, Long WH, Niu YF. Predictions of nuclear β-decay half-lives with machine learning and their impact on r-process nucleosynthesis. Phys Rev C (2019) 99:064307. doi:10.1103/PhysRevC.99.064307

CrossRef Full Text | Google Scholar

20. Wang ZA, Pei J, Liu Y, Qiang Y. Bayesian evaluation of incomplete fission yields. Phys Rev Lett (2019) 123:122501. doi:10.1103/PhysRevLett.123.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lovell AE, Mohan AT, Talou P. Quantifying uncertainties on fission fragment mass yields with mixture density networks. J Phys G: Nucl Part Phys (2020) 47:114001. doi:10.1088/1361-6471/ab9f58

CrossRef Full Text | Google Scholar

22. Melendez JA, Drischler C, Furnstahl RJ, Garcia AJ, Zhang X. Model reduction methods for nuclear emulators. J Phys G: Nucl Part Phys (2022) 49:102001. doi:10.1088/1361-6471/ac83dd

CrossRef Full Text | Google Scholar

23. Giuliani P, Godbey K, Bonilla E, Viens F, Piekarewicz J. Bayes goes fast: Uncertainty quantification for a covariant energy density functional emulated by the reduced basis method (2022). [Dataset]. doi:10.48550/ARXIV.2209.13039

CrossRef Full Text | Google Scholar

24. Bonilla E, Giuliani P, Godbey K, Lee D. Training and projecting: A reduced basis method emulator for many-body physics (2022). [Dataset]. doi:10.48550/ARXIV.2203.05284

CrossRef Full Text | Google Scholar

25. Lasseri RD, Regnier D, Ebran JP, Penon A. Taming nuclear complexity with a committee of multilayer neural networks. Phys Rev Lett (2020) 124:162502. doi:10.1103/PhysRevLett.124.162502

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Parr R, Yang W. International series of monographs on chemistry. New York: Oxford University Press (1989).Density functional theory of atoms and molecules

Google Scholar

27. Dreizler R, Gross E. Density functional theory: An approach to the quantum many-body problem. Springer-Verlag (1990). doi:10.1007/978-3-642-86105-5

CrossRef Full Text | Google Scholar

28. Engel J. Intrinsic-density functionals. Phys Rev C (2007) 75:014306. doi:10.1103/PhysRevC.75.014306

CrossRef Full Text | Google Scholar

29. Barnea N. Density functional theory for self-bound systems. Phys Rev C (2007) 76:067302. doi:10.1103/PhysRevC.76.067302

CrossRef Full Text | Google Scholar

30. Engel YM, Brink DM, Goeke K, Krieger SJ, Vautherin D. Time-dependent Hartree-Fock theory with Skyrme’s interaction. Nucl Phys A (1975) 249:215–38. doi:10.1016/0375-9474(75)90184-0

CrossRef Full Text | Google Scholar

31. Dobaczewski J, Dudek J. Time-Odd components in the rotating mean field and identical bands. Acta Phys Pol B (1996) 27:45.

Google Scholar

32. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys (2003) 75:121–80. doi:10.1103/RevModPhys.75.121

CrossRef Full Text | Google Scholar

33. Lesinski T, Bender M, Bennaceur K, Duguet T, Meyer J. Tensor part of the Skyrme energy density functional: Spherical nuclei. Phys Rev C (2007) 76:014312. doi:10.1103/PhysRevC.76.014312

CrossRef Full Text | Google Scholar

34. Schunck N, Quinlan KR, Bernstein J. A Bayesian analysis of nuclear deformation properties with Skyrme energy functionals. J Phys G: Nucl Part Phys (2020) 47:104002. doi:10.1088/1361-6471/aba4fa

CrossRef Full Text | Google Scholar

35. Dobaczewski J, Flocard H, Treiner J. Hartree-Fock-Bogolyubov description of nuclei near the neutron-drip line. Nucl Phys A (1984) 422:103–39. doi:10.1016/0375-9474(84)90433-0

CrossRef Full Text | Google Scholar

36. Vautherin D, Brink DM. Hartree-Fock calculations with skyrme’s interaction. I. Spherical nuclei. Phys Rev C (1972) 5:626–47. doi:10.1103/PhysRevC.5.626

CrossRef Full Text | Google Scholar

37. Dobaczewski J, Dudek J. Solution of the Skyrme-Hartree-Fock equations in the Cartesian deformed harmonic oscillator basis I. The method. Comput Phys Commun (1997) 102:166–82. doi:10.1016/S0010-4655(97)00004-0

CrossRef Full Text | Google Scholar

38. Bender M, Bennaceur K, Duguet T, Heenen PH, Lesinski T, Meyer J. Tensor part of the Skyrme energy density functional. II. Deformation properties of magic and semi-magic nuclei. Phys Rev C (2009) 80:064302. doi:10.1103/PhysRevC.80.064302

CrossRef Full Text | Google Scholar

39. Hellemans V, Heenen PH, Bender M. Tensor part of the Skyrme energy density functional. III. Time-odd terms at high spin. Phys Rev C (2012) 85:014326. doi:10.1103/PhysRevC.85.014326

CrossRef Full Text | Google Scholar

40. Ryssens W, Hellemans V, Bender M, Heenen PH. Solution of the skyrme-hf+BCS equation on a 3D mesh, II: A new version of the Ev8 code. Comput Phys Commun (2015) 187:175–94. doi:10.1016/j.cpc.2014.10.001

CrossRef Full Text | Google Scholar

41. Valatin JG. Generalized Hartree-Fock method. Phys Rev (1961) 122:1012–20. doi:10.1103/PhysRev.122.1012

CrossRef Full Text | Google Scholar

42. Mang HJ. The self-consistent single-particle model in nuclear physics. Phys Rep (1975) 18:325–68. doi:10.1016/0370-1573(75)90012-5

CrossRef Full Text | Google Scholar

43. Blaizot JP, Ripka G. Quantum theory of finite systems. Cambridge: The MIT Press (1985).

Google Scholar

44. Ring P, Schuck P. The nuclear many-body problem. In: Texts and monographs in physics. Springer (2004).

Google Scholar

45. Dobaczewski J, Dudek J. Time-odd components in the mean field of rotating superdeformed nuclei. Phys Rev C (1995) 52:1827–39. doi:10.1103/PhysRevC.52.1827

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Stoitsov MV, Dobaczewski J, Nazarewicz W, Ring P. Axially deformed solution of the Skyrme-Hartree-Fock-Bogolyubov equations using the transformed harmonic oscillator basis. The program HFBTHO (v1.66p). Comput Phys Commun (2005) 167:43–63. doi:10.1016/j.cpc.2005.01.001

CrossRef Full Text | Google Scholar

47. Heyde K, Wood JL. Shape coexistence in atomic nuclei. Rev Mod Phys (2011) 83:1467–521. doi:10.1103/RevModPhys.83.1467

CrossRef Full Text | Google Scholar

48. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys (2016) 88:045004. doi:10.1103/RevModPhys.88.045004

CrossRef Full Text | Google Scholar

49. Griffin JJ, Wheeler JA. Collective motions in nuclei by the method of generator coordinates. Phys Rev (1957) 108:311–27. doi:10.1103/PhysRev.108.311

CrossRef Full Text | Google Scholar

50. Wa Wong C. Generator-coordinate methods in nuclear physics. Phys Rep (1975) 15:283–357. doi:10.1016/0370-1573(75)90036-8

CrossRef Full Text | Google Scholar

51. Reinhard PG, Goeke K. The generator coordinate method and quantised collective motion in nuclear systems. Rep Prog Phys (1987) 50:1–64. doi:10.1088/0034-4885/50/1/001

CrossRef Full Text | Google Scholar

52. Verriere M, Regnier D. The time-dependent generator coordinate method in nuclear physics. Front Phys (2020) 8:1. doi:10.3389/fphy.2020.00233

CrossRef Full Text | Google Scholar

53. Brink DM, Weiguny A. The generator coordinate theory of collective motion. Nucl Phys A (1968) 120:59–93. doi:10.1016/0375-9474(68)90059-6

CrossRef Full Text | Google Scholar

54. Onishi N, Une T. Local Gaussian approximation in the generator coordinate method. Prog Theor Phys (1975) 53:504–15. doi:10.1143/PTP.53.504

CrossRef Full Text | Google Scholar

55. Une T, Ikeda A, Onishi N. Collective Hamiltonian in the generator coordinate method with local Gaussian approximation. Prog Theor Phys (1976) 55:498–508. doi:10.1143/PTP.55.498

CrossRef Full Text | Google Scholar

56. Bloch C, Messiah A. The canonical form of an antisymmetric tensor and its application to the theory of superconductivity. Nucl Phys (1962) 39:95–106. doi:10.1016/0029-5582(62)90377-2

CrossRef Full Text | Google Scholar

57. Zumino B. Normal forms of complex matrices. J Math Phys (1962) 3:1055–7. doi:10.1063/1.1724294

CrossRef Full Text | Google Scholar

58. Marević P, Schunck N, Ney EM, Navarro Pérez R, Verriere M, O’Neal J. Axially-deformed solution of the Skyrme-Hartree-Fock-Bogoliubov equations using the transformed harmonic oscillator basis (iv) HFBTHO (v4.0): A new version of the program. Comput Phys Commun (2022) 276:108367. doi:10.1016/j.cpc.2022.108367

CrossRef Full Text | Google Scholar

59. Drischler C, Furnstahl RJ, Melendez JA, Phillips DR. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A bayesian approach with correlated uncertainties. Phys Rev Lett (2020) 125:202702. doi:10.1103/PhysRevLett.125.202702

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Kravvaris K, Quinlan KR, Quaglioni S, Wendt KA, Navrátil P. Quantifying uncertainties in neutron-α scattering with chiral nucleon-nucleon and three-nucleon forces. Phys Rev C (2020) 102:024616. doi:10.1103/PhysRevC.102.024616

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Acharya B, Bacca S. Gaussian process error modeling for chiral effective-field-theory calculations of np ↔ dγ at low energies. Phys Lett B (2022) 827:137011. doi:10.1016/j.physletb.2022.137011

CrossRef Full Text | Google Scholar

62. Pastore A, Shelley M, Baroni S, Diget CA. A new statistical method for the structure of the inner crust of neutron stars. J Phys G: Nucl Part Phys (2017) 44:094003. doi:10.1088/1361-6471/aa8207

CrossRef Full Text | Google Scholar

63. Kortelainen M, Lesinski T, Moré J, Nazarewicz W, Sarich J, Schunck N, et al. Nuclear energy density optimization. Phys Rev C (2010) 82:024313. doi:10.1103/PhysRevC.82.024313

CrossRef Full Text | Google Scholar

64. Kortelainen M, McDonnell J, Nazarewicz W, Reinhard PG, Sarich J, Schunck N, et al. Nuclear energy density optimization: Large deformations. Phys Rev C (2012) 85:024304. doi:10.1103/PhysRevC.85.024304

CrossRef Full Text | Google Scholar

65. Kortelainen M, McDonnell J, Nazarewicz W, Olsen E, Reinhard PG, Sarich J, et al. Nuclear energy density optimization: Shell structure. Phys Rev C (2014) 89:054314. doi:10.1103/PhysRevC.89.054314

CrossRef Full Text | Google Scholar

66. Higdon D, McDonnell JD, Schunck N, Sarich J, Wild SM. A Bayesian approach for parameter estimation and prediction using a computationally intensive model. J Phys G: Nucl Part Phys (2015) 42:034009. doi:10.1088/0954-3899/42/3/034009

CrossRef Full Text | Google Scholar

67. McDonnell JD, Schunck N, Higdon D, Sarich J, Wild SM, Nazarewicz W. Uncertainty quantification for nuclear density functional theory and information content of new measurements. Phys Rev Lett (2015) 114:122501. doi:10.1103/PhysRevLett.114.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Neufcourt L, Cao Y, Nazarewicz W, Viens F. Bayesian approach to model-based extrapolation of nuclear observables. Phys Rev C (2018) 98:034318. doi:10.1103/PhysRevC.98.034318

CrossRef Full Text | Google Scholar

69. Neufcourt L, Cao Y, Giuliani S, Nazarewicz W, Olsen E, Tarasov OB. Beyond the proton drip line: Bayesian analysis of proton-emitting nuclei. Phys Rev C (2020) 101:014319. doi:10.1103/PhysRevC.101.014319

CrossRef Full Text | Google Scholar

70. Neufcourt L, Cao Y, Giuliani SA, Nazarewicz W, Olsen E, Tarasov OB. Quantified limits of the nuclear landscape. Phys Rev C (2020) 101:044307. doi:10.1103/PhysRevC.101.044307

CrossRef Full Text | Google Scholar

71. Rasmussen CE, Williams CKI. Gaussian Processes for machine learning. Adaptive computation and machine learning. Cambridge, Mass: MIT Press (2006).

Google Scholar

72. Bartel J, Quentin P, Brack M, Guet C, Håkansson HB. Towards a better parametrisation of skyrme-like effective forces: A critical study of the SkM force. Nucl Phys A (1982) 386:79–100. doi:10.1016/0375-9474(82)90403-1

CrossRef Full Text | Google Scholar

73. Schunck N, Duke D, Carr H, Knoll A. Description of induced nuclear fission with Skyrme energy functionals: Static potential energy surfaces and fission fragment properties. Phys Rev C (2014) 90:054305. doi:10.1103/PhysRevC.90.054305

CrossRef Full Text | Google Scholar

74. Schunck N. Density functional theory approach to nuclear fission. Acta Phys Pol B (2013) 44:263. doi:10.5506/APhysPolB.44.263

CrossRef Full Text | Google Scholar

75. Dubray N, Regnier D. Numerical search of discontinuities in self-consistent potential energy surfaces. Comput Phys Commun (2012) 183:2035. doi:10.1016/j.cpc.2012.05.001

CrossRef Full Text | Google Scholar

76. Sadhukhan J. Microscopic theory for spontaneous fission. Front Phys (2020) 8:567171. doi:10.3389/fphy.2020.567171

CrossRef Full Text | Google Scholar

77. Bruinsma W, Perim E, Tebbutt W, Hosking S, Solin A, Turner R. Scalable exact inference in multi-output Gaussian processes. Proceedings of the 37th international Conference on machine learning (PMLR). Proc Machine Learn Res (2020) 119:1190.

Google Scholar

78. Álvarez MA, Rosasco L, Lawrence ND. Kernels for vector-valued functions: A review. FNT Machine Learn (2012) 4:195–266. doi:10.1561/2200000036

CrossRef Full Text | Google Scholar

79. Bender M, Bernard R, Bertsch G, Chiba S, Dobaczewski J, Dubray N, et al. Future of nuclear fission theory. J Phys G: Nucl Part Phys (2020) 47:113002. doi:10.1088/1361-6471/abab4f

CrossRef Full Text | Google Scholar

80. Schunck N. Microscopic description of induced fission. J Phys : Conf Ser (2013) 436:012058. doi:10.1088/1742-6596/436/1/012058

CrossRef Full Text | Google Scholar

81. Ryssens W, Heenen PH, Bender M. Numerical accuracy of mean-field calculations in coordinate space. Phys Rev C (2015) 92:064318. doi:10.1103/PhysRevC.92.064318

CrossRef Full Text | Google Scholar

82. Jin S, Bulgac A, Roche K, Wlazłowski G. Coordinate-space solver for superfluid many-fermion systems with the shifted conjugate-orthogonal conjugate-gradient method. Phys Rev C (2017) 95:044302. doi:10.1103/PhysRevC.95.044302

CrossRef Full Text | Google Scholar

83. Regnier D, Dubray N, Schunck N, Verrière M. Microscopic description of fission dynamics: Toward a 3D computation of the time dependent GCM equation. EPJ Web Conf (2017) 146:04043. doi:10.1051/epjconf/201714604043

CrossRef Full Text | Google Scholar

84. Zhao J, Nikšić T, Vretenar D. Microscopic self-consistent description of induced fission: Dynamical pairing degree of freedom. Phys Rev C (2021) 104:044612. doi:10.1103/PhysRevC.104.044612

CrossRef Full Text | Google Scholar

85. Lau NWT, Bernard RN, Simenel C. Smoothing of one- and two-dimensional discontinuities in potential energy surfaces. Phys Rev C (2022) 105:034617. doi:10.1103/PhysRevC.105.034617

CrossRef Full Text | Google Scholar

86. Baldi P. Autoencoders, unsupervised learning, and deep architectures. In Proceedings of ICML workshop on unsupervised and transfer learning (JMLR Workshop and Conference Proceedings) (2012), 37–49.

Google Scholar

87. Burda Y, Grosse R, Salakhutdinov R. Importance weighted autoencoders (2015). arXiv preprint arXiv:1509.00519.

Google Scholar

88. Chen M, Xu Z, Weinberger K, Sha F. Marginalized denoising autoencoders for domain adaptation (2012). arXiv preprint arXiv:1206.4683.

Google Scholar

89. Gong D, Liu L, Le V, Saha B, Mansour MR, Venkatesh S, et al. Memorizing normality to detect anomaly: Memory-augmented deep autoencoder for unsupervised anomaly detection. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. October 2019 (2019). p. 1705–14.

CrossRef Full Text | Google Scholar

90. Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. IEEE Trans Pattern Anal Mach Intell (2013) 35:1798–828. doi:10.1109/tpami.2013.50

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Zhang F, Du B, Zhang L. Saliency-guided unsupervised feature learning for scene classification. IEEE Trans Geosci Remote Sens (2014) 53:2175–84. doi:10.1109/tgrs.2014.2357078

CrossRef Full Text | Google Scholar

92. Yu J, Hong C, Rui Y, Tao D. Multitask autoencoder model for recovering human poses. IEEE Trans Ind Electron (2017) 65:5060–8. doi:10.1109/tie.2017.2739691

CrossRef Full Text | Google Scholar

93. von Neuman J, Wigner E. Uber merkwürdige diskrete Eigenwerte. Uber das Verhalten von Eigenwerten bei adiabatischen Prozessen. Physikalische Z (1929) 30:467–70.

Google Scholar

94. Teller E. The crossing of potential surfaces. J Phys Chem (1937) 41:109–16. doi:10.1021/j150379a010

CrossRef Full Text | Google Scholar

95. Longuet-Higgins HC, Öpik U, Pryce MHL, Sack RA. Studies of the jahn-teller effect. II. The dynamical problem. Proc R Soc Lond A (1958) 244:1. doi:10.1098/rspa.1958.0022

CrossRef Full Text | Google Scholar

96. Longuet-Higgins H. The intersection of potential energy surfaces in polyatomic molecules. Proc R Soc Lond A (1975) 344:147. doi:10.1098/rspa.1975.0095

CrossRef Full Text | Google Scholar

97.W Domcke, D Yarkony, and H Köppel, editors. Conical intersections: Theory, computation and experiment. Advanced series in physical chemistry, Vol. 17. World Scientific (2011). doi:10.1142/7803

CrossRef Full Text | Google Scholar

98. Larson J, Sjöqvist E, Öhberg P. Intersections in physics. An introduction to synthetic gauge theories. In Lecture notes in physics. Springer (2020). doi:10.1007/978-3-030-34882-3

CrossRef Full Text | Google Scholar

99. Haider Q, Gogny D. Microscopic approach to the generator coordinate method with pairing correlations and density-dependent forces. J Phys G: Nucl Part Phys (1992) 18:993–1022. doi:10.1088/0954-3899/18/6/003

CrossRef Full Text | Google Scholar

100. Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In: International conference on machine learning (PMLR) (2015). p. 448–56.

Google Scholar

101. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. J machine Learn Res (2014) 15:1929–58.

Google Scholar

102. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. June 2016 (2016). p. 770–8.

CrossRef Full Text | Google Scholar

103. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst (2012) 25.

Google Scholar

104. Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. In: European conference on computer vision. Springer (2014). p. 818–33.

CrossRef Full Text | Google Scholar

105. Sermanet P, Eigen D, Zhang X, Mathieu M, Fergus R, LeCun Y. Overfeat: Integrated recognition, localization and detection using convolutional networks (2013). arXiv preprint arXiv:1312.6229.

Google Scholar

106. Szegedy C, Ioffe S, Vanhoucke V, Alemi AA. Inception-v4, inception-resnet and the impact of residual connections on learning. San Francisco, CA: Thirty-first AAAI conference on artificial intelligence (2017).

Google Scholar

107. Li H, Xu Z, Taylor G, Studer C, Goldstein T. Visualizing the loss landscape of neural nets. Adv Neural Inf Process Syst (2018) 31.

Google Scholar

108. Zhang H, Wu C, Zhang Z, Zhu Y, Lin H, Zhang Z, et al. Resnet: Split-attention networks. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition September 2022 (2022), 2736–46.

Google Scholar

109. Radosavovic I, Kosaraju RP, Girshick R, He K, Dollár P. Designing network design spaces. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. June 2020. Seattle, WA, USA. IEEE (2020). p. 10428–36.

CrossRef Full Text | Google Scholar

110. Cubuk ED, Zoph B, Shlens J, Le QV. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition workshops. June 2020. Seattle, WA, USA. IEEE (2020). p. 702–3.

CrossRef Full Text | Google Scholar

111. Yun S, Han D, Oh SJ, Chun S, Choe J, Yoo Y. Cutmix: Regularization strategy to train strong classifiers with localizable features. In Proceedings of the IEEE/CVF international conference on computer vision. May 2019. IEEE (2019). p. 6023–32.

CrossRef Full Text | Google Scholar

112. Zhang H, Cisse M, Dauphin YN, Lopez-Paz D. mixup: Beyond empirical risk minimization. arXiv preprint arXiv:1710.09412 (2017).

Google Scholar

113. Wickramasinghe CS, Marino DL, Manic M. Resnet autoencoders for unsupervised feature learning from high-dimensional data: Deep models resistant to performance degradation. IEEE Access (2021) 9:40511–20. doi:10.1109/ACCESS.2021.3064819

CrossRef Full Text | Google Scholar

114. He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision February 2015 (2015), 1026–34.

CrossRef Full Text | Google Scholar

115. Kingma DP, Ba J. Adam: A method for stochastic optimization (2014). arXiv preprint arXiv:1412.6980.

Google Scholar

116. Deza M, Deza E. Encyclopedia of distances. Springer (2009). doi:10.1007/978-3-642-00234-2

CrossRef Full Text | Google Scholar

117. Dobaczewski J, Nazarewicz W, Werner TR, Berger JF, Chinn CR, Dechargé J. Mean-field description of ground-state properties of drip-line nuclei: Pairing and continuum effects. Phys Rev C (1996) 53:2809–40. doi:10.1103/PhysRevC.53.2809

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Warda M, Robledo LM. Microscopic description of cluster radioactivity in actinide nuclei. Phys Rev C (2011) 84:044608. doi:10.1103/PhysRevC.84.044608

CrossRef Full Text | Google Scholar

119. Warda M, Zdeb A, Robledo LM. Cluster radioactivity in superheavy nuclei. Phys Rev C (2018) 98:041602(R). doi:10.1103/PhysRevC.98.041602

CrossRef Full Text | Google Scholar

120. Matheson Z, Giuliani SA, Nazarewicz W, Sadhukhan J, Schunck N. Cluster radioactivity. Phys Rev C (2019) 99:041304. doi:10.1103/PhysRevC.99.041304${\mathrm{o}\mathrm{f}}_{118}^{294}{\mathrm{O}\mathrm{g}}_{176}$

CrossRef Full Text | Google Scholar