Sensing with sound enhanced acoustic metamaterials for fault diagnosis

Cost-effective technology for condition monitoring and fault diagnosis is of practical importance for equipment maintenance and accident prevention. Among many fault diagnosis methods, sound-based sensing technology has been highly regarded due to its rich information, non-contact and flexible installation advantages. However, noise from the environment and other machines can interfere with sound signals, decreasing the effectiveness of acoustic sensors. In this paper, a novel trumpet-shaped acoustic metamaterial (TSAM) with a high enhancement of sound wave selection is proposed to detect rotating machinery faults. Firstly, a numerical calculation was carried out to test the characteristics of the proposed metamaterials model. Secondly, a finite element simulation was implemented on the model to verify the properties of the designed metamaterials. Finally, an experiment was conducted based on an electrical fan to prove the effectiveness of the designed metamaterials. The results of the signal-to-noise ratio show more than 25% improvement, consistently demonstrating the potentiality of the designed acoustic metamaterials for enhancing the weak fault signal in acoustic sensing and the capabilities of contributing to a more cost-effective fault diagnosis technology.

Introduction

As sound waves propagate along a material medium, most often air, mechanical wave energy is transmitted [1]. Acoustic sensing technology, which takes advantage of the physics of sound, is regarded as one of the most effective non-destructive detecting techniques in the field of fault diagnosis [2–5] as sound waves contain more information than conventionally used vibrations. For example, a single microphone and microphone array can be flexibly installed to capture the operating acoustic signal of industrial machinery situated in a production hall [6]. The contactless sensors are strategically placed to optimize the quality of the recorded sounds. Nevertheless, the sound signals generated by machines can be contaminated and drowned out easily by typical factory environment noise [7], creating an excessively complex process for condition monitoring. Besides, conventional sound-based noise reduction technology involves a mass of electrical components and devices, such as electronic noise filters, which may potentially reduce the early-stage weak faults signal acquired from the machine. Therefore, it is necessary to develop an efficient sound sensing method for fault diagnosis of industrial machinery.

On the other hand, due to their unconventional properties to manipulate sound waves, acoustic metamaterials have received extensive attention as man-made structures. For instance, the gradient acoustic metamaterials (GAMs) achieve acoustic rainbow trapping [8], which traps broadband sound energy at multiple locations and focuses it selectively according to its frequency, indicating that they can be tailored for weak signal capturing. Also, some metamaterial-based devices have been developed to improve the detection of weak signals [9–12]. In recent years, GAMs with improved SNRs are effective in extracting weak periodic impulse signals. Chen et al. utilized a metamaterial with a gradient refractive index to extract pulse signals that had been drowned by noise as a result of improved signal-to-noise ratios [13]. Although there has been an increasing amount of research unveiled in enhancing signal sensing, how to apply to utilize the properties in practical application to capture weak signals for condition monitoring remains a slippery subject. A little previous research has been carried out, among the few cases, to detect nonlinear elastic sources, Miniaci et al. took the characteristics of filtration and focalizing shown by nonlinearity from the designed metamaterials, which were selected and reflected [14]. Moreover, G. Okudan et al. investigated integrating phononic crystal lenses on pipelines to amplify guided waves for improved ultrasonic inspection [15]. For single-sensor compressed identification of elastic vibrations, Jiang T et al. propose a metamaterial with randomized resonators coupled with randomly coupled local resonators [16]. It was proposed by Li C et al. that a smart metasurface shaft (SMST) could be used to identify vibration sources using a single sensor [17]. Overall, it is possible to capture the weak elastic signal using metamaterial-based signal-enhanced detection methods without applying conventional noise reduction techniques. It remains to be seen if metamaterials-based sensing can be high-performance to diagnose faults in machinery.

In this paper, a trumpet-shaped acoustic metamaterial (TSAM) with a high refractive index is invested. The TSAM has the potential of simple structure and easy modeling and thus fast optimization for flexible sensing performance to meet the needs in practice. Test results demonstrate that the TSAM is capable of magnifying the specific frequency range of the acoustic signals generated by operating machines, which contributes to the potential possibility of fault diagnosis with acoustic metamaterials. The remaining contents of this paper are organized as follows: Section 2 introduces the acoustic metamaterial design details including the geometrical design along with the analytical model and the finite element analysis for verification. Section 3 presents the experimental studies including the frequency response of a prototype of the proposed TSAM and the experimental verification of a defective electrical fan for efficiency. Section 4 is the conclusion of this paper.

Metamaterials design and numerical simulation

Geometrical design

Inspired by Li et al [18], through progressively turning evanescent signals into propagating waves, the authors demonstrated an acoustic metamaterial in fan-shaped that amplifies signals at subwavelength levels. In this paper, a trumpet-shaped acoustic metamaterial (TSAM) is designed as shown in Figure 1A. 24 circular slabs are arranged in an array whose radii are described by a function z(x) = 0.0006x²+9 along the x-axis as the geometric parameters are shown in Table 1. Compared with the structure which is assembled by arrays of rectangle slabs proposed by Chen et al [19], the gradient increment of the diameters aims to match the impedance between the air and the effective medium form by the designed metamaterials [9]. Moreover, in contrast to rectangle slabs [8, 10, 13], circle slabs ensure the overall symmetry of the metamaterial structure, even if the incident sound interacts with the TSAM through an arbitrary angle, the TSAM is capable to achieve equal sound enhancement when the distance between the sound source and the TSAM symmetric point is the same. As far as this article is concerned, sound pressure acquired from the center of the slabs is constant at any incident arbitrary angle that facilitates the signal acquisition which will be discussed in section 2. The combination of circular slabs and air forms an effective medium with refraction much higher than the air, shown in Figure 1B in a 2D schematic, which functions as a sound wave compressor to compress the sound wave propagates within the TSAM resulting in higher sound pressure amplitude.

FIGURE 1

FIGURE 1. (A) Schematic of trumpet-shaped acoustic metamaterials; (B) 2D effective medium schematic.

TABLE 1

TABLE 1. Geometric parameters (unit: mm).

Numerical analysis

Based on the geometrical acoustic design above, in this section, a numerical model was built and calculation was carried out to preliminarily demonstrate the properties of the TSAM. In the absence of any sound source, acoustic waves in a homogeneous medium are controlled by the following equation.

${\nabla }^{\mathbf{2}}\mathit{P}-\frac{\mathit{\rho }}{\mathit{\beta }}\bullet \frac{{\partial }^{\mathbf{2}}\mathit{P}}{\partial {\mathit{t}}^{\mathbf{2}}}=\mathbf{0}(1)$

In which, acoustic pressure is represented by P, and mass density and bulk modulus are denoted by two constitutive parameters ρ and β. The speed of sound v can be derived by ${\left(\beta /\rho \right)}^{0.5}$. If the effective medium is considered, the ρ and β can take extraordinary values such as negative, zero, density, or modulus. A primary concern with the TSAM proposed here is its gradual increase in refraction index. For simplicity, the effective medium of the proposed TSAM is shown in two dimensions as shown in Figure 1B. According to the following effective medium model [13], an array of circular aluminium slabs with air between them can be defined as a continuous effective medium, and the effective mass density ρ (along the x-axis and z-axis) and bulk modules β can be expressed as:

${\mathit{\rho }}_{\mathit{x}}={\mathit{F}}_{\mathit{r}}\bullet {\mathit{\rho }}_{\mathit{A}\mathit{l}}+\left(\mathbf{1}+{\mathit{F}}_{\mathit{r}}\right){\mathit{\rho }}_{\mathit{a}\mathit{i}\mathit{r}}(2)$

${\mathit{\rho }}_{\mathit{z}}=\frac{{\mathit{\rho }}_{\mathit{A}\mathit{l}}\bullet {\mathit{\rho }}_{\mathit{a}\mathit{i}\mathit{r}}}{{\left(\mathbf{1}-{\mathit{F}}_{\mathit{r}}\right)\mathit{\rho }}_{\mathit{A}\mathit{l}}+{\mathit{F}}_{\mathit{r}}\bullet {\mathit{\rho }}_{\mathit{a}\mathit{i}\mathit{r}}}(3)$

$\mathit{\beta }=\frac{{\mathit{\beta }}_{\mathit{A}\mathit{l}}\bullet {\mathit{\beta }}_{\mathit{a}\mathit{i}\mathit{r}}}{{\left(\mathbf{1}-{\mathit{F}}_{\mathit{r}}\right)\mathit{\beta }}_{\mathit{A}\mathit{l}}+{\mathit{F}}_{\mathit{r}}\bullet {\mathit{\beta }}_{\mathit{a}\mathit{i}\mathit{r}},}(4)$

where Fr is the filling ratio of circular slabs, in Section 3, a prototype of the proposed TSAM is fabricated with aluminum circular slabs, therefore, the density ${\rho }_{Al}=2700kg/m^3$ and the bulk modulus ${\beta }_{Al}=70GPa$ are set for numerical calculation in this section. Meanwhile, the bulk modulus and density of air are ${\beta }_{air}=1.4\times 10Pa$ and ${\rho }_{air}=1.2kg/m^3$ respectively. The analytical calculation is based on the approximation that the entire trumpet-shaped metamaterial structure can be decomposed into an unlimited number of uniform metamaterial sections, with the curl z(x) presents in Section 2.1, which is the function of the radii of the TSAM shown in Table 1, and effective refractive index for the metamaterial can be obtained as follow:

${\mathit{n}}_{\mathit{T}\mathit{S}\mathit{A}\mathit{M}}\left(\mathit{x},\mathit{f}\right)={\left({\mathit{n}}_{\mathit{a}\mathit{i}\mathit{r}}+\frac{{\mathit{\beta }}_{\mathit{a}\mathit{i}\mathit{r}}{\mathit{\rho }}_{\mathit{a}\mathit{i}\mathit{r}}}{{\mathit{\rho }}_{\mathit{z}}\mathit{\beta }}{\left(\mathbf{tan}\left[\mathit{\omega }\bullet \frac{\mathit{z}\left(\mathit{x}\right)}{\mathbf{2}}\bullet {\left(\frac{{\mathit{\rho }}_{\mathit{z}}}{\mathit{\beta }}\right)}^{\mathbf{0.5}}\right]\right)}^{\mathbf{2}}\right)}^{\mathbf{0.5}},(5)$

where ω = 2πf is the angular frequency. Combining the model proposed by Chen et al [10], an equation of the sound pressure along the x-axis and the frequency of the input sound, can be obtained according to Eq. 5:

${\mathit{P}}_{\mathit{T}\mathit{S}\mathit{A}\mathit{M}}\left(\mathit{x},\mathit{f}\right)=\frac{{\left(\mathbf{2}\mathit{\pi }{\mathit{\rho }}_{\mathit{a}\mathit{i}\mathit{r}}\right)}^{\mathbf{0.5}}\bullet {\left({\mathbf{1}-\mathit{n}}_{\mathit{m}\mathit{e}\mathit{t}\mathit{a}}\right)}^{-\mathbf{0.5}}}{\mathbf{cos}[\mathbf{arctan}({\mathit{\rho }}_{\mathit{z}}{\mathit{\rho }}_{\mathit{a}\mathit{i}\mathit{r}}^{-\mathbf{1}}{{(\mathit{n}}_{\mathit{m}\mathit{e}\mathit{t}\mathit{a}}^{\mathbf{2}}-\mathbf{1})}^{\mathbf{0.5}})]}.(6)$

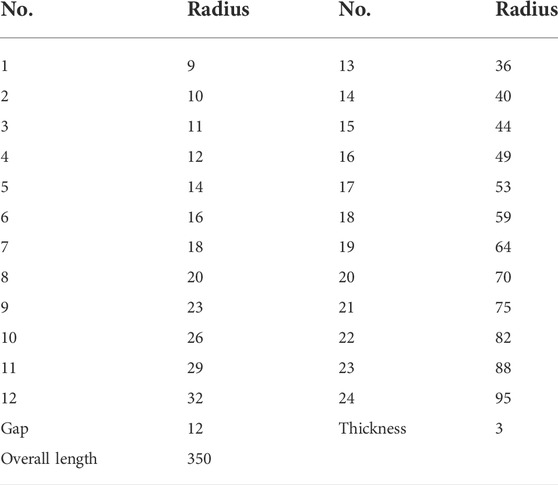
Based on Eqs 5, 6, a numerical calculation was conducted and Figure 2A demonstrates the results under the excitations of different single-frequency sounds. Taking five single frequency sounds for input excitations, significant amplifications appear along the position of the x-axis, which correlates to the TSAM’s specific locations namely the radius of the circular slabs z(x). From another point of view, shown in Figure 2B, taking five individual locations on the x-axis for observation, the model shows that different fixed locations target different frequency ranges of the acoustic signals. Overall, the analytical model shows that the further away from the origin (the higher the z(x) value), the lower the sound frequency it is targeting to enhance.

FIGURE 2

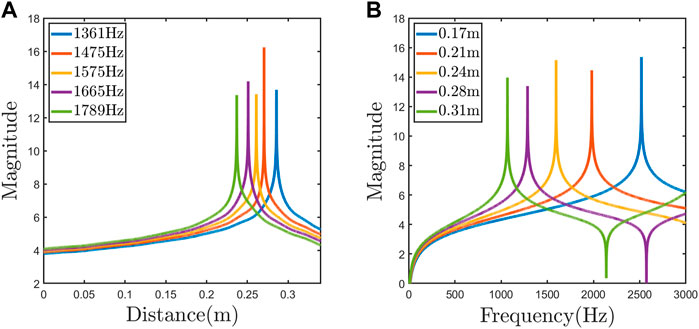
FIGURE 2. (A) Different single frequency sound excitation targeting at different locations on the x-axis of the TSAM; (B) Different locations on the x-axis of the TSAM targeting different sound frequencies.

Finite element analysis

To verify the analytic results further, a finite element analysis (FEA) was carried out to more accurately study the performance of the proposed TSAM, as FEA allows various influence parameters such as the discontinuous dimensions of the slabs and boundary conditions to be taken into account for more realistic analysis. As shown in Figure 3A, the sound pressure has been enhanced inside each slab gap under various single-frequency excitation. Along the x-axis, there is a sound pressure amplification (red rings) inside each slab gab in which a detecting point was set up, as illustrated in the figure by the black line. Moreover, for the larger diameter trumpet slab gaps, the frequency of amplified sound becomes lower, which is due to the higher effect of the effective refractive index achieved by the structure. These have verified the analytical analysis in the previous Section 1.2.

FIGURE 3

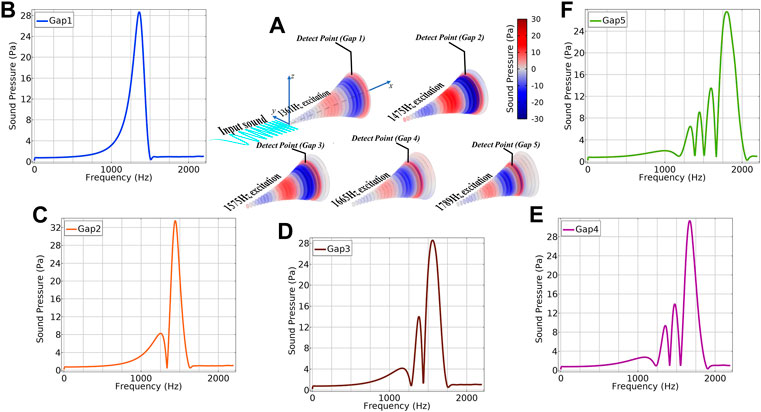
FIGURE 3. (A) Finite element analysis of TSAM under various excitation of 1361, 1475, 1575, 1665, and 1789 Hz, respectively; (B–F) Frequency responses of different detect points in Figure 3A.

The details of numerical results are presented in Figures 3B–F, which individually shows the frequency response of the TSAM ranging from 1Hz to 2500 Hz inside five successive gaps for the large diameter circular slabs when the input sound pressure is at 1 Pa. Amazingly, the structure allows a magnification gain of approximately 30 times for the gaps of interest. However, these finite element analysis results are preliminarily agreeable with the analytical calculation shown in Section 1.2, whether the TSAM functions as the results shown above in reality, still require further investigation in the following section.

Experimental verification

Acoustic metamaterials properties analysis

To verify the studies made in Sections 1, 2, a prototype of the proposed metamaterials was fabricated according to the geometrical parameters in Table 1. As shown in Figure 4A on the right, the prototype consists of 24 circular aluminium slabs penetrated through a threaded rod. A speaker connected to a signal generator is placed 1 m away from the tip of TSAM and sound was played with a frequency swept ranging from 1 Hz to 5000 Hz within 20 s. For the enhanced sound collection, an acoustic sensor array with eight channels was inserted inside the gap between two circular slabs shown in Figure 4B.

FIGURE 4

FIGURE 4. (A) Experimental setup and the prototype of TSAM (left lower) and experimental setup; (B) Schematic of sound data acquisition procedure and time waveform signal in Gap1∼Gap7 along with the signal collect outside the TSAM; (C) Frequency response of different detected areas in TSAM.

Based on the time domain sound signals, eight slab gaps are taken for demonstration, it shows that sound wave amplification occurs when a specific frequency sound excites on the specific slab gap, proving that the TSAM functions as a selective frequency enhancement device. It also demonstrates that the larger slabs, the lower the frequency that is targeted. In respect of the frequency domain, shown in Figure 4C, each slab gap manifests a narrow band amplification consistent with the time domain signal in Figure 4B. This experiment reveals that the TSAM is capable to split broadband sound signals selectively according to the frequency at various locations and generates a high local magnification on the sound amplitudes. Thus, the magnified frequency ranges of TSAM are individual with individual air gap locations.

Experimental studies of electrical fan fault detection with TSAM

To evaluate the performance of the proposed TSAM in fault diagnosis, a test was carried out to detect a small defect on one of the seven blades of an electrical fan, which is detailed in Figure 5A (left) and can be the common situation of pitting corrasions in many bladed systems. The distance between the fan and the tip of TSAM is 1 m. Acoustic signals were acquired from seven gaps and away from the structures, respectively for comparison. By using the second blade pass frequency as the central frequency, with sideband 200 Hz (upper and lower, respectively) to perform the envelope analysis. The envelope spectrum is more effective to highlight the asymmetric effect due to the fault. The envelope spectrums obtained are shown in Figure 5B. Compared with the sound signal collected in the air (No TSAM, yellow), whose frequency components can barely be seen, the other seven all exhibit significantly higher amplitudes at the rotating frequency and shows the high effectiveness of sound signal enhancement.

FIGURE 5

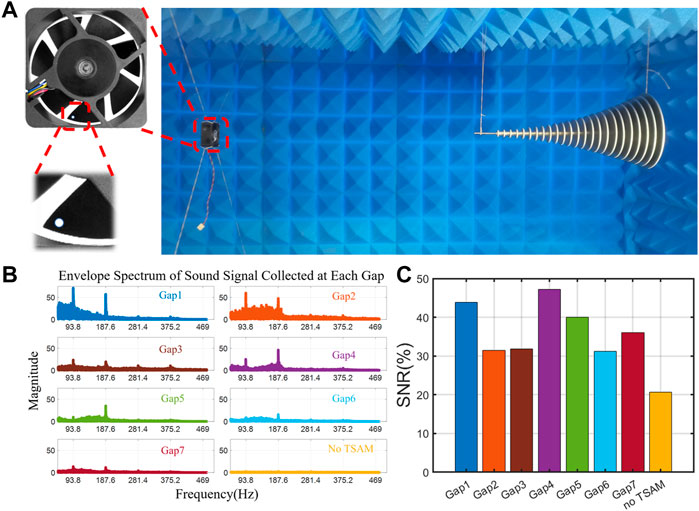
FIGURE 5. (A) A electrical fan with a diameter of 2 mm hole on one blade(left); (B) Envelope spectrum of the collected signal; (C) Full band SNR of the collected signals.

Despite the enhancement of the sound, it can be observed that all frequency components of the rotating defective fan are preserved in the sound signal acquired inside the TSAM, such functionality is highly critical for fault detection. In concern of the sound signal quality which is collected inside the gaps of TSAM, taking four harmonics of the fan rotational speed for observation on the SNRs, the seven signals collected inside the gaps show overwhelmingly up to 25% higher than the signals collected in the air (No TSAM), indicating the efficiency of fault detecting due to the improved signals from the TSAM.

Conclusion

This paper presents a novel acoustic structure based on acoustic metamaterial properties and evaluated it by monitoring and diagnosing the conditions of an electric fan. The conclusions are summarized as follows:

1) The proposed TSAM exhibits a strong narrow frequency band enhancement selectively, which improves the detective limit of the acoustic sensors for capturing the weak fault signal.

2) All information from the sound source is preserved after the enhancement by the TSAM due to the non-electronic components involved in the composition of the acoustic metamaterials.

3) Increased SNRs, being up to 25%, have been achieved in experimental tests indicating the possibility of applying acoustic metamaterial for high-performance fault diagnosis.

4) Acoustic metamaterials can be flexibly designed to target the concerned frequency band, which shows the potentiality of sensing enhancement practical application in other research fields.

In addition, the research also identified that multiband fusion, miniaturization, integration with electronics and manufacturing simplification, and so on to be addressed in future studies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SH: Experiment implementation, modeling, original draft. YL: Prototype fabrication, FEA, and editing. WT: Experimental setup and review. RD and FG: Signal processing, supervising, funding acquisition. QH and AB—supervised the Research.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52275102), the Special Projects in Key Areas of the Department of Education Guangdong Province (Grant No. 2022ZDZX3044), and the Young Innovative Talents Project of Department of Education Guangdong Province (Grant No. 2022KQNCX154).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1027895/full#supplementary-material

References

1. Hillhouse J. Sound that matters: Basic knowledge for electric motor application. IEEE Ind Appl Mag (2012) 18(1):38–45. doi:10.1109/mias.2011.943102

CrossRef Full Text | Google Scholar

2. Sun Y, Cao Y, Xie G, Wen T. Sound based fault diagnosis for RPMs based on multi-scale fractional permutation entropy and two-scale Algorithm. IEEE Trans Veh Technol (2021) 70(11):11184–92. doi:10.1109/tvt.2021.3090419

CrossRef Full Text | Google Scholar

3. Hou J, Ma J, Fang Z, Ming W, He W. Bearing fault diagnosis based on spatial features of 2.5 dimensional sound field. Shock and Vibration (2019) 2019:1–10. doi:10.1155/2019/4678491

CrossRef Full Text | Google Scholar

4. Naid A, Gu FS, Shao YM, Al-Arbi S, Ball A. Bispectrum analysis of motor current signals for fault diagnosis of reciprocating compressors. Key Eng Mater (2009) 413-414:505–11. doi:10.4028/www.scientific.net/kem.413-414.505

CrossRef Full Text | Google Scholar

5. Lu K, Gu JX, Fan H, Sun X, Li B, Gu F. Acoustics based monitoring and diagnostics for the progressive deterioration of helical gearboxes. Chin J Mech Eng (2021) 34(1):82. doi:10.1186/s10033-021-00603-1

CrossRef Full Text | Google Scholar

6. Liebetrau J. (2017). N.d.stackpath. [online] www.processingmagazine.com. Available from: https://www.processingmagazine.com/process-control-automation/article/15587140/predictive-maintenance-with-airborne-sound-analysis (Accessed September 16, 2021).

Google Scholar

7. Tagawa Y, Maskeliūnas R, Damaševičius R. Acoustic anomaly detection of mechanical failures in noisy real-life factory environments. Electronics (2021) 10(19):2329. doi:10.3390/electronics10192329

CrossRef Full Text | Google Scholar

8. Zhu J, Chen Y, Zhu X, Garcia-Vidal FJ, Yin X, Zhang W, et al. Acoustic rainbow trapping. Sci Rep (2013) 3(1):1728. doi:10.1038/srep01728

CrossRef Full Text | Google Scholar

9. Xinjing H, Yutian Y, Jinyu M, Jian L, Xiaobo R. An acoustic metamaterial-based sensor capable of multiband filtering and amplification. IEEE Sens J (2020) 20(8):4413–9. doi:10.1109/jsen.2019.2962279

CrossRef Full Text | Google Scholar

10. Chen Y, Liu H, Reilly M, Bae H, Yu M. Enhanced acoustic sensing through wave compression and pressure amplification in anisotropic metamaterials. Nat Commun (2014) 5(1):5247. doi:10.1038/ncomms6247

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chen YY, Zhu R, Barnhart MV, Huang GL. Enhanced flexural wave sensing by adaptive gradient-index metamaterials. Sci Rep (2016) 6(1):35048. doi:10.1038/srep35048

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Colombi A, Ageeva V, Smith RJ, Clare A, Patel R, Clark M, et al. Enhanced sensing and conversion of ultrasonic Rayleigh waves by elastic metasurfaces. Sci Rep (2017) 7(1):6750. doi:10.1038/s41598-017-07151-6

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chen T, Yu D, Wu B, Xia B. Weak signals detection by acoustic metamaterials-based sensor. IEEE Sens J (2021) 21(15):16815–25. doi:10.1109/jsen.2021.3076860

CrossRef Full Text | Google Scholar

14. Miniaci M, Gliozzi AS, Morvan B, Krushynska A, Bosia F, Scalerandi M, et al. Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Phys Rev Lett (2017) 118(21):214301. doi:10.1103/physrevlett.118.214301

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Danawe H, Okudan G, Ozevin D, Tol S. Conformal gradient-index phononic crystal lens for ultrasonic wave focusing in pipe-like structures. Appl Phys Lett (2020) 117(2):021906. doi:10.1063/5.0012316

CrossRef Full Text | Google Scholar

16. Jiang T, Li C, He Q, Peng ZK. Randomized resonant metamaterials for single-sensor identification of elastic vibrations. Nat Commun (2020) 11(1):2353. doi:10.1038/s41467-020-15950-1

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li C, Jiang T, He Q, Peng Z. Smart metasurface shaft for vibration source identification with a single sensor. J Sound Vibration (2021) 493:115836. doi:10.1016/j.jsv.2020.115836

CrossRef Full Text | Google Scholar

18. Li J, Fok L, Yin X, Bartal G, Zhang X. Experimental demonstration of an acoustic magnifying hyperlens. Nat Mater (2009) 8(12):931–4. doi:10.1038/nmat2561

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ganye R, Chen Y, Liu H, Bae H, Wen Z, Yu M. Characterization of wave physics in acoustic metamaterials using a fiber optic point detector. Appl Phys Lett (2016) 108(26):261906. doi:10.1063/1.4955058

CrossRef Full Text | Google Scholar