Coalescence preference dynamics for droplet growth during single-component fluid phase separation

When two unequal sized droplets coalesce to form a final product drop, the product forms closer to the larger of its two parents—a phenomenon known as the coalescence-preference dynamics. In this paper, using the state-of-the-art molecular dynamics simulations, we study the time-dependent properties of coalescence preference for phase segregating single-component fluids, over a broad range of fluid density and temperature. Hydrodynamics is fully taken into account. Coalescence time is observed to be shorter for parents with larger size ratio. Our simulation data also points towards an interesting power-law dependence of the coalescence time on the droplet size ratio, which is universal for both droplets and microbubbles.

1 Introduction

In the last decade there has been huge scientific involvement to understand the coalescence properties of bubbles and droplets. Coalescence and breakage of bubbles is common in nature; two bubbles upon touching each other try to reduce their surface energy in order to form a stable configuration [1] and during this process, which is known as coalescence, the droplets undergo changes in shape. Most of the literature for coalescence is dedicated to the study of liquid bridge, spreading and jumping of bubbles on a solid surface, coalescence of sessile droplets, etc [2–4]. Investigations on the coalescence preference dynamics are very few and started only recently [5–8]. When two liquid droplets (bubbles) touch each other and eventually coalesce to form a single final droplet (bubble), the spatial position of the product droplet (bubble) is observed to be closer to the larger of its two parents—a phenomenon known as coalescence preference (CP) dynamics. The relative positioning of the product drop (bubble) with respect to its parents has been reported earlier [5] to obey a power law scaling as a function of the parent size inequality. The higher the difference in the size of the two parents, the closer the final droplet forms to the larger parent. Experimentally, the quantification of such spatial and temporal properties of coalescence preference is highly challenging due to the hurdles involved with the precision measurements of the droplet centers and their radii. In highly dense fluids, this becomes even harder because of the overlap of nearby droplets. From computer simulation point of view, such studies are difficult because of the requirement of large system sizes (in order to avoid finite-size effects) which in turn makes the molecular dynamics simulations very expensive. Beside, to reach the limit of large droplet size ratio one requires a high droplet size dispersion which is difficult to achieve. Despite these obstacles, there have been successful attempts in the last decade trying to understand the coalescence preference for droplets [5, 6], microbubbles [5]; albeit for spatial properties. Time-dependent properties of coalescence preference are very rarely studied [7] and requires significant future investigations encompassing theory, experiments, and computer simulations. Knowledge on the universal features of various spatial and temporal quantities and the relevant power-law exponents are also crucial for a better understanding of this phenomenon.

An important class of systems which show coalescence of droplets are phase segregating fluids. The mechanism and dynamics of phase separation in fluids depend on a variety of control parameters, viz., fluid critical density, fluid temperature, viscosity, hydrodynamic effects, etc. A single-component fluid exhibits a second-order phase transition at its critical point of vapor–liquid transition which is exemplified schematically in Figure 1. Here, T_c marks the critical temperature above which the fluid happens to be in a homogeneous state. Density of the fluid at the critical point is ρ_c. The equilibrium state below T_c is the coexistence of liquid and vapor phases. When an initially homogeneous fluid at a very high temperature (T > T_c) is suddenly quenched below T_c, it falls out-of-equilibrium and undergoes a non-equilibrium phase separation process [9, 10]. If the fluid is quenched at its critical density ρ_c percolating domain structure is formed which grows with time. On the other hand, when the fluid is rapidly quenched at an off-critical density (marked by a cross in Figure 1), phase segregation proceeds via the formation of liquid droplets floating in the background vapor phase. With time, these liquid droplets undergo Brownian motion, they collide with each other [11, 12] and form bigger coalesced drops. This coalescence process conserves the total mass of the colliding droplets [13, 14] and takes place under the influence of hydrodynamics.

FIGURE 1

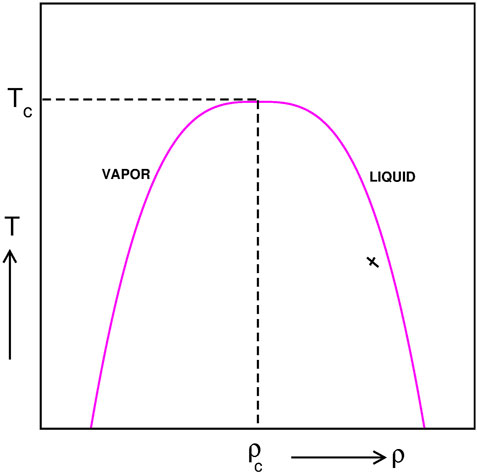
FIGURE 1. Schematic phase diagram of a single-component fluid in the temperature-density plane. T_c and ρ_c mark the critical temperature and critical density, respectively. Above T_c the fluid is in a homogeneous state and below T_c it is in a two-phase coexistence state. Upon a temperature quench from a high temperature inside the binodal at ρ_c percolating domain morphology is observed. Cross refers to an off-critical quench for which droplets form and they grow in size by coalescence among each other.

In this paper, using the state-of-the-art molecular dynamics (MD) simulations, we study the coalescence preference of liquid droplets during phase separation of a three-dimensional off-critical single-component fluid. The mechanism of coalescence of droplets involve hydrodynamics. Our primary focus is on the effects of the droplet size ratio on the time-dependent properties of coalescence preference (CP). To the best of our knowledge, this is the first study on the temporal properties of CP for phase segregating liquids.

A typical coalescence event is explained in Figure 2 schematically. Here, L, S, p mark the centres of the larger parent, smaller parent, and the product, respectively. Larger parent has radius R_L and the smaller one R_S. The distance between the product and the larger (smaller) parent is denoted by a_L (a_S). As reported in earlier studies in the literature [5], the relative positioning of the product droplet exhibits an algebraic scaling with respect to the parent size ratio as $(a_L/a_S)\sim {(R_L/R_S)}^{-q}$, where, q is the associated power-law exponent. Earlier experiments reveal that q ≃ 4.3 for droplet coalescence and q ≃ 5 for free bubbles [5]. Simple theoretical arguments involving the surface energy minimization led to a value of q ≃ 5.3. Such differences clearly point towards the influence of fluid density, droplet number density, etc., on the overall coalescence process. Effects of density on the spatial proximity of the product towards the larger parent was investigated experimentally for microbubbles [6]. There it was observed that for a dense bubble system presence of too many neighbouring bubbles might restrict the closeness of the product towards the bigger parent and hence can lead to a lower value of the relevant scaling exponent approx. 2 (rather than 5). On the other hand, droplet coalescence during phase separation in a single-component fluid exhibits q ≃ 3; here the driving mechanism involves the formation of the product at the centre-of-mass position of the parents [8].

FIGURE 2

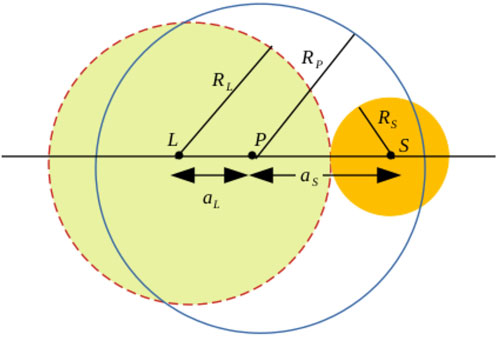
FIGURE 2. Schematic of two unequal-sized coalescing parent droplets with centres at L (large) and S (small) and the product droplet with a centre at P. The separation distances between the larger and smaller parents from the centre of the coalesced drop are marked as a_L and a_S, respectively. The radii of the droplets are denoted by R_L (larger parent), R_S (smaller parent), and R_P (product).

In this paper, we focus on the temporal properties of such coalescence events. Particular focus is on the coalescence time τ which is defined as the time required for the product droplet to form completely starting from the time when the two parents just touch each other. Our study reveals that the larger the size inequality of the parent droplets, the shorter time it takes for the product to form. Within the range of droplet size dispersion available in our study, our MD simulation data indicates the presence of a power-law dependence of τ on the droplet size ratio: $\tau \sim {(R_L/R_S)}^{-n}$. An algebraic behavior was also reported earlier for microbubbles from Lattice-Boltzmann simulations.

2 Model and methods

2.1 Model

A single-component fluid is considered which is modelled by mono-disperse particles of diameter σ and mass m which are interacting with each other via a 12–6 Lennard-Jones potential

$U\left(r_{ij}\right)=4{\epsilon }_{ij}\left[{\left(\frac{\sigma }{r_{ij}}\right)}^{12}-{\left(\frac{\sigma }{r_{ij}}\right)}^6\right],(1)$

where, ɛ is the interaction strength and r_ij is the spatial distance between two particles i and j. To reduce computational time, this potential is truncated at a suitable distance r = r_c = 2.5σ and further modified [15, 16] to make both the potential and force continuous at r_c as follows:

$\mathcal{U}\left(r_{ij}=|{\vec{r}}_i-{\vec{r}}_j|\right)=U\left(r_{ij}\right)-U\left(r_c\right)-\left(r_{ij}-r_c\right){\left.\frac{dU}{dr}\right|}_{r_{ij}=r_c};r_{ij}<r_c,(2)$

and 0 otherwise. Here, the density is expressed as ρ = Nσ³/L³; N being the total number of particles in a cubic simulation box of side length L. Periodic boundary conditions [17] are applied along all Cartesian directions. The phase diagram of this model fluid in the temperature-density plane (equivalent to Figure 1) was studied before [18] which estimated the values of the critical density ρ_c ≃ 0.3 and the critical temperature k_BT_c ≃ 0.9ɛ, for ɛ = 1. Based on this knowledge on the critical point we decided the quench temperature T of the fluid to be 0.67T_c which corresponds to a phase segregated state.

2.2 Simulation method

The initial configurations of the fluid are prepared at a very high temperature T_i = 5T_c using molecular dynamics (MD) simulation method [17, 19]. For this purpose, particles are assigned random positions within a cubic simulation box of length L by making sure that there is no particle overlap. Initial velocity is given from a Gaussian distribution at T_i = 5T_c. Next, the positions and velocities of the particles are updated within the MD scheme [20]. A velocity Verlet algorithm is used for the velocity update. Inter-particle forces for this purpose is calculated using Eq. 2. By running MD steps over a sufficiently long time, an equilibrium configuration at the temperature 5T_c is obtained. Next, this configuration is rendered a sudden temperature change at T_f = 0.67T_c. For this purpose, particles are given new velocities from a Gaussian distribution at T_f following the equipartition theorem. Next, the particle positions and velocities are updated again within the MD simulation [19] in the canonical ensemble using the Nosé-Hoover thermostat (NHT) [21]. A thermostat is required to maintain the system temperature to a desired fixed value (in this case, T_f). During MD runs, Newton’s equations of motion are solved using the velocity-Verlet algorithm, with a time step of integration dt = 0.005τ₀; ${\tau }_0=\sqrt{m{\sigma }^2/\epsilon }$ being the LJ time unit here. Periodic boundary conditions [17] are applied along all Cartesian spatial directions. T values mentioned here are all in the unit of k_B/ɛ. While the MD simulation runs are going on following a temperature quench from T_i to T_f, data for particle position are stored from which droplet configurations are captured.

2.3 Identification of droplets

In order to be able to identify the droplets from the MD simulation data, a smart mapping technique is applied [22]. First, the local density $\bar{\rho }$ around each constituent particle in the fluid is calculated. If $\bar{\rho }$ is larger than a critical value the particle is marked as a member of any of the existing liquid droplets. Now, the spatial distances among these marked particles are calculated and based on their proximity towards each other, various droplets are identified. Following this method, one can easily access information about the number of particles in each droplet, the volume and the radius of each droplet. From this, one can calculate the droplet radius R. While calculating this, two assumptions are made [1]: droplets have spherical shape and [2] that the local density within one droplet is constant N₀ = 4πρ₀R³/3 (N₀ being number of particles in a droplet and ρ₀ being the local density within the droplet). This leads to the fact the volume of a droplet is proportional to the cube of its radius R. Once the coordinates of all particles constituting a droplet is identified, its centre location is identified using the centre-of-mass rule. A system configuration at a certain time contains multiple droplets. By looking at configurations at different times, we first identify a pair of droplets which are undergoing a coalescence event as a function of time. We locate the centres of these two coalescing droplets at the moment they touch each other. Next, at subsequent times (as the coalescence is going on) the centres of these two droplets are recorded until a final almost spherical product drop has formed. Thus, we record the locations of the two parents and the final product. When the locations of the two parent droplets have coincided with each other and they no longer change with time - the final product has formed. It was shown in an earlier study [8] that these coalescence events are volume conserving: V_P = V_S + V_L, where Vs. are the volumes of the product, smaller and larger parents, respectively (Figure 3).

FIGURE 3

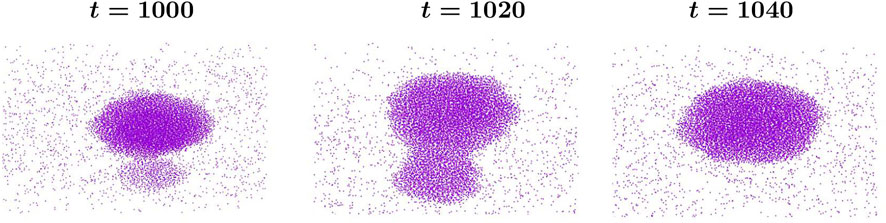
FIGURE 3. Molecular dynamics simulation snapshots of a coalescence event at different times t expressed in units of τ₀. See main text for the definition of τ₀. Two droplets touch at time t =1000, a thin liquid bridge forms and evolves with time until a single product drop forms at t =1040, in the background of the low-density vapor phase. System size and temperature are L =100 and T =0.68T_c, respectively. Phase separation progresses via the coalescence of liquid droplets.

2.4 Definition of coalescence time

Coalescence time for a coalescence event here is defined as the time interval from the moment two droplets just touch to the time when their centres have coincided with each other and no longer change. This will be further illustrated in Figure 4.

FIGURE 4

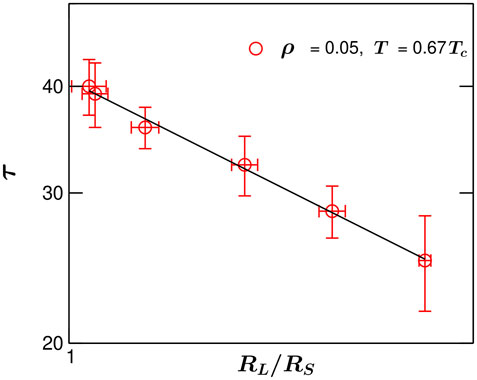
FIGURE 4. Coalescence time τ vs. the parent droplet size ratio R_L/R_S on the double-logarithmic scale, during droplet coalescence in a phase-segregating single-component fluid. Data correspond to the overall system density ρ =0.05 and the quench temperature T =0.67T_c and coalescence events are collected from various system sizes L*. The solid line refers to a power-law decay with an exponent n =1.1.

3 Results

Figure 4 represents the time evolution of two unequal sized coalescing droplets. Data are from molecular dynamics (MD) simulations. Morphologies at a few subsequent times are shown. Time t is in unit of τ₀ defined before. Various stages of the coalescence event are shown here: (a) touching of the two droplets, (b) formation of a dumbell-like neck, and (c) the final single product drop. Note that these droplets are three-dimensional and they are spherical only in a statistical sense. The constituent particles of the background low-density vapor phase are also marked in the snapshots. Clearly, the droplet density is much higher than the background fluid. The physical mechanism of this coalescence is the Brownian coagulation as described in [14].

In Figure 5 the dependence of the coalescence time τ on the droplet size ratio is presented for a value of density ρ = 0.05 and the quench temperature T = 0.67T_c. Here, τ is defined as the time required for a coalescence process to complete starting from the first touching between the two parents. The dependence of τ on the parent size ratio R_L/R_S is plotted on a double-logarithmic scale. One major hurdle with the simulation of such droplet coalescence is that the droplet size dispersion very low. Hence, finding coalescence of droplets of very different sizes is rare. Thus the x − axis in this plot is limited to a rather short window. Because these droplets are three-dimensional, pinpointing the exact time when they touch is also difficult. This leads to a large errorbar in the coalescence time τ. Each point in Figure 5 corresponds to 7-8 coalescence events and the errorbars are calculated by considering the average of all these coalesence events at a particular combination of R_L/R_S. Note that the errorbar in R_L/R_S arises from the fact that the numerical mapping of the spherical droplets is very tricky in three spatial dimensions and this makes the estimate of dropler radius and thus R_L/R_S subjected to error. Due to the same reason the estimataion of the exact time when two droplets touch each other is also prone to error. In Figure 5, the solid line corresponds to a power-law behavior [7].

$\tau \sim {\left(R_L/R_S\right)}^{-n},(3)$

where, n is the associated dynamic exponent. This phenomenological relation describes the dependence of coalescence time on the size inequality of the parents. For a finite positive value of n, coalescence time τ decreases as the parent size ratio R_L/R_S becomes larger. In the limiting case of R_L/R_S → ∞, one obtains τ → 0. An algebraic trend is captured within our MD simulation data; albeit over a rather short size ratio range. It is evident that the formation of a product drop takes lesser time for parents with more size inequality. In Figure 4, the solid line refers to a fit to the data using Eq. 3. Which yields n ≃ 1.1. Chi-square of fitting is 2.744 and the correlation coefficient 0.993. This value of n for liquid droplets is rather different from the one (n ≃ 0.7) observed in case of bubbles [7].

FIGURE 5

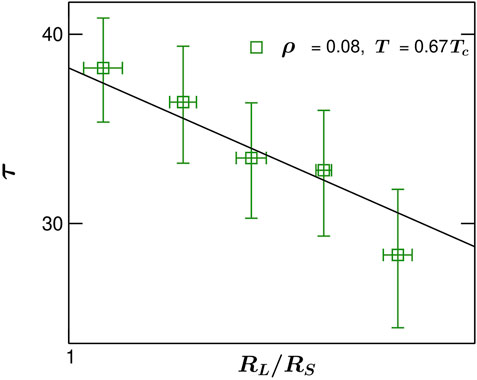
FIGURE 5. Same as Figure 4, but for density ρ =0.08 and temperature T =0.67T_c. Symbols correspond to molecular dynamics simulation data and the solid line is a fit to that with n ≃0.67.

Next, in order to study the effects of density change on the temporal decay exponent, in Figure 5, we present the temporal scaling of τ for a higher density ρ = 0.08 and temperature same as in Figure 4 (T = 0.67T_c). Both the ρ values are chosen judicially such that at those densities one observes spherical droplets in the fluid. It was demonstrated [12] that as the density of a fluid changes beyond a certain threshold value one observes percolating morphology (not droplets). The ρ values used in this work are suitable for droplet coalescence events. In Figure 5, the symbols stand for the MD simulation data and the solid line is a fit. The value of the power-law decay exponent n turns out to be slightly lower 0.67. However, at this point we do not aim to conclude about the dependence of this decay exponent on the fluid density due to the lack of very high precision data. With higher computer resources and more refined temporal and spatial resolutions one can of course investigate the dependence on density.

Our study points towards the presence of an algebraic dependence of coalescence time τ during coalescence on the parent size ratio R_L/R_S which appear to be universal for both microbubbles [23] and droplets. However, it seems like the value of the temporal exponent n is susceptible to bubbles/droplets. For bubbles the reported exponent value is 0.7 whereas our work points towards a value 1.1 for droplets. Here we point out that the density and viscosity of the background host fluid will influence the coalescence preference dynamics and hence the associated power-law exponents as well. For droplets which are suspended in a vapor phase the background density is much lower as compared to the bubbles suspended in a liquid. Hence, differences in the exponents for droplets and bubbles are also expected.

4 Summary

In conclusion, we present the first molecular dynamics simulation study of the coalescence preference dynamics for liquid droplets in a single-component fluid undergoing phase separation. The droplets undergo coalescence during which the total mass of the two coalescing droplets is conserved. The effects of the parent droplet size ratio for unequal-sized droplets is investigated systematically in details. It is observed that the formation of the product droplet is faster for parent droplets with stronger size inequality. Unequal sized droplets always coalesce much faster than equal sized droplets. Interestingly, our results indicates the presence of a power-law dependence of coalescence time τ on the droplet size ratio R_L/R_S. The associated exponent n as estimated from our molecular dynamics data n ≃ 1.1 is slightly different from that for microbubbles in water. Because of the short coalescence time and rather narrow range of droplet size, quantitative analysis of such scaling behavior within the framework of molecular dynamics simulations is quite challenging. Also, tracking the three dimensional droplets is another tricky job. In future, we will undertake the study of flow pattern around two coalescing droplets in order to understand how this might affect the coalescence time. Investigating similar phenomenon for liquid droplets in a binary fluid will provide important information about universality which we leave out as a future exercise. We hope this work will promote future studies on the time-dependence of coalescence preference for which till date there is no report from experiments. To the best of our knowledge, this is the first study on the temporal scaling of coalescence preference dynamics for non-equilibrium phase segregation phenomena.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JS contributed in the analysis of the data and writing the manuscript. SR conceived the project and contributed to the analysis of the data, writing the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lohse D, Zhang X. Surface nanobubbles and nanodroplets. Rev Mod Phys (2015) 87:981–1035. doi:10.1103/revmodphys.87.981

CrossRef Full Text | Google Scholar

2. Koplik J. Surface impacts and collisions of particle-laden nanodrops. Phys Fluids (1994) (2015) 27:082001. doi:10.1063/1.4928029

CrossRef Full Text | Google Scholar

3. Gross M, Steinbach I, Raabe D, Varnik F. Viscous coalescence of droplets: A lattice Boltzmann study. Phys Fluids (2013) 25:052101. doi:10.1063/1.4803178

CrossRef Full Text | Google Scholar

4. Li T, Li M, Zhang L, Yan M, Li H. Molecular dynamics study of the temperature-dependent coalescence of liquid nanodrops: Implications for microfluidics. ACS Appl Nano Mater (2019) 12:7978–88. doi:10.1021/acsanm.9b02018

CrossRef Full Text | Google Scholar

5. Weon BM, Je JH. Coalescence preference depends on size inequality. Phys Rev Lett (2012) 108:224501. doi:10.1103/physrevlett.108.224501

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kim Y, Lim SJ, Gim B, Weon BM. Coalescence preference in densely packed microbubbles. Sci Rep (2015) 5:7739. doi:10.1038/srep07739

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Chen R, Yu H, Zhu L, Patil RM, Lee T. Spatial and temporal scaling of unequal microbubble coalescence. Aiche J (2017) 63:1441–50. doi:10.1002/aic.15504

CrossRef Full Text | Google Scholar

8. Roy S. Coalescence preference and droplet size inequality during fluid phase segregation. EPL (2018) 121:34001. doi:10.1209/0295-5075/121/34001

CrossRef Full Text | Google Scholar

9. Bray AJ. Theory of phase-ordering kinetics. Adv Phys X (2002) 51:481–587. doi:10.1080/00018730110117433

CrossRef Full Text | Google Scholar

10.S Puri, and V Wadhawan, editors. Kinetics of phase transitions. Boca Raton: CRC Press (2009).

Google Scholar

11. Roy S, Das SK. Dynamics and growth of droplets close to the two-phase coexistence curve in fluids. Soft Matter (2013) 9:4178–87. doi:10.1039/c3sm50196e

CrossRef Full Text | Google Scholar

12. Roy S, Das SK. Effects of domain morphology on kinetics of fluid phase separation. J Chem Phys (2013) 139:044911. doi:10.1063/1.4816372

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Binder K. In: RW Cahn, P Haasen, and EJ Kramer, editors. Phase transformation of materials, 5. VCH, Weinheim (1991), 405.

Google Scholar

14. Binder K, Stauffer D. Theory for the slowing down of the relaxation and spinodal decomposition of binary mixtures. Phys Rev Lett (1974) 33:1006–9. doi:10.1103/physrevlett.33.1006

CrossRef Full Text | Google Scholar

15. Das SK, Horbach J, Binder K, Fisher ME, Sengers JV. Static and dynamic critical behavior of a symmetrical binary fluid: A computer simulation. J Chem Phys (2006) 125:024506. doi:10.1063/1.2215613

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Roy S, Das SK. Finite-size scaling study of shear viscosity anomaly at liquid-liquid criticality. J Chem Phys (2014) 141:234502. doi:10.1063/1.4903810

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Allen MP, Tildesley DJ. Computer simulations of liquids. Oxford: Clavendon (1987).

Google Scholar

18. Midya J, Das SK. Publisher’s note: “Finite-size scaling study of dynamic critical phenomena in a vapor-liquid transition” [J. Chem. Phys. 146, 044503 (2017)]. J Chem Phys (2017) 146:069901. doi:10.1063/1.4976556

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Frenkel D, Smit B. Understanding molecular simulations:from algorithm to applications. San Diego: Academic Press (2002).

Google Scholar

20. Roy S, Das SK. Study of critical dynamics in fluids via molecular dynamics in canonical ensemble. Eur Phys J E (2015) 38:132. doi:10.1140/epje/i2015-15132-2

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Martyna GJ, Klein ML, Tuckerman M. Nosé–Hoover chains: The canonical ensemble via continuous dynamics. J Chem Phys (1992) 4:2635–43. doi:10.1063/1.463940

CrossRef Full Text | Google Scholar

22. Roy S, Das SK. Nucleation and growth of droplets in vapor-liquid transitions. Phys Rev E (2012) 85:050602. doi:10.1103/physreve.85.050602

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chen R, Yu H, Zeng J, Zhu L. General power-law temporal scaling for unequal-size microbubble coalescence. Phys Rev E (2020) 101:023106. doi:10.1103/physreve.101.023106

PubMed Abstract | CrossRef Full Text | Google Scholar