Kerr nonlinearity-assisted quadratic microcomb

Generation of nonlinear frequency combs in χ⁽³⁾ optical microresonators has attracted tremendous research interest during the last decade. Recently, realization of the microcomb owing to χ⁽²⁾ optical nonlinearity in the microresonator promises new breakthroughs and is a big scientific challenge. Moreover, it is of high scientific interest that the presence of both second- and third-order nonlinearities results in complex cavity dynamics. In particular, the role of χ⁽³⁾ nonlinearity in the generation of the quadratic microcomb is still far from being well understood. Here, we demonstrate the interaction between the second- and third-order nonlinearity in the lithium niobate microresonator, which can provide a new way of phase matching to control the mode-locking condition and pulse number for the quadratic microcomb. Our results verify that the Kerr nonlinearity can benefit the quadratic microcomb. The principle can be further extended to other material platforms to provide more manipulation methods for comb generation based on χ⁽²⁾ nonlinearity at mid-infrared.

1 Introduction

On-chip generation of optical frequency combs via the Kerr nonlinearity has attracted significant interest in recent years [1–3] owing to their benefits for applications ranging spectroscopy [4–6], optical communications [6, 7], ranging [8, 9], frequency synthesis [10], astrocombs [11, 12], and optical clocks [13, 14]. In such Kerr resonators, cascaded four-wave mixing (FWM) processes lead to the formation, around the pump frequency, of a uniform frequency comb, where self- and cross-phase modulation (SPM and XPM) compensate the unequal cavity mode spacing induced by the group velocity dispersion [15]. Because of the relatively low strength of third-order nonlinearity, generation of Kerr combs requires high pump power. In addition, the pump frequency must be close to the zero-dispersion point for the ideal phase-matching of the effective FWM, which limits the wavelength range of the comb because the comb lines are generated near the pump. The dispersion of the microresonator will lead to a finite bandwidth of the comb generation process because the cascaded FWM is less efficient once the comb modes are not commensurate with the cavity mode spectrum. Although SPM and XPM can compensate this mismatching by nonlinear optical mode pulling, but the high pump power is necessary.

Recently, it was shown that the generation of quadratic combs is possible in noncentrosymmetric materials possessing quadratic nonlinearity, such as LiNbO₃ (LN) or LiTaO₃ (LTO) [16–21]. They potentially offer lower pump power thresholds by using the generally stronger χ⁽²⁾ nonlinearities [22] and permit the direct generation of combs in spectral regions where the generation of conventional Kerr combs is difficult to achieve, for e.g., because no suitable pump sources are available or because the dispersion properties of the material are not conducive to comb generation [17, 23–25]. However, in general, the pure quadratic nonlinear resonators also contain third-order nonlinearity. Compared with the purely second-order system, the participation of the third-order nonlinearity can affect the comb mode-locking behaviors, resulting in complex dynamics that are far from well understood. Here, we numerically demonstrate the dynamics of quadratic soliton in a continuous wave (cw)-driven doubly resonant degenerate micro-optical parametric oscillator (DR-DμOPO) and focussed in particular our attention on the role of χ⁽³⁾ effect, which can benefit the mode-locking situation. We can control the pulse number of steady-state solitons by varying the magnitude of the χ⁽³⁾ nonlinear strength. Interestingly, there is a range for χ⁽³⁾ in which single soliton stably exists, and the peak power of the soliton decreases with the increase in χ⁽³⁾. This phenomenon suggests that χ⁽³⁾ nonlinear effect can not only manipulate the relative phase between the comb lines for mode locking but also affect the phase matching in the microresonator. Our results provide a new way to control the quadratic soliton with the help of third-order nonlinearity.

2 Theoretical model and simulation results

Figure 1 shows a schematic of a cw-pumped z-cut-LN DR-DμOPO system in which the field evolution in the retarded time frame is simulated. We consider slowly varying electric field envelopes A and B with their carrier frequencies ω₀ and 2ω₀, respectively [17–19]. Optical fields A and B circling in the DR-DμOPO with both quadratic and cubic nonlinearity obey the coupled equations:

$\frac{\partial A}{\partial z}=\left(-\frac{{\alpha }_s}{2}-i\frac{k_s^{″}}{2}\frac{{\partial }^2}{\partial {\tau }^2}\right)A+i\kappa B{A}^{\ast }{e}^{-i\mathrm{\Delta }kz}+i{\gamma }_1|A{|}^{2}A+i2{\gamma }_{12}|B{|}^{2}A,(1)$

$\frac{\partial B}{\partial z}=\left[-\frac{{\alpha }_p}{2}-\mathrm{\Delta }{k}^{\prime }\frac{\partial }{\partial \tau }-i\frac{k_p^{″}}{2}\frac{{\partial }^2}{\partial {\tau }^2}\right]B+i\kappa A^2{e}^{i\mathrm{\Delta }kz}+i{\gamma }_2|B{|}^{2}B+i2{\gamma }_{21}|A{|}^{2}B,(2)$

and the boundary conditions are:

$A_{m+1}\left(0,\tau \right)=\sqrt{1-{\theta }_s}{A}_m\left(L,\tau \right)e^{-i{\delta }_s},(3)$

$B_{m+1}\left(0,\tau \right)=\sqrt{1-{\theta }_p}{B}_m\left(L,\tau \right)e^{-i{\delta }_p}+\sqrt{{\theta }_p}{B}_{in},(4)$

where A and B is the signal and pump field envelopes, respectively, z is the longitudinal coordinate, α_s,p are the propagation losses, Δk is the wave-vector mismatch, Δk′ is the group velocity mismatch, $k_{s,p}^{″}$ are the group-velocity dispersion (GVD) coefficients, τ is a fast time variable in a reference frame moving at the group velocity of the fundamental frequency ω₀, L is the nonlinear cavity length, m is an integer means the mth roundtrips, θ_s,p are the coupler transmission coefficients, and δ_s,p are signal- and pump-resonance phase detuning. γ₁ and γ₂ are the SPM coefficients, γ₁₂ and γ₂₁ are the XPM coefficients, γ₁ = γ₁₂ = 2πn₃/λ_sA_eff, γ₂ = γ₂₁ = 2πn₃/λ_pA_eff, where n₃ is the nonlinear index, λ_s,p are the wavelengths of the signal and pump field, and A_eff is the effective mode area. $\kappa =\sqrt{2}{\omega }_0{d}_{\mathit{eff}}/(A_{\mathit{eff}}\sqrt{c^3{n}_s^2{n}_p{ϵ}_0})$ is the normalized second-order nonlinear coupling coefficient, where d_eff is the effective second-order nonlinear coefficient, c is the speed of light, ϵ₀ is the vacuum permittivity, and n_s,p are the linear refractive indices. High-order dispersion and nonlinearity are neglected for simplicity. B_in is the cw pump power.

FIGURE 1

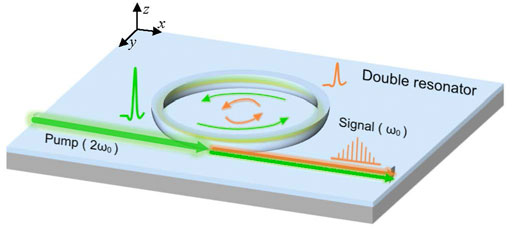
FIGURE 1. Schematic of the deterministic single quadratic soliton generation in the DR-DμOPO with both quadratic and cubic nonlinearities.

To elucidate the χ⁽³⁾ nonlinear effect on quadratic comb generation, we choose the physical parameters as follows: L = 1 mm, α_s = 11.2 dB/m, α_p = 23.6 dB/m, $k_s^{″}$ = −330.2 fs²/mm, $k_p^{″}$ = −164.1 fs²/mm, κ = 17 W^−1/2 m⁻¹, Δk′= 156 ps/m, FSR= 129 GHz, and |B_in|² = 0.3 W. We solve the coupled-wave equations (Eqs. 1, 2) by using the split-step Fourier method and the fourth-order Runge–Kutta method. We first consider the case of pure χ⁽²⁾ nonlinearity by setting γ₁ = γ₂ = γ₁₂ = γ₂₁ = 0 and the quasi-phase-matched condition Δk = 0. Our simulations, beginning from noise, are iterated for 0.5 million roundtrips and the results are obtained during a sweep of the laser frequency across the resonance, which is similar to the method commonly used for the excitation of cavity soliton states in Kerr resonators [26]. Figure 2A shows the temporal evolution and spectral dynamics of the signal field A during the pump frequency scanning process. At the start, the intracavity power increases and reaches above the OPO threshold with pump frequency accessing the cavity resonance. The temporal profiles exhibit Turing patterns corresponding to the superposition of optical pulses in the microresonator, and the spectrum appears to have two non-degenerate comb-like structures. The number of pulses in the cavity decreases as the power further increases. For the detuning δ_p = 1.8 GHz, we obtain two irregular solitons and the corresponding narrow spectrum, as shown in Figure 2B. Then, we use the same parameters as mentioned previously and add the third-order nonlinear effect by setting γ₁ = γ₁₂ = 1.16 W⁻¹m⁻¹ and γ₂ = γ₂₁ = 2.32 W⁻¹m⁻¹ to simulate the waveform inner cavity evolutionary processes. The temporal evolution of the signal field A is shown in Figure 2C. In the beginning, the temporal envelop for the non-degenerate OPO comb with an even number of optical pulses is observed. After Turing patterns, the intracavity pulse number decreases one by one with the increment of the detuning (i.e., intracavity power). The spectral bandwidth becomes broader than the pure second-order nonlinearity comb because of the optimized phase matching. For the detuning δ_p = 1.87 GHz, we obtain the single soliton and smooth sech² spectrum (Figure 2D). The relative phase between the comb lines (red dots in Figure 2D) becomes uniform compared with pure second-order nonlinearity (red dots in Figure 2B), which means that the third-order nonlinearity (SPM and XPM) can effectively manipulate the relative phase to realize the mode-locking condition. It is obvious that χ⁽³⁾ nonlinearity can affect the dynamics and benefit the mode-locking microcomb from second-order nonlinearity.

FIGURE 2

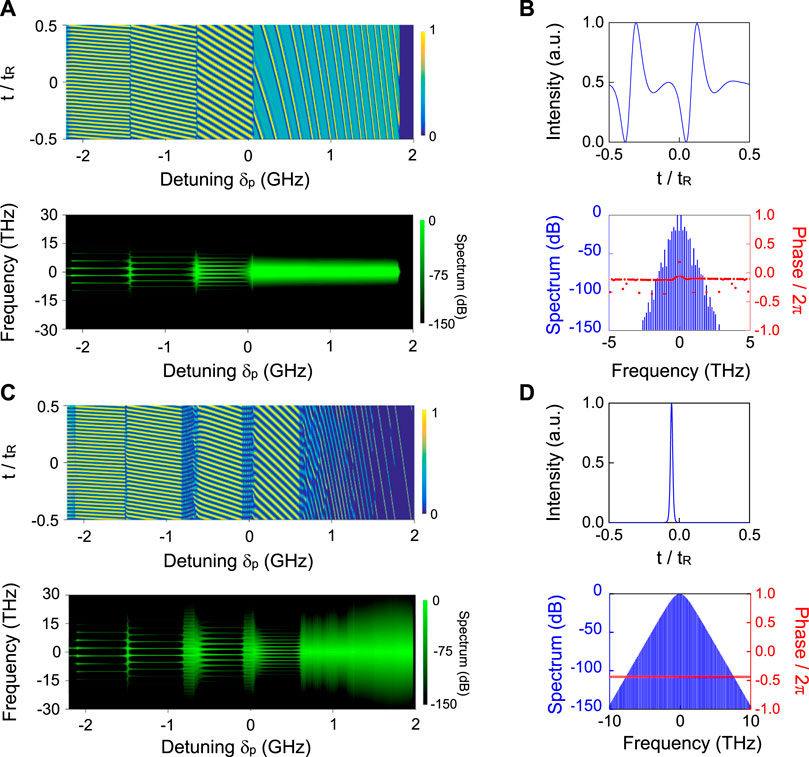
FIGURE 2. Temporal and spectral dynamics versus pump detuning δ_p in the DR-DμOPO (A) without (γ₁ = γ₂ = γ₁₂ = γ₂₁ = 0) and (C) with(γ₁ = γ₁₂ = 1.16 W⁻¹m⁻¹ and γ₂ = γ₂₁ = 2.32 W⁻¹m⁻¹) third-order nonlinearity. Temporal profile and the corresponding spectrum (B) without third-order nonlinearity for the detuning δ_p = 1.8 GHz and (D) with third-order nonlinearity for the detuning δ_p = 1.87 GHz. t_R is the round-trip time.

For second-order nonlinear materials, for example, LN and LTO, quasi-phase-matching (QPM) based on the period polling technique provides an effective and controllable method to increase the nonlinear conversion efficiency. Recently, third-order optical nonlinearities in graphene have been demonstrated to be large [27, 28] and have been predicted to be highly dependent on the Fermi energy of graphene, which can be readily changed by chemical doping or electrostatic gating [29, 30]. This prediction suggests that graphene can be used to make integrated optical systems with large and electrically tunable third-order nonlinearities. Therefore, we have a chance to control the second- and third-order nonlinearities simultaneously by combining QPM and graphene in an LN microresonator. To get a clear insight about what role χ⁽³⁾ nonlinearity has played, we investigate the intracavity dynamics with varied χ⁽³⁾. For simplicity, we set γ₀ = 1.16 W⁻¹m⁻¹, γ₂ = 2γ₁, and change γ₁ coefficient from 0 to 5γ₀. The output pulse number has an obvious step-like curve with the increment of χ⁽³⁾ nonlinearity, as shown in Figure 3. For small γ₁, the pulse number is still two (purple color). In the second step, the single soliton arises when γ₁ increases from γ₀ to 2.5γ₀ (green color). If γ₁ further increases, the pulse number becomes two (yellow color) and three (blue color). It means there is a suitable value of phase from third-order nonlinearity (SPM and XPM) to compensate the phase difference between the OPO comb lines. In other words, the phase difference between OPO comb lines is not unlimited. The insets in Figure 3 show the temporal profiles, spectrum, and relative phase for different γ₁. It is obvious that third-order nonlinearity can change the relative phase (i.e., mode-locking situation). This is the reason that the single pulse becomes a multiple pulse if γ₁ is too large.

FIGURE 3

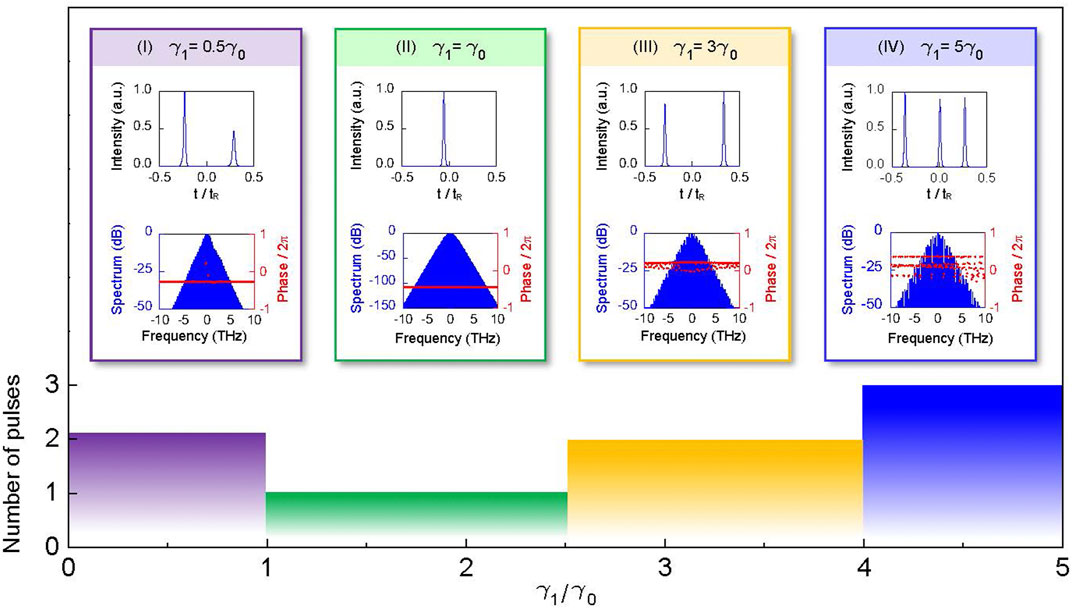
FIGURE 3. Pulse number of the quadratic soliton in the DR-DμOPO varies with χ⁽³⁾ nonlinearity. (I)–(IV) Spectral profile and the corresponding spectrum for different χ⁽³⁾ nonlinearity. t_R is the round-trip time.

In addition, the third-order nonlinearity also affects the phase matching and conversion efficiency of the OPO process. It is worth noting that the peak power of the single pulse decreases with the increment of χ⁽³⁾ nonlinearity, as shown in Figure 4A. In cw-driven DR-DμOPO, the energy of signal field A is mainly from the pump field B through the OPO process determined by the phase matching. Figure 4B shows the relationship between the peak power of the single pulse and phase mismatch Δk. By comparing the two curves in Figures 4A,B, we believe that the SPM and XPM play the same role with phase mismatch for the generation of the quadratic microcomb.

FIGURE 4

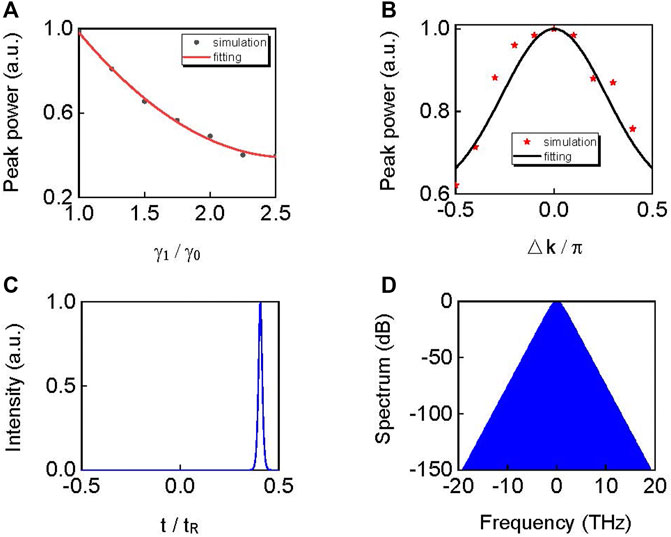
FIGURE 4. Variation of the peak power of the single pulse with (A) χ⁽³⁾ nonlinearity and (B) phase mismatching Δk. (C) Temporal profile and (D) the corresponding spectrum for γ₁ = 3γ₀ when the pump power is 0.15 W.

It is well known that third-order nonlinearity is not only related to χ⁽³⁾ nonlinear strength but also determined by the intracavity field power. This provides a flexible method to control the soliton state. As shown in Figure 3, there are two pulses for γ₁ = 3γ₀. If we reduce the pump power to 0.15 W, the mode-locked single soliton will be realized. Figures 4C,D show the temporal profile and spectrum, respectively. It indicates that modulating χ⁽³⁾ nonlinear strength by adjusting the pump power is the most feasible method for inducing single soliton generation.

3 Discussion and conclusion

In summary, we theoretically study the quadratic soliton generation in DR-DμOPO containing third-order nonlinearity. We show, for the first time, that third-order nonlinearity can benefit the mode-locking of the quadratic soliton by manipulating the relative phase between the comb lines. Then, we find that there is a range for χ⁽³⁾ nonlinearity in which single soliton can be generated deterministically. Results of numerical simulations have also shown that third-order nonlinearity can not only control the pulse number but also affect the generation efficiency of the quadratic soliton through phase matching. In the case of a stable single pulse, small third-order nonlinearity will be better for the output power. Technically, the heterogeneous waveguide of LN and other materials [31] can be used to balance second- and third-order nonlinearities in the microresonator. In addition, by integrating the LN waveguide with a monolayer of graphene, third-order nonlinear depends on the Fermi energy in graphene, which will provide another way to electrically control the nonlinear optical response in the microresonator [32, 33]. The more flexible method is to choose suitable pump power because the SPM and XPM are also related to the intracavity power. We expect that our results will be useful in understanding the dynamics of the nonlinear processes in quadratic microresonators and will contribute to the efficient generation of the coherent frequency combs in such systems. χ⁽²⁾ and χ⁽³⁾ microresonators provide a unique opportunity for quadratic soliton generation at the mid-infrared spectral range with high pump-to-comb conversion efficiency that may lead to significant enhancement of the precision measurements and optical signal processing.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

KW performed the theoretical simulations and analyzed the data. KW, YL, and H-TW wrote the manuscript. YL and H-TW planned and supervised the project. All authors discussed the results.

Funding

This work was supported financially by the National Key R&D Program of China (2019YFA0705000, 2019YFA0308700, and 2020YFA0309500) and the National Natural Science Foundation of China (12074197, 12074196, and 11922406).

Acknowledgments

The authors would like to acknowledge the support by the Collaborative Innovation Center of Extreme Optics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chang L, Liu S, Bowers JE. Integrated optical frequency comb technologies. Nat Photon (2022) 16:95–108. doi:10.1038/s41566-021-00945-1

CrossRef Full Text | Google Scholar

2. Gaeta AL, Lipson M, Kippenberg TJ. Photonic-chip-based frequency combs. Nat Photon (2019) 13:158–69. doi:10.1038/s41566-019-0358-x

CrossRef Full Text | Google Scholar

3. Kippenberg TJ, Gaeta AL, Lipson M, Gorodetsky ML. Dissipative kerr solitons in optical microresonators. Science (2018) 361:eaan8083. doi:10.1126/science.aan8083

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Suh MG, Yang QF, Yang KY, Yi X, Vahala KJ. Microresonator soliton dual-comb spectroscopy. Science (2016) 354:600–3. doi:10.1126/science.aah6516

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Coddington I, Newbury N, Swann W. Dual-comb spectroscopy. Optica (2016) 3:414–26. doi:10.1364/optica.3.000414

CrossRef Full Text | Google Scholar

6. Yu M, Okawachi Y, Griffith AG, Picqué N, Lipson M, Gaeta AL. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat Commun (2018) 9:1869–6. doi:10.1038/s41467-018-04350-1

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Pfeifle J, Brasch V, Lauermann M, Yu Y, Wegner D, Herr T, et al. Coherent terabit communications with microresonator kerr frequency combs. Nat Photon (2014) 8:375–80. doi:10.1038/nphoton.2014.57

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Trocha P, Karpov M, Ganin D, Pfeiffer MH, Kordts A, Wolf S, et al. Ultrafast optical ranging using microresonator soliton frequency combs. Science (2018) 359:887–91. doi:10.1126/science.aao3924

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Suh MG, Vahala KJ. Soliton microcomb range measurement. Science (2018) 359:884–7. doi:10.1126/science.aao1968

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Spencer DT, Drake T, Briles TC, Stone J, Sinclair LC, Fredrick C, et al. An optical-frequency synthesizer using integrated photonics. Nature (2018) 557:81–5. doi:10.1038/s41586-018-0065-7

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Obrzud E, Rainer M, Harutyunyan A, Anderson MH, Liu J, Geiselmann M, et al. A microphotonic astrocomb. Nat Photon (2019) 13:31–5. doi:10.1038/s41566-018-0309-y

CrossRef Full Text | Google Scholar

12. Suh MG, Yi X, Lai YH, Leifer S, Grudinin IS, Vasisht G, et al. Searching for exoplanets using a microresonator astrocomb. Nat Photon (2019) 13:25–30. doi:10.1038/s41566-018-0312-3

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Papp SB, Beha K, Del’Haye P, Quinlan F, Lee H, Vahala KJ, et al. Microresonator frequency comb optical clock. Optica (2014) 1:10–4. doi:10.1364/optica.1.000010

CrossRef Full Text | Google Scholar

14. Newman ZL, Maurice V, Drake T, Stone JR, Briles TC, Spencer DT, et al. Architecture for the photonic integration of an optical atomic clock. Optica (2019) 6:680–5. doi:10.1364/optica.6.000680

CrossRef Full Text | Google Scholar

15. Herr T, Hartinger K, Riemensberger J, Wang C, Gavartin E, Holzwarth R, et al. Universal formation dynamics and noise of kerr-frequency combs in microresonators. Nat Photon (2012) 6:480–7. doi:10.1038/nphoton.2012.127

CrossRef Full Text | Google Scholar

16. Ulvila V, Phillips CR, Halonen L, Vainio M. Frequency comb generation by a continuous-wave-pumped optical parametric oscillator based on cascading quadratic nonlinearities. Opt Lett (2013) 38:4281–4. doi:10.1364/ol.38.004281

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hansson T, Leo F, Erkintalo M, Coen S, Ricciardi I, De Rosa M, et al. Singly resonant second-harmonic-generation frequency combs. Phys Rev A (Coll Park) (2017) 95:013805. doi:10.1103/physreva.95.013805

CrossRef Full Text | Google Scholar

18. Leo F, Hansson T, Ricciardi I, De Rosa M, Coen S, Wabnitz S, et al. Walk-off-induced modulation instability, temporal pattern formation, and frequency comb generation in cavity-enhanced second-harmonic generation. Phys Rev Lett (2016) 116:033901. doi:10.1103/physrevlett.116.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mosca S, Parisi M, Ricciardi I, Leo F, Hansson T, Erkintalo M, et al. Modulation instability induced frequency comb generation in a continuously pumped optical parametric oscillator. Phys Rev Lett (2018) 121:093903. doi:10.1103/physrevlett.121.093903

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Xue X, Leo F, Xuan Y, Jaramillo-Villegas JA, Wang PH, Leaird DE, et al. Second-harmonic-assisted four-wave mixing in chip-based microresonator frequency comb generation. Light Sci Appl (2017) 6:e16253. doi:10.1038/lsa.2016.253

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Herr SJ, Brasch V, Szabados J, Obrzud E, Jia Y, Lecomte S, et al. Frequency comb up-and down-conversion in synchronously driven χ (2) optical microresonators. Opt Lett (2018) 43:5745–8. doi:10.1364/ol.43.005745

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Szabados J, Sturman B, Breunig I. Frequency comb generation threshold via second-harmonic excitation in χ (2) optical microresonators. APL Photon (2020) 5:116102. doi:10.1063/5.0021424

CrossRef Full Text | Google Scholar

23. Villois A, Kondratiev N, Breunig I, Puzyrev DN, Skryabin DV. Frequency combs in a microring optical parametric oscillator. Opt Lett (2019) 44:4443–6. doi:10.1364/ol.44.004443

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Mosca S, Ricciardi I, Parisi M, Maddaloni P, Santamaria L, De Natale P, et al. Direct generation of optical frequency combs in χ (2) nonlinear cavities. Nanophotonics (2016) 5:316–31. doi:10.1515/nanoph-2016-0023

CrossRef Full Text | Google Scholar

25. Nie M, Huang SW. Quadratic solitons in singly resonant degenerate optical parametric oscillators. Phys Rev Appl (2020) 13:044046. doi:10.1103/physrevapplied.13.044046

CrossRef Full Text | Google Scholar

26. Li Y, Huang SW, Li B, Liu H, Yang J, Vinod AK, et al. Real-time transition dynamics and stability of chip-scale dispersion-managed frequency microcombs. Light Sci Appl (2020) 9:52–10. doi:10.1038/s41377-020-0290-3

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Jiang T, Huang D, Cheng J, Fan X, Zhang Z, Shan Y, et al. Gate-tunable third-order nonlinear optical response of massless Dirac fermions in graphene. Nat Photon (2018) 12:430–6. doi:10.1038/s41566-018-0175-7

CrossRef Full Text | Google Scholar

28. Vermeulen N, Castelló-Lurbe D, Khoder M, Pasternak I, Krajewska A, Ciuk T, et al. Graphene’s nonlinear-optical physics revealed through exponentially growing self-phase modulation. Nat Commun (2018) 9:2675–9. doi:10.1038/s41467-018-05081-z

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Alexander K, Savostianova NA, Mikhailov SA, Kuyken B, Van Thourhout D. Electrically tunable optical nonlinearities in graphene-covered sin waveguides characterized by four-wave mixing. ACS Photon (2017) 4:3039–44. doi:10.1021/acsphotonics.7b00559

CrossRef Full Text | Google Scholar

30. Alexander K, Savostianova NA, Mikhailov SA, Van Thourhout D, Kuyken B. Gate-tunable nonlinear refraction and absorption in graphene-covered silicon nitride waveguides. ACS Photon (2018) 5:4944–50. doi:10.1021/acsphotonics.8b01132

CrossRef Full Text | Google Scholar

31. Honardoost A, Khan S, Gonzalez GC, Tremblay JE, Yadav A, Richardson K, et al. Heterogeneous integration of thin-film lithium niobate and chalcogenide waveguides on silicon. In: 2017 IEEE Photonics Conference (IPC) (IEEE); Oct. 01-05, 2017; Orlando United States (2017). p. 545–6.

CrossRef Full Text | Google Scholar

32. Yao B, Huang SW, Liu Y, Vinod AK, Choi C, Hoff M, et al. Gate-tunable frequency combs in graphene–nitride microresonators. Nature (2018) 558:410–4. doi:10.1038/s41586-018-0216-x

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Qin C, Jia K, Li Q, Tan T, Wang X, Guo Y, et al. Electrically controllable laser frequency combs in graphene-fibre microresonators. Light Sci Appl (2020) 9:185–9. doi:10.1038/s41377-020-00419-z

PubMed Abstract | CrossRef Full Text | Google Scholar