Compact neutron source from head-on collision of high energy density plasma jets

We propose a new scheme to generate a neutron source with a short duration, and the scheme is validated in two-dimensional radiation hydrodynamic simulations. When a laser beam irradiates a deuterated polystyrene cone with a half-opening angle of $60°$, high energy density plasma jets are produced due to the converging effect. As two laser-driven counter-propagating jets collide in a head-on configuration, the kinetic energy converts into internal energy efficiently, inducing a significant increase in density and temperature. Then, deuteron–deuteron thermonuclear reactions are triggered, and plenty of neutrons are released. The simulation results show that the total neutron yield is as high as $6.6\times {10}^8$ with a duration of 103 ps, providing a new way to achieve ultrafast diagnosis with high resolution in experiments.

Introduction

Neutron sources have been utilized across a wide range, such as material probing, nuclear waste treatment, material science [1, 2], and fast neutron imaging [3, 4]. Compared to X-ray radiographs, neutron radiographs are more sensitive to low-Z material and could provide complementary information, allowing robust measurement of interior temperature [5–7]. Although conventional neutron sources, for example, nuclear reactors and accelerator-based spallation, have abilities to provide high-flux neutrons, they are restricted in use due to enormous facilities and expensive costs. The advent of high-intensity lasers, providing a new access to pulsed neutron sources, has the potential to bring a further increase in neutron flux and brightness [8, 9]. When a PW-class intensity laser irradiates a solid target, the ions are accelerated to MeV energy by target normal sheath acceleration [10, 11]. Then the energetic ion beams are dumped into secondary low-Z converter targets to emit directional neutron beams [12–14]. Moreover, the cluster target also creates a dense fusion environment under laser irradiation and produces neutrons by Coulomb explosion [15–18]. The schemes of inertial confinement fusion (ICF) could also produce high-flux neutrons with narrow-band energy distribution, usually achieved by stagnation of ablated plasma [19–21]. However, the arrangement of multiple laser beams and elaborating target fabrication increases the difficulties of experimental operation [22–24].

As a new kind of target structure, the conical target is widely employed in experiments [25–27]. The uniquely converging configuration contributes to generating plasma jets with wide parameter range, which is considered an alternative tool to study astrophysical jets [28, 29]. Based on our previous work about high energy density jets, we propose a scheme of the compact source from the collision of high energy density jets [30]. When a laser beam irradiates the hollow cone which is made of deuterated polystyrene, high energy density plasma jets driven by ablation pressure are produced. Then the collision of counter-propagating jets takes place in a head-on configuration, converts kinetic energy into internal energy efficiently, and induces a significant increase in temperature and density. Eventually, the stagnation layer forms near the middle plane, and plenty of neutrons are released during the confinement period. Two-dimensional simulations show that the neutron yield can reach $6.6\times {10}^8$ with a duration of 103 ps, providing a robust way to achieve ultrafast diagnosis with high resolution in laboratory experiments.

Numerical model

The numerical code used is briefly outlined here. FLASH is an open-source radiation hydrodynamic code and has the capabilities to simulate the laser-driven high energy density physics experiments, such as nanosecond laser-plasma interaction, inertial confinement fusion, and laboratory astrophysics [31–33]. In FLASH, Euler’s governing equations are evolved by using a directionally unsplit solver and coupled with laser energy deposition, multigroup radiation transport, and electron thermal conduction. In view of the multi-temperature treatment of plasma, where ion temperature, electron temperature, and radiation temperature are not necessarily equal, the governing equations are given as

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \mathit{v}\right)=0(1)$

$\frac{\partial }{\partial t}\left(\rho \mathit{v}\right)+\nabla \cdot \left(\rho \mathit{v}\mathit{v}\right)+\nabla P=0(2)$

$\frac{\partial }{\partial t}\left(\rho E\right)+\nabla \cdot \left[\left(\rho E+P\right)\mathit{v}\right]=Q_{\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}-\nabla \cdot \mathit{q},(3)$

where $\rho$ is the mass density, $\mathit{v}$ is the fluid velocity, and $Q_{\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}$ represents the energy source due to laser heating. Moreover, $P$ is the total pressure defined as the sum of the ion, electron, and radiation pressure. $E$ is the total specific energy which includes the specific internal energy of the electrons, ions, and radiation field along with the specific kinetic energy. $\mathit{q}$ is the total heat flux including radiation and electron conductivity components. FLASH has been carefully compared with the published results from the HYDRA code, and both codes yield results that are in excellent agreement with the experimental data [32, 34]. Based on the original FLASH code, the thermonuclear reaction module has been extended. It is known that the neutron generation rate per volume for D–D thermonuclear reaction is expressed as ${\mathrm{d}Y}_n/\mathrm{d}t=\frac{1}{2}{n}_D^2⟨\sigma v⟩$, where $⟨\sigma v⟩$ is an averaged reactivity based on Maxwellian velocity distribution [35]. In thermal equilibrium, the reactivity can be written as

$⟨\sigma v⟩=\frac{4\pi }{{\left(2\pi m_{\mathrm{r}}\right)}^{1/2}}\frac{1}{{\left(k_{\mathrm{B}}T\right)}^{3/2}}{\int }_0^{\infty }\sigma \left(ϵ\right)ϵ\exp \left(-ϵ/k_{\mathrm{B}}T\right)dϵ,(4)$

where $\sigma \left(ϵ\right)$ is the cross-section. In the range of temperature $1\sim 100\mathrm{k}\mathrm{e}\mathrm{V}$, the reactivity is accurately fitted by the functional form $⟨\sigma v⟩=C_1{\zeta }^{-5/6}{\xi }^2\exp \left(-3{\zeta }^{-1/3}\xi \right)$ with $\zeta =1-\frac{C_{2}T+C_4{T}^2+C_6{T}^3}{1+C_{3}T+C_5{T}^2+C_7{T}^3}$ and $\xi =C_0/T^{1/3}$, where the coefficients for D–D thermonuclear reactions are referred [36]. The error of approximation is less than 0.35% when the ion temperature ranges from 0.2 to 100 keV. It is mentioned that the reactivity would be slightly overestimated if the corrected $S$ factor is implemented [37, 38]. In the extended module, the total neutron yield is calculated as $Y_n=\int \frac{1}{2}{n}_D^2⟨\sigma v⟩\mathrm{d}\mathrm{V}\mathrm{d}t$, where $\mathrm{d}t$ is the simulation time step. The thermonuclear reaction module is benchmarked with the laser-driven spherically convergent plasma fusion (SCPF) experiments [39]. In experiments, the total neutron yield is $1.7\times {10}^9$ with a maximum ion temperature of 6.4 keV.

To validate the newly extended thermonuclear reaction module, a two-dimensional radiation hydrodynamic simulation is carried out to simulate the SCPF experiments. According to the experiment setup, the gold spherical hohlraum has an inner diameter of $R_h=\mathrm{1,700}\mu \mathrm{m}$ with a shell thickness of $25\mu \mathrm{m}$. The fuel layer, composed of deuterated polystyrene, is lined in the inner wall with a thickness of $40\mu \mathrm{m}$. There are two laser entrance holes with a diameter of $\mathrm{1,000}\mu \mathrm{m}$ located at the top and bottom poles. Multiple laser beams, operating at a wavelength of $0.35\mu \mathrm{m}$, energy of $5.8\mathrm{k}\mathrm{J}$, and pulse duration of $1\mathrm{n}\mathrm{s}$, irradiate the equatorial plane of the spherical hohlraum at an angle of 45° with respect to the symmetry axis. Figure 1 shows the spatial distribution of mass density and ion temperature at 0.5 and 1.5 ns, respectively. Under laser irradiation, the plasma expands with an average velocity of $128\mathrm{k}\mathrm{m}/\mathrm{s}$ and maximum ion temperature of 1.1 keV at 0.5 ns. Then, the counter-propagating ablated fuel plasma converges and collides near the central axis. The collision region is cylindrical with a peak ion temperature of 6.1 keV and a number density of more than ${10}^{21}{\mathrm{c}\mathrm{m}}^{-3}$. The thermonuclear reaction is triggered and plenty of neutrons are released. Finally, the neutron yield calculated by FLASH code is $Y_n=2.01\times {10}^9$ for the uniform grid and $Y_n={1.93\times 10}^9$ for adaptive refinement grids that are both in good agreement with experimental results of ${1.7\times 10}^9$. Throughout the aforementioned simulation, it is believed that the thermonuclear module is accurate and could support our future work. The yield discrepancy may come from the initial condition setting, such as fuel layer density, input laser energy, and duration that are not accurately given in the reference. It is mentioned that the extended thermonuclear module only accesses the temporal evolution of neutron yield. The other quantities, for example, energy spread and angular distribution, rely on precise cross section, velocity distribution, and neutron transport in plasma, which is currently beyond the ability of the FLASH code.

FIGURE 1

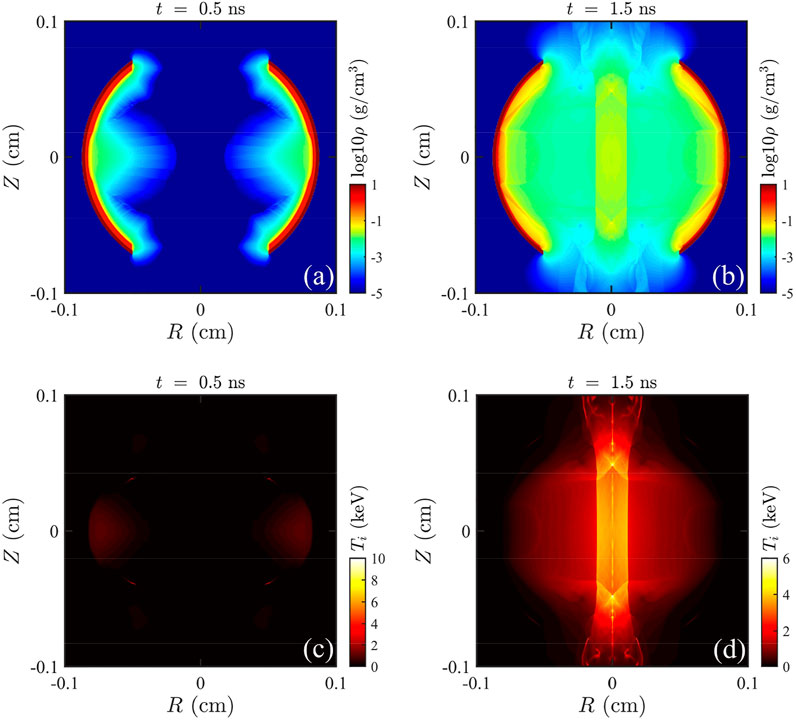
FIGURE 1. Spatial distribution in simulating the SCPF experiments of mass density distribution with color bar of decimal logarithmic scale at 0.5 ns (A) and 1.5 ns (B). The lower panel (C,D) corresponds to the ion temperature at the same moment.

Simulation results and discussions

Based on the extended thermonuclear reaction module, we propose a new scheme of compact neutron sources from the head-on collision of plasma jets. The schematic diagram is depicted in Figure 2. The gray part denotes deuterated polystyrene (CD) cone with a density of $\rho =0.9\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$, an opening radius of $250\mu \mathrm{m}$, half-opening angle of $\theta =60°$, and a thickness along the Z-axis of $d_0=15\mu \mathrm{m}$. Under the mirrored configuration, the separation distance between two cone tips is set as $L=800\mu \mathrm{m}$. Two laser beams, operating at a wavelength of $\lambda =0.35\mu \mathrm{m}$, normally irradiate the cone outer surface separately. The time profile comprises an increase of 0.05 ns, followed by a plateau of 0.95 ns, and a decrease of 0.05 ns. The laser intensity is $I={10}^{15}\mathrm{W}/{\mathrm{c}\mathrm{m}}^2$ with a focal waist of $250\mu \mathrm{m}$, equal to the cone radius. The size of the computational domain (R-Z plane) is set to be 400 μm × 1,000 µm, and the minimum grid size is 0.52 µm × 0.52 µm. The equation of state (EOS) in a tabular form is given by the FEOS code, which is based on the Helmholtz free energy function and tested against different types of experiments [40]. The mean opacity coefficients are generated by the SNOP code, tabulated as a function of density and temperature [41].

FIGURE 2

FIGURE 2. Schematic of neutron source from head-on collision of counter-propagating plasma jets.

Figure 3 shows the neutron yield (red line) and generation rate (blue line) in our radiation hydrodynamic simulation. Before $t=0.9\mathrm{n}\mathrm{s}$, the neutron generation rate integrated over the whole simulation domain rises from ${\mathrm{d}{Y}_n/\mathrm{d}t=10}^5{\mathrm{s}}^{-1}$ to ${10}^{16}{\mathrm{s}}^{-1}$, and the yield rises slowly to ${Y_n=2.7\times 10}^6$, less than 0.5% of the total yield. Since $t=0.9\mathrm{n}\mathrm{s}$, plenty of neutrons are released and the generation rate reaches a peak value of $5.4\times {10}^{18}{\mathrm{s}}^{-1}$ at $t=1.2\mathrm{n}\mathrm{s}$, subsequently decreasing to ${10}^{12}{\mathrm{s}}^{-1}$ until $t=2.0\mathrm{n}\mathrm{s}$. Finally, the total neutron yield is $Y_n=6.6\times {10}^8$, and the duration of the released neutron is $\tau \approx 103\mathrm{p}\mathrm{s}$ at the full width of half maximum.

FIGURE 3

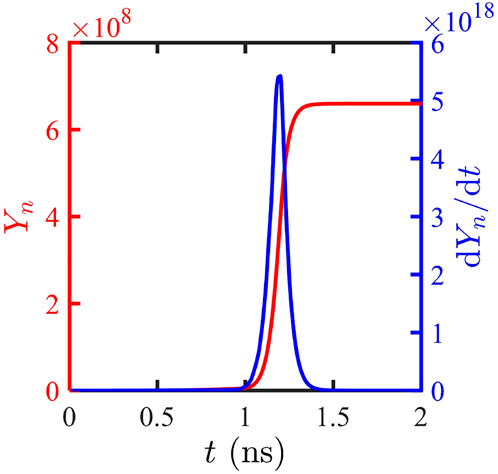
FIGURE 3. Neutron yield (red line) and generation rate integrated over the whole domain (blue line) evolve over time.

If the ion kinetic energy is much larger than the internal energy, they are not in thermal equilibrium with the background plasma. The approximate reactivity is no longer suitable, which means that the beam–target reaction should be employed rather than the thermonuclear reaction. Although the beam–target reaction is not involved in the extended module, we can still analyze the proportion of beam–target neutrons theoretically. There are two channels for D–D thermonuclear reactions with almost the same cross-section

$\mathrm{D}+\mathrm{D}\to \mathrm{p}\left(3.02\mathrm{M}\mathrm{e}\mathrm{V}\right)+\mathrm{T}\left(1.01\mathrm{M}\mathrm{e}\mathrm{V}\right),(5)$

$\mathrm{D}+\mathrm{D}\to {}_2{}^3\mathrm{H}\mathrm{e}\left(0.82\mathrm{e}\mathrm{V}\right)+\mathrm{n}\left(2.45\mathrm{M}\mathrm{e}\mathrm{V}\right),(6)$

where T, p, and n denote tritium nucleus, protons, and neutrons, respectively [35]. The 2.45 MeV neutrons at a velocity of $2.16\times {10}^4\mathrm{k}\mathrm{m}{\mathrm{s}}^{-1}$ are produced through channel D (d,n) ${}_2{}^3\mathrm{H}\mathrm{e}$, along with additional T ions generated with the kinetic energy of $1.01\mathrm{M}\mathrm{e}\mathrm{V}$. The velocity of T ions is about $v_T=\sqrt{2E/m_T}\approx 8.0\times {10}^3\mathrm{k}\mathrm{m}/\mathrm{s}$, far greater than the thermal velocity of the D nucleus in collision areas. During the confinement time, it is difficult for the T nucleus to slow down and reach thermal equilibrium with D. At that time, the beam–target reaction model is more suitable for the secondary D-T nuclear reaction. The generation rate of D-T neutrons per unit volume could be expressed as $d{Y}_{\mathrm{D}\mathrm{T}}/dt=n_D{n}_T{\sigma }_{DT}{v}_T$, where $\sigma =0.3715\times {10}^{-24}\mathrm{c}{\mathrm{m}}^2$ is the beam–target cross-section. The number density of T ions is approximately $n_T=\frac{1}{2}{n}_D^2{<\sigma v>}_{DD}\tau$. One can see that the number density $n_T$ is equal to the number of 2.45eV neutrons. Because Eqs 5, 6 occur simultaneously with almost the same probability, the ratio of D-T beam–target neutrons to 2.45 MeV D–D thermonuclear neutrons is

$\frac{d{Y}_{\mathrm{D}\mathrm{T}}/dt}{d{Y}_{\mathrm{D}\mathrm{D}}/dt}=n_D{\sigma }_{DT}{v}_T\tau .(7)$

The aforementioned parameters are substituted into the Eq. 7, and the ratio is as low as 0.5%.

The formation of plasma jets is of vital importance in our proposed scheme. When a laser normally irradiates the cone, the outer surface vaporizes rapidly to form blow-out corona plasma. The laser energy is only deposited near the critical surface where the laser frequency is equal to the plasma frequency, and then the laser energy is transferred to the electrons by the inverse bremsstrahlung mechanism. Then, the deposited energy is transported inward to the unablated region by the electron thermal conduction. The ablation pressure drives the shock wave, and promotes the cone movement. Figure 4 shows the spatial distribution of plasma mass density and ion temperature at different moments. Benefiting from the converging effect of the cone, the plasma jets are formed due to the collision and extrusion with an average density of $\rho \approx 2.5\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$ and the maximum density of $5\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$ at $t=0.8\mathrm{n}\mathrm{s}$, which is shown in Figure 4A. Figure 4D shows that the ion temperature increases up to $139\mathrm{e}\mathrm{V}$ due to the preheating of the shock wave. Under the driving force of the ablation force, the cone gradually converges to the central axis $R=0$. Then, the lateral collision decreases the width of the jets and promotes further formation of plasma jets. As the laser is switched off at $t=1.0\mathrm{n}\mathrm{s}$, the plasma jets have formed with an aspect ratio of $\sim 5$. Hereafter, a head-on collision of counter-propagating jets occurs at $t=1.2\mathrm{n}\mathrm{s}$ near the middle plane ($Z=500\mu \mathrm{m}$), which is shown in Figures 4B,E. In the collision area, the density doubles to $\rho \approx 2.1{\mathrm{g}/\mathrm{c}\mathrm{m}}^3$, and the ion temperature increases to more than $2.0\mathrm{k}\mathrm{e}\mathrm{V}$. The D–D thermonuclear reaction is triggered and plenty of neutrons are released. In the collision area, the neutron generation rate is as high as ${\mathrm{d}Y}_n/\mathrm{d}t=\frac{1}{2}{n}_D^2{<\sigma v>}_{DD}=4\times {10}^{25}{\mathrm{c}\mathrm{m}}^{-3}/\mathrm{s}$. Structurally, the collision area is similar to a hotspot with ultrahigh pressure of 2.5 Gbar. The plasma cannot maintain the burning state due to the lack of confinement. As shown in Figures 4C,F, the hotspot-like plasma expands at a velocity of sound speed. The average density and temperature decrease to $\rho \approx 0.4{\mathrm{g}/\mathrm{c}\mathrm{m}}^3$ and $T\approx 0.3\mathrm{k}\mathrm{e}\mathrm{V}$, respectively. The neutron generation rate is $1.2\times {10}^{19}{\mathrm{c}\mathrm{m}}^{-3}/\mathrm{s}$, six orders of magnitudes lower than that at $t=1.2\mathrm{n}\mathrm{s}$.

FIGURE 4

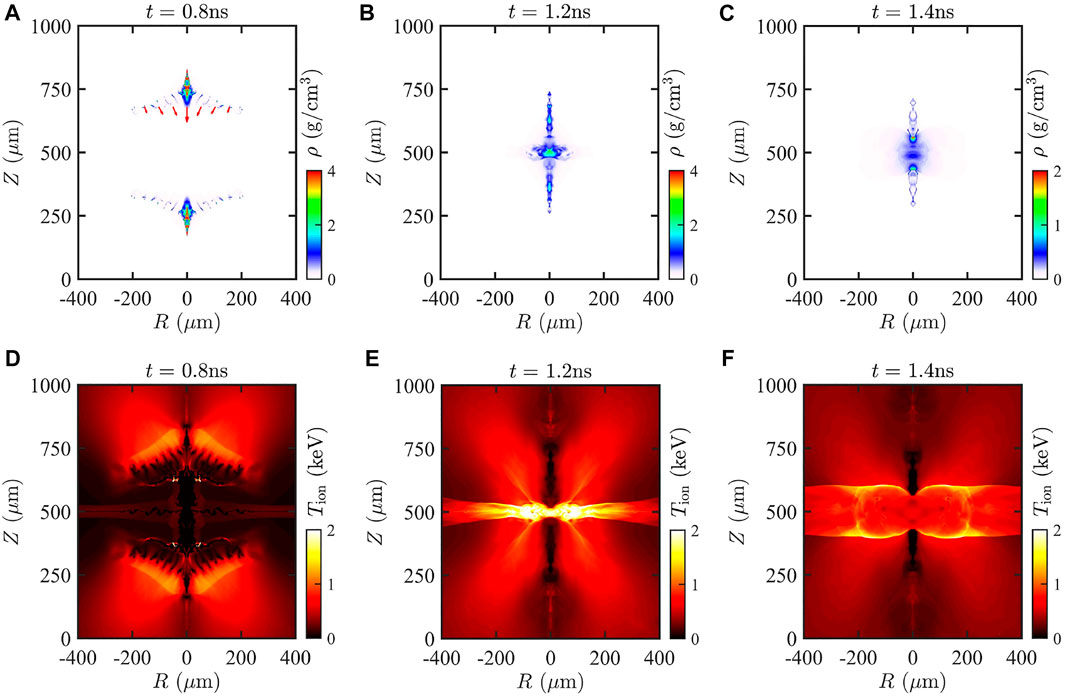
FIGURE 4. Spatial distribution of density at $t=0.8\mathrm{n}\mathrm{s}$ (A), $t=1.2\mathrm{n}\mathrm{s}$ (B), and $t=1.4\mathrm{n}\mathrm{s}$ (C). The low panel (D–F) shows the ion temperature corresponding to the same moments. The arrow in (A) represents the velocity vector.

The velocity is another important characteristic to describe the whole hydrodynamic process from jet formation to collision. Figure 5 shows the velocity distribution near the central axis $R=0$ at different moments. At $t=0.8\mathrm{n}\mathrm{s}$, the plasma jets move toward the middle plane at a velocity of $v\approx 938\mathrm{k}\mathrm{m}/\mathrm{s}$. It is mentioned that the corona, marked by the arrow “corona,” has collided at $t=0.8\mathrm{n}\mathrm{s}$, and they have no effect on the main part of the jets due to low density. When a head-on collision of plasma jets occurs at $t=1.2\mathrm{n}\mathrm{s}$, the axial velocity dramatically decreases, and the kinetic energy is converted into internal energy, leading to neutron generation. Then the high pressure causes the hotspot-like plasma to expand due to the lack of confinement.

FIGURE 5

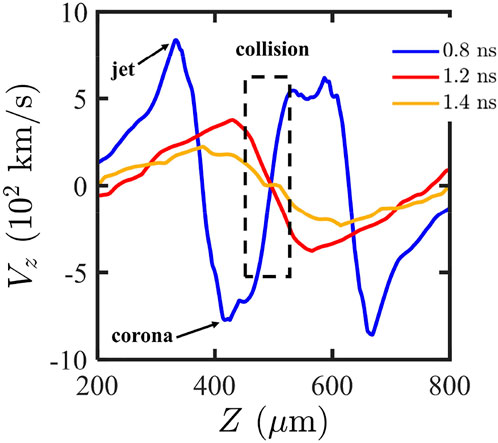
FIGURE 5. Velocity distribution along $R=0$ at $t=0.8\mathrm{n}\mathrm{s}$ (blue-line), $t=1.2\mathrm{n}\mathrm{s}$ (red-line), and $t=1.4\mathrm{n}\mathrm{s}$ (orange-line). The dashed square denotes the collision area and the arrows denote the jet and corona plasma at $t=0.8\mathrm{n}\mathrm{s}$.

As mentioned previously, the confinement time of the hotspot-like plasma is of vital importance to neutron yield. After the head-on collision of plasma jets, the rarefaction wave propagates outward from the center at acoustic speed $C_s$, causing hotspot-like plasma deformation. In the isentropic model, the acoustic speed could be expressed as $C_s=\sqrt{\gamma P/\rho }$, where the adiabatic index is $\gamma =1.67$, the thermal pressure is $P\approx 2.5\mathrm{G}\mathrm{b}\mathrm{a}\mathrm{r}$, and the mass density is $\rho \approx 2.1{\mathrm{g}/\mathrm{c}\mathrm{m}}^3$. The aforementioned plasma parameters are substituted, and the sound speed is calculated to be $C_s=446\mathrm{k}\mathrm{m}/\mathrm{s}$. The duration of the neutron source is approximately equal to the time when the rarefaction wave arrives at the edge. Assuming that the plasma jets before collision are cylinder-shaped with a radius of $r\approx 50\mu \mathrm{m}$ and the collision area is spherical with the same size, the confinement time can be derived as $\tau =\frac{r}{C_s}=0.1\mathrm{n}\mathrm{s}$, which is in good agreement with neutron duration in Figure 3.

The D–D thermonuclear reactions generate not only neutrons but also charged particles. Compared with the internal and kinetic energy density of CD plasma, the deposited energy from newly generated particles could be ignored. Generally, if the areal density is larger than $4.7\mathrm{g}/{\mathrm{c}\mathrm{m}}^2$, the neutron energy could be deposited effectively. Notably, this condition is hardly satisfied in the collision area and almost all neutrons eventually escape without elastic collision due to a long mean free path. The important characteristic of our simulation is the conversion between kinetic energy and internal energy. Figure 6 shows the distribution of energy density per volume along the central axis $R=0$ at different moments. At $t=0.8\mathrm{n}\mathrm{s}$, the maximum internal energy density is $E_{\mathrm{i}\mathrm{n}\mathrm{t}}=1.3\times {10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$, and the average one is $0.33\times {10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$ with a temperature of $T\approx 210\mathrm{e}\mathrm{V}$. The kinetic energy density is $E_{\mathrm{k}\mathrm{i}\mathrm{n}}=3.9\times {10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}{/\mathrm{c}\mathrm{m}}^3$. which is shown by red line in Figure 6A. When two counter-propagating plasma jets collide at the middle plane, the axial velocity dramatically decreases to $53\mathrm{k}\mathrm{m}/\mathrm{s}$. The conversion efficiency between kinetic energy to internal energy is about 55%. Figure 6B shows that the maximum internal energy density increases significantly up to $4.3\times {10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$, and the kinetic energy density decreases to $0.31\times {10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$ at $t=1.2$ns. Then, the hotspot-like plasma expands freely due to lack of confinement. At $t=1.4\mathrm{n}\mathrm{s}$, the kinetic and inertial energy density is $0.11\times {10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$ and $0.37\times {10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$, respectively.

FIGURE 6

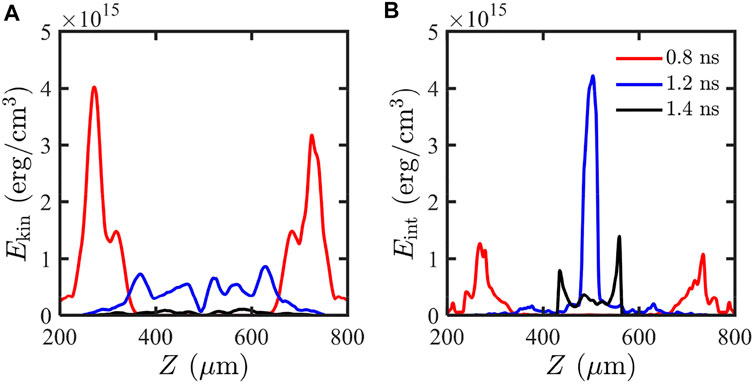
FIGURE 6. Distribution of kinetic energy density (A) and inertial energy density (B) at $t=0.8\mathrm{n}\mathrm{s}$ (red line), $t=1.2\mathrm{n}\mathrm{s}$ (blue line), and $t=1.4\mathrm{n}\mathrm{s}$ (black line).

Figure 7 shows the ion temperature and maximum density evolve as the half-opening angle $\theta$ and the distance between cone tips $L$. The diagnosis moment is chosen when the maximum density occurs in the collision area. The boundary of hotspot-like plasma is chosen as the isothermal contour of $T_{ion}=1\mathrm{k}\mathrm{e}\mathrm{V}$. Here, two kinds of plasma size are defined, which are along the Z-axis $r_z$ and R-axis $r_Z$, respectively, from the central point $\left(0,500\mu \mathrm{m}\right)$.

FIGURE 7

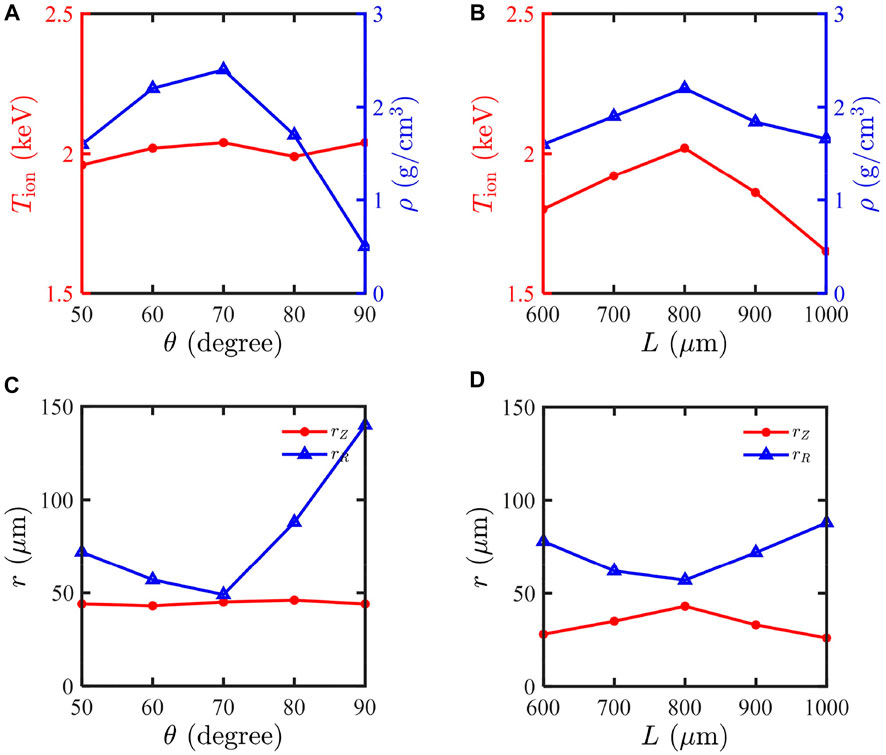
FIGURE 7. Maximum density and ion temperature evolve as the opening angle (A) and the distance of cone tips (B). (C,D) correspond to the hotspot-like plasma along the R-axis and Z-axis under the same condition.

The acceleration distance is mainly related to the distance between cone tips, but not to the opening angle. Notably, the kinetic energy of plasma jets increases as the distance increases. When the distance of cone tips is fixed as $L=800\mu \mathrm{m}$, whose results are shown in Figures 7A,C, the plasma has an equal acceleration distance along the Z-axis under the laser irradiation, and then subsequent collisions cause almost equal kinetic energy to be converted into internal energy. Therefore, the ion temperature, $T_{ion}\sim 2\mathrm{k}\mathrm{e}\mathrm{V}$, hardly changes with the opening angle with $T_{ion}\sim 2\mathrm{k}\mathrm{e}\mathrm{V}$. Moreover, the temperature distribution along the Z-axis, peaked at $2\mathrm{k}\mathrm{e}\mathrm{V}$, is almost the same, meaning that the same Z-size if the isothermal contour of $1\mathrm{k}\mathrm{e}\mathrm{V}$ is considered as the boundary. However, the opening angle has an important influence on jet formation and collision. After convergence near the symmetry axis, the plasma begins to expand along the R-axis due to high thermal pressure. If the angle is small (e.g., $50°$ and $60°$), plasma convergence takes place earlier than collision, which means that convergence and collision do not occur at the same time. When the angle increases to $80°$ or $90°$, the cone is shaped like a plane target and the convergence effect is not evident. In the two aforementioned cases, the collision is more likely to occur between two planes rather than the jets. In other words, the plasma convergence and jet collision do not match each other, resulting in a decrease in density and an increase in size along the R-axis. The simulation results show that the density reaches a peak value at an angle of 7$0°$, with the smallest R-size of $49\mu \mathrm{m}$. When the half-opening angle is fixed at $60°$, as shown in Figures 7B,D, the plasma has an insufficient acceleration if the distance is short, for example, $600\mu \mathrm{m}$ or $700\mu \mathrm{m}$. However, if the distance is overlong, the excessive internal energy is converted into radiation energy. Two aforementioned cases would decrease the ion temperature. The low temperature also narrows the hotspot size along the Z-axis. Moreover, the short or long distance also causes a mismatch between convergence and collision, which increases R-size and decreases density. In conclusion, one can see that the Z-size has a similar tendency with the ion temperature, and the R-size has a contrary evolution with the collision density.

The angle and distance would influence neutron yield. Figure 8 shows the neutron yield and duration evolve as the half-opening angle $\theta$ and the distance of separated cone tips $L$. In the case of a large angle, the cone is prone to the planar target. The weak convergence decreases the mass density in the collision area. It is known that the reactivity is proportional to the square of number density. Although the hotspot-like plasma becomes larger along the R-axis, the neutron yield would decrease. As shown in Figure 8A, the maximum yield is $12.3\times {10}^8$ in the case of $\theta =70°$, corresponding to the optimized angle for energy a point conversion efficiency and jet formation in our previous work [30]. Additionally, the neutron source with an overlarge R-size cannot be seen as, perhaps reducing the diagnosis resolution. Figure 8B shows the relationship between the neutron qualities and the distance of cone tips. The longer distance between the cone tips increases the accelerating time and axial velocity, and the neutron yield is enhanced as the separation distances increase. When the distance is larger than $800\mu \mathrm{m}$, the long-time radiation reduces ion temperature in the collision area, inducing a decrease in the yield. The parameter scanning shows that the neutron duration for different angles and tip distance is still as short as 100 ps

FIGURE 8

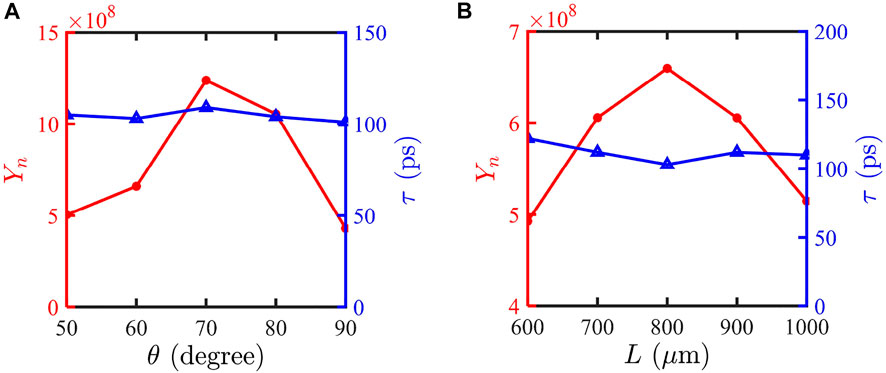
FIGURE 8. Yield (red-circle lines) and duration (blue-triangle lines) evolve as the cone angle (A) and the distance of separate cone tips (B). The distance of cone tips is fixed as $L=800\mu m$ in (A), and the half-opening angle is fixed as $\theta =60°$ in (B).

There is no essential difference between the hot but underdense plasma colliding approach and our proposed scheme. They increase neutron production rate and yield in different ways. Generally, higher intensity laser is required to increase plasma temperature. As for the stationary ablation model, the temperature in corona plasma is only in correction with the laser parameters, for example, intensity, energy absorption rate, and wavelength. However, by optimizing the target structure, high density can be achieved although the laser intensity is fixed. A scheme of overdense but cold plasma colliding is easier to implement in experiments.

Table 1 shows the comparison of the laser-driven neutron source. The neutron yield in our scheme is close to the beam–target interaction. Assuming that neutrons are emitted isotropically throughout the whole solid angle, the flux is estimated as $Y_n/4\pi ={10}^7/\mathrm{s}\mathrm{r}\sim {10}^8/\mathrm{s}\mathrm{r}$. From the perspective of laser energy, our scheme is not cost-effective at present. Our proposed scheme could be seen as a simplified model of inertial confinement fusion. The kinetic energy of D ions is on the order of keV in the collision area and the cross-section of the D–D nuclear reaction is much lower than that in the beam–target reaction. Fortunately, high ion number density overcomes the disadvantages of the low cross-section. After a fusion reaction, the product energy, for example, neutron or other ions, is on the order of MeV. According to the laws of conservation of energy and conservation of momentum, the keV ion energy hardly affects the MeV neutron energy generated. This is the reason that thermonuclear neutrons can be regarded as monoenergetic. The monoenergetic characteristic of neutron beams is the important advantage of the proposed scheme compared with the scheme of MeV ions dumped on low-Z converter targets with widely distributed energy spectrum. In addition, the implementation of a nanosecond laser, which allows easier enhancement of output energy, has the potential to achieve a higher yield in the future. Finally, our scheme is easily employed in experiments although the yield would be degraded. In the future, we hope to enhance neutron yield by mainly optimizing target structure.

TABLE 1

TABLE 1. The comparison of the laser-driven neutron sources.

Conclusion

In this study, we propose a new scheme of the compact neutron source. The laser-driven plasma jets are generated due to the convergence effect of the cone target. Under the mirrored geometric structure, two counter-propagating jets collide near the middle plane and form hotspot-like plasma. The conversion from kinetic to internal energy increases the ion temperature, and the D–D thermonuclear reaction is triggered. Plenty of neutrons are released and the neutron yield is as high as $6.6\times {10}^8$. Further simulation results show that the maximum yield is achieved in the case of half-opening angle of $70°$ and the distance between separated cone tips of $800\mu \mathrm{m}$. Our work not only reveals the temporal and spatial evolution of collision plasma, but also serves as a reference for the future study of fast ignition.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

Y-ZK contributed to the conception and ideas. YC and Y-ZK developed the newly extended thermonuclear module based on the original FLASH code. YC performed the numerical simulations and data analysis. YC completed the writing of the manuscript. X-HY, Y-YM, and F-QS contributed significantly to the analysis and manuscript preparation.

Funding

This work was supported by the Strategic Priority Research Program of the Chinese Academy of Science (Grant No. XDA25050200), the National Natural Science Foundation of China (Grant Nos 12175309, 11775305, 11975308, and 12005297), the fund of Science Challenge Project (No. TZ2018001), the State Key Laboratory of Laser Interaction with Matter (No. SKLLIM1908).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Svergun DI, Koch MHJ. Advances in structure analysis using small-angle scattering in solution. Curr Opin Struct Biol (2002) 12(5):654–60. doi:10.1016/s0959-440x(02)00363-9

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Noguere G, Cserpak F, Ingelbrecht C, Plompen AJM, Quetel CR, Schillebeeckx P. Non-destructive analysis of materials by neutron resonance transmission. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2007) 575(3):476–88. doi:10.1016/j.nima.2007.02.085

CrossRef Full Text | Google Scholar

3. Strobl M, Manke I, Kardjilov N, Hilger A, Dawson M, Banhart J. Advances in neutron radiography and tomography. J Phys D Appl Phys (2009) 42(24):243001. doi:10.1088/0022-3727/42/24/243001

CrossRef Full Text | Google Scholar

4. Higginson DP, McNaney JM, Swift DC, Bartal T, Hey DS, Kodama R, et al. Laser generated neutron source for neutron resonance spectroscopy. Phys Plasmas (2010) 17(10):100701. doi:10.1063/1.3484218

CrossRef Full Text | Google Scholar

5. Yuan VW, Bowman JD, Funk DJ, Morgan GL, Rabie RL, Ragan CE, et al. Shock temperature measurement using neutron resonance spectroscopy. Phys Rev Lett (2005) 94(12):125504. doi:10.1103/physrevlett.94.125504

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Swift DC, Seifter A, Holtkamp DB, Yuan VW, Bowman D, Clark DA. Explanation of anomalous shock temperatures in shock-loaded Mo samples measured using neutron resonance spectroscopy. Phys Rev B (2008) 77(9):092102. doi:10.1103/physrevb.77.092102

CrossRef Full Text | Google Scholar

7. Abe Y, Sunahara A, Lee S, Yanagawa T, Zhang Z, Arikawa Y, et al. Production of intense, pulsed, and point-like neutron source from deuterated plastic cavity by mono-directional kilo-joule laser irradiation. Appl Phys Lett (2017) 111(23):233506. doi:10.1063/1.5016531

CrossRef Full Text | Google Scholar

8. Danson C, Hillier D, Hopps N, Neely D. Petawatt class lasers worldwide. High Pow Laser Sci Eng (2015) 3:e3. doi:10.1017/hpl.2014.52

CrossRef Full Text | Google Scholar

9. Guler N, Volegov P, Favalli A, Merrill FE, Falk K, Jung D, et al. Neutron imaging with the short-pulse laser driven neutron source at the Trident laser facility. J Appl Phys (2016) 120(15):154901. doi:10.1063/1.4964248

CrossRef Full Text | Google Scholar

10. Wilks SC, Langdon AB, Cowan TE, Roth M, Singh M, Hatchett S, et al. Energetic proton generation in ultra-intense laser–solid interactions. Phys Plasmas (2001) 8(2):542–9. doi:10.1063/1.1333697

CrossRef Full Text | Google Scholar

11. Snavely RA, Key MH, Hatchett SP, Cowan TE, Roth M, Phillips TW, et al. Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys Rev Lett (2000) 85(14):2945–8. doi:10.1103/physrevlett.85.2945

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Higginson DP, McNaney JM, Swift DC, Petrov GM, Davis J, Frenje JA, et al. Production of neutrons up to 18 MeV in high-intensity, short-pulse laser matter interactions. Phys Plasmas (2011) 18(10):100703. doi:10.1063/1.3654040

CrossRef Full Text | Google Scholar

13. Zhao JR, Zhang XP, Yuan DW, Li YT, Li DZ, Rhee YJ, et al. A novel laser-collider used to produce monoenergetic 13.3 MeV 7Li (d, n) neutrons. Sci Rep (2016) 6(1):27363. doi:10.1038/srep27363

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kleinschmidt A, Bagnoud V, Deppert O, Favalli A, Frydrych S, Hornung J, et al. Intense, directed neutron beams from a laser-driven neutron source at PHELIX. Phys Plasmas (2018) 25(5):053101. doi:10.1063/1.5006613

CrossRef Full Text | Google Scholar

15. Ditmire T, Tisch JWG, Springate E, Mason MB, Hay N, Smith RA, et al. High-energy ions produced in explosions of superheated atomic clusters. Nature (1997) 386(6620):54–6. doi:10.1038/386054a0

CrossRef Full Text | Google Scholar

16. Ditmire T, Zweiback J, Yanovsky VP, Cowan TE, Hays G, Wharton KB. Nuclear fusion in gases of deuterium clusters heated with a femtosecond laser. Phys Plasmas (2000) 7(5):1993–8. doi:10.1063/1.874020

CrossRef Full Text | Google Scholar

17. Bang W, Dyer G, Quevedo HJ, Bernstein AC, Gaul E, Rougk J, et al. Optimum laser intensity for the production of energetic deuterium ions from laser-cluster interaction. Phys Plasmas (2013) 20(9):093104. doi:10.1063/1.4821611

CrossRef Full Text | Google Scholar

18. Ditmire T, Zweiback J, Yanovsky VP, Cowan TE, Hays G, Wharton KB. Nuclear fusion from explosions of femtosecond laser-heated deuterium clusters. Nature (1999) 398(6727):489–92. doi:10.1038/19037

CrossRef Full Text | Google Scholar

19. He M-Q, Cai H-B, Zhang H, Dong Q-L, Zhou C-T, Wu S-Z, et al. A spherical shell target scheme for laser-driven neutron sources. Phys Plasmas (2015) 22(12):123103. doi:10.1063/1.4936828

CrossRef Full Text | Google Scholar

20. Zhao JR, Zhang XP, Yuan DW, Chen LM, Li YT, Fu CB, et al. Neutron yield enhancement in laser-induced deuterium-deuterium fusion using a novel shaped target. Rev Scientific Instr (2015) 86(6):063505. doi:10.1063/1.4922912

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhang X, Zhao J, Yuan D, Fu C, Bao J, Chen L, et al. Deuteron-deuteron fusion in laser-driven counter-streaming collisionless plasmas. Phys Rev C (2017) 96(5):055801. doi:10.1103/physrevc.96.055801

CrossRef Full Text | Google Scholar

22. Craxton RS, Anderson KS, Boehly TR, Goncharov VN, Harding DR, Knauer JP, et al. Direct-drive inertial confinement fusion: A review. Phys Plasmas (2015) 22(11):110501. doi:10.1063/1.4934714

CrossRef Full Text | Google Scholar

23. Betti R, Hurricane OA. Inertial-confinement fusion with lasers. Nat Phys (2016) 12(5):435–48. doi:10.1038/nphys3736

CrossRef Full Text | Google Scholar

24. Bose A, Woo KM, Nora R, Betti R. Hydrodynamic scaling of the deceleration-phase Rayleigh–Taylor instability. Phys Plasmas (2015) 22(7):072702. doi:10.1063/1.4923438

CrossRef Full Text | Google Scholar

25. Hu L-X, Yu T-P, Shao F-Q, Zhu Q-J, Yin Y, Ma Y-Y. Enhanced dense attosecond electron bunch generation by irradiating an intense laser on a cone target. Phys Plasmas (2015) 22(12):033104. doi:10.1063/1.4913984

CrossRef Full Text | Google Scholar

26. Zhu X-L, Yu T-P, Sheng Z-M, Yin Y, Turcu ICE, Pukhov A. Dense GeV electron–positron pairs generated by lasers in near-critical-density plasmas. Nat Commun (2016) 7(1):13686–8. doi:10.1038/ncomms13686

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhang J, Wang W, Yang XH, Wu D, Ma YY, Jiao J, et al. Double-cone ignition scheme for inertial confinement fusion. Phil Trans R Soc A (2020) 378:20200015. doi:10.1098/rsta.2020.0015

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Shigemori K, Kodama R, Farley DR, Koase T, Estabrook KG, Remington BA, et al. Experiments on radiative collapse in laser-produced plasmas relevant to astrophysical jets. Phys Rev E (2000) 62(6):8838–41. doi:10.1103/physreve.62.8838

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Li CK, Tzeferacos P, Lamb D, Gregori G, Norreys PA, Rosenberg MJ, et al. Scaled laboratory experiments explain the kink behaviour of the Crab Nebula jet. Nat Commun (2016) 7(1):13081. doi:10.1038/ncomms13081

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ke YZ, Yang XH, Ma YY, Xu BB, Ge ZY, Gan LF, et al. High-energy-density plasma jet generated by laser-cone interaction. Phys Plasmas (2018) 25(4):042706. doi:10.1063/1.5021137

CrossRef Full Text | Google Scholar

31. Fryxell B, Olson K, Ricker P, Timmes FX, Zingale M, Lamb DQ, et al. Flash: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophys J Suppl Ser (2000) 131(1):273–334. doi:10.1086/317361

CrossRef Full Text | Google Scholar

32. Joggerst CC, Nelson A, Woodward P, Lovekin C, Masser T, Fryer CL, et al. Cross-code comparisons of mixing during the implosion of dense cylindrical and spherical shells. J Comput Phys (2014) 275:154–73. doi:10.1016/j.jcp.2014.06.037

CrossRef Full Text | Google Scholar

33. Derigs D, Winters AR, Gassner GJ, Walch S. A novel high-order, entropy stable, 3D AMR MHD solver with guaranteed positive pressure. J Comput Phys (2016) 317:223–56. doi:10.1016/j.jcp.2016.04.048

CrossRef Full Text | Google Scholar

34. Orban C, Fatenejad M, Lamb DQ. Code-to-code comparison and validation of the radiation-hydrodynamics capabilities of the FLASH code using a laboratory astrophysical jet. Phys Plasmas (2022) 29(5):053901. doi:10.1063/5.0079493

CrossRef Full Text | Google Scholar

35. Atzeni S, Meyertervehn J Plasma Physics & Controlled Fusion, 46 (2004). p. 1805.

Google Scholar

36. Bosch HS, Hale GM. Improved formulas for fusion cross-sections and thermal reactivities. Nucl Fusion (1992) 32(4):611–31. doi:10.1088/0029-5515/32/4/i07

CrossRef Full Text | Google Scholar

37. Tumino A, Spitaleri C, Mukhamedzhanov AM, Typel S, Aliotta M, Burjan V, et al. Low-energy d+d fusion reactions via the Trojan Horse Method. Phys Lett B (2011) 700(2):111–5. doi:10.1016/j.physletb.2011.05.001

CrossRef Full Text | Google Scholar

38. Tumino A, Spartà R, Spitaleri C, Mukhamedzhanov AM, Typel S, Pizzone RG, et al. NEW DETERMINATION OF THE²H(d, p)³H AND²H(d, n)³He REACTION RATES AT ASTROPHYSICAL ENERGIES. Astrophys J (2014) 785(2):96. doi:10.1088/0004-637x/785/2/96

CrossRef Full Text | Google Scholar

39. Ren G, Yan J, Liu J, Lan K, Chen YH, Huo WY, et al. Neutron generation by laser-driven spherically convergent plasma fusion. Phys Rev Lett (2017) 118(16):165001. doi:10.1103/physrevlett.118.165001

PubMed Abstract | CrossRef Full Text | Google Scholar

40. More RM, Warren KH, Young DA, Zimmerman GB. A new quotidian equation of state (QEOS) for hot dense matter. Phys Fluids (1994) (1988) 31(10):3059–78. doi:10.1063/1.866963

CrossRef Full Text | Google Scholar

41. Eidmann K. Radiation transport and atomic physics modeling in high-energy-density laser-produced plasmas. Laser Part Beams (1994) 12(2):223–44. doi:10.1017/s0263034600007709

CrossRef Full Text | Google Scholar