The hydrogen bond rotation of confined water affected by quantum resonance tunnelling

In this work, we report quantum tunnelling effects on the confined water chain flipping, different from the spatial size and even electronic correlation effects of the confinement environment. First-principles calculations and analyses confirm that quantum tunnelling from the water chain itself enhances the hydrogen bond rotation. Importantly, the neglected resonant tunnelling can result in tunnelling rotation of hydrogen bonds with a probability close to 1 through the provided 0.6 eV energy, while the probability of generally recognized sequential tunnelling is only 10⁻⁶. Not only that, compared to sequential tunnelling, resonant tunnelling leads to a 20 K higher flipping temperature of the water chain. Additionally, the ratio of the resonant tunnelling probability to the thermal disturbance probability at 200 K is at least ten times larger than that of sequential tunnelling, which further illustrates the enhancement of hydrogen bond rotation brought about by resonant tunnelling.

Introduction

To achieve effective regulation of the water transport process, an important goal is to deeply understand the confined hydrogen bond (H-bond) rotation mechanism at the atomic level. Quantum effects have been reported to be essential and should be carefully considered on a microscopic scale [1–7], including quantum effects related to water, such as properties of electronic correlation [8–10], nuclear quantum effects [11, 12] and tunnelling [13, 14]. This suggests that quantum effects play an important role in understanding the nature of water and even regulating its behavior. More importantly, some studies show that the H-bond rotation of water is affected by quantum effects [8, 15]. As a microstructure, a hydrogen atom has a very small mass, which leads to the existence of tunnelling effects from the water chain itself during H-bond rotation. Moreover, a recent experiment revealed that quantum coherence can effectively improve the tunnelling effects [1]. This inspired us to explore the deep effect of the quantum properties of a water chain on the H-bond rotation.

Currently, many studies have been performed on the transport and H-bonds of confined water [16–23], including on the step-by-step rotation behavior of confined water and its intrinsic mechanism [24]. Many studies have shown that the flipping of confined water is affected by the spatial size [25–30]. For example, the transport of confined water has a high conductivity [28, 29], and the water flux through a carbon nanotube (CNT) has a linear relationship with the radius of the CNT when the length is much larger than the radius [30]. However, due to the inherent complexity of the molecular system, the understanding of the mechanism of water chain flipping under confinement is still unclear. The experimental technique has been greatly improved compared with the past, which has resulted in water chains formed in CNTs with diameters as small as 0.548 nm, and an extremely high freezing temperature has been detected [31, 32]. However, observing the details of the mechanism of water chain flipping in a short time, much less regulating the mechanism of water chain flipping, is still a great challenge. Considering that the tunnelling effects, especially the previously often neglected quantum coherence, have a more fundamental significance in quantum physics, studying the resonance effects caused by the coherence that exists when a water chain flips in a confined space from the perspective of the basic principles of tunnelling is necessary.

In this work, we study the possible flipping of a water chain under quasi-one-dimensional (1D) confinement and find that the quantum tunnelling cannot be ignored. Significantly, quantum resonant tunnelling brings different effects than generally recognized tunnelling and thermal processes. Here, the calculation results show that the H-bond rotation of the water chain in a 1D-CNT is obviously affected by tunnelling, especially resonant tunnelling. Compared with the tunnelling without considering quantum coherence, the resonant tunnelling with considering quantum coherence can achieve a higher probability with less provided energies, which leads to an increase of water chain flipping temperature by 20 K. Therefore, our work opens a new perspective for the quantum regulation of water chain flipping in channels.

Computational methods

For first-principles calculations, the empirical-dispersion-corrected hybrid Perdew-Burke-Ernzerhof (PBE0-D3) method of density functional theory was carried out in the Gaussian 09 package [33–35]. The basis sets 6-311+G (d, p) and 6-31G (d) were used for water and the CNT, respectively. The armchair-type single-walled (6, 6) CNT was employed, and the diameter and length were set to 8.20 Å and 20 Å, respectively. After CNT preoptimization, we froze all of the atoms of the CNT to ensure constant confinement effects on the water. In the CNT, three water molecules were selected to form the water chain. The water chain was along the tube axis, and the molecules were connected to each other by H-bonds. Based on the different initial geometries of the water chain, we searched the structures for extreme points (including equilibrium and transition states) in the rotation of water molecules in the CNT and traced the reaction paths of the flipping for the water chain according to the intrinsic reaction coordinate [36, 37]. The reduced masses are 1.0834 amu and 1.0955 amu for the water chain flipping along the path containing L-type and D-type defective intermediates.

For the formula without considering quantum coherence, the Wentzel-Kramers-Brillouin (WKB) approximation is used for calculating the tunnelling probability for a single barrier using the following formula [38, 39]:

$\mathit{P}=\mathit{Exp}\left[-\frac{\mathbf{2}}{\mathit{\hslash }}{\int }_{{\mathit{x}}_{\mathbf{1}}}^{{\mathit{x}}_{\mathbf{2}}}\sqrt{\mathbf{2}\mathit{m}\left(\mathit{V}\left(\mathit{x}\right)-\mathit{E}\right)}\mathit{d}\mathit{x}\right](1)$

where ℏ is the reduced Planck constant, V(x) represents the potential energy surface (PES) function with the coordinate x as the variable, expressed by a Gaussian fitting function, and x₁ and x₂ are the two coordinates when V(x) and E are equal. The tunnelling probability for double barriers is obtained by multiplying the tunnelling probability of two single barriers.

For the formula considering quantum coherence, the steady-state Schrödinger equation of N multiple barriers is strictly solved. For the convenience of calculation, the equivalent square barrier is used to fit the PES. In detail, we first take the half-height width of the left-side barrier as the square barrier width to obtain the approximate equivalent square barrier. Then, the local minimum value is taken as the axis of symmetry to obtain the ideal double barrier model. This equivalent square barrier method is an approximation based on the principle that original barrier and approximate square barrier have the same tunnelling probability. The general expression of the Schrödinger equation can be written as follows:

${\mathit{\psi }}_{\mathit{j}}={\mathit{C}}_{\mathbf{2}\mathit{j}-\mathbf{1}}\mathit{exp}\left(\mathit{i}{\mathit{k}}_{\mathit{j}}\mathit{x}\right)+{\mathit{C}}_{\mathbf{2}\mathit{j}}\mathit{exp}\left(-\mathit{i}{\mathit{k}}_{\mathit{j}}\mathit{x}\right)(2)$

in which C_2j-1 represents the transmission amplitude, C_2j is the reflection amplitude and k_j is the wavenumber. The tunnelling probability is defined as the ratio of the flow of particles out of the barrier to the flow of particles into the barrier as follows:

$\mathit{T}=\frac{{\left|{\mathit{C}}_{\mathbf{4}\mathit{N}+\mathbf{1}}\right|}^{\mathbf{2}}}{{\left|{\mathit{C}}_{\mathbf{1}}\right|}^{\mathbf{2}}}(3)$

For the thermodynamic model, the Boltzmann distribution is used to describe the probability of crossing the barrier from the classical perspective as follows:

${\mathit{P}}_{\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{m}\mathit{a}\mathit{l}}=\mathit{Exp}\left(-\frac{\mathit{\Delta }\mathit{E}}{\mathit{k}\mathit{T}}\right)(4)$

where k is the Boltzmann constant and T is the temperature. ΔE represents the relative energy between the initial provided energy and the barrier peak. Additionally, to compare the classical and quantum methods of crossing the barrier, the ratio of the quantum tunnelling probability to the thermal disturbance probability is studied.

Results and discussion

To study the possible flipping of a water chain under confinement, the water molecules in a CNT that form a 1D chain are examined (Figure 1A). We give two reaction paths, and the corresponding PESs of flipping are shown in Figure 1B. There are five extreme points along each reaction path: two structures with lower energies (reactant and product, labelled Min1 and Min2), two transition state structures (labelled TS1 and TS2), and an intermediate structure (labelled Int). These structures are shown in Figure 1C. This suggests that the flipping of the water chain is a step-by-step process, and the formation of the intermediate is necessary, which is consistent with our previous study [24]. For the two reaction paths, the main difference lies in the structure of the intermediate. In detail, when the water chain flips along the nanotube axis in the opposite direction to the H-bonds, the heights of the energy barriers of the two transition states to be overcome are approximately 0.660 eV, and an intermediate with an energy of approximately 0.524 eV is formed. This structure has the two hydrogen atoms in the middle water molecule forming H-bonds with the oxygen atoms of the two adjacent water molecules. We call this the intermediate with an L-type defect [40]. The H-bonds are oriented towards the middle water molecule. When the water chain flips along the direction of the H-bond, it needs to overcome two energy barriers with heights of approximately 0.640 eV. Additionally, the intermediate formed has an energy of approximately 0.477 eV. In this structure, the oxygen atom in the middle water molecule forms H-bonds with the hydrogen atoms of the two adjacent water molecules. The H-bonds are oriented towards both ends of the water molecules, which is called the intermediate with a D-type defect [40]. The energy of the intermediate with an L-type defect is approximately 10⁻² eV higher than that of the intermediate with a D-type defect. This indicates that the water chain is more likely to flip along the path of the intermediate with a D-type defect.

FIGURE 1

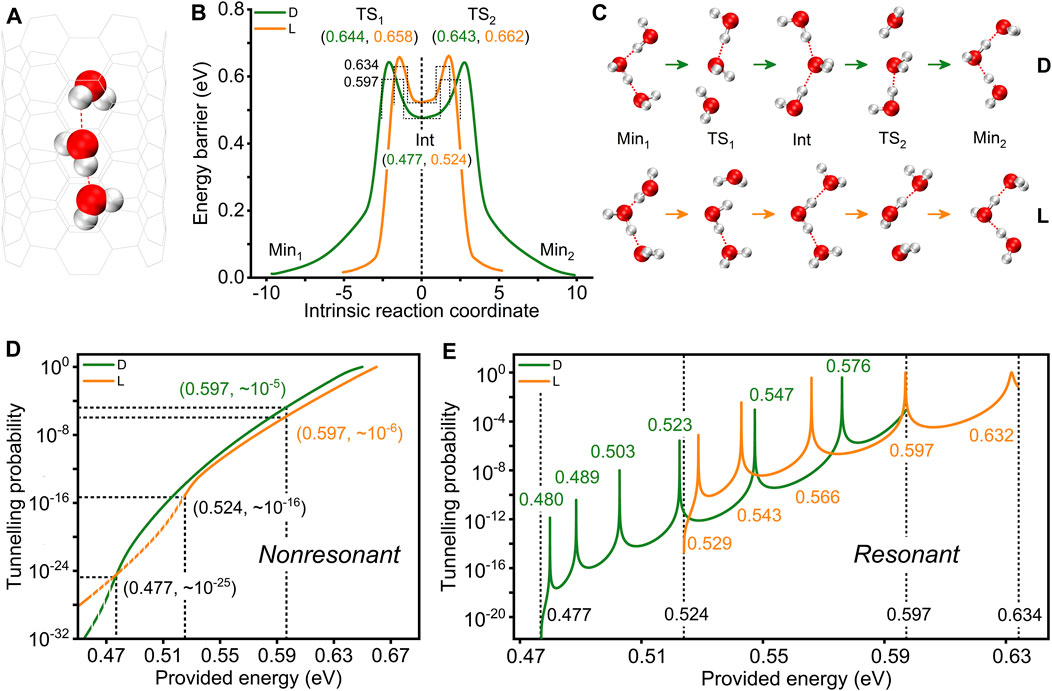
FIGURE 1. Different mechanisms by which the water chain with three water molecules in the CNT achieves reorientation. (A) Model of the confined water chain. (B) PESs of the water chain flipping. Dotted lines are the equivalent square energy barriers obtained by fitting the double barriers of the PESs. (C) Water chain structures corresponding to each extreme point on the PESs. (D) Variation in the quantum tunnelling probability with provided energy without considering coherence. The dotted and solid lines indicate the tunnelling probability at provided energies below and above the intermediate energies, respectively. (E) Variation in the quantum tunnelling probability with provided energy considering coherence. According to the square barriers, the energy height provided are 0.477–0.597 eV and 0.524–0.634 eV, corresponding to the two reaction paths. The dotted lines represent the provided energy at the start or end of the two reaction paths. Green and yellow represent the reaction paths containing D-type and L-type defective intermediates, respectively.

Reorientation of the water chain can be achieved not only through step-by-step flipping by classical thermodynamic perturbations but also by quantum tunnelling. Here, to obtain the sequential tunnelling probability for double barriers without considering the quantum coherence, the WKB approximation is applied [39, 40]. We considered the difficulty of the water chain to achieve reorientation by quantum tunnelling at different provided energies. As shown in Figure 1D, with an increase in the provided energy, the tunnelling probability gradually increases. Taking the path containing the L-type defective intermediate as an example, the tunnelling probabilities are approximately 10⁻²⁵, 10⁻¹⁶ and 10⁻⁶ when the provided energies are approximately 0.477 eV, 0.524 eV and 0.597 eV, respectively. For the two paths containing L-type and D-type defective intermediates, when the provided energy is approximately 0.477 eV, the two tunnelling probabilities are almost equal. However, when the provided energy is larger than 0.477 eV, the tunnelling probability of the water chain along the path containing the L-type defective intermediate is less than that along the path containing the D-type defective intermediate. For example, at the provided energy of 0.597 eV, the tunnelling probabilities are approximately 10⁻⁶ and 10⁻⁵ for the reaction paths containing the L-type and D-type defective intermediates, respectively. When the provided energy is less than 0.477 eV, the tunnelling probability of the water chain along the path containing the L-type defective intermediate is greater than that along the path containing the D-type defective intermediate.

In addition to quantum tunnelling, thermal effects can also cause the water chain to flip. To clearly show the relationship between tunnelling and thermal disturbance with temperature and provided energy, we treat thermal disturbance and tunnelling as independent probability events. Under this condition, we compare the probabilities of the water chain achieving reorientation by quantum tunnelling and thermal disturbance (25–200 K). As shown in Figure 2A, when the provided energies at the double barriers of the two reaction paths are given, the probability of water chain flipping by thermal disturbance increases with the temperature. When the temperature is lower than 84 K, quantum tunnelling is more dominant than thermal disturbance. At temperatures above 120 K, thermal disturbance plays a dominant role, rather than quantum tunnelling. Therefore, we infer that at room temperature, thermal disturbance is more likely to cause the water chain to flip.

FIGURE 2

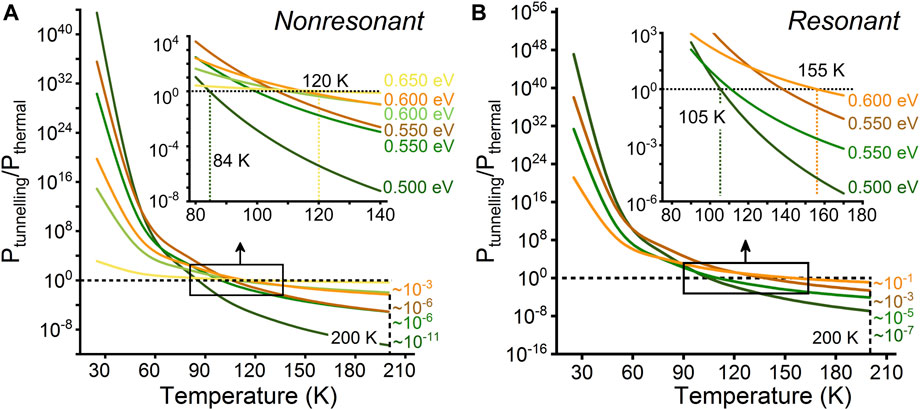
FIGURE 2. Ratio of the tunnelling probability to the thermal disturbance probability for the water chain in the CNT to achieve reorientation at certain provided energies and different temperatures. (A) Coherence is not considered in the tunnelling probability calculation. (B) Coherence is considered in the tunnelling probability calculation. The temperature range is 25–200 K, and the interval is 25 K “∼” is the magnitude.

Remarkably, due to the narrow width (approximately 1.9 Å and 2.5 Å for the reaction paths containing the L-type defect and D-type defect, and the values are similar to the previous article predicting hydrogen atom resonance tunneling [41]) of the well between the double barriers along the reaction path, the quantum coherence should not be ignored. Therefore, a discussion of the quantum tunnelling effects while considering coherence, that is, resonant tunnelling, is necessary. The tunnelling probability is defined as the ratio of the flow of particles out of the barrier to the flow of particles into the barrier. As shown in Figure 1E, with an increase in the provided energy, the tunnelling probability increases and decreases at times, showing a nonlinear change. This is significantly different from the quantum tunnelling probability without considering coherence. In addition, according to the peaks in Figure 1E, compared with quantum tunnelling without coherence, quantum tunnelling with coherence can achieve a higher probability at smaller provided energy. Taking the path containing the L-type defective intermediate as an example, the probabilities of quantum tunnelling without and with consideration of coherence are approximately 10⁻¹⁵, 10⁻¹², 10⁻¹⁰, 10⁻⁶, and 10⁻³ and 10⁻⁶, 10⁻³, 10⁻¹, 10⁰, and 100 when the provided energies at the double barrier are approximately 0.529 eV, 0.543 eV, 0.566 eV, 0.597 eV and 0.632 eV, respectively. In a word, at some specific provided energies, such as about 0.6 eV (detailed value is 0.597 eV), the resonant tunnelling with consideration of coherence greatly improves the tunnelling probability compared with sequential tunnelling (see in Figures 1D,E), which means that neglected quantum coherence may play an important role in the process of water chain flipping.

Our previous study has demonstrated that the persistent time (t) of the H-bond alignment for the confined water chain was closely related to the PES of flipping [24]. It is negatively correlation with the probability that the water chain achieves flipping by overcoming energy barriers. And the relationship between the number of water molecules (n) and the persistent time is written:

$\mathit{Log}\left(\mathit{t}\right)=\mathit{a}\times \mathit{n}+\mathit{b}(5)$

where a is the dynamic parameter of thermodynamic flipping under the traditional perspective. In this work, we found that the quantum tunneling, especially resonant tunneling, from the water chain itself has a positive impact on its flipping. This means that the existence of quantum tunnelling effects will reduce the persistent time (i.e., reducing the value of a), thereby enhancing the effect of water chain flipping. It is reported that with the increase of water molecules [24], water chain rotation becomes more difficult, which is expected to lead to relatively weak quantum tunneling effects.

Furthermore, we compare the probabilities of the water chain achieving reorientation via two different mechanisms (quantum tunnelling considering coherence and thermal disturbance), as shown in Figure 2B. The results show that when the temperature is lower than 105 K, tunnelling is dominant compared with thermal disturbance. When the temperature is higher than 155 K, thermal disturbance gradually becomes dominant. This temperature is approximately 20 K higher than that without considering coherence, indicating that the neglect of quantum coherence could lead to underestimation of the tunnelling capability. In addition, the ratios of the tunnelling probability to the thermal disturbance probability at 200 K are analyzed (Figure 2). For example, the ratios with coherence and without coherence are approximately 10⁻¹¹ and 10⁻⁷ when the provided energy is 0.5 eV for the reaction path containing the D defect, respectively. This further suggests that H-bond rotation is greater affected by quantum tunnelling than is generally recognized due to the presence of quantum coherence. Importantly, resonant tunnelling has been experimentally observed in hydrogen atom systems with an energy precision of 10⁻³ eV in previous report, which is equivalent to the resolution when considering resonant tunneling in this manuscript [1]. This suggests that there are opportunities for experimental observation and even regulation of water chain flipping in channels in the future, and our work is expected to provide theoretical guidance.

Although the approximation method in one-dimensional coordinates is widely used in the study of general tunnelling [42], it necessarily has some potential drawbacks in the study of resonant tunnelling. One of the problems neglected due to simplification is decoherence, i.e., the coherence breaking process caused by the interaction between the reaction coordinates and other coordinates under the influence of external environmental perturbations, which will correspondingly attenuate the effect of resonance tunnelling. However, it is well known that, the multidimensional quantum dynamics has remained difficult to describe properly with simulations up to now. We hope that our work will provide understanding of physical images and expect that further discussions on other factors can be performed in the future.

Conclusion

In summary, we shown the quantum tunnelling effects from the water chain itself under ideal conditions, which enhance the H-bond rotation. Importantly, compared with the generally recognized sequential tunnelling, the resonant tunnelling that considers quantum coherence can achieve a higher probability given less provided energy, which further enhances the rotation of the water chain. This work enriches the understanding of quantum tunneling effects on H-bonds and highlights the enhanced water chain rotation effect of previously neglected resonant tunneling due to quantum coherence, which is hoped to enable quantum regulation of the H-bond rotation mechanisms for confined water.

This paper is dedicated to the 70th anniversary of physics in Jilin University.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XY and LJ performed the theoretical simulations. ZW supervised the work. XY, LJ, YZ, ZZ, RL, and ZW discussed the results. XY, LJ, and ZW wrote the article.

Funding

This work was supported by the 2020-JCJQ project (GFJQ2126-007) and the National Natural Science Foundation of China (under grant number 11974136).

Acknowledgments

ZW also acknowledges the assistance of the High-Performance Computing Center of Jilin University and National Supercomputing Center in Shanghai.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yang T, Huang L, Xiao C, Chen J, Wang T, Dai D, et al. Enhanced reactivity of fluorine with para-hydrogen in cold interstellar clouds by resonance-induced quantum tunnelling. Nat Chem (2019) 11:744–9. doi:10.1038/s41557-019-0280-3

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Meng X, Guo J, Peng J, Chen J, Wang Z, Shi JR, et al. Direct visualization of concerted proton tunnelling in a water nanocluster. Nat Phys (2015) 11:235–9. doi:10.1038/nphys3225

CrossRef Full Text | Google Scholar

3. Benolt M, Marx D, Parrinello M. Tunnelling and zero-point motion in high-pressure ice. Nature (1998) 392:258–61. doi:10.1038/32609

CrossRef Full Text | Google Scholar

4. Ranea VA, Michaelides A, Ramírez R, De Andres PL, Vergés JA, King DA. Water dimer diffusion on Pd{111} assisted by an H-bond donor-acceptor tunneling exchange. Phys Rev Lett (2004) 92:136104–4. doi:10.1103/PhysRevLett.92.136104

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhang Q, Wahnström G, Björketun ME, Gao S, Wang E. Path integral treatment of proton transport processes inBaZrO3. Phys Rev Lett (2008) 101:215902–4. doi:10.1103/PhysRevLett.101.215902

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Quack M, Seyfang G. Atomic and molecular tunneling processes in chemistry. Amsterdam, Netherlands: Elsevier (2021). doi:10.1016/b978-0-12-817234-6.00012-x

CrossRef Full Text | Google Scholar

7. Ryzhkin MI, Ryzhkin IA, Kashin AM, Zavorotnaya UM, Sinitsyn VV. Quantum protons in one-dimensional water. J Phys Chem C (2022) 126:8100–6. doi:10.1021/acs.jpcc.2c01140

CrossRef Full Text | Google Scholar

8. Zhang D, Yang X, Jiang W, Jin L, Gao Y, Wang Z. Pauli repulsion enhances mobility of ultraconfined water. ACS Nano (2021) 15:2490–6. doi:10.1021/acsnano.0c06508

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Li D, Zhang Z, Jiang W, Zhu Y, Gao Y, Wang Z. Uncooperative effect of hydrogen bond on water dimer. Chin Phys Lett (2021) 38:013101. doi:10.1088/0256-307X/38/1/013101

CrossRef Full Text | Google Scholar

10. Liu R, Wang R, Li D, Zhu Y, Yang X, Wang Z. An ab initio study on boundaries for characterizing cooperative effect of hydrogen bonds by intermolecular compression. Chin Chem Lett (2022):107857. doi:10.1016/j.cclet.2022.107857

CrossRef Full Text | Google Scholar

11. Zhou L, Wiebe J, Wiesendanger R, Gambardella P, Baxevanis B, Khajetoorians AA, et al. Nuclear quantum effects of hydrogen bonds probed by tip-enhanced inelastic electron tunneling. Science (2016) 352:321–5. doi:10.1126/science.aaf2042

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Ceriotti M, Fang W, Kusalik PG, McKenzie RH, Michaelides A, Morales MA, et al. Nuclear quantum effects in water and aqueous systems: Experiment, theory, and current challenges. Chem Rev (2016) 116:7529–50. doi:10.1021/acs.chemrev.5b00674

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Kolesnikov AI, Anovitz LM, Mamontov E, Podlesnyak A, Ehlers G. Strong anisotropic dynamics of ultra-confined water. J Phys Chem B (2014) 118:13414–9. doi:10.1021/jp505355b

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Gorshunov BP, Zhukova ES, Torgashev VI, Lebedev VV, Shakurov GS, Kremer RK, et al. Quantum behavior of water molecules confined to nanocavities in gemstones. J Phys Chem Lett (2013) 4:2015–20. doi:10.1021/jz400782j

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Jeremy O, Richardson SCA, Lobsiger S, Reid AA, Temelso B, Shields GC, et al. Concerted hydrogen-bond breaking by quantum tunneling in the water hexamer prism. Science (2016) 351:1310–3. doi:10.1126/science.aae0012

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wang L, Zhao J, Li F, Fang H, Lu JP. First-principles study of water chains encapsulated in single-walled carbon nanotube. J Phys Chem C (2009) 113:5368–75. doi:10.1021/jp808873r

CrossRef Full Text | Google Scholar

17. Hummer G, Rasaiah JC, Noworyta JP. Water conduction through the hydrophobic channel of a carbon nanotube. Nature (2001) 414:188–90. doi:10.1038/35102535

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Joseph S, Aluru NR. Pumping of confined water in carbon nanotubes by rotation-translation coupling. Phys Rev Lett (2008) 101:064502–4. doi:10.1103/PhysRevLett.101.064502

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Striolo A. The mechanism of water diffusion in narrow carbon nanotubes. Nano Lett (2006) 6:633–9. doi:10.1021/nl052254u

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kalra A, Garde S, Hummer G. Osmotic water transport through carbon nanotube membranes. Proc Natl Acad Sci U S A (2003) 100:10175–80. doi:10.1073/pnas.1633354100

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhang D, Zhang Z, Jiang W, Gao Y, Wang Z. Effect of confinement on water rotation: Via quantum tunnelling. Nanoscale (2018) 10:18622–6. doi:10.1039/c8nr05137b

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Liu X, Pang H, Liu X, Li Q, Zhang N, Mao L, et al. Orderly porous covalent organic frameworks-based materials: Superior adsorbents for pollutants removal from aqueous solutions. Innovation (Camb) (2021) 2:100076. doi:10.1016/j.xinn.2021.100076

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Mondal D, Dandekar BR, Ahmad M, Mondal A, Mondal J, Talukdar P. Selective and rapid water transportation across a self-assembled peptide-diol channel via the formation of a dual water array. Chem Sci (2022) 13:9614–23. doi:10.1039/d2sc01737g

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jin L, Zhang D, Zhu Y, Yang X, Gao Y, Wang Z. A step-by-step process-induced unidirectional oriented water wire in the nanotube. J Phys Chem Lett (2021) 12:350–4. doi:10.1021/acs.jpclett.0c03340

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Alexiadis A, Kassinos S. Molecular simulation of water in carbon nanotubes. Chem Rev (2008) 108:5014–34. doi:10.1021/cr078140f

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chen X, Cao G, Han A, Punyamurtula VK, Liu L, Culligan PJ, et al. Nanoscale fluid transport: Size and rate effects. Nano Lett (2008) 8:2988–92. doi:10.1021/nl802046b

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wang J, Zhu Y, Zhou J, Lu X-H. Diameter and helicity effects on static properties of water molecules confined in carbon nanotubes. Phys Chem Chem Phys (2004) 6:829–35. doi:10.1039/B313307A

CrossRef Full Text | Google Scholar

28. Majumder M, Chopra N, Andrews R, Hinds BJ. Enhanced flow in carbon nanotubes. Nature (2005) 438:44. doi:10.1038/438044a

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Joseph S, Aluru NR. Why are carbon nanotubes fast transporters of water? Nano Lett (2008) 8:452–8. doi:10.1021/nl072385q

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Feng JW, Ding HM, Ren CL, Ma YQ. Pumping of water by rotating chiral carbon nanotube. Nanoscale (2014) 6:13606–12. doi:10.1039/c4nr03407d

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Cambré S, Schoeters B, Luyckx S, Goovaerts E, Wenseleers W. Experimental observation of single-file water filling of thin single-wall carbon nanotubes down to chiral index (5, 3). Phys Rev Lett (2010) 104:207401–4. doi:10.1103/PhysRevLett.104.207401

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Agrawal KV, Shimizu S, Drahushuk LW, Kilcoyne D, Strano MS. Observation of extreme phase transition temperatures of water confined inside isolated carbon nanotubes. Nat Nanotechnol (2017) 12:267–73. doi:10.1038/nnano.2016.254

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Adamo C, Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J Chem Phys (1999) 110:6158–70. doi:10.1063/1.478522

CrossRef Full Text | Google Scholar

34. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 09, revision D.01. (2016).

Google Scholar

35. Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys (2010) 132:154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Fukui K. Formulation of the reaction coordinate. J Phys Chem (1970) 74:4161–3. doi:10.1021/j100717a029

CrossRef Full Text | Google Scholar

37. Gonzalez C, Schlegel HB. Reaction path following in mass-weighted internal coordinates. J Phys Chem (1990) 94:5523–7. doi:10.1021/j100377a021

CrossRef Full Text | Google Scholar

38. Kramers HA. Wellenmechanik und halbzahlige Quantisierung. Z Physik (1926) 39:828–40. doi:10.1007/BF01451751

CrossRef Full Text | Google Scholar

39. Wentzel G. Eine Verallgemeinerung der Quantenbedingungen für die Zwecke der Wellenmechanik. Z Physik (1926) 38:518–29. doi:10.1007/BF01397171

CrossRef Full Text | Google Scholar

40. Dellago C, Naor MM, Hummer G. Proton transport through water-filled carbon nanotubes. Phys Rev Lett (2003) 90:105902. doi:10.1103/PhysRevLett.90.105902

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Bi C, Yang Y. Atomic resonant tunneling in the surface diffusion of H atoms on Pt(111). J Phys Chem C (2021) 125:464–80. doi:10.1021/acs.jpcc.0c08906

CrossRef Full Text | Google Scholar

42. Schreiner PR. Quantum mechanical tunneling is essential to understanding chemical reactivity. Trends Chem (2020) 2:980–9. doi:10.1016/j.trechm.2020.08.006

CrossRef Full Text | Google Scholar