Multi-party semi-quantum key distribution protocol based on hyperentangled Bell states

Semi-quantum key distribution allows generating a raw key between two communication participants, in which the sender is a quantum participant and the receiver is a classical participant. This article presents an original semi-quantum key distribution protocol based on hyperentangled Bell states. The hyperentangled Bell states can be entangled simultaneously in polarization and spatial degrees of freedom, enhancing channel capacity. According to the characteristics of hyperentangled Bell states, the proposed protocol is more efficient than the protocol based on Bell states. Moreover, the measure–resend attack, the intercept–resend attack, and the entangle–measure attack are analyzed in detail. The security analysis demonstrates that the proposed protocol is secure. In addition, a multi-party semi-quantum key distribution scheme based on hyperentangled Bell states is proposed, which can realize key distribution between one quantum participant and multiple classical participants.

1 Introduction

A traditional cryptographic protocol is the foundation of information security in public network channels [1–3]. With the successful development of quantum computers and quantum computing, the traditional classical encryption algorithm based on mathematical problems has been seriously threatened [4]. Different from traditional cryptography, quantum cryptography is based on quantum physics [5] and information science to guarantee communication security [6]. Therefore, quantum information processing has gained increasing attention for potential applications such as quantum communication technology and quantum computing. Quantum communication technology is based on quantum cryptography to solve the potential problem of channel eavesdropping, which has provable security. Quantum communication includes quantum key distribution (QKD) [7, 8], quantum secure direction communication (QSDC) [9, 10], quantum secret sharing (QSS) [11, 12], quantum private comparison (QPC) [13, 14] etc. Quantum key distribution protocol, as a significant field of quantum cryptography, is a quantum cryptography protocol, which can be verified theoretically and experimentally.

The BB84 protocol [15], the initial quantum key distribution protocol, was presented by Bennett and Brassard in 1984. It guarantees the secure transmission of keys between two participants. The BB84 protocol had gained widespread attention when it was proposed, and many researchers began to study the QKD protocol since BB84 was presented, such as Ekert91 protocol [16], BBM92 protocol [17], SARG04 protocol [18], and so on. In recent years, the latest protocols and the development of QKD were presented [19–22]. However, the traditional QKD protocols require all communication participants to have quantum capability and quantum devices [23], which are too complex and expensive to realize. At present, only a few environments can be implemented. These are also important factors hindering QKD’s current development.

Aiming at the problems faced in complex quantum operations and expensive quantum devices, the concept of “semi-quantum” was proposed for the first time by Boyer et al. [24]. They proposed the first semi-quantum key distribution protocol in 2007. Alice, a sender, has quantum capability, and Bob, a receiver, has classical capability. The classical capability is restricted within the following operations : (1) reflecting the qubits with no disturbance ; (2) measuring the qubits with basis Z; (3) preparing the fresh qubits with basis Z; and (4) reordering the qubits via delay lines. Because the concept of “semi-quantum” requires less quantum power and resources and is easy to implement, it has received extensive attention, has been studied by an increasing number of scholars, and even extended to other directions such as semi-quantum distribution (SQKD) protocols [25–33], semi-quantum secret sharing (SQSS) protocols [34–37], semi-quantum private comparison (SQPC) protocols [38–41], etc. In 2009, Zou et al. [25] put forward five SQKD protocols based on three quantum states, two quantum states, and one quantum state, and strong proofs are given. In 2011, an SQKD protocol based on Bell states was devised by Wang et al. [26]. Without invoking the classical participant’s measurement capability, an efficient SQKD protocol was designed by Zou et al. [27] in 2015. In 2017, an SQKD protocol that limits the quantum sender’s measurement capabilities was presented by Krawec et al. [28]. Two semi-quantum key distribution protocols based on GHZ states were proposed by Zhu et al. [29] in 2018. The presented protocol had higher noise tolerance than the “fully quantum” protocol. Iqbal et al. [30] designed an SQKD protocol based on high-dimensional quantum states which increased the noise tolerance in 2019. In 2020, Ye et al. [31] proposed a novel SQKD based on single photons in both polarization and spatial-mode degrees of freedom, which improved the capacity of quantum communication. In 2021, Tian et al. [32] presented an efficient SQKD based on EPR and single-particle hybridization, which has higher efficiency than that found in the similar literature. An efficient SQKD protocol based on single photons in both polarization and spatial-mode degrees of freedom was proposed by Ye et al. [33], which has double quantum communication capacity.

The hyperentangled states not only contain the entanglement between multi-particles but also multi-dimensional entanglements, such as spatial degree of freedom and polarization degree of freedom [42]. The way to transmit secret information safely is to measure the spatial degree of freedom and polarization degree of freedom of a photon by hyperentangled Bell state measurement to change the spatial degree of freedom and polarization degree of freedom of another photon.

To improve the efficiency and security of information transmission, reducing the responsibility of the protocol, this study proposes a semi-quantum key distribution protocol based on hyperentangled Bell states. In addition, the security analysis of the protocol shows that the proposed protocol can effectively resist the measure–resend attack, intercept–resend attack, and entangle–measure attack. It is demonstrated that the proposed protocol is efficient and secure. In the process of key distribution, sometimes not only two participants but also multiple participants are required. Considering that more scenarios are applicable, we design a semi-quantum key distribution protocol that satisfies multiple participants and achieves more than the previous key distribution between two participants.

This article is organized as follows: Section 2 proposes the semi-quantum distribution protocol, Section 3 gives the security proof and comparison of the protocol, Section 4 designs the multi-party semi-quantum distribution protocol, and Section 5 summarizes it.

2 Semi-quantum key distribution protocol

In this section, we introduce the hyperentangled Bell states and propose an SQKD protocol based on the hyperentangled Bell states.

2.1 The hyperentangled Bell states

We present the hyperentangled Bell states as follows:

${|\mathrm{\Phi }\rangle }_{ps}^{12}={|\mu \rangle }_p^{12}\otimes {|\nu \rangle }_s^{12},(1)$

where 1 and 2 represent the two qubits in the hyperentangled Bell states and p, s represent the polarization degree of freedom and the spatial degree of freedom, respectively.

Under the polarization degree of freedom ${|\mu \rangle }_p^{12}$, the Bell states can be described as follows:

${|{\varphi }^{\pm }\rangle }_p^{12}=\frac{1}{\sqrt{2}}\left(|HH\rangle \pm |VV\rangle \right),(2)$

${|{\psi }^{\pm }\rangle }_p^{12}=\frac{1}{\sqrt{2}}\left(|HV\rangle \pm |VH\rangle \right),(3)$

where |H⟩, |V⟩ are the horizontal and the vertical polarizations, respectively.

Under the spatial degree of freedom ${|\nu \rangle }_s^{12}$, the Bell state can be described as follows:

${|{\varphi }^{\pm }\rangle }_s^{12}=\frac{1}{\sqrt{2}}\left(|RR\rangle \pm |LL\rangle \right),(4)$

${|{\psi }^{\pm }\rangle }_s^{12}=\frac{1}{\sqrt{2}}\left(|RL\rangle \pm |LR\rangle \right),(5)$

where |R⟩, |L⟩ are orthogonal spatial states.

2.2 Protocol

Based on hyperentangled Bell states, the quantum sender Alice and the classical receiver Bob can produce secure keys. In this protocol, Alice has full quantum capabilities, with the potential to generate and measure the qubits with an arbitrary basis. Bob has classical capabilities, with the potential to only prepare and measure the qubits with Z basis. The proposed protocol comprises the following six steps.

Step 1: Alice generated N = 4n hyperentangled Bell states, which are chosen from sets $\{|{\varphi }^{\pm }{\rangle }_p^{12}\otimes |{\varphi }^{\pm }{\rangle }_s^{12},|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\varphi }^{\pm }{\rangle }_s^{12},|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12},|{\varphi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12}\}$, where 1, 2 represent the two particles of each state. Alice implemented particle 1 to compose the sequence A = {A₁, A₂, … , A_N} and particle 2 to compose the sequence B = {B₁, B₂, … , B_N}. Then, she held the A sequence in her hands and transmitted the B sequence to Bob.

Step 2: When Bob received the qubits, he randomly performed two operations. CTRL operation: reflecting the qubits to Alice with no disturbance and SIFT operation: measuring the qubits with base Z_P ⊗ Z_S and resending the same states to Alice.

Step 3: When the qubits arrived, Alice notified Bob that she has received them. Bob announced the operations of qubits, which he performed.

Step 4: Alice and Bob conducted eavesdropping detection. For CTRL particles, Alice combined particle 2 with the corresponding particle 1 and recorded hyperentangled Bell state measurements. The measurement results should be the same as what Alice sent. If the error rate exceeds the threshold value, Alice and Bob will terminate this protocol. Otherwise, they will move on to the next step.

Step 5: For SIFT particles, Alice carried out Z_P ⊗ Z_S base measurement on particle 1. Alice randomly selected n measurement results from particle 1, in which Bob chose SIFT operation. Alice and Bob checked the error rate, and Alice’s measurements should be equal to Bob’s measurements. If the error rate is higher than the threshold value, the protocol will be discarded. Otherwise, they will proceed with the next step.

Step 6: Alice and Bob performed error correcting code (ECC) and privacy amplification (PA) for the remaining n measurement results, in which Bob chose SIFT operation to obtain the final keys.

Table 1 gives a description of Alice’s and Bob’s operations when Alice transmitted $|{\varphi }^{+}{\rangle }_p^2\otimes |{\varphi }^{+}{\rangle }_s^2$ to Bob.

TABLE 1

TABLE 1. One example description of Alice’s and Bob’s operations.

3 Security analysis and comparison

A malicious eavesdropper, Eve, attempted to obtain the significant keys between Alice and Bob in this communication. Eve may attack keys by the measure–resend attack, intercept–resend attack, and entangle–resend attack.

3.1 Measure–resend attack

When Alice transmitted qubits to Bob via the quantum channel, Eve measured qubits from Alice and sent the measured qubits to Bob. Eve is eager to obtain the significant operations, which is chosen by Bob. Unfortunately, no matter what measures Eve took, errors will be introduced. When Alice and Bob conduct eavesdropping detection, Eve will be found.

Without loss of generality, Alice prepared the hyperentangled Bell states $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$ and sent the particle 2 sequence to Bob. The security analysis of hyperentangled Bell states $|{\varphi }^{-}{\rangle }_p^{12}\otimes |{\varphi }^{-}{\rangle }_s^{12}$, $|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\varphi }^{\pm }{\rangle }_s^{12}$, $|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12}$ and $|{\varphi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }\left.{\rangle }_s^{12}\right\}$ are similar to $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$.

Eve intercepted the particles and recorded base Z_P ⊗ Z_S measurement on $|{\varphi }^{+}{\rangle }_p^2\otimes |{\varphi }^{+}{\rangle }_s^2$. The qubit is collapsed to |0⟩ ⊗|0⟩, |0⟩ ⊗|1⟩, |1⟩ ⊗|0⟩, or |1⟩ ⊗|1⟩, each with 25% probability. After measurement, we suppose that Eve transmitted the states |0⟩ ⊗|0⟩ to Bob (if Eve’s measurement results are the rest of three results, the analysis is similar to the mentioned analysis). When Bob received the qubits, he chose CTRL operation or SIFT operation at random. If Bob chose CTRL operation, Alice performed hyperentangled Bell state measurement on the reflected qubit and the remaining qubit. Because Eve destroyed particle 2 from the hyperentangled Bell states, particle 2 has been changed, which is differently sent by Alice. The hyperentangled Bell states are collapsed to $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$, $|{\varphi }^{-}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$, $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{-}{\rangle }_s^{12}$ and $|{\varphi }^{-}{\rangle }_p^{12}\otimes |{\varphi }^{-}{\rangle }_s^{12}$, each with 25% probability. Alice can gain the initial measurement results $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$ with 1/4 probability. Therefore, Eve will be detected with the probability of 75% by the security check of Step 4. If Bob chose CTRL operation, there is no error introduced in this case. So Eve will not be detected.

Therefore, the proposed protocol can resist the measure–resend attack.

3.2 Intercept–resend attack

When Alice transmitted qubits to Bob via the quantum channel, Eve intercepted qubits from Alice and resent faked qubits, which were generated by Eve to Bob. Eve wanted to figure out which operation Bob had chosen. Unfortunately, irrespective of the measures taken by Eve, errors will be introduced. When Alice and Bob conduct eavesdropping detection, Eve will be found.

Without loss of generality, Alice prepares the hyperentangled Bell states $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$ and sends the particle 2 sequence to Bob. The security analysis of hyperentangled Bell states $|{\psi }^{-}{\rangle }_p^{12}\otimes |{\varphi }^{-}{\rangle }_s^{12}$, $|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12}$ and $|{\varphi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }\left.{\rangle }_s^{12}\right\}$ are similar to $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$.

Eve intercepted the particles and generated hyperentangled Bell states $|{\varphi }^{-}{\rangle }_p^{12}\otimes |{\varphi }^{-}{\rangle }_s^{12}$ (if Eve generated the remaining three hyperentangled Bell states, the analysis is similar to the mentioned analysis). Eve transmitted particle 2 to Bob because Eve reflected the qubits directly from Alice, and if Bob selected CTRL operation, there is no error introduced in this case. If Bob selects SIFT operation, the received qubits will be measured with base Z_P ⊗ Z_S, and the qubits will collapse to |0⟩ ⊗|0⟩, |0⟩ ⊗|1⟩, |1⟩ ⊗|0⟩, and |1⟩ ⊗|1⟩, each with 25% probability. When Alice received qubits, the received qubits with base Z_P ⊗ Z_S will be measured with ease, and the qubits will collapse to |0⟩ ⊗|0⟩, |0⟩ ⊗|1⟩, |1⟩ ⊗|0⟩, and |1⟩ ⊗|1⟩, each with 25% probability. Alice and Bob obtain the same measurement results with 1/4 probability. Therefore, Eve can be detected with the probability of 75% by the security check of Step 5.

Therefore, the proposed protocol can resist the intercept–resend attack.

3.3 Entangle–measure attack

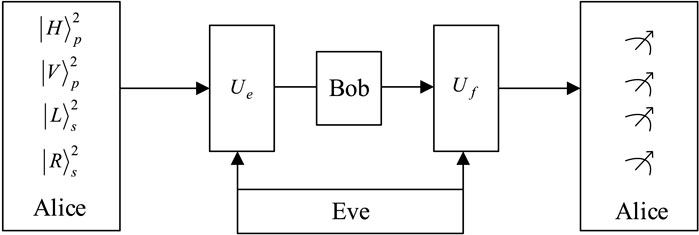
When Alice transmitted qubits to Bob via the quantum channel, Eve entangled the ancillary qubits to the transmitted qubits from Alice. When the qubits were transmitted back to Alice, Eve measured the transmitted qubits to obtain Bob’s measurement results. The implementation of the entangle–measure attack is shown in Figure 1. Unfortunately, irrespective of the measures taken by Eve, errors will be introduced. When Alice and Bob conduct eavesdropping detection, Eve will be found.

FIGURE 1

FIGURE 1. Entangle–measure attacks with two operations U_e and U_f.

Without loss of generality, it is assumed that Alice sent $|{\varphi }^{+}{\rangle }_p^2\otimes |{\varphi }^{+}{\rangle }_s^2$ to Bob and Eve performed unitary operation U_e to entangle the ancillary qubit |e⟩ with the target qubits and sent to Bob. When the qubits returned to Alice, Eve measured the ancillary qubit |e⟩ to get the information. For the target qubits $|{\varphi }^{+}{\rangle }_p^2\otimes |{\varphi }^{+}{\rangle }_s^2$, which are sent by Alice, after U_e, the states become as follows:

$\begin{array}{c}\hfill U_e\left({|H\rangle }_p^2\otimes {|R\rangle }_s^2\right)|e\rangle =\left({|H\rangle }_p^2|e_{hh}\rangle +{|V\rangle }_p^2|e_{hv}\rangle \right)\otimes \left({|R\rangle }_s^2|e_{rr}\rangle +{|L\rangle }_s^2|e_{rl}\rangle \right),\end{array}(6)$

$\begin{array}{c}\hfill U_e\left({|H\rangle }_p^2\otimes {|L\rangle }_s^2\right)|e\rangle =\left({|H\rangle }_p^2|e_{hh}\rangle +{|V\rangle }_p^2|e_{hv}\rangle \right)\otimes \left({|R\rangle }_s^2|e_{lr}\rangle +{|L\rangle }_s^2|e_{ll}\rangle \right),\end{array}(7)$

$\begin{array}{c}\hfill U_e\left({|V\rangle }_p^2\otimes {|R\rangle }_s^2\right)|e\rangle =\left({|H\rangle }_p^2|e_{vh}\rangle +{|V\rangle }_p^2|e_{vv}\rangle \right)\otimes \left({|R\rangle }_s^2|e_{rr}\rangle +{|L\rangle }_s^2|e_{rl}\rangle \right),\end{array}(8)$

$\begin{array}{c}\hfill U_e\left({|V\rangle }_p^2\otimes {|L\rangle }_s^2\right)|e\rangle =\left({|H\rangle }_p^2|e_{vh}\rangle +|V{\rangle }_p^2|e_{vv}\rangle \right)\otimes \left(|R{\rangle }_s^2|e_{lr}\rangle +|L{\rangle }_s^2|e_{ll}\rangle \right),\end{array}(9)$

where |e_hh⟩, |e_hv⟩, |e_vh⟩, |e_vv⟩, |e_rr⟩, |e_rl⟩, |e_lr⟩, and |e_ll⟩ are the pure ancillary states, which are controlled by the operation U_e.

Eve expected to pass the eavesdropping detection, where the operation U_e does not introduce errors. According to Eqs. 6–9, it can be inferred that

$|e_{hv}\rangle =|e_{rl}\rangle =|e_{lr}\rangle =|e_{vh}\rangle =0.(10)$

Then, Eve sent the qubits to Bob. Bob selected CTRL operation or SIFT operation on the qubits when he received them, and Bob returned the qubits to Alice. Eve carried out unitary operation U_f on the qubits which Bob transmitted back to Alice.

Case 1: Bob performed SIFT operation and returned the qubits to Alice. Eve performed U_f on the states sent back to Alice.

$\begin{array}{c}\hfill U_f\left(|H{\rangle }_p^2|e_{hh}\rangle \otimes |R{\rangle }_s^2|e_{rr}\rangle \right)=|H{\rangle }_p^2|f_{hh}\rangle \otimes |R{\rangle }_s^2|f_{rr}\rangle ,\end{array}(11)$

$\begin{array}{c}\hfill U_f\left(|H{\rangle }_p^2\right.|e_{hh}\rangle \otimes \left(|L{\rangle }_s^2|e_{ll}\rangle \right)=|H{\rangle }_p^2|f_{hh}\rangle \otimes |L{\rangle }_s^2|f_{ll}\rangle ,\end{array}(12)$

$\begin{array}{c}\hfill U_f\left(|V{\rangle }_p^2|e_{vv}\rangle \otimes |R{\rangle }_s^2|e_{rr}\rangle \right)=|V{\rangle }_p^2|f_{vv}\rangle \otimes |R{\rangle }_s^2|f_{rr}\rangle ,\end{array}(13)$

$\begin{array}{c}\hfill U_f\left(|V{\rangle }_p^2|e_{vv}\rangle \otimes |L{\rangle }_s^2|e_{ll}\rangle \right)=|V{\rangle }_p^2|f_{vv}\rangle \otimes |L{\rangle }_s^2|f_{ll}\rangle .\end{array}(14)$

Case 2: Bob performed CTRL operation and did nothing on the qubits. Therefore, after entangling the ancillary particle on the hyperentangled Bell states, the states become as follows:

$\begin{array}{cc}\hfill & U_f\left(|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}\right)\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\left(\left(|H^1\rangle \left(|H^2\rangle |f_{hh}\rangle +|V^2\rangle |f_{hv}\rangle \right)+|V^1\rangle \left(|H^2\rangle |f_{vh}\rangle +|V^2\rangle |f_{vv}\rangle \right)\right)\right.\hfill \\ \hfill & \otimes \left(|R^1\rangle \left(|R^2\rangle |f_{rr}\rangle +|L^2\rangle |f_{rl}\rangle \right)+|L^1\rangle \left(|R^2\rangle |f_{lr}\rangle +|L^2\rangle |f_{ll}\rangle \right)\right)\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\left(\left(|H^1{H}^2\rangle |f_{hh}\rangle +|H^1{V}^2\rangle |f_{hv}\rangle +|V^1{H}^2\rangle |f_{vh}\rangle +|V^1{V}^2\rangle |f_{vv}\rangle \right)\right.\hfill \\ \hfill & \otimes \left.\left(|R^1{R}^2\rangle |f_{rr}\rangle +|R^1{L}^2\rangle |f_{rl}\rangle +|L^1{R}^2\rangle |f_{lr}\rangle +|L^1{L}^2\rangle |f_{ll}\rangle \right)\right)\hfill \\ \hfill & =\frac{1}{2}\left(\left(|{\varphi }^{+}{\rangle }_p^{12}+|{\varphi }^{-}{\rangle }_p^{12}\right)|f_{hh}\rangle +\left(|{\psi }^{+}{\rangle }_p^{12}+|{\psi }^{-}{\rangle }_p^{12}\right)|f_{hv}\rangle \right.\hfill \\ \hfill & +\left.\left(|{\psi }^{+}{\rangle }_p^{12}-|{\psi }^{-}{\rangle }_p^{12}\right)|f_{vh}\rangle +\left(|{\varphi }^{+}{\rangle }_p^{12}-|{\varphi }^{-}{\rangle }_p^{12}\right)|f_{vv}\rangle \right)\hfill \\ \hfill & \otimes \left(\left(|{\varphi }^{+}{\rangle }_s^{12}+|{\varphi }^{-}{\rangle }_s^{12}\right)|f_{rr}\rangle +\left(|{\psi }^{+}{\rangle }_s^{12}+|{\psi }^{-}{\rangle }_s^{12}\right)|f_{rl}\rangle \right.\hfill \\ \hfill & +\left.\left.\left(|{\psi }^{+}{\rangle }_s^{12}-|{\psi }^{-}{\rangle }_s^{12}\right)|f_{lr}\rangle +\left(|{\varphi }^{+}{\rangle }_s^{12}-|{\varphi }^{-}{\rangle }_s^{12}\right)|f_{ll}\rangle \right)\right)\hfill \\ \hfill & =\frac{1}{2}\left(|{\varphi }^{+}{\rangle }_p^{12}|f_{hh}\rangle +|{\varphi }^{-}{\rangle }_p^{12}|f_{hh}\rangle +\left(|{\psi }^{+}{\rangle }_p^{12}+|{\psi }^{-}{\rangle }_p^{12}\right)|f_{hv}\rangle \right.\hfill \\ \hfill & +\left.\left(|{\psi }^{+}{\rangle }_p^{12}-|{\psi }^{-}{\rangle }_p^{12}\right)|f_{vh}\rangle +|{\varphi }^{+}{\rangle }_p^{12}|f_{vv}\rangle -|{\varphi }^{-}{\rangle }_p^{12}|f_{vv}\rangle \right)\hfill \\ \hfill & \otimes \left(|{\varphi }^{+}{\rangle }_s^{12}|f_{rr}\rangle +|{\varphi }^{-}{\rangle }_s^{12}|f_{rr}\rangle +\left(|{\psi }^{+}{\rangle }_s^{12}+|{\psi }^{-}{\rangle }_s^{12}\right)|f_{rl}\rangle \right.\hfill \\ \hfill & +\left.\left(|{\psi }^{+}{\rangle }_s^{12}-|{\psi }^{-}{\rangle }_s^{12}\right)|f_{lr}\rangle +|{\varphi }^{+}{\rangle }_s^{12}|f_{ll}\rangle -|{\varphi }^{-}{\rangle }_s^{12}|f_{ll}\rangle \right)\hfill \\ \hfill & =\frac{1}{2}\left(|{\varphi }^{+}{\rangle }_p^{12}\left(|f_{hh}\rangle +|f_{vv}\rangle \right)+|{\varphi }^{-}{\rangle }_p^{12}\left(|f_{hh}\rangle -|f_{vv}\rangle \right)+\left(|{\psi }^{+}{\rangle }_p^{12}+|{\psi }^{-}{\rangle }_p^{12}\right)|f_{hv}\rangle \right.\hfill \\ \hfill & +\left.\left(|{\psi }^{+}{\rangle }_p^{12}-|{\psi }^{-}{\rangle }_p^{12}\right)|f_{vh}\rangle \right)\hfill \\ \hfill & \otimes \left(|{\varphi }^{+}{\rangle }_s^{12}\left(|f_{rr}\rangle +|f_{ll}\rangle \right)+|{\varphi }^{-}{\rangle }_s^{12}\left(|f_{rr}\rangle -|f_{ll}\rangle \right)+\left(|{\psi }^{+}{\rangle }_s^{12}+|{\psi }^{-}{\rangle }_s^{12}\right)|f_{rl}\rangle \right.\hfill \\ \hfill & +\left.\left(|{\psi }^{+}{\rangle }_s^{12}-|{\psi }^{-}{\rangle }_s^{12}\right)|f_{lr}\rangle \right).\hfill \end{array}(15)$

Eve expected to pass the eavesdropping detection, so U_f should not change the states which were sent by Alice. Therefore, from Eq. 15, it can be inferred that

$|f_{hh}\rangle -|f_{vv}\rangle =0,(16)$

$|f_{rr}\rangle -|f_{ll}\rangle =0,(17)$

$|f_{hv}\rangle =|f_{vh}\rangle =|f_{rl}\rangle =|f_{lr}\rangle =0.(18)$

According to Eqs. 16–18, Eqs. 11–14 can be rewritten as follows:

$\begin{array}{c}\hfill U_f\left(|H{\rangle }_p^2|e_{hh}\rangle \otimes |R{\rangle }_s^2|e_{rr}\rangle \right)=|H{\rangle }_p^2|f_{hh}\rangle \otimes |R{\rangle }_s^2|f_{rr}\rangle ,\end{array}(19)$

$\begin{array}{cc}\hfill U_f\left(|H{\rangle }_p^2|e_{hh}\rangle \otimes |L{\rangle }_s^2|e_{ll}\rangle \right)& =|H{\rangle }_p^2|f_{hh}\rangle \otimes |L{\rangle }_s^2|f_{ll}\rangle \hfill \\ \hfill & =|H{\rangle }_p^2|f_{hh}\rangle \otimes |L{\rangle }_s^2|f_{rr}\rangle ,\hfill \end{array}(20)$

$\begin{array}{cc}\hfill U_f\left(|V{\rangle }_p^2|e_{vv}\rangle \otimes |R{\rangle }_s^2|e_{rr}\rangle \right)& =|V{\rangle }_p^2|f_{vv}\rangle \otimes |R{\rangle }_s^2|f_{rr}\rangle \hfill \\ \hfill & =|V{\rangle }_p^2|f_{hh}\rangle \otimes |R{\rangle }_s^2|f_{rr}\rangle ,\hfill \end{array}(21)$

$\begin{array}{cc}\hfill U_f\left(|V{\rangle }_p^2|e_{vv}\rangle \otimes |L{\rangle }_s^2|e_{ll}\rangle \right)& =|V{\rangle }_p^2|f_{vv}\rangle \otimes |L{\rangle }_s^2|f_{ll}\rangle \hfill \\ \hfill & =|V{\rangle }_p^2|f_{hh}\rangle \otimes |L{\rangle }_s^2|f_{rr}\rangle .\hfill \end{array}(22)$

According to the aforementioned equations, Eve’s probes are dependent on the corresponding states. Once Eve acquired the information, the eavesdropping behavior will introduce the error and be detected. So, Eve cannot acquire any valuable information.

For security analysis of qubits $|{\psi }^{-}{\rangle }_p^{12}\otimes |{\varphi }^{-}{\rangle }_s^{12}$, $|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12}$, $|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\varphi }^{\pm }{\rangle }_s^{12}$, and $|{\varphi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12}$ are similar to $|{\varphi }^{+}{\rangle }_p^{12}\otimes |{\varphi }^{+}{\rangle }_s^{12}$.

Consequently, the proposed protocol can resist the entangle–measure attack.

3.4 Comparison

The efficiency of key distribution can be improved by using the properties of hyperentangled Bell states. For example, Bell states can transmit two bits of classical information each time, while hyperentangled Bell states can transmit four bits of classical information each time, twice as much as Bell states. Specifically, the proposed protocols transmitted two bits in each interaction, and the previous SQKD based on the Bell state can only transmit one bit.

The efficiency qubit can use equation η = c/(q + b) for calculation, where c represents the compared classical participants, q represents particles generated by the quantum participant, and b represents particles generated by the classical participant. In Boyer et al. [24], the quantum resource is single photon; Alice prepared eight particles, and Bob measured and prepared four particles. Hence, η = c/(q + b) = 1/(8 + 4) = 1/12. Wang et al. [26] used the Bell states to describe an SQPC protocol, wherein Alice generated four particles and Bob measured and prepared two particles. Therefore, η = c/(q + b) = 1/(4 + 2) = 1/6. Zhu et al. [29] employed GHZ states to construct an SQPC protocol. Therefore, η = c/(q + b) = 1/(12 + 2) = 1/14. In Ye et al. [33], the single photon in two degrees of freedom is used to implement quantum key distribution. Alice prepared six particles, and Bob measured and prepared three particles. So, η = c/(q + b) = 2/(6 + 3) = 2/9. In the proposed protocol, SQKD is based on hyperentangled Bell states, Alice randomly prepared eight particles, and Bob measured and prepared four particles. Hence, η = c/(q + b) = 2/(8 + 4) = 1/6.

Table 2 shows the comparison between the proposed protocol and some protocols. It can be seen that this protocol and protocol [33] expand the degree of freedom of particles from a single degree of freedom to two degrees of freedom. This increases the communication capacity. The proposed protocol takes Bell states as an example to discuss the multiple degrees of freedom of the entangled state, which provides an indication for further research of various entangled states (GHZ states, cluster states, etc.).

TABLE 2

TABLE 2. Comparison.

4 Multi-party semi-quantum key distribution protocol

In this section, the previously proposed protocol is extended to a multi-party semi-quantum key distribution protocol (MPSQKD), which can realize that one quantum participant distributes keys among T (T > 1) classical participants.

Here, set U₁, U₂, … , U_T is referred as existing classical participants. In MPSQKD, only Alice has full quantum capability and can perform any quantum operation. Others are limited to measuring and preparing qubits with base Z_P ⊗ Z_S and realize the key distribution with the help of Alice. The following steps are part of the MPSQKD protocol.

Step 1: Alice generated 2^T+1N hyperentangled Bell states in the set $\{|{\varphi }^{\pm }{\rangle }_p^{12}\otimes |{\varphi }^{\pm }{\rangle }_s^{12},|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\varphi }^{\pm }{\rangle }_s^{12},|{\psi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12},|{\varphi }^{\pm }{\rangle }_p^{12}\otimes |{\psi }^{\pm }{\rangle }_s^{12}\}$. Subsequently, Alice transmitted particle 2 of each hyperentangled Bell state to the first user U₁.

Step 2: T classical participants are sorted in the order of U₁, U₂, … , U_T. The former classical participant randomly selected measurement or reflection operation and then back to the latter participant. The last participant randomly selected a measurement or reflection operation back to Alice.

Step 3: After Alice received all the qubits, U₁, U₂, … , U_T published their specific choices.

Step 4: According to the operation of their choices, Alice will take a different operation.

Case 1: When all classical participants chose SIFT operation, the measurement results of U₁, U₂, … , U_T will be raw keys.

Case 2: When all classical participants chose CTRL operation, Alice will check whether an eavesdropper arises. The results announced by Alice should be the same as prepared. Once the error rate is higher than the threshold, the protocol will be terminal.

Case 3: the classical participants discarded the qubits whose operations performed differently.

Step 5: T classical participants recorded some measurement results to check the eavesdropper of Case 1.

Step 6: U₁, U₂, … , U_T will own the final keys after promulgating the error correcting code (ECC) and privacy amplification (PA) data.

5 Conclusion

In this study, a novel semi-quantum key distribution protocol based on the hyperentangled Bell states is proposed. Alice has quantum capability and transmitted the hyperentangled Bell states to the classical participant Bob. Bob randomly performed two operations on the received qubits. Communication participants used the hyperentangled Bell states to realize the secure transmission. The security analysis proves that this scheme can effectively resist the measure–resend attack, intercept–resend attack, and entangle–measure attack. Hence, the proposed protocol is secure. The hyperentangled states dramatically improves the efficiency of key transmission, which effectively improves the efficiency and feasibility of the protocol. Moreover, a multi-party scenario protocol based on the hyperentangled Bell stats is presented, realizing key distribution for multiple classical participants. The proposed protocol is the first SQKD protocol based on multi-degree of freedom entangled states, which has a certain guiding role for future research.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YT is responsible for proposing innovative points, designing protocol steps, analyzing and designing, and writing paper. JL is responsible for the overall structure and content design of the paper. CY is responsible for paper preparation, protocol correctness and security analysis. CL is responsible for the polishing and proofreading of paper.

Funding

This work is supported by the Open Fund of Advanced Cryptography and System Security Key Laboratory of Sichuan Province No. SKLACSS-202108, the National Natural Science Foundation of China under Grant Nos. 92046001 and 61962009, the Fundamental Research Funds for the Central Universities under Grant 2019XD-A02, and the Open Research Project of the State Key Laboratory of Media Convergence and Communication under Grant KLMCC2020KF006.

Acknowledgments

We would like to thank the anonymous reviewers for their detailed reviews and valuable comments, which have enhanced the quality of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Xia ZH, Jiang LQ, Liu DD, Li LH, Jeon B. Boew: A content-based image retrieval scheme using bag-of-encrypted-words in cloud computing. IEEE Trans Comput (2019)(1) 1.

Google Scholar

2. Xia ZH, Wang L, Tang J, Xiong N, Weng J. A privacy-preserving image retrieval scheme using secure local binary pattern in cloud computing. IEEE Trans Netw Sci Eng (2020) 8(1):318–30. doi:10.1109/tnse.2020.3038218

CrossRef Full Text | Google Scholar

3. Xia ZH, Zhou WH, Xiong LZ, Weng J, Xiong NX. Str: Secure computation on additive shares using the share-transform-reveal strategy. IEEE Trans Comput (2021) 1. doi:10.1109/tc.2021.3073171

CrossRef Full Text | Google Scholar

4. Aumasson JP. The impact of quantum computing on cryptography. Computer Fraud Security (2017) 2017(6):8–11. doi:10.1016/s1361-3723(17)30051-9

CrossRef Full Text | Google Scholar

5. Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inf Theor (1976) 22(6):644–54. doi:10.1109/tit.1976.1055638

CrossRef Full Text | Google Scholar

6. Pan XB, Chen XB, Xu G, Ahmad H, Yang YX, Li ZP, et al. Controlled quantum network coding without loss of information. Comput Mater Continua (2021) 69(3):3967–79. doi:10.32604/cmc.2021.017087

CrossRef Full Text | Google Scholar

7. Guo GP, Li CF, Shi BS, Li J, Guo GC. Quantum key distribution scheme with orthogonal product states. Phys Rev A (Coll Park) (2001) 64(4):042301. doi:10.1103/physreva.64.042301

CrossRef Full Text | Google Scholar

8. Kronberg DA, Nikolaeva AS, Kurochkin YV, Fedorov AK. Quantum soft filtering for the improved security analysis of the coherent one-way quantum-key-distribution protocol. Phys Rev A (Coll Park) (2020) 101(3):032334. doi:10.1103/physreva.101.032334

CrossRef Full Text | Google Scholar

9. Deng FG, Long GL, Liu XS. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys Rev A (Coll Park) (2003) 68(4):042317–114. doi:10.1103/physreva.68.042317

CrossRef Full Text | Google Scholar

10. Sun Z, Song L, Huang Q, Yin L, Long G, Lu J, et al. Toward practical quantum secure direct communication: A quantum-memory-free protocol and code design. IEEE Trans Commun (2020) 68(9):5778–92. doi:10.1109/tcomm.2020.3006201

CrossRef Full Text | Google Scholar

11. Hillery M, Nek V., Berthiaume A. Quantum secret sharing. Phys Rev A (Coll Park) (1999) 59(3):1829–34. doi:10.1103/physreva.59.1829

CrossRef Full Text | Google Scholar

12. Yang CW, Tsai CW. Efficient and secure dynamic quantum secret sharing protocol based on Bell states. Quan Inf Process (2020) 19(5):162–14. doi:10.1007/s11128-020-02662-0

CrossRef Full Text | Google Scholar

13. Yang YG, Wen QY. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J Phys A: Math Theor (2009) 42(5):055305. doi:10.1088/1751-8113/42/5/055305

CrossRef Full Text | Google Scholar

14. Lang YF. Quantum private comparison using single Bell state. Int J Theor Phys (Dordr) (2021) 60:4030–6. doi:10.1007/s10773-021-04937-3

CrossRef Full Text | Google Scholar

15. Bennett CH, Brassard G. Quantum cryptography: Public key distribution and coin tossing. In: Proceedings of the IEEE international conference on computers, systems and signal processing. Bangalore (1984). p. 175–9.

Google Scholar

16. EkertArtur K. Quantum cryptography based on Bell’s theorem. Phys Rev Lett (1991) 67(6):661–3. doi:10.1103/physrevlett.67.661

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bennett CH. Quantum cryptography using any two nonorthogonal states. Phys Rev Lett (1992) 68:3121–4. doi:10.1103/physrevlett.68.3121

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Scarani V, Acin A, Ribordy G, Gisin N. Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulses implementations. Phys Rev Lett (2004) 92(5):057901.1–057901.4.

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Yan X, Zhou N, Gong L, Wang Y, Wen X. High-dimensional quantum key distribution based on qudits transmission with quantum Fourier transform. Quan Inf Process (2019) 18(9):271–14. doi:10.1007/s11128-019-2368-5

CrossRef Full Text | Google Scholar

20. Srikara S, Thapliyal K, Pathak A. Continuous variable B92 quantum key distribution protocol using single photon added and subtracted coherent states. Quan Inf Process (2020) 19(10):371–16. doi:10.1007/s11128-020-02872-6

CrossRef Full Text | Google Scholar

21. Wu X, Wang Y, Huang D, Guo Y. Multi-mode plug-and-play dual-phase-modulated continuous-variable quantum key distribution. Quan Inf Process (2021) 20(4):143–21. doi:10.1007/s11128-021-03076-2

CrossRef Full Text | Google Scholar

22. Li CY, Ye CQ, Tian Y, Chen XB, Li J. Cluster-state-based quantum secret sharing for users with different abilities. Quan Inf Process (2021) 20(12):385–14. doi:10.1007/s11128-021-03327-2

CrossRef Full Text | Google Scholar

23. Bennett CH, Wiesner SJ. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys Rev Lett (1992) 69(20):2881–4. doi:10.1103/physrevlett.69.2881

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Boyer M, Kenigsberg D, Mor T. Quantum key distribution with classical Bob. Phys Rev Lett (2007) 99(14):140501. doi:10.1103/physrevlett.99.140501

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zou X, Qiu D, Li L, Wu L, Li L. Semi-quantum key distribution using less than four quantum states. Phys Rev A (Coll Park) (2009) 79(5):052312–1747. doi:10.1103/physreva.79.052312

CrossRef Full Text | Google Scholar

26. Wang J, Zhang S, Zhang Q, Tang CJ. Semi-quantum key distribution using entangled states. Chin Phys Lett (2011) 28(10):100301. doi:10.1088/0256-307x/28/10/100301

CrossRef Full Text | Google Scholar

27. Zou X, Qiu D, Zhang S, Mateus P. Semi-quantum key distribution without invoking the classical party’s measurement capability. Quan Inf Process (2015) 14(8):2981–96. doi:10.1007/s11128-015-1015-z

CrossRef Full Text | Google Scholar

28. Krawec WO, Geiss EP. Limited resource semi-quantum key distribution. arXiv preprint arXiv:1710.05076 (2017).

Google Scholar

29. Zhu KN, Zhou NR, Wang YQ, Wen XJ. Semi-quantum key distribution protocols with GHZ states. Int J Theor Phys (Dordr) (2018) 57(12):3621–31. doi:10.1007/s10773-018-3875-3

CrossRef Full Text | Google Scholar

30. Iqbal H, Krawec WO. Semi-quantum cryptography. Quan Inf Process (2020) 19(3):97–52. doi:10.1007/s11128-020-2595-9

CrossRef Full Text | Google Scholar

31. Ye TY, Li HK, Hu JL. Semi-quantum key distribution with single photons in both polarization and spatial-mode degrees of freedom. Int J Theor Phys (Dordr) (2020) 59(9):2807–15. doi:10.1007/s10773-020-04540-y

CrossRef Full Text | Google Scholar

32. Tian Y, Li J, Yuan KG, Li CY, Li HJ, Chen XB. An efficient semi-quantum key distribution protocol based on EPR and single-particle hybridization. Quan Inf Comput (2021) 21(7-8):563–76. doi:10.26421/qic21.7-8-3

CrossRef Full Text | Google Scholar

33. Ye TY, Geng MJ, Xu TJ, Chen Y. Efficient semiquantum key distribution based on single photons in both polarization and spatial-mode degrees of freedom. Quan Inf Process (2022) 21(4):123–1. doi:10.1007/s11128-022-03457-1

CrossRef Full Text | Google Scholar

34. Tsai CW, Chang YC, Lai YH, Yang CW. Cryptanalysis of limited resource semi-quantum secret sharing. Quan Inf Process (2020) 19(8):224–8. doi:10.1007/s11128-020-02690-w

CrossRef Full Text | Google Scholar

35. Li XY, Chang Y, Zhang SB. Multi-party semi-quantum secret sharing scheme based on Bell states. In: International conference on artificial intelligence and security. Cham: Springer (2020). p. 280–8.

CrossRef Full Text | Google Scholar

36. Tian Y, Li J, Chen XB, Ye CQ, Li HJ. An efficient semi-quantum secret sharing protocol of specific bits. Quan Inf Process (2021) 20(6):217–1. doi:10.1007/s11128-021-03157-2

CrossRef Full Text | Google Scholar

37. Wang Y, Lou X, Fan Z, Wang S, Huang G. Verifiable multi-dimensional (t, n) threshold quantum secret sharing based on quantum walk. Int J Theor Phys (Dordr) (2022) 61(2):24–17. doi:10.1007/s10773-022-05009-w

CrossRef Full Text | Google Scholar

38. Ye TY, Ye CQ. Measure-resend semi-quantum private comparison without entanglement. Int J Theor Phys (Dordr) (2018) 57(12):3819–34. doi:10.1007/s10773-018-3894-0

CrossRef Full Text | Google Scholar

39. Jiang LZ. Semi-quantum private comparison based on Bell states. Quan Inf Process (2020) 19(6):180–21. doi:10.1007/s11128-020-02674-w

CrossRef Full Text | Google Scholar

40. Tian Y, Li J, Chen XB, Ye CQ, Li CY, Hou YY. An efficient semi-quantum private comparison without pre-shared keys. Quan Inf Process (2021) 20(11):360–13. doi:10.1007/s11128-021-03294-8

CrossRef Full Text | Google Scholar

41. Ye CQ, Li J, Chen XB, Tian Y. Efficient semi-quantum private comparison without using entanglement resource and pre-shared key. Quan Inf Process (2021) 20(8):1–19.

CrossRef Full Text | Google Scholar

42. Yang YG, Wen QY, Zhu FC. Multi-party multi-level quantum key distribution protocol based on entanglement swapping. Acta Phys Sin (2005) 54(12):5544–8. doi:10.7498/aps.54.5544

CrossRef Full Text | Google Scholar