Topological defects of dipolar bose-einstein condensates with dresselhaus spin-orbit coupling in an anharmonic trap

We consider the topological defects and spin structures of binary Bose-Einstein condensates (BECs) with Dresselhaus spin-orbit coupling (D-SOC) and dipole-dipole interaction (DDI) in an anharmonic trap. The combined effects of D-SOC, DDI and anharmonic trap on the ground-state phases of the system are analyzed. Our results show various structural phase transitions can be achieved by adjusting the magnitudes of the D-SOC and DDI. Meantime, a ground-state phase diagram is given as a function of the D-SOC and DDI strengths. In addition, we find that tuning the D-SOC and the DDI can derive novel rich topological configurations, including ghost vortex, half-quantum vortex, skyrmion pair, vertical skyrmion string and horizontal skyrmion string.

1 Introduction

One of the most fascinating developments in physics has been the production of quantum gases with magnetic dipole-dipole interaction (DDI), especially the Bose-Einstein condensates (BECs) with DDI in recent years [1–4]. The DDI, unlike the s-wave contact interaction, is long-range and anisotropic, which has great influence on the dynamics and steady-state property of the BECs [5–10]. So the enthusiasm for dipolar gases has been growing. In particular, the experimental realization of dipolar atoms with large magnetic dipole moments such as Cr [1]and Dy [11] and Er [12] provides an opportunity to induce novel ground-state properties and various fascinating phenomena of dipolar quantum gases [5, 7, 13–17], which has strongly stimulated research interest in dipolar gases.

On the other hand, the experimental realization of spin-orbit coupling (SOC) in ultracold quantum gases is a tremendous breakthrough and the spin-orbit-coupled quantum gases have become one of the frontier research fields in physics [18–23]. The general SOC being of either Bychkov-Rashba [24] or Dresselhaus [25] type which couples the internal states and orbit motion of the atoms offers an ideal simulation platform for studying the few-body and many-body quantum phenomena in condensed matter physics, nuclear physics and astrophysics, and provides an unique opportunity for exploring novel quantum states in ultracold atomic gases such as BECs [26–28]. Relevant studies show that the spin-1/2 BECs with SOC can exhibit rich topological structures, such as heliciform-stripe phase [29], supersolid phase [23], topological superfluid phase [21], soliton excitation [30, 31], half-quantum vortex [32–34], giant vortex, skyrmion, and multidomain pattern [35–38]. Obviously, the combined effects of DDI and SOC on spinor BECs seems to arouse great research interest and recently attracted considerable attention [7, 39, 40].

To the best of our knowledge, the property of the dipolar two-component BECs placed in an anharmonic trap (a harmonic trap plus a quartic distortion) is rarely involved. Such an anharmonic trap can confine the BECs even for Ω/ω_⊥ > 1, and therefore allowing a more controlled investigation of possible new states. The anharmonic trap has been discussed in the literatures [41, 42], and in the first Ref, ground states of rotating spin-orbit-coupled spin-1/2 BECs are studied, and the latter are dynamics of rotating spin-orbit-coupled spin-1 BECs with in-plane gradient magnetic field, respectively. For the spin-orbit interaction, we consider the Dresselhaus SOC (D-SOC) which can be realized under current experimental conditions [18, 19, 21, 22, 43, 44]. By using the imaginary-time propagation method based in the Peaceman-Rachford method [45, 46], we obtain the ground state of the system. The basic idea of the Peaceman-Rachford method is to translate a two-dimensional problem into one-dimensional problems, and the method can be easily extended to three-dimensional situations. The imaginary-time propagation algorithm with Peaceman-Rachford approach has good convergence, strong stability and high accuracy. A test of convergence and accuracy for the algorithm is given by the virial theorem, which fixes rigorous relationships among the different contributions to the kinetic and potential energies of system. A second test is provided by the fast convergent values of the energy functional and component wave functions of the system. Furthermore, it can also be tested by the same convergent results for different trial wave functions. All the tests have been verified in our numerical computations. Our results show that as two new degrees of freedom, the D-SOC ans DDI can be used to obtain the desired ground-state phases and to control the phase transition between different ground states. In addition, the combined effects of DDI, D-SOC and anharmonic trap can exhibit rich vortex defects and various kinds of skyrmion structures. The rest of this paper is organized as follows. In the next section, the theoretical model is presented. In Section 3, the results and discussion are shown. The main results of the paper are summarized in Section 4.

2 Model

We consider a quasi-two-dimensional system of two-component BECs with D-SOC. For the sake of discussion, we assume DDI exists only in component 1. In the framework of the mean field, the energy functional of such a system can be well described as follows.

$\begin{array}{ccc}\hfill E& =\hfill & \int \sum _{j=\mathrm{1,2}}\left(\frac{{\hslash }^2{\left|▿{\psi }_j\right|}^2}{2m}+V\left(r\right){\left|{\psi }_j\right|}^2+\frac{g_j}{2}{\left|{\psi }_j\right|}^4+k\hslash {\psi }_j^{\ast }\left[{\left(-1\right)}^{3-j}\frac{\partial {\psi }_{3-j}}{\partial x}+i\frac{\partial {\psi }_{3-j}}{\partial y}\right]\right)d^{2}r\hfill \\ \hfill & \hfill & +\int g_{12}{\left|{\psi }_1\right|}^2{\left|{\psi }_2\right|}^2{d}^{2}r+\int {\varphi }_1{\left|{\psi }_1\right|}^2{d}^{2}r\hfill \end{array}(1)$

where ψ_j (j = 1, 2) represent the two-componet (i.e., dipolar and nondipolar) wave functions, and they are normalized as $\int \left[{\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2\right]dxdy=N$, with N being the total particle number. g_j = 4πℏ²a_j/m (j = 1, 2) and g₁₂ = 2πℏ²a₁₂/m denote the intra- and intercomponent coupling strengths, where m is the atomic mass, a_j (j = 1, 2)and a₁₂ are s-wave scattering lengths between intra- and intercomponent atoms. The D-SOC term is given by $v_D=ik\hslash \left({\widehat{\sigma }}_y{\partial }_x+{\widehat{\sigma }}_x{\partial }_y\right)$ [18], where ${\widehat{\sigma }}_x$ and ${\widehat{\sigma }}_y$ are Pauli matrices, and k denotes the SOC strength. The external anharmonic trap is expressed as [38, 42].

$V\left(r\right)=\frac{1}{2}m{\omega }_{\perp }^2\left(r^2+\lambda \frac{r^4}{a_0^2}\right)=\frac{1}{2}m{\omega }_{\perp }\left(\frac{r^2}{a_0^2}+\lambda \frac{r^4}{a_0^4}\right),(2)$

where ω_⊥ denotes the radial trap frequency and $a_0=\sqrt{\hslash /m{\omega }_z}$ is the harmonic-oscillator length. Here $r=\sqrt{x^2+y^2}$ is the radial coordinate in two-dimensions, and λ is a dimensionless constant that characterizes the anharmonicity of the trap. ϕ₁ denote the DDI of intraspecies of component 1, and it can be expressed as [47, 48].

${\varphi }_1=c_1\int d{\mathbf{r}}^{\prime }{U}_{dd}\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right){\left|{\psi }_1\left({\mathbf{r}}^{\prime }\right)\right|}^2,(3)$

Here $c_1={\mu }_0{\mu }_1^2/4\pi$ is magnetic dipole constant of intraspecies in component 1, μ₀ is the vacuum magnetic permeability, and μ₁ denote magnetic dipole moment of component 1. Let us consider the simplest case in which the dipoles are polarized. Then U_dd(R) is given by [49].

$U_{dd}\left(\mathbf{R}\right)=\left(1-3{\cos }^2\theta \right)/R^3,(4)$

where θ is the angle between the direction of polarization and the relative position of atoms.

By introducing the notations $\tilde{r}=r/a_0,\tilde{t}={\omega }_{\perp }t$, $\tilde{V}(r)=V(r)/\hslash {\omega }_{\perp }=\left({\tilde{r}}^2+\lambda {\tilde{r}}^4\right)/2$, ${\tilde{\varphi }}_1={\varphi }_1/\hslash {\omega }_{\perp }$, ${\tilde{\psi }}_j={\psi }_j{a}_0/\sqrt{N}(j=\mathrm{1,2})$, we obtain the dimensionless coupled Gross-Pitaevskii (GP) equations by using a variational method,

$i{\partial }_t{\psi }_1=\left(-\frac{1}{2}{\nabla }^2+V+{\beta }_{11}{\left|{\psi }_1\right|}^2+{\beta }_{12}{\left|{\psi }_2\right|}^2+{\varphi }_1\right){\psi }_1+k\left({\partial }_x+i{\partial }_y\right){\psi }_2,(5)$

$i{\partial }_t{\psi }_2=\left(-\frac{1}{2}{\nabla }^2+V+{\beta }_{22}{\left|{\psi }_2\right|}^2+{\beta }_{12}{\left|{\psi }_1\right|}^2\right){\psi }_2+k\left(-{\partial }_x+i{\partial }_y\right){\psi }_1.(6)$

where the tilde is omitted for simplicity. Note that β_jj = 4πa_jN (j = 1, 2) and β₁₂ = β₂₁ = 2πa₁₂N are the dimensionless intra- and interspecies coupling strengths, respectively. For the present system, its interactions is composed of s-wave, D-SOC and DDI. Here, we introduce a dimensionless quantity to describe the magnitude of the DDI relative to the contact interaction [6, 49, 50],

${\epsilon }_{dd}=a_{dd}/a_1=\frac{{\mu }_0{\mu }_1^{2}m}{12\pi {\hslash }^2{a}_1},(7)$

where a_dd presents the scattering length characterizing the DDI. Note that we assume that these dipoles are arranged side by side along z direction. In this context, the DDI becomes an isotropic repulsion (or attraction) and can be equivalent to a contact interaction. Therefore, the DDI can be rewritten as the form of effective contact interaction [6, 49, 50], ${\varphi }_1={\beta }_{11}{\epsilon }_{dd}{\left|{\psi }_1\right|}^2$. Clearly the total interaction coefficient between atoms for component 1 can be expressed by (1 + ɛ_dd)β₁₁. Thus by varying the DDI strength ɛ_dd, the D-SOC strength k, and the interaction strengths β₁₁, β₂₂ and β₁₂, we can obtain different ground-state phases.

In order to describe the spacial distribution of the topological structure, we adopt a nonlinear Sigma model [51, 52], in which a normalized complex-valued spinor $\mathit{\chi }={\left[{\chi }_1,{\chi }_2\right]}^T$ with ${\left|{\chi }_1\right|}^2+{\left|{\chi }_2\right|}^2=1$ is introduced. The main idea of the nonlinear Sigma model is that pseudospin representation of the order parameter of a system with internal degrees of freedom is useful to obtain a physical understanding by mapping the system to a magnetic system. In this context, two-component BECs can be treated as a spin-1/2 BEC. An exact mathematical correspondence can be established between the two systems, where ψ₁ (ψ₂) corresponds to the up (down) component of the spin-1/2 spinor. The detailed discussion can be referred to Refs. [51–53]. The total density of the system is expressed by $\rho ={\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2$, where the corresponding two-components wave functions can be expressed as ${\psi }_1=\sqrt{\rho }{\chi }_1$ and ${\psi }_2=\sqrt{\rho }{\chi }_2$, In the pseudospin representation, the spin density is given by $\mathbf{S}=\bar{\mathit{\chi }}\mathit{\sigma }\mathit{\chi }$in which σ = (σ_x, σ_y, σ_z) are the pauli matrices. The components of S can be written as [37, 54, 55].

$S_x=2\left|{\chi }_1\right|\left|{\chi }_2\right|\cos \left({\theta }_1-{\theta }_2\right),(8)$

$S_y=-2\left|{\chi }_1\right|\left|{\chi }_2\right|\sin \left({\theta }_1-{\theta }_2\right),(9)$

$S_z={\left|{\chi }_1\right|}^2-{\left|{\chi }_2\right|}^2,(10)$

with θ_j (j = 1, 2) being the phase of component wave function ψ_j and ${\left|\mathbf{S}\right|}^2=S_x^2+S_y^2+S_z^2=1$.

3 Results and discussion

Here the system is complex. As far as we know, there is no analytical solution for this system. In the following, we numerically solve the GP Eqs 5, 6 and obtain the ground states of the system by using the imaginary-time propagation method in terms of standard imaginary time evolution [45, 46, 56]. In the present work, we systematically investigate the combined effects of DDI, D-SOC on the ground states of the BECs in an anharmonic trap. Without loss of generality we fix the interaction parameters β₁₁ = 50, β₂₂ = 100, and β₁₂ = 150 and choose the typical parameter of the anharmonic trap λ = 0.5 throughout this paper, and vary the DDI strength ɛ_dd or the D-SOC strength k. It is shown that the system can display intriguing properties which are not found in other systems.

Firstly, we give a ground-state phase diagram spanned by the D-SOC strength k and the DDI strength ɛ_dd. There are nine different phases marked by A-I, which differs in terms of their density and phase distributions. In the following discussion, we will give a detailed description of each phase. The density and phase distributions of the nine different phases A-I in Figure 1 are shown in Figures 2A–F and Figures 3A,D,F, respectively. In Figure 2 and Figure 3, the upper two rows are the density profiles ${\left|{\psi }_1\right|}^2$ and ${\left|{\psi }_2\right|}^2$ of two components, the lower rows denote the corresponding phase distributions θ₁ = arg ψ₁, θ₂ = arg ψ₂, respectively.

FIGURE 1

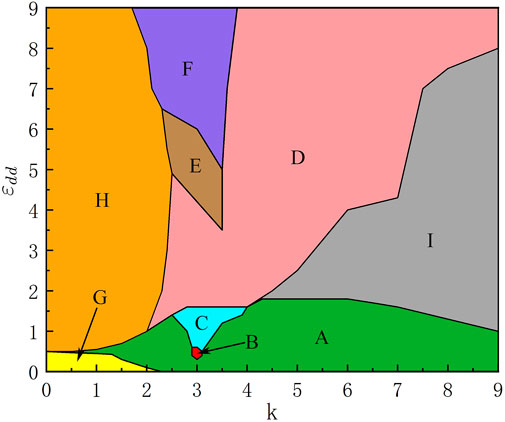
FIGURE 1. (Color online) Ground-state phase diagram of the Dresselhaus spin-orbit-coupled dipolar BECs in an anharmonic trap with respect to k and ɛ_dd for β₁₁ = 50, β₂₂ = 100 and β₁₂ = 150. There are nine different phases marked by (A–I).

FIGURE 2

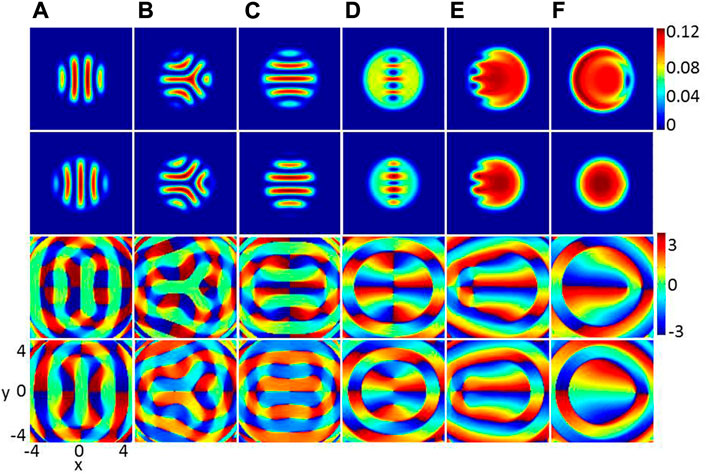
FIGURE 2. (Color online)Ground states of two-component BECs with DDI and D-SOC in an anharmonic trap, where β₁₁ = 50, β₂₂ = 100, β₁₂ = 150, and k = 3. (A) ɛ_dd = 0, (B) ɛ_dd = 0.4, (C) ɛ_dd = 1.5. (D) ɛ_dd = 3.5, (E) ɛ_dd = 5 and (F) ɛ_dd = 8. The rows from top to bottom denote ${\left|{\psi }_1\right|}^2$, ${\left|{\psi }_2\right|}^2$, argψ₁, and argψ₂, respectively. The unit length is a₀.

FIGURE 3

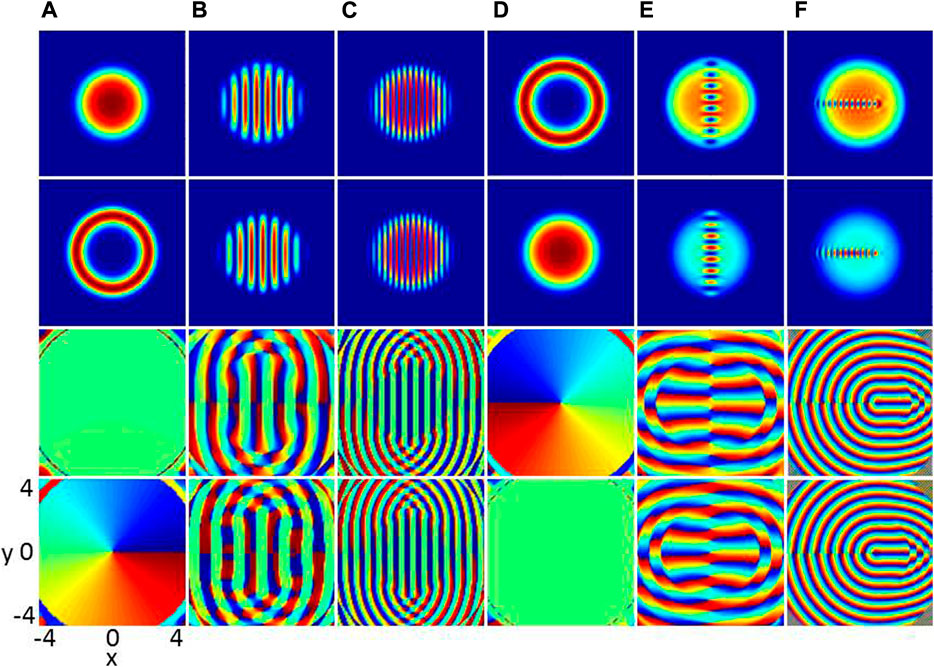
FIGURE 3. (Color online) Ground states of two-component BECs with different DDI and D-SOC in an anharmonic trap, where β₁₁ = 50, β₂₂ = 100 and β₁₂ = 150, (A) ɛ_dd = 0.2, k = 0.5, (B)ɛ_dd = 0.2, k = 5, (C) ɛ_dd = 0.2, k = 9, (D) ɛ_dd = 5, k = 0.5, (E) ɛ_dd = 5, k = 5, and (F) ɛ_dd = 5, k = 9. The rows from top to bottom denote ${\left|{\psi }_1\right|}^2$, ${\left|{\psi }_2\right|}^2$, argψ₁, and argψ₂, respectively. The unit length is a₀.

We start from the case where the DDI are weak and D-SOC is increased, which is indicated by the green region A in Figure 1. In this phase, the density for each component forms a set of stripes in both the dipolar component (component 1) and the non-dipolar component (component 2), and the two components are spatially separated (see the top two rows in Figure 2A) and the stripe density profiles were studied in [37], where the stripe profile are observed in a harmonic trap for large δ (δ = β₁₂/β, with β₁₁ = β₂₂). However, in the present system, the stripe exists due to the strong repulsive interspecies contract interaction ${\beta }_{12}^2>{\beta }_{11}{\beta }_{22}$, β₁₁ ≠ β₁₂ and the tight binding of the anharmonic trap. From the lower two rows of Figure 2A, we can find that several ghost vortices are generated in the outskirt of each component and they carry no angular momentum and energy [57–60]. With relatively weak DDI and D-SOC, the B phase emerges, as shown in the red region of Figure 1. The component densities evolve into curve-like patterns, and some visible phase defects are generated in component 2 (see Figure 2B). The above phenomenon has not been reported in the previous literature. With the slightly strong inclusion of DDI, the B phase transforms to the C phase as the ground states, as shown in Figure 1. Typical density distributions are shown in Figure 2C, in which the densities exhibit horizontal stripe pattern and both the component densities exhibit good symmetry concerning the vertical principal axes of the atom cloud. Note that here the horizontal stripe phase is remarkably similar to the stripe phase reported in literature [61]. The latter case result from a Rashba spin-orbit-coupled spin $\frac{1}{2}$ BEC without DDI in a harmonic trap (see Figure 2C in reference [61]). However, in the present system, the horizontal stripe exsists due to the complex competition among D-SOC, DDI and anharmonic trap. Meantime, we find that vertical votex string composed of vortex and antivortex along x = 0 appear in componet 2 (see the last row in Figure 2C). When the DDI strength further increases, the C phase transforms to the D phase, as shown in Figure 1. The typical ground state is that the stripe phase disappear and ordinary visible vortices which form obvious visible vortex chain along x = 0 axis in each component due to the enhanced DDI occur in the two components (see rows 1 and 2 in Figure 2D), where the system exhibit partial phase mixing in spite of the two components being separated initially, and the vortices in each component constitute clockwise vortex structure (see rows 3 and 4 in Figure 2D). This D phase occupies the largest region of the ground-state phase diagram in Figure 1.

Next, we move to the case of relatively strong DDI strength and weak D-SOC. The system supports the E phase, which is denoted by the brown region in Figure 1. The density and phase distributions of E phase are shown in Figure 1E, where the vortices deviate the central region of the external potential and tend to form an irregular vortex and anti-vortex cluster (see Figure 2E). The above is resulted from the competition among the increasing repulsive DDI, D-SOC and the anharmonic trap. In the limit of weak D-SOC and strong DDI, the phase transforms from the E phase to the F phase, as shown in Figure 1. The ground state of the system remains obvious phase mixing and exhibits disk shaped. We see that component 1 is a disk with a vortice being at the edge of the BECs, but there is no any topological defects in component 2. This point can be understood. Physically, when DDI increases, in view of the analytical effective interaction (1 + ɛ_dd)β₁₁, the increased total repulsive interaction in component 1 lead to reduction of the system energy and therefore there is less and less phase defects.

In the limit of weak DDI and D-SOC, the system sustains the G phase. Typical density and phase distributions of such a phase are shown in Figure 3A. The component 1 is a disk, in which most of the particles reside, and is surrounded by a thin, low-population annulus as the other component. The circulation with 2π in this annulus. Here, the ground state is the known half-quantum vortex state [32, 33, 60], which is characterized by one vortex in component and no vortex in the other component (see the third and fourth rows of Figure 3A). To get a deeper physical insight into this system, we study the ground-state phase diagram with weak DDI and but strong D-SOC, With the increase of the D-SOC, the phase transforms from the G phase to the A phase, as shown in Figure 1. The density and phase distributions are shown in Figures 3B,C, we find the ground becomes a vertical and dense stripe rofile. The main reason is that the increased D-SOC offers more energy and angular momentum to the system. In addition, these stripe profiles are quite different from the ground-state structures observed in conventional anisotropic SOC in toroidal trap [29] and SOC in harmonic trap [62].

Finally, we move to another case of strong DDI (e.g. ɛ_dd = 5). When the D-SOC increases, the phase transforms from H phase to E phase and then to D phase, and finally to I phase, as shown in Figure 1. The typical ground-state structure in H phase is shown in Figure 3D, where component 1 and component 2 in this system are exchanged approximately with those in phase G. Under the limit of strong DDI and D-SOC, the I phase emerges as the ground state, as shown in the gray region of Figure 1. The density and phase distributions of I phase are shown in Figure 3F, where transverse vortex chain instead of longitudinal vortex chain are formed in the BECs. The main reason is that when the D-SOC is enough strong, the number of vortices increasing significantly and the transverse structure of vortex chain is stable.

4 Spin texture

To further elucidate the ground-state properties, we now analyze the spin densities and spin textures of the system. In Figure 4, we show the spin densities. The DDI and D-SOC strengths in Figure 4 are A) ɛ_dd = 5, k = 3, B) ɛ_dd = 5, k = 5 and C) ɛ_dd = 5, k = 9, respectively. The density distributions and phase distributions corresponding to Figures 4A–C are given in Figure 2E, Figure 3E and Figure 3F, respectively. In the spin representation, the red region denotes spin-up and the blue region denotes spin-down. From Figures 4A,C, spin components S_x and S_z obeys an even-parity distribution along the x direction, while S_y shows odd-parity distribution along the x-direction, where the odd or even parity distributions along the y direction are not satisfied due to the long-range and anisotropic feature of the DDI. For the case of ɛ_dd = 5, k = 5 [see Figure 4B], S_x component of the spin density obeys the even-parity distribution along the x direction and odd-parity distribution along the y direction, while the situation is the reverse for S_y, i.e. S_y displays the odd-parity distribution along the x direction and even-parity distribution along the y direction. However, S_z satisfies even-paity distribution along both x and y directions.

FIGURE 4

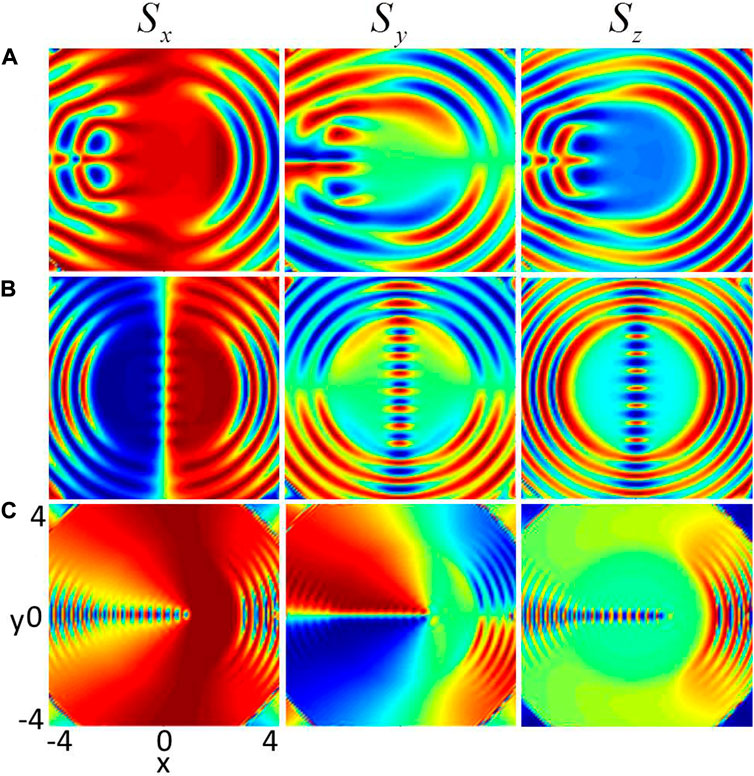
FIGURE 4. (Color online) Spin densities of dipolar BECs with D-SOC in an anharmonic trap. (A) ɛ_dd = 5, k = 3,(B) ɛ_dd = 5, k = 5 and (C) ɛ_dd = 5, k = 9. The corresponding ground states in (A), (B) and (C) are presented in Figure 2E, Figure 3E and Figure 3F. The columns from left to right are spin density S_x, S_y, S_z, respectively. The unit length is a₀.

The alternating appearance of the blue and red petals (see Figure 4) in spin component S_z means that some regular spin domains are formed in the spin representation. In addition, a special topological structure of skyrmion string is formed in the spin representation in Figures 4B,C. It is well known that the spin domain wall for two-component condensate system without rotation and SOC is a typicallly classical Neel wall, where the spin flips only along the vertical direction of the wall. However, our numerical simulation of the spin texture shows that in the region of spin domain wall the spin flips not only along the vertical direction of domian wall but also along the domain-wall direction, which denotes that the observed spin domain wall is a new type of domain wall.

The skyrmion is a type of topological soliton, which was originally suggested in nuclear physics by Skyrme to elucidate baryons as a quasiparticle excitation with spin pointing in all directions to wrap a sphere [60, 63]. Physically, the skyrmions are associated with vortex structures in the component density profiles, and the particle density should obey the continuity condition due to the quantum fluid nature of the BECs. Here the topological charge can be written as Q = ∫q(r)dxdy with the topological charge density $q(\mathbf{r})=\frac{1}{4\pi }\mathbf{S}•(\frac{\partial \mathbf{S}}{\partial x}\times \frac{\partial \mathbf{S}}{\partial y})$. Shown in the upper row of Figure 5 are the typical topological charge densities and the corresponding spin textures of the system, where the ground states of the three columns in Figure 5 are given in Figure 2E, Figures 3E,F, respectively. The corresponding local amplification of the spin textures are presented in the corresponding lower row, so one can better see the details of the spin textures. Note that the topological charge density (Figure 5A) and the corresponding texture (Figure 5B) are both approximately symmetric with respect to y = 0 axis. Our numerical calculation shows that the yellow spots in Figures 5B,C denote a skyrmion with local topological charge Q = 1. Obviously, the radial-out skyrmions in Figure 5B forms a skyrmion pair. Considering the limited resolution, in Figures 5D,G we only display the topological density and corresponding spin texture Figures 5E,Hin a limited domain, and the typical local enlargements of the spin texture are exhibited in Figures 5F,I, respectively. Our computation results show that the local topological charge in Figures 5F,I is Q = 1, and the total topological charge in Figures 5E,H are Q = 7 and Q = 11, respectively. Therefore the spin structure of Figure 5E is a skyrmion chain that is composed of a string of hyperbolic skyrmions in spin space and that of Figure 5H is consistes of circular skyrmion chain. Obviously, the skyrmion configurations observed in the present system are remarkably different from the previously reported results in two-component BECs.

FIGURE 5

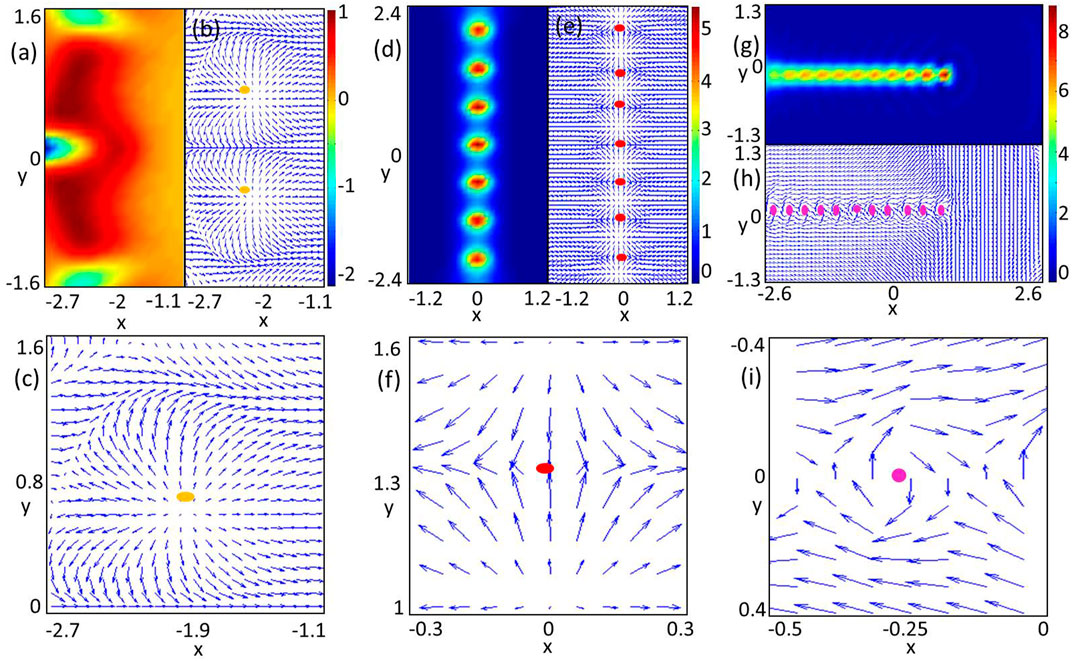
FIGURE 5. (Color online) Topological charge densities and spin textures. (A) Topological charge density, (B) the corresponding spin texture, and (C) the local amplification of the spin texture, where the ground state is given in Figure 2E. (D) Topological charge density, (E) the corresponding spin texture, and (F) the local amplification of the spin texture, where the ground-state is shown in Figure 3E. (G) Topological charge density, (H) the corresponding spin texture, and (I) the local amplification of the spin texture, where the ground state is seen in Figure 3F. Note that the yellow spots in (B) and (C) denote radial-out skyrmion, the red spots in (E) and (F) present hyperbolic skyrmion, and the purple spots are circular skyrmion.

5 Conclusion

In summary, we investigate the topological defects and spin structures of binary BECs with D-SOC and DDI in an anharmonic trap. Combined effects of D-SOC, DDI and anharmonic trap on the ground states of the system are analyzed and discussed in detail. As two new degrees of freedom, the DDI and D-SOC can be used to obtain the desired ground-state phases and to control the phase transition between various ground states. In particular, the system displays novel topological structures and spin textures, such as including ghost vortex, half-quantum vortex, skyrmion pair, vertical skyrmion string and horizontal skyrmion string. These exotic topological defects and spin textures can be tested and observed in the future experiments, and therefore the work presents fantastic perspective for topological excitations in cold atom physics and condensed matter physics.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HY: Conceptualization, Formal analysis, Data curation, Writing—review. YG: Formal analysis. BY: Investigation. JZ: Supervision, Writing—review editing.

Funding

This work was supported by Shanxi Education Department Fund (2020L0546).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Griesmaier A, Werner J, Hensler S, Stuhler J, Pfau T. Bose-Einstein condensation of chromium. Phys Rev Lett (2005) 94:160401. doi:10.1103/physrevlett.94.160401

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ray MW, Ruokokoski E, Tiurev K, Möttönen M, Hall DS. Observation of isolated monopoles in a quantum field. Science (2015) 348:544–7. doi:10.1126/science.1258289

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chomaz L, van Bijnen RMW, Petter D, Faraoni1 G, Baier S, Becher JH, et al. Observation of roton mode population in a dipolar quantum gas. Nat Phys (2018) 14:442–6. doi:10.1038/s41567-018-0054-7

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Tanzi L, Lucioni E, Famä F, Catani J, Fioretti A, Gabbanini C, et al. Observation of a dipolar quantum gas with metastable supersolid properties. Phys Rev Lett (2019) 122:130405. doi:10.1103/physrevlett.122.130405

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Santos L, Shlyapnikov G, Lewenstein M. Roton-maxon spectrum and stability of trapped dipolar bose-einstein condensates. Phys Rev Lett (2003) 90:250403. doi:10.1103/physrevlett.90.250403

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kawaguchi Y, Ueda M. Spinor bose-einstein condensates. Phys Rep (2012) 520:253–381. doi:10.1016/j.physrep.2012.07.005

CrossRef Full Text | Google Scholar

7. Deng Y, Cheng J, Jing H, Sun CP, Yi S. Spin-orbit-coupled dipolar Bose-Einstein condensates. Phys Rev Lett (2012) 108:125301. doi:10.1103/physrevlett.108.125301

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kadau H, Schmitt M, Wenzel M, Wink C, Maier T, Ferrier-Barbut I, et al. Observing the rosensweig instability of a quantum ferrofluid. Nature (2016) 530:194–7. doi:10.1038/nature16485

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Prasad SB, Bland T, Mulkerin BC, Parker NG, Martin AM. Vortex lattice formation in dipolar Bose-Einstein condensates via rotation of the polarization. Phys Rev A (Coll Park) (2019) 100:023625. doi:10.1103/physreva.100.023625

CrossRef Full Text | Google Scholar

10. Oldziejewski R, Górecki W, Pawłowski K, Rzazewski K. Strongly correlated quantum droplets in quasi-1d dipolar Bose gas. Phys Rev Lett (2020) 124:090401. doi:10.1103/physrevlett.124.090401

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lu M, Burdick NQ, Youn SH, Lev BL. Strongly dipolar Bose-Einstein condensate of dysprosium. Phys Rev Lett (2011) 107:190401. doi:10.1103/physrevlett.107.190401

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Aikawa K, Frisch A, Mark M, Baier S, Rietzler A, Grimm R, et al. Bose-Einstein condensation of erbium. Phys Rev Lett (2012) 108:210401. doi:10.1103/physrevlett.108.210401

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Jiang X, Fan Z, Chen Z, Pang W, Li Y, Malomed BA. Two-dimensional solitons in dipolar Bose-Einstein condensates with spin-orbit coupling. Phys Rev A (Coll Park) (2016) 93:023633. doi:10.1103/physreva.93.023633

CrossRef Full Text | Google Scholar

14. Kawaguchi Y, Saito H, Ueda M. Einstein-de Haas effect in dipolar Bose-Einstein condensates. Phys Rev Lett (2006) 96:080405. doi:10.1103/physrevlett.96.080405

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wilson RM, Ronen S, Bohn JL, Pu H. Manifestations of the roton mode in dipolar Bose-Einstein condensates. Phys Rev Lett (2008) 100:245302. doi:10.1103/physrevlett.100.245302

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lahaye T, Metz J, Froehlich B, Koch T, Meister M, Griesmaier A, et al. D-wave collapse and explosion of a dipolar bose-einstein condensate. Phys Rev Lett (2008) 101:080401. doi:10.1103/physrevlett.101.080401

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ticknor C, Wilson RM, Bohn JL. Anisotropic superfluidity in a dipolar Bose gas. Phys Rev Lett (2011) 106:065301. doi:10.1103/physrevlett.106.065301

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lin YJ, Jiménez-García K, Spielman IB. Spin-orbit-coupled bose-einstein condensates. Nature (2011) 471:83–6. doi:10.1038/nature09887

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Cheuk LW, Sommer AT, Hadzibabic Z, Yefsah T, Bakr WS, Zwierlein MW. Spin-injection spectroscopy of a spin-orbit coupled Fermi gas. Phys Rev Lett (2012) 109:095302. doi:10.1103/physrevlett.109.095302

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Qu C, Hamner C, Gong M, Zhang C, Engels P. Observation of zitterbewegung in a spin-orbit-coupled Bose-Einstein condensate. Phys Rev A (Coll Park) (2013) 88:021604. doi:10.1103/physreva.88.021604

CrossRef Full Text | Google Scholar

21. Wu Z, Zhang L, Sun W, Xu XT, Wang BZ, Ji SC, et al. Realization of two-dimensional spin-orbit coupling for Bose-Einstein condensates. Science (2016) 354:83–8. doi:10.1126/science.aaf6689

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Huang L, Meng Z, Wang P, Peng P, Zhang SL, Chen L, et al. Experimental realization of two-dimensional synthetic spin-orbit coupling in ultracold Fermi gases. Nat Phys (2016) 12:540–4. doi:10.1038/nphys3672

CrossRef Full Text | Google Scholar

23. Li JR, Lee J, Huang W, Burchesky S, Shteynas B, Top FC, et al. A stripe phase with supersolid properties in spin–orbit-coupled Bose–Einstein condensates. Nature (2017) 543:91–4. doi:10.1038/nature21431

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bychkov YA, Rashba EI. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J Phys C: Solid State Phys (1984) 17:6039–45. doi:10.1088/0022-3719/17/33/015

CrossRef Full Text | Google Scholar

25. Dresselhaus G. Spin-orbit coupling effects in zinc blende structures. Phys Rev (1955) 100:580–6. doi:10.1103/physrev.100.580

CrossRef Full Text | Google Scholar

26. Dalibard J, Gerbier F, Juzeliunas G, Ohberg P. Colloquium: Artificial gauge potentials for neutral atoms nas G, öhberg P. Colloquium: artificial gauge potentials for neutral atoms. Rev Mod Phys (2011) 83:1523–43. doi:10.1103/revmodphys.83.1523

CrossRef Full Text | Google Scholar

27. Galitski V, Spielman IB. Spin-orbit coupling in quantum gases. Nature (2013) 494:49.

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhai H. Degenerate quantum gases with spin–orbit coupling: a review. Rep Prog Phys (2015) 78:026001. doi:10.1088/0034-4885/78/2/026001

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang H, Wen L, Yang H, Shi C, Li J. Vortex states and spin textures of rotating spin-orbit-coupled Bose-Einstein condensates in a toroidal trap. J Phys B: Mol Opt Phys (2017) 50:155301. doi:10.1088/1361-6455/aa7afd

CrossRef Full Text | Google Scholar

30. Sakaguchi H, Malomed BA. Flipping-shuttle oscillations of bright one-and two-dimensional solitons in spin-orbit-coupled Bose-Einstein condensates with rabi mixing. Phys Rev A (Coll Park) (2017) 96:043620. doi:10.1103/physreva.96.043620

CrossRef Full Text | Google Scholar

31. Gautam S, Adhikari SK. Three-dimensional vortex-bright solitons in a spin-orbit-coupled spin-1 condensate. Phys Rev A (Coll Park) (2018) 97:013629. doi:10.1103/physreva.97.013629

CrossRef Full Text | Google Scholar

32. Hu H, Ramachandhran B, Pu H, Liu XJ. Spin-orbit coupled weakly interacting Bose-Einstein condensates in harmonic traps. Phys Rev Lett (2012) 108:010402. doi:10.1103/physrevlett.108.010402

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Ramachandhran B, Opanchuk B, Liu XJ, Pu H, Drummond PD, Hu H. Half-quantum vortex state in a spin-orbit-coupled Bose-Einstein condensate. Phys Rev A (Coll Park) (2012) 85:023606. doi:10.1103/physreva.85.023606

CrossRef Full Text | Google Scholar

34. Li X, Wang Q, Wang H, Shi C, Jardine M, Wen L. Ground-state properties of spin-orbit-coupled dipolar Bose-Einstein condensates with in-plane gradient magnetic field. J Phys B: Mol Opt Phys (2019) 52:155302. doi:10.1088/1361-6455/ab2a9b

CrossRef Full Text | Google Scholar

35. Zhou XF, Zhou J, Wu C. Vortex structures of rotating spin-orbit-coupled Bose-Einstein condensates. Phys Rev A (Coll Park) (2011) 84:063624. doi:10.1103/physreva.84.063624

CrossRef Full Text | Google Scholar

36. Radić J, Sedrakyan TA, Spielman IB, Galitski V. Vortices in spin-orbit-coupled Bose-Einstein condensates. Phys Rev A (Coll Park) (2011) 84:063604. doi:10.1103/physreva.84.063604

CrossRef Full Text | Google Scholar

37. Aftalion A, Mason P. Phase diagrams and Thomas-Fermi estimates for spin-orbit-coupled Bose-Einstein condensates under rotation. Phys Rev A (Coll Park) (2013) 88:023610. doi:10.1103/physreva.88.023610

CrossRef Full Text | Google Scholar

38. Fetter AL. Vortex dynamics in spin-orbit-coupled Bose-Einstein condensates. Phys Rev A (Coll Park) (2014) 89:023629. doi:10.1103/physreva.89.023629

CrossRef Full Text | Google Scholar

39. Gopalakrishnan S, Martin I, Demler EA. Quantum quasicrystals of spin-orbit-coupled dipolar bosons. Phys Rev Lett (2013) 111:185304. doi:10.1103/physrevlett.111.185304

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Kato M, Zhang XF, Sasaki D, Saito H. Twisted spin vortices in a spin-1 Bose-Einstein condensate with rashba spin-orbit coupling and dipole-dipole interaction. Phys Rev A (Coll Park) (2016) 94:043633. doi:10.1103/physreva.94.043633

CrossRef Full Text | Google Scholar

41. Shi CX, Wen L, Wang Q, Yang H, Wang H. Topological defects of spin–orbit coupled bose–einstein condensates in a rotating anharmonic trap. J Phys Soc Jpn (2018) 87:094003. doi:10.7566/jpsj.87.094003

CrossRef Full Text | Google Scholar

42. Yang H, Zhang Q, Jian ZH. Dynamics of rotating spin-orbit-coupled spin-1 Bose-Einstein condensates with in-plane gradient magnetic field in an anharmonic trap. Front Phys (2022) 10:910818. doi:10.3389/fphy.2022.910818

CrossRef Full Text | Google Scholar

43. Goldman N, Juzelinūas G, Öhberg P, Spielman IB. Light-induced gauge fields for ultracold atoms. Rep Prog Phys (2014) 77:126401. doi:10.1088/0034-4885/77/12/126401

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kolkowitz S, Bromley SL, Bothwell T, Wall ML, Marti GE, Koller AP, et al. Spin-orbit-coupled fermions in an optical lattice clock. Nature (2017) 542:66–70. doi:10.1038/nature20811

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Peaceman DW, Rachford HH. The numerical solution of parabolic and elliptic differential equations. J Soc Ind Appl Maths (1955) 3:28–41. doi:10.1137/0103003

CrossRef Full Text | Google Scholar

46. Wen L, Qiao Y, Xu Y, Mao L. Structure of two-component Bose-Einstein condensates with respective vortex-antivortex superposition states. Phys Rev A (Coll Park) (2013) 87:033604. doi:10.1103/physreva.87.033604

CrossRef Full Text | Google Scholar

47. Lahaye T, Menotti C, Santos L, Lewenstein M, Pfau T. The physics of dipolar bosonic quantum gases. Rep Prog Phys (2009) 72:126401. doi:10.1088/0034-4885/72/12/126401

CrossRef Full Text | Google Scholar

48. Yi S, You L. Trapped atomic condensates with anisotropic interactions. Phys Rev A (Coll Park) (2000) 61:041604. doi:10.1103/physreva.61.041604

CrossRef Full Text | Google Scholar

49. Ueda M. Fundamentals and New frontiers of Bose-Einstein condensation. Singapore: World Scientific (2010).

Google Scholar

50. Zhang X, Zhang P, Chen GP, Dong B, Tan RB, Zhang SG. Ground state of a two-component dipolar bose-einstein condensate confined in a coupled annular potential. Acta Phys Sin (2015) 64:060302. doi:10.7498/aps.64.060302

CrossRef Full Text | Google Scholar

51. Kasamatsu K, Tsubota M, Ueda M. Vortex molecules in coherently coupled two-component Bose-Einstein condensates. Phys Rev Lett (2004) 93:250406. doi:10.1103/physrevlett.93.250406

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Kasamatsu K, Tsubota M, Ueda M. Spin textures in rotating two-component Bose-Einstein condensates. Phys Rev A (Coll Park) (2005) 71:043611. doi:10.1103/physreva.71.043611

CrossRef Full Text | Google Scholar

53. Mizushima T, Machida K, Kita T. Mermin-ho vortex in ferromagnetic spinor Bose-Einstein condensates. Phys Rev Lett (2002) 89:030401. doi:10.1103/physrevlett.89.030401

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Han W, Zhang S, Jin J, Liu WM. Half-vortex sheets and domain-wall trains of rotating two-component Bose-Einstein condensates in spin-dependent optical lattices. Phys Rev A (Coll Park) (2012) 85:043626. doi:10.1103/physreva.85.043626

CrossRef Full Text | Google Scholar

55. Liu CF, Fan H, Zhang YC, Wang DS, Liu WM. Circular-hyperbolic skyrmion in rotating pseudo-spin-1/2 Bose-Einstein condensates with spin-orbit coupling. Phys Rev A (Coll Park) (2012) 86:053616. doi:10.1103/physreva.86.053616

CrossRef Full Text | Google Scholar

56. Zhang Y, Mao L, Zhang C. Mean-field dynamics of spin-orbit coupled Bose-Einstein condensates. Phys Rev Lett (2012) 108:035302. doi:10.1103/physrevlett.108.035302

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Kasamatsu K, Tsubota M, Ueda M. Nonlinear dynamics of vortex lattice formation in a rotating Bose-Einstein condensate. Phys Rev A (Coll Park) (2003) 67:033610. doi:10.1103/physreva.67.033610

CrossRef Full Text | Google Scholar

58. Wen L, Xiong H, Wu B. Hidden vortices in a Bose-Einstein condensate in a rotating double-well potential. Phys Rev A (Coll Park) (2010) 82:053627. doi:10.1103/physreva.82.053627

CrossRef Full Text | Google Scholar

59. Wen LH, Luo XB. Formation and structure of vortex lattices in a rotating double-well Bose-Einstein condensate. Laser Phys Lett (2012) 9:618–24. doi:10.7452/lapl.201210044

CrossRef Full Text | Google Scholar

60. Yang H, Wang Q, Su N, Wen L. Topological excitations in rotating Bose-Einstein condensates with rashba-dresselhaus spin-orbit coupling in a two-dimensional optical lattice. Eur Phys J Plus (2019) 134:589. doi:10.1140/epjp/i2019-12988-y

CrossRef Full Text | Google Scholar

61. Zhang YP, Mao L, Zhang C. Mean-field dynamics of spin-orbit coupled Bose-Einstein condensates. Phys Rev Lett (2012) 108:035302. doi:10.1103/physrevlett.108.035302

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Wang C, Gao C, Jian CM, Zhai H. Spin-orbit coupled spinor Bose-Einstein condensates. Phys Rev Lett (2010) 105:160403. doi:10.1103/physrevlett.105.160403

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Skyrme THR. A unified field theory of mesons and baryons. Nucl Phys (1962) 31:556–69. doi:10.1016/0029-5582(62)90775-7

CrossRef Full Text | Google Scholar