A globally accurate potential energy surface and quantum dynamics calculations on the Be(1S) + H2(v0 = 0, j0 = 0) → BeH + H reaction

The reactive collision between Be atom and H₂ molecule has received great interest both experimentally and theoretically due to its significant role in hydrogen storage, astrophysics, quantum chemistry and other fields, but the corresponding dynamics calculations have not been reported. Herein, a globally accurate ground-state BeH₂ PES is represented using the neural network strategy based on 12371 high-level ab initio points. On this newly constructed PES, the quantum time-dependent wave packet calculations on the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction are performed to study the microscopic dynamics mechanisms. The calculated results indicate that this reaction follows the complex-forming mechanism near the reactive threshold, whereas a direct H-abstraction process gradually plays the dominant role when the collision energy is large enough. The newly constructed PES can be used for further dynamics calculations on the BeH₂ reactive system, such as the rovibrational excitations and isotopic substitutions of the H₂ molecule, and the presented dynamics data would be of importance in experimental research at a finer level.

1 Introduction

In recent decades, the interactions between beryllium atom and hydrogen molecules have been of great attention because of their significance in astrophysics, hydrogen storage, quantum chemistry and other fields. On the one hand, the collision product BeH₂ molecule presents the fundamental and technological interest in potential applications, such as the nuclear materials and rocket fuel technology [1, 2], owing to its small mass and large hydrogen-to-metal mass ratios. Moreover, the molecular BeH₂, with a simple electronic structure, has become an excellent candidate for testing new computational methods for quantum chemistry [3–6]. On the other hand, the further product BeH molecule in the collision process of Be + H₂ is a popular testing target for the electronic structure calculations in open-shell systems [7, 8]. In addition, BeH is also an important interstellar molecule, which has been identified in stars and comets [9, 10].

Various experimental studies on the BeH₂ system have been implemented [11–18]. Tague and Andrews first detected the BeH₂ in molecular form by using infrared spectroscopy and the matrix isolation technique [11]. In their experiment, the pulsed laser evaporated Be atoms react with the hydrogen, and the primary product BeH and BeH₂ are largely favored compared with the other four more complex product molecules of Be₂H, HBeHBeH, HBe(H)₂BeH and HBeBeH. [12] synthesized the gaseous BeH₂ molecule using an electrical discharge facility, which is verified by infrared emission spectroscopy. Their study concluded that the stable BeH₂ is a linearly symmetric molecule with the BeH bond length of 1.334 Å. The high-precision infrared emission spectra of the BeH₂ and BeD₂ molecules were measured by [14]. The antisymmetric stretching modes and some hot bands of the two molecules were studied and the spectroscopic data were accurately determined. In their later study [17], the new vibration-rotation hot bands of the BeH₂ molecule were analyzed, and an accurate value was obtained for the frequency of the bending vibrational mode.

In the theoretical aspect, numerous ab initio calculations on the BeH₂ molecule have also been performed [19–26]. Martin and Lee [19] accurately calculated the quartic force field of BeH₂ using the CCSD(T) method, and the obtained spectroscopic constants are consistent with the corresponding experimental measurements. Hrenar et al. reported the first potential energy surface (PES) of the BeH₂ molecule used for the vibrational configuration-interaction calculations by a multilevel scheme [23]. Their calculated results can reproduce the experimental values of the gas phase measurements and matrix isolation. The ground-state equilibrium structure and PES of BeH₂ were calculated utilizing the CCSD(T) method combined with the cc-pVTZ through cc-pV6Z basis sets by Koput and Peterson [24]. Furthermore, the rovibrational energy levels of BeH₂ and its isotopic variations of BeD₂ and BeHD were accurately calculated by a variational method. The newest PES of the BeH₂ system was constructed by Li and Roy [25] utilizing the three-dimensional spline interpolation over 6,864 energy points with the internally contracted multi-reference configuration interaction (icMRCI)/aug-cc-pV5Z level. On this PES, the spectral constants of the BeH₂ and BeD₂ molecules were accurately calculated and the corresponding data of the BeHD molecule were predicted.

Although the BeH₂ system has received great attention both experimentally and theoretically, most of those studies focused on its structural and spectral properties, and the dynamics mechanisms of the Be + H₂ reaction process have not been reported up to now. In theory, the most reliable approach for obtaining the accurate dynamics information of a chemical reaction is to implement rigorous quantum scattering calculations on a globally high-precision PES [27, 28]. The previous PESs of the BeH₂ system are extremely reliable and accurate for describing the BeH₂ complex, whereas they are not suitable for the reaction dynamics calculations since some key regions where the reaction could reach are not included. Therefore, constructing a global and accurate BeH₂ PES is a crucial premise for studying the microscopic dynamics mechanisms of this reactive system.

Herein, a high-fidelity ground-state BeH₂ PES is represented based on a mass of high-precision ab initio energy points and the permutation invariant polynomial-neural network (PIP-NN) scheme [29, 30]. Moreover, the quantum dynamics calculations at the state-resolved level for the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction are carried out by the time-dependent wave packet (TDWP) method [31, 32] on this newly constructed PES. The computational details and the characteristics of the PES are given in Section 2. Section 3 displays the calculated dynamics results and the relevant discussion of the dynamics mechanisms for the title reaction and Section 4 concludes this work.

2 Ground-state BeH₂ potential energy surface

2.1 Ab initio calculations

The energy points of the BeH₂ system at the 1¹A′ state are calculated using the icMRCI method [33, 34] with the Davidson correction (+Q). The molecular orbitals are optimized by the complete active space self-consistent field (CASSCF) method [35, 36] before the MRCI calculations are carried out. The CASSCF orbitals are determined by the state-averaged calculations with equal weight for the 1¹A′, 2¹A′, 1¹A″ and 2¹A″ states. The active space is composed of nine active orbitals (8a′ + 1a″). The aug-cc-pV5Z basis set [37] is used for both the two different atoms. The energies calculated for the symmetrical configuration of Be-H₂ is defined by 0.8 ≤ R_HH/a₀ ≤ 8.0, 0.1 ≤ R_Be-HH/a₀ ≤ 16.0, 0 ≤ θ ≤ π/2, and the configuration of H-BeH is constructed by 2.0 ≤ R_BeH/a₀ ≤ 10.0, 0.1 ≤ R_H-BeH/a₀ ≤ 16.0, 0 ≤ θ′ ≤ π, Here, the ab initio calculations are performed utilizing Molpro 2012 software [38].

2.2 Permutation invariant polynomial-neural network fitting

The ground-state BeH₂ PES can be expressed by the summing of the two-body potentials and three-body potential:

$V\left(R_1,R_2,R_3\right)={\displaystyle \sum }_{i=1}^3{V}_i^{\left(2\right)}\left(R_i\right)+V^{\left(3\right)}\left(R_1,R_2,R_3\right)\cdot f\left(\mathit{R}\right)(1)$

where R_i (i = 1, 2, 3) are the bond length of Be-H_a, H_a-H_b and Be-H_b, respectively. A switch function f(R) is used to get a better representation in the asymptotic areas of the PES, and its form is written as:

$f\left(\mathit{R}\right)=\prod _{n=\mathrm{1,2,3}}\left(1-\frac{1}{2}\left(1+\tanh \left(\frac{R_n-R_{\mathrm{d}}}{R_{\mathrm{w}}}\right)\right)\right)(2)$

where R_d and R_w are the central position and the constant of switch strength, respectively.

The two-body potentials are obtained by a feedforward NN structure, which consists of two hidden layers with five neurons. A total of 69 and 53 ab initio points are calculated to fit the potential energy curves (PECs) of HH and BeH, respectively, and the corresponding root mean square error (RMSE) are 0.036 and 0.385 meV. Figure 1 shows that the fitting PECs of H₂(X¹Σ_g⁺) and BeH(X¹Σ⁺) molecules can pass through the center of each ab initio point. To further demonstrate the accuracy of the two-body potentials, Table 1 displays that the spectroscopic constants of the two diatomic molecules determined on the analytical PECs are in good agreement with the corresponding experimental data [39–41], suggesting the presented PES are sufficiently accurate for representing the reactant and product channels when the dynamics calculations are carried out.

FIGURE 1

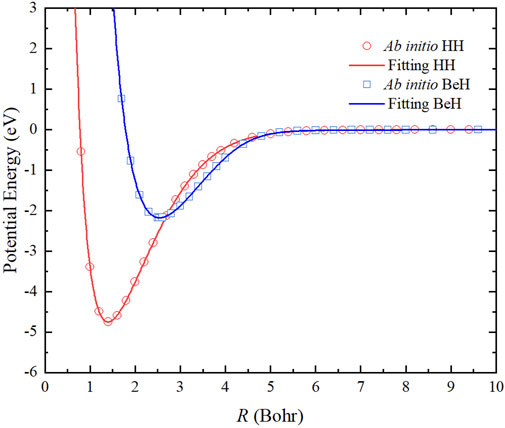
FIGURE 1. Comparison of the ab initio data and the NN fitting results of the PECs of H₂(X¹Σ_g⁺) and BeH(X¹Σ⁺).

TABLE 1

TABLE 1. Spectroscopic constants of H₂(X¹Σ_g⁺) and BeH(X¹Σ⁺).

The global ground-state BeH₂ PES is represented by the PIP-NN strategy [29, 30], which can rigorously assure that the constructed PES satisfies the exchange symmetry of the two hydrogen atoms, and this scheme has been widely and successfully applied to lots of molecular systems [42–51]. First, the fundamental invariants can be expressed as:

$P_i=\exp \left(-\alpha R_i\right)\left(i=\mathrm{1,2,3}\right)(3)$

where α is a constant between 0 and 1, and here the value of α is set as 0.2. Second, the symmetrized polynomial vector G = {G_i} is constructed as:

$G_1=\left(P_1+P_3\right)/2(4)$

$G_2=P_1\times P_3(5)$

$G_3=P_2(6)$

Finally, G is normalized as the input of the NN model:

$I_i=\frac{2\left(G_i-G_{i,\min }\right)}{\left(G_{i,\max }-G_{i,\min }\right)}-1,\left(i=\mathrm{1,2,3}\right)(7)$

where G_i,max and G_i,min are the maximum and minimum values of G_i, respectively.

The NN model used for constructing the global CaH₂⁺ PES consists of two hidden layers with 12 neurons. The hyperbolic tangent function and linear function are used as the transfer functions φ in the 1–2, 2–3 layers, and 3–4 layers, respectively. The finally analytical expansion of the final PES can be presented as:

$y={\phi }^{\left(3\right)}\left(b_1^{\left(3\right)}+{\displaystyle \sum }_{i=1}^{12}{w}_{i1}^{\left(3\right)}{\phi }^{\left(2\right)}\left(b_i^{\left(2\right)}+{\displaystyle \sum }_{j=1}^{12}{w}_{ji}^{\left(2\right)}{\phi }^{\left(1\right)}\left(b_j^{\left(1\right)}+{\displaystyle \sum }_{k=1}^3{w}_{kj}^{\left(1\right)}{I}_k\right)\right)\right)(8)$

where y represents the normalized potential energy. The connecting weight w and bias b between the adjacent two layers are iteratively optimized by the Levenberg–Marquardt algorithm [52]. Here, a total of 12371 molecular configurations are picked out to take part in the PIP-NN fitting, which are randomly classified into 90% training data, 5% testing data, and 5% validation data to avoid over-fitting. The parameters of w and b of the analysis PES are determined by the training data; the testing data are used to evaluate the generalization performance of the trained PES and the training should stop immediately when the testing error starts to rise; the validation data can be used for the initial assessment and adjustment of the NN model. The distribution of the fitting errors of the ground-state BeH₂ PES is plotted in Figure 2. This figure shows that the constructed PES can keep small fitting errors in the whole energy area. The overall RMSE of the PIP-NN PES is only 1.972 meV, and the energy points with an absolutely fitting error less than 0.005 eV can reach 97.2% of all the selected configurations, implying the fitting PES is globally accurate and suitable for performing the reaction dynamics studies on the BeH₂ system.

FIGURE. 2

FIGURE. 2. Distribution of the PIP-NN fitting errors of the ground-state BeH₂ PES.

2.3 Topographic characteristics of potential energy surface

Figures 3A,B display the contour plots of the PIP-NN PES at the D_∞h and C_2v symmetries, respectively. Excellent exchange symmetry of the PIP-PES is displayed in Figure 3A. There is a deep well with an energy minimum of −6.382 eV below the asymptotic H-Be-H at R₁ = R₃ = 2.515 a₀, and it is also the global minimum (GM) of the ground-state BeH₂ PES, which has been demonstrated in the previous theoretical and experimental studies [14, 25]. At the relatively low collision energy, the Be atom collides with the H₂ molecule with the remarkable elongation of the HH bond, and the BeH product is formed by the dissociation of the collinear BeH₂ molecule. For panel (B), a saddle point structure with the energy value of −2.156 eV is presented at R₂ = 2.269 a₀, R_Be-HH = 2.561 a₀, which is corresponding to the transition state (TS) of the BeH₂ system and dominates the collision process of the H- exchange path of H_a + BeH_b → H_b + BeH_a. The valley at R₂ = 1.401 a₀ corresponds to the Be(¹S) + H₂ channel, and the GM is also shown at R₂ = 5.030 a₀, R_Be-HH = 0 a₀ since the D_∞h configuration is a limitation of the C_2v symmetry.

FIGURE 3

FIGURE 3. Contour plots of the ground-state BeH₂ PES at the (A) D_∞h and (B) C_2v symmetries.

Table 2 lists the structures, energy values and vibrational frequencies of the GM and TS for the ground-state BeH₂ calculated at the PIP-NN PES, and the available experimental and ab initio values are also presented. The energy values are relative to the Be(¹S) + H₂ asymptotic channel. The newly constructed PES can accurately reproduce the geometries and the corresponding energies of the two stationary points, and the vibrational frequency v₂ is consistent with the experimental [14, 17] and extremely high-precision ab initio data [25] well. There exist some deviations for the values of v₁ and v₃ between the data calculated on the PIP-NN PES and the experimental or ab initio results, which are caused by the small fitting error because the harmonic frequencies are very sensitive to the small difference of PES, but they nearly do not affect the subsequent reaction dynamics results. In general, the PIP-NN PES can precisely represent the characteristics of the GM and TS of the ground-state BeH₂.

TABLE 2

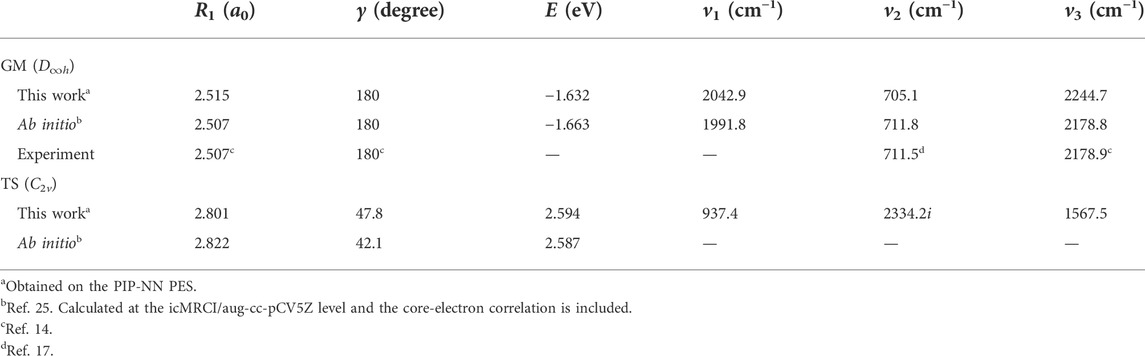
TABLE 2. Structures, energies and vibrational frequencies of the GM and TS for the ground-state BeH₂.

The contour maps of the ground-state BeH₂ PES at four fixed Be-H-H approaching angles (45°, 90°, 135°, and 180°) are presented in Figure 4. It is clear that the constructed PES is smooth in the entire configuration space, and there is no non-physical structure for each angle, suggesting the over-fitting behavior does not exist during the fitting PES. For the PES at every angle, the bottom valley is the Be(¹S) + H₂ channel, and the left valley is corresponding to the BeH + H channel. The energy of the bottom channel is lower than the left channel, indicating that the Be(¹S) + H₂ → BeH + H reaction is endothermic. For the angles of 45° and 90°, the reactant and product channels are connected by a barrier structure, which is generated by the avoid crossing behavior of the 2¹A′ state. The energy value of the barrier is higher than the energy of the product channel, implying the larger collision energy is needed to initiate this reaction by the collision approach with a relatively small Be-H-H approaching angle. In addition, a potential well with the depth of 2.496 eV relative to the BeH + H asymptotic region is shown when the approaching angle is at 45°, and many bound states or quasi-bound states can be supported by this well. For the angles of 135° and 180°, no well or barrier exists in the PES, thus the title reaction proceeds via a direct H-abstraction process when the collision angle becomes larger enough.

FIGURE 4

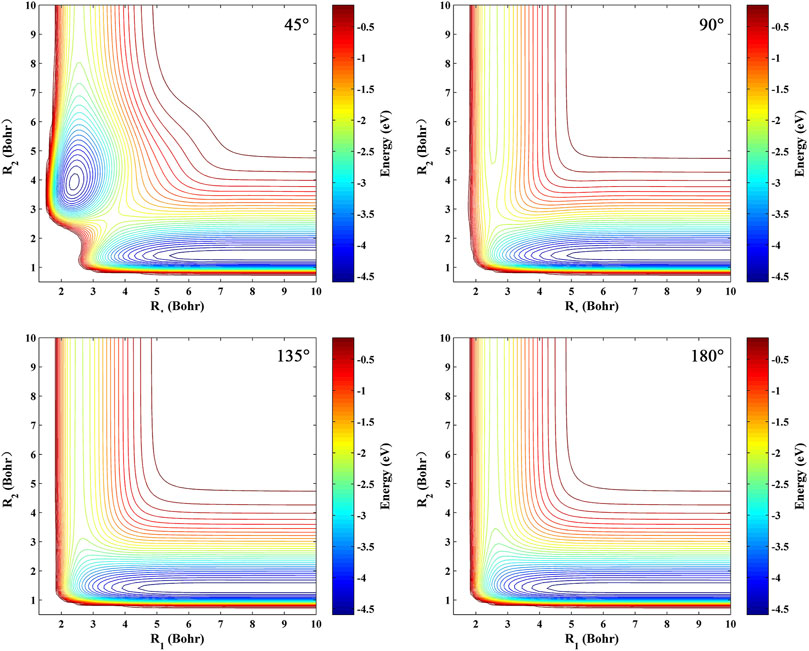
FIGURE 4. Contour plots of the ground-state BeH₂ PES at four Be-H-H angles (45°, 90°, 135°, and 180°).

Figure 5 shows the minimum energy paths (MEPs) of the Be(¹S) + H₂ → BeH + H reaction at four Be-H-H approaching angles (45°, 90°, 135°, 180°), calculated by scanning the ground-state BeH₂ PES with the fixed angle shown in Figure 4 at different coordinates to obtain the energy minimum. In addition, the global MEP generated by scanning the whole PES is also given in this plot, which plays the dominant role in determining the microscopic mechanisms of the title reaction, especially at relatively low energy. Under the action of collision energy, the reactants pass a barrier with the height of 2.096 eV relative to the reactant asymptotic region, and then a linear H-Be-H complex is formed on the well, which corresponds to the GM of the PES, finally, a Be-H bond is broken to generate the BeH molecule in the product channel. When the zero-point energies of the reactant and product molecules are taken into consideration, the endothermicity of the Be(¹S) + H₂ → BeH + H reaction calculated on this newly constructed PES is 2.716 eV.

FIGURE 5

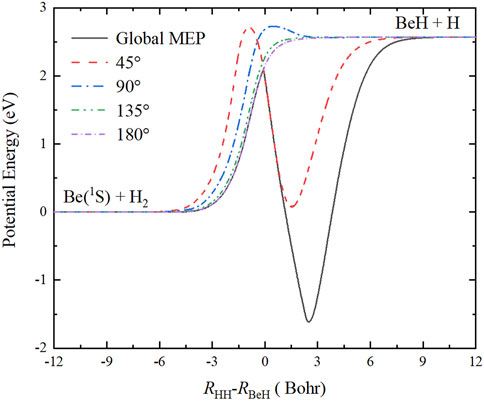
FIGURE 5. Global MEP and the MEPs at four Ca⁺-H-H angles (45°, 90°, 135°, and 180°) of the Be(¹S) + H₂ → BeH + H reaction obtained on the ground-state BeH₂ PES.

Figure 6A displays the contour plot of the ground-state BeH₂ PES in the case of the Be atom moving around the H₂ molecule fixed at its equilibrium distance. It is clear that the Be atom is always repelled by the H₂ molecule, so initiating the title reaction is difficult when the HH bond is stabilized at its equilibrium structure. As shown in Figure 3A, when the HH bond is elongated 5.030 a₀, there exist the attractive interactions between the Be atom and the H₂ molecule, and a stable BeH₂ complex is formed. A similar map to Figure 6A but for a H atom moving around the BeH fixed at its equilibrium distance is displayed in Figure 6B. Different from the case of Figure 6A, it appears the attractive interactions between the H atom and BeH molecule, and the well around the Be atom is deeper than the well around another H atom, suggesting that this H atom prefers to get out from the side of H atom of BeH in the product region.

FIGURE 6

FIGURE 6. (A) Contour plot of the ground-state BeH₂ PES when the Be atom moves around the H₂ molecule with the fixed bond length at 1.401 a₀ (B) Contour plot of the ground-state BeH₂ PES when a H atom moves around the BeH molecule with the fixed bond length at 2.544 a₀.

3 Quantum dynamics calculations

For most of the triatomic and some tetratomic reactive systems, the quantum TDWP method [31, 32, 53–55] is a high-efficiency and accurate tool for calculating the dynamics data. The full-dimensional quantum dynamics calculations of the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction are carried out on this newly constructed PIP-NN PES by the TDWP method for understanding the state-resolved dynamics mechanisms. The Coriolis coupling effect is included in the quantum TDWP calculations. Here, only the main equations in the TDWP calculations are displayed below. The Hamiltonian of the title reaction can be expressed as:

$\widehat{H}=-\frac{{\mathit{\hslash }}^2}{2{\mu }_R}\frac{{\partial }^2}{\partial R^2}-\frac{{\mathit{\hslash }}^2}{2{\mu }_r}\frac{{\partial }^2}{\partial r^2}+\frac{{\left(\widehat{J}-\widehat{j}\right)}^2}{2{\mu }_R{R}^2}+\frac{{\widehat{j}}^2}{2{\mu }_r{r}^2}+\widehat{V}(9)$

where µ_r and µ_R are the reduced masses associated with r and R in the Jacobi coordinate, respectively. J and j express the total angular momentum quantum number of BeH₂ and rotational angular momentum quantum number of H₂, respectively. The initial wave packet consists of a Gaussian type wave function, a rovibrational eigenfunction of H₂, and an eigenfunction of the total angular momentum, written as:

${\mathrm{\Psi }}_{a{v}_0{j}_0{l}_0}^{JM\epsilon }\left(t=0\right)=G\left(R_{\alpha }\right){\varphi }_{v_0}\left(r_{\alpha }\right)j_0\left({\theta }_{\alpha }\right)|JM{j}_0{l}_0\epsilon \rangle (10)$

To avoid the reflection of wave packet at the grid edge, the absorption potential used in the TDWP calculations is defined as:

$D\left(x\right)=\{\begin{array}{cc}\exp \left[-{\Delta }_t\cdot C_a\cdot {\left(\frac{x-x_a}{x_b-x_a}\right)}^2\right],& x_a\le x\le x_b\\ \exp \left[-{\Delta }_t\cdot C_b\cdot {\left(\frac{x-x_b}{x_{\mathrm{e}\mathrm{n}\mathrm{d}}-x_b}\right)}^2\right]\times \exp \left(-{\Delta }_t\cdot C_a\right),& x_b<x\le x_{\mathrm{e}\mathrm{n}\mathrm{d}}\end{array}(11)$

where C_i and x_i (i = a, b) represent the strength and positions of the absorption potential, respectively. Here, the time evolution of the wave packet is realized by the split operator scheme [56] and using the reactant coordinate-based method [57, 58] to extract the state-resolved S-matrix. The rovibrationally state-resolved reaction probability obtained by the S-matrix is expressed as:

$P_{vj\leftarrow v_0{j}_0}^J=\frac{1}{2j_0+1}{\displaystyle \sum }_K{{\displaystyle \sum }_{K_0}\left|S_{vjK\leftarrow v_0{j}_0{K}_0}^J\right|}^2(12)$

The state-resolved integral cross sections (ICSs) are calculated by summing the probabilities of all the calculated partial wave J:

${\sigma }_{vj\leftarrow v_0{j}_0}=\frac{\pi }{\left(2j_0+1\right)k_{v_0{j}_0}^2}{\displaystyle \sum }_K{\displaystyle \sum }_{K_0}{\displaystyle \sum }_J\left(2J+1\right){\left|S_{vjK\leftarrow v_0{j}_0{K}_0}^J\right|}^2(13)$

where $k_{v_{\mathit{0}}{j}_{\mathit{0}}}$ is the momenta in the entrance channel. The state-resolved differential cross sections (DCSs) can be obtained by the following equation:

$\frac{d{\sigma }_{vj\leftarrow v_0{j}_0}\left(\vartheta ,E\right)}{d\mathrm{\Omega }}=\frac{1}{\left(2j_0+1\right)}{{\displaystyle \sum }_K{\displaystyle \sum }_{K_0}\left|\frac{1}{2i{k}_{v_0{j}_0}}{\displaystyle \sum }_J\left(2J+1\right)d_{K{K}_0}^J\left(\vartheta \right)S_{vjK\leftarrow v_0{j}_0{K}_0}^J\right|}^2(14)$

where$d_{K{K}_0}^J\left(\vartheta \right)$ represents the reduced Wigner matrix, and$\vartheta$express the scattering angle.

In this work, the reactant H₂ molecule is set at its ground-rovibrational state of v₀ = 0, j₀ = 0, and the number of partial waves is calculated up to 65, which can obtain the convergent ICS and DCS up to the collision energy of 5.0 eV. In Table 3, the main parameters determined by many times tests of convergence in the TDWP calculations are listed.

TABLE 3

TABLE 3. Main numerical parameters in the TDWP calculations.

The collision energy dependence of total reaction probabilities for the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction with four partial waves (J = 0, 20, 40 and 50) are presented in Figure 7A. For J = 0, the curve exhibits relatively dense oscillation structures, which are attributed to the potential well on the reactive path. The title reaction is dominated by the global MEP and there is a well with the depth of 1.632 eV, resulting in obvious quantum resonances because numerous bound and quasi-bound states can be formed in the well. As the increase of J values, the reactive threshold becomes larger and the oscillations are gradually weakened. This is because the increasing centrifugal barrier reduces and even smooths the effective potential well, and the other collision channels shown in Figure 5 are opened, causing the amplitudes of oscillations on the reaction probability curves become less pronounced. Figure 7B shows the collision energy dependence of total ICS for the title reaction. The total ICS value increases monotonically with the increase of collision energy, which is consistent with the characteristic of an endothermic reaction. Compared to the reaction probabilities, there is no oscillation structures on the ICS curve due to the superposition of all the calculated partial waves.

FIGURE 7

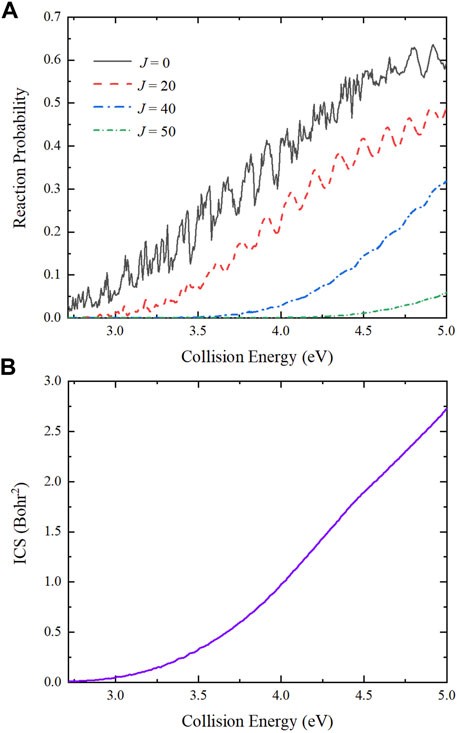
FIGURE 7. Collision energy dependence of (A) total reaction probabilities with four partial waves (J = 0, 20, 40 and 50) and (B) total ICS of the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction calculated by the TDWP method on the ground-state BeH₂ PES.

To understand the dynamics mechanisms of the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction at the state-to-state level, the rovibrationally state-resolved ICSs of the product BeH molecule at four collision energies (3.0, 4.0, 4.5, and 5.0 eV) are shown in Figure 8. For the collision energy of 3.0 eV, the BeH molecule only can be excited to the lowest three vibrational states, but the maximum of the rotational quantum number can reach j′ = 21 at v′ = 0, and the peak value of the rovibrationally state-resolved ICS is located at v′ = 0, j′ = 16. The presented vibrationally cold and rotationally hot distribution conforms to the complex-forming mechanism. More rovibrational states become available with the increase of collision energy, and there is a population inversion of the vibrational quantum number. For the collision energy of 5.0 eV, the product BeH molecule can populate at very high rovibrational states (v′ = 10, j′ = 28), suggesting more collision energy is effectively transformed into the internal energy of the product molecule. The contributions of high-order partial waves are larger and more reaction paths are gradually opened as the collision energy increases, thus the lifetime of the forming BeH₂ complex becomes shorter and the title reaction prefers a direct H-abstraction process when the collision energy is large enough.

FIGURE 8

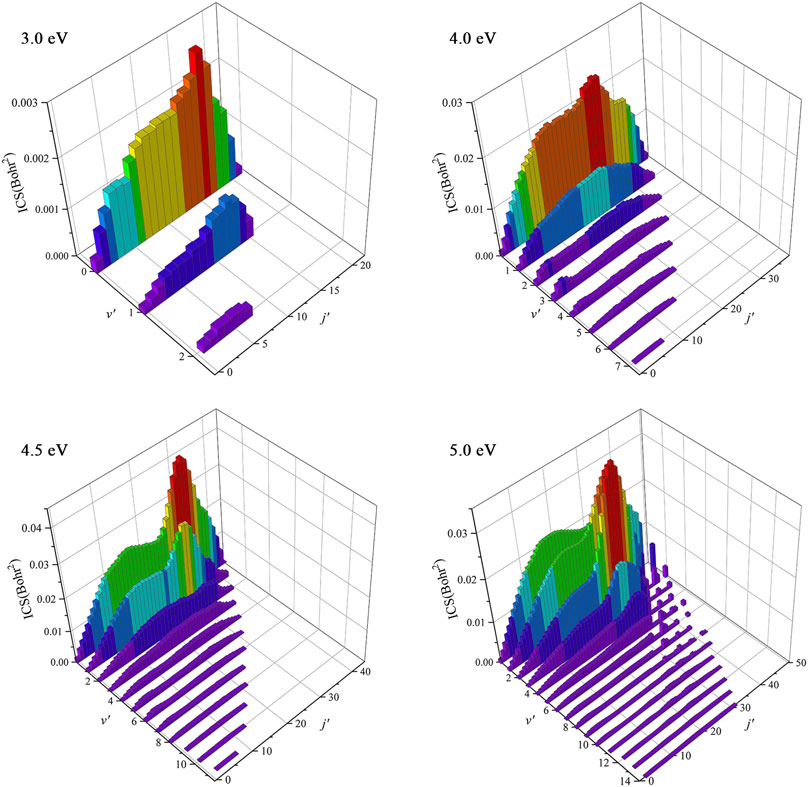
FIGURE 8. Rovibrationally state-resolved ICSs of the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction at four collision energies (3.0, 4.0, 4.5, and 5.0 eV) calculated by the TDWP method on the ground-state BeH₂ PES.

To study the dynamics process of the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction more intuitively by giving the angular distribution of the product molecule, Figure 9 presents the total DCSs varying with the scattering angle and collision energy. It is clear that the peak values of the angular distribution are located at the two extreme angles (0° and 180°) and the forward-backward symmetric DCSs are displayed when the collision energy is slightly larger than the reactive threshold, which is due to the forming of a BeH₂ complex supported by the potential well on the global MEP. With the increase of collision energy, the product BeH molecule increasingly prefers the forward scattering, showing an obviously non-statistical behavior. It also can be explained by the increasing contributions of the centrifugal barriers and more open reactive paths without a well at large collision energy. The calculated results of the total DCS further imply that the title reaction follows the complex-forming mechanism near the reactive threshold, whereas s direct H-abstraction process gradually plays a dominant role at high collision energy.

FIGURE 9

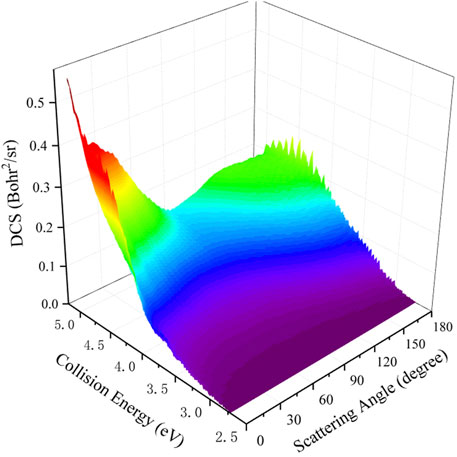
FIGURE 9. Total DCS of the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction as a function of scattering angle and collision energy calculated by the TDWP method on the ground-state BeH₂ PES.

4 Conclusion

In this paper, a globally accurate ground-state BeH₂ PES is structured using the PIP-NN scheme based on 12371 ab initio points calculated at the icMRCI + Q/aug-cc-pCV5Z level. The PES can accurately reproduce the original ab initio data in each region, and the global fitting RMSE is only 1.972 meV. The molecular constants of H₂(X¹Σ_g⁺) and BeH(X¹Σ⁺) calculated on the PES are consistent with the corresponding experimental data, and the PES can reproduce the characteristics of stationary points well. The GM and TS of the ground-state BeH₂ correspond to the D_∞h and C_2v symmetries, respectively. The topographic features of the PES are described in detail. On this newly constructed PES, the dynamics calculations are performed on the Be(¹S) + H₂(v₀ = 0, j₀ = 0) → BeH + H reaction at the state-to-state level by the quantum TDWP method for understanding the microscopic mechanisms. The endothermicity of the title reaction determined by the PES is 2.716 eV. There exist obvious oscillation structures on the curves of reaction probabilities since the well on the global MEP can support numerous bound and quasi-bound states, and the total ICS increases monotonically with the increase of collision energy. The rovibrationally state-resolved ICSs present vibrationally cold and rotationally hot distribution at relatively low collision energy, and the product BeH molecule can populate at very high rovibrational states. The total DCSs are forward-backward symmetric when the collision energy is slightly larger than the reactive threshold, but only the forward scatting is presented at high collision energy. The dynamics results indicate that the title reaction follows the complex-forming mechanism near the reactive threshold, whereas a direct H-abstraction process gradually plays the dominant role at high collision energy. Further dynamics studies for this reaction system can be carried out on the presented PES, such as the effects of rovibrational excitations and isotopic substitutions of the H₂ molecule, and the dynamics data calculated in this paper would be of importance in the experimental studies on the title reaction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZY wrote the original manuscript, constructed the theoretical models and performed the calculations. MC proposed the idea, supervised the research work and revised the manuscript. ZY and MC discussed and analysed the results.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 11774043).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Senin MD, Akhachinskii VV, Markushkin YE, Chirin NA, Kopytin LM, Mikhalenko IP, et al. The production, structure, and properties of beryllium hydride. Inorg Mater (1993) 29:1416–20.

Google Scholar

2. Nechiporenko GN, Lempert DB. An analysis of energy potentialities of composite solid propellants containing beryllium or beryllium hydride as an energetic component. Chem Phys Rep (1998) 17:1927–47.

Google Scholar

3. Szalay PG, Bartlett RJ. Approximately extensive modifications of the multireference configuration-interaction method: A theoretical and practical analysis. J Chem Phys (1995) 103:3600–12. doi:10.1063/1.470243

CrossRef Full Text | Google Scholar

4. Mahapatra US, Datta B, Mukherjee D. A size-consistent state-specific multireference coupled cluster theory: Formal developments and molecular applications. J Chem Phys (1999) 110:6171–88. doi:10.1063/1.478523

CrossRef Full Text | Google Scholar

5. Mazziotti DA. Comparison of contracted Schrödinger and coupled-cluster theories. Phys Rev A (Coll Park) (1999) 60:4396–408. doi:10.1103/physreva.60.4396

CrossRef Full Text | Google Scholar

6. Baer R, Neuhauser D. Molecular electronic structure using auxiliary field Monte Carlo, plane-waves, and pseudopotentials. J Chem Phys (2000) 112:1679–84. doi:10.1063/1.480733

CrossRef Full Text | Google Scholar

7. Meissner H, Paldus J. Direct iterative solution of the generalized bloch equation. IV. Application to H₂, LiH, BeH, and CH₂. J Chem Phys (2000) 113:2622–37. doi:10.1063/1.1305323

CrossRef Full Text | Google Scholar

8. Fülscher MP, Serrano-Andrés L. Quasi diabatic CASSCF state functions. Mol Phys (2002) 100:903–9. doi:10.1080/00268970110101590

CrossRef Full Text | Google Scholar

9. Sauval AJ, Tatum JB. A set of partition-functions and equilibrium constants for 300 diatomic-molecules of astrophysical interest. Astrophys J Suppl Ser (1984) 56:193–209. doi:10.1086/190980

CrossRef Full Text | Google Scholar

10. Singh M. Thirty-one new diatomic-molecules in cosmic objects spectra. Astrophys Space Sci (1988) 140:421–7. doi:10.1007/BF00638995

CrossRef Full Text | Google Scholar

11. Tague TJ, Andrews L. Reactions of beryllium atoms with hydrogen. Matrix infrared-spectra of novel product molecules. J Am Chem Soc (1993) 115:12111–6. doi:10.1021/ja00078a057

CrossRef Full Text | Google Scholar

12. Bernath PF, Shayesteh A, Tereszchuk K, Colin R. The vibration-rotation emission spectrum of free BeH₂. Science (2002) 297:1323–4. doi:10.1126/science.1074580

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sampath S, Lantzky KM, Benmore CJ, Neuefeind J, Siewenie JE, Egelstaff PA, et al. Structural quantum isotope effects in amorphous beryllium hydride. J Chem Phys (2003) 119:12499–502. doi:10.1063/1.1626638

CrossRef Full Text | Google Scholar

14. Shayesteh A, Tereszchuk K, Bernath PF, Colin R. Infrared emission spectra of BeH₂ and BeD₂. J Chem Phys (2003) 118:3622–7. doi:10.1063/1.1539850

CrossRef Full Text | Google Scholar

15. Wang XF, Andrews L. One-dimensional BeH₂ polymers: Infrared spectra and theoretical calculations. Inorg Chem (2005) 44:610–4. doi:10.1021/ic048464b

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Sampath S, Kolesnikov AI, Lantzky KM, Yarger JL. Vibrational dynamics of amorphous beryllium hydride and lithium beryllium hydrides. J Chem Phys (2008) 128:134512. doi:10.1063/1.2842079

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Motallebipour MS, Shayesteh A. Determination of v₂ fundamental band origin for BeH₂ and BeD₂ from deperturbation analysis of hot bands. J Chem Phys (2016) 145:074310. doi:10.1063/1.4960551

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Pépin CM, Loubeyre P. Layered structure and re-entrant disproportionation observed in crystalline BeH₂ under pressure. Phys Rev B (2016) 93:224104. doi:10.1103/PhysRevB.93.224104

CrossRef Full Text | Google Scholar

19. Martin JML, Lee TJ. Accurate ab initio quartic force-fields for borane and BeH₂. Chem Phys Lett (1992) 200:502–10. doi:10.1016/0009-2614(92)80082-M

CrossRef Full Text | Google Scholar

20. Ben Amor N, Maynau D. Size-consistent self-consistent configuration interaction from a complete active space. Chem Phys Lett (1998) 286:211–20. doi:10.1016/S0009-2614(98)00104-3

CrossRef Full Text | Google Scholar

21. Hinze J, Friedrich O, Sundermann A. A study of some unusual hydrides: BeH₂, BeH₆⁺ and SH₆. Mol Phys (1999) 96:711–8. doi:10.1080/00268979909483007

CrossRef Full Text | Google Scholar

22. Hantsch U, Winkler B, Milman V. The isotypism of BeH₂ and SiO₂: An ab initio study. Chem Phys Lett (2003) 378:343–8. doi:10.1016/S0009-2614(03)01333-2

CrossRef Full Text | Google Scholar

23. Hrenar T, Werner HJ, Rauhut G. Towards accurate ab initio calculations on the vibrational modes of the alkaline Earth metal hydrides. Phys Chem Chem Phys (2005) 7:3123–5. doi:10.1039/b508779a

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Koput J, Peterson KA. Ab initio prediction of the potential energy surface and vibration-rotation energy levels of BeH₂. J Chem Phys (2006) 125:044306. doi:10.1063/1.2212932

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Li H, Le Roy RJ. An accurate ab initio potential energy surface and calculated spectroscopic constants for BeH₂, BeD₂, and BeHD. J Chem Phys (2006) 125:044307. doi:10.1063/1.2212933

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Vasiliu M, Peterson KA, Dixon DA. Benchmark-quality atomization energies for BeH and BeH₂. J Chem Theor Comput (2017) 13:649–53. doi:10.1021/acs.jctc.6b01154

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Jiang B, Li J, Guo H. High-fidelity potential energy surfaces for gas-phase and gas-surface scattering processes from machine learning. J Phys Chem Lett (2020) 11:5120–31. doi:10.1021/acs.jpclett.0c00989

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Li J, Zhao B, Xie DQ, Guo H. Advances and new challenges to bimolecular reaction dynamics theory. J Phys Chem Lett (2020) 11:8844–60. doi:10.1021/acs.jpclett.0c02501

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Jiang B, Guo H. Permutation invariant polynomial neural network approach to fitting potential energy surfaces. J Chem Phys (2013) 139:054112. doi:10.1063/1.4817187

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Jiang B, Li J, Guo H. Potential energy surfaces from high fidelity fitting of ab initio points: The permutation invariant polynomial - neural network approach. Int Rev Phys Chem (2016) 35:479–506. doi:10.1080/0144235X.2016.1200347

CrossRef Full Text | Google Scholar

31. Sun ZG, Lee SY, Guo H, Zhang DH. Comparison of second-order split operator and Chebyshev propagator in wave packet based state-to-state reactive scattering calculations. J Chem Phys (2009) 130:174102. doi:10.1063/1.3126363

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Sun ZG, Guo H, Zhang DH. Extraction of state-to-state reactive scattering attributes from wave packet in reactant Jacobi coordinates. J Chem Phys (2010) 132:084112. doi:10.1063/1.3328109

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Werner HJ, Knowles PJ. An efficient internally contracted multiconfiguration reference configuration-interaction method. J Chem Phys (1988) 89:5803–14. doi:10.1063/1.455556

CrossRef Full Text | Google Scholar

34. Knowles PJ, Werner HJ. An efficient method for the evaluation of coupling-coefficients in configuration-interaction calculations. Chem Phys Lett (1988) 145:514–22. doi:10.1016/0009-2614(88)87412-8

CrossRef Full Text | Google Scholar

35. Werner HJ, Knowles PJ. A second order multiconfiguration SCF procedure with optimum convergence. J Chem Phys (1985) 82:5053–63. doi:10.1063/1.448627

CrossRef Full Text | Google Scholar

36. Knowles PJ, Werner HJ. An efficient second-order MC SCF method for long configuration expansions. Chem Phys Lett (1985) 115:259–67. doi:10.1016/0009-2614(85)80025-7

CrossRef Full Text | Google Scholar

37. Kendall RA, Dunning TH, Harrison RJ. Electron affinities of the first‐row atoms revisited. Systematic basis sets and wave functions. J Chem Phys (1992) 96:6796–806. doi:10.1063/1.462569

CrossRef Full Text | Google Scholar

38. Werner HJ, Knowles PJ, Knizia G, Manby FR, Schutz M. Molpro: A general-purpose quantum chemistry program package. Wires Comput Mol Sci (2012) 2:242–53. doi:10.1002/wcms.82

CrossRef Full Text | Google Scholar

39. Huber KP, Herzberg G. Molecular spectra and molecular structure, vol. 4, Constants of diatomic molecules. New York: Van Nostrand Reinhold (1979).

Google Scholar

40. Le Roy RJ, Appadoo DRT, Colin R, Bernath PF. On the X² Σ⁺, A²Π, and C² Σ⁺ states of BeH, BeD, and BeT. J Mol Spectrosc (2006) 236:178–88. doi:10.1016/j.jms.2006.01.010

CrossRef Full Text | Google Scholar

41. Horne R, Colin R. A²Π-X²Σ⁺ band system of BeH and BeD in absorption. B Soc Chim Belg (1972) 81:93. doi:10.1002/bscb.19720810108

CrossRef Full Text | Google Scholar

42. Yang ZJ, Chen HH, Chen MD. Representing globally accurate reactive potential energy surfaces with complex topography by combining Gaussian process regression and neural networks. Phys Chem Chem Phys (2022) 24:12827–36. doi:10.1039/d2cp00719c

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Song KS, Song HW, Li J. Validating experiments for the reaction H₂ + NH₂^- by dynamical calculations on an accurate full-dimensional potential energy surface. Phys Chem Chem Phys (2022) 24:10160–7. doi:10.1039/d2cp00870j

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Zuo JX, Croft JFE, Yao Q, Balakrishnan N, Guo H. Full-dimensional potential energy surface for ro-vibrationally inelastic scattering between H₂ molecules. J Chem Theor Comput (2021) 17:6747–56. doi:10.1021/acs.jctc.1c00882

CrossRef Full Text | Google Scholar

45. Varga Z, Liu Y, Li J, Paukku Y, Guo H, Truhlar DG. Potential energy surfaces for high-energy N + O₂ collisions. J Chem Phys (2021) 154:084304. doi:10.1063/5.0039771

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Yang ZJ, Wang SF, Yuan JC, Chen MD. Neural network potential energy surface and dynamical isotope effects for the N⁺(³P) + H₂ → NH+ + H reaction. Phys Chem Chem Phys (2019) 21:22203–14. doi:10.1039/c9cp02798j

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Yuan JC, He D, Wang SF, Chen MD, Han KL. Diabatic potential energy surfaces of MgH₂⁺ and dynamic studies for the Mg⁺(3p) + H₂ → MgH⁺ + H reaction. Phys Chem Chem Phys (2018) 20:6638–47. doi:10.1039/c7cp08679b

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Yang TG, Li AY, Chen GK, Yao Q, Suits AG, Guo H, et al. Isomer-specific kinetics of the C⁺ + H₂O reaction at the temperature of interstellar clouds. Sci Adv (2021) 7:eabe4080. doi:10.1126/sciadv.abe4080

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Yang DZ, Zuo JX, Huang J, Hu XX, Dawes R, Xie DQ, et al. A global full-dimensional potential energy surface for the K₂Rb₂ complex and its lifetime. J Phys Chem Lett (2020) 11:2605–10. doi:10.1021/acs.jpclett.0c00518

PubMed Abstract | CrossRef Full Text | Google Scholar

50. He D, Yuan JC, Li HX, Chen MD. A new potential energy surface of LiHCl system and dynamic studies for the Li(²S) + HCl(X¹ Σ⁺) → LiCl(X¹ Σ⁺) + H(²S) reaction. J Chem Phys (2016) 145:234312. doi:10.1063/1.4972229

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Li J, Varga Z, Truhlar DG, Guo H. Many-body permutationally invariant polynomial neural network potential energy surface for N₄. J Chem Theor Comput (2020) 16:4822–32. doi:10.1021/acs.jctc.0c00430

CrossRef Full Text | Google Scholar

52. Hagan MT, Menhaj MB. Training feedforward networks with the marquardt algorithm. IEEE Trans Neural Netw (1994) 5:989–93. doi:10.1109/72.329697

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Huang JY, Liu S, Zhang DH, Krems RV. Time-dependent wave packet dynamics calculations of cross sections for ultracold scattering of molecules. Phys Rev Lett (2018) 120:143401. doi:10.1103/PhysRevLett.120.143401

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Buren B, Chen MD, Sun ZG, Guo H. Quantum wave packet treatment of cold nonadiabatic reactive scattering at the state-to-state level. J Phys Chem A (2021) 125:10111–20. doi:10.1021/acs.jpca.1c08105

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Buren B, Chen MD. Wave packet approach to adiabatic and nonadiabatic dynamics of cold inelastic scatterings. Molecules (2022) 27:2912. doi:10.3390/molecules27092912

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Feit MD, Fleck JA, Steiger A. Solution of the Schrödinger equation by a spectral method. J Comput Phys (1982) 47:412–33. doi:10.1016/0021-9991(82)90091-2

CrossRef Full Text | Google Scholar

57. Gómez-Carrasco S, Roncero O. Coordinate transformation methods to calculate state-to-state reaction probabilities with wave packet treatments. J Chem Phys (2006) 125:054102. doi:10.1063/1.2218337

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Sun ZG, Lin X, Lee SY, Zhang DH. A reactant-coordinate-based time-dependent wave packet method for triatomic state-to-state reaction dynamics: Application to the H + O₂ reaction. J Phys Chem A (2009) 113:4145–54. doi:10.1021/jp810512j

PubMed Abstract | CrossRef Full Text | Google Scholar