Impact of dispersion and intracavity polarization state on pump power fixed point in a Yb-fiber frequency comb

We experimentally explored the relationship between the pump power fixed point and the net-cavity dispersion in a Yb-fiber optical frequency comb. By continuously adjusting the distance of the grating pair in the Yb-fiber oscillator, we measured the pump power fixed point frequency in different dispersion regimes and different intracavity polarization states. We find that the fixed point frequency for pump power is not always near the carrier frequency but changes significantly with the net-cavity dispersion and polarization. Especially at the near zero-dispersion point, the fixed point has a local minimum, which is less than tens of THz and far lower than the carrier frequency. This is the first time to completely reveal the influence of net-cavity dispersion and intracavity polarization state on the fixed point in the experiment.

Introduction

Fiber optical frequency combs are widely utilized in a variety of precision measurement fields due to their small size, low power consumption, and good robustness [1, 2]. A low noise mode-locked fiber oscillator is essential for the comb tightly phase-locking and precision measurement applications. In fiber oscillators, the net-cavity dispersion plays an important role in mode-locking laser dynamics and determines the level of frequency noise on the frequency comb [3, 4]. When tuning net-cavity dispersion from negative to positive [5, 6], the major pulse-shaping mechanisms include soliton regime [7, 8], stretched-pulse regime [9], self-similar regime [10], all-normal-dispersion (ANDi) regime [11]. The relative intensity noise (RIN) [12–14], timing jitter [12, 15], comb-line frequency noise and free-running linewidth of carrier envelop offset frequency (f_ceo) [14, 16, 17] of mode-locked fiber lasers all depend on the net-cavity dispersion and pulse-shaping mechanisms. The analytical theory [4, 18], numerical simulations [17, 19] and experiments have shown that RIN, timing jitter, comb-line frequency noise and f_ceo linewidth can be minimized at the near-zero dispersion in free-running mode-locked fiber lasers. Recently, these noise characteristics have been verified in the fully polarization maintaining nonlinear amplifying loop mirrors mode-locked oscillator [20, 21]. However, a fully stable optical frequency comb is required to lock both the f_ceo and repetition frequency (f_rep) at the same time. At this point, we should consider not only the f_ceo’s free-running linewidth, but the variation of the f_ceo with pump power, and the cross-talk between f_ceo locking and f_rep locking [22].

In fiber optical frequency comb, piezoelectric transducer (PZT), electro-optic modulator (EOM) [23], or optically pumped [24] are typically used to control the cavity length and lock the f_rep to a microwave reference or a comb line (f_n) to an optical reference, and the f_ceo is locked by feedback the pump power. We expect that the actuators that control the f_rep and f_ceo are orthogonal, which means that when the two frequencies are locked at the same time, two feedback loops have zero cross-talk [22]. In reality, PZT, EOM, and pump power will exert influence on both f_rep and f_ceo. The motion law of the longitudinal mode of the optical frequency comb is explained by the elastic tape model [25]. Based on this model, fixed point theory is developed and used to characterize the effect of an actuator or an intracavity noise source on the f_rep and f_ceo [25, 26]. When a comb parameter X (actuator or noise source) is altered, the comb will expand or breathe around the fixed point frequency (FPF) ${\nu }_{\mathrm{f}\mathrm{i}\mathrm{x}}^X$ ,

${\nu }_{\mathrm{f}\mathrm{i}\mathrm{x}}^X=n_{\mathrm{f}\mathrm{i}\mathrm{x}}^X{f}_{\mathrm{r}\mathrm{e}\mathrm{p}}+f_{\mathrm{c}\mathrm{e}\mathrm{o}}=\left(-{\mathrm{d}}_X{f}_{\mathrm{c}\mathrm{e}\mathrm{o}}/{\mathrm{d}}_X{f}_{\mathrm{r}\mathrm{e}\mathrm{p}}\right)f_{\mathrm{r}\mathrm{e}\mathrm{p}}+f_{\mathrm{c}\mathrm{e}\mathrm{o}}(1)$

where$n_{\mathrm{f}\mathrm{i}\mathrm{x}}^X$represents the number of fixed comb teeth, ${\mathrm{d}}_X{f}_{\mathrm{c}\mathrm{e}\mathrm{o}}$ and ${\mathrm{d}}_X{f}_{\mathrm{r}\mathrm{e}\mathrm{p}}$ represent the derivatives of f_ceo and f_rep with respect to X. Compared with PZT and EOM, the influence mechanism of pump power on f_rep and f_ceo is more complex [27]. Soliton perturbation theory and experiments show that the pump power FPF is near the carrier frequency and will deviate from the carrier frequency due to the self-phase modulation (SPM) [26–28]. In 2017, Ken Kashiwagi et al reported that the variations of FPF with polarization state exceeds PHz range in a soliton fiber laser [29]. However, the above results are measured in the soliton regime. For other mode-locked regimes, especially the stretched-pulse regime with minimal RIN, timing jitter and comb-line noise, the pump power FPF has not been characterized in detail yet.

In this work, we investigate the impact of net-cavity dispersion on the FPF of pump power in a 200 MHz Yb: doped fiber frequency comb. By adjusting the spacing of the grating pair, the net-cavity dispersion will change, and the oscillator will be in different mode-locked regimes. The measurement results show that the intracavity dispersion has a significant effect on the FPF. In particular, there is a minimum FPF at near-zero dispersion, the lowest is only 2.5 THz, which is unfavorable to f_ceo and f_rep (especially f_n) locking at the same time. In addition, with the change of dispersion, there is a negative correlation between the variation of f_ceo and the variation of f_rep, rather than a linear relationship as described in the early literature [28]. In the slightly positive dispersion regime, there is a local maximum of FPF, and the linewidth of f_ceo free-running is as narrow as that in zero-dispersion point, so it can be used for f_ceo locking.

Experiment setup

Figure 1 depicts the experimental setup. A standard nonlinear polarization evolution (NPE) mode-locked ytterbium-doped fiber oscillator with a repetition rate of 200 MHz was employed in this study. We use a pair of 1,000 lines/mm gratings with a dispersion of –6,000 fs²/mm at 1,030 nm to continually adjust the net dispersion in the cavity. A single-mode laser diode with a wavelength of 976 nm serves as the pump source for the oscillators. The oscillator output power is roughly 50 mW when the pump power is 373 mW. A 90:5:5 fiber beam splitter divides the oscillator output into three channels for amplification, measurement of repetition rate, and spectrum monitoring, respectively. After a one-stage Yb: doped fiber amplifier and pulse compression, the supercontinuum spectrum is generated using a tapered photonic crystal fiber (PCF), and the f_ceo signal is obtained using a standard f-2f interferometer.

FIGURE 1

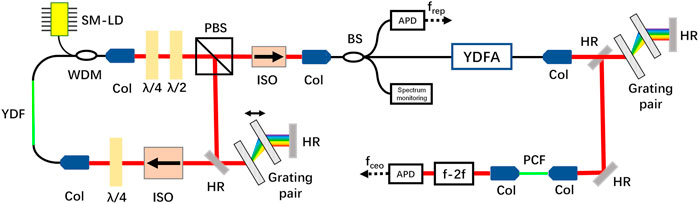
FIGURE 1. Experimental setup. SM LD, single-mode laser diode; YDF, Yb: doped fiber, Col, collimator; WDM, wavelength division multiplexer; λ/4, quarter-wave plate; λ/2, half-wave plate; ISO, isolator; PBS, polarizing beam splitter; HR, high reflection mirror; BS, beam splitter; YDFA, Yb: doped fiber amplifier; APD, avalanche photodetector; PCF, photonic crystal fiber, f_ceo: carrier-envelope offset; Black solid line, passive fiber; Green solid line, gain fiber or PCF; Red solid line, optical path, Black dashed line: electronic wire.

NPE mode-locking is realized by randomly rotating three wave plates in the oscillator cavity. The output spectrum of the oscillator changes as the spacing of the grating pair changes. When the grating pair spacing is raised from 2.5 to 5 mm, the oscillator can maintain stable mode-locking. To investigate the relationship between FPF and net-cavity dispersion, we adjust the grating pair spacing by 0.1 mm each time, corresponding to the dispersion shift of 600 fs². The spectrum and pump-induced variations of f_rep (Δf_rep) and f_ceo (Δf_ceo) are measured in each dispersion point. By optimization of the oscillator, it is ensured that the mode-locking can be maintained while moving the grating, without alerting other parameters such as the position of the wave plate and the pump power. This setting is to avoid the influence of other parameters on FPF as much as possible [29].

Considering that the positions of three-wave plates in the soliton domain will certainly affect the FPF [29], we measured the spectrum, Δf_rep and Δf_ceo under four different wave plate setting states. We completely disrupt the three-wave plates in the cavity to find a new mode-locking state instead of slightly adjusting the angle of the wave plates as described in the literature [29]. Since the position of the wave plates for NPE mode locking is a somewhat random process, the four intracavity polarization states (PS) are also random characteristics.

Result and discussion

The spectra of four states of several selected grating spacing are shown in Figure 2. As the separation between grating pairs increases, the spectra and zero dispersion point change as well. According to the definition in literature [14], we define the net-cavity dispersion using the second-order dispersion value at the nominal center wavelength (1,036 nm for all spectra in Figure 2). The position with the grating pair spacing of 3.6 mm is defined as the zero dispersion point. At the zero dispersion point, the oscillator operates in the stretched-pulse regime, and the FWHM (full width at half maximum) of the spectrum is the widest. With the increase of net-cavity dispersion, the spectral width narrows gradually, and the sharp peaks on the edges of the spectrum become stronger. Since the dispersion of optical fiber and optical element is positive at 1,035 nm, it is impossible to realize conventional optical soliton. When the negative dispersion increases, the spectral width also narrows. At the same grating spacing, the spectra of the four intracavity PS are different.

FIGURE 2

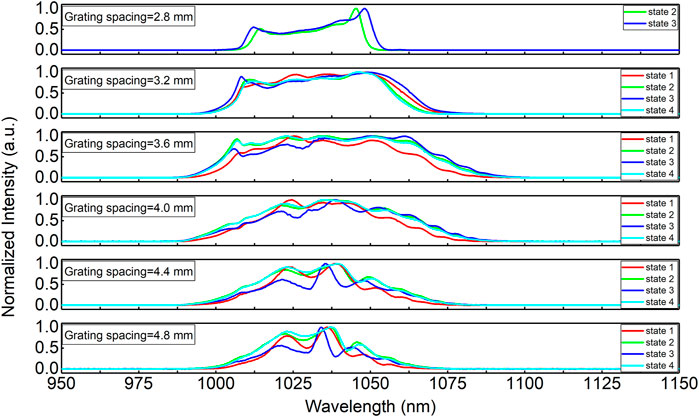
FIGURE 2. Oscillator spectra in different grating spacings and different intracavity polarization states.

Even though the df_rep/dP and df_ceo/dP have been described in soliton perturbative theory [27], calculating them in different dispersion and the different mode-locking regime is difficult. The most reliable method is to measure the value of the variation of f_ceo (Δf_ceo)and f_rep (Δf_ceo) with the pump power. Figure 3 shows the values of Δf_ceo/ΔP and Δf_rep/ΔP in the different spacing of grating pairs and four different intracavity PS. At each point, the Δf_rep is recorded using a frequency counter (Agilent 53132A) with the pump power changing by ±1.3% (from 368 to 378 mW), and Δf_ceo is measured using a spectrum analyzer (R&S FSW26). The f_rep and f_ceo vary linearly with the ±1.3% pump power change, so we have df_ceo/dP≈Δf_ceo/ΔP, df_rep/dP≈Δf_rep/ΔP. We selected partial dispersion points and polarization states to calculate the errors of Δf_rep/ΔP and Δf_ceo/ΔP relative to df_rep/dP and df_ceo/dP, which are all within 10%. In different states, for example, state 1 (red line) can only maintain stable mode-locking when the grating pair spacing is 3.2–4.9 mm, but state 3 (blue line) can maintain stable mode-locking when the grating pair spacing is 2.6–5.0 mm.

FIGURE 3

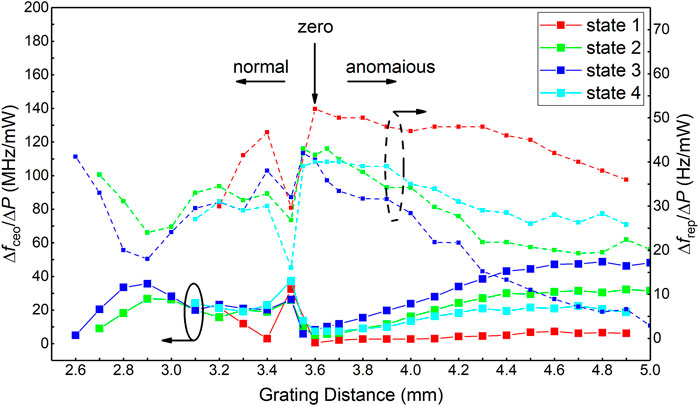
FIGURE 3. Pump power induced variation of f_ceo (solid line) and f_rep (dash line) with dispersion and different wave plate setting states.

The influence of net-cavity dispersion and intracavity PS on the values of Δf_ceo/ΔP and Δf_rep/ΔP is significant. At zero dispersion point, there is a local maximum of Δf_rep/ΔP and a minimum of Δf_ceo/ΔP. The Δf_rep/ΔP and Δf_ceo/ΔP curves exhibit a negative correlation with dispersion change, that is, when Δf_rep/ΔP increases, the Δf_ceo/ΔP decreases. In the same dispersion point, Δf_rep/ΔP and Δf_ceo/ΔP also show a negative correlation with the change of polarization state. Similar negative correlation between f_ceo and f_rep noise have been discovered in literature [30, 31]. This tendency indicates that the FPF of the pump power cannot remain constant while dispersion and intracavity PS change.

Figure 4 shows the FPF calculated from the data in Figure 3. The zero dispersion point is our most concerned point because it is proved that the f_ceo linewidth here is the narrowest [14]. In four different intracavity PS, the FPF has a minimum at the zero dispersion point. All the fixed points are lower than 40 THz, and the smallest one is only 2.5 THz. Such a low FPF shows that when we lock the f_ceo with the feedback pump power, the change of f_ceo is very small, but it has a greater impact on the comb-line frequency in the optical regime. Thus, the zero dispersion point is not appropriate to lock the f_ceo with pump current. Due to the broadband spectrum, short pulsewidth and high peak power of fiber lasers working in the stretched-pulse regime, the extremely small FPF may be caused by strong SPM at near-zero dispersion point.

FIGURE 4

FIGURE 4. The pump power FPF versus net-cavity dispersion and intracavity polarization state.

In the negative dispersion regime, the FPF increases with the negative dispersion, but the rise rate depends on the PS. When the grating separation from 3.6 to 4.9 mm (net-cavity dispersion from 0 to -7,800 fs²), the FPF of the state 1 (red line) always stays below 50 THz, but the FPF variation of the state 3 (blue line) has exceeded PHz. In Figure 2 negative dispersion regime (Grating spacing = 4.8 mm), the influence of intracavity PS on the spectrum is related to that on the FPF. The spectra of states 2 and state 4 are similar, and their FPF are also close. The spectral shape and central wavelength of state 3 are far away from the other three states, and its FPF is also much larger than that of the other three states. This is consistent with the results measured in the literature [29]. But the how the spectrum affects the FPF needs further exploration.

At the slightly positive dispersion point (+600 fs²), each of the four wave plate setting states has a local maximum FPF, which is close to the carrier frequency. In the more positive dispersion regime, with the increase of positive dispersion, the FPF does not follow monotonically but fluctuates. The influence of wave plate setting states on FPF is not as significant as that in the negative dispersion regime. In our experiment, the free-running linewidth of f_ceo is almost 100 kHz between the grating spacing from 3.2 to 4.6 mm (dispersion from -6,000 fs² to +2400 fs²) in four wave plate setting states. In the region of more positive dispersion and more negative dispersion, the linewidth of f_ceo will increase sharply, which is similar to that described in the literature [14]. Thus, the slightly positive dispersion point, in which the FPF close to the carrier frequency and linewidth is almost the same as that at near-zero dispersion, is suitable for locking f_ceo with pump power. According to the stretcher-pulse analytical theory, the chirp parameter is near zero at negative dispersion and increases at positive dispersion [18]. The combined action of chirp parameter, wave plate setting state and pulse-shaping mechanisms may thus induce the change of FPF in the positive dispersion. In the negative dispersion regime, the chirp parameter is near zero, so the FPF changes monotonically only under the influence of dispersion.

Conclusion

In conclusion, we completely measured the change of pump power fixed point with the net-cavity dispersion and intracavity polarization states in a Yb-fiber frequency comb for the first time. We found that the FPF is significantly affected by net-cavity dispersion and PS, instead of always close to the carrier frequency. At the zero-dispersion point, the FPF has a local minimum, corresponding to the minimal RIN, timing jitter and free-running f_ceo linewidth, but not suitable to lock both f_ceo and f_rep (especially f_n) at this point since the FPF is much lower than the carrier frequency at the zero-dispersion point. In the negative dispersion regime, the impact of intracavity PS on the FPF is more significant, even exceeding PHz. A local maximum value of FPF emerges in the slightly positive dispersion regime where the linewidth of f_ceo is identical to that at the zero-dispersion point. This is highly conducive to lock f_ceo and f_n simultaneously. This research brings us to access a suitable FPF to implement a better lock of the comb by adjusting the net-cavity dispersion and intracavity polarization states.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XS, HH, and ZW contributed to the design and experimental schemes. XS, HH, and JM performed the experiments and are responsible for the data processing. XS, HH, JM, MZ, and ZW contributed to writing and editing the manuscript.

Funding

This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA1502040404, XDB2101040004); National Natural Science Foundation of China (60808007, 61378040, 11078022, 91850209).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Diddams SA. The evolving optical frequency comb [Invited]. J Opt Soc Am B (2010) 27:B51–B62. doi:10.1364/josab.27.000b51

CrossRef Full Text | Google Scholar

2. Sinclair LC, Deschênes J-D, Sonderhouse L, Swann WC, Khader IH, Baumann E, et al. Invited article: A compact optically coherent fiber frequency comb. Rev Sci Instrum (2015) 86:081301. doi:10.1063/1.4928163

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Agrawal GP. Nonlinear fiber optics. In: Nonlinear Science at the dawn of the 21st century. Springer (2000). p. 195–211.

Google Scholar

4. Haus HA, Mecozzi A. Noise of mode-locked lasers. IEEE J Quan Electron (1993) 29:983–96. doi:10.1109/3.206583

CrossRef Full Text | Google Scholar

5. Hofer M, Ober M, Haberl F, Fermann M. Characterization of ultrashort pulse formation in passively mode-locked fiber lasers. IEEE J Quan Electron (1992) 28:720–8. doi:10.1109/3.124997

CrossRef Full Text | Google Scholar

6. Kim J, Song YJ. Ultralow-noise mode-locked fiber lasers and frequency combs: Principles, status, and applications. Adv Opt Photon (2016) 8:465–540. doi:10.1364/aop.8.000465

CrossRef Full Text | Google Scholar

7. Mollenauer LF, Stolen RH. The soliton laser. Opt Lett (1984) 9:13–5. doi:10.1364/ol.9.000013

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Haus H, Islam M. Theory of the soliton laser. IEEE J Quan Electron (1985) 21:1172–88. doi:10.1109/jqe.1985.1072805

CrossRef Full Text | Google Scholar

9. Tamura K, Nelson L, Haus H, Ippen E. Soliton versus nonsoliton operation of fiber ring lasers. Appl Phys Lett (1994) 64:149–51. doi:10.1063/1.111547

CrossRef Full Text | Google Scholar

10. Chong A, Wright LG, Wise FW. Ultrafast fiber lasers based on self-similar pulse evolution: A review of current progress. Rep Prog Phys (2015) 78:113901. doi:10.1088/0034-4885/78/11/113901

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chong A, Buckley J, Renninger W, Wise F. All-normal-dispersion femtosecond fiber laser. Opt Express (2006) 14:10095–100. doi:10.1364/oe.14.010095

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Song Y, Kim C, Jung K, Kim H, Kim J. Timing jitter optimization of mode-locked Yb-fiber lasers toward the attosecond regime. Opt Express (2011) 19:14518–25. doi:10.1364/oe.19.014518

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Budunoğlu IL, Ülgüdür C, Oktem B, Ilday FÖ. Intensity noise of mode-locked fiber lasers. Opt Lett (2009) 34:2516–8. doi:10.1364/ol.34.002516

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Nugent-Glandorf L, Johnson TA, Kobayashi Y, Diddams SA. Impact of dispersion on amplitude and frequency noise in a Yb-fiber laser comb. Opt Lett (2011) 36:1578–80. doi:10.1364/ol.36.001578

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Song Y, Jung K, Kim J. Impact of pulse dynamics on timing jitter in mode-locked fiber lasers. Opt Lett (2011) 36:1761–3. doi:10.1364/ol.36.001761

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Li P, Wang G, Li C, Wang A, Zhang Z, Meng F, et al. Characterization of the carrier envelope offset frequency from a 490 MHz Yb-fiber-ring laser. Opt Express (2012) 20:16017–22. doi:10.1364/oe.20.016017

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Paschotta R. Timing jitter and phase noise of mode-locked fiber lasers. Opt Express (2010) 18:5041–54. doi:10.1364/oe.18.005041

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Namiki S, Haus HA. Noise of the stretched pulse fiber laser. I. Theory. IEEE J Quan Electron (1997) 33:649–59. doi:10.1109/3.572138

CrossRef Full Text | Google Scholar

19. Paschotta R. Noise of mode-locked lasers (Part II): Timing jitter and other fluctuations. Appl Phys B (2004) 79:163–73. doi:10.1007/s00340-004-1548-9

CrossRef Full Text | Google Scholar

20. Mayer AS, Grosinger W, Fellinger J, Winkler G, Perner LW, Droste S, et al. Flexible all-PM NALM Yb: Fiber laser design for frequency comb applications: Operation regimes and their noise properties. Opt Express (2020) 28:18946–68. doi:10.1364/oe.394543

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Edelmann M, Hua Y, Şafak K, Kärtner FX. Intrinsic amplitude-noise suppression in fiber lasers mode-locked with nonlinear amplifying loop mirrors. Opt Lett (2021) 46:1752–5. doi:10.1364/ol.415718

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kuse N, Lee C-C, Jiang J, Mohr C, Schibli T, Fermann M. Ultra-low noise all polarization-maintaining Er fiber-based optical frequency combs facilitated with a graphene modulator. Opt Express (2015) 23:24342–50. doi:10.1364/oe.23.024342

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Hudson DD, Holman KW, Jones RJ, Cundiff ST, Ye J, Jones DJ. Mode-locked fiber laser frequency-controlled with an intracavity electro-optic modulator. Opt Lett (2005) 30:2948–50. doi:10.1364/ol.30.002948

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Okubo S, Gunji K, Onae A, Schramm M, Nakamura K, Hong F-L, et al. All-optically stabilized frequency comb. Appl Phys Express (2015) 8:122701. doi:10.7567/apex.8.122701

CrossRef Full Text | Google Scholar

25. Telle HR, Lipphardt B, Stenger J. Kerr-lens, mode-locked lasers as transfer oscillators for optical frequency measurements. Appl Phys B: Lasers Opt (2002) 74:1–6. doi:10.1007/s003400100735

CrossRef Full Text | Google Scholar

26. Newbury NR, Swann WC. Low-noise fiber-laser frequency combs (Invited). J Opt Soc Am B (2007) 24:1756–70. doi:10.1364/josab.24.001756

CrossRef Full Text | Google Scholar

27. Newbury NR, Washburn BR. Theory of the frequency comb output from a femtosecond fiber laser. IEEE J Quan Electron (2005) 41:1388–402. doi:10.1109/jqe.2005.857657

CrossRef Full Text | Google Scholar

28. Washburn B, Swann WC, Newbury NR. Response dynamics of the frequency comb output from a femtosecond fiber laser. Opt Express (2005) 13:10622–33. doi:10.1364/opex.13.010622

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kashiwagi K, Inaba H. Fixed point variations of a frequency comb generated by a passively mode-locked fiber laser. IEICE Electron Express (2017) 14:20170710. doi:10.1587/elex.14.20170710

CrossRef Full Text | Google Scholar

30. Dolgovskiy V, Bucalovic N, Thomann P, Schori C, Di Domenico G, Schilt S. Cross-influence between the two servo loops of a fully stabilized Er:fiber optical frequency comb. J Opt Soc Am B (2012) 29:2944–57. doi:10.1364/josab.29.002944

CrossRef Full Text | Google Scholar

31. Tian HC, Yang WK, Kwon D, Li RM, Zhao YW, Kim J, et al. Optical frequency comb noise spectra analysis using an asymmetric fiber delay line interferometer. Opt Express (2020) 28:9232–43. doi:10.1364/oe.386231

PubMed Abstract | CrossRef Full Text | Google Scholar