A new non-entangled quantum secret sharing protocol among different nodes in further quantum networks

As an important branch of quantum secure multi-party computation, quantum secret sharing (QSS) can distribute secret information among dishonest network nodes without revealing the secrets. In this study, a new four-party QSS protocol based on locally indistinguishable orthogonal product (LIOP) states is first proposed for quantum network communication. Then, the general multiparty QSS model based on LIOP states will be expanded. Combined with the property of LIOP states and obfuscating operation, the source node can send the secrets to different destination nodes in the quantum network. Accordingly, it is proven that the destination nodes have to work together to recover the shared secrets against some existing attacks. Furthermore, no entangled resources and complicated operations are required in the presented protocol. We hope the results could make positive effects to the development of quantum secure communication in the future.

1 Introduction

With the rapid development of the Internet, the security of information is becoming more and more important. Cryptography, as one of the fastest developing fields in modern science, is the basic theory to guarantee information security. Due to the development of quantum algorithms [1, 2], classical cryptographic protocols based on computational complexity are facing great security threats. Applying quantum theory to the research of cryptography, quantum cryptography has made a scientific breakthrough in cryptography. In 2002, Long et al. first discussed the quantum secure direct communication idea and analyzed its application in further quantum networks [3]. In 2008, Ma et al. proposed a group quantum communication network based on quantum secret sharing (QSS) among multiple nodes [4]. Afterward, QSS is becoming an important application in the quantum network [5–12].

QSS is the use of quantum technology to distribute secrets to a group of sharers. In QSS, a secret can only be recovered by all authorized sharers working together. As an important branch of quantum secure multi-party computation, QSS has attracted much attention. In 1999, Hillery et al. proposed the first QSS protocol [13]. On this basis, Karlsson et al. designed a Bell state secret sharing protocol [14]. In 2004, Xiao et al. generalized Hillery’s protocol to arbitrary multi-parties, effectively solving the limitation to secret sharing among multiple parties [15]. In 2017, Qin et al. proposed a QSS protocol using the n-qudit GHZ states [16]. In 2019, Zhang et al. gave an n-party QSS model based on multiparty entangled states [17]. In 2020, Mansour et al. presented a QSS protocol using maximally entangled multi-qudit states [18]. In 2021, Hu et al. proposed a novel dynamic QSS protocol in the high-dimensional quantum system based on transmitted particles and local unitary operations [19].

During the study, it can be seen that most of the existing QSS protocols are achieved by entangled states. As we know, the preparation of entangled states is difficult. It is necessary to propose more practical QSS protocols. The local indistinguishability of orthogonal product states is one of the hot topics in quantum information field recently. In 2015, Yu et al. constructed a set of orthogonal product states which cannot be perfectly distinguished by local operations and classical communication (LOCC) [20]. The indistinguishable orthogonal product (LIOP) states are easier to prepare than the entangled ones. It exhibits the overall non-locality of a wide range of applications in quantum cryptographic protocols. For example, Guo et al. proposed a quantum key distribution (QKD) protocol based on LIOP states in 2001 [21]. In 2007, Yang et al. presented a QSS protocol based on LIOP states [22]. In 2019, Jiang et al. proposed a quantum voting protocol based on LIOP states [23]. In 2020, Jiang et al. implemented a trusted third-party e-payment protocol on LIOP states [24].

In this study, we proposed a practical new four-party QSS protocol for LIOP states in quantum networks. First, the source node encodes the secret information into LIOP states. Second, the source node safely obfuscates the particles in the sequence and sends the corresponding particles to different destination nodes. Finally, all destination nodes work together to recover the secrets. Then, we generalize the protocol to any number of parties. According to the property of LIOP states, even if an attacker obtains n − 1 (n ≥ 3) particles of orthogonal product states, it is impossible to determine the shared messages.

The rest of the study is organized as follows. In Section 2, we introduce two LIOP states: X-LIOP states and F-LIOP states. With the introduced LIOP states, a new specific four-party QSS protocol and an extended multi-party QSS protocol are presented in Section 3 and Section 4. The security of the protocol is discussed in Section 5. A brief conclusion is given in Section 6.

2 Preliminaries

Here, we introduce the following specific form and properties of LIOP states, which will be used in the following protocols. It is well known that a set of orthogonal states is locally indistinguishable if it cannot be completely distinguished by LOCC [25].

Definition 1. In a 2 ⊗ 2 ⊗⋯⊗ 2 quantum system, the product basis that contains the following 2n orthogonal product states

$\begin{array}{cc}\hfill |{\varphi }_1\rangle & =\frac{1}{\sqrt{2}}|{0\rangle }_1|{1\rangle }_2|{1\rangle }_3\cdots |{1\rangle }_{n-1}{\left(|0\rangle +|1\rangle \right)}_n,\hfill \\ \hfill |{\varphi }_2\rangle & =\frac{1}{\sqrt{2}}|{1\rangle }_1|{1\rangle }_2|{1\rangle }_3\cdots {\left(|0\rangle +|1\rangle \right)}_{n-1}|{0\rangle }_n,\hfill \\ \hfill & \cdots \hfill \\ \hfill |{\varphi }_n\rangle & =\frac{1}{\sqrt{2}}{\left(|0\rangle +|1\rangle \right)}_1|{0\rangle }_2|{1\rangle }_3\cdots |{1\rangle }_{n-1}|{1\rangle }_n,\hfill \\ \hfill |{\varphi }_{n+1}\rangle & =\frac{1}{\sqrt{2}}|{0\rangle }_1|{1\rangle }_2|{1\rangle }_3\cdots |{1\rangle }_{n-1}{\left(|0\rangle -|1\rangle \right)}_n,\hfill \\ \hfill |{\varphi }_{n+2}\rangle & =\frac{1}{\sqrt{2}}|{1\rangle }_1|{1\rangle }_2|{1\rangle }_3\cdots {\left(|0\rangle -|1\rangle \right)}_{n-1}|{0\rangle }_n,\hfill \\ \hfill & \cdots \hfill \\ \hfill |{\varphi }_{2n}\rangle & =\frac{1}{\sqrt{2}}{\left(|0\rangle -|1\rangle \right)}_1|{0\rangle }_2|{1\rangle }_3\cdots |{1\rangle }_{n-1}|{1\rangle }_n\hfill \end{array}(1)$

cannot be perfectly distinguished by LOCC, where n ≥ 3, and the subscript i of the state $\frac{1}{\sqrt{2}}|{0\rangle }_1|{1\rangle }_2|{1\rangle }_3\cdots |{1\rangle }_{n-1}{(|0\rangle +|1\rangle )}_n$ denotes that the corresponding subsystem belong to the i-th party. In order to simplify the following protocol, the states aforementioned are named X-LIOP states.We can get the special case of n = 3, i.e., the following Definition 2.

Definition 2. In a 2 ⊗ 2 ⊗ 2 quantum system, the product basis that contains the following six orthogonal product states

$\begin{array}{cc}\hfill |{\varphi }_1\rangle & =\frac{1}{\sqrt{2}}|{0\rangle }_1|{1\rangle }_2{\left(|0\rangle +|1\rangle \right)}_3,\hfill \\ \hfill |{\varphi }_2\rangle & =\frac{1}{\sqrt{2}}|{1\rangle }_1{\left(|0\rangle +|1\rangle \right)}_2|{0\rangle }_3,\hfill \\ \hfill |{\varphi }_3\rangle & =\frac{1}{\sqrt{2}}{\left(|0\rangle +|1\rangle \right)}_1|{0\rangle }_2|{1\rangle }_3,\hfill \\ \hfill |{\varphi }_4\rangle & =\frac{1}{\sqrt{2}}|{0\rangle }_1|{1\rangle }_2{\left(|0\rangle -|1\rangle \right)}_3,\hfill \\ \hfill |{\varphi }_5\rangle & =\frac{1}{\sqrt{2}}|{1\rangle }_1{\left(|0\rangle -|1\rangle \right)}_2|{0\rangle }_3,\hfill \\ \hfill |{\varphi }_6\rangle & =\frac{1}{\sqrt{2}}{\left(|0\rangle -|1\rangle \right)}_1|{0\rangle }_2|{1\rangle }_3\hfill \end{array}(2)$

cannot be perfectly distinguished by LOCC. In order to simplify the subsequent protocol, the states aforementioned are named F-LIOP states.In Refs. [26, 27], these states are proven not to be perfectly distinguished by LOCC. We can find some properties of them.

Property 1. Even if n − 1 (n ≥ 3) particles of orthogonal product states are obtained, the exact form cannot be determined.

Property 2. Each particle can be transmitted independently.

Property 3. An operation on one of the particles does not affect the other particles.

3 Four-party quantum secret sharing protocol based on F-LIOP states

3.1 Proposed protocol

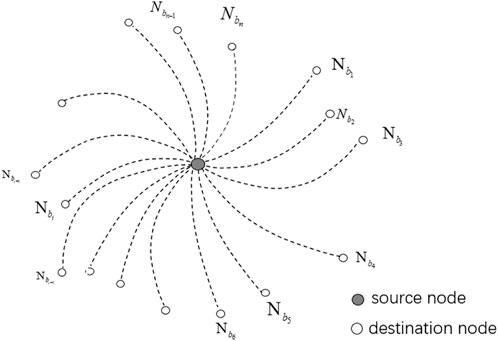
In this section, a four-party QSS protocol applied in the quantum network based on F-LIOP states is proposed. The network graph has two types of nodes (Figure 1): the source node (N_a) wants to distribute secrets, and destination nodes $(N_{b_1},N_{b_2},N_{b_3})$ receive secrets. The secrets can only be recovered if all destination nodes collaborate. The specific description is as follows:

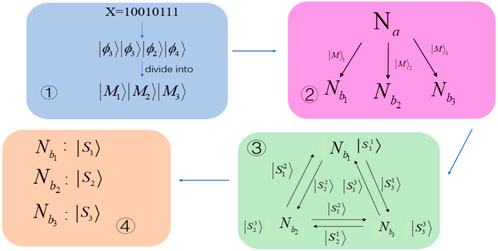
Step 1) N_a divides the secret message X into n groups, i.e., x₁, …, x_n, where x_i ∈ {00, 01, 10, 11}, i = 1, 2, …, n.

Step 2) N_a encodes the secret message X to a quantum sequence |S⟩, and according to the following rules, it should be accepted by all the nodes:

$\begin{array}{cc}\hfill & 00\mapsto |{\varphi }_1\rangle ,01\mapsto |{\varphi }_2\rangle \hfill \\ \hfill & 10\mapsto |{\varphi }_3\rangle ,11\mapsto |{\varphi }_4\rangle .\hfill \end{array}(3)$

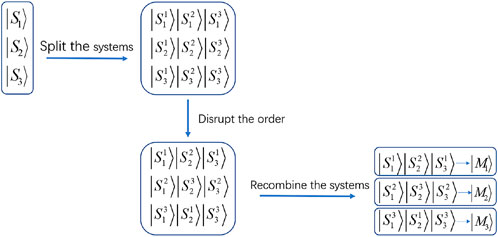
Step 3) N_a generates three identical sequences |S⟩, where the i-th sequence is denoted by |S_i⟩, i = 1, 2, 3. N_a splits |S_i⟩ into three subsystems, i.e., $|S_i^1\rangle ,|S_i^2\rangle ,|S_i^3\rangle$. Then, N_a generates three sequences |M₁⟩, |M₂⟩, and |M₃⟩, where $|M_1\rangle =\{|S_1^1\rangle ,|S_2^2\rangle ,|S_3^1\rangle \}$, $|M_2\rangle =\{|S_1^2\rangle ,|S_2^3\rangle ,|S_3^2\rangle \}$, and $|M_3\rangle =\{|S_1^3\rangle ,|S_2^1\rangle ,|S_3^3\rangle \}$. The distribution of the particles is shown in Figure 2.

Step 4) N_a takes the left states composed of |ϕ₅⟩, |ϕ₆⟩ as decoy states to randomly insert the quantum sequence |M_t⟩ to form |M_t⟩′, where t = 1, 2, 3. Finally, |M_t⟩′ is sent to $N_{b_l}$ randomly, where l = 1, 2, 3. In this case, $N_{b_l}$ does not know which particle they receive.

Step 5) After receiving the sequence |M_t⟩′ from N_a, $N_{b_l}$ sends an acknowledgment to N_a. Then, N_a announces both the basis and the positions of the decoy photons in |M_t⟩′. $N_{b_l}$ measures the decoy states. According to the measurement results of $N_{b_l}$, N_a performs eavesdropping detection. If no eavesdropping is detected, the protocol will continue to the next step. Otherwise, it will be aborted and will restart from Step 1.

Step 6) After the eavesdropping check, $N_{b_l}$ has the sequence |M_t⟩. Then, $N_{b_l}$ sends the j-th group of particles |M_t⟩ with the decoy states to $N_{b_j}$, where the decoy states are chosen from {| + ⟩, | − ⟩, |0⟩, |1⟩}, and where j = 1, 2, 3.

Step 7) After receiving the sequences from $N_{b_l}$, $N_{b_j}$ sends him a confirmation. $N_{b_l}$ announces both the basis and the positions of the decoy photons. According to the measurement results of $N_{b_j}(j\ne l)$, $N_{b_l}$ performs eavesdropping detection. If no eavesdropping is detected, the protocol will continue to the next step; otherwise, it will be aborted.

Step 8) After the eavesdropping check, $N_{b_l}$ has $|S_l^1\rangle ,|S_l^2\rangle ,|S_l^3\rangle$, i.e., |S_l⟩. Then, the quantum sequence |S_l⟩ is measured under the basis of Eq. 2, and ${\bar{X}}_l$ is recovered. N_a announces the measurement basis and order of all sequences.

Step 9) $N_{b_1},N_{b_2}$ and $N_{b_3}$ hold the same particles and perform the same operations. Therefore, if the protocol is valid, ${\bar{X}}_1,{\bar{X}}_2,{\bar{X}}_3$ and the secret X must be the same. Intuitively, if ${\bar{X}}_1={\bar{X}}_2={\bar{X}}_3=X$, the protocol will be valid; otherwise, the protocol fails.

FIGURE 1

FIGURE 1. Communication in N_a and $N_{b_i}$.

FIGURE 2

FIGURE 2. Generation process of the |M⟩ sequence.

3.2 Example

To illustrate our protocol more clearly, the following example is proposed. For convenience, eavesdropping detection is ignored. Suppose $N_a^{\prime }s$ secret is 10010111, it can been encoded as |ϕ₃⟩, |ϕ₂⟩, |ϕ₂⟩, |ϕ₄⟩.

Therefore,

$|S_1^1\rangle =\{|+\rangle ,|1\rangle ,|1\rangle ,|0\rangle \}=|S_2^1\rangle =|S_3^1\rangle$,

$|S_1^2\rangle =\{|0\rangle ,|+\rangle ,|+\rangle ,|1\rangle \}=|S_2^2\rangle =|S_3^2\rangle$, and

$|S_1^3\rangle =\{|1\rangle ,|0\rangle ,|0\rangle ,|-\rangle \}=|S_2^3\rangle =|S_3^3\rangle$.

Then, we get

$|M_1\rangle =\{|S_1^1\rangle ,|S_2^2\rangle ,|S_3^1\rangle \}=\{|+\rangle ,|1\rangle ,|1\rangle ,|0\rangle ;|0\rangle ,|+\rangle ,|+\rangle ,|1\rangle ;|+\rangle ,|1\rangle ,|1\rangle ,|0\rangle \}$,

$|M_2\rangle =\{|S_1^2\rangle ,|S_2^3\rangle ,|S_3^2\rangle \}=\{|0\rangle ,|+\rangle ,|+\rangle ,|1\rangle ;|1\rangle ,|0\rangle ,|0\rangle ,|-\rangle ;|0\rangle ,|+\rangle ,|+\rangle ,|1\rangle \}$, and

$|M_3\rangle =\{|S_1^3\rangle ,|S_2^1\rangle ,|S_3^3\rangle \}=\{|1\rangle ,|0\rangle ,|0\rangle ,|-\rangle ;|+\rangle ,|1\rangle ,|1\rangle ,|0\rangle ;|1\rangle ,|0\rangle ,|0\rangle ,|-\rangle \}$.

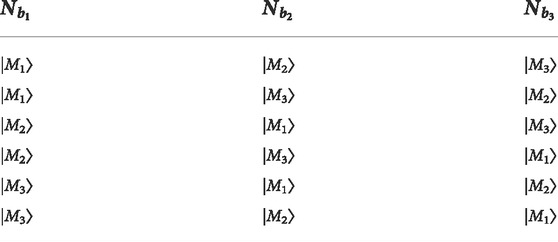
Here, we assume that N_a sends |M₁⟩, |M₂⟩, |M₃⟩ to $N_{b_1},N_{b_2},N_{b_3}$, respectively (This is just one of the cases; see Table 1).

TABLE 1

TABLE 1. $N_{b_l}$ received the sequence |M_t⟩.

Then, $N_{b_1}$ $(N_{b_2},N_{b_3})$ sends $|S_2^2\rangle$ $(|S_1^2\rangle ,|S_1^3\rangle )$ to $N_{b_2}$($N_{b_1},N_{b_1}$). In the same way, $N_{b_1}$ ($N_{b_2},N_{b_3}$) sends $|S_3^1\rangle$ ($|S_3^2\rangle ,|S_2^1\rangle$) to $N_{b_3}(N_{b_3},N_{b_2})$. $N_{b_1}$ ($N_{b_2},N_{b_3}$) holds $|S_1^1\rangle (|S_2^3\rangle ,|S_3^3\rangle )$ on its own. Then, $N_{b_1}$ gets$(|S_1^1\rangle ,|S_1^2\rangle ,|S_1^3\rangle )=|S_1\rangle$, $N_{b_2}$ gets |S₂⟩, and $N_{b_3}$ gets |S₃⟩. $N_{b_1}$ ($N_{b_2},N_{b_3}$) measures the quantum sequence |S₁⟩(|S₂⟩, |S₃⟩). According to the measurement basis and order of all sequences announced by N_a, the secret can be obtained. The specific procedures can be seen in Figure 3.

FIGURE 3

FIGURE 3. Process of quantum secret sharing.

4 Multi-party quantum secret sharing protocol based on X-LIOP states

In this section, we generalize the QSS protocol to any multi-party based on X-LIOP states applied in the quantum network. There are source node (N_a) and n destination nodes $(N_{b_1},N_{b_2},\dots ,N_{b_n})$. The secrets can be recovered only when the destination nodes cooperate together. The protocol can be described as follows. Here, we denote different m-bit sequences as $a_1=000\cdots 000,a_2=000\cdots 001,a_3=000\cdots 011,\dots ,a_{2^{m-2}}=111\cdots 101,a_{2^{m-1}}=111\cdots 110,a_{2^m}=$111 ⋯ 111, where m = ⌊ log₂n⌋.

Step1)N_a divides the secret message X into n groups, i.e., x₁, …, x_n, where $x_i\in \{a_1,a_2,a_3,\dots ,a_{2^{m-2}},a_{2^{m-1}},a_{2^m}\},i=\mathrm{1,2},\dots ,n$.

Step2)N_a encodes the secret message X to a quantum sequence |S⟩ according to the following rules accepted by all the nodes:

$\begin{array}{c}\hfill a_i\mapsto |{\varphi }_i\rangle \left(i=\mathrm{1,2},\dots ,2^m\right).\hfill \end{array}(4)$

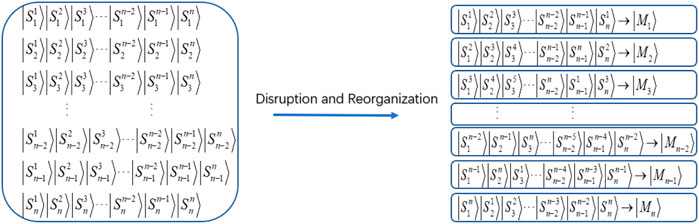
Step3)N_a creates n identical sequences |S⟩, where the i-th sequence is denoted by |S_i⟩ and i = 1, 2, …, n. N_a splits |S_i⟩ into n systems, i.e., $|S_i^1\rangle ,|S_i^2\rangle ,\dots ,|S_i^n\rangle$. N_a generates n sequences |M₁⟩, |M₂⟩, …, |M_n⟩, where $|M_1\rangle =\{|S_1^1\rangle ,|S_2^2\rangle ,\dots ,|S_{n-1}^{n-1}\rangle ,|S_n^1\rangle \}$, $|M_2\rangle =\{|S_1^2\rangle ,|S_2^3\rangle ,\dots ,|S_{n-1}^n\rangle ,|S_n^2\rangle \}$, …, and $|M_n\rangle =\{|S_1^n\rangle ,|S_2^1\rangle ,\dots ,|S_{n-1}^{n-2}\rangle ,|S_n^n\rangle \}$ (Figure 4).

Step4)N_a randomly inserts n unencoded orthogonal products into the quantum sequence as the decoy states and generates |M_t⟩′, where t = 1, 2, 3, …, n. Finally, |M_t⟩′ is given to $N_{b_l}$ randomly, where l = 1, 2, 3, …, n. Therefore, $N_{b_l}$ does not know which particle it gains.

Step5)After getting the sequence |M_t⟩′ from N_a, $N_{b_l}$ sends an acknowledgment to the sender. N_a announces the basis and the positions of the decoy photons in |M_t⟩′, and $N_{b_l}$ measures these decoy states. According to the measurement results of $N_{b_l}$, N_a checks eavesdropping. If N_a does not detect eavesdropping, the protocol will continue to perform the next step. Otherwise, it will stop and restart from Step 1.

Step6)After detecting eavesdropping, $N_{b_l}$ gets sequence |M_t⟩, and $N_{b_l}$ generates n decoy states that are selected from {| + ⟩, | − ⟩, |0⟩, |1⟩}. Then, decoy states are randomly inserted into the sequence |M_t⟩, and then, the j-th group of particles is sent to $N_{b_j}$, where j = 1, 2 …, n.

Step7)After receiving the sequences from $N_{b_l}$, $N_{b_j}$ sends $N_{b_l}$ a confirmation. Then, $N_{b_l}$ announces the basis and the positions of the decoy photons. According to the measurement results of $N_{b_j}$, $N_{b_l}$ performs eavesdropping detection. If no eavesdropping is detected, the protocol will continue to the next step; otherwise, it will stop.

Step8)After the eavesdropping check, $N_{b_l}$ gets $|S_l^1\rangle ,|S_l^2\rangle ,|S_l^3\rangle ,\dots ,|S_l^n\rangle$, i.e., |S_l⟩. Then, the quantum sequence |S_l⟩ is measured under the basis of Eq. 1, and ${\bar{X}}_l$ is recovered. N_a announces the measurement basis and order of all sequences.

Step9)$N_{b_1},N_{b_2},\dots ,N_{b_n}$ keep the same particles and perform the same operations. Therefore, if the protocol is effective, ${\bar{X}}_1,{\bar{X}}_2,{\bar{X}}_3,\dots ,{\bar{X}}_n$ and the secret X must be the same. Intuitively, if ${\bar{X}}_1={\bar{X}}_2={\bar{X}}_3=\cdots ={\bar{X}}_n=X$, the protocol will be effective; otherwise, the protocol fails.

FIGURE 4

FIGURE 4. Generation process of the |M⟩ sequence.

5 Security analysis

In this section, we analyze the attack performed by the internal and external malicious nodes.

5.1 Internal attack

Since the internal nodes directly take part in the process of the protocol, the malicious internal nodes can perform more strong attacks than the external ones. Here, we analyzed two types of participant attacks: information leak attacks and forgery attacks.

5.1.1 Information leak attack

Here, we consider information leak attacks and assume that malicious nodes can guess the secret messages together. In order to show that the following three cases are analyzed, without loss of generality, we assume that r nodes are malicious.

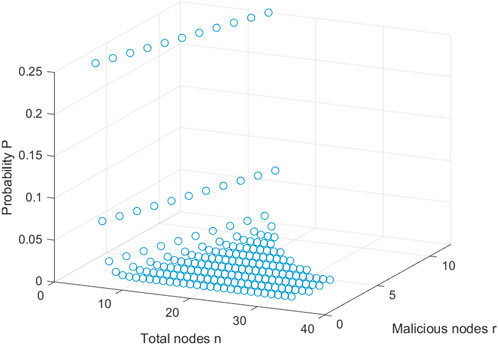
Case 1: Since r malicious nodes conspire, they will send the corresponding particles according to the normal process. Hence, the r particles of r malicious nodes are correctly arranged, and the left (n − r) correct particles are required. As the states of each part come from {| + ⟩, | − ⟩, |0⟩, |1⟩}, the probability of the malicious nodes intuitively guessing one particle is $\frac{1}{4}$, and the probability of guessing n − r particles is

$\begin{array}{c}\hfill P_1={\left(\frac{1}{4}\right)}^{n-r}.\hfill \end{array}(5)$

For the malicious nodes, the successful probability to obtain the secrets is shown in Figure 5.

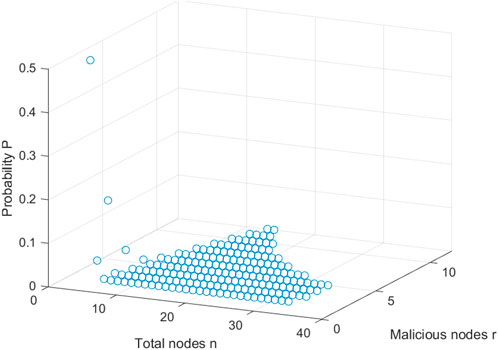
Case 2: In the same case, the r malicious nodes can also use other methods to guess the remaining particles. It is observed that the malicious nodes have a total of r × (n − r) particles left in their hands. If malicious nodes want to guess the secrets, they will arrange the remaining r × (n − r) particles correctly, and only one arrangement of particles is correct. Therefore, the successful probability to obtain the secrets is

$\begin{array}{c}\hfill P_2=\frac{1}{\left(r\times \left(n-r\right)\right)!}.\hfill \end{array}(6)$

FIGURE 5

FIGURE 5. Successful probability to obtain the secrets in Case 1.

For malicious nodes, the successful probability to obtain the secrets is shown in Figure 6.

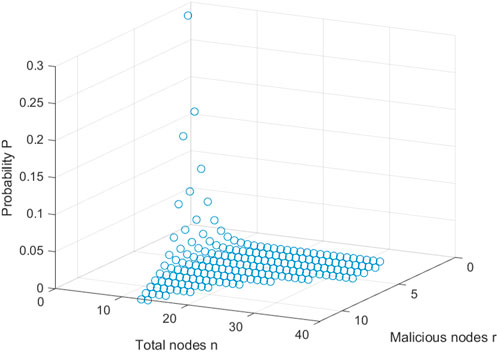
Case 3: Moreover, the r malicious nodes can perform the following different attacks as they give all the particles in their hands to one malicious node. In this sense, the malicious node independently guesses the secrets with the successful probability of

$\begin{array}{c}\hfill P_3=\frac{C_{r+1}^1\times {\left(C_r^1\right)}^{n-2}\times C_{r-1}^1}{C_{r\times n}^n}=\frac{\left(r+1\right)\times \left(r^{n-2}\right)\times \left(r-1\right)\times \left(n!\right)}{\left(r\times n\right)\times \left(r\times n-1\right)\times \cdots \times \left(r\times n-n+1\right)}.\hfill \end{array}(7)$

FIGURE 6

FIGURE 6. Successful probability to obtain the secrets in Case 2.

For malicious nodes, the successful probability to obtain the secrets is shown in Figure 7.

FIGURE 7

FIGURE 7. Successful probability to obtain the secrets in Case 3.

Above all, the probability of malicious nodes guessing the secrets successfully can be shown as

$\begin{array}{c}\hfill P=\mathit{max}\left\{P_1,P_2,P_3\right\}.\hfill \end{array}(8)$

From the analysis mentioned previously, it can be seen for all malicious nodes without all the particles, and the probability to guessing the secrets tends to be 0. According to the property of the LIOP states, our protocol can resist information leak attacks.

5.1.2 Forgery attack

A forgery attack is an easily overlooked but important attack in the QSS protocol. Forgery attack means that malicious nodes can obtain secret messages and successfully forge secret messages so that other nodes get the wrong secret messages. This attack was proposed by Zhang et al. in 2013 [28] and was also mentioned by Sutradhar et al. in 2020 [29]. In the protocol, a forgery attack is also considered. The secrets are encoded as LIOP states, and particles are transmitted between all destination nodes. Therefore, it is possible for malicious nodes to complete the forgery attack.

When malicious nodes change | + ⟩ (| − ⟩) to | − ⟩ (| + ⟩), they have a certain probability to complete the forgery attack. So, the secrets encoded as |ϕ₁⟩ (|ϕ₄⟩) are forged and are encoded as |ϕ₄⟩ (|ϕ₁⟩) in Eq. 3. In the multi-party QSS protocol, the secrets are encoded most in the first n states in Eq. 1. The secrets are not encoded in LIOP states with | − ⟩ states. Therefore, this attack is only possible in the four-party QSS protocol.

5.1.2.1 Individual attack

Here, we assume that the malicious node can only perform a forgery attack on its own. When a malicious node gets all $|S_i^3\rangle$ and $N_a^{\prime }s$, secret messages encoded as |ϕ₁⟩or|ϕ₄⟩, it can successfully forge secrets 00 to secrets 11 or secrets 11 to secrets 00, as in Eq. 3, i = 1, 2, 3. The probability that the secret messages are encoded as |ϕ₁⟩or|ϕ₄⟩

$\begin{array}{c}\hfill P_a=\frac{1}{2}.\hfill \end{array}(9)$

Next, we analyze the probability that the malicious node gets all $|S_i^3\rangle$. When we assume that $N_{b_1}$ or $N_{b_3}$ is a malicious node, we will find that it is impossible for them to get all sequences $|S_i^3\rangle$. Only when it is assumed that $N_{b_2}$ is a malicious node and obtains sequence |M₃⟩, the individual has a certain probability to acquire all sequences $|S_i^3\rangle$. Therefore, the probability that $N_{b_2}$ obtains all $|S_i^3\rangle$ is

$\begin{array}{c}\hfill P_b=\frac{1}{3}.\hfill \end{array}(10)$

So, the probability that the individual wants to successfully forge the secrets is

$\begin{array}{c}\hfill P=P_a\times P_b=\frac{1}{2}\times \frac{1}{3}=\frac{1}{6}.\hfill \end{array}(11)$

For the n length of the quantum sequences, it is not difficult to see that the probability of the malicious node successfully forging secrets P′ tends to be zero with the increase in n in Eq. 12.

$\begin{array}{c}\hfill P^{\prime }=P^n={\left(\frac{1}{6}\right)}^n.\hfill \end{array}(12)$

5.1.2.2 Collusion attack

A more serious threat than an individual attack is that some attackers cooperate to forge secrets. Since this attack in this study only exists in the four-party QSS protocol, there are at most two malicious nodes here. When the malicious nodes obtain the secret messages of all sequences $|S_i^3\rangle$ and $N_a^{\prime }s$ secret messages encoded as |ϕ₁⟩ or |ϕ₄⟩, the malicious nodes can successfully forge secret messages 00 to secret messages 11 or forge secret messages 11 to secret messages 00. The secret messages are encoded as |ϕ₁⟩or|ϕ₄⟩ with the probability

$\begin{array}{c}\hfill P_a=\frac{1}{2}.\hfill \end{array}(13)$

We analyze the probability of malicious nodes obtaining all sequences $|S_i^3\rangle$. A total of three cases were found to be possible to get $|S_i^3\rangle$.

Case 1: $N_{b_1}$ and $N_{b_2}$ are malicious nodes.

Case 2: $N_{b_2}$ and $N_{b_3}$ are malicious nodes.

Case 3: $N_{b_1}$ and $N_{b_3}$ are malicious nodes.

First, we analyze Case 1, and when they get sequence |M₃⟩, they can obtain sequences $|S_i^3\rangle$. The probability of Case 1 is

$\begin{array}{c}\hfill P_{b_1}=\frac{1}{3}.\hfill \end{array}(14)$

Next, we see Case 2; when they obtain sequence |M₃⟩, the success probability is

$\begin{array}{c}\hfill P_{b_2}=\frac{1}{3}.\hfill \end{array}(15)$

Finally, during Case 3, when they receive sequence |M₂⟩, the successful probability is

$\begin{array}{c}\hfill P_{b_3}=\frac{1}{3}.\hfill \end{array}(16)$

Therefore, the successful probability of malicious nodes forging messages is

$\begin{array}{c}\hfill P_1=P_a\times P_{b_1}=\frac{1}{6},P_2=P_a\times P_{b_2}=\frac{1}{6},P_3=P_a\times P_{b_3}=\frac{1}{6}.\hfill \end{array}(17)$

For the length of n of the quantum sequences, it is not difficult to see that in Eq. 18, as n increases, the probability $P_i^{\prime }$ of malicious nodes successfully forging secrets tends to be zero, where i = 1, 2, 3.

$\begin{array}{c}\hfill P_1^{\prime }=P_1^n={\left(\frac{1}{6}\right)}^n,P_2^{\prime }=P_2^n={\left(\frac{1}{6}\right)}^n,P_3^{\prime }=P_3^n={\left(\frac{1}{6}\right)}^n.\hfill \end{array}(18)$

They want to successfully forge the secret without being discovered is almost impossible. Therefore, the protocol is safe against internal attacks.

5.2 External attack

Unlike internal attackers, external attackers are illegal eavesdroppers from outside. We analyze intercept-replay attacks, intercept-measure-replay attacks, and entangle-measure attacks in the following sections.

5.2.1 Intercept-resend (IR) attack

Eve is an eavesdropper who wants to obtain the secrets of the source node. In order to obtain secrets, he can intercept secrets in Step 4 and Step 6 and complete the attack. Eve prepares large quantities of {| + ⟩, | − ⟩, |0⟩, |1⟩}. Eve intercepts the sequences |M_t⟩ and sends the sequences prepared on his own to $N_{b_l}$ at the same time. The probability of Eve guessing one particle is $\frac{1}{4}$, and the probability of guessing n particles is ${(\frac{1}{4})}^n$; the probability approximates to zero. Therefore, when N_a and $N_{b_l}$ perform eavesdropping detection, $N_{b_l}$ has a high probability of getting wrong measurements, and N_a will find that it has eavesdropped. N_a will give up sharing secrets, so Eve will not get any secret messages.

5.2.2 Intercept-measure-resend (IMR) attack

Eve receives the sequences |M_t⟩ and measures them in the computational basis. After the measurement, the sequences are resent to $N_{b_l}$. Considering one of the particles in the measured sequence, if $N_{b_l}$ measurement basis is the same as Eve′s selection, Eve will get $N_{b_l}$ measurement basis, which means Eve will get secrets. However, Eve does not distinguish between secret particles and decoy particles, so they do not get useful secret messages.

Similar to the IR attack and IMR attack, Eve is an external attacker, while in the entanglement and measurement attack, Eve has less information than an internal attacker and, therefore, has a higher probability of failure.

6 Discussion and conclusion

We compare and summarize the QSS protocols based on LIOP states in Table 2. R denotes a rearrangement operation, and H denotes a random three-level Hadamard transform.

TABLE 2

TABLE 2. Comparison among some different QSS protocols.

Compared with the existing QSS protocols based on LIOP states, our protocol can be extended to the arbitrary multi-party. In addition, we only use the characteristics of the states themselves to perform arrangement operations and do not require local measurement. In this case, two new QSS protocols based on LIOP states are proposed and may be applied in further quantum networks. The four-party QSS protocol is a special case of the multi-party QSS protocol. However, the secrets are encoded into different forms and attack strategies are different. To improve the efficiency, two more states are introduced in the four-party QSS protocol for encoding. Hence, the necessary forgery attack is discussed. For the multi-party QSS protocol, it is not difficult to see that the forgery attack can be naturally resisted.

In conclusion, combining with the property of LIOP states and obfuscating operation, the source nodes and destination nodes can complete the secret sharing in the quantum network. The destination nodes work together to recover the secrets. Since the LIOP states are more convenient to prepare than the entangled ones, the protocol is easily realized. Moreover, with regard to the property of LIOP states, it is proven that our protocol can be secure against the existing attacks. We hope this can be helpful to the further development of quantum networks.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

Conceptualization, S-JF and K-JZ; methodology, S-JF; software, S-JF; validation, S-JF, K-JZ, LZ, and K-CH; writing—original draft preparation, S-JF; writing—review and editing, S-JF and K-JZ. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grant 61802118 and Natural Science Foundation of Heilongjiang Province under Grant YQ2020F013, LH2019F031. The work of K-JZ was supported by the Advanced Programs of Heilongjiang Province for the overseas scholars and the Outstanding Youth Fund of Heilongjiang University. This research is supported by the Heilongjiang Provincial Key Laboratory of the Theory and Computation of Complex Systems.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev Soc Ind Appl Math (1999) 41(2):303–32. doi:10.1137/S0036144598347011

CrossRef Full Text | Google Scholar

2. Grover LK. A fast quantum mechanical algorithm for database search. In: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing (1996). p. 212–9. doi:10.1145/237814.237866

CrossRef Full Text | Google Scholar

3. Long GL, Liu XS. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys Rev A (Coll Park) (2002) 65(3):032302. doi:10.1103/PhysRevA.65.032302

CrossRef Full Text | Google Scholar

4. Ma H, Guo Z. A group quantum communication network using quantum secret sharing. In: 2008 IFIP International Conference on Network and Parallel Computing; 2008 October 18–21; Shanghai, China (2008). p. 549–52. IEEE. doi:10.1109/NPC.2008.42

CrossRef Full Text | Google Scholar

5. Zidan M, Abdel-Aty A-H, El-Sadek A, Zanaty EA, Abdel-Aty M. Low-cost autonomous perceptron neural network inspired by quantum computation. AIP Conf Proc (2017) 1905:020005. doi:10.1063/1.5012145

CrossRef Full Text | Google Scholar

6. Noor KI, Noor MA, Mohamed HM. Quantum approach to starlike functions. Appl Math Inf Sci (2021) 15(4):437–41. doi:10.18576/amis/150405

CrossRef Full Text | Google Scholar

7. Bogolyubov NN, Soldatov AV. Time-convolutionless master equation for multi-level open quantum systems with initial system-environment correlations. Appl Math Inf Sci (2020) 14(5):771–80. doi:10.18576/amis/140504

CrossRef Full Text | Google Scholar

8. Said T, Chouikh A, Bennai M. N two-transmon-qubit quantum logic gates realized in a circuit QED system. Appl Math Inf Sci (2019) 13(5):839–46. doi:10.18576/amis/130518

CrossRef Full Text | Google Scholar

9. Zidan M, Abdel-Aty A-H, Younes A, El-khayat I, Abdel-Aty M. A novel algorithm based on entanglement measurement for improving speed of quantum algorithms. Appl Math Inf Sci (2018) 12(1):265–9. doi:10.18576/amis/120127

CrossRef Full Text | Google Scholar

10. Abdel-Aty A-H, Kadry H, Zidan M, Zanaty EA, Abdel-Aty M. A quantum classification algorithm for classification incomplete patterns based on entanglement measure. J Intell Fuzzy Syst (2020) 38(3):2809–16. doi:10.3233/JIFS-179566

CrossRef Full Text | Google Scholar

11. Ye TY, Li HK, Hu JL. Semi-quantum key distribution with single photons in both polarization and spatial-mode degrees of freedom. Int J Theor Phys (Dordr) (2020) 59(9):2807–15. doi:10.1007/s10773-020-04540-y

CrossRef Full Text | Google Scholar

12. Ye TY, Geng MJ, Xu TJ, Chen Y. Efficient semiquantum key distribution based on single photons in both polarization and spatial-mode degrees of freedom. Quan Inf Process (2022) 21(4):123. doi:10.1007/s11128-022-03457-1

CrossRef Full Text | Google Scholar

13. Hillery M, Buvek V, Berthiaume A. Quantum secret sharing. Phys Rev A (Coll Park) (1999) 59(3):1829–34. doi:10.1103/PhysRevA.59.1829

CrossRef Full Text | Google Scholar

14. Karlsson A, Koashi M, Imoto N. Quantum entanglement for secret sharing and secret splitting. Phys Rev A (Coll Park) (1999) 59(1):162–8. doi:10.1103/PhysRevA.59.162

CrossRef Full Text | Google Scholar

15. Xiao L, Long GL, Deng FG, Pan JW. Efficient multiparty quantum-secret-sharing schemes. Phys Rev A (Coll Park) (2004) 69(5):052307. doi:10.1103/PhysRevA.69.052307

CrossRef Full Text | Google Scholar

16. Qin H, Dai Y. Dynamic quantum secret sharing by using d-dimensional GHZ state. Quan Inf Process (2017) 16(3):64–13. doi:10.1007/s11128-017-1525-y

CrossRef Full Text | Google Scholar

17. Zhang KJ, Zhang X, Jia HY, Zhang L. A new n-party quantum secret sharing model based on multiparty entangled states. Quan Inf Process (2019) 18(3):81–15. doi:10.1007/s11128-019-2201-1

CrossRef Full Text | Google Scholar

18. Mansour M, Dahbi Z. Quantum secret sharing protocol using maximally entangled multi-qudit states. Int J Theor Phys (Dordr) (2020) 59(12):3876–87. doi:10.1007/s10773-020-04639-2

CrossRef Full Text | Google Scholar

19. Hu W, Zhou RG, Li X, Fan P, Tan C. A novel dynamic quantum secret sharing in high-dimensional quantum system. Quan Inf Process (2021) 20(5):159–28. doi:10.1007/s11128-021-03103-2

CrossRef Full Text | Google Scholar

20. Yu S, Oh CH. Detecting the local indistinguishability of maximally entangled states (2015). arXiv preprint arXiv:1502.01274. Available at: https://arxiv.org/abs/1502.01274 (Accessed Feb 4, 2015).doi:10.48550/arXiv.1502.01274

CrossRef Full Text | Google Scholar

21. Guo GP, Li CF, Shi BS, Li J, Guo GC. Quantum key distribution scheme with orthogonal product states. Phys Rev A (Coll Park) (2001) 64(4):042301. doi:10.1103/PhysRevA.64.042301

CrossRef Full Text | Google Scholar

22. Yang Y, Wen Q, Zhu F. An efficient quantum secret sharing protocol with orthogonal product states. Sci China Ser G: Phys Mech Astron (2007) 50(3):331–8. doi:10.1007/s11433-007-0028-8

CrossRef Full Text | Google Scholar

23. Jiang DH, Wang J, Liang XQ, Xu GB, Qi HF. Quantum voting scheme based on locally indistinguishable orthogonal product states. Int J Theor Phys (Dordr) (2020) 59(2):436–44. doi:10.1007/s10773-019-04337-8

CrossRef Full Text | Google Scholar

24. Jiang DH, Hu QZ, Liang XQ, Xu GB. A trusted third-party E-payment protocol based on locally indistinguishable orthogonal product states. Int J Theor Phys (Dordr) (2020) 59(5):1442–50. doi:10.1007/s10773-020-04413-4

CrossRef Full Text | Google Scholar

25. Walgate J, Hardy L. Nonlocality, asymmetry, and distinguishing bipartite states. Phys Rev Lett (2002) 89(14):147901. doi:10.1103/PhysRevLett.89.147901

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Xu GB, Wen QY, Qin SJ, Yang YH, Gao F. Quantum nonlocality of multipartite orthogonal product states. Phys Rev A (Coll Park) (2016) 93(3):032341. doi:10.1103/PhysRevA.93.032341

CrossRef Full Text | Google Scholar

27. Feng Y, Shi Y. Characterizing locally indistinguishable orthogonal product states. IEEE Trans Inf Theor (2009) 55(6):2799–806. doi:10.1109/TIT.2009.2018330

CrossRef Full Text | Google Scholar

28. Zhang K, Qin S. The Cryptanalysis of Yuan et al.’s Multiparty Quantum Secret Sharing Protocol. Int J Theor Phys (Dordr) (2013) 52(11):3953–9. doi:10.1007/s10773-013-1706-0

CrossRef Full Text | Google Scholar

29. Sutradhar K, Om H. Efficient quantum secret sharing without a trusted player. Quan Inf Process (2020) 19(2):73–15. doi:10.1007/s11128-019-2571-4

CrossRef Full Text | Google Scholar

30. Hsu LY, Li CM. Quantum secret sharing using product states. Phys Rev A (Coll Park) (2005) 71(2):022321. doi:10.1103/PhysRevA.71.022321

CrossRef Full Text | Google Scholar

31. Xu J, Chen HW, Liu WJ, Liu ZH. An efficient quantum secret sharing scheme based on orthogonal product states. In: IEEE Congress on Evolutionary Computation; 2010 July 18–23; Barcelona, Spain (2010). p. 1–4. IEEE. doi:10.1109/CEC.2010.5586410

CrossRef Full Text | Google Scholar