
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 17 October 2022
Sec. Biophysics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1020619
Self-assembly of membrane inclusions plays a key role in biological processes such as cellular signalling and trafficking and has potential applications for designing interfacial devices such as sensors and actuators. Despite intensive studies of curvature-mediated interactions, how membrane curvature modulates interactions between flat disk-like inclusions, adsorbed on vesicles, remains unknown. We use Monte Carlo simulations of a triangulated vesicle with simulated annealing to explore curvature-mediated interactions between disk-like rigid inclusions, induced by membrane elastic energy. We distinguish two distinct short and long-range curvature-mediated interactions for disk distances below and above the vesicle diameter. We observe short-range neutral interactions in the limit of small disks, where the vesicle appears as a flat bilayer to the disks. Beyond a certain size of disk-like inclusions, we find a transition from neutral to attractive short-range forces. Consistent with experiments, we also show that upon deflating vesicles, previously-attracted disks experience repulsive interactions. Our findings show how the vesicle curvature and the relative size between the disks and the vesicle determine the character of membrane-mediated interactions between adsorbed disk-like inclusions.
Ubiquitous in cellular environments and central to the cell and cellular organelles, biological membranes constitute the most important interfacial surfaces in living organisms. Self-assembly of colloidal particles and proteins, at the membrane interface, is crucial to several cellular functions and processes such as signalling and endocytosis [1, 2]. Clustering of membrane macromolecules, that are either embedded in or adsorbed on the membrane, is essential for membrane domain formation which is linked to the cell adhesion and membrane budding [3, 4]. Membrane-mediated interactions result either from equilibrium membrane deformations or from membrane thermal fluctuations, referred to as static and dynamic interactions, respectively [5]. Whereas, static forces due to membrane deformations represent the ground-state forces originating in membrane elasticity, entropic forces resulting from thermal fluctuations are a special case of more general Casimir-like forces [6]. Inclusions, bound to or incorporated in the membrane, suppress local membrane shape fluctuations thereby giving rise to entropic forces between them. Fluctuation-induced interactions, intensively studied for membranes, are attractive for finite temperatures [7–11].
Interactions between inclusions at membranes are classified into two main categories of direct and indirect forces. Direct interactions including van der Waals and electrostatic forces, and hydrogen binding are induced by chemical and physical forces between particles and biomolecules [1]. Indirect or membrane-mediated interactions are, however, generated by a sort of physical perturbation applied to the membrane bilayer structure or its shape by the attached/embedded inclusions. Indirect membrane-mediated interactions include those induced by the membrane tension [12], by membrane thickness perturbation [13, 14], or by perturbing membrane curvature [9, 15–20].
Membrane curvature has been found to play a significant role in cellular signalling and trafficking [21–23], in conferring cells and cellular organelles their morphology [21, 24], and in many cellular functions and cellular processes such as division, migration, and vesicle trafficking [21, 24]. Curved inclusions impose their curvature on the host membrane by strongly adhering to the membrane. Biomembranes respond by reorganizing their shape together with the associated inclusions to minimize membrane curvature-energy resulting in membrane-mediated interactions between inclusions. These interactions have been found to be repulsive between two isotropically and weakly curved inclusions on planar membranes in absence of thermal fluctuations [9, 15, 25]. Elongated inclusions with anisotropic curvature such as scaffolding BAR proteins and proteins of reticulon family, however, attract each other enabling them create and maintain highly-curved membrane structures such as membrane tubules [26, 27]. Membrane curvature has been also shown to induce attractive interactions between partially adsorbed spherical particles on vesicles [28, 29], regulated by the particle interaction range [30], and particle wrapping fraction [31]. Membrane-mediated interactions between curved inclusions on flat membranes are intensely studied. However, little is known about curvature-mediated interactions between flat inclusions on vesicles.
Flat rigid inclusions exemplify both rigid particles such as Shiga toxin molecules [2], and solid membrane domains with different shapes [32–34]. Like curved inclusions, flat inclusions also experience both fluctuation and elasticity-induced interactions on membranes. Entropic forces, resulting from modified membrane shape fluctuations around flat rigid inclusions with sufficiently strong binding to the membrane, have been found capable of clustering these inclusions [2, 6]. Two-dimensional theoretical analysis has revealed the importance of membrane elasticity on short and long-range interactions between flat inclusions [18, 34]. Yet a general three dimensional analysis is missing.
Here, we use Monte Carlo simulations of a three-dimensional membrane model with simulated annealing to understand pairwise interactions, induced by membrane elastic energy, between rigid flat disks adsorbed on a vesicle [28]. In absence of thermal fluctuations, the shape of the vesicle with adsorbed disks is found by minimizing the total energy E of the system
composed of membrane curvature or bending energy Ebe, the adhesion energy Ead between the vesicle and the disks, and the two harmonic terms EA and EV to maintain the vesicle area A and its volume V close to their target values A0 and V0, respectively. Area and volume coefficients KA and KV are chosen sufficiently large to ensure that the relative errors of the vesicle area and its volume from their target values are less than 1% [28]. Here, κ is the bending rigidity, κG is the modulus of the Gaussian curvature, and M, K, and C0 are mean, Gaussian, and spontaneous curvatures of the membrane, respectively [35]. The integral in Eq. (1) is computed over the vesicle area A and the adhesion strength U is taken to be large enough to ensure the strong adhesion limit between the vesicle and the disks. In this regime, the entire disk surface is adhered to the vesicle with the disk adhesion area Aad equal to the disk area
We perform two different sets of simulations with spherical vesicles without volume constraint, KV = 0, and deflated vesicles with constrained volumes, KV > 0. For all vesicles, the vesicle area is preserved at the target vesicle area A0 equal to the area of the initial spherical vesicle as shown in the left panel of Figure 1A. The vesicles are characterized by the fixed vesicle radius
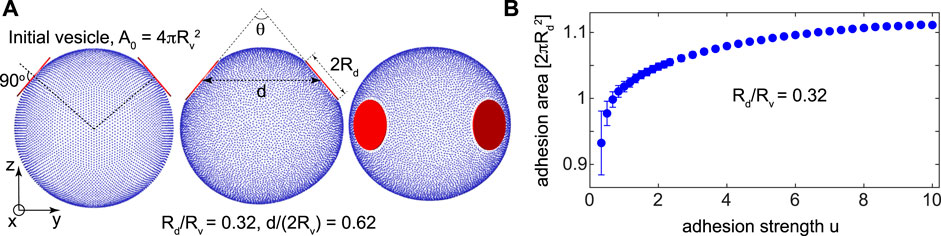
FIGURE 1. The initial spherical vesicle of fixed area
We perform Monte Carlo simulations of a triangulated vesicle model which has been successfully applied to understand membrane remodelling in contact with different inclusions [30]. Combining Monte Carlo simulations with simulated annealing, we find the elastic energy of the vesicle in the limit of low temperature, where thermal fluctuations of the membrane are suppressed. The resulting membrane-mediated interactions are thus purely induced by membrane elastic energy without entropic contributions. The triangulated vesicles with high resolution are composed of nn = 10,242 mesh nodes, ne = 30,720 edges, and nt = 20,480 triangles. Mesh nodes are displaced to reorganize membrane shape while mesh edges are flipped to fulfill fluidity of the membrane [28]. Circular disks are modelled as three dimensional cylindrical objects with radius Rd and a small height hd = 0.016Rv, taken to be sufficiently small to impose the flat shape of the disk on the bound membrane segment.
To ensure that the disks are in the strong adhesion limit, we vary the adhesion strength U between the disks and the vesicle and find the adhesion area of the disks from ten simulations at each adhesion strength. The adhesion area, graphed in Figure 1B, is found to saturate for an adhesion strength u = 10 for a typical disk size Rd/Rv = 0.32. The same adhesion strength u = 10 is then used in all simulations to ensure that the disks are always in the strong adhesion regime. All mesh nodes inside the disk cylinder are assumed adhered to the disk. The adhesion area Aad is then the sum ∑i Ai over the area contributions Ai (i = 1..nn) of all adhered nodes.
To find the total energy of the vesicle and the disks as a function of the disk distance, we fix the disk centers at a given distance d between them. The two disks are allowed to freely and independently rotate around an axis perpendicular to the system plane of symmetry that contains the line connecting disk centers i.e. the axis x in Figure 1. We then perform simulated annealing minimization to find the vesicle shape and the orientation of the disks with minimum total energy. Each Monte Carlo step is composed of randomly moving all nodes, flipping all edges, and independently rotating both disks. Random disk rotation is performed either clockwise or counter clockwise each time up to one degree with uniform probability distribution. The same minimization is then repeated for different disk distances as well as various disk sizes and the total energy curves are obtained for a range of system parameters. More details on Monte Carlo and simulated annealing simulations can be found in similar simulations with the same model [28].
We find that short-range membrane-mediated interactions between adsorbed disks on spherical vesicles without constrained volume are attractive for disks beyond a certain relative size with respect to the vesicle. Consistent with experiments [34], we show that for disks adsorbed on a deflated vesicle with sufficiently small volume the attractive interactions turn into repulsive ones.
Curvature-mediated interactions are induced and regulated by the local changes in membrane curvature due to adsorbed inclusions. Assuming a negligible spontaneous curvature C0 = 0, vesicles differ from flat bilayers in the sense that they are naturally curved due to their spherical shape. This inherent curvature can be further intensified or weakened by changing the overall shape of the vesicle through vesicle deflation. To distinguish these two effects, we first start with spherical vesicles without volume constraint and then turn to deflated vesicles with different volumes.
We start with simulated annealing simulations of two flat disks adhered to a spherical vesicle whose unconstrained volume can freely change. In our simulations this is achieved by choosing KV = 0. These vesicles are thus simulated in a constant-area ensemble. The centers of the two disks are initially placed at a distance d from each other with a symmetrical angular position in such a way that the disk plane is tangent to the vesicle surface and is perpendicular to the plane containing the centers of the disks and the vesicle i.e. frontal plane yz in Figure 1A. We then equilibrate the vesicle and the disks with Monte Carlo simulations at room temperature during which the vesicle remodels and the disks rotate around the axis x as shown in Figure 1A. Using simulated annealing, membrane shape fluctuations are then suppressed by reducing the temperature to almost zero thereby finding the system configuration with minimum total energy. For each disk distance d, we perform ten simulations and find the mean and standard deviation of the total energy. The disk distance is then varied and the total energy is found for different disk distances, a procedure which is repeated for different disk sizes Rd/Rv.
During initial Monte Carlo equilibration and subsequent annealing, the disks independently rotate in the frontal plane, the yz plane in Figure 1A, with two different angles which are almost identical in the final structure with minimum total energy. Because of the symmetry, the total energy of the vesicle and the disks depends on the relative angular position θ ∈ [0 180o] of the two disks. Video S1 shows both Monte Carlo equilibration and simulated annealing of the vesicle with two disks of size Rd/Rv = 0.32 at a distance d/(2Rv) = 0.62. The two disks freely rotate, with fixed centers, to minimize the total energy of the final nearly-symmetrical structure.
We first find the total energy curves for disks with relatively small sizes Rd/Rv = (0.16, 0.24). Figure 2 shows the total energy E of these vesicles as a function of the distance d between the disks. The total energy E is almost constant up to a relatively large distance of d/(2Rv) = 1 for both disk sizes Rd/Rv = (0.16, 0.24). This disk distance is equal to the vesicle diameter d = 2Rv as shown by the red dotted lines on energy curves in Figure 2. Curvature-mediated interactions between these small disks are thus neutral at short and intermediate distances without an obvious energetic tendency of the disks to mutually attract or repel. This is mainly due to the fact that in the limit of very small disks, the vesicle effectively appears to the disks as a flat bilayer with negligible curvature. Therefore, even if the disks impose their shape on the vesicle by strong binding, the vesicle spherical shape is barely perturbed. Membrane-mediated interactions are thus neutral, similar to those between flat disks adsorbed on a flat bilayer. At large distances, however, the total energy increases tending to bring the disks back to intermediate distances leading to long-range attractive interactions between the adsorbed disks. This is reflected in the rise of the total energy for disk distances beyond the vesicle diameter d > 2Rv i.e. to the right of the red dotted lines in Figure 2. Inspecting vesicle snapshots in the right panels of Figure 2 reveals that the rise in the total energy is indeed due to a change in the global vesicle shape which transforms into an oval stretched vesicle with larger bending energy. This can be seen, for instance, in the rightmost panel in Figure 2B. Bending and adhesion energies of these vesicle are shown in Supplementary Datasheet S1.
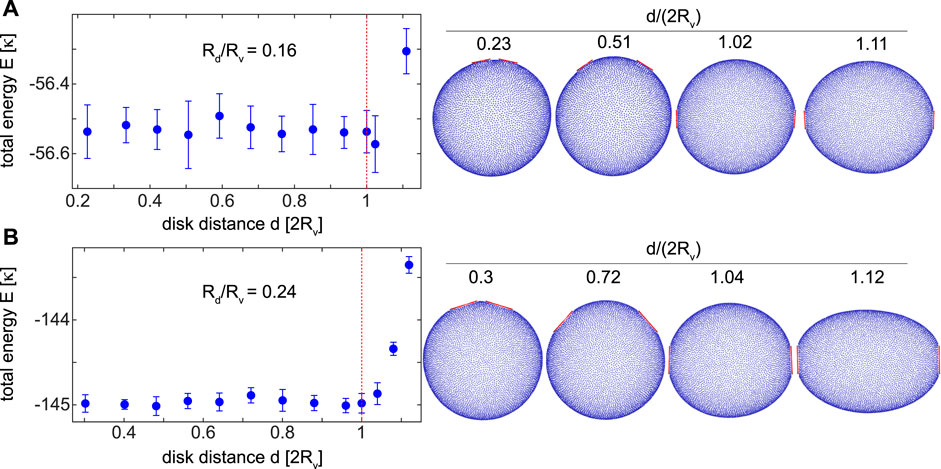
FIGURE 2. The total energy E/κ of a spherical vesicle with disks of relatively small sizes (A) Rd/Rv =0.16 and (B) Rd/Rv =0.24 with corresponding vesicle shapes in the right panels. Each point reflects the mean and the standard deviation of the total energy from ten simulations. Small disks experience short-range neutral interactions for disk distances below the vesicle diameter d ≤2Rv and long-range attraction beyond the vesicle diameter d ≥2Rv. The red dotted line corresponds to the diameter of the initial spherical vesicle d =2Rv.
We then examine disks with larger sizes Rd/Rv = (0.32, 0.4, 0.48). Figure 3 displays the total energy E for vesicles with these disks as well as some snapshots of the minimum-energy vesicles. Unlike total energies of smaller disk sizes Rd/Rv = (0.16, 0.24), which remain almost constant at intermediate and close distances with small fluctuations, the total energies of the larger disks exhibit a monotonically increasing trend, see energy curves in left panels of Figures 3A–C. Although it is not straightforward to recognize the exact transition size Rd/Rv, beyond which the total energy monotonically increases with the disk distance d also for distances d < 2Rv, the transition obviously occurs for some disk size in 0.24 < Rd/Rv < 0.32. Monotonically increasing total energy of the vesicle and the two adsorbed disks implies attractive interactions between the disks that lead to their self-assembly at the vesicle interface. Bending and adhesion energies of these vesicles are shown in Supplementary Datasheet S2.
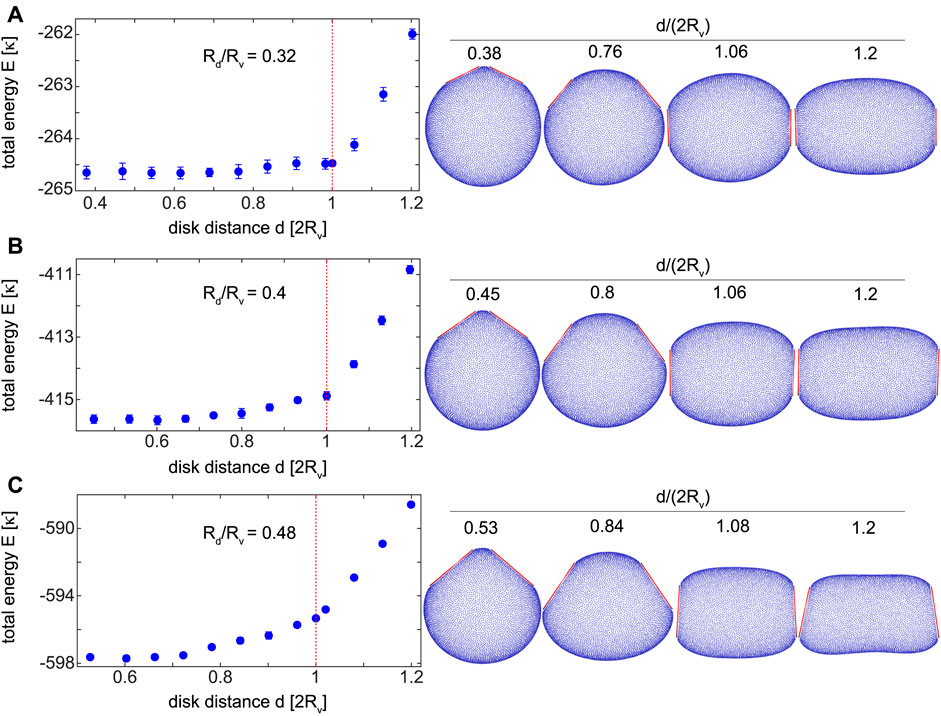
FIGURE 3. The total energy E/κ of a spherical vesicle with disk sizes (A) Rd/Rv =0.32, (B) Rd/Rv =0.4, and (C) Rd/Rv =0.48 with corresponding vesicle shapes in the right panels. Each point reflects the mean and the standard deviation of the total energy from ten simulations. For large disk sizes Rd/Rv >0.3, both short and long-range interactions are attractive as shown for disk distances below and beyond the vesicle diameter 2Rv i.e. the red dotted line.
We have shown so far that the attractive or repulsive character of curvature-mediated interactions between adsorbed disks on a vesicle is determined by the relative size of the disks and the vesicle. More precisely, we have found an approximate transition disk size beyond which neutral interactions turn into attractive ones. How these membrane-mediated interactions are induced by membrane curvature needs more careful consideration.
Membrane-mediated interactions are known to be always neutral for flat disks adsorbed on flat bilayers simply because flat disks do not distort the shape of the flat bilayer upon adhesion. The same disks adsorbed on a vesicle, however, perturb the naturally-curved shape of the initially-spherical vesicle and consequently experience either repulsive or attractive interactions. This class of membrane-mediated interactions, commonly short-ranged, are categorized as curvature-mediated interactions irrespective of their repulsive or attractive character. The size-dependent transition from neutral to attractive forces we found here, falls in this class of short-range curvature-mediated forces that acts on short and intermediate disk distances. For adsorbed disks on vesicles, there is another class of curvature-mediated interactions induced be the overall shape transition of the vesicle from an almost spherical vesicle into an stretched oval-shaped vesicle. These long range interactions, typically-attractive and commonly observed for all disk sizes, are a result of the relatively large rise in the total energy for a disk distance larger than the vesicle diameter. In other words, regardless of the disk size, all pairs of adsorbed disks with different sizes experience long-range attractive forces of the second type. It is worth noting that the second class is indeed exclusive to vesicles and does not exist even for curved inclusions adsorbed on flat bilayers. We classify these two types as short-range and long-range curvature-mediated interactions, induced by local and global shape changes of the vesicle, respectively. To distinguish these two types of curvature-mediated interactions, we focus on the relative angular position of the disks.
The two short and long-range curvature-mediated forces act on disks depending on whether the disks are distanced closer or farther than the vesicle diameter 2Rv. Equivalently, the disks start to transform the vesicle into oval shapes, as soon as they are located on the two sides of the vesicle almost parallel to each other with negligible angle θ. Figure 4 shows the relative angular position θ of the two disks as a function of the disk distance for different disk sizes Rd/Rv ∈ [0.16 0.48], see the blue dots. The red solid line shows the angle between the surface tangents of the spherical vesicle with radius Rv as a function of the distance between the tangent point on the vesicle. As expected, we observe that the disk relative angle decreases with the disk distance till a distance d/(2Rv) = 1 equal to the vesicle diameter beyond which the disks become almost parallel with negligible θ. Interestingly, we observe that irrespective of the disk size the relative angle vanishes when the disk distance equals the vesicle diameter. We verify this by adding more data points just before d/(2Rv) = 1 in different panels of Figure 4 corresponding to all disk sizes. We can thus use the disk distance d = 2Rv to distinguish short and long-range curvature-mediated interactions as indicated by red vertical dashed lines at d/(2Rv) = 1 in Figures 2, 3. Based on this criterion, curvature-mediated interactions between adsorbed disks on a vesicle are attractive if they exhibit monotonically increasing total energy for disk distances in the range d/(2Rv) ≤ 1. The criterion is quantified by the energy change ΔE defined as the difference in the total energy between touching disks and those distanced by the vesicle diameter d = 2Rv, graphed in the phase diagram in Figure 4F. Comparing the blue dots and the red curves in Figures 4A–E reveals that in the limit of small disks Rd/(2RV) → 0 the two angles are equal. In this limit, where the vesicle appears as a flat bilayer to the disks, the minimum-energy structure is the one with two disks tangent to the vesicle surface.
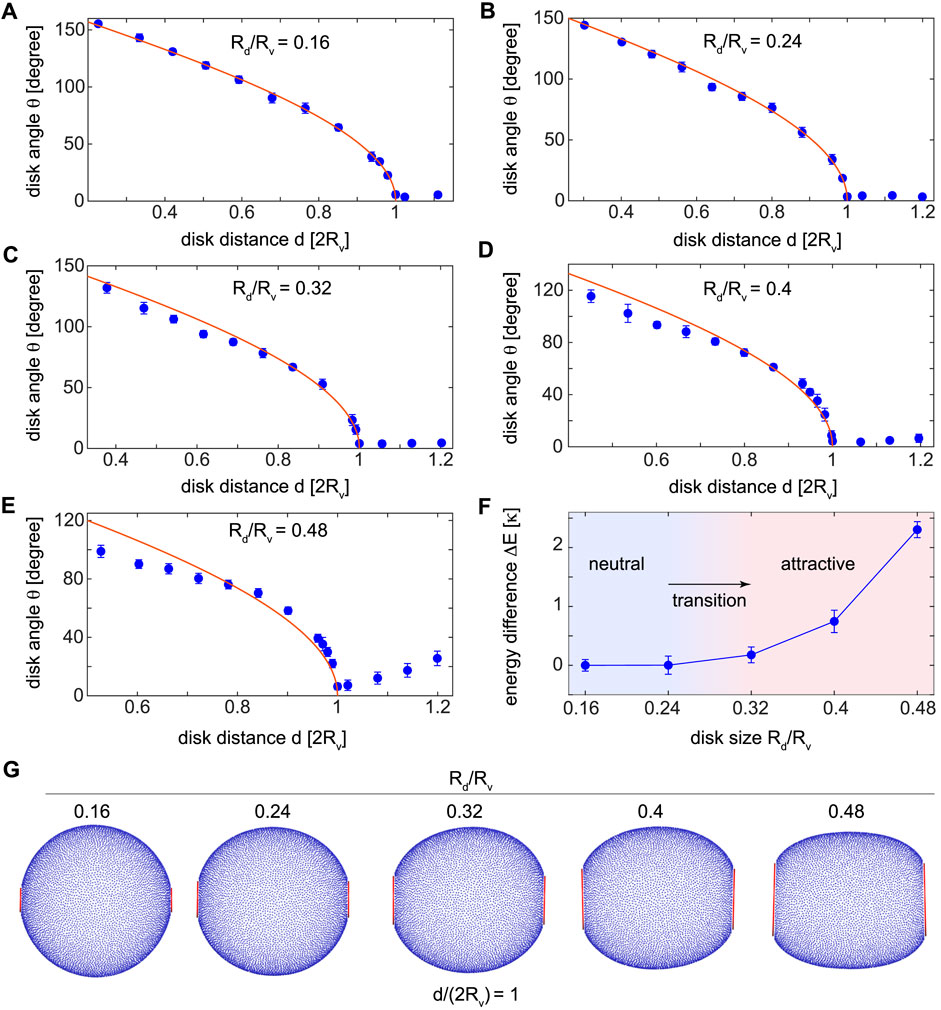
FIGURE 4. (A–E) The relative angular position θ of the two disks with different sizes Rd/Rv =0.16 to Rd/Rv =0.48 adsorbed on spherical vesicles. Each point reflects the mean and the standard deviation of the relative angle from ten simulations. The solid red line shows the angle between the surface tangents of a spherical vesicle with radius Rv as a function of the distance between the tangent point on the vesicle. The angle θ reduces for disk distances below the vesicle diameter and vanishes beyond that when the disks are distant enough to become almost parallel. (F) The difference in the total energy ΔE of the touching disks and the disks distanced by d =2Rv determines the transition disk size 0.24< Rd/Rv <0.32 for which the short-range curvature-mediated interactions change from neutral to attractive interactions. (G) Vesicle shapes with disks distanced by the vesicle diameter for which the two disks become parallel.
For the small disk sizes Rd/Rv = (0.16, 0.24), the total energy is almost equal for the smallest disk distance and the disks distanced by d = 2Rv resulting in ΔE ≈ 0, see Figure 4F and the energy curves in Figure 2. For disk distances below the vesicle diameter, the total energy fluctuates around an almost constant level leading to neutral short-range curvature-mediated interactions between the disks. For larger disk sizes Rd/Rv = (0.32, 0.4, 0.48), however, we observe an increasing total energy even at disk distances closer than the transition distance d = 2Rv with positive energy differences ΔE > 0, see Figure 4F. This corresponds to the attractive short-range interactions discussed earlier. Within the precision of our high resolution discrete vesicles, the transition between the neutral and attractive short-range interactions occurs at some disk size in the range 0.24 < Rd/Rv < 0.32 as shown on the phase diagram in Figure 4F. Minimum-energy vesicles, with disks distanced by the vesicle diameter d = 2Rv, are shown in Figure 4G. Small disks with Rd/Rv = (0.16, 0.24) barely change the spherical shape of the vesicle and thus lead to neutral interactions as reflected in ΔE ≈ 0 in Figure 4F. By contrast, larger disks with Rd/Rv = (0.32, 0.4, 0.48) distort the initial spherical shape of the vesicle strong enough to induce short-range attractive forces. These curvature-mediated interactions can be modified by controlling the global shape of the vesicle via changing the vesicle volume.
Vesicles in cellular environment are subject to osmotic stress commonly imposed by concentration gradient of biological material between the vesicle interior and the surrounding bulk solution. The resulting change in the vesicle volume leads to a variety of vesicle morphologies such as red-blood-cell-like, tubular and cup-shaped vesicles ubiquitously found in the cell and cellular organelles. Here, we explore curvature-mediated interactions between adsorbed disks on deflated vesicles with different reduced volumes. Deflated vesicles are simulated in a constant-area constant-volume ensemble wherein both area and volume of the vesicle are preserved by choosing KA, KV > 0. This is equivalent to a constant-reduced-volume ensemble. To understand how curvature-mediated interactions are regulated by the vesicle volume, we focus on a fixed disk size. Figure 5 shows the total energy of vesicles with reduced volumes v = 0.92 to v = 0.99 and two adsorbed disks of size Rd/Rv = 0.32.
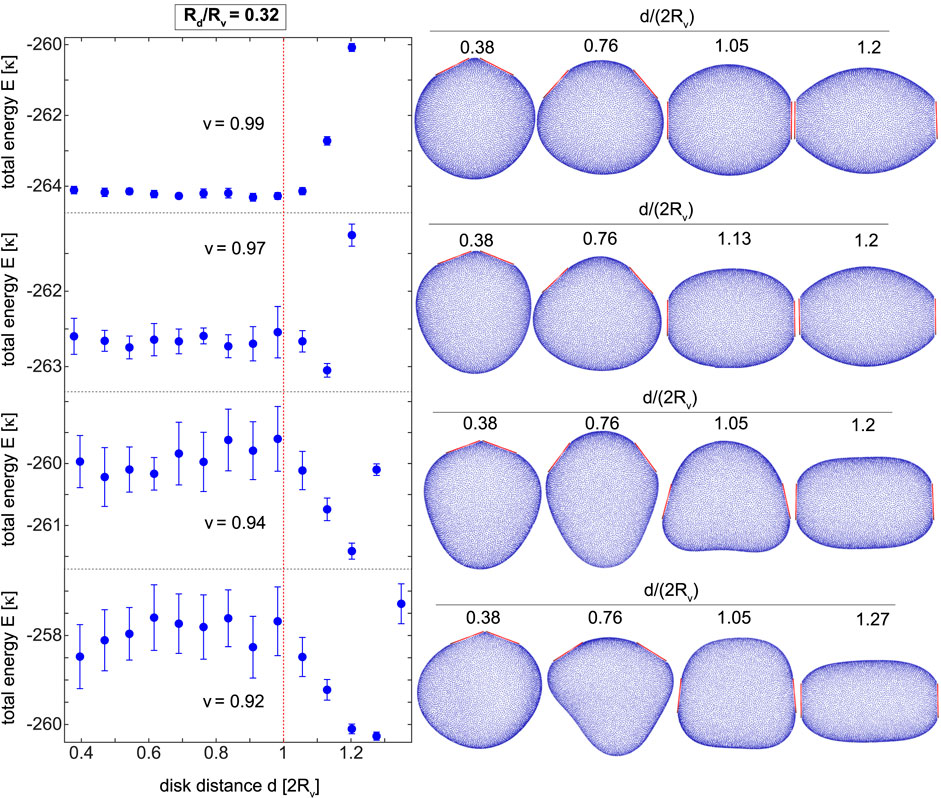
FIGURE 5. The total energy E/κ of deflated vesicles of different reduces volumes v =0.92 to v =0.99 with disks of fixed size Rd/Rv =0.32 with some vesicle shapes on the right panel. Each point reflects the mean and the standard deviation of the total energy from ten simulations. The short-range interactions become neutral upon vesicle deflation and the long-range interactions become repulsive resulting in repulsive curvature-mediated forces between the disks. The stable elongated vesicle occurs at larger disk distances for vesicles with smaller volumes.
For a spherical vesicle with disks of size Rd/Rv = 0.32, we found attractive short-range interactions with monotonically increasing total energy for disk distances d ≤ 2Rv, see the energy curve in Figure 3A. Same disks adsorbed on a deflated vesicle with the largest volume v = 0.99, experience neutral short-range interactions as reflected in the almost flat energy curve for d/(2Rv) ≤ 1, see the upper left panel of Figure 5. For this relatively large volume, the long-range interactions are still attractive with increasing total energy for large disk distances d ≥ 2Rv. Further decrease in the vesicle volume, corresponding to v ≤ 0.97, leads to a minimum in the total energy at a relatively large disk distance beyond the vesicle diameter d > 2Rv i.e. on the right side of the red dotted line in Figure 5. This stable oval vesicle occurs at larger disk distances for smaller vesicle volumes shifting from d/(2Rv) = 1.13 for v = 0.97 to d/(2Rv) = 1.27 for v = 0.92. The right panel of Figure 5 illustrates these stable vesicles for different vesicle volumes as well as some other vesicles at various disk distances. At larger disk distances, beyond the stable minimum-energy vesicle, the overall shape of the deflated vesicle is further stretched resulting in yet larger total energies. Therefore, the adsorbed disks with neutral or attractive interactions start to experience repulsive interactions upon deflating the vesicle. These repulsive forces are stronger for smaller vesicle volumes due to the larger depth of the total energy well around the stable vesicle. As shown experimentally, these volume-controlled interactions and accordingly their attractive or repulsive character can be reversibly adjusted upon vesicle deflation/inflation [34].
We use Monte Carlo simulations with simulated annealing of a discrete triangulated vesicle with adsorbed flat disks to examine curvature-mediated interactions between the disks induced by membrane elastic energy. Computing the total energies of the vesicle and the disks with a high-resolution vesicle model, we find curvature-mediated interactions between the adsorbed disks on spherical vesicles with freely varying volume as well as deflated non-spherical vesicles with fixed constrained volumes. We find the total energy of the vesicle and the disks in the limit of close-to-zero temperatures where thermal fluctuations are absent. Therefore, the pairwise interactions we report here are exclusively resulting from membrane elasticity and are different from those induced by membrane thermal fluctuations.
In contrast to disks adsorbed on flat bilayers, curvature-mediated interactions between adsorbed disks on spherical vesicles are always attractive at large disk distances, regardless of the disk size. This is due to the shape transformations of the vesicles that adopt elongated oval shapes with increasing bending energies for large disk distances. Therefore, we introduce the short and long-range interactions to recognize the character of curvature-mediated forces. Short and long-range curvature-mediated forces are differentiated by the disk distance below and beyond the diameter of the initial spherical vesicle. Attractive long-range forces due to changes in the vesicle global shape act at large disks distances. Short-range forces are, however, resulting from local shape changes of almost spherical vesicles whose shapes are locally distorted by the adsorbed disks.
Very small disks to which the vesicle appears as a flat bilayer, experience neutral interactions similar to adsorbed disks on a flat bilayer. Beyond a disk size, found to be between 24% and 32% of the vesicle size, we find short-range attractive interactions between the two disks leading to the self-assembly of sufficiently-large disks. Unlike particles with large volume-to-area ratio such as spherical inclusions which are typically wrapped by the membrane [28], disk-like particles with small volume-to-area ratio are adsorbed on the membrane. We note that a disk with a relative diameter 24%–32% with respect to the vesicle only covers 5%–10% of the vesicle area and is therefore relatively small compared to the vesicle. Although we expect multi-body attractions and consequent clustering of multiple such disks on a vesicle, any conclusion about many body interactions between the disks requires simulating three disks on the vesicle and remains to be studied in future works. The long-range forces, corresponding to large disk distances beyond the vesicle diameter, are found to be always attractive for disks adsorbed on stretched vesicles with freely-varying volume.
We find curvature-mediated short-range interactions to be attractive for disk sizes Rd/Rv = (0.32, 0.4, 0.48) and neutral for Rd/Rv = (0.16, 0.24) as seen in Figure 4F. These interactions are induced by membrane elasticity and are different from fluctuation-induced interactions. Fluctuation-induced Casimir-like interactions between rigid disks on membranes are known to have interaction energies of about
We then simulate non-spherical deflated vesicles of different volumes with adsorbed disks of various sizes. Our results show that disks adsorbed on deflated vesicles with smaller volumes experience neutral or repulsive interactions driving them to a stable structure of an elongated vesicle with distant disks. The vesicle volume can be thus used to reversibly control the attractive or repulsive nature of curvature-mediated interactions between adsorbed disks. Overall, we demonstrate how vesicle volume together with the relative size of the flat inclusions and the vesicle determine the attractive or repulsive character of pairwise curvature-mediated interactions originating in membrane elastic energy. Our results have important implications for rigid or relatively stiff membrane domains as well as for flat rigid inclusions adsorbed on vesicle membranes or curved membrane patches for both biological and biomimetic membranes.
All relevant data is contained within the article.
AB designed the research. EA-H and AS performed the simulations. AB wrote the original draft. EA-H, AS, and AB reviewed and edited the article.
This work was partially supported by the Max Planck Partner Group in UNAM, Bilkent University funded by the Max Planck Society.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1020619/full#supplementary-material
1. Johannes L, Pezeshkian W, Ipsen JH, Shillcock JC. Clustering on membranes: fluctuations and more. Trends Cell Biol (2018) 28:405–15. doi:10.1016/j.tcb.2018.01.009
2. Pezeshkian W, Gao H, Arumugam S, Becken U, Bassereau P, Florent JC. Mechanism of shiga toxin clustering on membranes. ACS nano (2017) 11:314–24. doi:10.1021/acsnano.6b05706
3. Monks CR, Freiberg BA, Kupfer H, Sciaky N, Kupfer A. Three-dimensional segregation of supramolecular activation clusters in t cells. Nature (1998) 395:82–6. doi:10.1038/25764
4. Schekman R, Orci L. Coat proteins and vesicle budding. Science (1996) 271:1526–33. doi:10.1126/science.271.5255.1526
5. Weikl TR. Dynamic phase separation of fluid membranes with rigid inclusions. Phys Rev E (2002) 66:061915. doi:10.1103/physreve.66.061915
6. Yolcu C, Deserno M. Membrane-mediated interactions between rigid inclusions: an effective field theory. Phys Rev E (2012) 86:031906. doi:10.1103/physreve.86.031906
7. Park JM, Lubensky T. Interactions between membrane inclusions on fluctuating membranes. J Phys France (1996) 6:1217–35. doi:10.1051/jp1:1996125
8. Weikl T. Fluctuation-induced aggregation of rigid membrane inclusions. Europhys Lett (2001) 54:547–53. doi:10.1209/epl/i2001-00281-7
9. Goulian M, Bruinsma R, Pincus P. Long-range forces in heterogeneous fluid membranes. Europhys Lett (1993) 22:145–50. doi:10.1209/0295-5075/22/2/012
10. Helfrich W, Weikl T. Two direct methods to calculate fluctuation forces between rigid objects embedded in fluid membranes. The Eur Phys J E (2001) 5:423–39. doi:10.1007/s101890170049
11. Golestanian R, Goulian M, Kardar M. Fluctuation-induced interactions between rods on a membrane. Phys Rev E (1996) 54:6725–34. doi:10.1103/physreve.54.6725
12. Sens P, Johannes L, Bassereau P. Biophysical approaches to protein-induced membrane deformations in trafficking. Curr Opin Cel Biol (2008) 20:476–82. doi:10.1016/j.ceb.2008.04.004
13. Fournier JB. Coupling between membrane tilt-difference and dilation: a new “ripple” instability and multiple crystalline inclusions phases. Europhys Lett (1998) 43:725–30. doi:10.1209/epl/i1998-00424-4
14. May S, Ben-Shaul A. Molecular theory of lipid-protein interaction and the lα-hii transition. Biophysical J (1999) 76:751–67. doi:10.1016/s0006-3495(99)77241-3
15. Weikl T, Kozlov M, Helfrich W. Interaction of conical membrane inclusions: Effect of lateral tension. Phys Rev E (1998) 57:6988–95. doi:10.1103/physreve.57.6988
16. Kim K, Neu J, Oster G. Curvature-mediated interactions between membrane proteins. Biophys J (1998) 75:2274–91. doi:10.1016/s0006-3495(98)77672-6
17. Sintes T, Baumgärtner A. Interaction of wedge-shaped proteins in flat bilayer membranes. J Phys Chem B (1998) 102:7050–7. doi:10.1021/jp9807266
18. Biscari P, Bisi F, Rosso R. Curvature effects on membrane-mediated interactions of inclusions. J Math Biol (2002) 45:37–56. doi:10.1007/s002850200142
19. Breidenich M, Netz R, Lipowsky R. The shape of polymer-decorated membranes. Europhys Lett (2000) 49:431–7. doi:10.1209/epl/i2000-00167-2
20. Auth T, Gompper G. Budding and vesiculation induced by conical membrane inclusions. Phys Rev E (2009) 80:031901. doi:10.1103/physreve.80.031901
21. McMahon HT, Boucrot E. Membrane curvature at a glance. J Cel Sci (2015) 128:1065–70. doi:10.1242/jcs.114454
22. Tian A, Baumgart T. Sorting of lipids and proteins in membrane curvature gradients. Biophysical J (2009) 96:2676–88. doi:10.1016/j.bpj.2008.11.067
23. Lou HY, Zhao W, Zeng Y, Cui B. The role of membrane curvature in nanoscale topography-induced intracellular signaling. Acc Chem Res (2018) 51:1046–53. doi:10.1021/acs.accounts.7b00594
24. Shibata Y, Hu J, Kozlov MM, Rapoport TA. Mechanisms shaping the membranes of cellular organelles. Annu Rev Cel Dev Biol (2009) 25:329–54. doi:10.1146/annurev.cellbio.042308.113324
25. Dommersnes P, Fournier J, Galatola P. Long-range elastic forces between membrane inclusions in spherical vesicles. Europhys Lett (1998) 42:233–8. doi:10.1209/epl/i1998-00235-7
26. Schweitzer Y, Kozlov MM. Membrane-mediated interaction between strongly anisotropic protein scaffolds. Plos Comput Biol (2015) 11:e1004054. doi:10.1371/journal.pcbi.1004054
27. Bonazzi F, Weikl TR. Membrane morphologies induced by arc-shaped scaffolds are determined by arc angle and coverage. Biophys J (2019) 116:1239–47. doi:10.1016/j.bpj.2019.02.017
28. Bahrami AH, Lipowsky R, Weikl TR. Tubulation and aggregation of spherical nanoparticles adsorbed on vesicles. Phys Rev Lett (2012) 109:188102. doi:10.1103/physrevlett.109.188102
29. Van Der Wel C, Vahid A, Šarić A, Idema T, Heinrich D, Kraft DJ. Lipid membrane-mediated attraction between curvature inducing objects. Sci Rep (2016) 6:32825–10. doi:10.1038/srep32825
30. Bahrami AH, Raatz M, Agudo-Canalejo J, Michel R, Curtis EM, Hall CK. Wrapping of nanoparticles by membranes. Adv Colloid Interf Sci (2014) 208:214–24. doi:10.1016/j.cis.2014.02.012
31. Bahrami AH, Weikl TR. Curvature-mediated assembly of janus nanoparticles on membrane vesicles. Nano Lett (2018) 18:1259–63. doi:10.1021/acs.nanolett.7b04855
32. Li L, Cheng JX. Coexisting stripe-and patch-shaped domains in giant unilamellar vesicles. Biochemistry (2006) 45:11819–26. doi:10.1021/bi060808h
33. Chen D, Santore MM. Large effect of membrane tension on the fluid–solid phase transitions of two-component phosphatidylcholine vesicles. Proc Natl Acad Sci U S A (2014) 111:179–84. doi:10.1073/pnas.1314993111
34. Xin W, Wu H, Grason GM, Santore MM. Switchable positioning of plate-like inclusions in lipid membranes: Elastically mediated interactions of planar colloids in 2d fluids. Sci Adv (2021) 7:eabf1943. doi:10.1126/sciadv.abf1943
35. Deuling H, Helfrich W. The curvature elasticity of fluid membranes: a catalogue of vesicle shapes. J Phys France (1976) 37:1335–45. doi:10.1051/jphys:0197600370110133500
36. Noruzifar E, Wagner J, Zandi R. Scattering approach for fluctuation-induced interactions at fluid interfaces. Phys Rev E (2013) 88:042314. doi:10.1103/physreve.88.042314
Keywords: vesicle, membrane curvature, rigid disks, elastic energy, monte carlo simulations, simulated annealing, pairwise interactions
Citation: Alizadeh-Haghighi E, Karaei Shiraz A and Bahrami AH (2022) Membrane-mediated interactions between disk-like inclusions adsorbed on vesicles. Front. Phys. 10:1020619. doi: 10.3389/fphy.2022.1020619
Received: 16 August 2022; Accepted: 29 September 2022;
Published: 17 October 2022.
Edited by:
Thomas R. Weikl, Max Planck Institute of Colloids and Interfaces, GermanyReviewed by:
Thorsten Auth, Helmholtz Association of German Research Centres (HZ), GermanyCopyright © 2022 Alizadeh-Haghighi, Karaei Shiraz and Bahrami. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amir H. Bahrami, YmFocmFtaUB1bmFtLmJpbGtlbnQuZWR1LnRy
†These authors contributed equally to this work and share first authorship
‡ORCID ID: Amir H. Bahrami, orcid.org/0000-0001-5841-2516
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.