Magnetic anisotropy-controlled vortex nano-oscillator for neuromorphic computing

Chiral magnetic vortex has shown great potential for high-density magnetic storage, modern telecommunication and computation devices, thanks to its topological stability and rich dynamic behaviours. Particularly, the synchronization of magnetic vortex nano-oscillators leads to the emergence of fascinating collective phenomena used for microwave generator and neuromorphic computing. In this work, by means of micromagnetic simulations, we create stable chiral magnetic vortices by exploiting the chiral coupling principle and study the gyrotropic motion of the vortex core under spin-transfer torques. The gyrotropic oscillation frequency can be tuned by injecting spin-polarised current as well as the change of the magnetic anisotropy in the vortex area, resulting from the modification of the vortex confine potential and the size of the vortex core. Two vortex nano-oscillators can be synchronized wherein the synchronization state can be modulated by the spin-polarised current and the magnetic anisotropy. Moreover, we demonstrate that the magnetic anisotropy can modify the synchronization patterns when integrating six vortices into an oscillator network, making it potentially serve as an oscillator-based neural network. Our work provides a new route to constructing a flexible oscillator network for neuromorphic computing hardware.

Introduction

Polar vortex magnetic texture has nonlinear spin swirling alignment with nontrivial topology. The unique magnetic configuration occurs as a result of the energy competition between various interactions, including magnetic exchange interaction, dipolar interaction, and importantly, the antisymmetric Dzyaloshinskii-Moriya interaction (DMI) [1–3]. The magnetic vortex, usually with nanoscale dimensions, can have superior stability thanks to the topological protection, and is less prone to defect pinning, which enables the efficient displacement with a low electric current [4]. The driving current can be as low as 10⁶ A/m² which is five orders of magnitude lower than the current required for domain-wall motion [5]. These properties help to realize excellent spintronic devices for high-density data storage, non-volatile logic operation and nanoscale microwave generator [6, 7]. Moreover, the particle-like characteristic of the magnetic vortex enables the potential application as magnetic synapses [8]. The local manipulation of creation, motion and deletion of magnetic vortices have been applied to mimic the potentiation and depression behaviours of biological synapses, thus showing great promises for artificial neural networks [9–11].

The magnetic vortex has rich dynamic behaviours with a broad frequency range from 0.1–100 GHz [12–14]. Response dynamics of magnetic vortices under external fields can be classified into two modes: breath mode and gyration mode. On one hand, the dynamical shrinkage/expansion of the vortex texture can be manipulated by perpendicular a. c. Magnetic field [15, 16], a. c. Current [17], or spin-orbital torques [17, 18]. On the other hand, since the inherent dynamics of magnetic vortex is gyrotropic, self-sustained magnetic oscillation can be obtained via spin transfer torques that compensate the intrinsic magnetic damping, which suggests great potential for applications in spin-torque nano-oscillators [13, 14, 19, 20]. The radio-frequency oscillation gives an electric power output in the pico-watt to nano-watt range [21, 22], which can be further enhanced by placing the nano-oscillators in arrays or networks. In such nano-oscillators, the interactions between the individual vortex nano-oscillator result in the phase locking, with all nano-oscillators oscillating in a common frequency, termed as synchronization [23]. Synchronization between magnetic nano-oscillators usually occurs as a result of exchange interactions in close proximity [24, 25], long-range dipolar coupling [14, 23, 26, 27], propagating spin waves [28] or emitted power through microwave currents [29]. The phase locking can act as an ‘anchor’ to stablise the self-sustained oscillations that is crucial for radio-frequency applications. More importantly, the nonlinear dynamics of synchronized magnetic nano-oscillators enables the development of neuromorphic computing architectures, particularly associative memories with information encoding in the individual phases of large scale arrays of interacting nano-oscillators [14]. Intercorrelated magnetic vortex oscillators provide extended possibilities to embrace the dynamical nature of the brains through interactions [14, 30–32], aiming to solve complex problems efficiently within small networks. The synchronization can also mimic the periodic spiking and synaptic communication of neurons. A coupled network of spin-torque nano-oscillators can learn to perform computational tasks through synchronization, for applications in speech, pattern recognition, where each synchronization pattern can be used directly as an output for the neural networks [31, 33]. Therefore, finding an efficient way to manipulate the synchronization is crucial for magnetic vortex oscillator-based neuromorphic computing devices.

The nonlinear dynamics of magnetic vortex oscillators results in easy adaption of their frequencies to the external stimuli or other associative oscillators. The modified dynamics of individual oscillator can in turn influence the synchronization [14], and hence large varieties of synchronization patterns can be obtained when different external stimuli are implemented. Indeed, magnetic field and spin-polarised current have been reported to successfully tune the dynamic properties of magnetic vortex nano-oscillators [19, 20, 34, 35]. Since the oscillation frequency depends on the vortex potential energy, the magnetic anisotropy of the vortex region, which directly influences the magnetic anisotropy energy, can provide a new route to modulating the oscillation dynamics. In experiment, the magnetic anisotropy can be readily modified via voltage controlled perpendicular magnetic anisotropy (VCMA) effect [36–39].

In this work, using micromagnetic simulation, we introduce magnetic anisotropy as a degree of freedom to manipulate the oscillation dynamics and the synchronization of magnetic vortices. The vortex structure for a single oscillator is generated through chiral coupling principle between adjacent regions with in-plane (IP) and out-of-plane (OOP) anisotropy inside a magnetic vortex, and is stabilised via interfacial DMI. Although magnetic vortex can be formed and the oscillation and synchronization phenomena can be realized without DMI [12, 34, 40, 41], the presence of DMI, on the other hand, has been reported to obtain a large frequency and can protect the magnetic texture of the magnetic vortex under a large spin current, thus making the vortex more stable and favouring the development of microwave signal generator [42]. Also, DMI can help to realize small magnetic nano-oscillators (as small as 10 nm) [43, 44]. The DMI-stabilised chirally coupled nanomagnets have been experimentally demonstrated to realize current-driven domain-wall logic, synthetic antiferromagnets and Ising-like artificial spin ices [45–48]. Here, by altering the magnetic anisotropy of the vortex region from IP to OOP, i.e. by increasing the value of magnetic anisotropy constant, we show that the oscillation frequency of a magnetic vortex increases significantly. This magnetic anisotropy-dependence of the oscillation dynamics can be used to modulate the synchronization of two vortex oscillators, based on which we design an oscillator network which is capable of programming synchronization configurations used for pattern recognition. As compared to the spin-current-based vortex oscillator reported previously, here magnetic anisotropy is introduced as a new degree of freedom to tune the dynamics, and the mechanism for dynamics modulation is explained in a more comprehensive way. Moreover, the spin current and the magnetic anisotropy can be combined to tune the synchronization configuration and potentially provide extended flexibility for neuromorphic computing.

Methods

To study the oscillation dynamics of the magnetic vortex, micromagnetic simulations were carried out with the MuMa×3 code [49] using a computation box with 2 × 2 × 1 nm³ discretization. The MuMax3 utilises the Landau– Lifshitz–Gilbert–Slonczewski (LLG) equation as the basic formalism for describing the low-energy magnetisation dynamics (for details, see Appendix A). The magnetic parameters are taken from the experimentally reported chirally coupled nanomagnet based on Pt/Co/AlOx multilayer, with a saturation magnetisation M_S = 1.0 MA/m, exchange constant A = 16 pJ/m, interfacial DMI constant D = −1.5 mJ/m⁻² favouring left-handed chirality, uniaxial anisotropy constant of the OOP region K₀ = 7.03 × 10⁵ J/m², and Gilbert damping constant α = 0.01. A circular region with a diameter of 100 nm (named as vortex region hereafter) is embedded inside the computation box with a fixed OOP magnetic anisotropy (named as OOP region hereafter) to form the vortex-like magnetic texture. To reach the vortex-like magnetic texture, the magnetisation in the OOP region is set to the +z direction, while the magnetisation in the vortex region is set to its opposite direction, after which the system is relaxed. Self-sustained oscillation of the vortex core is then obtained by injecting a spin polarised current along the +z direction in the vortex region. The x component of the average magnetisation (M_Vx) in the vortex region, which is closely correlated to the oscillation of the core, is used to illustrate the dynamic behaviour of the vortex [50]. The oscillation frequency is obtained from the frequency spectra converted via fast Fourier transformation (FFT) on the time-dependent M_Vx with the simulation running over a period of 150 ns. To study the influence of anisotropy on the oscillation frequency, the magnetic anisotropy constant of the vortex region is varied from 0. To study the synchronization phenomena. Several vortices are separated with each other by a certain distance to create a network. The synchronization spectra are obtained by superimposing the frequency spectra of each single vortex. When mutual phase-locking occurs, the spectra exhibit a strengthened intensity with a common shared peak, otherwise separated peaks with much weaker intensities are observed. All the simulations are performed at zero absolute temperature without considering the thermal magnetisation fluctuations.

Results and discussions

Single oscillator

We first consider the dynamics of a single vortex. As shown in Figure 1, a circular region with variable magnetic anisotropy (vortex region) is embedded in a slab with a fixed uniaxial OOP anisotropy (OOP region). When the uniaxial magnetic anisotropy constant of the vortex region (K_V) is initially set to be 0, the vortex region has an IP anisotropy, and the chiral vortex magnetic texture is stabilised by the interfacial DMI: H_DM = –D_ij · (m_i × m_j) where D_ij denotes the DMI vector of interfacial-type DMI, and the DMI energy is given by $U_{DMI}=D\int dV\left(m_z\frac{\delta m_x}{\delta x}-m_x\frac{\delta m_z}{\delta x}+m_z\frac{\delta m_y}{\delta y}-m_y\frac{\delta m_z}{\delta y}\right)$. Unlike the symmetric exchange interaction that favours collinear alignment of magnetic moments, DMI prefers an orthogonal arrangement between the neighbouring spins [45], and here in the Pt/Co/AlO_x system it gives a fixed left-handed chirality determined by the negative sign of the Dzyaloshinskii vector D_ij. Hence, the chiral coupling generates skyrmion-like spin texture in the vortex region which induces a core pointing along the OOP direction opposite to that in the outside OOP regions [23, 50]. The equilibrium position of the core in the absence of external stimulus is located in the geometry centre of the vortex region for a relatively large DMI strength (|D_ij|≥0.75 mJ/m²) [50] (Figure 1A). When the DMI strength is too small, the equilibrium position of the core is at a finite distance away from the centre, whereas the vortex texture may turn into helical state for a large DMI strength [50, 51]. In order to stimulate the gyrotropic motion of the vortex core with STT, a spin-polarised current is perpendicularly injected in the vortex region. The self-sustained oscillation can only be obtained when the current is injected here in the +z direction, while the current injected in the -z direction breaks the balance between the forces (Figure 1B). Due to the rapid dissipation of the injected current and the much lower SOT current-to-spin conversion efficiency cf. the STT current-to-spin conversion efficiency [52, 53], the SOT spin current generated in Pt is negligible as compared to the spin current generated via STT and not considered in our structure. In order to quickly reach the steady precession state, a preset process is needed [54–56], which is done here by a applying a magnetic field of 5 mT parallel to the plane to preset the vortex core away from the geometry centre. The magnetic field is then removed. If there is no external stimulus, the vortex core relaxes back to the centre following a damped gyrotropic trajectory (black curve in Figure 2A and left inset of Figure 2B). In the presence of STT, the energy dissipation can be counter-balanced by injecting a continuous spin-polarised current in the plain normal direction (z direction) through an OOP magnetized top layer via a magnetic tunnelling junction in adjacent to the magnetic disk in experiments (Figure 1B). When the current density J is above a threshold, self-sustained oscillation of the core with a finite distance away from the geometry centre can be obtained (red curve in Figure 2A and middle inset in Figure 2B). As shown by the snapshots taken from different time for the oscillation at J = 5.5 × 10⁸ A/m² (insets of Figure 2A), all vortex cores keep the same distance away from the geometry centre. Figure 2B shows the spectra for oscillation frequency as a function of spin current J when K_V = 0. The oscillation frequency increases with the increase of J, while a larger current (above 1.35 × 10⁹ A/m²) destroys the self-sustained oscillation, leading to the collapse of the vortex structure (blue curve in Figure 2A and right inset of Figure 2B). When K_V increases to 4 × 10⁵ J/m³, the frequency of the whole spectra increases and the modulation of oscillation frequency occurs at a higher current (Figure 2C). The detailed mechanism for the modulation in oscillation frequency will be discussed later.

FIGURE 1

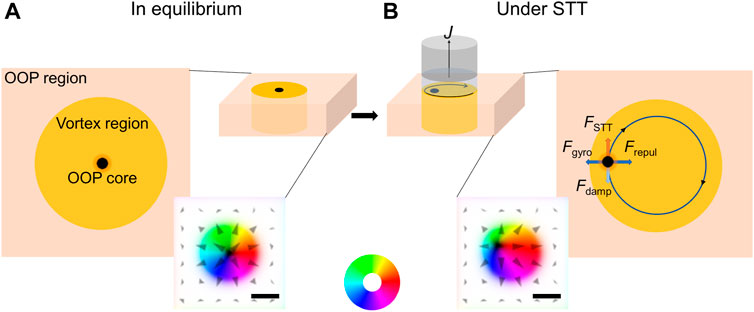
FIGURE 1. Schematic illustration of a magnetic vortex structure where circular vortex regions with tunable anisotropy are surrounded by regions with fixed out-of-plane (OOP) anisotropy and a core with out-of-plane magnetisation is induced: (A) in equilibrium and (B) in oscillation under spin-polarised current. The insets show the magnetisation configuration of the simulated area. Magnetisation along the +z and–z direction is indicated in white and black, while the magnetisation direction in the vortex region is given by the colour wheel. Scale bar: 50 nm.

FIGURE 2

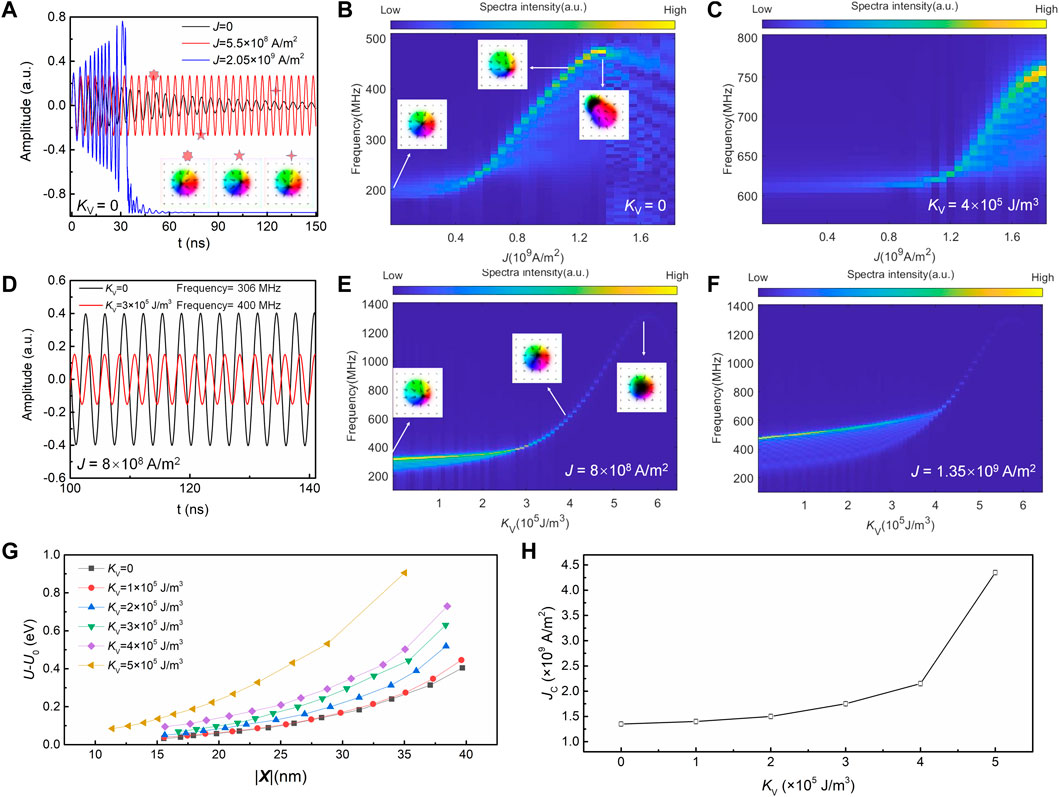
FIGURE 2. (A) Oscillation amplitudes of x component of average magnetisation in the vortex when the spin polarised current J = 0 (black), J = 5.5 × 10⁸ A/m² (red) and J = 2.05 × 10⁹ A/m² (blue). Dependence of oscillation frequency on J for (B) the anisotropy constant of vortex region K_V = 0 and (C) K_V = 4 × 10⁵ J/m³. (D) Oscillation amplitudes of x component of average magnetisation in the vortex region when K_V = 0 (black) and K_V = 3 × 10⁵ J/m³ (red) for J = 8 × 10⁸ A/m². Dependence of oscillation frequency on K_V for (E) J = 8 × 10⁸ A/m² and (F) J = 1.35 × 10⁹ A/m². (G) Dependence of the potential energy (U) on the variation of the core displacement (|X|) at different K_V values. (H) The change of upper limit current density (J_C) for the self-sustained oscillation with the change in K_V.

Note that the required STT current density (10⁸–10⁹ A/m²) is much lower than the spin-orbital-torque (SOT) current density (10¹¹ A/m²) in a similar structure [57] which is due to the following reasons: First, the charge-to-spin conversion efficiency in the STT (around 0.5 in Pt/Co system [52]) is usually higher as compared to SOT (around 0.1 in Pt [53]). Second, the spin current drives a gyrotropic motion of magnetic oscillator around the equilibrium spin texture, while the SOT switching needs to overcome the magnetic anisotropy and rotate the magnetisation for 180°. So the oscillation spin current density is lower than that for switching the magnetisation. Meanwhile, we have not considered the pinning effect which may increases the required spin current density in the real devices.

To study the influence of magnetic anisotropy on the dynamic behaviour of a single vortex, we fix the electric current J = 8.0 × 10⁸ A/m² and vary the magnetic anisotropy constant K_V from 0. When K_V is equal to 0, due to chiral coupling the vortex region forms a stable skyrmion-like spin texture with a small OOP core (left inset of Figure 2E) as a result of exchange singularity [23, 50]. The self-sustained oscillation, as shown in Figure 2D (curve in black for K_V = 0), has a constant amplitude with a fixed period of 32.6 ns, corresponding to a frequency of 306 MHz. With the increase of K_V, the oscillation frequency first increases slowly when K_V <3 × 10⁵ J/m³, and then increases drastically when K_V >3 × 10⁵ J/m³ (Figure 2E). Meanwhile, the size of the vortex core, as shown in the middle and right inset of Figure 2E (for K_V = 4 × 10⁵ J/m³), undergoes a significant expansion. The red oscillation curve in Figure 2D (representing the oscillation at K_V = 3 × 10⁵ J/m³), as compared to the black curve (K_V = 0) has a shorter oscillation period (25 ns) with a larger frequency (400 MHz). The oscillation amplitude, which is proportional to the average magnetisation of the vortex region, also decreases, due to the expansion of the core region and the reduction of the IP magnetised region. Interestingly, when K_V is beyond a critical point of ∼5.8 × 10⁵ J/m³, the spectra intensity gradually vanishes, indicating the breakdown of the self-sustained oscillation. As shown in the right inset of Figure 2E, the size of OOP core enlarges to be almost equal to the vortex region when K_V = 5.8 × 10⁵ J/m³, resulting in the annihilation of the vortex structure. A similar phenomenon is observed when J is increased to 13.5 × 10⁸ A/m² (Figure 2F), where the frequency increases less rapidly with the increasing of K_V, with a peak reaching at a similar K_V = 5.8 × 10⁵ J/m³ before the vortex structure collapses. The annihilation of the vortex structure due to the modification of magnetic anisotropy has been realized experimentally through VCMA effects [36, 37, 58, 59], where a well-defined IP anisotropy in the radial vortex region is crucial for maintaining the noncolinear spin texture of vortex structure through DMI. When K_V increases, the antisymmetric DMI is gradually taken over by the symmetric exchange interaction, while the latter favours a colinear and parallel spin alignment between adjacent regions, which eventually results in the collapse of the noncolinear vortex spin texture.

To further understand the tunable dynamic behaviour of the vortex oscillation under the influence of J and K_V, we refer to the centre-of-mass dynamics of the magnetic vortex oscillator, which has been well-modelled by the single collective variable Thiele equation [60–62].

$\mathit{G}\times \frac{d\mathit{X}}{dt}+\frac{\partial U\left(\mathit{X}\right)}{\partial \mathit{X}}+\alpha D\frac{d\mathit{X}}{dt}+F_{STT}=0(1)$

The first term represents the gyrotropic force (also termed as Magnus force), where $\mathit{G}=-\frac{4\pi Q{\mu }_{0}d{M}_S}{\gamma }{\mathit{e}}_z$ is the gyrovector, with skyrmion number Q = ±1 for isolated skyrmion. M_S is the saturation magnetisation, d is the film thickness, $\gamma$ is the gyromagnetic ratio, ${\mu }_0$ is the vacuum permeability and ${\mathit{e}}_z$ is the unit vector. The rigid profile of the vortex core is described by its position X = X (x(t), y(t)) in the plane, and its velocity is given by $\frac{d\mathit{X}}{dt}$. The gyrotropic force is radial outward which primarily acts to expel the core to the outer shell of the vortex [62]. The second term represents the repulsive (or restoring) force which originates from the edge effect: when the core moves close to the boundary of the vortex structure, the magnetic charges distributed at the cylindrical side wall will generate a centripetal confine potential U (X) to regulate the core inside the vortex region [63]. As can be seen from the form, this second term $\frac{\partial U\left(\mathit{X}\right)}{\partial \mathit{X}}$ represents a conservative force acting on the vortex core that is derived from the total free energy of the system [13]. The edge-induced repulsive force together with the remanent gyrotropic force provide the centripetal force to sustain the circular motion of the core [54], as illustrated in Figure 1B. The last two terms in Eq. (1) represent the damping force and spin transfer forces, respectively [54]. The spin polarised current perpendicular to the layers results in a torque force on the vortex core, which can be balanced by the dissipative force, and, in overall, they jointly support orbital motion of the vortex core [23]. It is worthwhile to mention that Eq. (1) describes an intrinsically non-Newtonian dynamics, which means that the response of the vortex core to a conservative force is gyrotropic, i.e. in a direction perpendicular to the force, instead of accelerating in a direction collinear with the force. This gyrotropic dynamics therefore underpins the persistent oscillations of the vortex core under the four different contributions [13], as depicted in Figure 1B.

We first consider the role of spin polarised current J. As discussed above, the confining potential provides an inward radial repulsive force (second term in Eq. 1) to confine the vortex inside the vortex region, while the spin transfer torque (STT force, the last term in Eq. (1)) arising from J tends to drive the core outward toward the edge, so does the gyrotropic force (first term in Eq. (1)). With the increase in J, the radius of the steady state orbit increases (as shown in the middle inset of Figure 2B in comparison with the left inset), as a larger dissipation rate is required to compensate the increase in spin torques [50]. The gyrotropc force increases as well to counterbalance the increase in the STT force, resulting in the increase in the velocity of the core $\frac{d\mathit{X}}{dt}$ [64]. This entails higher oscillation frequencies above the intrinsic resonance frequency (Figures 2B,C). On the other hand, the radial inward repulsive force has an upper limit because of the limited confine potential U (X) [62]. The increase in J therefore leads to a growing outward net force to push the core towards the boundary. When J reaches a critical value, the core cannot be confined inside the vortex region and eventually be pushed out (as shown in the right inset of Figure 2B), leading to the collapse of the vortex spin texture [62]. To more effectively confine the core and maintain the vortex, the upper critical current density should be increased. This can be done by increasing the edge potential using nanoring with high perpendicular magnetic anisotropy [62]. As discussed below, the increase in the K_V in the vortex region can serve as an alternative stabiliser to increase the confine potential.

We now turn to understand the role of K_V on the oscillation dynamics. The intrinsic oscillation frequency is determined by the curvature of the confining potential at the equilibrium core position in the absence of STT force [50]. We first calculate the relative potential energy of system (U-U₀, where U₀ is the potential energy when the core is in the centre) with respect to different core distances from the centre (|X|) at different K_V values in the absence of STT (Figure 2G). Since the equilibrium position of the core is in the centre, U-U₀ increases when the core displaces away from the centre. Interestingly, when K_V increases, U-U₀ increases more rapidly with displacement, especially at large K_V values, indicating that the potential energy becomes higher when the core has the same displacement. This, on one hand, directly increases the slope of the curve as observed in Figure 2G, corresponding to an enhanced $\frac{\partial U\left(\mathit{X}\right)}{\partial \mathit{X}}$, and causes the increase of the repulsive force (second term in Eq. 1). The increase in the repulsive force can in turn be counterbalanced by increasing the gyrotropic force (first term in Eq. 1) when J is fixed, as long as self-sustained oscillation is maintained. The increase in gyrotropic force eventually leads to the increase in the velocity $\frac{d\mathit{X}}{dt}$ and hence the oscillation frequency of the vortex core increases (Figures 2E,F). On the other hand, the increase in confine potential caused by the increase in K_V requires a larger STT current to maintain the oscillation, which elevates the upper limit of the critical current density (J_C) for the self-sustained oscillation before the annihilation occurs. Figure 2H shows the J_C under a 150 ns running interval: when K_V increases from 0 to 5 × 10⁵ J/m³, J_C increases monotonically from 1.35 × 10⁹ A/m² to 4.25 × 10⁹ A/m².

The potential energy is closely correlated to the evolution of the vortex structure. As mentioned above, the vortex core expands rapidly when K_V increases (insets in Figure 2E), which leads to the shrinkage of the noncolinear spin region. The enlarged OOP core and the reduced vortex area make it more difficult for the core to move, and thus a higher exchange energy is needed, which results in the increase in the overall potential energy and the oscillation frequency. Hence, the tuning of the oscillation frequency by K_V is understood.

Synchronization of two oscillators

We next turn to investigate how the spin current and magnetic anisotropy affect the mutual interactions for a couple of oscillators. In the simulation, two vortex oscillators are placed with a given distance, while the J and K_V are varied (Figure 3A). As mentioned earlier, interacting non-identical oscillators with different intrinsic frequencies tend to undergo resonance at a common frequency when their oscillation frequencies are within an certain locking range, resulting in the synchronization phenomena [23, 50]. Figure 3B shows the synchronization spectra as a function of the current density for a pair of oscillators (named as one and 2) with a 100 nm distance when K_V = 0. When the spin polarised current of oscillator 1 (J₁) is fixed at 8 × 10⁸ A/m² and that of oscillator 2 (J₂) varies from 0 to 1.25 × 10⁹ A/m², two distinct frequency peaks are observed at small J₂, and then they merge into one peak with an enhanced intensity, undergoing synchronization when J₂ ranges between 6 × 10⁸ A/m² and 1 × 10⁹ A/m². The merged peak diverge again when J₂ > 1 × 10⁹ A/m². In order to study the influence of magnetic anisotropy on the synchronization, the magnetic anisotropy constant in the vortex region of oscillator 1 (K_V1) is fixed at 1 × 10⁵ J/m³ while that of oscillator (K_V2) varies from 0 to 3 × 10⁵ J/m³. We first study the case where different currents are injected into the two oscillators: J₁ (8 × 10⁸ A/m²) ≠ J₂ (6.5 × 10⁸ A/m²). As shown in Figure 3C, the two oscillators synchronize with each other when K_V2 ranges from 6 × 10⁴ J/m³ to 1.5 × 10⁵ J/m³. The synchronized region ΔK_V2, defined as the length of the interval between the starting and ending point of K_V2 of the synchronization region, is estimated to be 0.9 × 10⁵ J/m³. It is noteworthy that the frequency spectra and synchronization region keep unchanged when the two different oscillators swap their relative positions, as shown in Figure 3D, indicating that the contributions from two oscillators are switchable with regard to position.

FIGURE 3

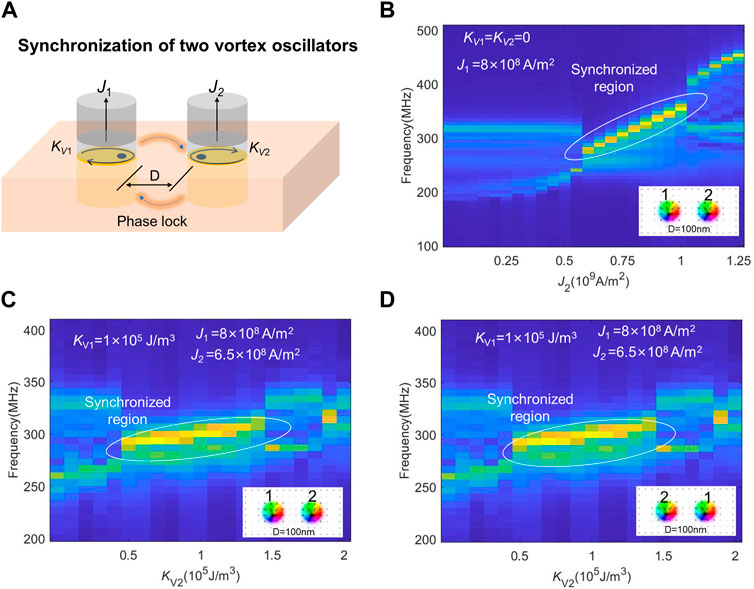
FIGURE 3. (A) Schematic illustration for the synchronization of two non-identical vortex nano-oscillators with varying spin polarised current density (J) and anisotropy constant of the vortex region (K_V). (B) Synchronization frequency spectra for two oscillators separated by a distance of 100 nm with varying J when the K_V for both oscillators are 0. The injected current density for oscillator 1 (J₁) is fixed at 8 × 10⁸ A/m² while that of oscillator 2 (J₂) is varied. (C) Synchronization frequency spectra for two oscillators separated by a distance of 100 nm with varying K_V when the J for both oscillators are fixed at 8 × 10⁸ A/m². The anisotropy constant of the vortex region for oscillator 1 (K_V1) is fixed at 1 × 10⁵ J/m³ while that of oscillator 2 (K_V2) is varied. (D) Synchronization frequency spectra when oscillator one and two switch their positions.

The synchronization of nano-oscillators in this system can be realized through propagating spin waves or dipolar interactions [14], where the distance between the oscillators plays a crucial role to determine the synchronization stability and coupling strength [50]. Here, to better understand the distance effect, the separation between the oscillators is varied from 60 to 150 nm. Figures 4A–C show the synchronization spectra with a distance of 60, 80 and 100 nm, respectively, for J₁ (8 × 10⁸ A/m²) ≠ J₂ (6.5 × 10⁸ A/m²) (termed as ‘nonequal case’) and Figures 4D–F show the respective spectra for J₁ (8 × 10⁸ A/m²) = J₂ (8 × 10⁸ A/m²) (termed as ‘equal case’). In both cases, the synchronization range ΔK_V2 decreases with the increase in separation distance (Figure 4G), which could be attributed to the decay in coupling strength [50]. Interestingly, the decrease in ΔK_V2 for the nonequal case is much more rapid than the equal case: at a small distance of 60 nm, ΔK_V2 of the nonequal case is similar to that of the equal case, both having a large synchronization interval of ∼3 × 10⁵ J/m³; in contrast, when the distance increases to 150 nm, ΔK_V2 for the equal case keeps at a sizable value 1.7 × 10⁵ J/m³, while for the nonequal case it decays to 0.1 × 10⁵ J/m³. This stark difference is a clear indication of the faster decay for the overall strength of oscillator interaction with the increase in separation distance when the two current densities are different, which could be due to the relative contribution from different source of interaction (dipolar interaction or spin wave propagation) changes when the current density and distance are different.

FIGURE 4

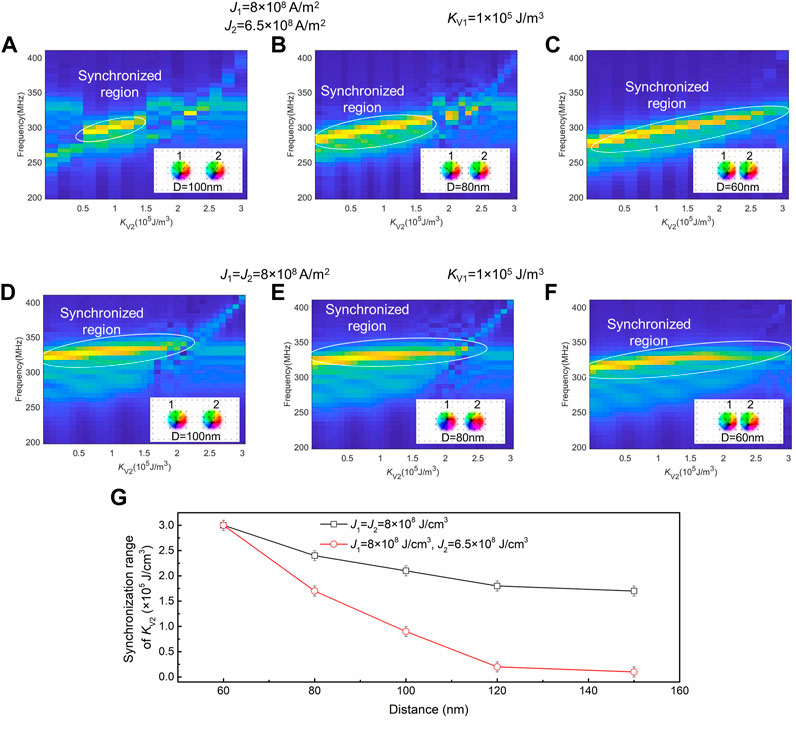
FIGURE 4. (A–C) Influence of oscillator distance on the synchronization frequency spectra for two oscillators with varying anisotropy (K_V) when the current density (J) for the two oscillators are nonequal (J₁ = 8 × 10⁸ A/m² and J₂ = 6.5 × 10⁸ A/m²): (A) D = 100 nm (B) D = 80 nm and (C) D = 60 nm. The anisotropy constant of the vortex region for oscillator 1 (K_V1) is fixed at 1 × 10⁵ J/m³ while that of oscillator 2 (K_V2) is varied. (D–F) Influence of oscillator distance on the synchronization frequency spectra for two oscillators with varying anisotropy (K_V) when the current density (J) for both oscillators are equal (J₁ = J₂ = 8 × 10⁸ A/m²): (A) D = 100 nm (B) D = 80 nm and (C) D = 60 nm. The anisotropy constant of the vortex region for oscillator 1 (K_V1) is fixed at 1 × 10⁵ J/m³ while that of oscillator 2 (K_V2) is varied. (G) The change of synchronization range with varying the distance of the two oscillators. The error bar is taken as the interval of the variation of the anisotropy constant in the simulation.

Synchronization of multiple oscillators for neural networks

The synchronization of nano-oscillators is of great interest for neuromorphic computing. As a proof-of-concept demonstration, we design a neural network comprised of six vortex oscillators (A, B and 1, 2, 3, 4) (Figure 5A), and explore the ability of coupled vortex nano-oscillators to work as a model system for neuromorphic computing via anisotropy control. Figure 5B shows the schematic for the intercorrelation between oscillators, neurons, inputs and outputs. The oscillators are separated from each other with a certain distance, with 1–4 (output neurons) surrounded by A and B (input oscillators), so that all oscillators can be mutually interacted with each other. As shown below, the change in K_V of the two input oscillators can modify the synchronization configurations of the whole neural network, mimicking the conversion of encoded inputs to classified output signals via programmable weighting mechanism [30]. Hence, the synchronization configuration between the six oscillators is interpreted here as the output signal.

FIGURE 5

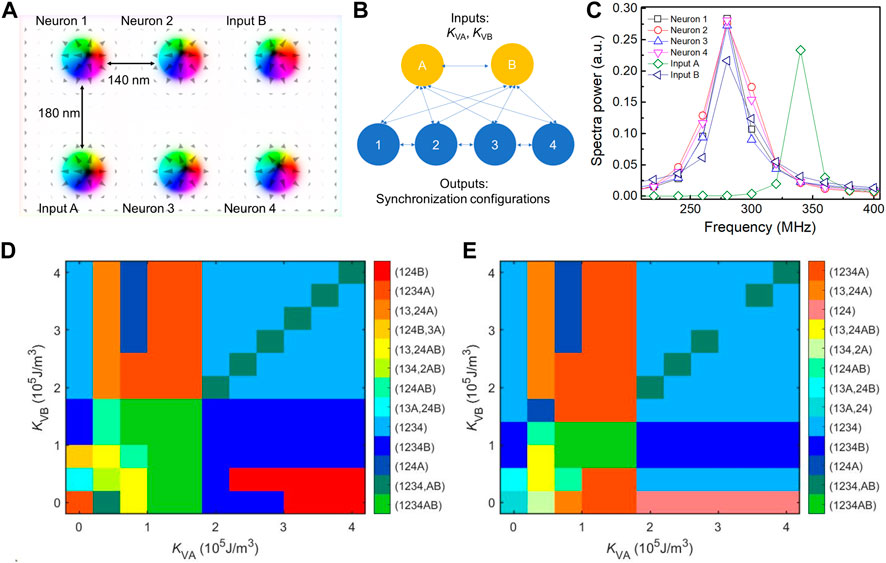
FIGURE 5. (A) Configuration of the neural network with two input oscillators (A,B) and four neuron oscillators (1,2,3,4). (B) Schematic illustration for the intercorrelation between the oscillators, neurons, inputs and outputs. (C) The output frequencies of the oscillators, for the case of K_VA = 2.4 × 10⁵ J/m³, K_VB = 1.6 × 10⁵ J/m³. J and for all the oscillators are fixed at 8 × 10⁸ A/m², and K_V for neurons 1,2,3,4 are 1.1 × 10⁵ J/m³, 0.8 × 10⁵ J/m³, 1.2 × 10⁵ J/m³, 0.9 × 10⁵ J/m³, respectively. (D) 2D synchronization map with varying K_VA and K_VB when J_B = 8 × 10⁸ A/m². (E) 2D synchronization map with varying K_VA and K_VB when J_B = 9 × 10⁸ A/m².

To begin with, we set up one input signal using the magnetic anisotropy of either oscillator A or B (K_VA or K_VB), and then increase to two input signals by adopting both K_VA and K_VB. The current density J for all the oscillators is set to be 8 × 10⁸ A/m², and the K_V for the output neurons 1, 2, 3, and four are set to be 1.1 × 10⁵ J/m³, 0.8 × 10⁵ J/m³, 1.2 × 10⁵ J/m³, 0.9 × 10⁵ J/m³, respectively. When K_VA and K_VB are varied from 0 to 4 × 10⁵ J/m³, the frequency patterns of the neural network are converged and allocated to different synchronization configurations appearing at different K_VA and K_VB values. For example, when K_VA = 2.4 × 10⁵ J/m³ and K_VB = 1.6 × 10⁵ J/m³, five oscillators (1, 2, 3, 4 and B) are synchronized into one common frequency (Figure 5C) during a running period of 50 ns, corresponding to an output synchronization code of (1234B). A total of 13 output patterns are obtained, as represented by 13 different colours organised into a two-dimensional colour map (Figure 5D), while only up to six configurations can be recognised with one input (either K_VA or K_VB). Interestingly, when J_B changes to 9 × 10⁸ A/m², the synchronization pattern is modified (Figure 5E): the synchronization codes (124B), (134, 2AB) and (124B, 3A) that appear in the case of J_B = 8 × 10⁸ A/m² now disappear, while another three codes (13A, 24), (134, 2A) and (124) emerge. This indicates that current can work jointly with the magnetic anisotropy to modulate the output synchronization patterns.

In the proof-of-concept neural network shown in Figure 5, we have six oscillators, each having independent current density and magnetic anisotropy. The neural network hence has twelve variables. Two variables (K_VA and K_VB) can act as inputs and tune the synchronization patterns as the outputs (Figure 5D). We also found that the synchronization pattern changes when the current density of one oscillator is changed (Figures 5E vs 5D), indicating that the output depends on the combination of all variables. When two variables (K_VA, K_VB) are defined as the inputs, the combination of the rest ten variables (K_V1 … K_V4, J₁, … , J₄ and J_A, J_B) can be defined as the weight and bias. When these ten parameters are changed, the weight and bias are changed, resulting in a different output pattern (as shown in Figures 5D,E). Therefore, we can train the neural network to get a target output pattern by adjusting the weight and bias parameters via a learning rule.

Conclusion

We propose a spintronic nano-oscillator based on the tunable magnetic anisotropy of a polar vortex magnetic structure. The increase of the magnetic anisotropy in the vortex region, which modifies the confine potential and the topology of the magnetic vortex texture, brings the oscillation frequency to higher values and increase the upper critical limit of the spin-polarised currents. The change in oscillation frequency can modify the synchronization between a pair of oscillators. Making use of the tunable dynamics, we show that a designed network of tunable magnetic vortex oscillators can serve as a model system for neuromorphic computing, which is capable to recognise different output synchronization configurations when the magnetic anisotropies of vortices are encoded as inputs. We also found that the output patterns are modified when the spin-polarised current changes. Since both the magnetic anisotropy and spin-polarised current can be experimentally tuned, our model system possesses great potential as a hardware for neuromorphic computing with large flexibility.

Data availability statement

The data presented in the study are deposited in the Zendo repository, accession number: https://zenodo.org/deposit/7149131.

Author contributions

ZLu and CY conceived and designed the project. CY, ZLi, and ZLu performed the simulation. CY and YW analysed the simulation data. CY and ZLu worked on the manuscript. All authors are contributed to the discussion on the data and revision of the manuscript.

Acknowledgments

The authors acknowledge funding from the National Natural Science Foundation of China (Grant Nos. 51731001, 52201287, 52271160, 11975035, 11805006, 11675006, 52027801, 52111530236), the National Key Research and Development Program of China (Grant No. 2021YFB3500300) and the China-Germany Collaboration Project (M-0199). CY acknowledges the funding from Boya postdoctoral fellowship, Peking University for support of the research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Appendix A: Basic formalism of the Mumax software

The MuMax3 code is based on the low-energy magnetisation dynamics in strong ferromagnets, which is well-described by the Landau–Lifshitz–Gilbert–Slonczewski (LLG) equation [65, 66]

$\frac{d\mathit{m}}{dt}=-\gamma {\mu }_0\mathit{m}\times H_{eff}+\alpha \mathit{m}\times \frac{d\mathit{m}}{dt}+\sigma J\mathit{m}\times \left(\mathit{m}\times \mathit{p}\right)(\mathrm{A1})$

where m = $\frac{\overrightarrow{M}}{M_S}$ is the normalised spin vector, M_S is the saturation magnetisation, γ is the gyromagnetic ratio, ${\mu }_0$ is the vacuum permeability, p is the electron polarization unit vector, J is the current density. The first term on the right hand side describes the precession of magnetisation induced by the local effective magnetic field

$H_{eff}=-\frac{1}{{\mu }_0{M}_S}\frac{\delta U}{\delta \mathit{m}}(\mathrm{A2})$

where U is the free energy of the system. $H_{eff}$ includes the perpendicular uniaxial magnetic anisotropy field, the exchange field, the demagnetization field, and field induced by the interfacial form of the Dzyaloshinskii–Moriya interaction (DMI). In a continuous magnetization model, the DMI energy is given by

$U_{DMI}=D\int dV\left(m_z\frac{\delta m_x}{\delta x}-m_x\frac{\delta m_z}{\delta x}+m_z\frac{\delta m_y}{\delta y}-m_y\frac{\delta m_z}{\delta y}\right)(\mathrm{A3})$

where D is the DMI constant and m_x, m_y, m_z are the components of the normalized magnetization vector m. The second term on the right is the Gilbert term representing viscous damping, where α is the Gilbert damping constant. The third term on the right hand is the Slonczewski term describing the torque arising from the coupling between the local magnetisation and the spin-polarised current flowing perpendicular to the film plane.

References

1. Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, et al. Skyrmion lattice in a chiral magnet. Science (80) (2009) 323:915–9. doi:10.1126/science.1166767

CrossRef Full Text | Google Scholar

2. Yu XZ, Onose Y, Kanazawa N, Park JH, Han JH, Matsui Y, et al. Real-space observation of a two-dimensional skyrmion crystal. Nature (2010) 465:901–4. doi:10.1038/nature09124

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Malozemoff A, Slonczewski J. Magnetic domain walls in bubble materials. New York: Academic Press (1979). doi:10.1016/C2013-0-06998-8

CrossRef Full Text | Google Scholar

4. Karakas V, Gokce A, Habiboglu AT, Arpaci S, Ozbozduman K, Cinar I, et al. Observation of magnetic radial vortex nucleation in a multilayer stack with tunable anisotropy. Sci Rep (2018) 8:7180. doi:10.1038/s41598-018-25392-x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Guo JH, Xia J, Zhang X, Pong PWT, Zhou Y. A ferromagnetic skyrmion-based nano-oscillator with modified perpendicular magnetic anisotropy. Phys Lett A (2021) 392:127157. doi:10.1016/j.physleta.2021.127157

CrossRef Full Text | Google Scholar

6. Tokura Y, Kanazawa N. Magnetic skyrmion materials. Chem Rev (2021) 121:2857–97. doi:10.1021/acs.chemrev.0c00297

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Fert A, Cros V, Sampaio J. Skyrmions on the track. Nat Nanotechnol (2013) 8:152–6. doi:10.1038/nnano.2013.29

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Nagaosa N, Tokura Y. Topological properties and dynamics of magnetic skyrmions. Nat Nanotechnol (2013) 8:899–911. doi:10.1038/nnano.2013.243

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Song KM, Jeong J-S, Pan B, Zhang X, Xia J, Cha S, et al. Skyrmion-based artificial synapses for neuromorphic computing. Nat Electron (2020) 3:148–55. doi:10.1038/s41928-020-0385-0

CrossRef Full Text | Google Scholar

10. Li S, Kang W, Huang Y, Zhang X, Zhou Y, Zhao W. Magnetic skyrmion-based artificial neuron device. Nanotechnology (2017) 28:31LT01. doi:10.1088/1361-6528/aa7af5

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yu Z, Shen M, Zeng Z, Liang S, Liu Y, Chen M, et al. Voltage-controlled skyrmion-based nanodevices for neuromorphic computing using a synthetic antiferromagnet. Nanoscale Adv (2020) 2:1309–17. doi:10.1039/D0NA00009D

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Choe S-B, Acremann Y, Scholl A, Bauer A, Doran A, Stöhr J, et al. Vortex core-driven magnetization dynamics. Science (80) (2004) 304:420–2. doi:10.1126/science.1095068

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Garcia-Sanchez F, Sampaio J, Reyren N, Cros V, Kim J. A skyrmion-based spin-torque nano-oscillator. New J Phys (2016) 18:075011. doi:10.1088/1367-2630/18/7/075011

CrossRef Full Text | Google Scholar

14. Locatelli N, Hamadeh A, Abreu Araujo F, Belanovsky AD, Skirdkov PN, Lebrun R, et al. Efficient synchronization of dipolarly coupled vortex-based spin transfer nano-oscillators. Sci Rep (2015) 5:17039. doi:10.1038/srep17039

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mochizuki M. Spin-wave modes and their intense excitation effects in skyrmion crystals. Phys Rev Lett (2012) 108:017601. doi:10.1103/PhysRevLett.108.017601

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Moon K-W, Kim D-H, Je S-G, Chun BS, Kim W, Qiu ZQ, et al. Skyrmion motion driven by oscillating magnetic field. Sci Rep (2016) 6:20360. doi:10.1038/srep20360

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Litzius K, Lemesh I, Krüger B, Bassirian P, Caretta L, Richter K, et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat Phys (2017) 13:170–5. doi:10.1038/nphys4000

CrossRef Full Text | Google Scholar

18. Woo S, Song KM, Han H-S, Jung M-S, Im M-Y, Lee K-S, et al. Spin-orbit torque-driven skyrmion dynamics revealed by time-resolved X-ray microscopy. Nat Commun (2017) 8:15573. doi:10.1038/ncomms15573

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Demidov VE, Urazhdin S, Ulrichs H, Tiberkevich V, Slavin A, Baither D, et al. Magnetic nano-oscillator driven by pure spin current. Nat Mater (2012) 11:1028–31. doi:10.1038/nmat3459

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Saha S, Flauger P, Abert C, Hrabec A, Luo Z, Zhou J, et al. Control of damping in perpendicularly magnetized thin films using spin-orbit torques. Phys Rev B (2020) 101:224401. doi:10.1103/PhysRevB.101.224401

CrossRef Full Text | Google Scholar

21. Abreu Araujo F, Darques M, Zvezdin KA, Khvalkovskiy AV, Locatelli N, Bouzehouane K, et al. Microwave signal emission in spin-torque vortex oscillators in metallic nanowires: Experimental measurements and micromagnetic numerical study. Phys Rev B (2012) 86:064424. doi:10.1103/PhysRevB.86.064424

CrossRef Full Text | Google Scholar

22. Kumar D, Barman S, Barman A. Magnetic vortex based transistor operations. Sci Rep (2015) 4:4108. doi:10.1038/srep04108

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zaspel CE. Synchronization in alternating linear chains of vortex-based spin-torque oscillators. J Magn Magn Mater (2019) 492:165683. doi:10.1016/j.jmmm.2019.165683

CrossRef Full Text | Google Scholar

24. Mancoff FB, Rizzo ND, Engel BN, Tehrani S. Phase-locking in double-point-contact spin-transfer devices. Nature (2005) 437:393–5. doi:10.1038/nature04036

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ruotolo A, Cros V, Georges B, Dussaux A, Grollier J, Deranlot C, et al. Phase-locking of magnetic vortices mediated by antivortices. Nat Nanotechnol (2009) 4:528–32. doi:10.1038/nnano.2009.143

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Slavin AN, Tiberkevich VS. Nonlinear self-phase-locking effect in an array of current-driven magnetic nanocontacts. Phys Rev B (2005) 72:092407. doi:10.1103/PhysRevB.72.092407

CrossRef Full Text | Google Scholar

27. Hrabec A, Křižáková V, Pizzini S, Sampaio J, Thiaville A, Rohart S, et al. Velocity enhancement by synchronization of magnetic domain walls. Phys Rev Lett (2018) 120:227204. doi:10.1103/PhysRevLett.120.227204

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kaka S, Pufall MR, Rippard WH, Silva TJ, Russek SE, Katine JA. Mutual phase-locking of microwave spin torque nano-oscillators. Nature (2005) 437:389–92. doi:10.1038/nature04035

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Grollier J, Cros V, Fert A. Synchronization of spin-transfer oscillators driven by stimulated microwave currents. Phys Rev B (2006) 73:060409. doi:10.1103/PhysRevB.73.060409

CrossRef Full Text | Google Scholar

30. Martins L, Jenkins AS, Alvarez LSE, Borme J, Böhnert T, Ventura J, et al. Non-volatile artificial synapse based on a vortex nano-oscillator. Sci Rep (2021) 11:16094. doi:10.1038/s41598-021-95569-4

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Nikonov DE, Csaba G, Porod W, Shibata T, Voils D, Hammerstrom D, et al. Coupled-oscillator associative memory array operation for pattern recognition. IEEE J Explor Solid-state Comput Devices Circuits (2015) 1:85–93. doi:10.1109/JXCDC.2015.2504049

CrossRef Full Text | Google Scholar

32. Vodenicarevic D, Locatelli N, Abreu Araujo F, Grollier J, Querlioz D. A nanotechnology-ready computing scheme based on a weakly coupled oscillator network. Sci Rep (2017) 7:44772. doi:10.1038/srep44772

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Romera M, Talatchian P, Tsunegi S, Abreu Araujo F, Cros V, Bortolotti P, et al. Vowel recognition with four coupled spin-torque nano-oscillators. Nature (2018) 563:230–4. doi:10.1038/s41586-018-0632-y

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Pribiag VS, Krivorotov IN, Fuchs GD, Braganca PM, Ozatay O, Sankey JC, et al. Magnetic vortex oscillator driven by d.c. spin-polarized current. Nat Phys (2007) 3:498–503. doi:10.1038/nphys619

CrossRef Full Text | Google Scholar

35. Yakata S, Tanaka T, Kiseki K, Matsuyama K, Kimura T. Wide range tuning of resonant frequency for a vortex core in a regular triangle magnet. Sci Rep (2013) 3:3567. doi:10.1038/srep03567

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Shiota Y, Nozaki T, Bonell F, Murakami S, Shinjo T, Suzuki Y. Induction of coherent magnetization switching in a few atomic layers of FeCo using voltage pulses. Nat Mater (2012) 11:39–43. doi:10.1038/nmat3172

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bhattacharya D, Razavi SA, Wu H, Dai B, Wang KL, Atulasimha J. Creation and annihilation of non-volatile fixed magnetic skyrmions using voltage control of magnetic anisotropy. Nat Electron (2020) 3:539–45. doi:10.1038/s41928-020-0432-x

CrossRef Full Text | Google Scholar

38. Wang W-G, Li M, Hageman S, Chien CL. Electric-field-assisted switching in magnetic tunnel junctions. Nat Mater (2012) 11:64–8. doi:10.1038/nmat3171

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Tan AJ, Huang M, Avci CO, Büttner F, Mann M, Hu W, et al. Magneto-ionic control of magnetism using a solid-state proton pump. Nat Mater (2019) 18:35–41. doi:10.1038/s41563-018-0211-5

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Yamada K, Kasai S, Nakatani Y, Kobayashi K, Kohno H, Thiaville A, et al. Electrical switching of the vortex core in a magnetic disk. Nat Mater (2007) 6:270–3. doi:10.1038/nmat1867

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Van Waeyenberge B, Puzic A, Stoll H, Chou KW, Tyliszczak T, Hertel R, et al. Magnetic vortex core reversal by excitation with short bursts of an alternating field. Nature (2006) 444:461–4. doi:10.1038/nature05240

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Chen S, Zhang S, Zhu Q, Liu X, Jin C, Wang J, et al. Effect of Dzyaloshinskii-Moriya interaction on the magnetic vortex oscillator driven by spin-polarized current. J Appl Phys (2015) 117:17B720. doi:10.1063/1.4915476

CrossRef Full Text | Google Scholar

43. Butenko AB, Leonov AA, Bogdanov AN, Rößler UK. Theory of vortex states in magnetic nanodisks with induced Dzyaloshinskii-Moriya interactions. Phys Rev B (2009) 80:134410. doi:10.1103/PhysRevB.80.134410

CrossRef Full Text | Google Scholar

44. Kwon HY, Kang SP, Wu YZ, Won C. Magnetic vortex generated by Dzyaloshinskii–Moriya interaction. J Appl Phys (2013) 113:133911. doi:10.1063/1.4799401

CrossRef Full Text | Google Scholar

45. Luo Z, Dao TP, Hrabec A, Vijayakumar J, Kleibert A, Baumgartner M, et al. Chirally coupled nanomagnets. Science (80) (2019) 363:1435–9. doi:10.1126/science.aau7913

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Luo Z, Hrabec A, Dao TP, Sala G, Finizio S, Feng J, et al. Current-driven magnetic domain-wall logic. Nature (2020) 579:214–8. doi:10.1038/s41586-020-2061-y

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wang RF, Nisoli C, Freitas RS, Li J, McConville W, Cooley BJ, et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature (2006) 439:303–6. doi:10.1038/nature04447

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Colbois J, Hofhuis K, Luo Z, Wang X, Hrabec A, Heyderman LJ, et al. Artificial out-of-plane Ising antiferromagnet on the kagome lattice with very small farther-neighbor couplings. Phys Rev B (2021) 104:024418. doi:10.1103/PhysRevB.104.024418

CrossRef Full Text | Google Scholar

49. Vansteenkiste A, Leliaert J, Dvornik M, Helsen M, Garcia-Sanchez F, Van Waeyenberge B. The design and verification of MuMax3. AIP Adv (2014) 4:107133. doi:10.1063/1.4899186

CrossRef Full Text | Google Scholar

50. Zeng Z, Luo Z, Heyderman LJ, Kim J-V, Hrabec A. Synchronization of chiral vortex nano-oscillators. Appl Phys Lett (2021) 118:222405. doi:10.1063/5.0048672

CrossRef Full Text | Google Scholar

51. Luo YM, Zhou C, Won C, Wu YZ. Effect of Dzyaloshinskii–Moriya interaction on magnetic vortex. AIP Adv (2014) 4:047136. doi:10.1063/1.4874135

CrossRef Full Text | Google Scholar

52. Rajanikanth A, Kasai S, Ohshima N, Hono K. Spin polarization of currents in Co/Pt multilayer and Co–Pt alloy thin films. Appl Phys Lett (2010) 97:022505. doi:10.1063/1.3460910

CrossRef Full Text | Google Scholar

53. Keller S, Mihalceanu L, Schweizer MR, Lang P, Heinz B, Geilen M, et al. Determination of the spin Hall angle in single-crystalline Pt films from spin pumping experiments. New J Phys (2018) 20:053002. doi:10.1088/1367-2630/aabc46

CrossRef Full Text | Google Scholar

54. Zhou S, Zheng C, Chen X, Liu Y. Skyrmion-based spin-torque nano-oscillator in synthetic antiferromagnetic nanodisks. J Appl Phys (2020) 128:033907. doi:10.1063/5.0013402

CrossRef Full Text | Google Scholar

55. Zhang S, Wang J, Zheng Q, Zhu Q, Liu X, Chen S, et al. Current-induced magnetic skyrmions oscillator. New J Phys (2015) 17:023061. doi:10.1088/1367-2630/17/2/023061

CrossRef Full Text | Google Scholar

56. Guo JH, Xia J, Zhang XC, Pong PWT, Wu YM, Chen H, et al. .A ferromagnetic skyrmion-based nano-oscillator with modified profile of Dzyaloshinskii-Moriya interaction. J Magn Magn Mater (2020) 496:165912. doi:10.1016/j.jmmm.2019.165912

CrossRef Full Text | Google Scholar

57. Liu L, Lee OJ, Gudmundsen TJ, Ralph DC, Buhrman RA. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys Rev Lett (2012) 109:096602. doi:10.1103/PhysRevLett.109.096602

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Schott M, Bernand-Mantel A, Ranno L, Pizzini S, Vogel J, Béa H, et al. The skyrmion switch: Turning magnetic skyrmion bubbles on and off with an electric field. Nano Lett (2017) 17:3006–12. doi:10.1021/acs.nanolett.7b00328

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Srivastava T, Schott M, Juge R, Křižáková V, Belmeguenai M, Roussigné Y, et al. Large-voltage tuning of dzyaloshinskii–moriya interactions: A route toward dynamic control of skyrmion chirality. Nano Lett (2018) 18:4871–7. doi:10.1021/acs.nanolett.8b01502

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Thiele AA. Steady-state motion of magnetic domains. Phys Rev Lett (1973) 30:230–3. doi:10.1103/PhysRevLett.30.230

CrossRef Full Text | Google Scholar

61. Huber DL. Dynamics of spin vortices in two-dimensional planar magnets. Phys Rev B (1982) 26:3758–65. doi:10.1103/PhysRevB.26.3758

CrossRef Full Text | Google Scholar

62. Feng Y, Xia J, Qiu L, Cai X, Shen L, Morvan FJ, et al. .A skyrmion-based spin-torque nano-oscillator with enhanced edge. J Magn Magn Mater (2019) 491:165610. doi:10.1016/j.jmmm.2019.165610

CrossRef Full Text | Google Scholar

63. Liu Y, Hou Z, Gliga S, Hertel R. Influence of the dynamic dipolar interaction on the current-induced core switch in vortex pairs. Phys Rev B (2009) 79:104435. doi:10.1103/PhysRevB.79.104435

CrossRef Full Text | Google Scholar

64. Das D, Muralidharan B, Tulapurkar A. Skyrmion based spin-torque nano-oscillator. J Magn Magn Mater (2019) 491:165608. doi:10.1016/j.jmmm.2019.165608

CrossRef Full Text | Google Scholar

65. Zhang S, Wang J, Zheng Q, Zhu Q, Liu X, Chen S, et al. Current-induced magnetic skyrmions oscillator. New J Phys (2015) 17:023061. doi:10.1088/1367-2630/17/2/023061

CrossRef Full Text | Google Scholar

66. Feng Y, Xia J, Qiu L, Cai X, Shen L, Morvan FJ, et al. .A skyrmion-based spin-torque nano-oscillator with enhanced edge. J Magn Magn Mater (2019) 491:165610. doi:10.1016/j.jmmm.2019.165610

CrossRef Full Text | Google Scholar