- Department of Physics, University of Surrey, Guildford, United Kingdom
Einstenium-254 (Z = 99, N = 155), can be prepared as a target for research into nuclear reaction studies. This work presents structure and reaction calculations of Es-254 and Ca-48 (Z = 20, N = 28), using the Skyrme-(Time-Dependent)-Energy-Density-Functional formalism. The reaction calculations show the initial parts of the heavy-ion reaction between the nuclei which, depending on the interaction parameters, can lead to capture to a compound nucleus of element 119. For collisions with the spherical 48Ca impinging on the tip of the prolate 254Es no fusion events are found. For collisions where the calcium approaches the belly of the einsteinium, capture occurs with the compound nucleus outlasting the lifetime of the calculation, indicating a possible fusion candidate. For a sample center-of-mass collision energy of 220 MeV, slightly non-central collisions, up to an impact parameter of 1 fm, also form long-lived compound nuclei.
1 Introduction
Einsteinium-254 (Z = 99, N = 155, J = 7 ground state [1]), with a half-life of 276 days [2], is a transuranic actinide which can be produced in sufficient quantities to prepare as a target in nuclear reaction experiments. Previous experimental studies of heavy-ion induced reactions on Es-254 include with 16,18O and 22Ne beams [3, 4], as well as in searches for superheavy elements with Ca-48 [5].
The theoretical study of the best reaction mechanisms and beam-target combinations is an important part of superheavy element (SHE) research, going hand-in-hand with the experimental efforts to understand SHE formation [6–8]. While many theoretical methods are used, as shown and referenced in the just-cited arcticles, the present work concentrates on calcualtions using the microscopic time-dependent Hartree-Fock (TDHF) method. This has the benefit of being relaticely parameter-free, at least in the reaction theory, using parameterised effective interactions fitted at the level of (mainly) ground state structure and nuclear matter properties. TDHF is the basic mean-field picture of nuclear dynamics and includes some significant effects not found in all theories, like the ability of the reacting nuclear systems to exhibit significant rearrangement of matter while accounting for shell structure and some correlation effects (e.g. through the Pauli principle). On the other hand, the mean-field approximation misses explicit two-body or higher collision terms, and is computationally costly enough to make extensive systematic calcualtions difficult. The method has previously been applied to study the formation of superheavy elements through fusion [9], and in particular the reaction of Bk-249 with Ca-48 and Ti-50 [10, 11]. More recently, the addition of projection methods after TDHF has allowed detailed studies of multinucleon transfer as a method for creating SHE [12].
In this contribution, we study the reaction 48Ca + 254Es using TDHF at energies above the Coulomb barrier to map out the reaction dynamics, and point researchers to futher possibilities for improved calculations and experiments in this area.
2 Formalism
2.1 Hartree-fock and time-depdendent hartree-fock
The calculations presented in this work use the Skyrme energy density functional, with static Hartree-Fock (HF) calculations to produce the ground state and time-dependent Hartree-Fock calculations for the calculation of collisions. Full details of the energy density functional and the methods of the static and time-dependnet Hartree-Fock calculcations can be found in the papers desribing the Sky3D code used here [13, 14]. For further details of the Skyrme density functional method in general, the reader is refered to review article of Bender [15]. Several useful reviews for the use of TDHF (and extensions) give further details of TDHF calculations for collisions [16–18].
2.2 Frozen hartree fock
As well as the standard HF + TDHF methods, we use the Frozen Hartree-Fock (FHF) approximation to give an intuitive picture of the heavy-ion fusion barrier. FHF, using the Skyrme interaction, involves forming a combined system of two nuclei, each obtained via its own static HF calculations. The two nuclei are placed a defined distance apart, and the total energy of the system calculated using the combined densities. Subtracting the energies of the individual nuclei gives the FHF potential [17]
By placing the nuclei at a range of separations
3 Static properties
In order to understand the starting point of the dynamics between 254Es and other nuclei, the static ground state properties of 254Es were studied.
In order to understand the choice of effective interaction on the ground state properties, the following Skyrme parameterisations were used in the ground state study: SV-min [21], a force whose parameters were fitted by a least-squares minimization of an error function based on observables with small correlation effects; SLy5 [22], a widely-used parameter set which includes a fit to the equation of state for pure neutron matter, intended to work well far from stability, and at densities away from saturation; and SLy5t [23] which adds perturbatively the Skyrme tensor force on top of the SLy5 parameters. The tensor terms can rearrange the single particle levels and so influence the shell gaps [24], and hence the ground state shapes of nuclei, including (in the context of the present study) potential fission daughter products.
Figure 1 shows the convergence of the total (binding) energy, and the shape parameters β2 and γ during the Hartree-Fock minimization procedure to determine the ground state. It is seen that in particular, the shape of the nucleus is very consistent between the forces, with a quadrupole deformation paramter of β2 ≃ 0.18 with small triaxial deformation parameter γ ≃ 5o. We note that odd protons and odd neutrons usually induce a small triaxiality on top of the typically axial even-even core they orbit.
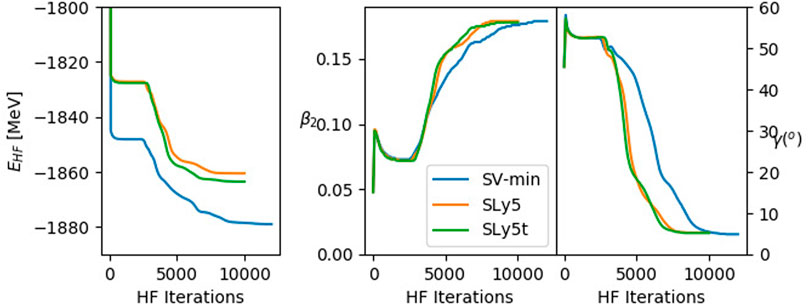
FIGURE 1. Convergence of total energy (left frame), β2 quadrupole deformation (middle frame) and γ deformation (right frame) as a function of Hartree-Fock iteration for three different Skyrme parameterisations, as discussed in the text.
The HF + TDHF calculations omit pairing. This is a common approximation for TDHF calculations, partly for expedition, and partly since the pairing dynamics are not considered to be prominent in fusion reactions where the massive rearangement of nucleons in large amplitude collective motion is the primary concern. However, pairing can have a significant effect on ground state deformations, which can have significant effects on fusion, and so we asses the effect of omitting pairing in the odd-odd 254Es nucleus by turning on pairing for the neighbouring even-even sytems with A = 254. Using the code ev8 [25] to allow shape-constrained calculations, the ground states of 254Cf (Z = 98) and 254Fm (Z = 100) were obtained with Skyrme parameterisation SLy4, and BCS pairing. In both cases the energy minima gave a similar shape to each other, and to that of the Sky3D calculation of 254Es using SLy5t without pairing. The minimum energy occurs at ⟨Q20⟩ = 978fm2 for the SLy5 force using ev8 with pairing, compared to ⟨Q20⟩ = 1036 fm2 for SLy5t using Sky3d without pairing, and we conclude that the lack of pairing makes little effect on the ground state shape.
4 Inter-ion potentials
Using the frozen Hartree-Fock approximation as described in Section 2 inter-ion potentials have been calculated to show the dependence of direction of approach on the reaction dynamics. Ground states for 254Es and 48Ca were calcualted with the SLy5t interaction and placed on a coordinate space grid with grid spacing in each cartesian direction of 1 fm. Each nucleus was moved in units of 1 fm, with centres along each coordinate axis to produce potential energies for approach along each of these three directions. For each of the three sets of data, spline interpolation is used to produce a smooth potential.
Figure 2 shows the curves for separation along each Cartesian axis. The x-direction is labelled “tip” since the tip of the deformed einsteinium nucleus is oriented in this direction. The y- and z-directions are labelled “belly-y” and “belly-z” respectively. One can see from the plot that the two belly curves are nearly equal since the einsteinium nucleus is nearly axially symmetric (while the calcium is spherical).
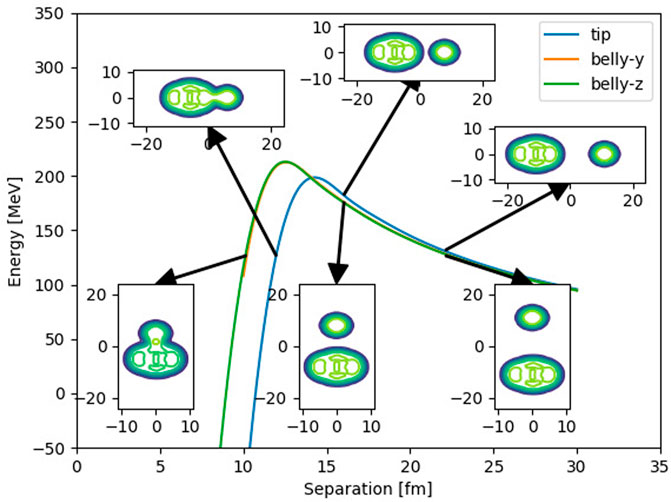
FIGURE 2. Frozen Hartree-Fock potentials of 254Es+48Ca showing orientation-dependence of potential barriers. Snapshots of the density slices in the z = 0 plane are shown in insets whose axis units are fm. The interaction used is SLy5t.
From the spline interpolation, the barrier heights are Vtip = 198.6 MeV in the tip direction and Vbelly = 213.0 MeV in the belly direction. As a general rule, these should be upper limits of the fusion barrier in TDHF calcualtions which allows for dynamic lowering of the barrier through shape changes as the nuclei approach. On the other hand, sub-barrier nucleon tranfer can actually increase the barrier if the neutron-proton asymmetry in one of the projectiles is very large [26]. In the present case, a lowering should be expected.
5 Time-dependent hartree-fock calculations
5.1 Approaching the tip
A systematic series of calculations from below the barrier up to high energies were peformed for reactions in which the spherical Ca-48 nucleus approaches the tip of Es-254 with an impact parameter b = 0. All calculations in this orientation were performed on a coordinate space grid of nx × ny × nz = 64 × 30 × 32 fm with 1 fm grid spacing. The centres of the nuclei were initialised at a separation of 24 fm.
Figure 3 shows a summary of all calculations in which the 48Ca nucleus approaches the tip of the 254Es. The following regions of reaction behaviour are observed:
• ECM < 193 Mev: 48Ca approaches 254Es but does not touch. Some Coulomb excitation seen through distortion of nuclei
• 193 MeV
• 250 MeV
• 500 MeV

FIGURE 3. Snapshots of time-dependent evolution of collisions of 48Ca coming in from the right to the tip of 254Es (left). Time runs to the right. Time separation between frames is 100 fm/c. Calculations are shown as far as a final frame where two clear separated nuclei are seen. The center-of-mass energies for each row are, starting from to top 180 MeV, 190 MeV, 192 MeV, 193 MeV, 194 MeV, 195 MeV, 196 MeV, 198 MeV, 200 MeV, 202 MeV, 220 Mev, 250 MeV, 300 MeV, 400 MeV, 500 MeV, 600 MeV, 800 MeV.
For no configuration was a fusion event found on the timescale of the simulation, with a many-nucleus final state in all cases. Curiously the longest lifetime found was quite far above the barrier at 500 MeV. We term the separation events quasifission rather than true fission because of the timescale and the apparent retention of a target-projectile cluster structure in the compound nucleus.
5.2 Approaching the belly
As with the tip-approaching calculations, a series of TDHF simulations of collisions where the impinging 48Ca approached the side or belly of the 254Es nucleus was performed. These calculations were performed in a nx × ny × nz = 30 × 30 × 64 fm box with grid spacing 1 fm. A summary figure of snapshots of the time-evolution of the collisions is shown in Figure 4.
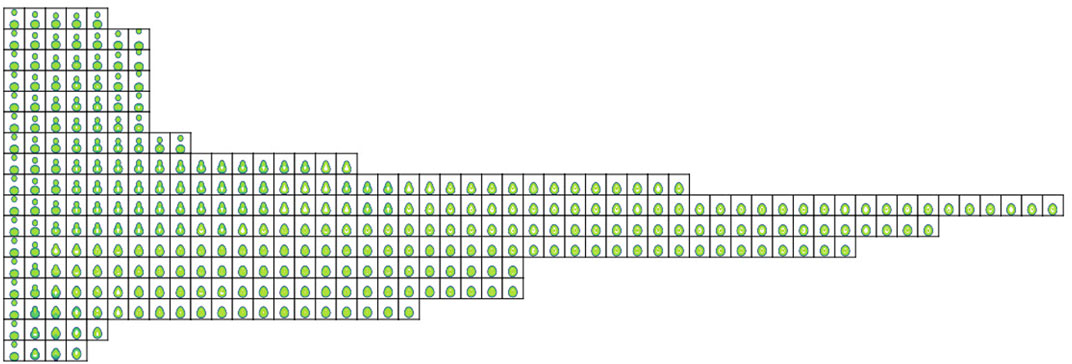
FIGURE 4. Snapshots of time-dependent evolution of collisions of 48Ca coming in from above to the belly of 254Es (left). Time runs to the right. Time separation between frames is 100 fm/c. The center-of-mass collision energy in each row is, starting from the top row, 180 MeV, 190 MeV, 200 MeV, 204 MeV, 206 MeV, 208 MeV, 210 MeV, 213 MeV, 216 MeV, 220 MeV, 240 MeV 350 MeV, 400 MeV, 500 MeV, 600 MeV, 700 MeV, 800 MeV.
For these side collisions, it is seen that.
• for ECM ≤ 210 MeV (compare with 213 MeV for the FHF barrier) the 48Ca does not fuse with the 254Es, though as one gets closer to the higher energy range, there is an increased contact time.
• for 213 MeV
• for ECM ≥700 MeV a fragment is immediately emitted from the CN, leaving a hot residue of a lighter system.
Similarly to the tip calculations, for energies slightly above the barrier, the impinging 48Ca nucleus attaches to the side of the 254Es and the CN retains this octupole shape for some time, after which the CN relaxes to a more spherical shape.
The more compact shape afforded by the collision to the belly compared to a collision to the tip is presumably the key factor in the longer lifetime of the compound nucleus, and has been seen in similar TDHF calculations: see e.g. Figure 3 of [9] for collisions of 48Ca + 238U at ECM = 203 MeV, where the tip configuration CN survives for around 3 zs and the belly configuration for around 15 zs. The longer lifetimes seen in 48Ca + 254Es may indicate enhanced stability of the Z = 119 CN compared to Cn, perhaps due to enhanced octupole shell gaps.
5.3 Cross-sections
These TDHF calculations alone do not allow a reliable fusion cross section calculation, as the decay of a superheavy CN can proceed through fission or light particle emission at a later time than a TDHF calculation but before any chance of detection of the element. The belly collisions show some amount of capture with an unknown final state, as we do not know without invoking a further theory how the CN will decay. However, we performed belly-orientation calculations with b = 1 fm, b = 2 fm, b = 3 fm and b = 4 fm for ECM = 220 MeV and found capture occuring at b = 1 fm but not b ≥ 2 fm. Thus, we can give an upper estimate of a geometrical capture cross section of σc ≃ πb2 = 4.7 ± 1.6 fm2 where the error indicates the low resolution to which we have determined the upper value of b. Note that this is for belly impingement only, and one would prefer an inclusive cross section integrated across angle, which would require computationally-demanding extensive further calculations. Given that the impingements to the tip do not fuse, the complete TDHF prediction would be lowered averaging over all orientations, assuming that intermediate angle configurations do not exhibit a structural effect in which capture is enhanced with respect to the belly configuration.
This figure of 4.7 fm2 = 4.7 × 10–26 cm2 can be compared to the upper limit of 3 × 10–31 cm2 for superheavy element fragments with spontaneous fission half-lives from fractions of a day to a few months, from the 1985 paper of Lougheed et al. [5].
For a more developed prediction, TDHF can be combined with other methods such a statistical models to predict long-time behaviour of the compound nucleus [27], but such methods are beyong the scope of the work presented here.
6 Conclusion
This study explored the reaction dynamics of 48Ca + 254Es heavy-ion reactions using time-dependent Hartree-Fock. For orientations where the interaction of the spherical calcium nucleus is to the belly of the prolate einsteinium, then the mean-field dynamics show capture to a compound nucleus which lives long enough to give a fused Z = 119 compound nucleus whose ultimate longevity should be understood throguh a suitale theory, such as the statistical model.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/pdstevenson/es254
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work is supported by the UK STFC from grant ST/V001108/1. This work was performed using the DiRAC Data Intensive service at Leicester, operated by the University of Leicester IT Services, which forms part of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The equipment was funded by BEIS capital funding via STFC capital grants ST/K000373/1 and ST/R002363/1 and STFC DiRAC Operations grant ST/R001014/1. DiRAC is part of the National e-Infrastructure.
Acknowledgments
The author would like to thank the University of Surrey for access to its High Performance Computing facility, where testing and development of codes took place. Further calculations made use of STFC DiRAC facilities, as noted in the Funding section.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Nothhelfer S, Albrecht-Schönzart TE, Block M, Chhetri P, Düllmann CE, Ezold JG, et al. Nuclear structure investigations of 253–255Es by laser spectroscopy. Phys Rev C (2022) 105:L021302. Publisher: American Physical Society. doi:10.1103/PhysRevC.105.L021302
2. Ahmad I, Unik JP. Half-life of 254Es. J Inorg Nucl Chem (1975) 37:1851–3. doi:10.1016/0022-1902(75)80900-6
3. Schadel M, Brüchle W, Brügger M, Gaggeler H, Moody KJ, Schardt D, et al. Transfer cross sections from reactions with 254Es as a target. Phys Rev C (1986) 33:1547–50. doi:10.1103/PhysRevC.33.1547
4. Moody KJ, Lougheed RW, Wild JF, Dougan RJ, Hulet EK, Hoff RW, et al. Decay properties of heavy mendelevium isotopes. Nucl Phys A (1993) 563:21–73. doi:10.1016/0375-9474(93)90010-U
5. Lougheed RW, Landrum JH, Hulet EK, Wild JF, Dougan RJ, Dougan AD, et al. Search for superheavy elements using the 48Ca+254Esg reaction. Phys Rev C (1985) 32:1760–3. Publisher: American Physical Society. doi:10.1103/PhysRevC.32.1760
6. Adamian GG, Antonenko NV, Diaz-Torres A, Heinz S. How to extend the chart of nuclides? Eur Phys J A (2020) 56:47. doi:10.1140/epja/s10050-020-00046-7
7. Loveland WD. The synthesis of new neutron-rich heavy nuclei. Front Phys (2019) 7:23. doi:10.3389/fphy.2019.00023
8. Oganessian YT, Utyonkov VK, Super-heavy element research. Rep Prog Phys 78. Publisher: IOP Publishing (2015). p. 036301. doi:10.1088/0034-4885/78/3/036301
9. Umar AS, Oberacker VE. Time-dependent HF approach to SHE dynamics. Nucl Phys A (2015) 944:238–56. doi:10.1016/j.nuclphysa.2015.02.011
10. Umar AS, Oberacker VE, Simenel C. Fusion and quasifission dynamics in the reactions 48Ca + 249Bk and 50Ti + 249Bk using a time-dependent Hartree-Fock approach. Phys Rev C (2016) 94:024605. doi:10.1103/PhysRevC.94.024605
11. Godbey K, Umar AS, Simenel C. Deformed shell effects in Ca-48 + Bk-249 quasifission fragments. Phys Rev C (2019) 100:024610. doi:10.1103/PhysRevC.100.024610, ,
12. Sekizawa K. TDHF theory and its extensions for the multinucleon transfer reaction: A mini review. Front Phys (2019) 7:20. doi:10.3389/fphy.2019.00020
13. Maruhn JA, Reinhard PG, Stevenson PD, Umar AS. The TDHF code Sky3D. Comput Phys Commun (2014) 185:2195–216. doi:10.1016/j.cpc.2014.04.008
14. Schuetrumpf B, Reinhard PG, Stevenson PD, Umar AS, Maruhn JA. The TDHF code Sky3D version 1.1. Comput Phys Commun (2018) 229:211–3. doi:10.1016/j.cpc.2018.03.012
15. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys (2003) 75:121–80. doi:10.1103/RevModPhys.75.121
16. Stevenson PD, Barton MC. Low-energy heavy-ion reactions and the Skyrme effective interaction. Prog Part Nucl Phys (2019) 104:142–64. doi:10.1016/j.ppnp.2018.09.002
17. Simenel C, Umar AS. Heavy-ion collisions and fission dynamics with the time-dependent Hartree–Fock theory and its extensions. Prog Part Nucl Phys (2018) 103:19–66. doi:10.1016/j.ppnp.2018.07.002
18. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys (2016) 88:045004–53. doi:10.1103/RevModPhys.88.045004
19. Umar AS, Oberacker VE. Heavy-ion interaction potential deduced from density-constrained time-dependent Hartree-Fock calculation. Phys Rev C (2006) 74:021601. doi:10.1103/PhysRevC.74.021601
20. Stevenson PD. Internuclear potentials from the Sky3D code. IOPSciNotes (2020) 1:025201. doi:10.1088/2633-1357/ab952a
21. Klüpfel P, Reinhard PG, Bürvenich TJ, Maruhn JA. Variations on a theme by Skyrme: A systematic study of adjustments of model parameters. Phys Rev C (2009) 79:034310. –23. doi:10.1103/physrevc.79.034310
22. Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl Phys A (1998) 635:231–56. doi:10.1016/s0375-9474(98)00180-8
23. Colò G, Sagawa H, Fracasso S, Bortignon P. Spin–orbit splitting and the tensor component of the Skyrme interaction. Phys Lett B (2007) 646:227–31. doi:10.1016/j.physletb.2007.01.033
24. Suckling EB, Stevenson PD. The effect of the tensor force on the predicted stability of superheavy nuclei. EPL (2010) 90:12001. doi:10.1209/0295-5075/90/12001
25. Ryssens W, Hellemans V, Bender M, Heenen PH. Solution of the skyrme-hf+BCS equation on a 3D mesh, II: A new version of the Ev8 code. Comput Phys Commun (2015) 187:175–94. doi:10.1016/j.cpc.2014.10.001
26. Vo-Phuoc K, Simenel C, Simpson EC. Fusion with exotic nuclei using a microscopic approach. EPJ Web Conf (2017) 163:00062. doi:10.1051/epjconf/201716300062
Keywords: nuclear reactions, superheavy elements, time-dependent methods, Skyrme forces, einsteinium
Citation: Stevenson PD (2022) Mean-field simulations of Es-254 + Ca-48 heavy-ion reactions. Front. Phys. 10:1019285. doi: 10.3389/fphy.2022.1019285
Received: 14 August 2022; Accepted: 14 October 2022;
Published: 25 October 2022.
Edited by:
Antonio Di Nitto, University of Naples Federico II, ItalyReviewed by:
Sait Umar, Vanderbilt University, United StatesKyle Samuel Godbey, Facility for Rare Isotope Beams, Michigan State University, United States
Copyright © 2022 Stevenson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Paul D. Stevenson, cC5zdGV2ZW5zb25Ac3VycmV5LmFjLnVr
 Paul D. Stevenson
Paul D. Stevenson