- School of Space Science and Physics, Shandong University, Weihai, China
We theoretically investigate tunable optical absorption properties of photonic crystals containing lossy materials as defects. It is found that a lossy defect can induce one or multiple perfect absorption peaks in the bandgap of photonic crystals and the number of the peaks mainly depends on the thickness of the defect layer. On the one hand, multiple complete absorption peaks can also emerge in the photonic bandgap when multiple lossy defects are inserted within the photonic crystals, and the resonant wavelengths of absorption peaks can be modulated by changing the distances among the defects. On the other hand, the optical absorption away from resonant wavelengths is nearly zero in the whole visible range. Such nanostructures can be used to engineer novel optical devices such as tunable single-channel and multi-channel perfect optical absorbers.
1 Introduction
The media, which can absorb the optical waves strongly, have many important applications, such as photovoltaics, sensors, photodetectors, and imaging [1–7]. Conventional optical absorbers based on bulk materials generally have some shortcomings including fixed material parameters, untunable absorption frequency, and absorption band, which restrict their applications. In recent years, artificial nanostructures attract much attention due to their advantages in realizing tunable optical absorption, where a typical nanostructure is a photonic crystal [6, 7].
Photonic crystals (PCs) are composed of periodic arrangements of materials with different refractive indices, which can be divided into one-dimensional (1D), two-dimensional (2D), or three-dimensional (3D) PCs. Periodic PCs have the photonic bandgap (which can also be called as photonic forbidden gap) so that they can also be named photonic bandgap materials. If defects are inserted into the PCs, defect modes (also named cavity modes) will appear in the photonic bandgap which can induce strong photonic localization [8–11]. On the other hand, the interface mode can also induce photonic localization with special nanostructures, such as photonic heterostructures composed of truncated PCs and thick metallic films [12–15], or different PCs [16]. The enhanced optical absorption can be realized based on the photonic localization in 1D nanostructures [12, 14, 15, 17]. In addition, many 2D and 3D nanostructures are also used to enhance optical absorption such as periodic air holes [18], elliptical nano-disk arrays [19], and metal nanocavity arrays [20]. Compared with 2D and 3D nanostructures, 1D PCs are simpler in the spatial dimension and easier to prepare, so many research works focus on modulating optical properties by 1D nanostructures [21–26] including enhancing optical absorption in PCs containing different defects [26–28]. Currently, the study of perfect absorption in a super wide band is less. In this study, we theoretically demonstrate that single-channel and multi-channel perfect optical absorption can be realized in 1D PCs containing one or multiple lossy defects in the whole visible region which is much larger than the photonic bandgap.
The study is organized as follows. Section 2 describes the tunable optical absorption properties of 1D PCs containing a lossy defect layer. Section 3 describes the tunable optical absorption properties of 1D PCs with multiple lossy defect layers. Finally, the conclusions are drawn in Section 4.
2 Tunable absorption properties of 1D PCs containing a lossy defect layer
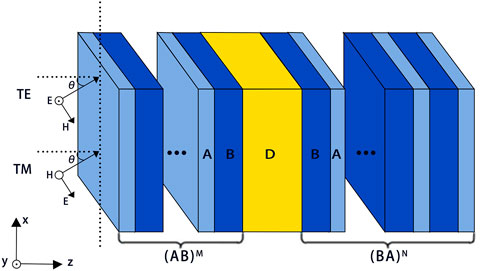
In this section, 1D PC containing a lossy defect layer is considered, which is denoted by (AB)MD(BA)N as is shown in Figure 1, where A and B denote TiO2 and SiO2 with refractive indices of nA = 2.123 and nB = 1.431, respectively [29, 30]. M and N represent periodic numbers of the optical barriers on both sides of defect layer D, respectively. For simplicity, the real part of the refractive index for the lossy defect layer D is identical to that of A, and the imaginary part of its refractive index is denoted by kD. The thicknesses of A and B are kept with dA = 66.24 nm and dB = 98.27 nm, respectively. The thickness of lossy layer D is changed to modulate the absorption properties of the defective PCs.
Based on the transfer matrix method [31], Figure 2A shows the simulated absorption spectra of symmetrical PC (AB)5D (BA)5 with kD = 0.006 and dD = 138.28 nm in the case of normal incidence. It can be seen that the maximum absorptance at the resonant wavelength of 570.65 nm is nearly 0.5. However, the asymmetrical nanostructures are easier to realize complete absorption [32, 33]. Therefore, we select the asymmetrical PC (AB)MD(BA)N to enhance the optical absorption in this study, the thickness of the defect layer D of which is fixed and the periodic number N is larger than M. Figure 2B shows that there is a perfect absorption peak at the wavelength of 570.58 nm in the whole visible region for asymmetrical PC (AB)5D(BA)20 with kD = 0.006 and dD = 138.28 nm. Moreover, by increasing the thickness of defect layer D to dD = 331.86 nm, two perfect absorption peaks at resonant wavelengths of 510.77 nm and 627.06 nm are obtained in the visible region as described in Figure 2C. It is worth noting that the photonic bandgap of the periodic PC (AB)N is from 499.35 nm to 643.74 nm, which is much narrower than the whole visible region. Therefore, the whole visible range can be regarded as a super wide band. Moreover, for the PC with a thicker defect layer, more perfect absorption peaks can be obtained in the visible region. The reason is that thicker lossy defect as the resonant cavity can induce more resonances in the photonic bandgap of the PC.
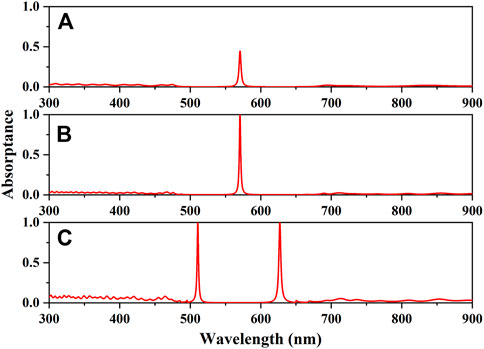
FIGURE 2. Absorption spectra of the PC (AB)MD(BA)N with kD = 0.006. (A) Symmetrical PC (AB)5D(BA)5 with dD = 138.28 nm. (B) Asymmetrical PC (AB)5D(BA)20 with dD = 138.28 nm. (C) (AB)5D (BA)20 with dD = 331.86 nm.
To understand the physical mechanism of the enhanced absorption more clearly, the electric field intensities in different PCs at defect wavelengths are shown in Figure 3, where the blue and red lines denote the intensities of symmetrical PC (AB)5D(BA)5 at the wavelength of 570.65 nm and asymmetrical nanostructure (AB)5D(BA)20 at the wavelength of 570.58 nm, respectively. (AB)5D(BA)20 has larger intensities than those in the former symmetrical PC so it has perfect absorption at the defect wavelength. The reason is that the absorptance is proportional to the electric field intensities in the lossy defect [14]. Moreover, the electric field intensities of (AB)5D(BA)20 with dD = 331.86 nm at the wavelengths of 510.77 nm and 627.06 nm are given in Figure 4A and 4B, respectively. It can be seen that the electric fields are mainly localized within lossy defect layer D.
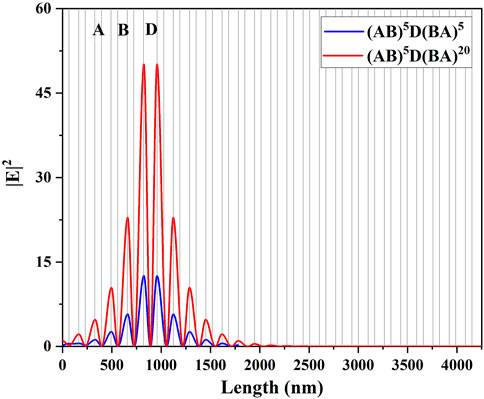
FIGURE 3. Simulated intensities of the electric field at the resonant wavelength of the PC (AB)MD(BA)N. Blue and red lines describe (AB)5D(BA)5 at the wavelength 570.65 nm and (AB)5D(BA)20 at the wavelength 570.58 nm, respectively. All parameters are the same as those used in Figure 2A and 2B.
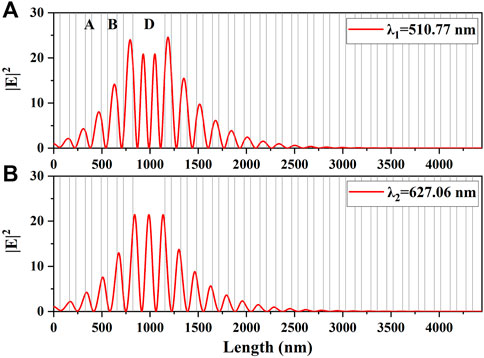
FIGURE 4. Simulated intensities of the electric field at absorption wavelengths of 510.77 nm (A) and 627.06 nm (B) for the PC (AB)MD(BA)N. All parameters are the same as those used in Figure 2C.
Furthermore, the oblique incidence and different polarizations are taken into consideration. The absorption spectra of asymmetrical PCs (AB)5D(BA)20 with different thicknesses of dD = 138.28 nm and dD = 331.86 nm are simulated in detail, as shown in Figure 5 and Figure 6, respectively. It can be found that the wavelengths of absorption peaks are blueshift with the increase of incident angle for both polarizations. Importantly, the values of absorption peaks for two different PCs are close to the unit, and those away from absorption wavelengths remain at a low level in a wide range of incidence and in broadband including photonic bandgap and passband, where the variation trends of two band edges with the incident angles are described by yellow lines in Figure 5. Therefore, these asymmetrical defective PCs can be used to fabricate single and multi-channel perfect absorbers in an ultrawide band.
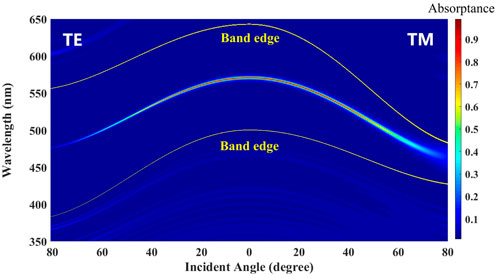
FIGURE 5. Absorption spectra of (AB)5D(BA)20 with different incident angles for TE and TM polarizations. The yellow lines denote the variation trends of two band edges with the incident angles. All parameters are the same as those used in Figure 2B.
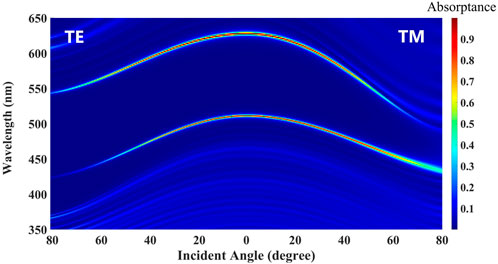
FIGURE 6. Absorption spectra of (AB)5D(BA)20 with different incident angles for TE and TM polarizations. All parameters are the same as those used in Figure 2C.
3 Tunable absorption properties of 1D PCs containing multiple lossy defect layers
In addition to changing the thickness of a defect layer in the PC to realize multiple absorptions, the same effect can also be obtained by inserting multiple lossy defect layers within the PC. In addition, the absorption wavelengths can be modulated by altering the distances among the defect layers. Herein, the asymmetrical PCs containing multiple defect layers are considered. First, the absorption properties of the PCs (AB)5D(BA)ND(AB)20 and (AB)5D(BA)ND(AB)ND(BA)20 are investigated by changing the periodic number N, as shown in Figure 7 and Figure 8, respectively. As shown in Figure 7, two perfect absorption peaks appear in the whole visible range for (AB)5D(BA)ND(AB)20 with kD = 0.0036 and dD = 128.5 nm. It can be seen that the gap between two absorption wavelengths tends to diminish when the periodic number becomes larger from N = 2 to N = 6. The reason is that the coupling effect between defect modes is stronger when the periodic number N is two rather than four or six [33]. A strong coupling effect can induce large splitting of the defect modes which is inversely proportional to the distance between the defect layers. In Figure 8, three perfect absorption peaks are obtained in the whole visible range for (AB)5D(BA)ND(AB)ND(BA)20 with kD = 0.0023 and dD = 130.3 nm. It is also found that the spacing among three absorption wavelengths becomes smaller with the increase of the periodic numbers from N = 2 to N = 6. Moreover, if more defect layers are inserted into the PCs, more perfect absorption peaks will be realized in the whole visible region. Therefore, such nanostructures are potential candidates for engineering tunable multi-channel perfect absorbers in the visible range.
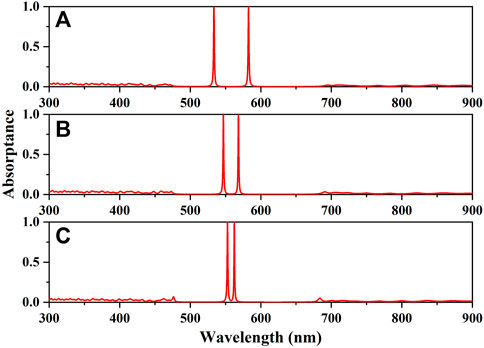
FIGURE 7. Absorption spectra of the PC (AB)5D(BA)ND(AB)20 with dD = 128.5 nm and kD = 0.0036. (A) N = 2. (B) N = 4. (C) N = 6.
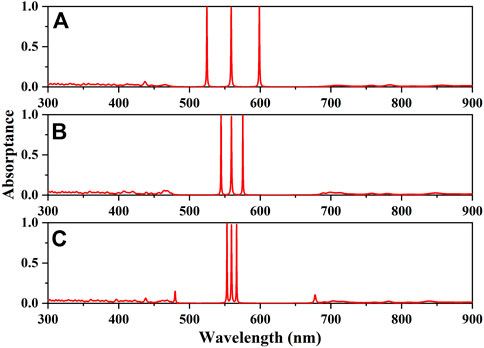
FIGURE 8. Absorption spectra of the PC (AB)5D(BA)ND(AB)ND(BA)20 with dD = 130.3 nm and kD = 0.0023. (A) N = 2. (B) N = 4. (C) N = 6.
At last, the influence of incident angles and polarizations on the absorption properties of PCs containing multiple defect layers has been studied. For simplicity, two PCs (AB)5D(BA)2D(AB)20 and (AB)5D(BA)2D(AB)2D(BA)20 are the same as those corresponding to Figure 7A and Figure 8A, respectively. In Figure 9 and Figure 10, the wavelengths of absorption peaks are blueshift with increase of the incident angles for TE and TM polarizations. In particular, the absorptance of all peaks remains nearly the unit in a wide range of incident angles, while the absorptances away from the defect wavelengths are very low in the whole visible region.
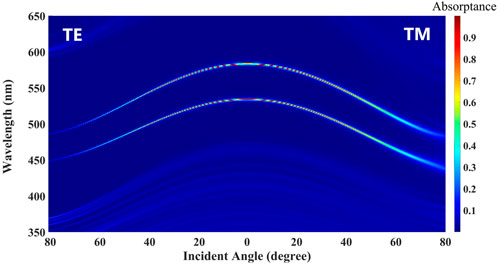
FIGURE 9. Absorption spectra of (AB)5D(BA)2D(AB)20 with different incident angles for TE and TM polarizations. All parameters are the same as those used in Figure 7A.
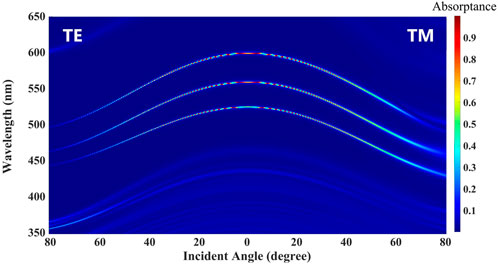
FIGURE 10. Absorption spectra of (AB)5D(BA)2D(AB)2D(BA)20 with different incident angles for TE and TM polarizations. All parameters are the same as those used in Figure 8A.
4 Conclusion
In summary, we have theoretically demonstrated that optical waves at defect wavelengths can be absorbed completely in asymmetrical PCs with lossy or multiple lossy defects. One or multiple perfect absorption peaks appear in the whole visible region. The number of absorption peaks can be modulated by changing the thickness of the defect layer or the defect number. Moreover, the distances among absorption wavelengths for PCs containing multiple defects can be tuned by altering the distances among the defects. These types of PCs with lossy defects will play an important role in modulating perfect optical absorption in the visible region.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
GD designed the research. RY, JL, HZ, and YZ performed the research and analyzed the data. GD, RY, and JL wrote the manuscript. GD, FL, and AW contributed to the revisions.
Funding
This research was funded by the Natural Science Foundation of Shandong Province (No. ZR2019MA055).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Hwang I, Choi D, Lee S, Seo JH, Kim KH, Yoon I, et al. Enhancement of light absorption in photovoltaic devices using textured polydimethylsiloxane stickers. ACS Appl Mater Inter (2017) 9:21276–82. doi:10.1021/acsami.7b04525
2. Chen Z, Weng Y, Liu J, Guo N, Yu Y, Xiao L. Dual-band perfect absorber for a mid-infrared photodetector based on a dielectric metal metasurface. Photon Res (2020) 9:27–33. doi:10.1364/PRJ.410554
3. Liu N, Mesch M, Weiss T, Hentschel M, Giessen H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett (2010) 10:2342–8. doi:10.1021/nl9041033
4. Lv J, Zhou M, Gu Q, Jiang X, Ying Y, Si G. Metamaterial lensing devices. Molecules (2019) 24:2460. doi:10.3390/molecules24132460
5. Landy NI, Sajuyigbe S, Mock JJ, Smith DR, Padilla WJ. Perfect metamaterial absorber. Phys Rev Lett (2008) 100:207402. doi:10.1103/PhysRevLett.100.207402
6. Thongrattanasiri S, Koppens FH, Garcia de Abajo FJ. Complete optical absorption in periodically patterned graphene. Phys Rev Lett (2012) 108:047401. doi:10.1103/PhysRevLett.108.047401
7. Wu JH, Artoni M, La Rocca GC Perfect absorption and no reflection in disordered photonic crystals. Phys Rev A (2017) 95:053862. doi:10.1103/PhysRevA.95.053862
8. Dissanayake SE, Wijewardena Gamalath KAIL. Point defects in GaAs photonic crystals. Int Lett Chem Phys Astron (2015) 43:91–102. doi:10.18052/www.scipress.com/ILCPA.43.91
9. Skoromets V, Němec H, Kadlec C, Fattakhova-Rohlfing D, Kužel P. Electric-field-tunable defect mode in one-dimensional photonic crystal operating in the terahertz range. Appl Phys Lett (2013) 102:241106. doi:10.1063/1.4809821
10. Dai X, Xiang Y, Wen S, He H Thermally tunable and omnidirectional terahertz photonic bandgap in the one-dimensional photonic crystals containing semiconductor InSb. J Appl Phys (2011) 109:053104. doi:10.1063/1.3549834
11. Lee KJ, Wu JW, Kim K. Defect modes in a one-dimensional photonic crystal with a chiral defect layer. Opt Mater Express (2014) 4:2542–50. doi:10.1364/OME.4.002542
12. Auguié B, Bruchhausen A, Fainstein A. Critical coupling to Tamm plasmons. J Opt (2015) 17:035003. doi:10.1088/2040-8978/17/3/035003
13. Kaliteevski M, Iorsh I, Brand S, Abram R, Chamberlain J, Kavokin A, et al. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys Rev B (2007) 76:165415. doi:10.1103/PhysRevB.76.165415
14. Du G, Jiang H, Wang Z, Yang Y, Wang Z, Lin H, et al. Heterostructure-based optical absorbers. J Opt Soc Am B (2010) 27:1757–62. doi:10.1364/JOSAB.27.001757
15. Lu G, Wu F, Zheng M, Chen C, Zhou X, Diao C, et al. Perfect optical absorbers in a wide range of incidence by photonic heterostructures containing layered hyperbolic metamaterials. Opt Express (2019) 27:5326–36. doi:10.1364/OE.27.005326
16. Kavokin AV, Shelykh IA, Malpuech G. Lossless interface modes at the boundary between two periodic dielectric structures. Phys Rev B (2005) 72:233102. doi:10.1103/PhysRevB.72.233102
17. Wu F, Wu X, Xiao S, Liu G, Li H. Broadband wide-angle multilayer absorber based on a broadband omnidirectional optical tamm state. Opt Express (2021) 29:23976–87. doi:10.1364/OE.434181
18. Chen L, Qiang Z, Zhou W, Brown G. Spectral selective absorption enhancement in photonic crystal defect cavities. Proc SPIE (2007) 6480:64801C. doi:10.1117/12.699410
19. Chen J, Zeng Y, Xu X, Chen X, Zhou Z, Shi P, et al. Plasmonic absorption enhancement in elliptical graphene arrays. Nanomaterials (2018) 8:175. doi:10.3390/nano8030175
20. Bonod N, Popov E. Total light absorption in a wide range of incidence by nanostructured metals without plasmons. Opt Lett (2008) 33:2398–400. doi:10.1364/OL.33.002398
21. Fan S, Villeneuve PR, Joannopoulos JD, Haus H. Channel drop tunneling through localized states. Phys Rev Lett (1998) 80:960–3. doi:10.1103/PhysRevLett.80.960
22. Cui L, Lu G, Zhang S, Liu F, Xin Y, Wang K, et al. Optical resonant tunneling in photonic heterostructures containing a tunable dielectric layer. AIP Adv (2017) 7:105108. doi:10.1063/1.5001691
23. Nkonde S, Jiang C. Photonic crystal waveband de-multiplexers. Results Phys (2018) 11:896–8. doi:10.1016/j.rinp.2018.10.061
24. Lin X, Wu W, Zhou H, Zhou K, Lan S. Enhancement of unidirectional transmission through the coupling of nonlinear photonic crystal defects. Opt Express (2006) 14:2429–39. doi:10.1364/oe.14.002429
25. Lin YC, Chou SH, Hsueh WJ Robust high-q filter with complete transmission by conjugated topological photonic crystals. Sci Rep (2020) 10:7040. doi:10.1038/s41598-020-64076-3
26. Qiu B, Lin Y, Arinze ES, Chiu A, Li L, Thon SM. Photonic band engineering in absorbing media for spectrally selective optoelectronic films. Opt Express (2018) 26:26933–45. doi:10.1364/OE.26.026933
27. Vincenti MA, de Ceglia D, Grande M, D'Orazio A, Scalora M. Nonlinear control of absorption in one-dimensional photonic crystal with the graphene-based defect. Opt Lett (2013) 38:3550–3. doi:10.1364/OL.38.003550
28. Liu Y, Xie X, Xie L, Yang Z, Yang H. Dual-band absorption characteristics of one-dimensional photonic crystal with graphene-based defect. Optik (2016) 127:3945–8. doi:10.1016/j.ijleo.2016.01.121
29. Du G, Zhou X, Pang C, Zhang K, Zhao Y, Lu G, et al. Efficient modulation of photonic bandgap and defect modes in all-dielectric photonic crystals by energetic ion beams. Adv Opt Mater (2020) 8:2000426. doi:10.1002/adom.202000426
30. Liu B, Lu G, Cui L, Li J, Sun F, Liu F, et al. Experimental investigation of multiple near-perfect absorptions in sandwich structures containing thin metallic films. Opt Express (2017) 25:13271–7. doi:10.1364/OE.25.013271
32. Piper JR, Fan S. Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided resonance. ACS Photon (2014) 1:347–53. doi:10.1021/ph400090p
Keywords: photonic crystals, photonic bandgap, optical absorption, photonic localization, defect modes
Citation: Yan R, Li J, Zhou H, Zhao Y, Liu F, Wu A and Du G (2022) Tunable perfect optical absorption in truncated photonic crystals with lossy defects. Front. Phys. 10:1019214. doi: 10.3389/fphy.2022.1019214
Received: 14 August 2022; Accepted: 26 August 2022;
Published: 19 September 2022.
Edited by:
Zhiwei Guo, Tongji University, ChinaCopyright © 2022 Yan, Li, Zhou, Zhao, Liu, Wu and Du. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guiqiang Du, ZGdxcWxAc2R1LmVkdS5jbg==
 Runze Yan
Runze Yan Junyang Li
Junyang Li Guiqiang Du
Guiqiang Du