All optical Q-switched laser based spiking neuron

This paper studies theoretically the use of a Q-switch laser with side light injection as a spiking all-optical neuron for photonic spiking neural networks (PSNN). Ordinary differential equations for the multi-section laser are presented, including terms for the side light injection for gain quenching and saturable absorption. The behaviour of the laser mimics that of a spiking neuron with ultrafast pico-second scale response and low power control signals.

1 Introduction

Neuromorphic computing aims to emulate the brain’s ability to process large amounts of information efficiently. Since the 1980s [1], this field has continued to evolve as we have improved our understanding of brain physiology, as well as hardware innovation. As a result, functional neuromorphic chips were first implemented using electronic platforms [2]. However, neuromorphic electronics is facing important limitations related to bandwidth and integration density [3, 4]. More recently, silicon photonics technology has emerged as a potential platform for scaling up neuromorphic devices [3], and might be an answer to meeting this technological challenge regarding complexity, interconnection and also power consumption especially when IIIV based devices can be integrated along other passive and active components [5, 6].

Neuromorphic hardware is based on models of artificial neural networks (ANNs). Spiking neural networks (SNNs) are the most bio-realistic form of them, as they operate using discrete spatio-temporal spikes, much like biological neurons [7]. Since they have a temporal aspect, SNNs are capable of processing spatio-temporal information, leading to more complex applications such as feature recognition, image classification, audio recognition, etc [3, 7]. In addition, unlike conventional ANNs, they only operate when spikes occur, which makes their hardware much more energy efficient.

Models of spike neurons have been proposed to simulate most biological features of neurons [8]. Among them, the Leaky Integrate-and-Fire (LIF) offers the best compromise between biological plausibility and practicality [2, 9], which explains its widespread use in the literature. In neuromorphic photonics, the excitability of spiking neurons has already been demonstrated by using excitable semiconductor lasers, also known as spiking lasers [10–12]. Saturable absorber is typically used in such lasers, resulting in non-linearities that give the lasers either bistability or spiking behavior [13]. The latter is usually the result of a Q-switch mechanism. Spiking lasers can be divided into two categories based on how optical spikes are generated: optical-electrical-optical (O/E/O) and all-optical [3]. In most cases, O/E/O spiking lasers rely on electronic circuits to control their excitable dynamics. In contrast, all-opticall lasers are directly excited by optical perturbations. Various all-optical laser designs have been proposed in references [14–16].

In this paper we first describe the architecture of an all-optical side light-injected Q-switch laser. Then, we solve his Ordinary Differential Equations (ODE) to determine its behavior as a spiking neuron: integration of incoming synaptic signals, exitability, inhibitability and spike response, refractory period. Once this is set, we demonstrate the cascadability and the optical memory ability of our laser in a two-neurons mutually coupled circuit.

2 Materials and methods

2.1 Side light injected Q-switch laser

Q-switched lasers have been proposed in [10] to serve as spiking neurons owing to their capacity to integrate in a leaky way the incoming energy over time and fire an output pulse when that energy increases above an internal threshold. Electrical command signals have been proposed and demonstrated [17–20] using balanced photodetectors to modulate the bias current of the gain section. Optical command signals have also been proposed in [21] but require a complex implementation. Indeed, as these signals are injected along the main laser cavity, they interact mainly with the gain section of the laser and hence provide only gain quenching (by increasing stimulated emission and hence reducing the exited carrier concentration). As a result, incoming pulses can only be used as inhibitors to the laser-neuron. Excitability requires the optical signals to be reversed, leading to additional hardware to be employed [21].

In [22], a side light-injected bistable laser was developed and tested for applications in all-optical digital signal processing. The laser was composed of five sub-sections along the main optical cavity. Three sections were devoted to pure gain with a direct bias (current injection) while one section was devoted to gain quenching and another one to saturable absorption. The two later sections had perpendicular waveguides connected to them, allowing light to be injected directly into those sections without creating a large crosstalk with the main waveguide. Overall, the laser was designed to have a bistable operation. In its general operation, the gain section is biased slightly under the laser threshold. By injecting light in the side waveguide connected to the gain quenching section (resp. the saturable absorption section), additional radiative recombinations by stimulated emission (resp. carrier excitation by photon absorption) occurs hence locally reducing (resp. increasing) the population inversion and as a result creating a sudden drop in the cavity gain (resp. drop in the cavity loss). Subsequently, the laser would switch-off (resp. switch-on). A similar behavior can be applied to a Q-switch laser to obtain all optical excitability or inhibition as in spiking neurons.

In the following section, we describe sush laser layout and parameters and write the ODEs describing its behaviour.

2.2 All-optical neuron model

The Q-switch laser is based on five sections as in [22]. A schematic view of its structure integrated on a silicon photonics platform is represented in Figure 1. Two side light injected sections are sandwiched between three generic gain sections which provide the main photon generation and amplification functions for the longitudinal laser cavity. The three gain sections are directly biased together by a single electrode (respective currents denoted i_G,1, i_G,2, and i_G,3) while the two other sections have their own electrical electrodes. A direct bias is also applied to the gain quenching section (i_Q) and a zero or small reverse bias to the SA section (i_SA). Using the formalism from [17] (Figure 2), we write the ODEs that describe the time evolution of the carriers and photons in the different sections of the laser. Note that there will be three different photon populations: the one in the longitudinal waveguide N_ph plus the ones in the lateral waveguides N_Q and N_SA. According to [23], the wavelengths of these photon populations have to be within the III-V material absorption spectrum but may not be exactly the same. However, for the sake of simplicity we will assume similar wavelengths and hence that the same gain/absorption coefficients can be used in the equations. First, for the carrier concentration in the main gain sections (m = 1, 2 or 3):

$\frac{\partial n_{\text{G},m}}{\partial t}=\frac{\eta i_{\text{G},m}}{q{V}_{\text{G},m}}-\frac{n_{\text{G},m}}{{\tau }_{\text{G}}}-\mathrm{\Gamma }{g}_{\text{G}}\left(n_{\text{G},m}-n_{\text{G},0}\right)\frac{N_{\text{ph}}}{V_{\text{tot}}}(1)$

where n_G,m is the carrier concentration in the considered section, η the current injection efficiency, V_G,m the section’s volume, τ_G the carrier lifetime, g_G the differential gain, n_G,0 the carrier density at transparency, N_ph the photon population in the overall longitudinal cavity and V_tot the total volume of the main cavity. Now, for the gain quenching section, we write:

$\frac{\partial n_{\text{Q}}}{\partial t}=\frac{\eta i_{\text{Q}}}{q{V}_{\text{Q}}}-\frac{n_{\text{Q}}}{{\tau }_{\text{Q}}}-\mathrm{\Gamma }{g}_{\text{Q}}\left(n_{\text{Q}}-n_{\text{Q},0}\right)\left(\frac{N_{\text{ph}}}{V_{\text{tot}}}+\frac{N_{\text{Q}}}{V_{\text{Q}}}\right)(2)$

FIGURE 1

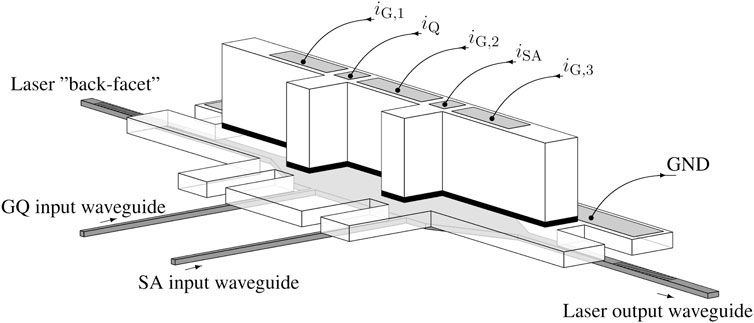
FIGURE 1. 3D-Schematic view of the neuron laser: the IIIV material is processed on top of an silicon photonics wafer to allow coupling between the underlying silicon waveguides and the gain material. Biasing currents are injected into the top electrodes (InP⁺) through the quantum wells (represented as a black layer) to the ground electrode (InP⁻). Two waveguides perpendicular to the main laser cavity are used to feed optical power directly into the GQ and SA parts of the laser. The detailed structure of the laser can be inferred from [5, 6].

FIGURE 2

FIGURE 2. Schematic view of the neuron laser detailing the different variables of the model.

For the saturable absorption region:

$\frac{\partial n_{\text{SA}}}{\partial t}=\frac{\eta i_{\text{SA}}}{q{V}_{\text{SA}}}-\frac{n_{\text{SA}}}{{\tau }_{\text{SA}}}-\mathrm{\Gamma }{g}_{\text{SA}}\left(n_{\text{SA}}-n_{\text{SA},0}\right)\left(\frac{N_{\text{ph}}}{V_{\text{tot}}}+\frac{N_{\text{SA}}}{V_{\text{SA}}}\right)(3)$

the parameters are self-explanatory. Note that V_tot = V_G,1 + V_Q + V_G,2 + V_SA + V_G,3. Finally, for the photon populations, we write:

$\begin{array}{ll}\hfill \frac{\partial N_{\text{ph}}}{\partial t}& =-\frac{N_{\text{ph}}}{{\tau }_{\text{ph,long}}}+\mathrm{\Gamma }\left[\sum _{m=1}^3{g}_{\text{G}}\left(n_{\text{G},m}-n_{\text{G},0}\right)\frac{V_{\text{G}},m}{V_{\text{tot}}}+g_{\text{Q}}\left(n_{\text{Q}}-n_{\text{Q},0}\right)\frac{V_{\text{Q}}}{V_{\text{tot}}}+g_{\text{SA}}\left(n_{\text{SA}}-n_{\text{SA},0}\right)\frac{V_{\text{SA}}}{V_{\text{tot}}}\right]N_{\text{ph}}\hfill \\ \hfill & +\sum _{m=1}^3{V}_{\text{G},m}\beta B_r{n}_{\text{G},m}^2+V_{\text{Q}}\beta B_r{n}_{\text{Q}}^2\hfill \end{array}(4)$

$\frac{\partial N_{\text{Q}}}{\partial t}=\frac{{\psi }_{\text{Q}}-N_{\text{Q}}}{{\tau }_{\text{ph,inj}}}+\mathrm{\Gamma }{g}_{\text{G}}\left(n_{\text{Q}}-n_{\text{G},0}\right)N_{\text{Q}}+V_{\text{Q}}\beta B_r{n}_{\text{Q}}^2(5)$

$\frac{\partial N_{\text{SA}}}{\partial t}=\frac{{\psi }_{\text{SA}}-N_{\text{SA}}}{{\tau }_{\text{ph,inj}}}+\mathrm{\Gamma }{g}_{\text{SA}}\left(n_{\text{SA}}-n_{\text{SA},0}\right)N_{\text{SA}}(6)$

where β and B_r are respectively the spontaneous emission coupling factor and the bimolecular recombination term. In Eqs 5, 6, the external injection terms ψ_Q and ψ_Q appear. They represent the photon flux entering from the lateral waveguides. The photon populations in the lateral waveguides have a different and much shorter life time τ_ph,inj than the longitudinal photons as they travel along the width of the active section and these sections are not equipped with mirrors so as to facilitate the external injection [23]. Note that the terms ψ_Q and ψ_SA are slowing the photon population decrease and hence appear with a positive sign in the equations. Also, there is no relative volumic term in Eqs 5, 6 as the photons and carriers considered in these equations occupy the same volumic space. To finish this mathematical framework and considering further simplfying the model, we note that the three gain sections can be combined in a single one with volume V_G = ∑V_G,m, carrier concentration n_G = ∑n_G,mV_G,m/V_G and total injected current i_G = ∑i_G,m.

The optical output of the laser is defined by the number of photons escaping the cavity N_ph,out = η_cN_ph leading to the expression of the optical output power [17]:

$P_{\text{out}}=\frac{{\eta }_c{N}_{\text{ph}}\mathrm{\Gamma }hc}{\lambda {\tau }_{\text{ph}}}(7)$

In the following section, we study the behavior of the side-light-injected Q-switched laser and compare it to a spiking neuron.

3 Results and discussion

In the following, using Matlab^®, we solve the above ODEs to demonstrate the similarity in terms of behavior between the Q-switch multi-section laser and a spiking neuron. For this we will use parameter values as detailed in table 1 taken from [17].

TABLE 1

TABLE 1. Parameters used in the DFB-SA laser neuron model [17].

3.1 Spiking threshold

First, we look at the self-pulsating threshold, i.e., the value of i_G above which the laser is self-pulsating. The overall biasing of the gain section denoted i_bias is uniformly split between the different gain sections i.e. the overall bias current density is kept the same in all gain sections: i_G = i_bias × V_G/(V_G + V_Q) and i_Q = i_bias × V_Q/(V_G + V_Q). We plot (Figure 3) the output pulse energy as a function of i_G without external injection (ψ_Q = 0 and ψ_SA = 0). We set to zero the bias current for the SA i_SA = 0.0 mA. We find a self-pulsating threshold of 14.4 mA. The pulses on the output are found to be approximatively 55ps full width half-maximum.

FIGURE 3

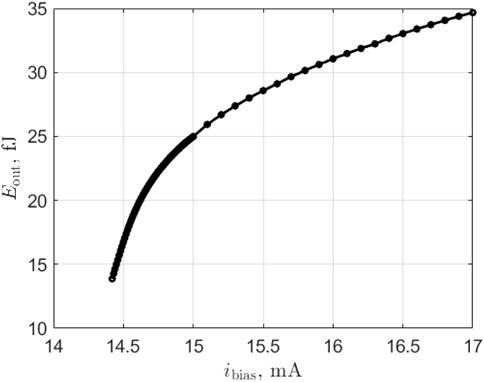
FIGURE 3. Output pulse energy vs bias current of the gain section for the laser-neuron. Self-pulsating threshold is i_bias = 14.4 mA.

3.2 Time traces

In order to highlight the neuronal behavior of the laser, we plot the time traces of the internal variables under different situations. The first case concerns the arrival in the SA of an excitatory pulse (of energy 60 fJ) and the triggering of an output spike event. Results are presented in Figure 4. At the input pulse arrival (t = 500ps), the SA photon population N_SA (black curve in the left hand side graph) increases sharply then returns to zero as those photons are either absorbed or exit the SA section on the other side (the transit time through the SA is τ_ph,inj in the lateral direction). These photons anyway, create a large number of carriers n_SA (grey curve in the right hand side graph) that saturates the absorber. As the SA has a fast dynamics, it recovers almost immediately (first peak in the n_SA curve), but not fully since the overall laser cavity gain increases in the meantime leading to a surge in the main photon population N_ph (grey curve in the left hand side graph) and a new peak in the SA carrier concentration. This results in the laser output switching on and, consequently, the depletion of the gain sections’ carrier population n_G and n_Q due to the large stimulated emission occurring. Finally, the reducing n_G closes the gain of the cavity, switching off the laser output and allowing the SA to recover fully its high loss state (n_SA → 0) while n_G and n_Q slowly recover their steady state value thanks to the gain section bias current (rate 1/τ_G). During that time, the laser can hardly trigger a new spike event; this is the equivalent of the relative refractory period in the spiking neuron. The second case highlights the integration of excitation signals. Now, two pulses are sent to the SA section at t = 500ps and t = 600ps each with an energy of 30 fJ. Results are presented in Figure 5. The arrival of the first input pulse at t = 500ps, creates a surge in the SA carrier population as explained above. The SA loss drops and the main photon population increases slightly but not enough to lead to a spiking event as shown by the dashed curves representing the evolution of the parameters if only a single pulse had been sent. Upon the arrival of the second pulse, the SA carrier population increases again sharply and now reaches a level sufficiently high to trigger a spiking event followed by a refractory period during which the laser slowly recovers. Finally, we illustrate the inhibition of a spiking event. An inhibitory pulse of energy 60 fJ is sent into the gain quenching section at t = 500ps and then an excitatory pulse of energy 60 fJ is sent into the SA section at t = 600ps and no spiking event occurs. Results are presented in Figure 6. Following the reception of the inhibitory pulse, the photon population of the GQ section surges (black dash-dot curve in the left hand side graph). This triggers a sharp drop in the carrier concentration of this section (black dash-dot curve in the right hand side graph). As the lifetime of the GQ section photons is very short, N_Q rapidly falls back to zero and the carrier concentration starts to recover. When the excitatory pulse reaches the SA at t = 600ps (black curve in the left hand side graph), the laser has not recovered yet and hence, although the carrier concentration of the SA section exhibits a large spike, there is only a small increase in the main photon population (gray curve in the left hand side graph) and no output spike is generated. Also, the carrier concentration of the main gain section n_G (as shown by the black curve in the right hand side graph) is nearly not affected. After this illustration of the similarity in behavior between the proposed side light-injected Q-switch laser and an spiking neuron (excitation, recovery, integration and inhibition), we now perform a more general behavioral study.

FIGURE 4

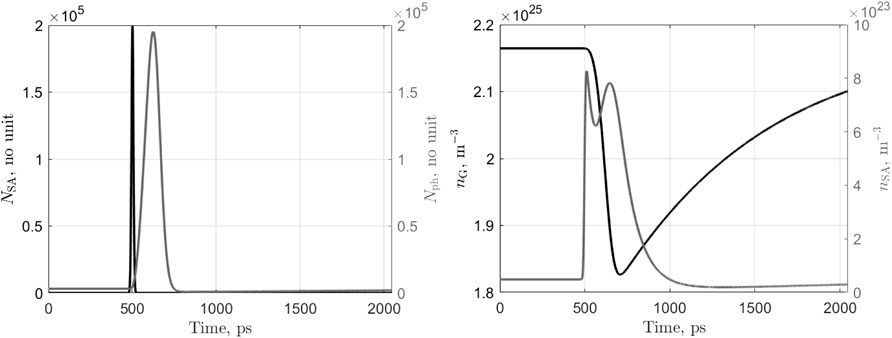
FIGURE 4. Time traces of the photons (left) and carriers (right) of the laser-neuron under i_bias = 13 mA and upon the arrival at t = 500ps of an exitatory pulse (in the SA section) of energy 60 fJ.

FIGURE 5

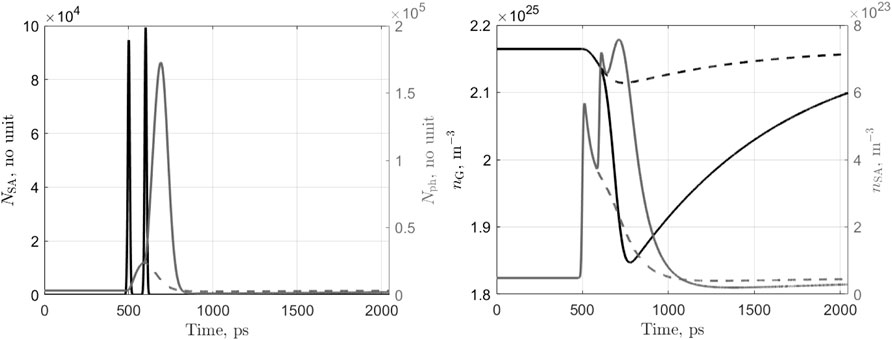
FIGURE 5. Time traces of the photons (left) and carriers (right) of the laser-neuron under i_bias = 13 mA and upon the arrival at t = 500ps and 600ps of two exitatory pulses (in the SA section) each of energy 30 fJ. The dashed curves show the evolution of the parameters if only the first pulse had been present.

FIGURE 6

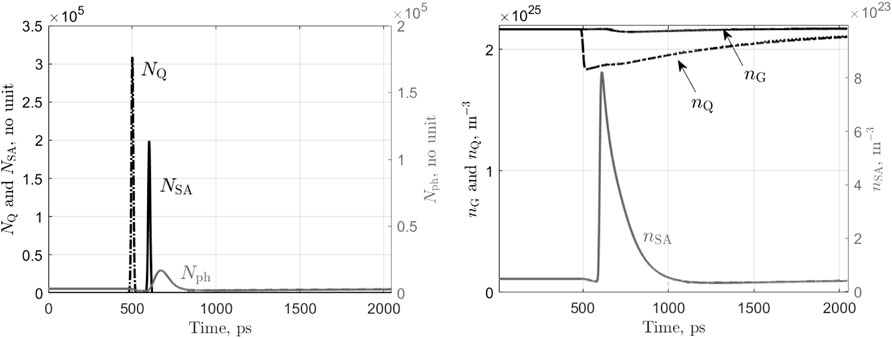
FIGURE 6. Time traces of the photons (left) and carriers (right) of the laser-neuron under i_bias = 13 mA and upon the arrival at t = 500ps of an inhibitory pulse (in the GQ section) of energy 60 fJ then at 600 ps of an exitatory pulse (in the SA section) of energy 60 fJ.

3.3 Excitation threshold

Next, we study the excitability by computing the output pulse energy E_out and timing T_S,out as a function of input pulse energy E_SA,in when the neurons bias is set below its self-pulsating threshold (we use i_bias = 13 mA). Results are shown in Figure 7. The input pulse consists of a Gaussian pulse of full width at half-maximum 55 ps matching the lasers output pulse characteristics. It enters the lateral waveguide connected to the SA part of the laser. We find that the excitation threshold of the spiking laser neuron is 48 pJ.

For input pulse energies above this value, the laser fires an output spike and under this value, it returns to its resting state.

As can be seen in 7 (top graph), the output pulse energy is not constant as can be expected from biological neurons but depends upon the input excitation strength. It can also be noted that the pulse output timing (7 bottom graph) decreases sharply above the threshold, then stabilizes around 70 ps after the input pulse arrival. This behavior, where the spike output timing is inversely proportional to the strength of the membrane voltage excitation, can also be found in neuron models such as the Hodgkin-Huxley and LIF ones [8].

FIGURE 7

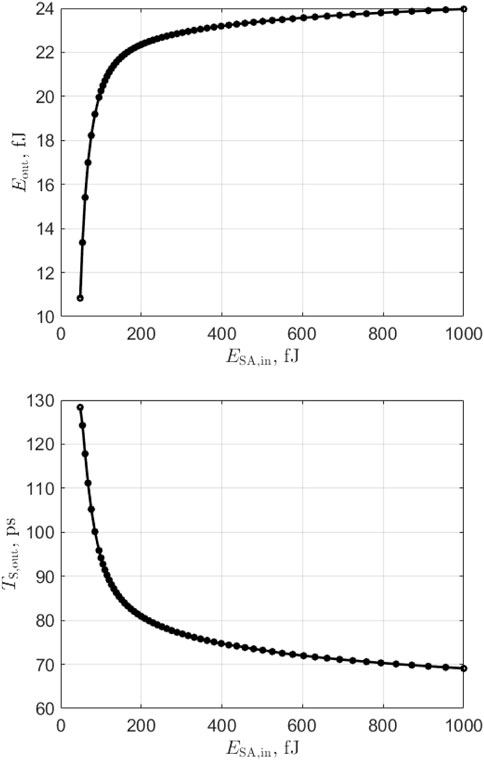
FIGURE 7. Simulation of output pulse energy (top) and spike timing (bottom) as a function of SA input pulse energy for i_bias = 13 mA. A minimum input pulse energy of 48 fJ is required to trigger an output spike.

3.4 Inhibition threshold

We now study the impact of sending an optical pulse on the gain quenching input. To do so, we plot (Figure 8) the pulse output energy E_out and timing T_S,out as a function of the pulse energy E_Q,in on the gain quenching section for various conditions of SA input pulse energy (above excitation threshold e.g. E_SA,in > 48 fJ) for the same gain section bias (i_bias = 13 mA). We thus can assess the inhibitory effect of the gain quenching section. Sending optical energy on the GQ section leads to a strong reduction of the output pulse energy or even a complete cancelation of the spiking event. The energy level required to suppress the spike event is about one order of magnitude lower than the required excitatory pulse energy to generate the output pulse. This can be explained by the high population inversion of the gain section and the strong stimulated emission created when the side light is input, multiplying the effect.

FIGURE 8

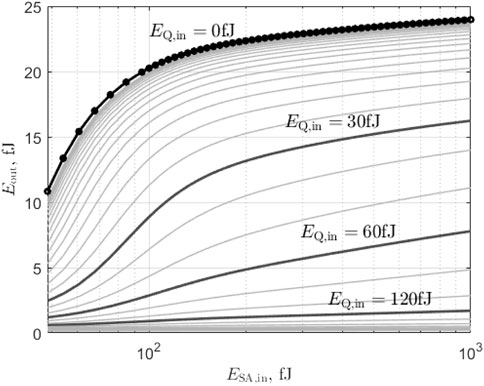
FIGURE 8. Simulation of output pulse energy as a function of SA input pulse energy for different GQ input pulse energy and for i_bias = 13 mA.

3.5 Refractory period

Next, we look at the refractory period of the laser-neuron (Figure 9). To do so, we trigger a spike event by sending an input pulse of energy E_SA,in ($>48$fJ for i_bias = 13 mA) at time T_S,in to the SA section and immediately send another triggering pulse at time T_S,in + ΔT_S with the same energy. Without refractoriness, the neuron should fire a first pulse of energy E_out,1 then a second output pulse of energy E_out,2. We plot the second output pulse energy as a function of E_SA,in and ΔT_S. For sufficiently large ΔT_S, we find as expected that E_out,2 = E_out,1. However, for ΔT_S < 3ns, E_out,2 is significantly lower than E_out,1 and even, for ΔT_S < 400ps there is no second pulse E_out,2 = 0.

FIGURE 9

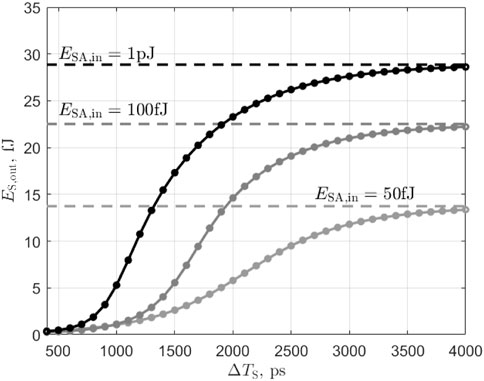
FIGURE 9. Simulation of output pulse energy as a function of SA input pulses energy for different delays between the input pulses and for i_bias = 13 mA. The laser receives two input pulses (SA section) of equal energy E_SA,in separated by ΔT_S. In response it emits up to two output pulses. The first output pulse energy is plotted with a dash line while the second pulse energy is plotted with a thick line and symbols.

3.6 Multistable system demonstration

We now verify the cascadability in the presented neuron, as well as its optical memory properties. Cascadability can be defined as the ability of a laser to drive one or many other lasers. This characteristic is therefore a necessary condition to design a large scale photonic spiking neural network (PSNN). A demonstration of these two properties can be done using a system of two interconnected lasers as shown in Figure 10, also known as a multistable system [10]. Here, the two lasers are considered identical and are both polarized with i_bias = 13 mA. They are also mutually coupled through an amplifier characterized by the coupling weight w = 5 (7 dB of optical gain), associated with a delay of τ_d = 2ns. Figure 11 shows the respective responses of the two lasers. The system is first turned on when an optical pulse of energy 100 fJ is injected into the first laser’s SA section (ON) at t = 200ps. The output spike of the laser is then amplified to allow the excitation of the second laser. This initiates both lasers to fire a train of spikes with a fixed period $\approx 2\times {\tau }_{\text{d}}$ as we can see in Figure 11. It takes about four round trips to stabilize the pulse power to about 80 fJ. We thus demonstrate on the one hand that our laser can be optically cascaded and on the other hand that it can store the information contained in a spike. We also show in the same example that the system can be turned off by stimulating the gain with an optical pulse of 100 fJ at t ≈ 85ns. The pulse train is interrupted in a couple of round trips.

FIGURE 10

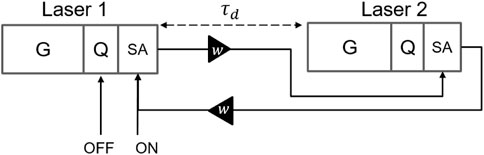
FIGURE 10. Cascadability circuit: two identical laser neurons are self-coupled with a delay of τ_d = 2ns and a gain of 7 dB (w = 5).

FIGURE 11

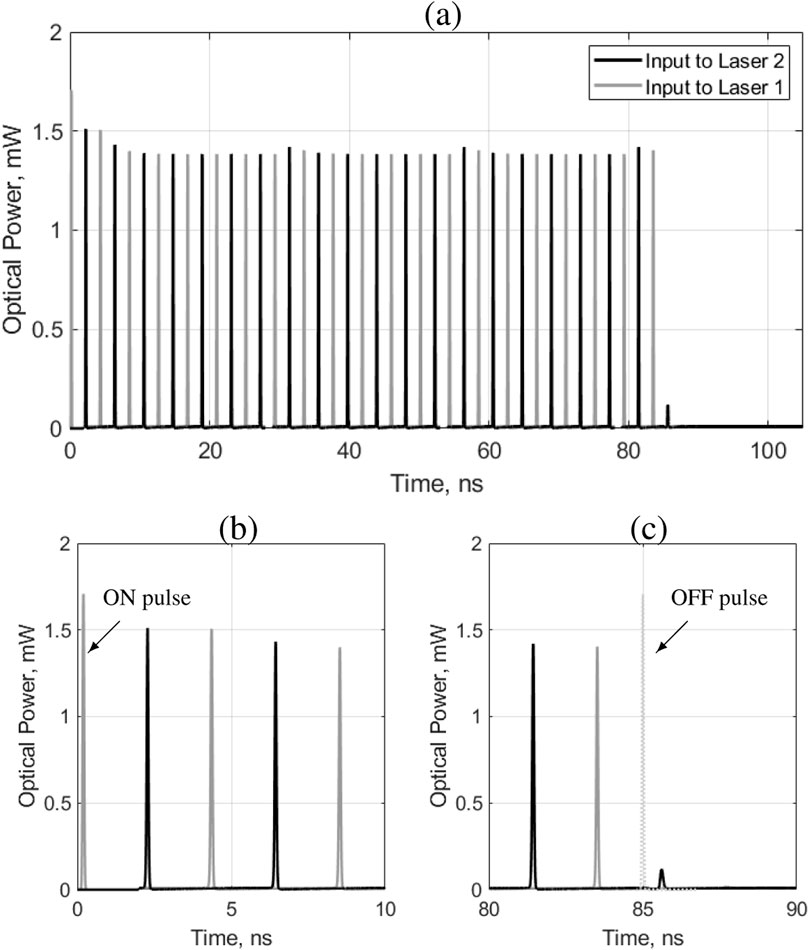
FIGURE 11. (A): Pulse train from two self-coupled laser neurons with 2ns delay and 7 dB of optical gain. Gray: input to laser 1 SA section. Black: input to laser 2 SA section. (B): focus on the start of the pulse train. (C): focus of the end of the pulse train.

4 Conclusion

In this paper, we have studied theoretically the use of a Q-switch laser with side light injection as an all-optical neuron for photonic spiking neural networks (PSNN). First, we have presented the Ordinary Differential Equations for the multi-section laser, including terms for the side light injection for gain quenching and saturable absorption. Then, solving numerically these equations, we have shown that the behaviour of the laser-neuron mimics that of spiking neuron (excitability, inhibitability, integration, refractoriness and cascadability) with ultrafast pico-second scale response and low power control signals. We have determined the self-pulsating and the optical excitability thresholds as well as quantified the inibitory effects and refractory period. Finally, we demonstrated the cascadability of the laser-neurons. Such all optical laser-neuron is suited for future high speed SNN hardware implementation especially considering integration platforms such as silicon photonics.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

KM-O and BC contributed to the overall study and analysis and wrote the full paper. BR contributed some background work regarding the use of spiking neurons in general neuromorphic circuits.

Funding

This work was supported by the French Public Authorities in the frame of the Important Project of Common European Interest (IPCEI) on Microelectronics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Roy K, Jaiswal A, Panda P. Towards spike-based machine intelligence with neuromorphic computing. Nature (2019) 575:607–17. doi:10.1038/s41586-019-1677-2

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Hendy H, Merkel C. Review of spike-based neuromorphic computing for brain-inspired vision: Biology, algorithms, and hardware. J Electron Imaging (2022) 31:010901. doi:10.1117/1.JEI.31.1.010901

CrossRef Full Text | Google Scholar

3. Shastri BJ, Tait AN, de Lima TF, Nahmias MA, Peng H-T, Prucnal PR. Principles of neuromorphic photonics. arXiv:1801.00016 [physics] (2018) doi:10.1007/978-3-642-27737-5_702-1

CrossRef Full Text | Google Scholar

4. Shastri BJ, Tait AN, Ferreira de Lima T, Pernice WHP, Bhaskaran H, Wright CD, et al. Photonics for artificial intelligence and neuromorphic computing. Nat Photon (2021) 15:102–14. doi:10.1038/s41566-020-00754-y

CrossRef Full Text | Google Scholar

5. Ona KM, Charbonnier B, Hassan K. Design of an integrated iii–v on silicon semiconductor laser for spiking neural networks. In: 2021 IEEE International Interconnect Technology Conference (IITC) (2021). p. 1. doi:10.1109/IITC51362.2021.9537482

CrossRef Full Text | Google Scholar

6. Szelag B, Hassan K, Adelmini L, Ribaud K, Roure MC, Sanchez L, et al. Cmos compatible iii-v/silicon laser integration on silicon photonics platform. In: 2019 IEEE Photonics Conference (IPC) (2019). p. 1. doi:10.1109/IPCon.2019.8908325

CrossRef Full Text | Google Scholar

7. Vreeken J. Spiking neural networks, an introduction. Utrecht: Utrecht University: Information and Computing Sciences (2003). Technical report UU-CS-2003-008 , 5.

Google Scholar

8. Gerstner W, Kistler WM. Spiking neuron models: Single neurons, populations, plasticity. Cambridge, U.K.; New York: Cambridge University Press (2002).

Google Scholar

9. Zeng Y, Stewart TC, Ibne Ferdous Z, Berdichevsky Y, Guo X. Temporal learning with biologically fitted SNN models. In: International Conference on Neuromorphic Systems 2021. Knoxville: ACM (2021). p. 1–8. doi:10.1145/3477145.3477153

CrossRef Full Text | Google Scholar

10. Nahmias MA, Shastri BJ, Tait AN, Prucnal PR. A leaky integrate-and-fire laser neuron for ultrafast cognitive computing. IEEE J Sel Top Quan Electron (2013) 19:1–12. doi:10.1109/JSTQE.2013.2257700

CrossRef Full Text | Google Scholar

11. Shastri BJ, Nahmias MA, Tait AN, Rodriguez AW, Wu B, Prucnal PR. Spike processing with a graphene excitable laser. Sci Rep (2016) 6:19126. doi:10.1038/srep19126

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Song ZW, Xiang SY, Ren ZX, Hong S, Wen AJ, Hao Y. Photonic spiking neural network based on excitable VCSELs-SA for sound azimuth detection. Opt Express (2020) 13:1561. doi:10.1364/oe.381229

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ueno M, Lang R. Conditions for self-sustained pulsation and bistability in semiconductor lasers. J Appl Phys (1985) 58:1689–92. doi:10.1063/1.336065

CrossRef Full Text | Google Scholar

14. Xiang J, Torchy A, Guo X, Su Y. All-optical spiking neuron based on passive microresonator. J Lightwave Technol (2020) 38:4019–29. doi:10.1109/JLT.2020.2986233

CrossRef Full Text | Google Scholar

15. Coomans W, Gelens L, Beri S, Danckaert J, Van der Sande G. Solitary and coupled semiconductor ring lasers as optical spiking neurons. Phys Rev E (2011) 84:036209. doi:10.1103/PhysRevE.84.036209

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Selmi F, Braive R, Beaudoin G, Sagnes I, Kuszelewicz R, Barbay S. Relative refractory period in an excitable semiconductor laser. Phys Rev Lett (2014) 112:183902. doi:10.1103/PhysRevLett.112.183902

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Shastri BJ, Nahmias MA, Tait AN, Wu B, Prucnal PR. Simpel: Circuit model for photonic spike processing laser neurons. Opt Express (2015) 23:8029–44. doi:10.1364/OE.23.008029

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Nahmias MA, Tait AN, Shastri BJ, de Lima TF, Prucnal PR. Excitable laser processing network node in hybrid silicon: Analysis and simulation. Opt Express (2015) 23:26800–13. doi:10.1364/OE.23.026800

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tait AN, de Lima TF, Zhou E, Wu AX, Nahmias MA, Shastri BJ, et al. Neuromorphic photonic networks using silicon photonic weight banks. Sci Rep (2017) 7:7430. doi:10.1038/s41598-017-07754-z

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Peng H-T, Angelatos G, de Lima TF, Nahmias MA, Tait AN, Abbaslou S, et al. Temporal information processing with an integrated laser neuron. IEEE J Sel Top Quan Electron (2020) 26:1–9. doi:10.1109/JSTQE.2019.2927582

CrossRef Full Text | Google Scholar

21. Robertson J, Hejda M, Bueno J, Hurtado A. Ultrafast optical integration and pattern classification for neuromorphic photonics based on spiking VCSEL neurons. Sci Rep (2020) 10:6098. doi:10.1038/s41598-020-62945-5

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Uenohara H, Kawamura Y, Iwamura H, Nonaka K, Tsuda H, Kurokawa T. Operation characteristics of a side-light-injection multiple-quantum-well bistable laser for all-optical switching. J Appl Phys (2008) (1994) 33:815–21. doi:10.1143/jjap.33.815

CrossRef Full Text | Google Scholar

23. Nonaka K, Tsuda H, Kurokawa T, Uenohara H, lwamura H. Side-injection light control bistable laser diode with ingaas/inp mqw saturable absorption region. In: 13th IEEE International Semiconductor Laser Conference (1992). p. 132–3. doi:10.1109/ISLC.1992.763607

CrossRef Full Text | Google Scholar