Abstract
All previously published data on the dynamics of ethylene glycol conveying copper and gold nanoparticles over a convective surface, nothing is known about the importance of dual branch solutions. Hybrid nanofluids improve the thermal conductivity of the fluid. The nanoparticles copper and gold having ethylene glycol as a base fluid are used here. The flow problem is described over a stretching/shrinking surface with the influence of Ohmic heating, non-linear radiation, and a convectively heated surface. Furthermore, the magnetic field strength is applied perpendicular to the direction of the flow. To control the fluid, flow-governing equations are numerically solved by using bvp4c, a built-in approach in MATLAB. For hybrid nanomaterials, the consequence of different physical parameters is discussed graphically and with tabular data. A comparison with previous findings reveals that the present findings are in good agreement. The results revealed that the coefficient of skin friction for the physically stable branch declines over a certain range of shrinking parameters; nonetheless, for the unstable branch, the reverse pattern is discovered. The magnetic force diminishes the flow field and energy dispersion in the upper branch but improves it in the lower branch.
1 Introduction
In industries, heat transfer is used in a wide range of applications to lower and raise temperatures. The conditions for energy exchange in a system are provided by heat transfer fluids, and the effects of these fluids depend on their physical characteristics, including thermal conductivity, viscosity, density, and heat capacity. The low thermal conductivity of typical fluids such as water, ethylene glycol, or oil cannot achieve significant heat exchange rates in thermal engineering equipment. To overcome this barrier, ultrafine solid particles contained in ordinary fluids can be used to improve their thermal conductivity. A nanofluid is defined as a suspension of nano-sized particles in a regular base fluid. In the formulation of the nanofluids, usually metals, carbon nanotubes, and carbides as nanoparticles are utilized. The metal nanoparticles incorporate gold and silver while copper oxide, zinc oxide, and aluminum oxide are included into the category of oxide nanoparticles. In comparison to suspensions with millimeter- or micrometer-sized particles, nanofluids exhibit greater stability, rheological characteristics, and significantly higher thermal conductivities [1]. In modern technology, the use of nanofluids is to promote system miniaturization by lowering particle clogging. Numerous researchers have recently examined, both experimentally and theoretically, how nanofluids can improve heat transmission in thermal engineering devices. In order to calculate the thermophysical properties of nanofluids, researchers have used a range of preparation techniques, features, and models. Choi [2] developed the idea of nanofluids by suggesting that nanoparticles be suspended in a base fluid. Following that, several researchers studied the heat transport of a nanofluid for various aspects, either experimentally or numerically. For instance, Tiwari and Das [3] reported their work on the mathematical models of nanofluids. The efficiency of particle micromixing in heavy metal reduction procedures under different inlet conditions was covered by Karvelas et al. [4]. Benos et al. [5] discussed the theoretical model for natural convection of the CNT–water nanofluid flow that incorporates the revised Hamilton–Crosser model. Kouz et al. [6] presented the analysis of the heat transfer and entropy generation of a water–Fe3O4/CNT hybrid magnetic nanofluid flow in a trapezoidal wavy enclosure with porous media. Song et al. [7] considered a convectively heated vertical surface to examine the nanofluid influenced by a haphazard motion with the Buongiorno model. The hydromagnetic flow phenomenon of the Casson nanofluid with the involvement of an exponentially shrunk sheet was scrutinized by Ishtiaq and Nadeem [8]. Many researchers have used the Tiwari–Das nanofluid model to examine many aspects of the flow, including in Ref. [9–26].
Thermal radiation’s effect on heat transfer is becoming increasingly significant in the design of modern energy conversion systems that operate at high temperatures. Furthermore, thermal radiation is used to solve a wide range of technological difficulties, including combustion, nuclear reactor safety, solar collectors, and furnace design. A nanofluid has distinct features than either particles or the base fluid, so studying the effects of thermal radiation on the flow and heat transfer characteristics in a nanofluid has garnered a lot of attention. Due to this fact, numerous researchers have investigated the effects of thermal radiation on the flow, heat transfer, and other different features in a nanofluid. In a single-phase model, Hady et al. [27] investigated the boundary layer viscous flow and heat transfer properties of a nanofluid across a nonlinearly stretching sheet in the presence of thermal radiation. Mahanthesh et al. [28] investigated the radiative flow of the water-based nanofluid over a convectively heated surface. Shoaib et al. [29] numerically investigated the rotational flow of the magnetized hybrid nanofluid with radiation effects across a stretching sheet. Mabood et al. [30] discussed the irreversibility analysis in hybrid nanomaterials with nonlinear thermal radiation and melting heat transfer. Jamaludin et al. [31] explored the stagnation-point flow of a nanofluid due to a stretching/shrinking surface in the existence of thermal radiation, suction, and a heat source/sink. The comparative analysis for the radiative flow of hybrid nanomaterials and nanomaterials in a permeable porous medium was performed by Yasir et al. [32]. Very recently, Yasir et al. [33] further explored the dynamics of ethylene glycol transporting copper and titania nanoparticles on a curved object in the presence of nonlinear thermal radiation and a heat source/sink. The interesting articles that depend on heat transport through nanoparticles are in Ref. [34–44].
The existing examination is being held out to explore the radiative stagnation-point flow of hybrid nanomaterials subject to a permeable shrinking surface. As evidenced by the literature, investigation of the hybrid nanofluid stagnation-point flow is uncommon. In this scenario, gold and copper are mixed into the ethylene glycol base fluid to formulate a hybrid nanofluid that implements a stagnation-point flow mechanism on a shrinking sheet. Furthermore, the association between the aligned magnetic field and wall suction was scrutinized. The shooting technique was used to solve the resulting nonlinear ordinary differential equations, and the solution was calculated in terms of velocity, temperature, local Nusselt number, and skin friction coefficient, all of which are dictated by relevant flow parameters. In our perspective, we have extremely competitively investigated this problem. The several originalities of the current analysis are emphasized as follows:
(a) To efficiently manage the flow, the boundary layer separation points for various control parameters are shown.
(b) It is observed that the suitable amount of control parameters improved the rates of skin friction and heat transfer.
(c) What is the consequence of gold and copper nanoparticles on the thermal conductivity of ethylene glycol over a shrinking surface?
2 Mathematical formulation
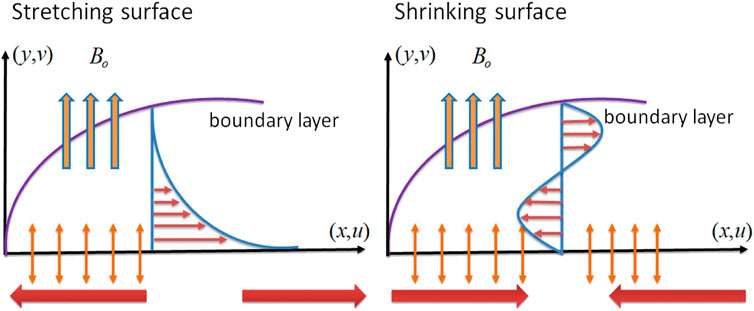
In the presence of a porous medium, the magnetized flow of a hybrid nanofluid over a permeable shrinking surface is considered. The physical coordinate system is depicted in Figure 1, where the x − axis is measured along the surface and the y − axis is normal to it. The hypothesis is that the velocity of the shrinking surface is and the free-stream velocity is . Furthermore, the surface temperature is Tw, while the ambient hybrid nanomaterial temperature is T∞. Tiwari and Das’ mathematical nanofluid model was used in this study. To investigate the thermal transport of a hybrid nanofluid, Ohmic heating and viscous dissipation with nonlinear thermal radiation over a convectively heated surface are taken into account.
FIGURE 1
The model equations for hybrid nanomaterials are as follows:
The related boundary conditions are as follows:where v and u symbolize the hybrid nanomaterial velocity components along the y and x directions, respectively. T is the fluid temperature, vw signifies the velocity mass flux, and the radiative heat flux qr is defined as follows:in which k∗ symbolizes the Stefan–Boltzmann constant and σ∗ represents the mean absorption coefficient.
Lettingwhich converts the governing Eqs. 2–4 as
with boundary conditionsHere, is the constant stretching/shrinking parameter, is the magnetic field, is the mass flux constant, is the porous media permeability parameter, is the Prandtl number, is the temperature ratio parameter, is the Eckert number, is the thermal radiation, and is the Biot number.
The skin friction coefficient Cf and heat transfer rate Nux are expressed aswhere τw and qw are defined asBy using equation , the dimensionless form of the equation iswhere is the local Reynolds number; μhnf, ρhnf, khnf, , and σhnf are the hybrid nanomaterials’ dynamic viscosity, effective density, thermal conductivity, heat capacity, and electrical conductivity, respectively, which are defined as [45]. Further, the thermo-physical properties also defined in Table 1,
TABLE 1
| Physical property | Nanoparticles | Base fluid | |
|---|---|---|---|
| Gold (Au) | Copper (Cu) | Ethylene glycol | |
| 2430 | |||
| k1 = 318 | k2 = 401 | 0.253 | |
| ρ1 = 19300 | ρ2 = 8933 | 1115 | |
| Pr | — | — | 2.0363 |
Thermo-physical properties of the base fluid and nanoparticles .
3 Graphical analysis
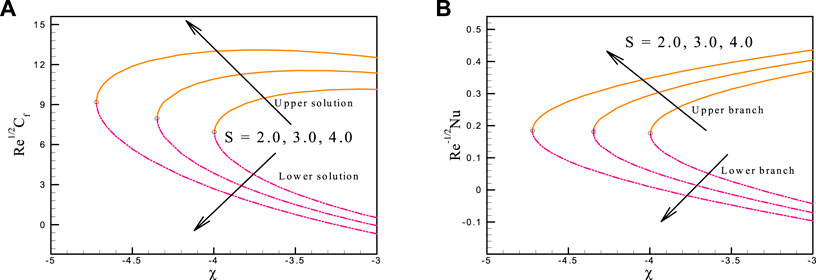
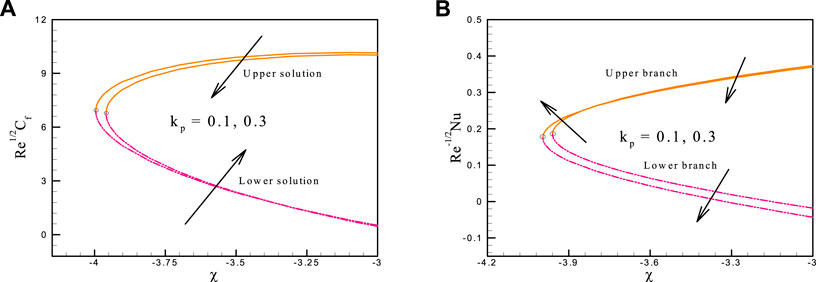
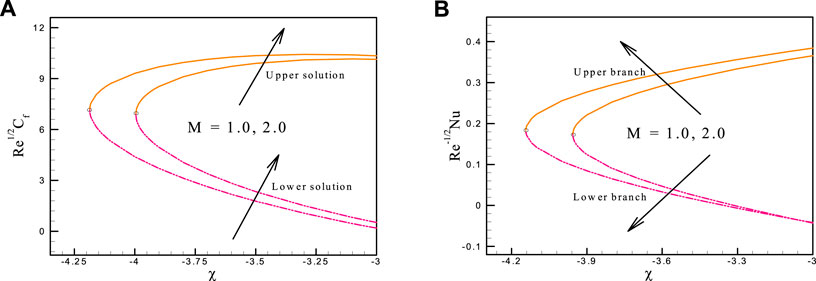
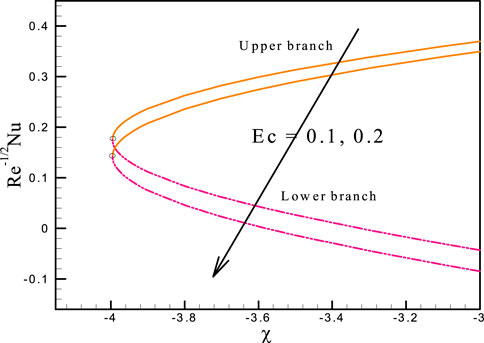
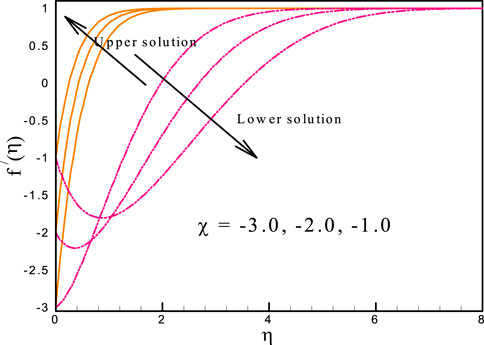
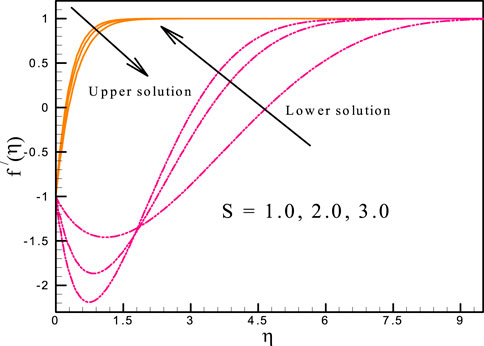
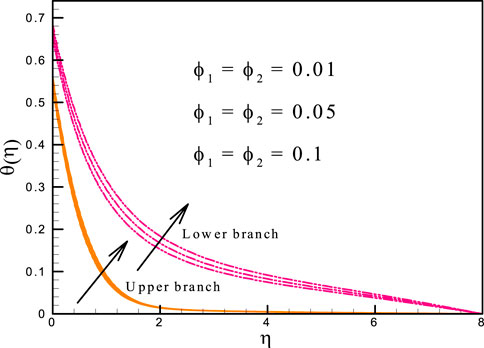
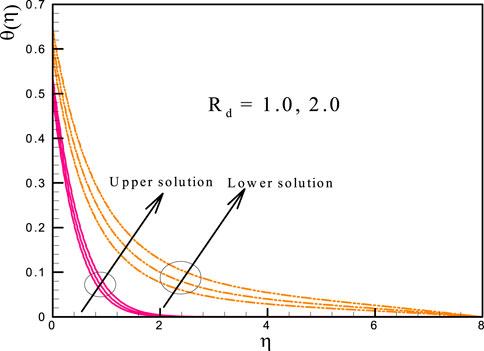
This study’s objectives include the following: (i) investigating the effects of relevant parameters on the flow and heat transfer; (ii) detecting the existence of dual solutions; and (iii) verifying the nature of the solution. As a result, the outcomes and discussions regarding the goal will be clarified in this part. The numerical solution is determined using the following control parameters: The results are presented in a graphical style to provide a better understanding of the effect of the physical parameter. The variation of and against χ with the interpretation of S are portrayed in Figures 2A, B. According to these figures, solutions exist in the range χc < χ for hybrid nanomaterials, but no solution occurs beyond the turning points, that is, when χ < χc. The region’s outcome route clearly widens as the value of S increases, with the bifurcation values of χc. Furthermore, in the physically stable branch of the solution, the skin friction coefficient increases, whereas in the unstable branch, the opposite tendency is observed. As the porous medium is taken into account in this model, so Figures 3A, B depict the fluctuation of and against the shrinking parameter χ with different values of the porosity parameter . It is seen that the boundary layer bifurcates at the crucial points χc = −3.9592 at and χc = −3.9954 at . This also implies that increasing the porosity parameter kp delays the bifurcation process. As a result of the increased porosity parameter k, the skin friction coefficient decreases for the upper solution and increases for the lower branch solution, while the local Nusselt number shows a decline trend. Furthermore, the rising behavior of the magnetic field parameter M on and is depicted in Figures 4A, B. The magnetic field is influenced more by the dispersion of Au nanoparticles in the nanofluid. The rate of heat transfer increases with the concentration of nanoparticles because intermolecular collisions increase the kinetic energy. Additionally, the skin friction coefficient demonstrates a similar impact. Figure 5 shows the influence of the Eckert number Ec on in the direction of χ. In the first and second solutions, raising Ec slows down the rate of heat transportation. However, the uncertainty in the boundary layer partition is unaffected by the increasing Eckert number. As a result, the dual branches are only applicable up to the identical critical value for all Ec values. Figure 6 represents the effects of shrinking velocity on the dimensionless velocity profile. It is observed that the velocity profile significantly decreases with shrinking velocity for the upper branch solution, while increases for the lower branch solution. The physical importance of this problem shows that in the case of dual solutions, the flow separates from the plate, which is very important for many practical problems. The fluctuation of the mass suction parameter S on the velocity profile in relation to the similarity variable η is shown in Figure 7. Here, it is noted that suction diminishes the thickness of the related boundary layer due to the physical increase in velocity distribution. Figure 8 depicts the effect of the volume percentage of nanoparticles on the temperature distribution. Because of an upsurge in the kinetic energy of the system, the fluid temperature inclines. This increase in kinetic energy promotes thermal transfer. Figure 9 demonstrates the influence of γ on the temperature distribution. The Biot number improves the temperature of the fluid in consort with the boundary layer thickness. In actuality, increasing the Biot number improves the penetration depth. To study the behavior of thermal distribution for distinct values of Ec,Figure 10 is sketched. Since Ec is derived from the appearance of the Joule heating result, the increment in Ec also indicates that a stronger heat generation from the electric current reference has been considered to the conducting sheet, which therefore generates the upgrade in temperature. Figure 11 is sketched to analyze the nature of temperature distribution for various values of . It is found that the fluid temperature and the associated thickness, both are enhanced on increasing θw. Figure 12 shows the effect of thermal radiation on , and it can be seen from this figure that rises as Rd is increased. This is because as Rd is increased, the fluid absorbs more heat, causing a rise in .
FIGURE 2
FIGURE 3
FIGURE 4
FIGURE 5
FIGURE 6
FIGURE 7
FIGURE 8
FIGURE 9
FIGURE 10
FIGURE 11
FIGURE 12
The numerical outputs of the existing analysis with those reported in Ref. [45] for distinct values of the shrinking parameter are scrutinized, and the outcomes are demonstrated in Table 2. The obtained results are extremely compact, providing confidence in the current procedure’s validity.
TABLE 2
| χ | Hafeez et al. [46] | Current results | ||
|---|---|---|---|---|
| Upper solution | Lower solution | Upper solution | Lower solution | |
| −0.25 | 1.4022331 | — | 1.4021311 | — |
| −0.50 | 1.4958565 | — | 1.4947538 | — |
| −0.75 | 1.4893224 | — | 1.4893124 | — |
| −1.00 | 1.3281191 | 0 | 1.3287901 | — |
| −1.15 | 1.0823058 | 0.1160042 | 1.0824134 | 0.1166937 |
| −1.20 | 0.9320782 | 0.2336751 | 0.9325191 | 0.2334401 |
Comparison of for distant values of χ.
4 Numerical solution procedure
By permitting the following condition to exist, we performed the procedure:
5 Conclusion
The goal of the current research is to identify the multiple solutions for the magneto-hybrid nanofluid flow due to a shrinking surface. Additionally, the incorporated consequences of Ohmic heating and non-linear thermal radiation over a convectively heated surface are discussed comprehensively through graphical structures. In this study, multiple solutions occur for various ranges of the shrinking parameter. This research can be summarized in the following way:
• The existence of a shrinking surface promotes the discovery of dual solutions.
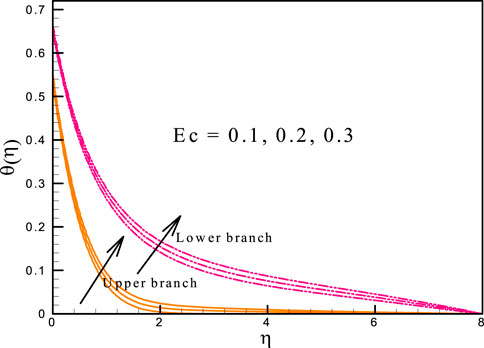
• It may be possible to decrease the flow velocity and raise the flow temperature by using higher joule heating and viscous dissipation effects.
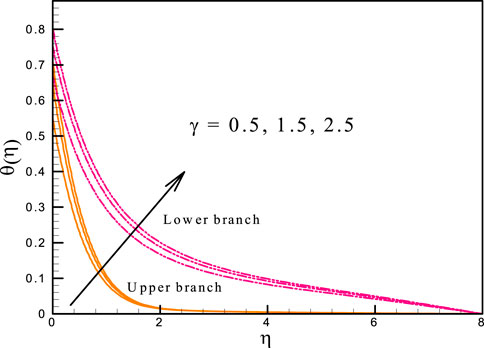
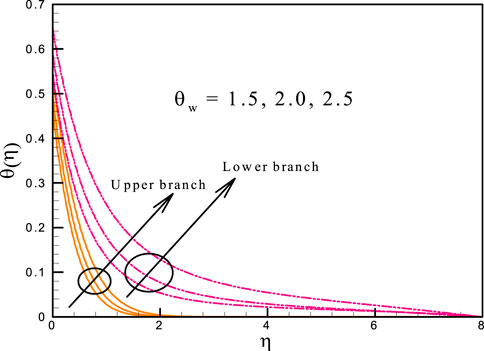
• For large values of the Biot number, the temperature distribution and thermal transport rate are more prominent.
• The suction parameter reduces the fluid velocity in the upper branch, while it is enhanced in the lower branch.
• In a physical stable branch, an increasing magnetic strength raises the skin friction coefficient.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Materials; further inquiries can be directed to the corresponding author.
Author contributions
MN: conceptualization, validation, writing review, and editing. SA: Conceptualization. ZW: Methodology, software. AA: Validation of results. ET‐e: Writing original draft preparation, MY: Helping in review processing.
Acknowledgments
The study was supported by the Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R52), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Nomenclature
- αhnf
thermal diffusivity [m2s−1]
- khnf
thermal conductivity [kgmK−1s−3]
specific heat [m2s−2K−1]
- μhnf
dynamic viscosity [kgm−1s−1]
- νhnf
kinematic viscosity [m2s−1]
- ρhnf
density [kgm−3]
- ϕ1
Au volume fraction
- ϕ2
Cu volume fraction
- u, v
velocity components [ms−1]
- T
fluid temperature [K]
- T∞
ambient temperature [K]
- M
magnetic parameter
- Pr
Prandtl number
- Rd
radiation parameter
- Ec
Eckert number
- χ
stretching/shrinking parameter
- f ′
dimensionless velocity
- θ
dimensionless temperature
References
1.
LiuMSLinMCCHuangITWangCC. Enhancement of thermal conductivity with carbon nanotube for nanofluids. Int Commun Heat Mass Transfer (2005) 32(9):1202–10. 10.1016/j.icheatmasstransfer.2005.05.005
2.
ChoiSUS. Enhancing thermal conductivity of fluids with nanoparticles. ASMEPublications-Fed (1995) 231:99–106.
3.
TiwariRKDasMK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf (2007) 50(9-10):2002–18. 10.1016/j.ijheatmasstransfer.2006.09.034
4.
KarvelasELiosisCBenosLKarakasidisTSarrisI. Micromixing efficiency of particles in heavy metal removal processes under various inlet conditions. Water (2019) 11(6):1135. 10.3390/w11061135
5.
BenosLTKarvelasEGSarrisIE. A theoretical model for the magnetohydrodynamic natural convection of a CNT-water nanofluid incorporating a renovated Hamilton-Crosser model. Int J Heat Mass Transf (2019) 135:548–60. 10.1016/j.ijheatmasstransfer.2019.01.148
6.
Al-KouzWAbderrahmaneAShamshuddinMDYounisOMohammedSBégOAet alHeat transfer and entropy generation analysis of water-Fe3O4/CNT hybrid magnetic nanofluid flow in a trapezoidal wavy enclosure containing porous media with the Galerkin finite element method. Eur Phys J Plus (2021) 136(11):1184. 10.1140/epjp/s13360-021-02192-3
7.
SongYQObideyiBDShahNAAnimasaunILMahrousYMChungJD. Significance of haphazard motion and thermal migration of alumina and copper nanoparticles across the dynamics of water and ethylene glycol on a convectively heated surface. Case Stud Therm Eng (2021) 26:101050. 10.1016/j.csite.2021.101050
8.
IshtiaqBNadeemS. Theoretical analysis of Casson nanofluid over a vertical exponentially shrinking sheet with inclined magnetic field. Waves in Random and Complex Media (2022) 1–17. 10.1080/17455030.2022.2103206
9.
SarrisIEKassinosSCCaratiD. Large-eddy simulations of the turbulent Hartmann flow close to the transitional regime. Phys Fluids (1994) (2007) 19(8):085109. 10.1063/1.2757710
10.
RiazAEllahiRSaitSM. Role of hybrid nanoparticles in thermal performance of peristaltic flow of Eyring–Powell fluid model. J Therm Anal Calorim (2021) 143(2):1021–35. 10.1007/s10973-020-09872-9
11.
RajaMAZShoaibMTabassumRKhanMIGowdaRPPrasannakumaraBCet alIntelligent computing for the dynamics of entropy optimized nanofluidic system under impacts of MHD along thick surface. Int J Mod Phys B (2021) 35(26):2150269. 10.1142/s0217979221502696
12.
ShamshuddinMDEidMR. Magnetized nanofluid flow of ferromagnetic nanoparticles from parallel stretchable rotating disk with variable viscosity and thermal conductivity. Chin J Phys (2021) 74:20–37. 10.1016/j.cjph.2021.07.038
13.
RiazAKhanSUDZeeshanAKhanSUHassanMMuhammadT. Thermal analysis of peristaltic flow of nanosized particles within a curved channel with second-order partial slip and porous medium. J Therm Anal Calorim (2021) 143(3):1997–2009. 10.1007/s10973-020-09454-9
14.
SowmyaGGireeshaBJAnimasaunILShahNA. Significance of buoyancy and lorentz forces on water-conveying iron (III) oxide and silver nanoparticles in a rectangular cavity mounted with two heated fins: heat transfer analysis. J Therm Anal Calorim (2021) 144(6):2369–84. 10.1007/s10973-021-10550-7
15.
SabuASMackolilJMahantheshBMathewA. Reiner-Rivlin nanomaterial heat transfer over a rotating disk with distinct heat source and multiple slip effects. Appl Math Mech (2021) 42(10):1495–510. 10.1007/s10483-021-2772-7
16.
MahantheshBShashikumarNSLorenziniG. Heat transfer enhancement due to nanoparticles, magnetic field, thermal and exponential space-dependent heat source aspects in nanoliquid flow past a stretchable spinning disk. J Therm Anal Calorim (2021) 145(6):3339–47. 10.1007/s10973-020-09927-x
17.
YasirMAhmedAKhanM. Carbon nanotubes based fluid flow past a moving thin needle examine through dual solutions: Stability analysis. J Energ Storage (2022) 48:103913. 10.1016/j.est.2021.103913
18.
UmavathiJCPatilSLMahantheshBBégOA. Unsteady squeezing flow of a magnetized nano-lubricant between parallel disks with Robin boundary conditions. Proc Inst Mech Eng N: J Nanomater Nanoengineering Nanosystems (2021) 235(3-4):67–81. 10.1177/23977914211036562
19.
SalawuSOShamshuddinMDBégOA. Influence of magnetization, variable viscosity and thermal conductivity on Von Karman swirling flow of H2O-FE3O4 and H2O-Mn-ZNFe2O4 ferromagnetic nanofluids from a spinning DISK: Smart spin coating simulation. Mater Sci Eng B (2022) 279:115659. 10.1016/j.mseb.2022.115659
20.
YasirMHafeezAKhanM. Thermal conductivity performance in hybrid (SWCNTs-CuO/Ehylene glycol) nanofluid flow: Dual solutions. Ain Shams Eng J (2022) 13(5):101703. 10.1016/j.asej.2022.101703
21.
GowdaRJPKumarRNPrasannakumaraBC. Two-phase Darcy-Forchheimer flow of dusty hybrid nanofluid with viscous dissipation over a cylinder. Int J Appl Comput Math (2021) 7(3):1–18. 10.1007/s40819-021-01033-2
22.
KumarRNGowdaRPAbusorrahAMMahrousYMAbu-HamdehNHIssakhovAet alImpact of magnetic dipole on ferromagnetic hybrid nanofluid flow over a stretching cylinder. Phys Scr (2021) 96(4):045215. 10.1088/1402-4896/abe324
23.
HouEWangFKhanMNAhmadSRehmanAAlmalikiAHet alFlow analysis of hybridized nanomaterial liquid flow in the existence of multiple slips and Hall current effect over a slendering stretching surface. Crystals (Basel) (2021) 11(12):1546. 10.3390/cryst11121546
24.
FerdowsMShamshuddinMDSalawuSORezaM. Computation of heat transfer in magnetised Blasius flow of nano-fluids with suspended carbon nanotubes through a moving flat plate. Int J Ambient Energ (2022) 1–9. 10.1080/01430750.2022.2075933
25.
AnimasaunILShahNAWakifAMahantheshBSivarajRKorikoOK. Ratio of momentum diffusivity to thermal diffusivity: introduction, meta-analysis, and scrutinization. Florida: CRC Press (2022).
26.
YasirMSarfrazMKhanMAlzahraniAKUllahMZ. Estimation of dual branch solutions for Homann flow of hybrid nanofluid towards biaxial shrinking surface. J Pet Sci Eng (2022) 218:110990. 10.1016/j.petrol.2022.110990
27.
HadyFMIbrahimFSAbdel-GaiedSMEidMR. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res Lett (2012) 7(1):229–13. 10.1186/1556-276x-7-229
28.
MahantheshBGireeshaBJGorlaRSR. Nonlinear radiative heat transfer in MHD three-dimensional flow of water based nanofluid over a non-linearly stretching sheet with convective boundary condition. J Niger Math Soc (2016) 35(1):178–98. 10.1016/j.jnnms.2016.02.003
29.
ShoaibMRajaMAZSabirMTIslamSShahZKumamPet alNumerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet. Sci Rep (2020) 10(1):18533–15. 10.1038/s41598-020-75254-8
30.
MaboodFYusufTAKhanWA. Cu–Al2O3–H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J Therm Anal Calorim (2021) 143(2):973–84. 10.1007/s10973-020-09720-w
31.
JamaludinANazarRPopI. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies (2019) 12(5):788. 10.3390/en12050788
32.
YasirMKhanM. Comparative analysis for radiative flow of Cu–Ag/blood and Cu/blood nanofluid through porous medium. J Pet Sci Eng (2022) 215:110650. 10.1016/j.petrol.2022.110650
33.
YasirMKhanMSarfrazMAbuzaidDUllahMZ. Exploration of the dynamics of ethylene glycol conveying copper and titania nanoparticles on a stretchable/shrinkable curved object: Stability analysis. Int Commun Heat Mass Transfer (2022) 137:106225. 10.1016/j.icheatmasstransfer.2022.106225
34.
MahantheshB. Flow and heat transport of nanomaterial with quadratic radiative heat flux and aggregation kinematics of nanoparticles. Int Commun Heat Mass Transfer (2021) 127:105521. 10.1016/j.icheatmasstransfer.2021.105521
35.
GowdaRJPKumarRNJyothiAMPrasannakumaraBCSarrisIE. Impact of binary chemical reaction and activation energy on heat and mass transfer of marangoni driven boundary layer flow of a non-Newtonian nanofluid. Processes (2021) 9(4):702. 10.3390/pr9040702
36.
AbdelmalekZKhanSUWaqasHRiazAKhanIATliliI. A mathematical model for bioconvection flow of Williamson nanofluid over a stretching cylinder featuring variable thermal conductivity, activation energy and second-order slip. J Therm Anal Calorim (2021) 144(1):205–17. 10.1007/s10973-020-09450-z
37.
RanaPMackolilJMahantheshBMuhammadT. Cattaneo-Christov Theory to model heat flux effect on nanoliquid slip flow over a spinning disk with nanoparticle aggregation and Hall current. Waves in Random and Complex Media (2022) 1–23. 10.1080/17455030.2022.2048127
38.
GowdaRJPKumarRNJyothiAMPrasannakumaraBCNisarKS. KKL correlation for simulation of nanofluid flow over a stretching sheet considering magnetic dipole and chemical reaction. ZAMM - J Appl Math Mech/Z Angew Mathematik Mechanik (2021) 101(11):e202000372. 10.1002/zamm.202000372
39.
RiazAZeeshanABhattiMM. Entropy analysis on a three-dimensional wavy flow of eyring–powell nanofluid: a comparative study. Math Probl Eng (2021). 10.1155/2021/6672158
40.
GowdaRJKumarRNRaufAPrasannakumaraBCShehzadSA. Magnetized flow of sutterby nanofluid through cattaneo-christov theory of heat diffusion and stefan blowing condition. Appl Nanosci (2021) 1–10. 10.1007/s13204-021-01863-y
41.
KhanMYasirMAlshomraniASSivasankaranSAladwaniYRAhmedA. Variable heat source in stagnation-point unsteady flow of magnetized Oldroyd-B fluid with cubic autocatalysis chemical reaction. Ain Shams Eng J (2022) 13(3):101610. 10.1016/j.asej.2021.10.005
42.
MaboodFMackolilJMahantheshBSEPRaufAShehzadSA. Dynamics of Sutterby fluid flow due to a spinning stretching disk with non-Fourier/Fick heat and mass flux models. Appl Math Mech (2021) 42(9):1247–58. 10.1007/s10483-021-2770-9
43.
KumarRNSureshaSGowdaRJMegalamaniSBPrasannakumaraBC. Exploring the impact of magnetic dipole on the radiative nanofluid flow over a stretching sheet by means of KKL model. Pramana - J Phys (2021) 95(4):180–9. 10.1007/s12043-021-02212-y
44.
GowdaRPMallikarjunaHBPrasannakumaraBCKumarRNManjunathaPT. Dynamics of thermal Marangoni stagnation point flow in dusty Casson nanofluid. Int J Model Simul (2021) 42 (5), 1–9. 10.1080/02286203.2021.1957330
45.
Abo-ElkhairREBhattiMMMekheimerKS. Magnetic force effects on peristaltic transport of hybrid bio-nanofluid (AuCu nanoparticles) with moderate Reynolds number: An expanding horizon. Int Commun Heat Mass Transfer (2021) 123:105228. 10.1016/j.icheatmasstransfer.2021.105228
46.
HafeezAYasirMKhanMMalikMYAlqahtaniAS. Buoyancy effect on the chemically reactive flow of Cross nanofluid over a shrinking surface: Dual solution. Int Commun Heat Mass Transfer (2021) 126:105438. 10.1016/j.icheatmasstransfer.2021.105438
Summary
Keywords
stretching/shrinking surface, stagnation-point flow, non-linear thermal radiation, hybrid nanomaterials, dual solution
Citation
Naveed Khan M, Alhowaity S, Wang Z, Alqahtani AM, Tag-eldin E and Yassen MF (2022) Significance of multiple solutions on the dynamics of ethylene glycol conveying gold and copper nanoparticles on a shrinking surface. Front. Phys. 10:1014644. doi: 10.3389/fphy.2022.1014644
Received
08 August 2022
Accepted
07 September 2022
Published
17 October 2022
Volume
10 - 2022
Edited by
Animasaun I. L., Federal University of Technology, Nigeria
Reviewed by
Sanatan Das, University of Gour Banga, India
Mohammed Shamshuddin, Vaagdevi College of Engineering, India
Mahanthesh B., Christ University, India
Updates
Copyright
© 2022 Naveed Khan, Alhowaity, Wang, Alqahtani, Tag-eldin and Yassen.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aisha M. Alqahtani, Alqahtani@pnu.edu.sa
This article was submitted to Interdisciplinary Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.