A new statistical thermodynamic mechanism for quantum mechanics

A new quantum mechanics mechanism theory based on statistical mechanics is introduced. This theory is based on corresponding changes in the number of states with associated energy changes at the observer and observed occurring at observer 1) reset and 2) observation. It is shown that a) the change in the number of states has different consequences than determining the “value” obtained at observation, where each state is a possible interaction between the system and the environment. The number of bits, as a measure of information content, is determined in discrete cell size increments. Two experiments are proposed to validate the introduced mechanism. The first experiment is to determine the spatial and temporal characteristics of energy changes and how they are related to the observer and observed during the entire measurement process. The second experiment is designed to determine timing between changes in the number of states in the system at observer reset. It is anticipated that these experiments will demonstrate no time delay, an entangled process, and, hence, explain delayed choice observations. Moreover, they would demonstrate that bits not stored in the system are transferred to the environment at observer reset, so when the number of inputs is greater than the number of outputs, an energy change occurs and interference is observed (wave characteristics). Conversely, if the number of inputs equals the number of outputs, no energy change occurs and no interference is observed (particle characteristics). It is envisioned that upon validating this mechanism theory, it will further the understanding of the measurement process and entanglement’s involvement in that process.

Introduction

Quantum mechanics is used as a very effective tool in explaining numerous physical phenomena as well as in many practical applications. There have been numerous attempts to explore and understand the fundamental mechanisms in quantum physics that are based on understanding the quantum measurement process. These measurements are frequently performed and described as “collapse of the wave function”. The mechanism between the inputs and outputs of observations is unknown. Feynman described the basis of understanding quantum mechanics is to understand the mechanism of the double-slit experiment [1], whereas Schrodinger described it based on the understanding of entanglement [2, 3]. Though there have been numerous descriptions of possible mechanisms, many are not testable and even the ones that are testable have not been shown to explain the observations.

This work introduces a new mechanism in which an observation provides new information to the observer regarding the state of the observed leaving the subsequent state of the observed unknowable by the observer unless the observer is reset (ability to make an observation). Using this theory, the changes in energy due to entropic changes can be used to determine when and where the energy changes due to an observation (measurement) can be determined. This mechanism postulates that information changes when observers are reset, that is, equivalent to adding observers, which decreases the number of superposition states at the observed and increases the number of states in the environment, resulting in increased energy in the environment. Observers’ observations have the opposite effect where the states are transferred to the system and energy in the environment is decreased. This is consistent with the conservation of energy.

Quantum mechanics is used to determining the probability of each possible observation. The number of possible observations is inversely proportional to the amount of information in a system, that is, the greater the number of possibilities, the less information is available which is associated with a corresponding increase in entropy. An observation is a result of what an observer is capable of observing after observer reset, which defines the domain of the possible observations. The amount of missing information is based on the resolution (cell size and type) used to define a state, that is, how the information is defined. A state is defined as a possible relationship between a system and the environment. As the domain of the observation decreases, the number of possible states decreases, and the probability of observing any given state that exists prior to the observation increases.

In order to validate the introduced concepts, two experiments are proposed. These experiments are designed to analyze energy changes in the observed and observer due to a change in the number of relationships in the system when 1) the observer is reset, 2) the observer makes the observation, and 3) the observer is again reset. The second experiment is designed to determine the time relationship between the reset of the observer and changes at the observed, particularly the possibility of no delay, which provides additional insight regarding the mechanism of an observation.

Historical background

Early interpretations for possible mechanisms of quantum mechanics were explained by Niels Bohr and Werner Heisenberg and summarized in the “Copenhagen interpretation” [4], which consists of several different but related views. Per these views, the properties of particles do not exist without an observer’s observation [5]. This was tested by an experiment designed by Bell, which verified that properties may not exist prior to observation [6]. Challenges to the Copenhagen interpretation came from Bohm, who proposed the pilot wave interpretation [7–9]. This was related to an earlier study by De Broglie known as the De Broglie–Bohm interpretation [10]. It is a non-local theory incorporating pilot waves, which has similarities to the transactional interpretation involving a wave from the source to the receiver and the receiver to the source [11]. A further challenge came from Everett who proposed the many worlds interpretation, which requires a splitting of universes each time there is a wave function collapse [12]. Other proposed mechanisms include a relational interpretation by Rovelli, which involves the correlation between the system and observers so different observers may observe different results [13]. Retro-causality has also been considered as a possible mechanism, where past events affect future events [14]. More recent interpretations include quantum information theories [15]. These theories range from predicting outcomes based on how the system was prepared to involving the consciousness of the observer [16]. However, these interpretations do not have experimental validation. The Copenhagen interpretation is the most mainstream, though it only applies to post measurements.

Similarly, information theory and statistical mechanics have been shown to be related. Shannon demonstrated the similarity between the equation for entropy and information [17–19], which has been verified experimentally [20]. Landauer’s results [21–24] followed by an in-depth analysis by Bennet [25–27] demonstrated that in a typical gate where the number of inputs is greater than the number of outputs, as in an ideal “AND” gate, energy is consumed not in the computation but in the reset of the gate so it can be reused. This decreases the number of relationships at the gate (reset reduces unknown information.) The number of superposition states at the gate decreases and energy is dissipated to the environment, which results in increased temperature. The information is copied into the inputs of the gate at no energy cost. The gate output is represented by only one value and has less information content than the inputs. No energy is used until the reverse computation is attempted. This is the reverse of the initial computation, in which one input (the previous output of the gate) results in two possible outputs (the two previous inputs to the gate), which are now in a superposition of states (four total number of possible states) [28, 29].

There are various definitions of entropy previously well-presented in the literature. These include the relationship between entropy and fractals, which are based on counting fractal dimensions applied to dynamic entropic systems to categorize loss of information [30–32]. The fractal distribution of prime numbers has also been applied to physical systems [32]. Fractal dimensions have been shown to provide a finer measure of the complexity of a set up to infinity as a mathematical abstraction; hence, it is not applicable to real-world physical systems. However, fractals that incorporate finite iterative recursiveness, pre-fractals, are useful in real-world applications that improve entropy computations [30, 31]. Discreteness, finite difference, is inherent in quantum mechanics, so infinite iterations cannot be used for the non-zero probability of events to measure entropy. Entropy needs to be compatible with a defined measure for diversity (a discrete scale Rényi entropy, a generalization of Shannon entropy) [30]. The Weierstrass spectrum derived from the fractal Weierstrass–Mandelbrot dimension function can be generated by a quantum mechanical Hamiltonian for a weakly singular potential [33]. The solutions for non-relativistic particles with discrete energy levels that satisfy Schrodinger’s equation are shown to form a geometric progression when the spectrum is compatible with the Weierstrass form for an initial fixed negative energy level under certain weakly singular potential [34].

More recent considerations for analyzing quantum mechanical systems are based on wavelet analysis, which is localized in both time and frequency and can be optimized by the selection of the proper scale factor for specific applications. Fractional wavelet transforms provide time and fractional domain information simultaneously, which are a generalization and improvement of the classical wavelet transform in the functional Fourier transform domain, localized only in frequency. Wavelet basis is used to investigate the function’s behavior in the time-frequency plane of the Heisenberg box. The choice of the family of wavelets affects how the wavelet transforms and has been evaluated for positive definite distributions, which have applications to quantum mechanics and the determination of entropy [30]. Adaptive multi-scale wavelet decomposition improves classical signal processing techniques by including graphical structure information in the analysis, and it has extended technological capabilities for graphic signal processing [35]. A relevant application has been in Shannon entropy-based adaptive decomposition algorithms [36].

Methodology

This theory introduces the mechanism in quantum mechanics as a function of entropy and information. Moreover, it makes an analogy between a computer “AND” gate and double-slit systems. Based on this analogy, several new interrelated concepts are introduced for the mechanism in quantum mechanics observed in multi-slit systems. These include the following:

1. Statistical mechanics is related to that of quantum mechanics. If the number of states (multiplicity), not value, is significant, then quantum mechanics can be related to statistical mechanics in physical systems. Both deal with the number of physical states that result in a macroscopic observation.

2. To eliminate interference in multi-slit experiments, the number of outputs (observers), including the final detector screen, must be equal to the number of inputs (states).

3. The information decreases at the slits when observers make an observation. Conversely, the information increases at the reset of the observers due to the existence of fewer possible interactions (paths) between the system and the environment.

4. The mechanism for the change in the number of states is an instantaneous, entanglement-type process.

Three independent assumptions are made, which are as follows:

1. Changes in the number of superposition states result in an energy change [37].

2. Observer’s reset and observation changes the number of superposition states at the observed.

3. The effect of reset and observation of the observer on the observed is near instantaneous as an entangled-type process. This effect is not communicated by a wave and does not have a known value, which is transferred at the speed of light or less.

The introduced theory is founded on the notion that quantum information is based on the number of states whereas classical information is based on the value of the state. The introduced theorem postulates that there is no delay between the reset of the observer and the beginning of changes in the number of relationships at the observed, which occurs in a near infinitesimal elapse of time. Based on the results, this may explain observations of dark energy and dark matter without additional particles since near instantaneous changes in the number of relationships with observer reset/observation at observed/observer also applies to astronomical distances.

Near instantaneous time increment

The near instantaneous time increment is defined as one Boltzmann time increment, which corresponds to the energy change due to 1 bit of information developed as follows.

Using statistical thermodynamics, if all the microstates possess the same probability, the entropy can be defined as follows [38, 39]:

$S_B=k_B\mathit{ln}\left(W\right),(1)$

where $k_B$ is the Boltzmann constant and $W$ is the number of microstates that are directly related to the macroscopic thermodynamic state; therefore, $S$ is temperature dependent. Analogously, Shannon entropy in information theory can be expressed in units of bits per cell size, defined as follows [18]:

$S_S=k_B{\log }_{2}W.(2)$

Therefore, $S_B=\mathit{ln}\left(2\right)S_S$, where $\mathit{ln}\left(2\right)$ is the conversion multiplier for Shannon entropy (defined in base $2$) to the physical entropy (defined in base $e$).

On the other hand, entropy can be related to the change in energy as follows:

$S=\frac{∆E}{T},(3)$

where $∆E$ is the change in energy, and $T$ is the temperature measured in Kelvin. Combining Eqs 2, 3, one obtains the following:

$k_B=\frac{∆E}{T{\log }_{2}W}.(4)$

Using Eq. 4, in an isothermal system, the energy for 1 bit corresponds to one unit change of Boltzmann constant, that is, ($W$ = 2); hence, (${\log }_{2}W=1$). Therefore, Eq. 4 becomes the following:

$k_B=\frac{∆E}{T}.(5)$

Considering Planck’s relationship,

$∆E=h\vartheta ,(6)$

where $h$ is Planck’s constant and $\vartheta$ is the wave frequency. The period (time) corresponding to the energy change due to 1 bit of information change is as follows:

$∆t=\frac{h}{∆E}.(7)$

Combining Eqs 5, 7, one obtains the following:

$∆t=\frac{h}{k_{B}T}.(8)$

Substituting the values for Boltzmann’s constant ($k_B=1.38064852\times {10}^{-23}{m}^2\mathrm{k}\mathrm{g}{s}^{-2}{K}^{-1}$) and Planck’s constant $\left(h=6.62607004\times {10}^{-34}{m}^2\mathrm{k}\mathrm{g}/\mathrm{s}\right.$), the time corresponding to the energy change due to 1 bit of information change is $∆t=4.8\times {10}^{-11}/T\left(\mathit{sec}\right)$, which defines the near-instantaneous time increment as one Boltzmann time increment.

Application of the developed theory to thermodynamics and quantum mechanics

This theory only considers ideal cases, that is, energy conversion occurs with no losses. It postulates that a change in the number of states, not value, has a significant energetic effect; thus, quantum mechanics is related to statistical mechanics in physical systems. This is because both quantum mechanics and statistical mechanics are a result of microscopic information not available to a macroscopic observation in a system. Therefore, a holistic analysis of the entire system, not individual components, for quantum mechanics and statistical mechanics is required. Fundamentally, using the aforementioned definition of states, entropy in statistical mechanics can be used to predict the probability of observations in quantum mechanics.

In thermodynamics, there is typically no corresponding relationship to superposition in quantum mechanics. In this theory, each possible relationship between the source and slits in the double (multi)-slit experiment is considered as a separate state. Since entropy is proportional to the number of states, the entropy in this case is proportional to the number of possible relationships. The number of states, including superposition states, is quantified by entropy in statistical mechanics. Quantum distinguishable and quantum indistinguishable states are individual states. In quantum mechanics experiments, if the number of states is greater than the number of outputs, superposition exists. In general, when information is added to any system, some states are eliminated, resulting in decreased entropy (information increased). This theory postulates that information is added at observer reset. By considering each possible relationship as a separate state, entropy is associated with a discrete version of a modified Feynman’s sum-over-histories.

In a physical system with probabilistic multiple states, there is an associated entropy corresponding to the number of ways the states can be distributed. This implies that a change in the number of superposition states changes the entropy, which has an associated change in thermal energy per unit of temperature not available for work. The experiment performed by Lucia and Hackermuller [40] indicates the validity of this concept. Moreover, as Schrodinger’s equation does not have direct temperature dependence, it may not predict the complete behavior of that system, though, the temperature dependence in Schrodinger’s equation may be inherent in the energy component. As such, the incorporation of entropy in the analysis, which has direct temperature dependence, may be a more complete description.

In the case explained previously, the entropy due to the number of distinguishable microstates is as follows:

$S_S^D=k_B{\log }_2{W}_D,(9)$

where $W_D$ is the number of distinguishable microstates. Similarly, the entropy due to the number of indistinguishable microstates is as follows:

$S_S^I=k_B{\log }_2{W}_I,(10)$

where $W_I$ is the number of indistinguishable microstates. Therefore, Eq. 2 can be written as follows:

$S_s=S_S^D+S_S^I.(11)$

The number of microstates obtained in Eqs 9, 10 (from a statistical mechanics point of view) perfectly correlates with the number of microstates obtained from quantum mechanics theory.

Multi-slit system

In multi-slit systems, the addition of one observer can result in a large change in the number of superposition states and consequent energy change at the observed. For any given number of slits, the energy change in the environment at reset or from observation is a result of changes in the number of indistinguishable states.

This will be demonstrated for multi-slit systems in the following.

For $N$, equal-sized (and therefore equally probable) slits and one source particle the number of distinguishable states is as follows:

$W_D=2^{\frac{N!}{\left(N-1\right)!1!}}=2^N.(12)$

Born’s rule, which predicts that quantum interference occurs from pairs of paths, has been validated through experiments [41]. For $N$ slits, incorporating the requirement for indistinguishable states to be a combination of pairs of relationships, the number of indistinguishable states at the slits with no slit observers is as follows:

$W_I=2^{\frac{N!}{\left(N-2\right)!1!1!}}=2^{N\left(N-1\right)}.(13)$

Entropy for cases with and without observers, distinguishable and indistinguishable, is different. The maximum entropy, for no path information observer, due to distinguishable and indistinguishable states is as follows:

$S_S=k_B{\log }_2{2}^N+k_B{\log }_2{2}^{N\left(N-1\right)}={k_{B}N}^2.(14)$

It is important to differentiate between the effect of closed systems, typical of thermodynamics, and open systems, typical of quantum mechanics. Adding or removing observers or slits occurs in an open system in which the number of states changes with the reset/observation of the observer leading to a change in entropy.

For $R$ added path information observers, total entropy at the slits decreases. In this case, although, the number of distinguishable states does not change (${W_D^R=W}_D$), the number of indistinguishable states is as follows:

$W_I^R=2^{\left(N-R\right)\left(N-R-1\right)}.(15)$

Therefore, the maximum entropy, for $R$ path information observers, due to distinguishable and indistinguishable states is as follows:

$S_S^R=k_B{\log }_2{2}^N+k_B{\log }_2{2}^{\left(N-R\right)\left(N-R-1\right)}=k_B\left(N^2+R^2-2NR+R\right)forR\le N-1(16)$

A screen observer is always considered to exist. Therefore, at least one observer is necessary to even say the source exists. This means for $R=N-1$, as expected, there are no indistinguishable states resulting in $S_S^R=N$ .

Proposed validating experiments

In order to validate the developed theory, two experiments are proposed, as explained below.

Experiment I: Investigating where and when energy changes occur in the measurement process

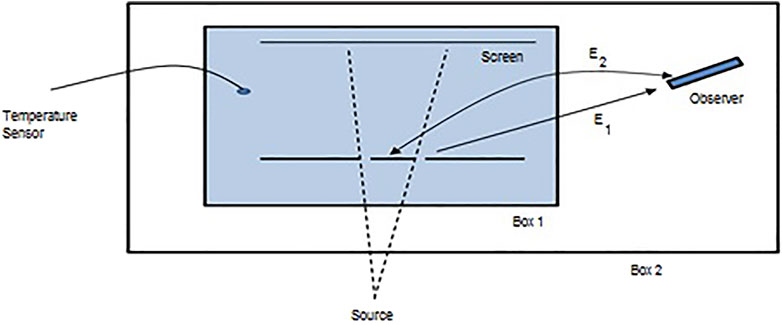
The first proposed experiment shows how the new theory applies to the double-slit experiment. Figure 1 shows the double-slit experiment enclosed in a transparent isothermal box (Box1). A slit observer is outside the transparent box but inside a bigger isothermal box (Box2). The screen observer can be inside or outside Box1. Note that the “slit observer” used throughout the discussion is equivalent to determining path information. A reset of both observers (slit and screen) is required to eliminate interference.

FIGURE 1

FIGURE 1. Schematics of the setup for experiment I.

Reset of the slit observer decreases the number of relationships at the slits by eliminating the superposition states releasing energy into Box1. Superposition states, that is, an increase in the number of relationships, are added at the slits post observation causing a decrease in the energy in Box1. Information associated with the aforementioned energy change is due to changes in the number of superposition states that occur with the reset and observation of the observer, not the value of the information.

To eliminate interference in double-slit systems requires two observers: a final screen observer and a path information observer. The screen is essentially an observer of the slit not observed by the path information observer. It is worth noting that the screen observer, as a photographic plate, has many resets that were performed in the factory at manufacturing. With a reset of the path information observer, this case will be distinguishable (no interference). Any subsequent cases will have indistinguishable states unless the slit observer is again reset.

Without screen and path information observers, no information, including the existence of the two slits, can be determined. In double-slit systems, the addition of a final detector screen (reset) adds information resulting in four possible source (environment) interactions with the slits (system). The reset or, equivalently, the addition of the slit observer, adds information further reducing the number to two possible relationships (eliminates superposition states).

In this proposed experiment, energy changes in the observed (Box1) and observer (Box2) are monitored independently during the process from observer reset through observation and through the next reset. At reset, information at the observed is increased until the observer makes an observation, when information at the observed again decreases. Energy will be transferred to the environment in Box1, that is, Assumption 1. This means the temperature in Box1 increases and the temperature at the slits decreases. An observation is a transfer of a shared state of at least 1 bit of information from the observed to the observer. The energy sequence and changes due to the final detector observer with a single reset and capable of making one observation (not a screen with multiple pre-resets) can also be determined using this experiment by observing changes in energy in Box1 and Box2 with a final detector observer inside and outside Box1. The proposed sequence is as follows:

1. Energy is required to reset the slit observer to enable making another observation. Every slit observer reset eliminates at least two states that are in superposition at the observed (collapse of the wave function). The two slits are in a known state after reset. Superposition states are always paired (Born’s rule).

2. Considering the entropy of the setup, if 1) the final detector screen is in place and 2) after the slit observer makes an observation of path information, there will be an increase in the number of relationships at the observed (slits) in Box1. In this case, energy is transferred from the environment to the slits. Superposition of states exists at the slits after the observers make an observation. The observer of the path information does not absorb the particle, so the screen observer still has the ability to observe the particle. The energy in the setup is assumed to change by at least 1 bit (using Eq. 5) $E\ge k_{B}T$. The magnitude of a 1 bit discrete energy change may be different from this, which possibly can be tested by experiment.

3. The temperature of Box1 changes because energy is dissipated to the environment at observer reset. Using this theory, the predicted temperature change and when it occurs will be different from those from existing theories. For 1 bit energy change,

$∆T=\frac{∆E}{M_s{C}_p}\ge \frac{k_{B}T}{M_s{C}_p},(17)$

where $∆T$ is a temperature change, $M_s$ is the mass of Box1, and $C_p$ is the heat capacity. The effect of energy changes due to the source can be determined by measuring any energy changes in Box1 and Box2 with the source absorbed by a photographic plate without any slits.

In the distinguishable case (commuting), the observation at the final detector screen is a result of the state of each slit as they exist simultaneously. In the indistinguishable case (non-commuting), since there is only 1 bit of information (one observer) and two states, the simultaneous state of both slits cannot be determined. The one observation, then, is a result of the combination of two relationships between slits and the environment, which is observed as a phase difference between the outputs.

The tendency for entropy to always increase is reflected in the tendency for the change in the number of indistinguishable relationships to be maximized. The information for such a system tends to be minimized, that is, the least amount of information that must be added to completely characterize the state of a system. The addition of an observer, reset, is the minimum information added to double-slit systems that decreases the number of possibilities, yet it can completely characterize the state of the system.

Experiment II: Investigating temporal changes in the measurement process

The second proposed experiment determines the observer/observed time relationship during the observation process. The domain space of the observer is either extending “out” to the environment or observing information “from” the environment into the observer. Moreover, determining which of the signals, from the observer or to the observer, affects the observations on a final detector screen, that is, whether or not interference is observed. This is a function of the time from observer reset to path information observation. Moving the observer relative to path information availability at a given velocity (increasing distance between observer and observed) requires less time from reset to path information than path information to observer. If there is no interference, then the signal from the observer to the path information is operative. If there is interference, then the signal from the path information to the observer is operative. Another possible situation is the case where to and from signal information is necessary for an observation. This has a different effect, a longer delay, than the unidirectional to or from requirement for an observation unless the signals are parallel, which requires a positive and negative signal in time, as postulated by Bohm [7–9].

This theory proposes that the observer/observed relationship is characterized as an entanglement process where it makes no difference how far the observer and observed are separated from each other, or how fast they move apart (a near-instantaneous effect.) The number of relationships in the observed begins to change instantaneously. The reset results in the ability to make one observation in the domain of the observer as long as the path information observer is added before the final detector screen (which absorbs the particle so no more observations of the particle–environmental interaction can be made.)

All indistinguishable binary states can be modeled as entangled since both indistinguishable states change simultaneously. At reset, indistinguishable states are transferred to the environment as a wave (energy in the environment) or additional states are added to the environment.

The change in the number of states at the slits when the observer is reset begins to change instantaneously; however, any change in the number of indistinguishable states that occur in time is theorized to be transferred in one Boltzmann time increment. This mechanism is independent of determining value information (path information) and explains delayed choice observations. Distinguishable states are independent, whereas indistinguishable states are dependent on two existing distinguishable states.

For double-slit experiments, an effective way to differentiate between the effect of reset and observation of the slit–particle interaction is to reset a distant observer as close in time as technically possible before the particle interacts with the final detector. Even at the speed of light, the path information signal cannot reach the observer before the particle is observed on the final detector screen. No interference indicates the change is similar to an entangled process. Using this concept, the delay in delayed choice experiments that eliminates interference can be quantified.

The entanglement mechanism is significant because it indicates if, when, and how observer reset affects the information at the slits (Box1.) If the time measurement of temperature changes is instantaneous, then determining when a temperature change occurs in Box1 and Box2, relative to reset, could provide the timing information. However, since temperature is a distributed process, the required time for temperature change may not have adequate resolution to determine this timing information.

Analogously, the proposed concepts can be applied to experiments involving the entanglement process. If there is a temperature change in the environment of the unobserved entangled particle with an observer reset of the observed particle, then the observer/observed relationship is an approximately instantaneous energy change. This energy change may be demonstrated in the case where there are sufficient entangled particles reset simultaneously with the same distance to the distal entangled particles located at approximately the same space surrounded by a box where temperature changes can be measured.

It is worth noting that in the proposed experiment there are subtle differences between interferometer models and double-slit systems, which have physical implications. In interferometer models, there is no delay between path information availability and observers of that path information. This is equivalent to the path information observer being at the same spatial location as the path information (when it becomes available in double-slit systems.) In double-slit systems, available path information and observers of the slit–environment relationship are physically separated in space. The delay in obtaining path information (value information) between observer reset and path information availability in double-slit systems does not exist in interferometer models. In double-slit systems, one observer of path information is added or removed and a constant final detector screen observer is in place. In the interferometer models, the added second half-mirror is equivalent to changing the distinguishable case with two observers to the indistinguishable case with one observer where path information is eliminated instantaneously. The detectors in interferometer models are equivalent to a final detector screen in double-slit systems. The two observers that measure the photon distal to the second half-mirror in the interferometer are equivalent to two points on the final detector screen. Removing the second half-mirror is equivalent to path information observer reset in double-slit systems. In this case, the two observers in the interferometer are equivalent to the two path information observers in double-slit systems. In delayed choice Mach–Zehnder interferometer experiments [42], where the decision to add a second half-mirror, eliminating path information is delayed, observer reset is also immediately eliminated (one observer eliminated) so interference post observation is observed.

Discussion and applications

The following scenarios demonstrate ways of approaching physical problems based on the theory developed in this work.

Theoretical applications

Mass and energy

In the indistinguishable case of multi-slit systems, missing information, associated with irreversibility, results in wave characteristics, which is a quantum mechanical result. Conversely, in the distinguishable case of multi-slit systems, the complete information results in particle characteristics, that is, the minimum number of states equal to the number of slits, which is a classical result.

Relationships require a “difference” which can be considered a fundamental concept that leads to observable physical phenomena. Slits are a difference in space. Entropy exists only as a measure of disorder in space, not time. The total number of Boltzmann energy states in increments of ($k_{B}T$) is a result of commuting, distinguishable states (existing information) plus indistinguishable states (due to missing information) which are binary, non-commuting differences between two distinguishable states in space.

Differences in space are considered to result in mass ($m$), since particle characteristics increase with distinguishability. Differences in time, characterized as a wave, are considered to result in energy ($E$). Those differences are defined in Planck states increments $h$, which results in wave characteristics. This theory can be applied to interpreting, $E=m{c}^2$ ($c$ is the speed of light) as a conversion of energy, as differences in time (wave) to bits (mass), as differences in space. Therefore, if the number of differences in space is mass, it can be expressed as the number of bits that exist between boundaries as a dimensionless quantity. Similarly, if the number of differences in time is energy, then energy can also be expressed as a dimensionless quantity.

Mass Equivalent of One Bit: One bit of energy increase, $k_{B}T$, increases the quantum mass ($kg$) by $\left(m_Q=E/c^2=\left(1.53e-40\right)T\right.$). It is worth noting that, depending on the temperature, $m_Q$ can have the same order of magnitude as the mass of a neutrino ($m_{neutrino}\ge \left(1e-38\right)kg$) [43]. Considering multiple Boltzmann interactions exist within a particle, internal particle temperature may be different from ambient temperature without thermal transfer of energy to the vacuum of empty space.

Gravity

“Gravity is explained as an entropic force caused by changes in the information associated with the position of material bodies” [44, 45]. In this scenario, information is associated with matter and its location (as entropy and information are only in space). The change in entropy results in an entropic force that takes the form of gravity. Entropic force is an effective macroscopic force that originates in a system with many states with a tendency for entropy to increase. Zero inertia is a consequence of a particle at rest will stay at rest because there is no entropy gradient. Zero entropy then becomes a reference point. There is finite entropy associated with each matter configuration. Quantum mechanics, based on entropy, as described here, can be incorporated into the macroscopic universe described by general relativity derived from entropic considerations [45].

Dark matter and dark energy

There are implications of this theory that apply to astronomical situations. Per this theory, the entangled relationship between the changes in a number of states at reset/observation in laboratory experiments also applies to astronomical distances [46]. The instantaneous change in the number of states due to observer observation is delayed until the signal information with meaning travels from the source to the observer up to or at the speed of light. Interactions in the universe between observer domain and observed is changed by resets and observations.

Dark matter can be a result of the number of resets in the entire universe that is external to, but is capable of interacting with, a Galaxy being much larger than the number of observations of that Galaxy. With an external reset, there is a transfer of a number of superposition states from the Galaxy to the external environment releasing a large amount of energy and mass equivalent to the environment around the Galaxy. Observers in the universe external to the Galaxy would observe only the surface of the Galaxy to be approximately uniformly distributed so the only effect would be gravitational and somewhat uniform, consistent with what is known about dark matter and explain the halo effect. An observation of the Galaxy occurs with a delay where classical energy has extended into space at the speed of light (wave) or less (matter). At observation by any observer external to the Galaxy, energy is reabsorbed by the Galaxy. The net difference in the time duration between multiple resets and observations results in the width of the halo.

An additional possible mechanism to consider is, if matter is differences in space and energy is differences in time, then dark matter/energy is prevalent as a higher density of matter around galaxies that is not observable as individual mass differences and changes in differences. The effect would have a large magnitude since there are many total particles (low density in a large space).

A Galaxy is dense compared to empty space. Although there is a low density of particles in empty space, there is a high probability that whenever there is an observable, it will be observed since there are many observers. Observers would be relatively close to the particles so the number of observations, “value” (equivalent to path information) information obtained after reset at the speed of light from particle to observer would occur with a small time duration compared to observers of Galaxies that are spaced relatively far apart so the effect of observation would dominate the effect of resets. The number of superposition states transferred from the environment to the observed (particle) would increase, decreasing the number of states and energy in the environment and comparable mass resulting in a negative entropic effect in the environment so if gravity is related to entropy, there would be a negative gravitational effect. The changes may be transient at an individual level but the net changes are approximately stable. The number of resets and observations could somehow combine to automatically result in a flat, expanding, or contracting universe.

Entanglement and wave/property duality

Per this theory, wave/particle duality can analogously be applied to wave/property duality. The property refers to the internal characteristics of particles (e.g., spin). This is applied to double-slit and Bell inequality systems. Particle properties are entangled, in a superposition of states, when information about their state is missing, equivalent to the indistinguishable case for double-slit systems. Indistinguishable states affect observations (non-zero phase difference); however, they cannot be observed directly. Quantum information only changes the amount of information (number of states) in space and does not provide information about the state (value) in space but affects the distribution of possible observations [47].

Per this theory, entanglement and double-slit systems are a result of the same quantum mechanical effect so interference between entangled properties such as frequencies or spin should be observable if there is missing information, equivalent to the indistinguishable case in double-slit systems. The entangled state has a superposition relationship between the distinguishable states of the property. Interference of spin is a result of wave characteristics existing for properties other than the mass of particles; a wave/property duality. The interference pattern is a result of the relative phase difference between the source and angle of a polarizer. For spin states, it is the angle of the Stern–Gerlach (S–G) observer relative to the angle of the entangled spin states. Similar to double-slit systems, interference of spin is non-commuting. The unobserved magnetic moment of the entangled pair rotates through a range of values and variable phase differences, resulting in the equivalent of interference in double-slit systems.

The experiments illustrating the violation of Bell’s inequality have confirmed that the behavior of entangled particles is consistent with quantum mechanics. The analogy, proposed below, demonstrates the mechanisms for the double-slit systems and Bell’s inequality violation is the same phenomenon. Superposition exists at the emission of wave or entangled spin states without polarization angle or spin state observers, equivalent to no path information observers.

Joint probabilities between two phases and two polarization systems, demonstrating a violation of Bell’s inequality, are equivalent to the phase difference in a double-slit system observed on a final detector screen. Different phase settings for polarizers correspond to different locations within slits. The number of photons at different locations of the double-slit final detector screen corresponds to two outputs (detection and no detection) of separated polarizers, measured at different angles. The four probability correlations used to determine Bell’s inequality experiment correspond to four probability correlations resulting in the observed distribution of photons at different locations on a final detector screen in double-slit systems. The correlation coefficient for Bell’s inequality determination and double-slit systems are the same when combined for angle differences of $67.5°$ and $22.5°$. The joint detection probabilities of outputs from Slit1 and Slit2 or outputs between two polarizers lead to the same probability distribution. Both are quantum mechanical, not classical results. In polarizer systems, the addition of a second polarizer at each end causes attenuation of the signal corresponding to attenuation from the initial peak on the final detector screen. The additional polarizer stretches out the space of the signal, similar to the additional space of the final detector screen.

Black holes

Information transfer across a boundary is particularly relevant to black hole theories [48]. This is because the mass (number of differences) in black holes is added in increments proportional to entropy which increases the Schwarzschild surface area; further indicating that there is a discrete relationship between mass and entropy (information). Therefore, gravity is the only observable for Schwarzschild black holes. With the addition of distinguishable states, the change in the number of outputs equals the change in the number of inputs, that is, a one-to-one correspondence exists between the number of bits in black holes (mass) and observable gravity. Based on the definition of information as minimal differences (1 bit), if the entire black hole evaporates, the same number of bits from the universe forming the black hole would re-enter the universe. In this case, no “quantum” information is lost.

An area (mass) change of the black hole presumably results in a $4l_p^2$ planar wave either emitted or absorbed. The area increment of $4l_p^2$ is the minimum increment in black holes. Black hole mass, which is proportional to the number of states (number of differences in space, i.e., entropy), represents a special case of matter where matter is maximal (maximum number of minimal difference) in a minimal distribution in space, that is, a spherical area. Each area increment of $4l_p^2$ is distinguishable, a distinct position within the sphere. The entire surface of the black hole consists only of differences, analogous to distinguishable slits.

For a non-rotating black hole with no charge, a Schwarzschild black hole [49], entropy is as follows:

$S_{BH}=\frac{A}{4l_p^2}{k}_B(18)$

where $A$, is the spherical area of the Schwarzschild radius. Using the developed theory, Eq. 18 can be written as follows:

$S_{BH}=N{k}_B(19)$

where $N$, is the number of relationships which is the number of minimum areas ($4l_p^2$) in the total area, $A$. The following provides the rationale for the above. The fundamental black hole boundary increments are a square of $2l_p$ on each side [48]. The minimum to establish a distinguishable state in one dimension requires $2l_p$, where the minimum linear state is Planck’s length, $l_p$, and to have a difference in a two-dimensional surface of a black hole, incorporating the one dimension’s difference, requires a $4l_p^2$ surface. A square with $4l_p^2$ area consists of two mass increments, one Boltzmann mass for each difference. The relationship between mass and number of bits is a constant at a given temperature as expected if bits result in mass. Based on the number of bits (entropy) in the black hole, Planck’s length, and temperature, the mass of the black hole can be obtained as follows:

$m_{BH}=\frac{2N{k}_{B}T}{c^2}(20)$

The fundamental non-black hole mass ($N=1$) is equivalent to one Boltzmann energy bit as follows:

$m_{non-BH}=\frac{k_{B}T}{c^2}(21)$

The difference between the ratio of mass to the number of bits in a particle and that of the black hole is a result of the existence of two bits per $4l_p^2$ area.

Copenhagen interpretation

Since this theory proposes that the number of states, that is, the amount of information that is observed, begins to change approximately instantaneously with observer reset/observation, an intermediate number of state changes between reset and observation is not observable. This is consistent with one aspect of the Copenhagen interpretation of quantum mechanics; namely, that the number of states cannot be determined between source and observation until “meaningful” information is observed [50]. This theory is not consistent with another aspect of the Copenhagen interpretation or Bell’s inequality interpretation since individual particles and/or properties of particles are real in the intermediate state even without an observation.

Uncertainty

The developed theory, which focuses on the entropic interpretation of quantum mechanics, includes interpreting wave-particle duality as a description of energy and matter, respectively. This would modify the uncertainty principle by combining measurement energy uncertainty with observer/observed matter uncertainty. Analogous to the inability of determining the measured energy of an interaction with greater accuracy than the limit set by Heisenberg uncertainty, a component of a particle cannot be determined with greater accuracy than the energy of a bit, $k_{B}T$, the minimum energy to establish an entropic difference in space. There are two types of uncertainties to consider with minimal values of 1) thermodynamic ($∆E\ge k_{B}T$) and, 2) Heisenberg uncertainty ($∆E∆t\ge h$). This work postulates that observational uncertainty is due to the quantum nature of an observation which limits the precision of an observation process interacting with the quantum nature of the observer/observed characterized by another quantum.

For uncorrelated, independent uncertainties between the quantum natures of an observation (${∆W}_{Observed}$) and the observer (${∆W}_{Observer}$), the following is observed:

${∆E}^2\ge {\left(\frac{h}{∆t}\right)}^2+{\left(k_{B}T{\mathit{log}}_2{∆W}_{Observed}\right)}^2+{\left(k_{B}T{\mathit{log}}_2{∆W}_{Observer}\right)}^2.(22)$

In the case of complete information in the observed and observer (${∆W}_{Observer}={∆W}_{Observed}=1$), the conventional equation for uncertainty ($∆E\ge h/∆t$) is achieved.

Zeno and anti-Zeno effect

The Zeno effect is a demonstration that resets (or observations) of the observing instrument affects the observed. This is due to internal changes of the particle since the probability of decay is not affected if decay occurs independent of the reset/observation [51, 52]. For the double-slit experiment, this is equivalent to the change of internal characteristics in Box1 with reset/observation of the observer.

Per this theory, each addition of an observer (reset) of the radioactive particle or double-slit experiment results in a transfer of indistinguishable states from the system’s internal components, slit, or elements in the radioactive particle, to the environment. When the energy transferred to the environment is equal to or greater than the energy equivalent of the radiated mass, radioactive decay can occur. Since decoherence is equivalent to reset/observation, this would occur with internal decoherence where the number of resets is greater than the number of observations, resulting in the observed decay times without external resets/observations.

Based on this theory, the Zeno and anti-Zeno effects are affected by external observer reset/observation. Events internal to the atom can be modeled as a change between the number of states pre and post-decay. When the number of resets is greater than the number of observations, there is a transfer of indistinguishable states between distinguishable states to the internal environment of the atom, resulting in decreased decay time, the anti-Zeno effect. The opposite occurs with observation, decreasing the energy in the internal environment of the radioactive particle, decreasing the probability of decay, increased decay time, the Zeno effect. After each external reset/observation, the system returns to the previous distinguishable/indistinguishable ratio until the next external change, analogous to changes in Box1. One can investigate if the same number of parallel resets/observations has the same effect on half-life as serial changes.

Another possible mechanism is that external reset/observation results in a change in the total energy of the atom. Reset would result in a decrease in the energy of the atom (radiated to the environment) and result in decay less likely, the Zeno effect, whereas observation would result in an increase of energy in the internal environment of the atom and result in decay more likely, the anti-Zeno effect.

Schrodinger’s cat

In the Schrodinger cat thought experiment [3], if the radioactive atom emits a particle, the flask breaks, fatally harming the cat, which, in the Copenhagen interpretation of quantum mechanics, is considered to be in a superposition of states until observed by an external observer. The interpretation of this thought experiment, based on the theory presented here, considers the flask to be an observer of the radioactive substance. There is one input, the state of the radioactive atom, and one output, the state of the flask; hence, there is no missing information. The state of the radioactive atom is not known without an observer (flask), not even having information of its existence. An entropy change is required to reset or add the observer, that is, adding a flask. With the addition of the flask, the radioactive particle is decayed or not decayed (one input and only one output). The emission of a particle from a radioactive source is transferred to the flask at the speed of light or less, resulting in an energy/entropy change in the detector (flask.)

Different interpretations of quantum mechanics result in various outcomes for the cat. These include superposition (alive and dead simultaneously), primarily based on the Copenhagen interpretation; while others consider the cat alive or dead [53]. An additional interpretation is presented here. Schrodinger’s cat is a model to demonstrate the timing of a change from a quantum superposition system to a classical system. Basically, when does superposition end (stop being a linear combination of states)? This is addressed herein; it changes at observer reset.

As mentioned before, entropy is in space only; that is, superposition is only in space at each time instant. A change in entropy is in time; however, the current conventional description of Schrodinger’s cat is based on superposition or entropy in time. Schrodinger’s cat thought experiment is currently based on the cat still being dead and alive after flask changes but, per this theory, with entropy change (state change) in the flask, the cat is dead. Therefore, there is a one-to-one relationship between the state of the cat and the state of the flask.

Practical applications

Quantum computing

Minimizing noise is one of the critical factors in extending the operation of quantum computing. To date, the focus has mainly been on minimizing the interference from environmental observers of states, frequently attributed to decoherence [54]. Based on the theory presented in this work, as the number of superposition states changes with reset and observation, noise immunity can be reduced. This can be accomplished by minimizing the effect of reset in addition to observation, increasing the number of qubits incorporated in the quantum computer.

Signal processing

Each state existing prior to a measurement can be determined by a transducer which is limited by what the transducer is capable of measuring, that is, its signal processing capabilities. Any parameters that have no transducer capable of measuring them may exist but be “hidden”. Based on the theory presented in this work, determination of what can be measured is performed before an experiment occurs, that is, which transducers are reset (capable of making an observation.) It does not limit hidden variables, but limits which hidden variables, if any, can be observed. One of the non-observable variables, per this theory, is how many states exist before the experiment was performed. For example, in the observation of double-slit systems, there is no indication that wave characteristics existed prior to the addition of a path information observer. Hence, per this theory, the change occurred from wave to particle characteristics when the additional observer was reset (added.)

Until recently, quantum signal processing has been limited to a single transform domain such as the frequency in classical processing. By considering wavelets in signal processing, which uses time and frequency with variable scaling, more efficient algorithms can be developed. For specific algorithmic problems, the efficiency is increased in many ways: decrease in storage requirements, number of required operations, and complexity. This application is context-sensitive (dependent on the characteristics of the data being processed and the measurement process); what works well for one set of data may not work well for another set of data [55]. Signal processing requires consideration of the type and number of observers before measurement and, frequently, the relationship between them at a given instant, so parallel information is obtained, such as amplitude and phase. Each observer requires a reset. By requiring fewer observer resets, the efficiency can be greatly improved.

The aforementioned approach can be applied to fractal modulation [56, 57]. Since quantum mechanics is, by definition, discrete, an integer version of wavelet analysis can provide improved and more realistic results [55]. This is consistent with the theory developed in this work, that is, there is a change in the integer number of bits at reset and observation.

Quantum artificial intelligence (QAI)

The use of quantum computing to enhance machine learning algorithms can considerably improve results; particularly for problems too complex for conventional digital computers. These include speech and language recognition, game theory, and decision-making [58]. Quantum Artificial Intelligence (QAI) has similarities to general intelligence as they both have intrinsic uncertainty. Therefore, the efficiency of QAI and general intelligence can be related to the reset effect on entropy change and even evolution [59]. It is possible that both employ parallel decision processes.

Summary and conclusion

In the theory proposed here, adding an observer (reset) decreases the number of relationships (eliminating non-commuting relationships) at slits as an entangled process. This begins instantaneously with reset and occurs in one Boltzmann time increment with an associated probability change. This is caused by the change in the number of possible states due to a change in the available and missing information. Two experiments are proposed to determine the energy and timing of changes during the observation process in multi-slit systems. Energy changes are monitored independently in the slit system and observers of slits: after reset of path information observers, at the observation of path information, and observation at a final detector screen. Therefore, where (at observer, observed), when (at reset, observation) and timing (entanglement) between observer reset/observation of energy (entropic) changes due to the observation process is determined. Transfer of “meaningful” information requires time and no usable transfer of “meaningful” information occurs at reset. After the transfer of meaningful information resulting in an observation, the number of relationships at the slits increases approximately instantaneously. This work proposes that the number of observers must equal the number of slits to eliminate interference in multi-slit experiments. The entropic interpretation of the quantum mechanical mechanism is applied to the Zeno and anti-Zeno effect, delayed choice, a different interpretation of Schrodinger’s cat, a modified uncertainty relationship, the relationship between wave/particle duality and energy and matter, and implications applicable to dark energy and matter. Upon the experimental validation of this theory, a better understanding of the quantum mechanical measurement processes may lead to applications in engineered devices such as quantum computing, signal processing, and quantum artificial intelligence.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Feynman RP. Feynman lectures on computation. In: RP Feynman, editor. Feynman lecures on computation. Boulder, Co: Westview Press (1969). p. 155–63.

Google Scholar

2. Schrodinger E, Born M. Discussion of probability relations between separated systems. Math Proc Camb Phil Soc (1935) 31(4):555–63. Bibcode:1935PCPS.31.555S. doi:10.1017/S0305004100013554

CrossRef Full Text | Google Scholar

3. Schrödinger E. Die gegenwärtige Situation in der Quantenmechanik (The present situation in quantum mechanics). Naturwissenschaften (1935) 23:807–12. Bibcode:1935NW.23.807S. doi:10.1007/bf01491891

CrossRef Full Text | Google Scholar

4. Wimmel H. Quantum physics & observed reality: A critical interpretation of quantum mechanics. Singapore: World Scientific (1992). Bibcode:1992qpor.book.....W. ISBN 978-981-02-1010-6.

Google Scholar

5. Faye J, Folse HJ. Niels Bohr and the philosophy of physics. Twenty-First-Century perspectives. London: Bloomsbury Academic (1997).

Google Scholar

6. Bell JS. Speakable and unspeakable in quantum mechanics. Cambridge University Press (1987). p. 65. ISBN 9780521368698. OCLC 15053677. Cambridge p. 65. ISBN 9780521368698. OCLC 15053677. Cambridge University Press.

Google Scholar

7. Bohm D. A suggested interpretation of the quantum theory in terms of 'hidden variables' I (Bibcode:1952PhRv. Phys Rev (1952) 8585(2):166B166–79. doi:10.1103/PhysRev.85.166

CrossRef Full Text | Google Scholar

8. Bohm D. A suggested interpretation of the quantum theory in terms of hidden variables, II. Phys Rev (1952) 85(2):180–93. Bibcode:1952PhRv.85.180B. doi:10.1103/PhysRev.85.180

CrossRef Full Text | Google Scholar

9. Bohm D. Wholeness and the implicate order. NY: Routledge (1983).

Google Scholar

10. Cushing JT, Fine A, Goldstein H. Bohmian mechanics and quantum theory: An appraisal. Berlin: Springer (1996).

Google Scholar

11. Cramer J. Transactional interpretation of quantum mechanics. Rev Mod Phys (2009) 58(3):795–8. ISBN 978-3-540-70622-9. doi:10.1007/978-3-540-70626-7_223

CrossRef Full Text | Google Scholar

12. Everett H, Wheeler JA, DeWitt BS, Cooper LN, Van Vechten D, Graham N. The many-worlds interpretation of quantum mechanic, A fundametnal expositon of hugh Everett, princeton series in physics. Princeton: NJ: Princeton University Press (1973).

Google Scholar

13. Rovelli C. Relational quantum mechanics. Int J Theor Phys (Dordr) (1996) 35:1637–78. doi:10.1007/bf02302261

CrossRef Full Text | Google Scholar

14. Wheeler JA, Feynman RP. Interaction with the absorber as the mechanism of radiation. Rev Mod Phys (1945) 17:157–81. doi:10.1103/RevModPhys.17.157

CrossRef Full Text | Google Scholar

15. Von Baeyer HC. Information: The new language of science. Cambridge: Harvard University Press (2004).

Google Scholar

16. Esfeld M. Wigner’s view of physical reality. Essay review of jagdish mehra. In: The collected works of eugene Paul widnger. Part B. Historical, phiosophical and socio-political papers. Volume VI: Philosophical reflections and synthesis, studies in history and philosophy of modern physics. Amsterdam: Elsevier Science Ltd (1999). p. 145–54. 30B.

Google Scholar

17. Machta J. Entropy, information, and computation. Am J Phys (1999) 67:1074–7. doi:10.1119/1.19085

CrossRef Full Text | Google Scholar

18. Shannon CE, Weaver W. The mathematical theory of communications. Urbana, IL: University of Illinois (1949).

Google Scholar

19. Sloane NJA, Wyner AD. Claude E. Shannon collected papers. Hoboken: Wiley-IEEE Press (1993).

Google Scholar

20. Bérut A, Arakelyan A, Petrosyan A, Ciliberto S, Dillenschneider R, Lutz E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature (2012) 483:187–9. doi:10.1038/nature10872

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Keyes RW, Landauer R. Minimal energy dissipation in logic. IBM J Res Dev (1970) 14:152–7. doi:10.1147/rd.142.0152

CrossRef Full Text | Google Scholar

22. Landauer R. Uncertainty principle and minimal energy dissipation in the computer. Int J Theor Phys (Dordr) (1982) 21(3/4):283–97. doi:10.1007/BF01857731

CrossRef Full Text | Google Scholar

23. Landauer R. Energy requirements in communication. Appl Phys Lett (1987) 51(24):2056–8. doi:10.1063/1.98291

CrossRef Full Text | Google Scholar

24. Landauer R, Woo JWF. Minimal energy dissipation and maximal error for the computational process. J Appl Phys (1971) 42:2301–8. doi:10.1063/1.1660540

CrossRef Full Text | Google Scholar

25. Bennet CH. The thermodynamics of computation-A review. Int J Theor Phys (Dordr) (1982) 21:905–40. doi:10.1007/bf02084158

CrossRef Full Text | Google Scholar

26. Bennet CH. Logical reversibility of computation. IBM J Res Dev (1987) 17:525–32. doi:10.1147/RD.176.0525

CrossRef Full Text | Google Scholar

27. Bennet CH. Notes on the history of reversible computation. IBM J Res Dev (1988) 32:16–23. doi:10.1147/rd.321.0016

CrossRef Full Text | Google Scholar

28. Feynman R, Leighton R, Sands M. Lectures on physics. Reading, MA: Addison-Wesley (1966). I, ch 37, and . III Ch. 1.

Google Scholar

29. Zurek WH. Complexity, entropy and the physics of information. Redwood City, CA: Addison-Wesley (1990).

Google Scholar

30. Guariglia E. Entropy and fractal antennas. Entropy (2016) 18(3):84. doi:10.3390/e18030084

CrossRef Full Text | Google Scholar

31. Guariglia E. Harmonic Sierpinski gasket and applications. Entropy (2018) 20(9):714. doi:10.3390/e20090714

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Guariglia E. Primality, fractality and image analysis. Entropy (2019) 21(3):304. doi:10.3390/e21030304

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Guariglia E. Fractional-wavelet Analysis of positive definite distributions and wavelets on D'(C). In: R Silvestrov, editor. Engineering mathematics II. Berlin, Germany: Springer (2017). p. 337–53.

CrossRef Full Text | Google Scholar

34. Berry MV, Lewis ZV, Nye JF. On the Weierstrass-Mandelbrot fractal function. Proc R Soc Lond Ser A (1980) 370(1743):459–84. doi:10.1098/rspa.1980.0044

CrossRef Full Text | Google Scholar

35. Zheng X, Tang YY, Zhou J. A framework of adaptive multiscale wavelet decomposition for signals on undirected graphs. IEEE Trans Signal Process (2019) 67(7):1696–711. doi:10.1109/tsp.2019.2896246

CrossRef Full Text | Google Scholar

36. Yang L, Su H, Zhong C, Meng Z, Luo H, Li X, et al. Hyperspectral image classification using wavelet transform-based smooth ordering. Int J Wavelets Multiresolut Inf Process (2019) 17(6):1950050. Article Number: 1950050. doi:10.1142/s0219691319500504

CrossRef Full Text | Google Scholar

37. Klatzow J, Becker JN, Ledingham PM, Weinzetl C, Kaczmarek KT, Saunders DJ, et al. Experimental demonstration of quantum effects in the operation of microscopic heat engines. Phys Rev Lett (2019) 122:110601. doi:10.1103/PhysRevLett.122.110601

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Boltzmann L. Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen. Wiener Berichte (1872) 66:275–370. in WA I, paper 23. doi:10.1142/9781848161337_0015

CrossRef Full Text | Google Scholar

39. Boltzmann L. Bermerkungen über einige Probleme der mechanische Wärmetheorie. Wiener Berichte (1877) 75:62–100. in WA II, paper 39.

Google Scholar

40. Lucia H, Hornberger K, Brezger B, Zeilinger A, Arndt M. Decoherence of matter waves by thermal emission of radiation. Nature (2004) 427:711–4. (arXiv:quant-ph/0402146). doi:10.1038/nature02276

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Sinha U, Couteau C, Jennewein T, Laflamme R, Weihs G. Ruling out multi-order interference in quantum mechanics. Science (2010) 329(5590):418–21. doi:10.1126/science.1190545

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Jacques V, Wu E, Grosshans F, Treussart F, Grangier P, Aspect A, et al. Experimental realization of wheeler's delayed-choice gedanken experiment. Science (2007) 315(5814):966–8. doi:10.1126/science.1136303

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Goobar A, Hannestad S, MortsellTuass H. The neutrino mass bound from WMAP-3, the baryon acoustic peak, the SNLS supernovae and the Lyman-α forest (2006). Available at: arxiv.org/pdf/astro-ph/0602155.pdf (Accessed July 20, 2021).

Google Scholar

44. Carroll SM, Remmen GN, What is the entropy in entropic gravity? (2016). ArXiv:1601.07558v3 [hep-th].

Google Scholar

45. Verlinde E. On the origin of gravity and the laws of Newton. J High Energ Phys (2011) 2011:29. arXiv:1001.0785v1 [hep-th]. doi:10.1007/JHEP04(2011)029

CrossRef Full Text | Google Scholar

46. Deng Y-H, Wang H, Ding X, Duan Z-C, Qin J, Chen MC, et al. Quantum interference between light sources separated by 150 million kilometers. Phys Rev Lett (2019) 123:080401. doi:10.1103/physrevlett.123.080401

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Berltmann RA, Zeilinger A. Quantum [Un]speakables: From Bell to quantum information. Berlin: Springer (2002). p. 119–50.

Google Scholar

48. Bekenstein JD. Black holes and the second law. Lett Nuovo Cimento (1972) 4(15):737–40. doi:10.1007/bf02757029

CrossRef Full Text | Google Scholar

49. Bekenstein JD. Black holes and entropy. Phys Rev D (1973) 7(15):2333–46. doi:10.1103/physrevd.7.2333

CrossRef Full Text | Google Scholar

50. Faye J. Copenhagen interpretation of quantum mechanics. In: EN Zalta, editor. The stanford encyclopedia of philosophy winter 2019 edition. Stanford, CA: Stanford Encyclopedia of Philosophy (2019).

Google Scholar

51. Itano WM, Heinzen DH, Bollinger JJ, Wineland DJ. Quantum Zeno effect. Phys Rev A (Coll Park) (1990) 41:2295–300. doi:10.1103/physreva.41.2295

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Misra BJ, Sudarshan EC. The Zeno's paradox in quantum theory. J Math Phys (1977) 18(4):756–63. doi:10.1063/1.523304

CrossRef Full Text | Google Scholar

53. Polkinghorne JC. The quantum world. Princeton, NJ: Princeton University Press (1985). p. 67.

Google Scholar

54. Joos E, Zeh H. The emergence of classical properties through interaction with the environment. Z Physik B - Condensed Matter (1985) 59:223–43. doi:10.1007/bf01725541

CrossRef Full Text | Google Scholar

55. Gutierrez FAC, Uribe CF, Perez Sansalvador JCP, Gomez GR. Quantum approach to the integer wavelet transform and its application to quantum lossless compression. Puebla, Mexico: The National Institute of Astrophysics, Optics and Electronics (2021). Technical Report No. CCC-22-001, Tonantzintla.

Google Scholar

56. Eldar YC, Oppenheim AV. Quantum signal processing. IEEE Signal Process Mag (2002) 19(6):12–32. doi:10.1109/msp.2002.1043298

CrossRef Full Text | Google Scholar

57. Wornell GW, Oppenheim AV. Wavelet-based representations for a class of self-similar signals with application to fractal modulation. IEEE Trans Inf Theor (1992) 38:785–800. doi:10.1109/18.119736

CrossRef Full Text | Google Scholar

58. Papatheodorou TS, Christodoulakis DN, Karanikolas NN. Current trends in informatics. Athens: New Technologies Publications (2007). p. 469–77. A.

Google Scholar

59. Keshmiri S. Entropy and the brain: An overview. Entropy (Basel) (2020) 22(9):917. doi:10.3390/e22090917

PubMed Abstract | CrossRef Full Text | Google Scholar