A spatially non-overlapping dual-wavelength 2D FBG for the measurement of temperature and strain

This work designed a dual-wavelength 2D fiber Bragg grating (FBG) engraved on the single-mode fiber to measure the temperature and strain. The FBG is composed of two sub-gratings that are not overlapped spatially at the same location of the fiber core. Experiments showed that the temperature and strain sensitivities of this grating were separately measured to be 10.64 p.m./°C and 0.882,731 p.m./μɛ at the central wavelength of 1,548 nm, and 10.74 p.m./°C and 0.916,080 p.m./μɛ at the central wavelength of 1,550 nm. These coefficients constitute a coefficient matrix that can solve the problem of cross sensitivity between temperature and strain, which has been verified by varying central wavelengths caused by the synchronous change of temperature and strain.

1 Introduction

The reflection wavelength of a fiber Bragg grating (FBG) changes with physical quantities, such as temperature and strain. The former phenomenon originates from thermal expansion [1, 2] and thermo-optic effects [3, 4] while the latter one originates from photoelastic effect [5, 6]. FBG is a fiber optic sensor that has been most widely used to measure these physical quantities in optical communication and sensing fields because of its numerous advantages [7], such as small volume, low insertion loss, high sensitivity, strong anti-interference capability, easy coupling to optical fibers at a low loss, etc.

In practical application, it is a pressing problem to eliminate the cross sensitivity between temperature and strain [8–10]. The current solutions include reference to fiber gratings [11–13], the combination of different gratings [14–18], the fusion of fiber gratings with different cladding diameters [19–21], chirped fiber gratings [22], Fabry-Perot (FP)cavities [23–26], and microstructured fiber gratings [27–30]. Among these methods, referring to fiber gratings requires that the two gratings must have identical structures and parameters, raising higher requirements for fabricating. The combination of FBG with the long-period fiber grating (LPFG) can easily separate the variable quantities of temperature and strain because the LPFG is highly sensitive to temperature and extremely insensitive to strain [31]. However, the LPFG has a larger bandwidth, which limits the measurement accuracy. Therefore, this combination is inapplicable to the large-scale wavelength division multiplexing system.

The chirped fiber gratings measure the strain and temperature based on the intensity of the reflected light, and for this reason, reference signals shall be provided to eliminate the fluctuation of light source power. The fusion of fiber gratings with different cladding diameters, as well as the methods of FP cavities and microstructured fiber gratings cannot be widely used because of the high requirements for their fabrication. Meanwhile, the overlapping dual-wavelength FBG [32, 33] is designed, which helps cope with the issue of cross sensitivity between temperature and strain from a new perspective. However, multiple exposures are needed to overlap the gratings of different periods at the same location, which complicates the fabricating process, and consequently, the consistency of these gratings cannot be guaranteed.

This work proposed a 2D FBG based on the 2D spatial mask to design a dual-wavelength grating that could be easily engraved with a compact structure, thus measuring the temperature and strain. The dual-wavelength 2D FBG was successfully engraved using the universal phase mask at one time, during which the two sub-gratings were highly consistent and therefore could be engraved repeatedly. The response of this grating to temperature and strain was measured experimentally, based on which a coefficient matrix for these two physical quantities was deduced. Experimental results demonstrate that the 2D FBG can be potentially used to solve the problem of cross sensitivity between temperature and strain.

2 Preparation of the 2D FBG

Using the 2D spatial phase mask with multiple periodic structures, the fabricating spots could have a dibit encoding structure. When these spots acted on the fiber core to be engraved, the refractive indexes were modulated in both axial and radial directions of the core on the same scale, thus forming multiple sub-gratings that were parallel along the axial direction. This process concerned both axial and radial dimensions, which was known as the 2D FBG, as shown in Figure 1A.

FIGURE 1

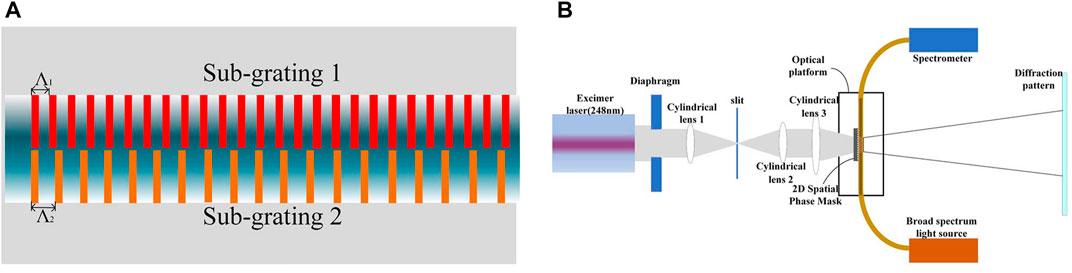
FIGURE 1. The schematic diagram for the fabricating system of 2D FBG. (A) Schematic diagram of the grating distribution of the 2D FBG (viewed along the longitudinal direction). (B) Schematic diagram of the optical path of the 2D fiber grating fabricating system (viewed from above).

As shown in Figure 1B, after passing through the 2D spatial phase mask, the ultraviolet beam from the excimer laser can emit the diffracted light with a spatial encoding structure. With near-field diffraction, the interference fringes of such light in various orders can be converged on the fiber core that is to be engraved. Then, the core medium with light sensitivity records the spatial intensity distribution of these fringes based on the fluctuation of refractive indexes, thus achieving the light-sensitive engraving of this core on a sub-wavelength scale. The 2D FBG with high consistency and stability was engraved by a single exposure of phase mask.

In this experiment, the 2D FBG was prepared with a 2D spatial phase mask that was 50 mm long. Using a mask encoded in 2D space, the 2D FBG was fabricated in the fiber core by ultraviolet photolithography. The KrF excimer laser (FPMLA-MLI-248 nm), with the pulse energy of 160 mJ and the repetition frequency of 30 Hz, was collimated through the cylindrical lens 1. The slit served as a spatial filter to control the widths of the light beam and cylindrical lens 2, forming a rectangular beam that passed through the cylindrical lens three and focused on the fiber core through the 2D spatial mask. The optical fiber to be engraved, with its coating removed, was clamped at an angle of 5° using the system installed on the mechanical stage. In this system, the 2D spatial phase mask composed of several periodic structures that were separated by one 1-μm gap was close to but not connected to the fiber (the distance between them was less than 1 mm). The horizontal gap of this mask was adjusted to make it evenly distributed in the center of the fiber core.

How the grating’s reflection and transmission spectra evolved during the exposure was monitored in real-time using the amplified spontaneous emission (ASE) broadband light source (BBS,JF8143-C-band) and optical spectrum analyzer (OSA, ADVANTEST-Q8384). After being shaped and focused, the laser beam projected multiple periodic structures and their gaps onto the optical fiber to engrave a 2D FBG. If there was a small angle between the fiber axis and the septal line of the 2D spatial phase mask, a slope line could be observed on the screen placed behind the optical fiber in +1 and -1 diffraction fringes, in which case, the fiber should can be adjusted. To monitor the spectra of the 2D FBG during the fabricating process, this fiber’s output end was connected to the OSA, and the other end was connected to the BBS. The fiber was adjusted vertically till these spectra were symmetrical, thus making the periodic structures symmetrically distributed on the fiber core. It is worth mentioning that this FBG preparation system in Figure 1B is a typical setting, in which the 2D spatial phase mask shall be designed specially and aligned more strictly in the vertical direction.

The spatial phase masks with their respective periods of 1,548.51 nm and 1,550.12 nm were adopted to engrave a 5 mm-long dual-wavelength 2D FBG with spectral characteristics on the single-mode fiber (SM28e). Figure 2 presents the spectrogram. In the above spectrogram, the central wavelengths which correspond to the maximum reflection were 1,548.062 nm and 1,550.015 nm, respectively, and the peak reflection intensity exceeded 85%. The uneven sub-peaks were caused by the alignment between the optical fiber and the mask’s datum line, having no effect on the change of central wavelengths and exerting little impact on the sensing of temperature and strain. Therefore, the fabricating technique shall be precisely designed and improved to realize the 2D FBG with smooth spectra.

FIGURE 2

FIGURE 2. The spectra of 2D FBG at room temperature.

3 Principles of the temperature and strain sensing

The central reflection wavelength of the FBG can meet the Bragg condition as Eq. 1 [34].

${\lambda }_{\text{Brg}}=2n_{\mathrm{e}\mathrm{ff}}\mathrm{\Lambda }(1)$

where n_eff refers to the effective refractive index, and Λ is the grating period. When the strain and temperature change simultaneously in the 2D FBG, the Bragg condition can be expressed as Eq. 2. Where ɛ represents the strain magnitude of the grating and T represents the temperature of the environment where the grating is located.

$\left[\begin{array}{c}\hfill {\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{1}}\hfill \\ \hfill {\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{2}}\hfill \end{array}\right]=2\left[\begin{array}{c}\hfill n_{\mathrm{e}\mathrm{ff}\mathrm{1}}\left(\epsilon ,T\right){\mathrm{\Lambda }}_1\left(\epsilon ,T\right)\hfill \\ \hfill n_{\mathrm{e}\mathrm{ff}\mathrm{2}}\left(\epsilon ,T\right){\mathrm{\Lambda }}_2\left(\epsilon ,T\right)\hfill \end{array}\right](2)$

The change in the center wavelength can be expressed as Eq. 3.

$\left[\begin{array}{c}\hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{1}}\hfill \\ \hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{2}}\hfill \end{array}\right]=2\left[\begin{array}{c}\hfill \mathrm{\Delta }{n}_{\mathrm{e}\mathrm{ff}\mathrm{1}}{\mathrm{\Lambda }}_1+n_{\mathrm{e}\mathrm{ff}\mathrm{1}}\mathrm{\Delta }{\mathrm{\Lambda }}_1\hfill \\ \hfill \mathrm{\Delta }{n}_{\mathrm{e}\mathrm{ff}\mathrm{2}}{\mathrm{\Lambda }}_2+n_{\mathrm{e}\mathrm{ff}\mathrm{2}}\mathrm{\Delta }{\mathrm{\Lambda }}_2\hfill \end{array}\right](3)$

As shown in Eq. 4, the relative change of the Bragg wavelength can be obtained by Equation (2)–(3).

$\left[\begin{array}{c}\hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{1}}/{\lambda }_{\mathrm{B}\mathrm{1}}\hfill \\ \hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{2}}/{\lambda }_{\mathrm{B}\mathrm{2}}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \mathrm{\Delta }{n}_{\mathrm{e}\mathrm{ff}\mathrm{1}}/n_{\mathrm{e}\mathrm{ff}\mathrm{1}}+\mathrm{\Delta }{\mathrm{\Lambda }}_1/{\mathrm{\Lambda }}_1\hfill \\ \hfill \mathrm{\Delta }{n}_{\mathrm{e}\mathrm{ff}\mathrm{2}}/n_{\mathrm{e}\mathrm{ff}\mathrm{2}}+\mathrm{\Delta }{\mathrm{\Lambda }}_2/{\mathrm{\Lambda }}_2\hfill \end{array}\right](4)$

When the temperature varies under a constant strain, the central wavelength changes under thermal expansion and thermo-optic effects, based on which Eq. 5 [35] is obtained.

$\left[\begin{array}{c}\hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{1}}/{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{1}}\hfill \\ \hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{2}}/{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{2}}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\alpha }_1\hfill \\ \hfill {\alpha }_2\hfill \end{array}\right]\mathrm{\Delta }T+\left[\begin{array}{c}\hfill {\xi }_1\hfill \\ \hfill {\xi }_2\hfill \end{array}\right]\mathrm{\Delta }T(5)$

where α and ξ are thermal expansion and thermo-optic coefficients of the optical fiber, respectively.

When the strain varies at a constant temperature, the central wavelength changes under the photoelastic effect, thus obtaining Eq. 6 [16].

$\left[\begin{array}{c}\hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{1}}/{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{1}}\hfill \\ \hfill \mathrm{\Delta }{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{2}}/{\lambda }_{\mathrm{B}\mathrm{r}\mathrm{g}\mathrm{2}}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 1-P_{e1}\hfill \\ \hfill 1-P_{e2}\hfill \end{array}\right]\mathrm{\Delta }\epsilon (6)$

where P_e represents the photoelastic coefficient [36] of the optical fiber. In addition, there is the equation of $P_{e1}=P_{e2}=n_{\mathit{eff}}^2\left[P_{12}-v\left(P_{11}+P_{12}\right)\right]/2$[16], in which P₁₁ and P₁₂ are photoelastic coefficients of the fiber core and cladding, respectively.

When the strain and temperature change synchronously, the central wavelength of the FBG varies according to Eq. 7.

$\mathrm{\Delta }{\lambda }_{\mathit{Brg}}\left(\epsilon ,T\right)=K_{\epsilon }\mathrm{\Delta }\epsilon +K_T\mathrm{\Delta }T(7)$

where K_ɛ and K_T are strain and temperature coefficients, respectively. The change of the central reflection wavelengths in both sub-gratings of the 2D FBG is expressed as Eq. 8.

$\left[\begin{array}{c}\hfill \mathrm{\Delta }{\lambda }_{\mathit{Brg1}}\hfill \\ \hfill \mathrm{\Delta }{\lambda }_{\mathit{Brg2}}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill K_{\epsilon 1}\hfill & \hfill K_{T1}\hfill \\ \hfill K_{\epsilon 2}\hfill & \hfill K_{T2}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathrm{\Delta }\epsilon \hfill \\ \hfill \mathrm{\Delta }T\hfill \end{array}\right](8)$

The coefficient matrix for the dual-wavelength grating was obtained by measuring the coefficients of temperature and strain during their respective variations. Therefore, the measured stress and temperature change can be obtained by analyzing the change of the central wavelength of the grating. It should be noted that the cross sensitivity between strain and temperature can only be eliminated under the following condition as Eq. 9 when the dual-wavelength grating is adopted.

$\frac{K_{\epsilon 1}}{K_{\epsilon 2}}\ne \frac{K_{T1}}{K_{T2}}(9)$

3.1 Results and discussion

Herein, we measured the strain and temperature characteristics of the 2D FBG. Using the test system for temperature sensing performance in Figure 3, the light emitted from the BBS was transmitted into the 2D FBG through a fiber optic circulator, and the reflected light was sent out by this circulator into the OSA. The 2D FBG that was straightly fixed onto the surface of a sheet metal was placed in a water tank at constant temperatures which were measured at 5-degree intervals from 35 to 100°C.

FIGURE 3

FIGURE 3. The schematic diagram for the fabricating system of 2D FBG.

As shown by the experimental results in Figure 4, the central wavelengths of both sub-gratings moved towards the long wavelength with increased temperatures. The data fitting curves indicated that the change of two wavelengths had a strong linear response to temperature, with the temperature sensitivity being 10.64 p.m./°C and 10.74 p.m./°C, and the value of R² being 0.99957 and 0.99963. According to Eq. 5, when α and ξ showed their respective values of 5.5 × 10^–7/°C and 7 × 10^–6/°C in the silica-based optical fiber [37], the temperature sensitivity of two sub-gratings should be 11.6 p.m./°C and 11.7 p.m./°C in theory, which were close to the above-measured values (10.64 p.m./°C and 10.74 p.m./°C). Thereinto, the error was primarily caused by the slight temperature fluctuation in the water tank and the limited measurement accuracy of the OSA.

FIGURE 4

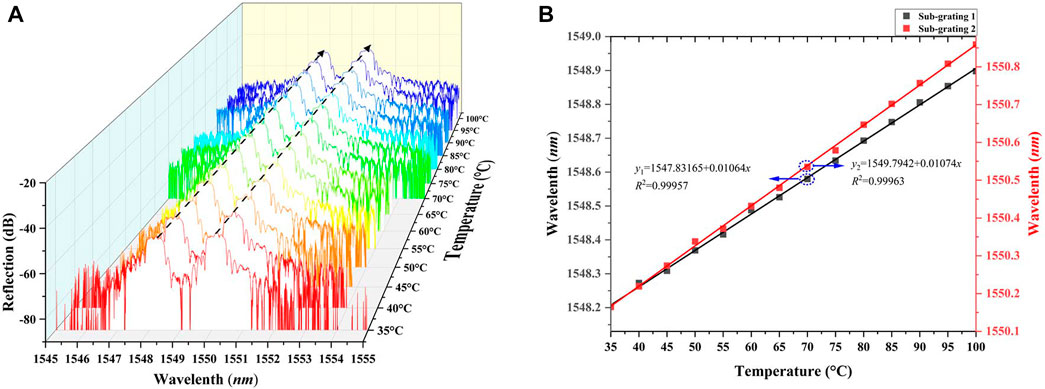
FIGURE 4. Results of the temperature sensing experiment. (A) Reflection spectra of 2D FBG at different temperatures. (B) The center wavelength and linear curve fitting results of the two sub-gratings of 2D FBG at different temperatures.

Figure 5 presents the test system for strain sensing performance. The 2D FBG was fixed onto two sliders on the horizontal guide rail, of which one was immovable and the other was slideable. The latter was connected to a mass block through a fixed pulley and moved by changing the mass of this block to cause the strain of the grating. In this process, the Si O ₂ had its Young’s modulus of 72 GPa; the acceleration of gravity was set at 9.8 g/cm³; the strain was 110 μɛ for every mass change of 10 g in the mass block. The strain response was measured using 0 ∼ 13 weights successively, with each weight being about 2.5 g.

FIGURE 5

FIGURE 5. The schematic diagram for the strain sensing system.

As shown in Figure 6, experimental results showed that the central wavelengths of both sub-gratings had a strong linear response to strain, during which the strain sensitivity was 0.882,731 pm/μɛ and 0.916,080 pm/μɛɛ, and the value of R² was 0.99849 and 0.99819. According to Eq. 6, when the photoelastic coefficients of the fiber core and cladding were set at P₁₁ = 0.121 and P₁₂ = 0.27 under the condition of ν = 0.17, respectively [37], the theoretical strain sensitivity of two sub-gratings should be 1.2086 pm/μɛɛ and 1.2101 pm/μɛ.

FIGURE 6

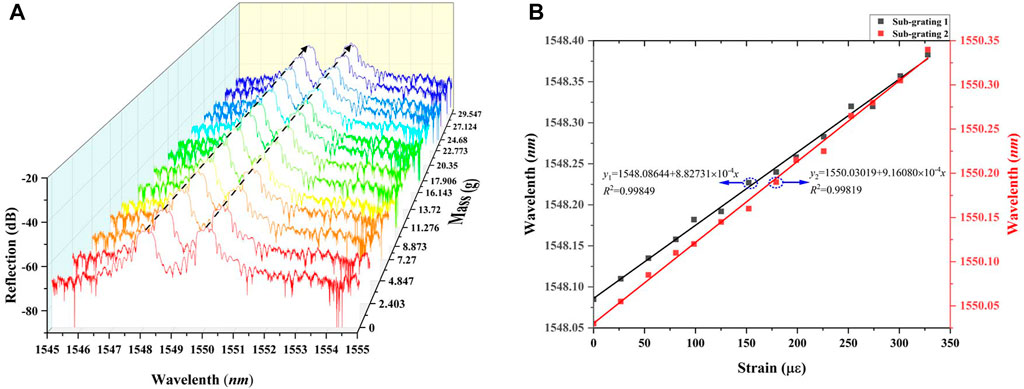
FIGURE 6. Results of the strain sensing experiment at room temperature (25 °C). (A) Reflection spectra of 2D FBG at different strain. (B) The center wavelength and linear curve fitting results of the two sub-gratings of 2D FBG at different strain.

In the experiment, the OSA with resolution 10 p.m. is employed, so the resolution of temperature and strain can reach 0.93°C and 10.8 μɛ, respectively. The comparison of the characteristics between several methods for measurement of temperature and strain among the published works is presented in Table 1. As can be seen from Table 1, most of the published works achieves simultaneous measurement of temperature and strain by increasing the types of optical fibers, the form of fiber gratings, adding photosensitive materials, and constructing interferometer structures. This proposed sensor is completed at one time in a single-mode fiber, the structure is compact and simple, the results are accurate and stable is relatively complicated.

TABLE 1

TABLE 1. Comparison between several methods for measurement of temperature and strain.

The spectrogram also presents the intensity of the reflected light at the central wavelength under different temperatures and strains, as shown in Figure 7. It can be seen that the intensity response of both sub-gratings changes slightly with varying temperatures and strains, and the two sub-gratings fluctuate in consistent trends. This indicates that the temperature and strain only have a small impact on the reflection intensity of the grating, which further verifies the good synchronicity and high stability of both sub-gratings.

FIGURE 7

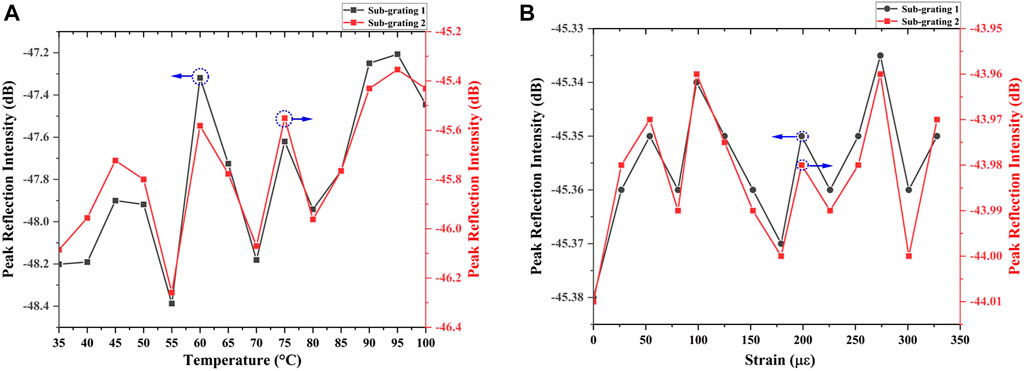
FIGURE 7. Synchronization test results of two sub-gratings. (A) The peak reflection intensity of 2D FBG in temperature sensing experiments. (B) The peak reflection intensity of 2D FBG in strain sensing experiments.

The above results indicate that this dual-wavelength grating can be used for the strain and temperature sensing, with its response to temperature and strain expressed as Eq. (10).

$\left[\begin{array}{c}\hfill \mathrm{\Delta }{\lambda }_{B1}\hfill \\ \hfill \mathrm{\Delta }{\lambda }_{B2}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 0.8827\hfill & \hfill 10.64\hfill \\ \hfill 0.9161\hfill & \hfill 10.74\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathrm{\Delta }\epsilon \hfill \\ \hfill \mathrm{\Delta }T\hfill \end{array}\right](10)$

based on which, Eq. 11 are deduced.

$\begin{array}{c}{K}_{\epsilon 1}/K_{\epsilon 2}=0.9636\hfill \\ K_{T1}/K_{T2}=0.9907\hfill \end{array}(11)$

According to Eq. 8, this dual-wavelength grating meets the requirements of dual-parameter sensing and therefore can be used to cope with the cross sensitivity between temperature and strain in the sensing process. This result was verified by cooling the grating region locally under constant strains, thus revealing the change of the central wavelength using different mass blocks (0 g, 9.5 g, 17 g, and 22 g) at 40°C, 42°C, and 45°C, respectively, as shown in Figure 8. The measured data in this experiment are in line with those calculated with a coefficient matrix, which validates that the 2D FBG can achieve the strain and temperature sensing simultaneously and improve the cross sensitivity between strain and temperature effectively. It is also noted that this grating, with a compact structure, can be engraved without multiple exposures and produced in bulk, showing great advantages in practical application.

FIGURE 8

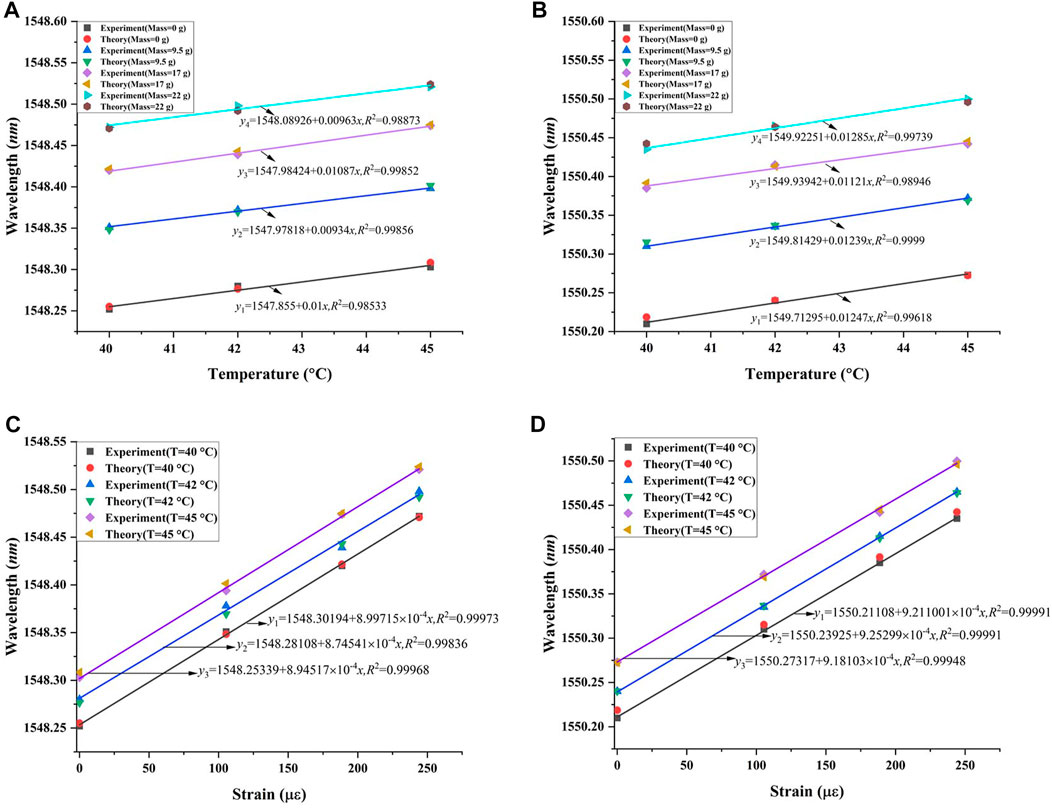
FIGURE 8. Results of the verification experiment on the cross sensitivity between temperature and strain. (A) Comparison of theoretical and experimental data and curve fitting results obtained from experimental data under the same strain at 1,548 nm. (B) Comparison of theoretical and experimental data and curve fitting results obtained from experimental data under the same strain at 1,550 nm. (C) Comparison of theoretical and experimental data and curve fitting results obtained from experimental data under the same temperature at 1,548 nm. (D) Comparison of theoretical and experimental data and curve fitting results obtained from experimental data under the same temperature at 1,550 nm.

During the verification, we revealed the temperature and strain responses at different central wavelengths based on the data of such wavelengths obtained from the OSA. As presented in Figure 9, the demodulated curves for both responses in the experiment changed in the same way with the theoretical ones. The mean relative errors of temperature and strain responses were computed to be 3.476 and 1.087%, respectively, which separated the cross sensitivity between temperature and strain.

FIGURE 9

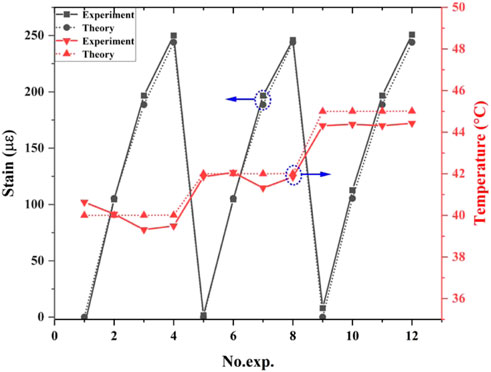
FIGURE 9. Comparison of theoretical (dashed lines) and experimental data (solid lines) curves for strain and temperature responses.

4 Conclusion

In summary, the spatially non-overlapping dual-wavelength 2D FBG engraved on the single-mode fiber in this work can be used to measure the temperature and strain simultaneously. Its temperature and strain coefficients are tested to be 10.64 pm/°C and 0.882,731 pm/μɛ at the central wavelength of 1,548 nm, and 10.74 pm/°C and 0.916,080 pm/μɛ at the central wavelength of 1,550 nm. Our experiments verify that using a coefficient matrix, it is feasible for this grating to eliminate the cross sensitivity between temperature and strain and achieve the simultaneous measurement of dual parameters. The values of temperature and strain responses inverted from this matrix during the simultaneous variation of both parameters have the mean relative errors of 3.476 and 1.087% with theoretical ones, respectively. Moreover, it is noted that this grating has a compact structure and can be engraved without multiple exposures and produced in bulk. Therefore, it is superior to existing fiber gratings in respect of dual-parameter sensing.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.

Author contributions

ZC, PX, and XG contributed to conception and design of the study. ZC and JW organized the database. JW, XG, and LM performed the statistical analysis. ZC, PX, CC, and JZ wrote the first draft of the manuscript. ZC, JW, JZ, CC, and LM wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Vendittozzi C, Felli F, Lupi C. Modeling fbg sensors sensitivity from cryogenic temperatures to room temperature as a function of metal coating thickness. Opt Fiber Tech (2018) 42:84–91. doi:10.1016/j.yofte.2018.02.017

CrossRef Full Text | Google Scholar

2. El-Amassi D, Taya S DV, Vigneswaran D. Temperature sensor utilizing a ternary photonic crystal with a polymer layer sandwiched between si and sio2 layers. J Theor Appl Phys (2018) 12:293–8. doi:10.1007/s40094-018-0308-x

CrossRef Full Text | Google Scholar

3. Jin L, Tan YN, Quan Z, Li MP, Guan BO. Strain-insensitive temperature sensing with a dual polarization fiber grating laser. Opt Express (2012) 20:6021–8. doi:10.1364/OE.20.006021

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wu F, Wu J, Guo Z, Jiang H, Sun Y, Li Y, et al. Giant enhancement of the goos-hänchen shift assisted by quasibound states in the continuum. Phys Rev Appl (2019) 12:014028. doi:10.1103/PhysRevApplied.12.014028

CrossRef Full Text | Google Scholar

5. Lin CY, Chern GW, Wang LA. Periodical corrugated structure for forming sampled fiber Bragg grating and long-period fiber grating with tunable coupling strength. J Lightwave Technol (2001) 19:1212–20. doi:10.1109/50.939803

CrossRef Full Text | Google Scholar

6. Jena S, Tokas R, Thakur S, Udupa D. Tunable mirrors and filters in 1d photonic crystals containing polymers. Physica E: Low-dimensional Syst Nanostructures (2019) 114:113627. doi:10.1016/j.physe.2019.113627

CrossRef Full Text | Google Scholar

7. Lin H, Fengyin L, Jun L. Slope detection based on grating sensors. Int J Onl Eng (2018) 14:147–59. doi:10.3991/ijoe.v14i11.9520

CrossRef Full Text | Google Scholar

8. Han GH, Zhang WG. Method of correlation function for analyzing cross-sensitivity of strain and temperature in fiber grating sensors. Optoelectron Lett (2007) 3:195–8. doi:10.1007/s11801-007-6166-4

CrossRef Full Text | Google Scholar

9. Farahi F, Webb D, Jones J, Jackson D. Simultaneous measurement of temperature and strain: cross-sensitivity considerations. J Lightwave Technol (1990) 8:138–42. doi:10.1109/50.47862

CrossRef Full Text | Google Scholar

10. Liu Q, Ran ZL, Rao YJ, Luo SC, Yang HQ, Huang Y. Highly integrated fp/fbg sensor for simultaneous measurement of high temperature and strain. IEEE Photon Technol Lett (2014) 26:1715–7. doi:10.1109/LPT.2014.2331359

CrossRef Full Text | Google Scholar

11. Wu H, Lin Q, Jiang Z, Zhang F, Li L, Zhao L. A temperature and strain sensor based on a cascade of double fiber Bragg grating. Meas Sci Technol (2019) 30:065104. doi:10.1088/1361-6501/ab093e

CrossRef Full Text | Google Scholar

12. Lima HF, Antunes PF, de Lemos Pinto J, Nogueira RN. Simultaneous measurement of strain and temperature with a single fiber Bragg grating written in a tapered optical fiber. IEEE Sens J (2010) 10:269–73. doi:10.1109/JSEN.2009.2030261

CrossRef Full Text | Google Scholar

13. Liang L, Liu M, Li Y, Li G, Yang K. Solutions of strain and temperature cross-sensitivity of long period fiber grating temperature sensing. Hongwai Yu Jiguang Gongcheng/Infrared Laser Eng (2015) 44:1020–3.

Google Scholar

14. Kipriksiz SE, Yücel M. Tilted fiber Bragg grating design for a simultaneous measurement of temperature and strain. Opt Quan Electron (2021) 53:6–15. doi:10.1007/s11082-020-02609-w

CrossRef Full Text | Google Scholar

15. Li B, Zhan X, Tang M, Gan L, Shen L, Huo L, et al. Long-period fiber gratings inscribed in few-mode fibers for discriminative determination. Opt Express (2019) 27:26307–16. doi:10.1364/OE.27.026307

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Frazão O, Santos JL. Simultaneous measurement of strain and temperature using a Bragg grating structure written in germanosilicate fibres. J Opt A: Pure Appl Opt (2004) 6:553–6. doi:10.1088/1464-4258/6/6/010

CrossRef Full Text | Google Scholar

17. Cavaleiro P, Araujo F, Ferreira L, Santos J, Farahi F. Simultaneous measurement of strain and temperature using Bragg gratings written in germanosilicate and boron-codoped germanosilicate fibers. IEEE Photon Technol Lett (1999) 11:1635–7. doi:10.1109/68.806871

CrossRef Full Text | Google Scholar

18. Hu Q, Wang P, Rao B, Wang M, Wang Z, Xu X. Simultaneous measurement of temperature and strain using double-cladding fiber based hybrid Bragg grating. OSA Continuum (2020) 3:1031–7. doi:10.1364/OSAC.389645

CrossRef Full Text | Google Scholar

19. Gao X, Xu J, Xie C, Zhang W, Pei L, Zheng J, et al. Strain-insensitive temperature sensor based on few-mode fiber and photonic crystal fiber. IEEE Photon J (2022) 14:1–7. doi:10.1109/JPHOT.2022.3183574

CrossRef Full Text | Google Scholar

20. Wang Y, Zhou Y, Wang X, Chen D, Lian Z, Lu C, et al. Simultaneous measurement of temperature and strain based on a hollow core Bragg fiber. Opt Lett (2020) 45:6122–5. doi:10.1364/OL.403722

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Shu X, Liu Y, Zhao D, Gwandu BAL, Floreani F, Zhang L, et al. Dependence of temperature and strain coefficients on fiber grating type and its application to simultaneous temperature and strain measurement. Opt Lett (2002) 27 9:701–3. doi:10.1364/ol.27.000701

PubMed Abstract | CrossRef Full Text | Google Scholar

22. jie Li L, Li D, hao Wang W, Han J. Research on the decoupling method of structure strain measurement based on pvdf sensors array. In: Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA); 21-24 Oct. 2016; China (2016). p. 433–7.

CrossRef Full Text | Google Scholar

23. Tian J, Jiao Y, Ji S, Dong X, Yao Y. Cascaded-cavity fabry–perot interferometer for simultaneous measurement of temperature and strain with cross-sensitivity compensation. Opt Commun (2018) 412:121–6. doi:10.1016/j.optcom.2017.12.005

CrossRef Full Text | Google Scholar

24. Tian K, Zhang M, Yu J, Jiang Y, Zhao H, Wang X, et al. High sensitivity, low temperature-crosstalk strain sensor based on a microsphere embedded fabry–perot interferometer. Sensors Actuators A: Phys (2020) 310:112048. doi:10.1016/j.sna.2020.112048

CrossRef Full Text | Google Scholar

25. Wang Y, Bao H, Ran Z, Huang J, Zhang S. Integrated fp/rfbg sensor with a micro-channel for dual-parameter measurement under high temperature. Appl Opt (2017) 56:4250–4. doi:10.1364/AO.56.004250

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Guan BO, Tam H, Chan H, Choy CL, Demokan M. Discrimination between strain and temperature with a single fiber Bragg grating. Microw Opt Technol Lett (2002) 33:200–2. doi:10.1002/mop.10275

CrossRef Full Text | Google Scholar

27. Zhang W, Wu X, Li S, Zhang G, Wang X, Yang Y, et al. Temperature insensitive strain measurement based on a novel mach-zehnder interferometer with tcf-pmpcf structure. J Mod Opt (2021) 68:839–46. doi:10.1080/09500340.2021.1952326

CrossRef Full Text | Google Scholar

28. Pereira L, Min R, Paixão T, Marques C, Woyessa G, Bang O, et al. Compact dual-strain sensitivity polymer optical fiber grating for multi-parameter sensing. J Lightwave Technol (2021) 39:2230–40. doi:10.1109/JLT.2020.3046077

CrossRef Full Text | Google Scholar

29. Tian S, Tang Y, Zhang Y, An R, Yuan Y, Zhu Y, et al. Simultaneous measurement of strain and temperature based on dual cross-axis interference polarization-maintaining fiber interferometer. J Lightwave Technol (2022) 40:4878–85. doi:10.1109/JLT.2022.3166276

CrossRef Full Text | Google Scholar

30. Cui W, Su JJ, Jiang PP, Wu B, Shen YH. High-resolution multiplexed fiber Bragg grating wavelength interrogation system based on tunable ld. Acta Photonica Sinica (2016) 45:59–66. doi:10.3788/gzxb20164507.0706003

CrossRef Full Text | Google Scholar

31. Nair AS, Kumar VPS, Joe H. Twist sensitivity of cladding-mode resonances and its cross-sensitivity to strain and temperature in a mechanically induced long-period fiber grating. Fiber Integrated Opt (2014) 33:347–59. doi:10.1080/01468030.2014.979958

CrossRef Full Text | Google Scholar

32. Tian Y, Chai Q, Meng Y, Liu Y, Ren J, Wang S, et al. An overlap-splicing-based cavity in fbg sensor for the measurement of strain and temperature. IEEE Photon Technol Lett (2017) 29:235–8. doi:10.1109/LPT.2016.2637361

CrossRef Full Text | Google Scholar

33. Pan Y, Liu T, Jiang J, Liu K, Wang S, Yin J, et al. Simultaneous measurement of temperature and strain using spheroidal-cavity-overlapped fbg. IEEE Photon J (2015) 7:1–6. doi:10.1109/JPHOT.2015.2493724

CrossRef Full Text | Google Scholar

34. Kersey A, Davis M, Patrick H, Leblanc M, Koo K, Askins C, et al. Fiber grating sensors. J Lightwave Technol (1997) 15:1442–63. doi:10.1109/50.618377

CrossRef Full Text | Google Scholar

35. Culshaw B. Optical fiber sensor technologies: opportunities and-perhaps-pitfalls. J Lightwave Technol (2004) 22:39–50. doi:10.1109/JLT.2003.822139

CrossRef Full Text | Google Scholar

36. Kaur G, Kaler RS, Kwatra N. On the optimization of fiber Bragg grating optical sensor using genetic algorithm to monitor the strain of civil structure with high sensitivity. Opt Eng (2016) 55:087103. doi:10.1117/1.OE.55.8.087103

CrossRef Full Text | Google Scholar

37. Sun X, Zeng L, Du H, Dong X, Chang Z, Hu Y, et al. Phase-shifted gratings fabricated with femtosecond laser by overlapped two types of fiber Bragg gratings. Opt Laser Tech (2020) 124:105969. doi:10.1016/j.optlastec.2019.105969

CrossRef Full Text | Google Scholar

38. Du WC, Tao XM, Tam HY. Fiber Bragg grating cavity sensor for simultaneous measurement of strain and temperature. IEEE Photon Technol Lett (1999) 11:105–7. doi:10.1109/68.736409

CrossRef Full Text | Google Scholar

39. Xie RW, Zhang XZ, Wang S, Jiang JF, Liu K, Zang CJ, et al. Research on influencing factors of fbg temperature sensors stability. Guangdianzi Jiguang/Journal of Optoelectronics Laser (2018) 29:363–9. doi:10.16136/j.joel.2018.04.0229

CrossRef Full Text | Google Scholar

40. Leal-Junior AG, Frizera A, Marques C. Thermal and mechanical analyses of fiber Bragg gratings-embedded polymer diaphragms. IEEE Photon Technol Lett (2020) 32:623–6. doi:10.1109/LPT.2020.2988554

CrossRef Full Text | Google Scholar

41. Zeng H, Geng T, Yang W, An M, Li J, Yang F, et al. Combining two types of gratings for simultaneous strain and temperature measurement. IEEE Photon Technol Lett (2016) 28:477–80. doi:10.1109/LPT.2015.2499378

CrossRef Full Text | Google Scholar

42. Yang W, Geng T, Yang J, Zhou A, Liu Z, Geng S, et al. A phase-shifted long period fiber grating based on filament heating method for simultaneous measurement of strain and temperature. J Opt (2015) 17:075801. doi:10.1088/2040-8978/17/7/075801

CrossRef Full Text | Google Scholar

43. Bai Z, Zhang W, Gao S, Zhang H, Wang L, Liu Y, et al. Simultaneous measurement of strain and temperature using a long period fiber grating based on waist-enlarged fusion bitapers. J Opt (2014) 16:045401. doi:10.1088/2040-8978/16/4/045401

CrossRef Full Text | Google Scholar

44. Brady GP, Kalli K, Webb DJ, Jackson DA, Reekie L, Archambault JL. Simultaneous measurement of temperature and strain using double-cladding fiber based hybrid Bragg grating. OSA Continuum (1997) 3:1031. doi:10.1364/OSAC.389645

CrossRef Full Text | Google Scholar