- 1School of Physics, Northwest University, Xi’an, China
- 2China Academy of Space Technology, Xi’an, China
- 3School of Electronics and Information, Northwestern Polytechnical University, Xi’an, China
The probability density analysis formula of the single orbital angular momentum (OAM) mode of an annular vortex beam with a focusing mirror in a turbulent atmosphere is derived theoretically, and the effects of different parameters on the OAM spectrum are investigated numerically, and the results show that the OAM diffusion of the annular vortex beam is weaker than the Gaussian vortex beam in a turbulent atmosphere under the same conditions, and the annular vortex beam with a focusing mirror can more effectively reduce the crosstalk of OAM modes. Our findings will be useful for improving FSO system performance.
1 Introduction
Vortex beams, carrying the OAM, have attracted many attentions because of its wide application, such as optical manipulation and trapping [1], imaging [2], quantum entanglement [3], free-space optical (FSO) communication [4] and so on. In particular, those beams with mutually orthogonal property have been used to multiplexing/demultiplexing in FSO communication for increase capacity and spectral efficiency [5, 6]. However, the major challenge for FSO communication based on the OAM multiplexing/demultiplexing is the disturbance of atmospheric turbulence. When the laser beam propagates in atmosphere, the energy of one OAM state will disperse to adjacent states because of the random fluctuation of the refraction index caused by the turbulence [7–10]. This phenomenon is called as the cross-talk of OAM modes. Obviously, the cross-talk of OAM modes affects the communication quality and the strong cross talk even leads to the failure of communication. In previous studies, the adaptive optics was adopted to compensate the beam’s OAM in turbulent atmosphere [11, 12], but the adaptive optics system is very complicated. In addition, the reconstruction accuracy and correcting efficiency are limited by the phase singularity resulting from the strong fluctuation of wavefront.
On the other hand, the laser beam with different beam profiles has different diffraction characteristics, which are important qualities in the area of FSO communication. The probability density of an OAM mode of Hankel-Bessel beams in atmospheric turbulence was reported [13]. It is found that Hankel-Bessel beams were a good light source for weakening turbulence spreading of the beams and mitigating the effects of turbulence on the probability density of the OAM mode. The Bessel beam based on the OAM multiplexing/demultiplexing in FSO communication with atmospheric turbulence was studied [7]. Under the same turbulence condition, they found that the bit error rates of transmitted signals carried by high order Bessel beams showed small values and fluctuations. The performance of a tailored Airy vortex beam array through atmospheric turbulence was numerically studied [14]. Airy vortex beam array can be a superior light source for effectively reducing the intermodal crosstalk and vortex splitting, thus leading to improvement in the FSO system performance. All of them are the no-diffracting beams. It is well known that no-diffracting beams own the self-healing property and can resist the disturbance of an opaque obstruction [15–17]. Therefore, the no-diffracting beams are naturally considered being applied to FSO communication based on the OAM multiplexing/demultiplexing. In fact, one common beam, i.e. the annular beam, seems to be advantageous on reducing the scintillation index in turbulent atmosphere [18, 19]. Meanwhile it can be used to effectively assist delivering laser power from orbit to the ground for its self-focusing effect propagating in atmosphere [20]. An annular beam can be easily generated [21] and have wide applications [22–26]. However, to the best of our knowledge, there is no report on the OAM properties of an annular vortex beam in turbulent atmosphere. In the present paper, we will study the OAM spectrum of an annular vortex beam in weak turbulent atmosphere. It is found that it, combined with the method that we proposed in recent paper [27], can be used to reduce the cross-talk of OAM modes.
2 Basic theory
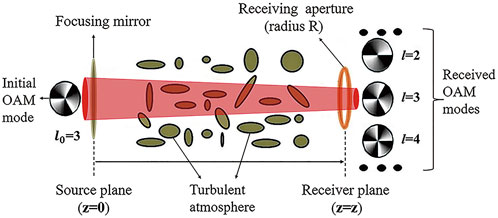
A vortex beam propagates in turbulent atmosphere with a focusing mirror is illustrated in Figure 1. Using the quantum description of a light beam, the complex amplitude of a beam, at any space point (r, ϕ, z), could be written as the superpositions of different OAM states [28], i.e.,
with the expansion coefficient
where l is the quantum number of the OAM mode. The average probability density of an OAM mode can be expressed as
where the angular brackets denote an ensemble average, the * means the complex conjugate. From this equation, the energy weight of each OAM mode can be calculated as
where R is the radius of the receiving aperture. Therefore, one can obtain the OAM spectrum of a beam, i.e., the normalized version of Eq. 4
In free space, the beam field in the receiver plane could be calculated with the help of the Huygens-Fresnel integral [29], as
where (ρ, φ) is the polar coordinates in the source plane, k = 2π/λ denotes the wavenumber with wavelength λ, E (ρ, φ, 0) represents the complex amplitude of a light beam in the source plane. The beam propagating in turbulent atmosphere is a complicated process. For convenience, we only consider the weak turbulence regime and hence the cumulative effect of the turbulence could be thought as a pure phase perturbation to the beam field in the receiver plane [30], i.e.,
exp [ψ(r, ϕ, z)] is the complex phase perturbation due to the atmospheric turbulence along the propagation channel and the Rytov approximation is adopted. By substituting Eq. 7 into Eq. 3, then we can get the expression as
where ⟨ exp [ψ*(r, ϕ1, z) + ψ(r, ϕ2, z)]⟩ is a phase correlation function and could be given by [31].
with
ρ0 is the spatial coherence radius of a spherical wave,
The expression for an annular beam was proposed by Mei [33] and a vortex beam with annular beam profile in the source plane can be expressed as
where ω0 is beam waist size of the Gaussian term,
This case was discussed in Ref. [27], which was proposed as a new method, using a focusing mirror, to reduce the cross-talk among different OAM modes in turbulent atmosphere. There, for simplicity, the basic Gaussian beam was adopted, but the special beam is used in the present paper. By substituting Eq. 11 into Eq. 6, with the help of the following integral formulas [34],
and
after tedious calculation, we obtain the propagating beam field in free space as
with
where Jn () and In() represent the first kind Bessel function and modified Bessel function with order-n, respectively. On substituting Eq. 15 and Eq. 9 into Eq. 8, integrating the equation with variable ϕ1 and ϕ2, the average probability density is obtained,
On substituting Eq. 16 into Eqs 4, 5, we can get the energy weight of each OAM mode for an annular vortex beam in turbulent atmosphere, namely, its OAM spectrum.
3 Numerical results and discussion
In this part, we will show our numerical calculation results. We set λ = 1,060 nm, F = z = 1,000 m, R = 0.1 m,
Figure 2 shows the OAM spectrum of an annular vortex beam in the receiver plane. C0 ≠ 0 denotes that there is a focusing mirror and C0 = 0 means that there is not a focusing mirror. For the convenience of comparing, a Gaussian vortex beam is also shown in the same figure. It is found that the energy of the central mode of the annular vortex beam increases 24.9% by comparing Figures 2A,C. It implies that using a focusing mirror can effectively reduce the influence of turbulence on OAM modes. Moreover, one can find that the energy of the central mode of the annular vortex beam is 0.807. It is larger than that of the Gaussian vortex beam under the same condition. This means that the annular vortex beams show a good result for reducing the influence of turbulence on the OAM mode.
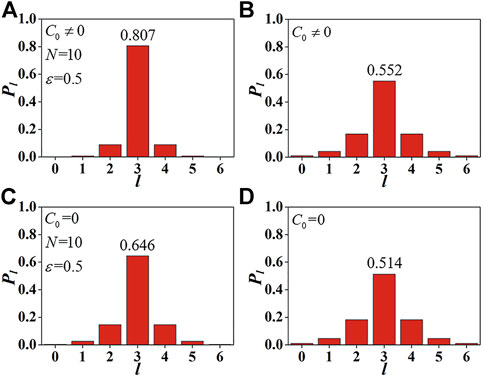
FIGURE 2. The OAM spectrum in the receiver plane for the annular vortex beam with ɛ = 0.5 (A,C) and the Gaussian vortex beam (B,D). C0 ≠ 0 and C0 = 0 denote the beam with a focusing mirror and without this mirror, respectively.
This can be explained by the theory used in Ref. [27], i.e., the annular vortex beam has a smaller transverse area in the receiver plane than Gaussian vortex beams which is illustrated by Figure 3. This figure shows the intensity evolution along the optical axis z and the normalized intensity distribution in the receiver plane for an annular vortex beam and a Gaussian vortex beam. If we use this definition of power in the bucket [35].
to define the effective radius of light beams and then we can calculate the effective interaction area
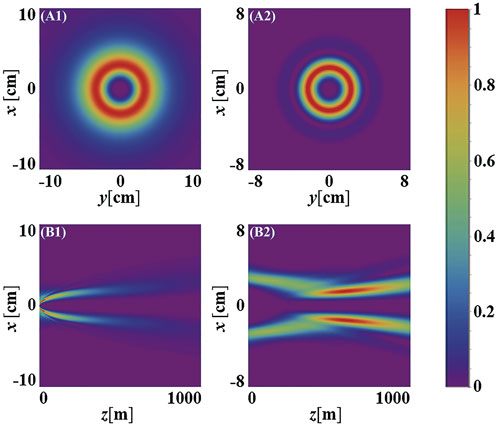
FIGURE 3. The beam spot in the receiver plane and the intensity evolution along the z − axis for a Gaussian vortex beam (A1,B1) and an annular vortex beam (A2,B2), respectively.
The influence of the beam order N of an annular vortex beam on the OAM spectrum in the receiver plane is plotted in Figure 4. On the one hand, it is found that the energy of the central mode Pl=3 for the annular beam with a focusing mirror increases as the beam order N increases. On the other hand, one can find that the energy of the central mode of the annular vortex beam with a focusing mirror is always larger than that of the annular vortex beam without a focusing mirror at arbitrary beam order N. This is shown again that the cross talk of the OAM mode can be largely reduced by using a focusing mirror. Therefore, in this paper, we only focus on the OAM spectrum for the annular vortex beam with a focusing mirror in turbulent atmosphere and we will not discuss the case without a focusing mirror in the next content. For comparing, the energy of the central mode Pl=3 for a Gaussian vortex beam is also plotted in Figure 4. It is found that the annular vortex beam is better on reducing the cross talk of OAM mode in turbulent atmosphere than the Gaussian vortex beam. The variation of energy of central mode Pl=3 as a function of the obscure ration ɛ of the annular vortex beam is plotted in Figure 5. One can find that Pl=3 increases when the value of ɛ increases. In other words, the cross talk of OAM mode is weak for annular vortex beams with a great value of ɛ.
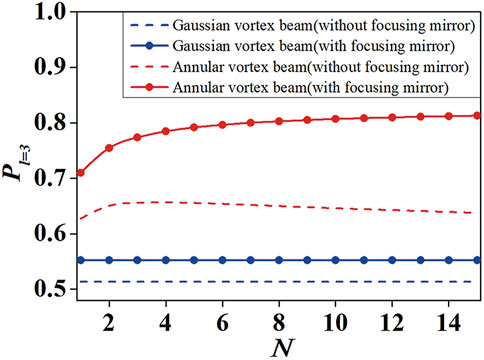
FIGURE 4. The variation of the energy of central mode Pl=3 as a function of beam order N for annular vortex beam in the receiver plane. The corresponding Gaussian vortex beam, dashed line, is plotted for comparing.
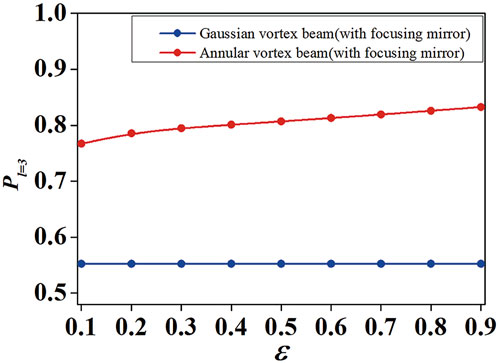
FIGURE 5. The variation of the energy of central mode Pl=3 as a function of obscure ratio ɛ for annular vortex beam in the receiver plane.
4 Numerical simulation
To illustrate the analytical results, we simulate the two beams propagating in turbulent atmosphere by using the random phase screen [36]. In this examples, we take λ = 1,060 nm, ω0 = 0.02 m, l0 = 3, li = 0.001 m, F = 1,000 m, N = 10 and ɛ = 0.5. The size of each phase screen is set as 0.28 m × 0.28 m with 512 w512 pixels. There are 13 screens among 1 km propagating distance. Every phase screen is characterized by an effective coherence diameter
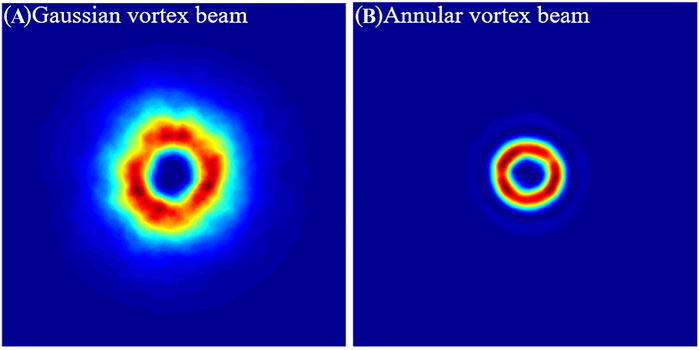
FIGURE 6. The beam spot (one realization) for a Gaussian vortex beam (A) and an annular vortex beam (B) in the receiver plane with l0 = 3,
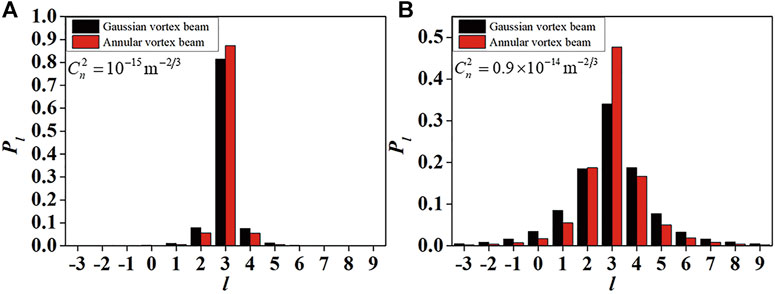
FIGURE 7. The OAM spectrum (averaged over 100 realizations) of an annular vortex beam and a Gaussian vortex beam in the receiver plane for different structural constant (A) 10-15 and (B) 0.9×10-14.
5 Conclusion
The OAM spectrum of an annular vortex beam in turbulent atmosphere was studied. The influence of different parameters was explored numerically. For comparing sake, the Gaussian vortex beam was also showed in this paper. We found that the cross talk of OAM modes was reduced largely by using the annular vortex beam with a focusing mirror. At the same time, the annular vortex beam had a better performance on reducing the cross talk of OAM modes than the Gaussian vortex beam. Moreover, at the initial quantum number l0 = 3, the annular vortex beam with a great beam number N or a large obscure ratio can more reduce the cross talk of OAM modes. The results obtained in this paper are useful for FSO communication.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
GW proposed the idea and directed the entire process, YZ and HL performed the theoretical derivation, JC performed the numerical simulation, JC and YZ wrote the first draft, and all authors participated in the revision of the manuscript and approved the final version.
Funding
National key Research and Development Project of China (2019YFA0705000); National Natural Science Foundation of China (NSFC) (12192254, 12074310, 11974281, 91750201); Natural Science Basic Research Plan in Shaanxi Province of China (Program No. 2021JM-315); Innovation Group of Jinan (2018GXRC010); Local Science and Technology Development Project of the Central Government (No. YDZX20203700001766).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. He H, Friese MEJ, Heckenberg NR, Rubinsztein-Dunlop H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys Rev Lett (1995) 75:826–9. doi:10.1103/PhysRevLett.75.826
2. Davis JA, McNamara DE, Cottrell DM, Campos J. Image processing with the radial hilbert transform: Theory and experiments. Opt Lett (2000) 25:99–101. doi:10.1364/OL.25.000099
3. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature (2001) 412:313–6. doi:10.1038/35085529
4. Gibson G, Courtial J, Padgett MJ, Vasnetsov M, Pas’ko V, Barnett SM, et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt Express (2004) 12:5448–56. doi:10.1364/OPEX.12.005448
5. Wang J, Yang JY, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat Photon (2012) 6:488–96. doi:10.1038/nphoton.2012.138
6. Lei T, Zhang M, Li Y, Jia P, Liu GN, Xu X, et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci Appl (2015) 4:e257. doi:10.1038/lsa.2015.30
7. Yuan Y, Lei T, Li Z, Li Y, Gao S, Xie Z, et al. Beam wander relieved orbital angular momentum communication in turbulent atmosphere using Bessel beams. Sci Rep (2017) 7:42276–7. doi:10.1038/srep42276
8. Wang J. Advances in communications using optical vortices. Photon Res (2016) 4:B14. doi:10.1364/PRJ.4.000B14
9. Anguita JA, Neifeld MA, Vasic BV. Turbulence-induced channel crosstalk in an orbital angular momentum-multiplexed free-space optical link. Appl Opt (2008) 47:2414–29. doi:10.1364/AO.47.002414
10. Krenn M, Fickler R, Fink M, Handsteiner J, Malik M, Scheidl T, et al. Communication with spatially modulated light through turbulent air across Vienna. New J Phys (2014) 16:113028. doi:10.1088/1367-2630/16/11/113028
11. Li N, Chu X, Zhang P, Feng X, Fan C, Qiao C. Compensation for the orbital angular momentum of a vortex beam in turbulent atmosphere by adaptive optics. Opt Laser Technol (2018) 98:7–11. doi:10.1016/j.optlastec.2017.07.028
12. Ren Y, Xie G, Huang H, Bao C, Yan Y, Ahmed N, et al. Adaptive optics compensation of multiple orbital angular momentum beams propagating through emulated atmospheric turbulence. Opt Lett (2014) 39:2845–8. doi:10.1364/OL.39.002845
13. Zhu Y, Liu X, Gao J, Zhang Y, Zhao F. Probability density of the orbital angular momentum mode of Hankel-Bessel beams in an atmospheric turbulence. Opt Express (2014) 22:7765–72. doi:10.1364/OE.22.007765
14. Yan X, Guo L, Cheng M, Li J. Controlling abruptly autofocusing vortex beams to mitigate crosstalk and vortex splitting in free-space optical communication. Opt Express (2018) 26:12605–19. doi:10.1364/OE.26.012605
15. Broky J, Siviloglou GA, Dogariu A, Christodoulides DN. Self-healing properties of optical Airy beams. Opt Express (2008) 16:12880–91. doi:10.1364/OE.16.012880
16. Chu X, Zhou G, Chen R. Analytical study of the self-healing property of Airy beams. Phys Rev A (Coll Park) (2012) 85:013815. doi:10.1103/PhysRevA.85.013815
17. Chu X. Analytical study on the self-healing property of Bessel beam. Eur Phys J D (2012) 66:259–5. doi:10.1140/epjd/e2012-30343-6
18. Vetelino FES, Andrews LC. Annular Gaussian beams in turbulent media. In: DG Voelz, and JC Ricklin, editors, Free-Space Laser Commun Active Laser Illumination. 5160. Proc. SPIE (2004). p. 86–97. doi:10.1117/12.507774
19. Gerçekcioğlu H, Baykal Y, Nakiboğlu C. Annular beam scintillations in strong turbulence. J Opt Soc Am A (2010) 27:1834–9. doi:10.1364/JOSAA.27.001834
20. Zhang Y, Ji X, Li X, Li Q, Yu H. Self-focusing effect of annular beams propagating in the atmosphere. Opt Express (2017) 25:21329–41. doi:10.1364/OE.25.021329
21. Sabatyan A, Meshginqalam B. Generation of annular beam by a novel class of Fresnel zone plate. Appl Opt (2014) 53:5995–6000. doi:10.1364/AO.53.005995
22. Liu S, Kong F, Shi S, Kovacevic R. Study of a hollow laser beam for cladding. Int J Adv Manuf Technol (2014) 73:147–59. doi:10.1007/s00170-014-5763-1
23. Zhang J, Shi S, Fu G, Shi J, Zhu G, Cheng D. Analysis on surface finish of thin-wall parts by laser metal deposition with annular beam. Opt Laser Technol (2019) 119:105605. doi:10.1016/j.optlastec.2019.105605
24. Lenton IC, Armstrong DJ, Stilgoe AB, Nieminen TA, Rubinsztein-Dunlop H. Orientation of swimming cells with annular beam optical tweezers. Opt Commun (2020) 459:124864. doi:10.1016/j.optcom.2019.124864
25. Lee DR, Gweon DG, Yoo H. Annular-beam dual-detection confocal reflectance microscopy for high-speed three-dimensional surface profiling with an extended volume. Meas Sci Technol (2020) 31:045403. doi:10.1088/1361-6501/ab4d2e
26. Lu X, Yang L, Xie H, Yang Z, Cui J, Wang Y. Simulations of the near-field enhancement on AFM tip irradiated by annular laser beam. IEEE Trans Nanotechnol (2019) 18:979–82. doi:10.1109/TNANO.2019.2938614
27. Zhou M, Zhou Y, Wu G, Cai Y. Reducing the cross-talk among different orbital angular momentum modes in turbulent atmosphere by using a focusing mirror. Opt Express (2019) 27:10280–7. doi:10.1364/OE.27.010280
28. Molina-Terriza G, Torres JP, Torner L. Management of the angular momentum of light: Preparation of photons in multidimensional vector states of angular momentum. Phys Rev Lett (2001) 88:013601. doi:10.1103/PhysRevLett.88.013601
29. Born M, Wolf E. Principles of optics: Electromagnetic theory of propagation, interference and diffraction of light. Cambridge University Press (2013).
30. Paterson C. Atmospheric turbulence and orbital angular momentum of single photons for optical communication. Phys Rev Lett (2005) 94:153901. doi:10.1103/PhysRevLett.94.153901
31. Zhu Y, Chen M, Zhang Y, Li Y. Propagation of the OAM mode carried by partially coherent modified Bessel–Gaussian beams in an anisotropic non-Kolmogorov marine atmosphere. J Opt Soc Am A (2016) 33:2277–83. doi:10.1364/JOSAA.33.002277
32. Wang F, Cai Y. Second-order statistics of a twisted Gaussian Schell-model beam in turbulent atmosphere. Opt Express (2010) 18:24661–72. doi:10.1364/OE.18.024661
33. Mei Z, Zhao D. Controllable dark-hollow beams and their propagation characteristics. J Opt Soc Am A (2005) 22:1898. doi:10.1364/JOSAA.22.001898
34. Gradshteyn IS, Ryzhik IM. Table of integrals, series, and products. London, United Kingdom: Academic Press (2014).
35. Siegman AE. How to (maybe) measure laser beam quality. In: M Dowley, editor. DPSS (diode pumped solid state) lasers: Applications and issues. OSA Trends Opt. Phonotic (1998). doi:10.1364/DLAI.1998.MQ1
Keywords: an annular vortex beam, cross talk, OAM, atmospheric turbulence, FSO
Citation: Cao J, Liang H, Zhou Y, Wu G and Pang X (2022) Mitigating the cross talk of orbital angular momentum modes in free-space optical communication by using an annular vortex beam and a focusing mirror. Front. Phys. 10:1013729. doi: 10.3389/fphy.2022.1013729
Received: 07 August 2022; Accepted: 28 September 2022;
Published: 14 October 2022.
Edited by:
Yahya Baykal, Çankaya University, TurkeyReviewed by:
Yuanjie Yang, University of Electronic Science and Technology of China, ChinaBernhard Johan Hoenders, University of Groningen, Netherlands
Copyright © 2022 Cao, Liang, Zhou, Wu and Pang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yunqin Zhou, emhvdXlxQHN0dS54aWRpYW4uZWR1LmNu; Gaofeng Wu, Z2Z3dUBud3UuZWR1LmNu; Xiaoyan Pang, eHlwYW5nQG53cHUuZWR1LmNu
 Jiaxuan Cao
Jiaxuan Cao Huijian Liang2
Huijian Liang2 Gaofeng Wu
Gaofeng Wu