A study on vague-valued hesitant fuzzy graph with application

The hesitant fuzzy graph (HFG) is one of the most powerful tools to find the strongest influential person in a network. Many problems of practical interest can be modeled and solved by using HFG algorithms. HFGs, belonging to the FG family, have good capabilities when faced with problems that cannot be expressed by FGs. The vague-valued hesitant fuzzy graph (VVHFG) is the generalization of the HFG. A VVHFG is a powerful and useful tool to find the influential person in various parts, such as meetings, conferences, and every group discussion. In this study, we introduce a new concept of the VVHFG. Our purpose is to develop a notion of the VVHFG and also to present some basic definitions, notations, remarks, and proofs related to VVHFGs. We propose a numerical method to find the most dominating person using our proposed work. Finally, an application of the VVHFG in decision-making has been introduced.

1 Introduction

Graphs, from ancient times to the present day, have played a very important role in various fields, including computer science and social networks, so that with the help of the vertices and edges of a graph, the relationships between objects and elements in a social group can be easily introduced. But, there are some phenomena in our lives that have a wide range of complexities that make it impossible for us to express certainty. These complexities and ambiguities were reduced with the introduction of FSs by Zadeh [1]. After introduction of fuzzy sets, FS-theory is included as part of large research fields. Since then, the theory of FSs has become a vigorous area of research in different disciplines, including life sciences, management, statistics, graph theory, and automata theory. The subject of FGs was proposed by Rosenfeld [2]. Analysis of uncertain problems by the fuzzy graph (FG) is important because it gives more integrity and flexibility to the system. An FG has good capabilities in dealing with problems that cannot be explained by weight graphs. They have been able to have wide applications even in fields such as psychology and identifying people based on cancerous behaviors. One of the advantages of the FG is its flexibility in reducing time and costs on economic issues, which has been welcomed by all managers of institutions and companies. Rashmanlou et al. [3] studied cubic fuzzy graphs. Pramanik et al. [4] presented an extension of the fuzzy competition graph and its uses in manufacturing industries. Pal [5] introduced antipodal interval-valued fuzzy graphs. Bera et al. [6] proposed certain types of m-polar, interval-valued fuzzy graphs.

Gau and Buehrer [7] proposed the concept of the vague set (VS) in 1993 by replacing the value of an element in a set with a subinterval of [0,1].

One type of the FG is the vague graph (VG). VGs have a variety of applications in other sciences, including biology, psychology, and medicine. Also, a VG could concentrate on determining the uncertainty coupled with the inconsistent and indeterminate information of any real-world problems, where FGs may not lead to adequate results. Ramakrishna [8] introduced the concept of VGs and studied some of their properties. After that, Akram et al. [9] introduced vague hypergraphs.

Cayley-VG and regularity were introduced by Akram et al. [10–12]. The concept of domination in VGs was introduced by Borzooei [13]. Rao et al. [14–16] studied certain properties of VGs and domination in vague incidence graphs. Borzooei et al. [17, 18] investigated isomorphic properties of neighborly irregular vague graphs. They also expressed new concepts of regular and highly irregular vague graphs with applications. New concepts of coloring in vague graphs with applications are presented by Krishna [19]. Kosari et al. [20, 21] expressed the notion of VG structure with application in medical diagnosis and also studied a novel description of the VG with application in transportation systems.

Torra [22, 23] developed the concept of a FS to a hesitant fuzzy set (HFS). The HFS is a powerful and effective tool to express uncertain information in multi-attribute decision-making processes as it permits the membership degree of an element to a set represented by several possible values in [0,1].

Many problems of practical interest can be modeled and solved by using HFG-algorithms. The HFG is a useful tool in modeling some problems, especially in the field of communication networks. HFGs was introduced by Pathinathan et al. [24] and extended in [25, 26]. Javaid et al. [27] studied new results of HFGs and their products. Karaaslan [28] investigated the HFGs and their applications in decision-making. Kalyan [29] defined k-regular domination in hesitancy as a fuzzy graph. Shakthivel [30] expressed domination in the hesitancy fuzzy graph. Inverse domination in HFGs and its properties was introduced by Shakthivel et al. [31]. Bai [32] investigated dual HFGs with applications to multi-attribute decision-making. The concept of isomorphic properties of m-polar fuzzy graphs is studied by Ghorai and Pal [33]. Pandey et al. [34] developed a notion of the FG in the setup of bipolar-valued hesitant fuzzy sets and so presented a new definition of a bipolar-valued hesitant fuzzy graph. Shi et al. [35] introduced the notion of homomorphism (HM) of VGs and discussed HM, isomorphism (IM), weak isomorphism (WI), and co-weak isomorphism (CWH) of VGs.

Although HFGs are better at expressing uncertain variables than FGs, they do not perform well in many real-world situations, such as IT management. Therefore, when the data come from several factors, it is necessary to use the VVHFG. VVHFGs, belonging to the FG family, have good capabilities when faced with problems that cannot be expressed by HFGs and VFGs. They are highly practical tools for the study of different computational intelligence and computer science domains. VVHFGs have several applications in real-life systems and applications where the level of the information inherited in the system varies with time and has different levels of accuracy. Homomorphisms (HMs) provide a way of simplifying the structure of objects one wishes to study, while preserving much of it that is of significance. It is not surprising that homomorphisms also appeared in graph theory and that they have proven useful in many areas. Therefore, in this study, we present a novel notion of the VVHFG and investigate HM, IM, WI, and CWI between VVHFGs and express some fundamental operations as a Cartesian product (CP), strong product (SP), and union on VVHFG. Finally, directed-VVHFGs and their application in decision-making have been given.

2 Preliminaries

In this section, we review some notions of vague graphs and their operations.

Definition 2.1. A graph is an ordered pair G* = (X, E) where X is the set of vertices of G* and E ⊆ X × X is the set of edges of G*. Suppose E is the set of all 2-element subsets of X that we denoted by ${\tilde{X}}^2$.(I) Let G₁ = (X₁, E₁) and G₂ = (X₂, E₂) be two graphs, then the CP of two graphs G₁ and G₂ denoted by G₁ × G₂ = (X₁ × X₂, E₁ × E₂) is defined as:

$X_1\times X_2=\left\{\left(s_1,s_2\right)|s_1\in X_1,s_2\in X_2\right\},$

$E_1\times E_2=\left\{\left(t,t_2\right)\left(t,k_2\right)|t\in X_1,t_2{k}_2\in E_2\right\}\cup \left\{\left(t_1,p\right)\left(k_1,p\right)|t_1{k}_1\in E_1,p\in X_2\right\}.$

(II) Let G₁ = (X₁, E₁) and G₂ = (X₂, E₂) be two graphs. Then, the SP of two graphs G₁ and G₂ denoted by G₁ ⊗ G₂ = {X₁ ⊗ X₂, E₁ ⊗ E₂} is defined as:

$X_1\times X_2=\left\{\left(s_1,s_2\right)|s_1\in X_1,s_2\in X_2\right\},$

$\begin{array}{ll}\hfill E_1\times E_2& =\left\{\left(t,t_2\right)\left(t,k_2\right)|t\in X_1,t_2{k}_2\in E_2\right\}\cup \left\{\left(t_1,p\right)\left(k_1,p\right)|t_1{k}_1\in E_1,p\in X_2\right\}\hfill \\ \hfill & \cup \left\{\left(t_1,t_2\right)\left(k_1,k_2\right)|t_1{k}_1\in E_1,t_2{k}_2\in E_2\right\}.\hfill \end{array}$

Definition 2.2. An FG on a graph G* = (X, E) is a pair G = (ψ, θ), where ψ: X → [0, 1] is an FS on X and θ: X × X → [0, 1] is a fuzzy relation on E, such that,

$\theta \left(mn\right)\le \min \left\{\psi \left(m\right),\psi \left(n\right)\right\},$

for all m, n ∈ X.

Definition 2.3. [7]"A vague set (VS) W is a pair (t_W, f_W) on set X where t_W and f_W are taken as real-valued functions which can be defined on X → [0, 1] so that t_W(m) + f_W(m) ≤ 1, ∀m ∈ X.

Definition 2.4. [8] Suppose G* = (X, E) is a crisp graph, a pair G = (W, Z) is named a VG on graph G* = (X, E) where W = (t_W, f_W) is a VS on X and Z = (t_Z, f_Z) is a VS on E ⊆ X × X such that,

$t_Z\left(mn\right)\le \min \left\{t_W\left(m\right),t_W\left(n\right)\right\},$

$f_Z\left(mn\right)\ge \max \left\{f_W\left(m\right),f_W\left(n\right)\right\},$

for all mn ∈ E.A VG G is named strong if

$t_Z\left(mn\right)=\min \left\{t_W\left(m\right),t_W\left(n\right)\right\},$

$f_Z\left(mn\right)=\max \left\{f_W\left(m\right),f_W\left(n\right)\right\},$

for all m, n ∈ X.

Definition 2.5. [11] Suppose G = (W, Z) is a VFG on G*, the degree of vertex m is defined as deg(m) = (d_t(m), d_f(m)) where

$d_t\left(m\right)=\sum _{m\ne n,n\in X}{t}_Z\left(mn\right),d_f\left(m\right)=\sum _{m\ne n,n\in X}{f}_Z\left(mn\right).$

The order of G is defined as

$O\left(G\right)=\left(\sum _{m\in X}{t}_W\left(m\right),\sum _{m\in X}{f}_W\left(m\right)\right).$

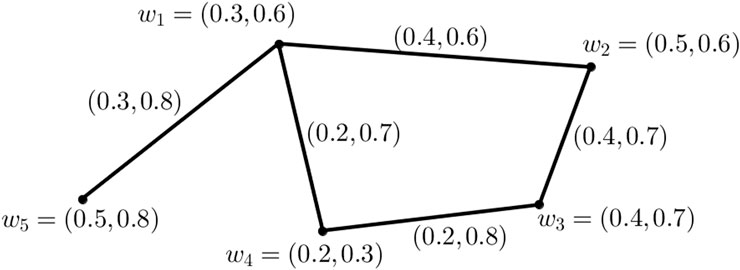
Example 2.6. Consider a graph G* = (X, E), where X = {w₁, w₂, w₃, w₄, w₅} and E = {w₁w₂, w₂w₃, w₃w₄, w₁w₅}. Suppose G = (W, Z) is a VFG of a graph G*, as shown in Figure 1.Graph G in Figure 1 is a VFG. Also, the degree of each vertex in the VFGG is d(w₁) = (0.9, 2.1), d(w₂) = (0.8, 1.3), d(w₃) = (0.6, 1.5), d(w₄) = (0.4, 1.5), and d(w₅) = (0.3, 0.8).

FIGURE 1

FIGURE 1. VFG.

Definition 2.7. A graph G = (X, E) is called a directed graph (digraph) if it has oriented edges and the arrows on the edges show the direction of each edge. Digraph G is displayed by ${\vec{G}}_d=(X,\vec{E})$.

2.1. Vague-valued hesitant fuzzy set

Definition 2.8. Suppose X is a set, a vague-valued hesitant fuzzy set (VVHFS) W on X is defined as:

$W=\left\{\left(a,W\left(a\right)\right)|a\in X\right\},$

where W(a) is a subset of values in [0, 1] × [0, 1]. We name W(a) a vague-valued hesitant fuzzy element (VVHFE) defined as

$W\left(a\right)=\left\{m_a|m_a\in \left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]\right\}.$

Here, $m_a=(m_a^t,m_a^f)$ is a vague-valued fuzzy number (VVFN) such that $m_a^t\in [\mathrm{0,1}]$ and $m_a^f\in [\mathrm{0,1}]$.

Definition 2.9. Suppose X is a non-empty universe, and for a ∈ X, suppose W(a), W₁(a), and W₂(a) are the VVHFEs, then,

$\ast W_1\left(a\right)\cup W_2\left(a\right)=\left\{\left(\max \left(m_{1a}^t,m_{2a}^t\right),\max \left(m_{1a}^f,m_{2a}^f\right)\right)|m_{1a}\in W_1\left(a\right),m_{2a}\in W_2\left(a\right)\right\},$

$\ast W_1\left(a\right)\cap W_2\left(a\right)=\left\{\left(\min \left(m_{1a}^t,m_{2a}^t\right),\min \left(m_{1a}^f,m_{2a}^f\right)\right)|m_{1a}\in W_1\left(a\right),m_{2a}\in W_2\left(a\right)\right\},$

$\ast W{(a)}^c=\{(1-m_a^t,1-m_a^f)|m_a\in W(a)\}$

Definition 2.10. Suppose $m_a=(m_a^t,m_a^f)\in W(a)$ is a VVFN, then the value of score S(m_a) is defined as

$S\left(m_a\right)=\frac{1}{2}\left(m_a^t-m_a^f\right).$

This means the degree of satisfaction corresponding to some characteristic features and the degree of satisfaction to some implicit contradictory features are related to a principle.

Definition 2.11. Suppose W(a) is a VVHFE, then the score function S(W(a)) is defined as

$S\left(W\left(a\right)\right)=\frac{1}{n\left(W\left(a\right)\right)}\sum _{m_a\in W\left(a\right)}S\left(m_a\right).$

Here, the number of vague -values in W(a) is denoted by n(W(a)), and m_a is the element in W(a), shown as the form of the VVFN.

Definition 2.12. Suppose W and Z are two VVHFSs on X. Then, score-based (SB) intersection and union of two VVHFEs W(a) and Z(a) are denoted by $W(a)\tilde{\wedge }Z(a)$ and $W(a)\tilde{\vee }Z(a)$ respectively, which is characterized by

$W\left(a\right)\tilde{\wedge }Z\left(a\right)=\left\{\begin{array}{c}\mathrm{W}(\mathrm{a})\mathrm{i}\mathrm{f}\mathrm{S}(\mathrm{W}(\mathrm{a}))<\mathrm{S}(\mathrm{Z}(\mathrm{a}))\hfill \\ \mathrm{Z}(\mathrm{a})\mathrm{i}\mathrm{f}\mathrm{S}(\mathrm{W}(\mathrm{a}))>\mathrm{S}(\mathrm{Z}(\mathrm{a}))\hfill \\ \mathrm{W}(\mathrm{a})\mathrm{o}\mathrm{r}\mathrm{Z}(\mathrm{a})\mathrm{i}\mathrm{f}\mathrm{S}(\mathrm{W}(\mathrm{a}))=\mathrm{S}(\mathrm{W}(\mathrm{a}))\hfill \end{array}\right.$

and

$W\left(a\right)\tilde{\vee }Z\left(a\right)=\left\{\begin{array}{c}\mathrm{W}(\mathrm{a})\mathrm{i}\mathrm{f}\mathrm{S}(\mathrm{W}(\mathrm{a}))>\mathrm{S}(\mathrm{Z}(\mathrm{a}))\hfill \\ \mathrm{Z}(\mathrm{a})\mathrm{i}\mathrm{f}\mathrm{S}(\mathrm{W}(\mathrm{a}))<\mathrm{S}(\mathrm{Z}(\mathrm{a}))\hfill \\ \mathrm{W}(\mathrm{a})\mathrm{o}\mathrm{r}\mathrm{Z}(\mathrm{a})\mathrm{i}\mathrm{f}\mathrm{S}(\mathrm{W}(\mathrm{a}))=\mathrm{S}(\mathrm{W}(\mathrm{a}))\hfill \end{array}\right.$

Definition 2.13. Suppose W and Z are two VVHFSs on set X, then $S(W(a)\tilde{\wedge }Z(a))=S(W(a))\wedge S(Z(a))$ and $S(W(a)\tilde{\vee }Z(a))=S(W(a))\vee S(Z(a))$.

2.2 Vague-valued hesitant fuzzy relation

Definition 2.14. Suppose W and Z are two VVHFSs on set X, then the SB CP of two VVHFSs W and Z is displayed by $W\tilde{\times }Z$ and specified by

$\begin{array}{ll}\hfill W\tilde{\times }Z& =\left\{<\left(a,b\right),\left(W\tilde{\times }Z\right)\left(a,b\right)>|\left(a,b\right)\in X\times X\right\},\hfill \\ \hfill & =\left\{<\left(a,b\right),W\left(a\right)\tilde{\times }Z\left(b\right)>|\left(a,b\right)\in X\times X\right\}.\hfill \end{array}$

Definition 2.15. Suppose X is a non-empty set and suppose W and Z are two VVHFSs on X, for a, b ∈ X, consider W(a, b): X × X → ([0, 1] × [0, 1]) is a VVHF relation on X, and then, we name W is SB VVHF relation on Z if,

$S\left(W\left(a,b\right)\right)\le S\left(Z\left(a\right)\right)\wedge S\left(Z\left(b\right)\right),$

for all a, b ∈ X.All the essential notations are shown in Table 1.

TABLE 1

TABLE 1. Some essential notations.

3 Vague-valued hesitant fuzzy graph

In this part, we introduce the definition of the VVHFG with some examples.

Definition 3.1. Suppose G* = (X, E) is a graph, a VVHFG on set X is an order pair G = (W, Z) where W and Z are VVHFSs in X and ${\tilde{X}}^2$, respectively. If W: X → [0, 1] × [0, 1] and $Z:{\tilde{X}}^2\to [\mathrm{0,1}]\times [\mathrm{0,1}]$ then, we have the following conditions

$S\left(Z\left(ab\right)\right)\le S\left(W\left(a\right)\right)\wedge S\left(W\left(b\right)\right),\forall ab\in {\tilde{X}}^2,$

$S\left(Z\left(ab\right)\right)=0,\forall ab\in \left({\tilde{X}}^2-E\right).$

Here, Z(ab) and W(a) are VVHFEs defined as

$Z\left(ab\right)=\left\{\left(n_{ab}^t,n_{ab}^f\right)|\left(n_{ab}^t,n_{ab}^f\right)\in \left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]\right\},$

and

$W\left(a\right)=\left\{\left(m_a^t,m_a^f\right)|\left(m_a^t,m_a^f\right)\in \left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]\right\}.$

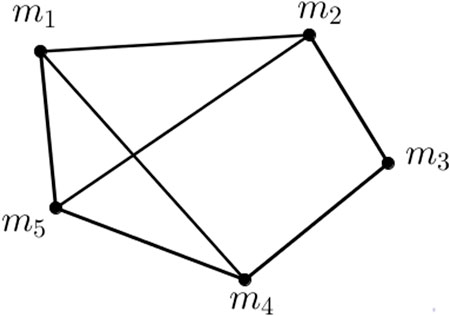
Example 3.2. Let there be five companies in the debate competition and Congress members choose one company as the best company according to three important properties, that is, profit-making, revenue, and influence power. Congress members evaluate the communication of three properties between five companies. Suppose X is a set of five companies {m₁, m₂, m₃, m₄, m₅} and E = {m₁m₂, m₂m₃, m₃m₄, m₄m₅, m₅m₁, m₂m₅, m₁m₄} is the communication of three properties among companies, we show the scores of vertices and edges in Table 2 and Table 3, respectively. A VVHFG is given in Figure 2.

TABLE 2

TABLE 2. VVHF table.

TABLE 3

TABLE 3. VVHF table.

FIGURE 2

FIGURE 2. VVHFG.

Definition 3.3. Suppose G = (W, Z) is a VVHFG on G* = (X, E), the SB degree of a vertex s₁ ∈ X in the VVHFG is denoted by $\mathfrak{D}\mathfrak{e}(s_1)$ and defined as $\mathfrak{D}\mathfrak{e}(s_1)={\sum }_{s\ne s_1\in X}S(Z(s_{1}s))$.For Example 3.2, we obtain the SB degree of every vertex in the VVHFG; therefore, we have $\mathfrak{D}\mathfrak{e}(m_1)=-0.7,\mathfrak{D}\mathfrak{e}(m_2)=-0.55,\mathfrak{D}\mathfrak{e}(m_3)=-0.358,\mathfrak{D}\mathfrak{e}(m_4)=-0.625,\mathfrak{D}\mathfrak{e}(m_5)=0.567$.

Definition 3.4. Suppose G₁ = (W₁, Z₁) and G₂ = (W₂, Z₂) are two VVHFGs on G* = (X, E), then we say that G₁ is the SB VVHF-subgraph of G₂, if it holds the conditions

$S\left(W_1\left(a\right)\right)\le S\left(W_2\left(a\right)\right),S\left(Z_1\left(ab\right)\right)\le S\left(Z_2\left(ab\right)\right),\forall a\in X,\forall ab\in {\tilde{X}}^2.$

3.1 Basic operations on VVHFGs

In this section, we express some basic operations like CP, SP, and union between VVHFGs, and also some properties in VVHFGs are established.

Definition 3.5. Suppose G₁ = (W₁, Z₁) and G₂ = (W₂, Z₂) are two VVHFGs on the graph G* = (X, E), we give some operations and related results for VVHFGs.CP: The CP of two VVHFGs denoted by $G_1\tilde{\times }{G}_2=(W_1\tilde{\times }{W}_2,Z_1\tilde{\times }{Z}_2)$ is defined as1) $(W_1\tilde{\times }{W}_2)(a_1,a_2)=W_1(a_1)\tilde{\wedge }{W}_2(a_2),\forall (a_1,a_2)\in X_1\times X_2$.2) $(Z_1\tilde{\times }{Z}_2)((a,a_2)(a,b_2))=W_1(a)\tilde{\wedge }{Z}_2(a_2{b}_2),\forall a\in X_1,a_2,b_2\in E_2$.3) $(Z_1\tilde{\times }{Z}_2)((a_1,e)(b_1,e))=Z_1(a_1{b}_1)\tilde{\wedge }{W}_2(e),\forall a_1{b}_1\in E_1,e\in X_2$.

Proposition 3.6. Suppose G₁ and G₂ are two VVHFGs, then $G_1\tilde{\times }{G}_2$ is a VVHFG.

Proof.. For every a ∈ X₁ and a₂, b₂ ∈ E₂, we have

$\begin{array}{ll}\hfill S\left(\left(Z_1\tilde{\times }{Z}_2\right)\left(\left(a,a_2\right)\left(a,b_2\right)\right)\right)& =S\left(W_1\left(a\right)\tilde{\wedge }{Z}_2\left(a_2{b}_2\right)\right)=S\left(W_1\left(a\right)\right)\wedge S\left(Z_2\left(a_2{b}_2\right)\right)\hfill \\ \hfill & \le S\left(W_1\left(a\right)\right)\wedge \left(S\left(W_2\left(a_2\right)\right)\wedge S\left(W_2\left(b_2\right)\right)\right)\hfill \\ \hfill & =\left(S\left(W_1\left(a\right)\right)\wedge S\left(W_2\left(a_2\right)\right)\right)\wedge \hfill \end{array}$

$\begin{array}{ll}\hfill \left(S\left(W_1\left(a\right)\right)\wedge S\left(W_2\left(b_2\right)\right)\right)& =S\left(W_1\left(a\right)\right)\tilde{\wedge }S\left(W_2\left(a_2\right)\right)\wedge S\left(W_1\left(a\right)\right)\tilde{\wedge }S\left(W_2\left(b_2\right)\right)\hfill \\ \hfill & =S\left(\left(W_1\tilde{\times }{W}_2\right)\left(a,a_2\right)\right)\wedge S\left(\left(W_1\tilde{\times }{W}_2\right)\left(a,b_2\right)\right).\hfill \end{array}$

For every e ∈ X₂ and a₁, b₁ ∈ E₁, we have

$\begin{array}{ll}\hfill S\left(\left(Z_1\tilde{\otimes }{Z}_2\right)\left(\left(a_1,e\right)\left(b_1,e\right)\right)\right)& =S\left(Z_1\left(a_1{b}_1\right)\tilde{\wedge }{W}_2\left(e\right)\right)=S\left(Z_1\left(a_1{b}_1\right)\right)\wedge S\left(W_2\left(e\right)\right)\hfill \\ \hfill & \le \left(S\left(W_1\left(a_1\right)\right)\wedge S\left(W_1\left(b_1\right)\right)\right)\wedge S\left(W_2\left(e\right)\right)\hfill \\ \hfill & =\left(S\left(W_1\left(a_1\right)\right)\wedge S\left(W_2\left(e\right)\right)\right)\wedge \hfill \end{array}$

$\begin{array}{ll}\hfill \left(S\left(W_1\left(b_1\right)\wedge S\left(W_2\left(e\right)\right)\right)\right.& =\left(S\left(W_1\left(a_1\right)\right)\tilde{\wedge }S\left(W_2\left(e\right)\right)\right)\wedge \left(S\left(W_1\left(b_1\right)\right)\tilde{\wedge }S\left(W_2\left(e\right)\right)\right)\hfill \\ \hfill & =S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(a_1,e\right)\right)\wedge S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(b_1,e\right)\right).\hfill \end{array}$

SP: The SP of two VVHFGs denoted by $G_1\tilde{\otimes }{G}_2=(W_1\tilde{\otimes }{W}_{2}and{Z}_1\tilde{\otimes }{Z}_2)$ is defined as1) $(W_1\tilde{\otimes }{W}_2)(a_1,a_2)=W_1(a_1)\tilde{\wedge }{W}_2(a_2),\forall (a_1,a_2)\in X_1\times X_2$.2) $(Z_1\tilde{\otimes }{Z}_2)((a,a_2)(a,b_2))=W_1(a)\tilde{\wedge }{Z}_2(a_2{b}_2),\forall a\in X_1,a_2,b_2\in E_2$.3) $(Z_1\tilde{\otimes }{Z}_2)((a_1,e)(b_1,e))=Z_1(a_1{b}_1)\tilde{\wedge }{W}_2(e),\forall a_1{b}_1\in E_1,e\in X_2$.4) $(Z_1\tilde{\otimes }{Z}_2)((a_1,a_2)(b_1,b_2))=Z_1(a_1{b}_1)\tilde{\wedge }{Z}_2(a_2{b}_2),\forall a_1{b}_1\in E_1,a_2{b}_2\in E_2$.

Proposition 3.7. Suppose G₁ and G₂ are two VVHFGs, then $G_1\tilde{\otimes }{G}_2$ is a VVHFG.

Proof.. For every a ∈ X₁ and a₂, b₂ ∈ E₂, we have

$\begin{array}{ll}\hfill S\left(\left(Z_1\tilde{\otimes }{Z}_2\right)\left(\left(a,a_2\right)\left(a,b_2\right)\right)\right)& =S\left(W_1\left(a\right)\tilde{\wedge }{Z}_2\left(a_2{b}_2\right)\right)=S\left(W_1\left(a\right)\right)\wedge S\left(Z_2\left(a_2{b}_2\right)\right)\hfill \\ \hfill & \le S\left(W_1\left(a\right)\right)\wedge \left(S\left(W_2\left(a_2\right)\right)\wedge S\left(W_2\left(b_2\right)\right)\right)\hfill \\ \hfill & =\left(S\left(W_1\left(a\right)\right)\wedge S\left(W_2\left(a_2\right)\right)\right)\wedge \hfill \end{array}$

$\begin{array}{ll}\hfill \left(S\left(W_1\left(a\right)\right)\wedge S\left(W_2\left(b_2\right)\right)\right)& =\left(S\left(W_1\left(a\right)\right)\tilde{\wedge }S\left(W_2\left(a_2\right)\right)\right)\wedge \left(S\left(W_1\left(a\right)\right)\tilde{\wedge }S\left(W_2\left(b_2\right)\right)\right)\hfill \\ \hfill & =S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(a,a_2\right)\right)\wedge S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(a,b_2\right)\right).\hfill \end{array}$

For every e ∈ X₂ and a₁, b₁ ∈ E₁, we have

$\begin{array}{ll}\hfill S\left(\left(Z_1\tilde{\otimes }{Z}_2\right)\left(\left(a_1,e\right)\left(b_1,e\right)\right)\right)& =S\left(Z_1\left(a_1{b}_1\right)\tilde{\wedge }{W}_2\left(e\right)\right)=S\left(Z_1\left(a_1{b}_1\right)\right)\wedge S\left(W_2\left(e\right)\right)\hfill \\ \hfill & \le \left.\left(S\left(W_1\left(a_1\right)\right)\wedge S\left(W_1\left(b_1\right)\right)\right)\wedge S\left(W_2\left(e\right)\right)\right)\hfill \\ \hfill & =\left(S\left(W_1\left(a_1\right)\right)\wedge S\left(W_2\left(e\right)\right)\right)\wedge \hfill \end{array}$

$\begin{array}{ll}\hfill \left(S\left(W_1\left(b_1\right)\right)\wedge S\left(W_2\left(e\right)\right)\right)& =S\left(W_1\left(a_1\right)\right)\tilde{\wedge }S\left(W_2\left(e\right)\right)\wedge S\left(W_1\left(b_1\right)\right)\tilde{\wedge }S\left(W_2\left(e\right)\right)\hfill \\ \hfill & =S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(a_1,e\right)\right)\wedge S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(b_1,e\right)\right).\hfill \end{array}$

For every a₁b₁ ∈ E₁ and a₂b₂ ∈ E₂, we have

$\begin{array}{ll}\hfill S\left(\left(Z_1\tilde{\times }{Z}_2\right)\left(\left(a_1,a_2\right)\left(b_1,b_2\right)\right)\right)& =S\left(Z_1\left(a_1{b}_1\right)\tilde{\wedge }{Z}_2\left(a_2{b}_2\right)\right)=S\left(Z_1\left(a_1{b}_1\right)\right)\wedge S\left(Z_2\left(a_2{b}_2\right)\right)\hfill \\ \hfill & \le \left(S\left(W_1\left(a_1\right)\right)\wedge S\left(W_1\left(b_1\right)\right)\wedge \left(S\left(W_2\left(a_2\right)\right)\wedge S\left(W_2\left(b_2\right)\right)\right.\right.\hfill \\ \hfill & =\left(S\left(W_1\left(a_1\right)\right)\wedge S\left(W_2\left(a_2\right)\right)\right)\wedge \left(S\left(W_2\left(b_1\right)\right)\wedge \left(S\left(W_2\left(b_2\right)\right)\right)\right.\hfill \\ \hfill & =\left(S\left(W_1\left(a_1\right)\right)\tilde{\wedge }S\left(W_2\left(a_2\right)\right)\wedge \left(S\left(W_1\left(b_1\right)\right)\tilde{\wedge }S\left(W_2\left(b_1\right)\right)\right)\right.\hfill \\ \hfill & =S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(a_1,a_2\right)\right)\wedge S\left(\left(W_1\tilde{\otimes }{W}_2\right)\left(b_1,b_2\right)\right).\hfill \end{array}$

Shown by G₁ ∪ G₂ = (W₁ ∪ W₂, Z₁ ∪ Z₂) s. t. S(W₁(a)) = 0 if a∉X₁ and S(W₂(a)) = 0 if a∉X₂ is defined as1) $(W_1\cup W_2)(a)=W_1(a)\tilde{\vee }{W}_2(a),\forall a\in X_1\cup X_2$.2) $(Z_1\cup Z_2)(ab)=Z_1(ab)\tilde{\vee }{Z}_2(ab),\forall ab\in E_1\cup E_2$.

Proposition 3.8. Suppose G₁ and G₂ are two VVHFGs, then G₁ ∪ G₂ is a VVHFG.

Proof. For every ab ∈ E₁ ∪ E₂, we have

$\begin{array}{ll}\hfill S\left(\left(Z_1\cup Z_2\right)\left(ab\right)\right)& =S\left(Z_1\left(ab\right)\tilde{\vee }{Z}_2\left(ab\right)\right)=S\left(Z_1\left(ab\right)\right)\vee S\left(Z_2\left(a_b\right)\right)\hfill \\ \hfill & \le \left(S\left(W_1\left(a\right)\right)\wedge S\left(W_1\left(b\right)\right)\right)\vee \left(S\left(W_2\left(a\right)\right)\wedge S\left(W_2\left(b\right)\right)\right)\hfill \\ \hfill & =\left(S\left(W_1\left(a\right)\right)\vee S\left(W_2\left(a\right)\right)\right)\wedge \left(S\left(W_1\left(b\right)\right)\vee S\left(W_2\left(b\right)\right)\right)\hfill \\ \hfill & =S\left(W_1\left(a\right)\right)\tilde{\vee }S\left(W_2\left(a\right)\right)\wedge S\left(W_1\left(b\right)\right)\tilde{\vee }S\left(W_2\left(b\right)\right)\hfill \\ \hfill & =S\left(\left(W_1\cup W_2\right)\left(a\right)\right)\wedge S\left(\left(W_1\cup W_2\right)\left(b\right)\right).\hfill \end{array}$

3.2 Isomorphism between vague-valued hesitant fuzzy graphs

In this part, we define the novel concepts of IM, HM, WI, and CWI on VVHFGs and discuss IM between VVHFGs.

Definition 3.9. Suppose G₁ and G₂ are two VVHFGs,a HM $\mathfrak{h}:G_1\to G_2$ is a mapping $\mathfrak{h}:X_1\to X_2$ satisfying the following conditions:1) $S(W_1(a_1))\le S(W_2(\mathfrak{h}(a_1))),\forall a_1\in X_1$.2) $S(Z_1(a_1{b}_1))\le S(Z_2(\mathfrak{h}(a_1)\mathfrak{h}(b_1))),\forall a_1{b}_1\in {\tilde{X}}_1^2$.An IM $\mathfrak{h}:G_1\to G_2$ is a bijective mapping (BM) $\mathfrak{h}:X_1\to X_2$ satisfying the following conditions:1) $S(W_1(a_1))=S(W_2(\mathfrak{h}(a_1))),\forall a_1\in X_1$.2) $S(Z_1(a_1{b}_1))=S(Z_2(\mathfrak{h}(a_1)\mathfrak{h}(b_1))),\forall a_1{b}_1\in {\tilde{X}}_1^2$.A WI $\mathfrak{h}:G_1\to G_2$ is a BM $\mathfrak{h}:X_1\to X_2$ satisfying the following conditions:1) $S(W_1(a_1))=S(W_2(\mathfrak{h}(a_1))),\forall a_1\in X_1$.2) $S(Z_1(a_1{b}_1))\le S(Z_2(\mathfrak{h}(a_1)\mathfrak{h}(b_1))),\forall a_1{b}_1\in {\tilde{X}}_1^2$.A CWI $\mathfrak{h}:G_1\to G_2$ is a BM $\mathfrak{h}:X_1\to X_2$ satisfying the following conditions:1) $S(W_1(a_1))\le S(W_2(\mathfrak{h}(a_1))),\forall a_1\in X_1$.2) $S(Z_1(a_1{b}_1))=S(Z_2(\mathfrak{h}(a_1)\mathfrak{h}(b_1))),\forall a_1{b}_1\in {\tilde{X}}_1^2$.

Remark 3.10. Suppose G = G₁ = G₂, so a HM of $\mathfrak{h}$ onto itself is called endomorphism. An IM $\mathfrak{h}$ on G* is named an automorphism (AM). Suppose $\mathfrak{h}:X_1\to X_2$ is a BM, then ${\mathfrak{h}}^{-1}:X_2\to X_1$ is a BM.

Remark 3.11. Suppose G = (W, Z) is a VVHFG of G* and suppose AM(G) is the set of all vague-valued hesitant AM of G $\mathfrak{g}:G\to G$ is considered a map and $\mathfrak{g}(a)=a,\forall a\in X$. It is clear $\mathfrak{g}\in Aut(G^{*})$.

Remark 3.12. Suppose G = G₁ = G₂, then the WI and CWI, indeed, become isomorphic.

Proposition 3.13. If G₁, G₂ and G₃ are VVHFGs, then the IM between these graphs is an equivalence relation.

Proof.. For reflexivity, we use identity mapping between VVHFGs, and it is obvious. We consider a function $\mathfrak{h}:X_1\to X_2$ is an IM on G₁ onto G₂ such that $\mathfrak{h}(v_1)=v_2,\forall v_1\in X_1$ with conditions

$S\left(W_1\left(v_1\right)\right)=S\left(W_2\left(\mathfrak{h}\left(v_1\right)\right)\right),$

$S\left(Z_1\left(v_1{u}_1\right)\right)=S\left(Z_2\left(\mathfrak{h}\left(v_1\right)\mathfrak{h}\left(u_1\right)\right)\right),\forall v_1\in X_1,\forall v_1{u}_1\in {\tilde{X}}_1^2.\left(1\right)$

Since $\mathfrak{h}$ is IM, we have ${\mathfrak{h}}^{-1}(v_2)=v_1,\forall v_2\in X_2$ satisfies condition (1), we have

$S\left(W_1\left({\mathfrak{h}}^{-1}\left(v_2\right)\right)\right)=S\left(W_2\left(v_2\right)\right),$

$S\left(Z_1\left({\mathfrak{h}}^{-1}\left(v_2\right){\mathfrak{h}}^{-1}\left(u_2\right)\right)\right)=S\left(Z_2\left(v_2{u}_2\right)\right),\forall v_2\in X_2,\forall v_2{u}_2\in {\tilde{X}}_2^2.$

So, a mapping ${\mathfrak{h}}^{-1}:X_2\to X_1$ is an IM from G₂ onto G₁. For transitivity, we consider ${\mathfrak{h}}_1:X_1\to X_2$ such that ${\mathfrak{h}}_1(v_1)=v_2,\forall v_1\in X_1$ and ${\mathfrak{h}}_2:X_2\to X_3$ such that ${\mathfrak{h}}_2(v_2)=v_3,\forall v_2\in X_2$ are IMs between G₁ onto G₂ and G₂ onto G₃, respectively. Thus, ${\mathfrak{h}}_{2}o{\mathfrak{h}}_1:X_1\to X_3$ is a composition of ${\mathfrak{h}}_1$ and ${\mathfrak{h}}_2$ such that $({\mathfrak{h}}_{2}o{\mathfrak{h}}_1)(v_1)={\mathfrak{h}}_2({\mathfrak{h}}_1(v_1)),\forall v_1\in X_1.$ Since the map ${\mathfrak{h}}_1:X_1\to X_2$ is an IM, we have

$S\left(W_1\left(v_1\right)\right)=S\left(W_2\left({\mathfrak{h}}_1\left(v_1\right)\right)\right)=S\left(W_2\left(v_2\right)\right),\forall v_1\in X_1,\left(2\right)$

$S\left(Z_1\left(v_1{u}_1\right)\right)=S\left(Z_2\left({\mathfrak{h}}_1\left(v_1\right){\mathfrak{h}}_1\left(u_1\right)\right)\right)=S\left(Z_2\left(v_2{u}_2\right)\right),\forall v_1{u}_1\in {\tilde{X}}_1^2.\left(3\right)$

Again, since the map ${\mathfrak{h}}_2:X_2\to X_3$ is an IM, we have

$S\left(W_2\left(v_2\right)\right)=S\left(W_3\left({\mathfrak{h}}_2\left(v_2\right)\right)\right)=S\left(W_3\left(v_3\right)\right),\forall v_2\in X_2,\left(4\right)$

$S\left(Z_2\left(v_2{u}_2\right)\right)=S\left(Z_3\left({\mathfrak{h}}_2\left(v_2\right){\mathfrak{h}}_2\left(u_2\right)\right)\right)=S\left(Z_3\left(v_3{u}_3\right)\right),\forall v_2{u}_2\in {\tilde{X}}_2^2.\left(5\right)$

From expressions (2) and (4), we have.$S(W_1(v_1))=S(W_2({\mathfrak{h}}_1(v_1)))=S(W_2(v_2))=S(W_3({\mathfrak{h}}_2(v_2)))=S(W_3({\mathfrak{h}}_2({\mathfrak{h}}_1(v_1))))=S(W_3({\mathfrak{h}}_{2}o{\mathfrak{h}}_1(v_1))),\forall v_1\in X_1$.From expressions (3) and (5), we have.$S(Z_1(v_1{u}_1))=S(Z_2({\mathfrak{h}}_1(v_1){\mathfrak{h}}_1(u_1)))=S(Z_2(v_2{u}_2))=S(Z_3({\mathfrak{h}}_2(v_2){\mathfrak{h}}_2(u_2)))=S\left(Z_3\right.({\mathfrak{h}}_2({\mathfrak{h}}_1((v_1)))({\mathfrak{h}}_2({\mathfrak{h}}_1((u_1))))=S(W_3({\mathfrak{h}}_{2}o{\mathfrak{h}}_1)(v_1)({\mathfrak{h}}_{2}o{\mathfrak{h}}_1)(u_1))),\forall v_1{u}_1\in {\tilde{X}}_1^2$.Hence, ${\mathfrak{h}}_{2}o{\mathfrak{h}}_1$ is an IM between G₁ and G₃. □

Proposition 3.14. If G₁, G₂ and G₃ are VVHFGs, then the WI between specified graphs is an equivalence relation.

Proof.. Reflexivityis trivial. For anti-symmetry, we consider a function $\mathfrak{h}:X_1\to X_2$ is a WI on G₁ onto G₂ such that ${\mathfrak{h}}_1(v_1)=v_2,\forall v_1\in X_1$ with conditions

$S\left(W_1\left(v_1\right)\right)=S\left(W_2\left({\mathfrak{h}}_1\left(v_1\right)\right)\right),$

$S\left(Z_1\left(v_1{u}_1\right)\right)\le S\left(Z_2\left({\mathfrak{h}}_1\left(v_1\right){\mathfrak{h}}_1\left(u_1\right)\right)\right)=S\left(Z_2\left(v_2{u}_2\right)\right),\forall v_1\in X_1,\forall v_1{u}_1\in {\tilde{X}}_1^2.\left(6\right)$

Let ${\mathfrak{h}}_2:X_2\to X_1$ is a WI between G₁ and G₂ such that ${\mathfrak{h}}_2(v_2)=v_1,\forall v_2\in X_2$ with condition

$S\left(W_2\left(v_2\right)\right)=S\left(W_1\left({\mathfrak{h}}_2\left(v_2\right)\right)\right),$

$S\left(Z_2\left(v_2{u}_2\right)\right)\le S\left(Z_2\left({\mathfrak{h}}_2\left(v_2\right){\mathfrak{h}}_2\left(u_2\right)\right)\right),\forall v_2\in X_2,\forall v_2{u}_2\in {\tilde{X}}_1^2.\left(7\right)$

We conclude from phrases (6) and (7) that these inequalities satisfy if and only if the VVHFGs are the same. Here, we indicate that G₁ and G₂ are similar because the number of edges and the corresponding edges have the same weights. Furthermore, the transitivity among graphs G₁, G₂ and G₃ is the same as in the previous statement. □

Proposition 3.15. Suppose G = (W, Z) is a VVHFG, AM(G) is the set of all AM on G. Then, (AM(G), o) forms a group.

Proof.. For every θ, η ∈ AM(G) and a, b ∈ X, we have

$\begin{array}{ll}\hfill S\left(Z\left(\left(\theta o\eta \right)\left(a\right)\left(\theta o\eta \right)\left(b\right)\right)\right)& =S\left(Z\left(\theta \left(\eta \left(a\right)\right)\left(\theta \left(\eta \left(b\right)\right)\right)\right.\right.\hfill \\ \hfill & =S\left(Z\left(\eta \left(a\right)\eta \left(b\right)\right)\right)\hfill \\ \hfill & =S\left(Z\left(ab\right)\right),\hfill \end{array}$

$\begin{array}{ll}\hfill S\left(W\left(\left(\theta o\eta \right)\left(a\right)\right)\right)& =S\left(W\left(\theta \left(\eta \left(a\right)\right)\right)\right)\hfill \\ \hfill & =S\left(W\left(\eta \left(a\right)\right)\right)\hfill \\ \hfill & =S\left(W\left(a\right)\right),\hfill \end{array}$

it is clear, θoη ∈ AM(G). Also, AM(G) is associative under the mapping composition. Suppose $\mathfrak{I}:G\to G$ is an identity mapping such that $\theta o\mathfrak{I}=\mathfrak{I}o\theta =\theta ,\forall \theta \in AM(G)$, for every θ ∈ Aut(G), we have θ⁻¹ ∈ G such that $S\left(W\left({\theta }^{-1}(x)\right)\right)=S\left(W\left(\theta \left({\theta }^{-1}(x)\right)\right)\right)=A(W((x)))$, $S(Z({\theta }^{-1}(x){\theta }^{-1}(y)))=S\left(Z\right.(\theta ({\theta }^{-1}(x))(\theta ({\theta }^{-1}(y))))=S(Z(XY))$. This proof is complete. □

4 Directed-VVHFGs and their application in decision-making

Definition 4.1. A directed-VVHFG ${\vec{G}}_d=(W,\vec{Z})$ of the graph G* = (X, E) with W: X → ([0, 1] × [0, 1]) and $W:{\tilde{X}}^2\to ([\mathrm{0,1}]\times [\mathrm{0,1}])$ satisfies the below conditions

$S\left(\vec{Z}\left(ab\right)\right)\le S\left(W\left(a\right)\right)\wedge S\left(W\left(b\right)\right),\forall ab\in {\tilde{X}}^2,$

$S\left(\vec{Z}\left(ab\right)\right)=0,\forall ab\in \left({\tilde{X}}^2-E\right).$

Definition 4.2. Suppose X is a set and {W_l(a)|a ∈ X, l = 1, 2, ….., p} is a collection of VVHFEs and $\omega ={({\omega }_1,{\omega }_2,\dots ..,{\omega }_p)}^T$ is the weight vector of $W_l(a)=(m_{la}^t,m_{la}^f)(l=\mathrm{1,2},\dots ..,p)$ with ω_l ∈ [0, 1] and ${\sum }_{l=1}^p{\omega }_l=1$, then the vague-valued hesitant fuzzy weighted averaging (VVHFWA) operator is a mapping VVHFWA:W^p → W, whereVVHFWA$(W_1(a),W_2(a),\dots \dots ,W_p(a))={\otimes }_{l=1}^p({\omega }_l\widetilde{W_l}(a))=$

$\begin{array}{ll}\hfill & \left\{\left(1-\prod _{l=1}^p{(1-m_{la}^t)}^{{\omega }_l},1-\prod _{l=1}^p{(1-m_{la}^f)}^{{\omega }_l}\right)|m_{1a}\in W_1(a),\right.\hfill \\ \hfill & \left.m_{2a}\in W_2(a),\dots \dots ,m_{pa}\in W_p(a)\right\},(8)\hfill \end{array}$

the VVHFWA operator is the vague -valued hesitant fuzzy averaging (VVHFA) operator, if we have $\omega ={(\frac{1}{p},\frac{1}{p},\dots \dots ,\frac{1}{p})}^T$. We can write Equation 8 as follows.VVHFA$(W_1(a),W_2(a),\dots \dots ,W_p(a))={\otimes }_{l=1}^p\left(\frac{1}{p}{W}_l(a)\right)=$

$\begin{array}{ll}\hfill & \left\{\left(1-\prod _{l=1}^p{(1-m_{la}^t)}^{\frac{1}{p}},1-\prod _{l=1}^p{(1-m_{la}^f)}^{\frac{1}{p}}\right)|m_{1a}\in W_1(a),\right.\hfill \\ \hfill & \left.m_{2a}\in W_2(a),\dots \dots ,m_{na}\in W_p(a)\right\}.(9)\hfill \end{array}$

Definition 4.3. Suppose ${\vec{G}}_d=(W,\vec{Z})$ is a directed-VVHFG on G* = (X, E) and σ_r, r = 1, 2, …., p is adjacent VVHF-vertices of σ_k ∈ X, by using expression (9), we define out-degree (OD) and in-degree (ID) of a vertex σ_k represented by O_d(σ_k) and I_d(σ_k), respectively:

$O_d\left({\sigma }_k\right)=\left\{\left(1-\prod _{l=1}^p\left(1-n_{{\sigma }_k{\sigma }_l}^t\right),1-\prod _{l=1}^p\left(1-n_{{\sigma }_k{\sigma }_l}^f\right)\right)|{\sigma }_k{\sigma }_l\in Z\right\},\left(10\right)$

$I_d\left({\sigma }_k\right)=\left\{\left(1-\prod _{l=1}^p\left(1-n_{{\sigma }_l{\sigma }_k}^t\right),1-\prod _{l=1}^p\left(1-n_{{\sigma }_l{\sigma }_k}^f\right)\right)|{\sigma }_l{\sigma }_k\in Z\right\}.\left(11\right)$

After finding the ID and OD of each vertex, we denote its score value by S(O_d(σ)) and S(I_d(σ)), respectively, and determine it from definition 9. To find the D-degree of every vertex σ_k, we use O_d(σ_k) − I_d(σ_k), where O_d(σ_k) and I_d(σ_k) denote the score value of OD and ID of vertex σ_k, respectively, and shown by Ω(σ_k).

4.1. Application of a directed-vague-valued hesitant fuzzy graph

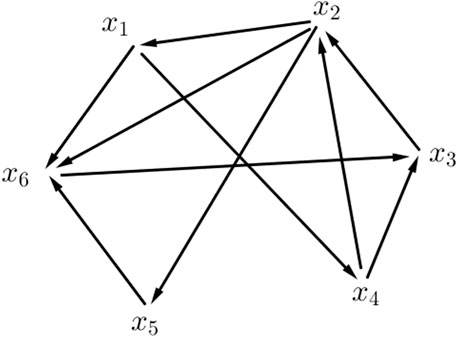
We cannot measure the value of influence of a person’s property, so we are always hesitant to evaluate the value of the influence of a person. On the other hand, if we do not have enough information about a person’s property, it will have a negative effect on him. In this section, we present a directed-VVHFG for such a subject. We consider the directed-VVHFG of the mental power of six people W = {x₁, x₂, x₃, x₄, x₅, x₆} in a scientific meeting (see Figure 3). Here, membership degrees are really valued and determine the mental power of people. Suppose W is the VVHFS on the set X as in Table 4, it indicates the mental power of people who are present in a scientific meeting. Suppose Z = {x₁x₄, x₁x₆, x₂x₁, x₂x₅, x₂x₆, x₃x₂, x₄x₂, x₄x₃, x₅x₆, x₆x₃} is the set of vague-valued directed hesitant edges as in Table 5, it determines the value of the influence of one person onto another person in a scientific meeting.

FIGURE 3

FIGURE 3. Directed-VVHFG.

TABLE 4

TABLE 4. VVHF membership of persons mental power.

TABLE 5

TABLE 5. Value of the influence of one person on another person.

Here, we determine the OD and ID of every person as In Table 6.

TABLE 6

TABLE 6. Out-degree and in-degree of every person.

Afterward, we obtained the score value of OD and ID of every person in the scientific meeting as in Table 7.

TABLE 7

TABLE 7. Score value of out-degree and in-degree.

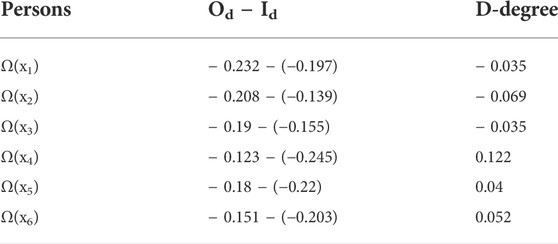
Finally, we determined the D-degree of every person in the scientific meeting as in Table 8.

TABLE 8

TABLE 8. Domination degree of every person.

It is clear that the most dominating person in a scientific meeting is x₄.

In HFG, all information is expressed with only one membership degree, which represents the satisfaction degree of an element corresponding to the set, and it ignores the degree of satisfaction of the element for some implicit counter property of the set. However, since the VVHFG simultaneously considers the membership and non-membership satisfaction degrees, we will use the following tables for comparative study between the VVHFG and HFG. In the HFG, the hesitant fuzzy table is composed only of the people’s satisfaction degrees corresponding to the set (in Tables 9, 10).

TABLE 9

TABLE 9. HF membership of persons mental power.

TABLE 10

TABLE 10. Value of influence of one person on another person.

Here, we determine the OD and ID of every person as in Table 11.

TABLE 11

TABLE 11. Out-degree and in-degree of every person.

Afterward, we obtained the score value of OD and ID of every person in the scientific meeting as in Table 12.

TABLE 12

TABLE 12. Score value of out-degree and in-degree.

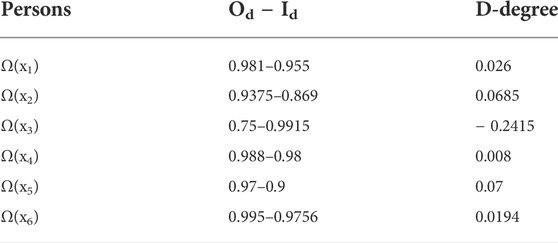
Finally, we determined the D-degree of every person in the scientific meeting as in Table 13.

TABLE 13

TABLE 13. Domination degree of every person.

It is clear that the most dominating person in a scientific meeting is x₅.

Through the HFG, the domination degree of each person in this scientific meeting is ranked as follows: clearly person x₅ is the most dominating person in the scientific meeting. When the results of the HFG and VVHFG are examined, we realize that the domination degree and ranking of dominating people change significantly in two cases. In the VVHFG, x₄ is the most dominating person in the scientific meeting, while in the HFG, person x₅ is the most dominating person in the scientific meeting. Furthermore, when we examine the mental power of people in two cases a significant difference between the two results is observed. The main reason for this difference is the capability of the VVHFG, and it is simultaneously considering the membership and non-membership degrees with no restriction, while the HFG considers only one membership value.

5 Conclusion

HFGs are useful tools to determine the membership degree of an element from some possible values. This is quite common in decision-making problems. A VVHFG can accurately characterize the ambiguity of all types of networks. So, in this work, the VVHFG structure and some concepts related to VVHFGs such as HM, IM, WI, and CWI are introduced, and operations of CP, SP, and union between two VVHFGs are defined. Likewise, we defined a new notion of the VVHFG called directed-VVHFG. This concept is a useful tool to present the different decision-making processes to find the D-degree of a person in a scientific meeting through directed-VVHFG. Finally, an application of the directed-VVHFG has been presented. In our future work, we will introduce new concepts of connectivity in VVHFGs and investigate some of their properties. Also, we will study new results of global dominating sets, perfect dominating sets, connected perfect dominating sets, regular perfect dominating sets, and independent perfect dominating sets on VVHFGs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All the authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (No. 62172116, 61972109) and the Guangzhou Academician and Expert Workstation (No. 20200115-9).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zadeh LA. Fuzzy sets. Inf Control (1965) 8:338–53. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar

2. Rosenfeld A. Fuzzy graphs. In: LA Zadeh, KS Fu, and M Shimura, editors. Fuzzy sets and their applications. New York, NY, USA: Academic Press (1975). p. 77–95.

CrossRef Full Text | Google Scholar

3. Rashmanlou H, Muhiuddin G, Amanathulla SK, Mofidnakhaei F, Pal M. A study on cubic graphs with novel application. J Intell Fuzzy Syst (2021) 40(1):89–101. doi:10.3233/jifs-182929

CrossRef Full Text | Google Scholar

4. Pramanik T, Muhiuddin G, Alanazi AM, Pal M. An extension of fuzzy competition graph and its uses in manufacturing industries. Mathematics (2020) 8:1008. doi:10.3390/math8061008

CrossRef Full Text | Google Scholar

5. Rashmanlou H, Pal M. Antipodal interval-valued fuzzy graphs. Int J Appl Fuzzy Sets Artif Intelligence (2013) 3:107–30.

Google Scholar

6. Sanchari B, Pal M. Certain types of m-polar interval-valued fuzzy graph. J Intell Fuzzy Syst (2020) 39(3):3137–50. doi:10.3233/jifs-191587

CrossRef Full Text | Google Scholar

7. Gau WML, Buehrer DJ. Vague sets. IEEE Trans Syst Man Cybern (1993) 23(2):610–4. doi:10.1109/21.229476

CrossRef Full Text | Google Scholar

8. Ramakrishna N. Vague graphs. Int J Comput Cogn (2009) 7:51–8.

Google Scholar

9. Akram M, Gani N, Saeid AB. Vague hypergraphs. J Intell Fuzzy Syst (2014) 26:647–53. doi:10.3233/ifs-120756

CrossRef Full Text | Google Scholar

10. Akram M, Samanta S, Pal M. Cayley vague graphs. J Fuzzy Maths (2017) 25(2):1–14.

Google Scholar

11. Akram M, Feng F, Sarwar S, Jun YB. Certain types of vague graphs. UPB Scientific Bull Ser A: Appl Mathematica Phys (2014) 76(1):141–54.

Google Scholar

12. Akram M, Dudek WA, Murtaza Yousaf M. Regularity in vague intersection graphs and vague line graphs, Abstract and Applied Analysis (2014). Article ID 525389, 10 pages.

Google Scholar

13. Borzooei R, Rashmanlou H. Domination in vague graphs and its applications. J Intell Fuzzy Syst (2015) 29(5):1933–40. doi:10.3233/ifs-151671

CrossRef Full Text | Google Scholar

14. Rao Y, Kosari S, Shao Z. Certain properties of vague graphs with a novel application. Mathematics (2020) 8(10):1647. doi:10.3390/math8101647

CrossRef Full Text | Google Scholar

15. Rao Y, Kosari S, Shao Z, Qiang X, Akhoundi M, Zhang X. Equitable domination in vague graphs with application in medical sciences. Front Phys 9. Article ID 635-642, 2021. doi:10.3389/fphy.2021.635642

CrossRef Full Text | Google Scholar

16. Rao Y, Kosari S, Shao Z, Cai R, Xinyue L. A Study on Domination in vague incidence graph and its application in medical sciences. Symmetry (2020) 12(11):1885. doi:10.3390/sym12111885

CrossRef Full Text | Google Scholar

17. Borzooei RA, Rashmanlou H, Jun YB, Mathew S. Isomorphic properties of neighborly irregular vague graphs. J Intell Fuzzy Syst (2016) 30:3261–70. doi:10.3233/ifs-152074

CrossRef Full Text | Google Scholar

18. Borzooei RA, Darabian E, Rashmanlou H, Azadi M. New concepts of regular and (highly) irregular vague graphs with applications. Fuzzy Inf Eng (2017) 9:161–79. doi:10.1016/j.fiae.2017.06.003

CrossRef Full Text | Google Scholar

19. Kishore Kumar PK, Lavanya S, Broumi S, Rashmanlou H. New concepts of coloring in vague graphs with application. J Intell Fuzzy Syst (2017) 33:1715–21. doi:10.3233/jifs-17489

CrossRef Full Text | Google Scholar

20. Kosari S, Rao Y, Jiang H, Liu X, Wu P, Shao Z. Vague graph Structure with Application in medical diagnosis. Symmetry (2020) 12(10):1582. doi:10.3390/sym12101582

CrossRef Full Text | Google Scholar

21. Kou Z, Kosari S, Akhoundi M. A novel description on vague graph with application in transportation systems. J Maths 2021:11. Article ID 4800499. doi:10.1155/2021/4800499

CrossRef Full Text | Google Scholar

22. Torra V. Hesitant fuzzy sets. Int J Intell Syst (2010) 25:529–39. doi:10.1002/int.20418

CrossRef Full Text | Google Scholar

23. Torra V, Narukawa Y. On hesitant fuzzy sets and decision. In: Proceedings of the 18th IEEE international conference on fuzzy systems. Korea: Jeju Island (2009). p. 1378–82.

CrossRef Full Text | Google Scholar

24. Pathinathan T, Jon Arockiaraj J, Jesintha Rosline J. Hesitancy fuzzy graphs. Indian J Sci Technol 8(35). doi:10.17485/ijst/2015/v8i35/86672

CrossRef Full Text | Google Scholar

25. Xu Z. Hesitant fuzzy sets and theory, studies in fuzziness and sof computing. Springer-Verlag Publications (2014).

Google Scholar

26. Zhu B, Xu Z, Xia M. Dual hesitant fuzzy sets. Journal of Applied Mathematics. Hindawi Publishing Corporation (2012). Article ID. 879629.

Google Scholar

27. Javaid M, Kashif A, Rashid T. Hesitant fuzzy graphs and their products. Fuzzy Inf Eng (2020) 12(2):238–52. doi:10.1080/16168658.2020.1817658

CrossRef Full Text | Google Scholar

28. Karaaslan F. Hesitant fuzzy graphs and their applications in decision making. J Intell Fuzzy Syst (2019) 36(3):2729–41. doi:10.3233/jifs-18865

CrossRef Full Text | Google Scholar

29. Sriram Kalyan SK. K-regular domination in hesitancy fuzzy graph. Int J Mod Agric (2021) 10(1):195–200.

Google Scholar

30. Shakthivel R, Vikramaprasad R, Vinoth Kumar N. Inverse domination in hesitancy fuzzy graphs. Solid State Technol (2020) 63(2):795–803.

Google Scholar

31. Shakthivel R, Vikramaprasad R, Vinothkumar N. Domination in hesitancy fuzzy graph. Int J Adv Sci Technol (2019) 28(16):1142–56.

Google Scholar

32. Bai W, Ding J, Zhang C. Dual hesitant fuzzy graphs with applications to multi-attribute decision making. Int J Cogn Comput Eng (2020) 1:18–26. doi:10.1016/j.ijcce.2020.09.002

CrossRef Full Text | Google Scholar

33. Ghorai G, Pal M. Some isomorphic properties of m-polar fuzzy graphs with applications. SpringerPlus (2016) 5(1):2104–25. doi:10.1186/s40064-016-3783-z

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Pandey SD, Ranadive AS, Samanta S. Bipolar-valued hesitant fuzzy graph and its application, social network analysis and mining. Granular Comput (2022) 4(3):559–83.

Google Scholar

35. Shi X, Kosari S, Mehdipoor N, Talebi AA, Muhiuddin G. Novel concepts in vague graphs with application in hospital’s management system. J Maths (2022) 1. Article ID 9129386. doi:10.1155/2022/9129386

CrossRef Full Text | Google Scholar