
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 06 October 2022
Sec. Interdisciplinary Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1005447
The present study aims to investigate the Casson nanofluids flow theoretically over a vertical Riga plate. The temperature and concentration with ramped and isothermal wall conditions are considered. Moreover, the fluid is considered electrically conducted. Concrete is considered as a base fluid while clay nanoparticles are added to it. The present flow regime is formulated in terms of a system of partial differential equations. Using dimensionless variables, the system of equations with the imposed boundary conditions is non-dimensionalized. The Laplace transform technique is used to calculate the exact solutions for the temperature, concentration, and velocity distributions. The effect of various embedded parameters on the velocity, temperature, and concentration fields are shown graphically and discussed physically. The variation in the skin friction for various values of clay nanoparticles volume fraction is shown in tabular form. The results indicate that adding 4% clay nanoparticles, enhanced the skin friction up to 7.04% in instance of ramped wall temperature (RWT) and 11.13% in isothermal wall temperature (IWT). This result is worth noting because the increase in skin friction causes rapid compaction of the cementitious materials and improves the tensile strength of the concrete.
Non-Newtonian liquids are a hard topic among scientists and researchers, due to their wide range of applications in industry, everyday life, and engineering. They are categorized into several different classes because of their complexity and variety in nature and rheology. There are many models that may represent the flow behavior of viscoelastic liquids. Non-Newtonian fluids are processed under laminar flow conditions due to their higher consistency. Yield-pseudo plastic materials are an example of viscoelastic fluid. Such fluids show a nonlinear flow curve that has been preceded by particular yield stress. The viscosity of a pseudo-plastic fluid decreases as the rate of shear increases. With low apparent viscosity, this type of material displays an infinite rate of shear, whereas, with infinite apparent viscosity, the shear rate is much less (approaches zero). The Casson fluid model is a shear-thinning non-Newtonian fluid that is related to viscoplastic behavior. This is used to explain the shear stress and shear rate properties of fluid flow in yogurt, tomato puree, food, and biological materials in various industrial processes [1]. The most well-known examples of this type of flow behavior include paints, printing inks, and dispensing systems. However, poor flow speed is observed when the rate of shear is reduced, pseudo-plasticity is unenviable because of this fact [2]. Among the various models that describe the flow behavior of viscoelastic liquids, the Casson fluid is considered to be more reliable. Furthermore, the essence of viscoelastic fluids is increased because these materials are the only ones that depict the behavior of blood flow in the human body [3]. Casson developed the constitutive law that describes the Casson fluid model when characterizing the flow curves for pigment suspension in Silicon suspension and printing ink. Because of the wide variety of applications, the Casson fluid flow has received a lot of attention in the research community [4]. Ullah et al. [3] delineated a nonlinearly extending sheet immersed in a porous medium with unsteady MHD mixed convection slip flow of Casson fluid. They also considered heat generation/absorption, thermal radiation, chemical reaction, and convective boundary conditions. Variable fluid parameters have an effect on the oblique stagnation point flow of a Casson nanofluid subjected to convective boundary conditions discussed by Prasad et al. [5]. [6] Investigated the exact solution of Casson fluid flow past through a stretching sheet. They have found that the velocity of the fluid decreases with increasing values of the Casson fluid parameter.
Nanofluids are the suspension of very small nanometer-sized solid particles into the base fluid. In contrast to the above, nanofluids offer a solution to the problem by mixing base fluids with non-agglomerated particles [7, 8]. Metals, metal oxides, ceramics, semiconductors, and clay are just a few of the materials that may be used to make nanofluids. In the area of construction and civil engineering, nanotechnology is one of the most modern fields of research. Concrete consists of a mixture of various aggregate materials like stone, sand, cement, and water. Nano concrete is made from nanomaterials or contains nanomaterials with a particle size of fewer than 500 nm. Nanoparticles are more accurately defined as recently developed concrete admixtures. Nanotechnology is a relatively new research area that covers a broad range in the field of civil engineering and construction studies. For example, they improve the hydration process of cement, thereby producing calcium-silica-hydrate, which increases the strength of cement-based products. By filling cement paste pores, nanoparticles with smaller particle sizes assist to enhance concrete’s microstructure and, as a result, increase its packing density. Many researchers have reported experimentally and theoretically different nanofluid models for different purposes. For example, some experimental findings on the integration of nanoparticles in cement-based concrete were published recently. Controlling the processes of hydration, strength production, and fracturing requires a detailed analysis of concrete-based material nanostructures. For many construction applications, for example, the development of new materials with properties like discoloration resistance is essential [9]. It is now possible to see the arrangement of materials at the microscopic level and even estimate their hardness, strength, and other fundamental characteristics by employing new and advanced technologies. In the construction execution process, construction joints are utilized to make construction work more accessible. Constructing joints would have a significant impact on concrete compressive strength. Construction joints are found in all concrete buildings [10]. Clay is a fine-grained natural soil material composed mostly of clay minerals. Clay is the most inorganic common raw material used in the products of ceramics, and they are produced commonly using traditional techniques. Most clay minerals are white or light in color, although natural clays may be brownish due to impurities like iron oxide. Clay nanoparticles’ research is focused on studying cement-based materials composition and fracture mechanisms [11, 12]. Clay nanoparticles’ major function is to increase the tensile strength of the concrete, decrease oxygen permeability, and improve heat resistance in the concrete. Clay nanoparticles are the ones that help to make cementitious materials stronger. The mechanical behavior of nano-enabled cement is strengthened by clay nanoparticles [13]. By improving the intersectional zone in cement and providing higher density concrete, nanoparticles will create an excellent filler effect. Clay nanoparticles improve the bulk strength of the concrete, commonly known as the structural packing model. The addition of clay nanoparticles to increase the strength of conventional concrete is discussed experimentally by Norhasri et al. [14]. Recent work on the Casson nanofluids by considering different aspects are seen in [15, 16].
Heat is a type of energy that may have been transferred from one region to another. Many manufacturing and industrial operations use heat transfer, such as heating phenomena, cooling chambers, drying processes, and engines [17–19]. Radiation, conduction, and convection are the three modes for transferring heat. Variations in ambient conditions, such as temperature, can cause a change in buoyancy forces and, as a result, a change in flow regime, which leads to a change in the governing correlation. The practical use of such correlations would be significantly enhanced if they could be used in a wide range of different ambient conditions. Similarly, mass transfer refers to the net movement of species from one place to another. The relative motion of species in a mixture due to concentration gradients is referred to as mass transfer. High-pressure pumps, filtering of crude oil, fractional distillation, and petrochemical refinement are only a few of the modern sciences and technologies that are using it. Mass transfer processes include evaporation, absorption, distillation, precipitation, filtration, and crystallization, to mention a few [20]. To better explain the process of moisture transport in clays during the drying process is experimentally investigated by Gong et al. [21]. Mainly due to the extraction of crude oil and other applications from the pores of the storage rocks, fluid flow through a porous media has been of significant interest in recent literature. Ali et al. [22] examined the impact of a vertical plate implanted in a porous media with changing surface temperature, concentration, and velocity on the flow of a water-based Brinkman-type nanofluid. Recently, Kataria and Patel [23] studied the influence of radiation and chemical reactions on Casson fluid flow passing through a porous media oscillating vertical plate. In polymer and chemical production equipment, the mass transfer effect is significant and has a wide range of applications [24]. Khan et al. [25] investigated the influence of mass in intermittent microwave convective drying modeling. Blood purification in the kidneys and liver, pond water evaporation, and alcohol distillation are a few examples of mass transfer phenomena. In non-Newtonian fluids, it plays a vital role in industries, pharmaceuticals, and biological processes [26–29].
Although, the uniform wall conditions are mostly used in the literature [30]. But many physical situations can not be described using these conditions. Such situations as nuclear heat transfer control, the process of various materials, heat transfer in turbines, some electric circuits, and heat transfer in buildings [31], need variable conditions. These variable conditions at the wall are termed ramped wall temperature. Due to the applications of the ramped wall conditions, Chandran et al. investigated the natural convection flow of fluid with ramped wall temperature [20]. The free convection laminar flow with ramped wall conditions is investigated by [32, 33], Seth et al. [34] examined radiative heat transfer in MHD flow by considering the impact of a porous material and a plate with a ramped wall temperature. When a system comes into contact with an external thermal reservoir, the isothermal process begins, and the change in the system occurs slowly enough for the system to continue to adapt to the reservoir’s temperature through heat exchange. Boiling water is an isothermal process because the temperature of the water remains constant at 100°C even though the addition of heat to the system as the water reaches its boiling point. The method is known as the isothermal wall temperature process [31].
Gallites and Lilausis [35] designed an electromagnetic actuator to provide crossing magnetic and electric fields that would suitably provoke the parallel Lorentz forces on the wall. When magnets and electrodes are alternatively connected with each other. These combinations of magnets and electrodes are known as Riga plates. In this electric and magnetic field, a transverse Lorentz force is produced, which contributes to the flow of the plate [36]. Riga plate in combination with Casson nanofluids flows has industrial and civil engineering applications. It also reduces the turbulence, making it possible to achieve effective control of flow as examined by Nasrin et al. [37]. Using Riga plate, submarines can achieve lower pressure drag by reducing surface friction and skin friction instead of boundary layer separation. The flow of nanofluid over the Riga plate with the effect of heat absorption and melting was reported by [38]. Pantokratoras and Magyari investigated many features of laminar fluid flow induced by the Riga plate [39]. Adeel et al. [40] investigated the mixing of boundary layers nanofluid flow generated by the Riga plate. By preventing boundary layer separation, the Riga plate may be useful for reducing drag [41]. One can find the applications of the Riga plate in the studies [42–54] and the references therein.
There is no study that has been reported in the published literature to find the closed form solutions for the EMHD Casson nanofluid flow in a porous medium over a vertical Riga plate with ramped wall temperature conditions. The objective of this study is to fill this research gaps by finding the exact solutions for the flow of a Casson nanofluid past through a vertical Riga plate embedded porous medium. The effects of thermal radiation and chemical reaction of the first order are also considered in this problem. Furthermore, the suspended nanoparticles (clay) in the base fluid (concrete) are taken. This study provides how the binding and tensile strength of the cementitious materials increase by adding clay nanoparticles in concrete. This work also provides to compare the ramped wall and isothermal boundary conditions graphically for velocity, temperature and concentration profiles. The Laplace transform method has been used to get the exact solutions to this problem. The tabular representation shows the impacts of different embedded parameters on Nusselt number, Sherwood number, and skin friction.
In the present research, the flow of unsteady, incompressible Casson nanofluids and buoyancy-driven through a semi-infinite vertical Riga-plate with ramped and constant wall conditions is investigated. The plate is taken along the x-axis. Assume that the Riga plate is initially at rest. The fluid occupies the space
The velocity, temperature and concentration fields for the above flow regime are:
The basic constitutive equations for the Casson fluid are given as:
whereas
Here
Where
The body forces
Keeping in mind Eq. 1 and using of Eqs 3–8 can be written in component form as:
Physical initial and boundary conditions of the problem are:
Here
The volume fraction of nanoparticles is denoted by
The following is a representation of the radiative flux
Where Sefan-Boltzmann constant and, the mean absorption coefficient are represented by
Using Equation 13 into Equation 12 and differentiated with respect to y to obtainearticle size of fewer than 500 talease confirm that it is correct.
Introduce the following dimensionless variables
Using Equation 17 into Equations 3–5, the following system of diemensionless equations are obtained:
The dimensionless initial and boundary conditions of the problem are:
During the dimensionalization, the following dimensionless parameters are obtained:
Applying the Laplace transform method to Eq. 19 and Eq. 21, then incorporating the transformed initial and boundary conditions to obtain:
The inverse Laplace transform of Eq. 22 for ramped wall temperature yields:
In the case of isothermal wall temperature, the solution becomes:
Using the Laplace Transform to Eq. 20 and Eq. 21, then incorporating the transformed initial and boundary conditions to obtain:
The inverse Laplace transform of Eq. 26 for ramped wall temperature yields:
In the case of isothermal wall temperature, the solution becomes:
Applying the Laplace transform to Eq. 18 and Eq. 21, then incorporating the transformed initial and boundary conditions to obtain:
The inverse Laplace transform of Eq. 30 cannot be calculated in terms of explicit functions. Zakian’s numerical technique is applied to find the inverse Laplace transform numerically. The weighted function enables the visual representation of the function. The technique based on Zakian’s algorithm is described in detail in [58].
The Nsselt number
The Sherwood number
The skin fraction
In this paper, the investigation of the exact solutions of unsteady Casson nanofluid passing through a vertical Riga plate with ramped and isothermal boundary conditions on the wall is carried out. Suspended clay nanoparticles in the base fluid (concrete) are taken. The property of the clay nanoparticles is to decrease oxygen permeability and increase the tensile strength of the base fluid. An analysis of the graphical results shows how different embedded parameters affect the velocity profile
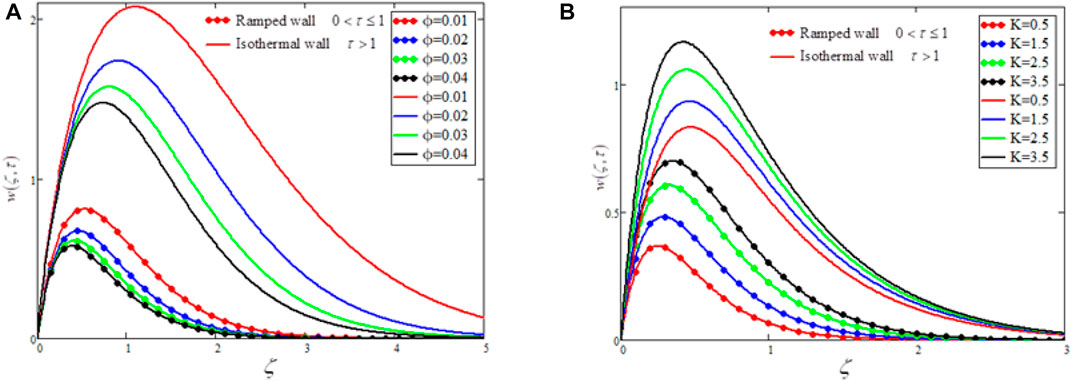
FIGURE 2. The effects of volume fraction parameter
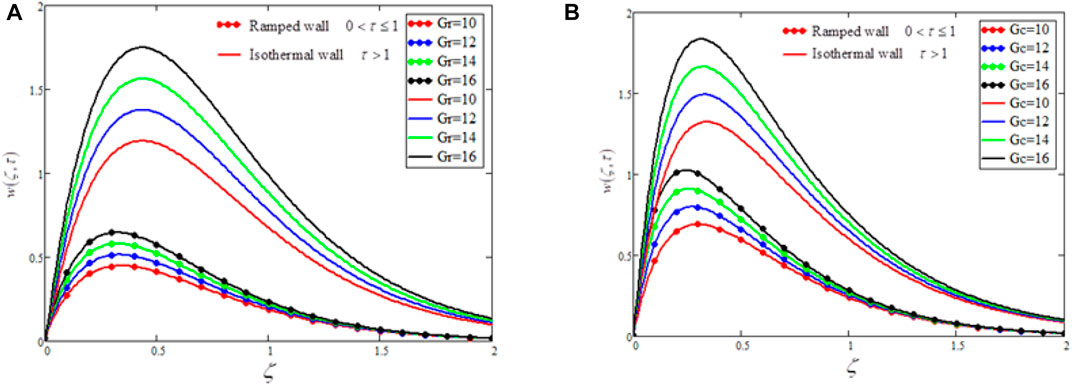
FIGURE 3. Velocity distribution for different values of Grashoof number
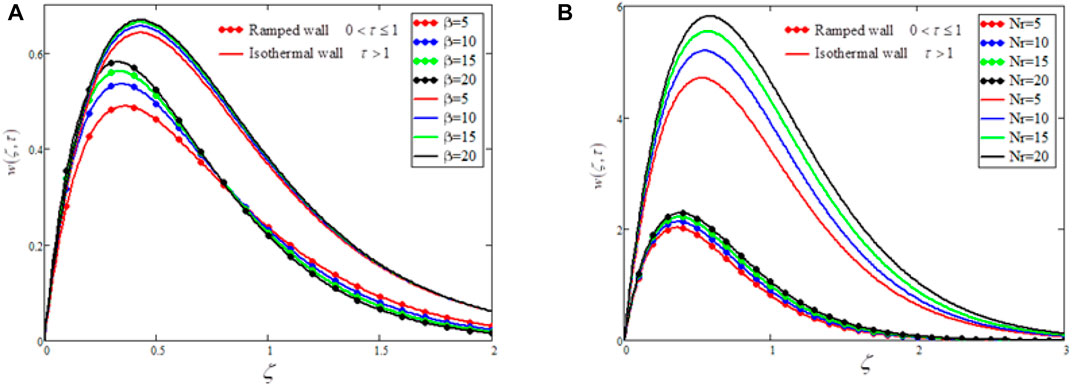
FIGURE 4. Variation in velocity distribution for various values of Casson fluids parameter
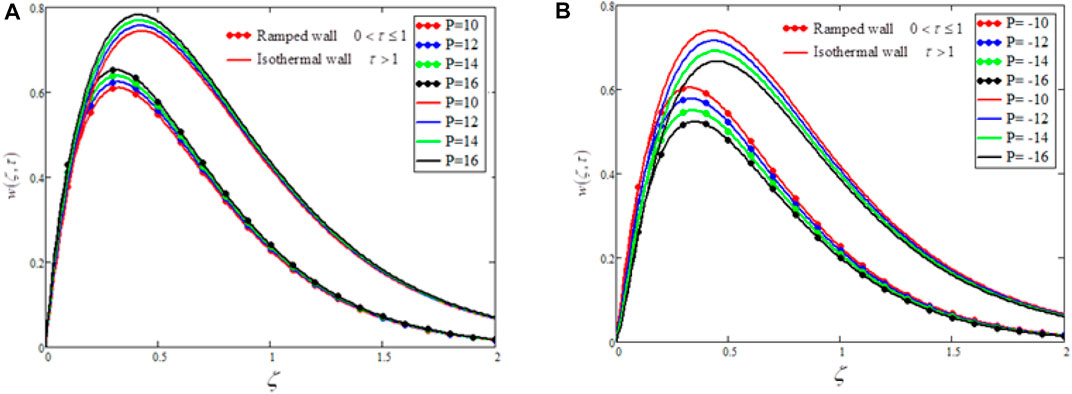
FIGURE 6. The effects of positive and negative values of modified Hartmann number
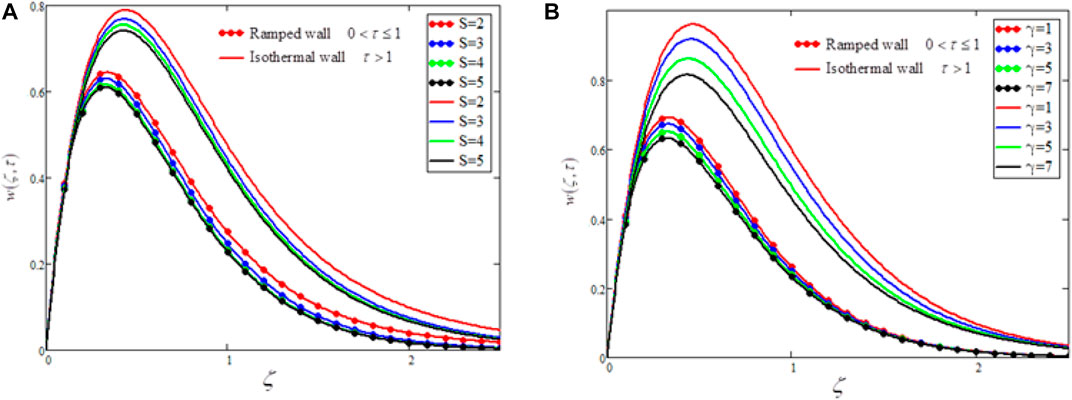
FIGURE 7. The effects of relation between viscosity and velocity
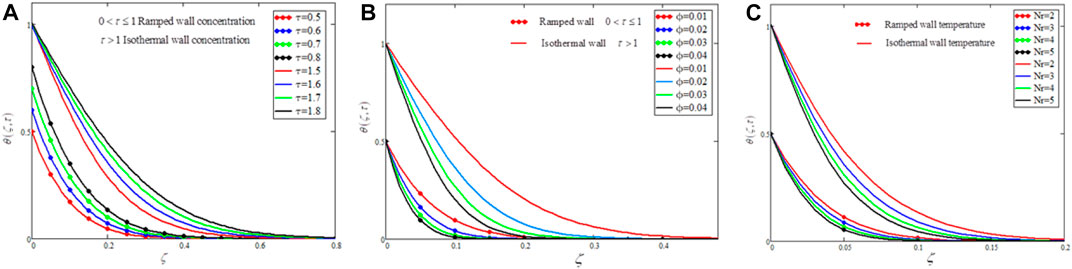
FIGURE 8. The effects of time
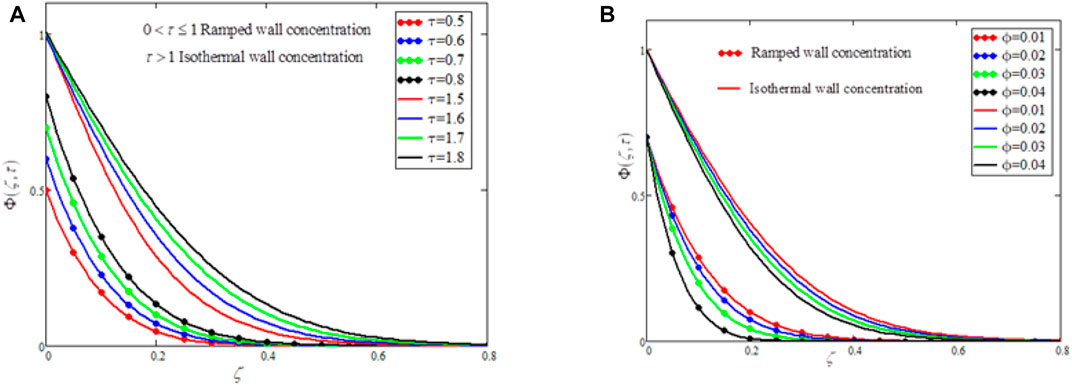
FIGURE 9. The effects of time
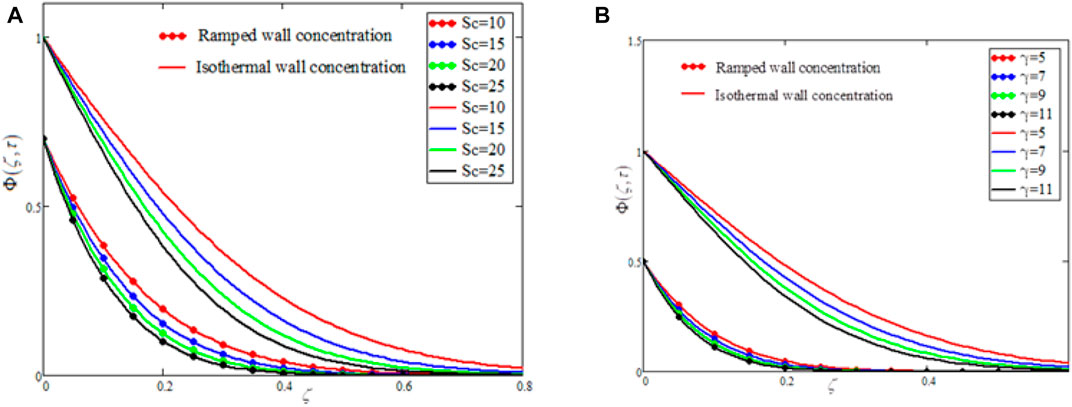
FIGURE 10. The effects of Schmidt number
The effect of volume fraction
Figure 4B illustrates the influence of the radiation parameter
The influence of time
The influence of time
Table 1 shows the thermo-physical properties of base fluid (concrete) and Clay nanoparticles. Table 2 depicts the changes in skin friction caused by various parameter values in both ramped and isothermal wall temperatures. The increasing values of
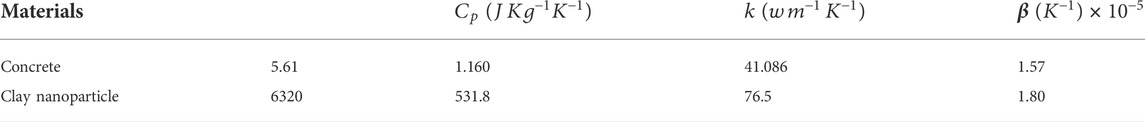
TABLE 1. Thermo-physical properties of base fluid (concrete) and Clay nanoparticles [13].
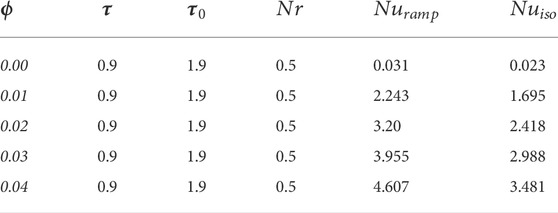
TABLE 3. The variations of the Nusselt number
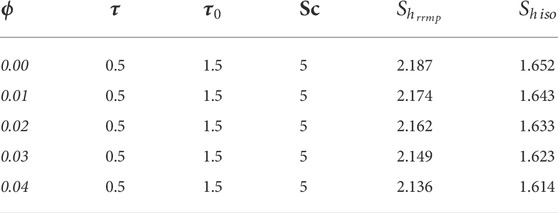
TABLE 4. The variations of the Sherwood number
This study presents the exact solutions for electromagnetic unsteady Casson nanofluid passing through a vertical Riga plate with ramped wall conditions. To obtain exact solutions for temperature, concentration, and velocity distributions, the Laplace transform method is used. All initial and boundary conditions are satisfied by the general solution provided. The graphical study reveals that concentration, velocity, and temperature profiles are larger for constant wall temperatures and smaller for ramped wall temperature and concentration. The effect of different embedded parameters on Sherwood number, skin friction, and Nusselt number, is numerically calculated and presented in tabular form. Based on the solutions to the problem and the graphical analysis, the following significant results are concluded.
• The positive values of the modified Hartmann number
• Velocity distribution of the nanofluids and the coefficient of skin friction are improved by a higher permeability
• The velocity is enhanced by increasing Casson fluid parameter
• Suspended clay nanoparticles in concrete-based Casson nanofluids enhanced skin friction up to 7.04% in RWT and 11.13% in IWT, which consequently enhance the tensile strength of the concrete.
• By increasing the value of
• The temperature is diminished by the uplifting radiation parameter
• Greater values of Schmidt number
Following are the future suggestions for the upcoming researchers to extend the above-mentioned problem.
• This problem can be extended to cylindrical co-ordinates.
• For various applications various nanoparticles can be introduced.
• Different non-Newtonian fluids, such as second-grade fluid, Jeffery fluid, Couple stress fluid, Maxwell fluid, and so on, may be modelled using the present approach.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
FA model problem. HK and NK solved the modeled problem analytically. HK and NK draw the graphs. Results and discussions have reviewed by IK and AM reviewed the whole manuscript. All authors reviewed the final manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Chhabra R, Richardson J. Oxford. auckland boston johannesburg melbourne New Delhi butterworth-heinemann. In: Non-Newtonian flow in the process industries: Fundamentals and engineering applications (1999).
2. cross MM. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J Colloid Science Undefined (1965).
3. Ullah I, Bhattacharyya K, Shafie S, Khan I. Unsteady MHD mixed convection slip flow of Casson fluid over nonlinearly stretching sheet embedded in a porous medium with chemical reaction, thermal radiation, heat generation/absorption and convective boundary conditions. PLoS ONE (2016) 11(10):e0165348. doi:10.1371/JOURNAL.PONE.0165348
4. Srinivas S, Kumar CK, Reddy AS. Pulsating flow of Casson fluid in a porous channel with thermal radiation, chemical reaction and applied magnetic field. Nonlinear Anal (2018) 23(2):213–33. doi:10.15388/NA.2018.2.5
5. Vaidya H, Prasad K, Vajravelu K, Wakif A, Basha NZ, Manjunatha G, et al. Effects of variable fluid properties on oblique stagnation point flow of a casson nanofluid with convective boundary conditions. Defect and Diffusion Forum (2020) 401:183–96. doi:10.4028/www.scientific.net/DDF.401.183
6. Khan U, Mebarek-Oudina F, Zaib A, Ishak A, Abu Bakar S, Sherif ESM, et al. An exact solution of a Casson fluid flow induced by dust particles with hybrid nanofluid over a stretching sheet subject to Lorentz forces. Waves in Random and Complex Media (2022) 1–14. doi:10.1080/17455030.2022.2102689
7. Shamshuddin M, Abderrahmane A, Koulali A, Eid MR, Shahzad F, Jamshed W. Thermal and solutal performance of Cu/CuO nanoparticles on a non-linear radially stretching surface with heat source/sink and varying chemical reaction effects. Int Commun Heat Mass Transfer (2021) 129:105710. doi:10.1016/j.icheatmasstransfer.2021.105710
8. Ram MS, Ashok N, Salawu SO, Shamshuddin MD. Significance of cross diffusion and uneven heat source/sink on the variable reactive 2D Casson flowing fluid through an infinite plate with heat and Ohmic dissipation. Int J Model Simulation (2022) 1–15. doi:10.1080/02286203.2022.2084007
9. Sobolev K, Flores I, Torres-Martinez LM, Valdez PL, Zarazua E, Cuellar EL. Engineering of SiONanoparticles for optimal performance in nano cement-based materials. Nanotechnology in Construction (2009) 3:139–48. doi:10.1007/978-3-642-00980-8_18
10. Gerges NN, Issa CA, Fawaz S. Effect of construction joints on the splitting tensile strength of concrete. Case Stud Construction Mater (2015) 3:83–91. doi:10.1016/J.CSCM.2015.07.001
12. Bartos PJM. Nanotechnology in construction: A roadmap for development. American Concrete Institute, ACI Special Publication (2008). p. 1–14. doi:10.1007/978-3-642-00980-8_2/COVER
13. Murtaza S, Iftekhar M, Ali F, Khan I. Exact analysis of non-linear electro-osmotic flow of generalized Maxwell nanofluid: Applications in concrete based nano-materials. IEEE Access (2020) 8:96738–47. doi:10.1109/ACCESS.2020.2988259
14. Norhasri M, Hamidah M, Fadzil AM. Applications of using nano material in concrete: A review. Construction Building Mater (2017) 133:91–7. doi:10.1016/j.conbuildmat.2016.12.005
15. Khan U, Zaib A, Ishak A, Roy NC, Bakar SA, Muhammad T, et al. Exact solutions for MHD axisymmetric hybrid nanofluid flow and heat transfer over a permeable non-linear radially shrinking/stretching surface with mutual impacts of thermal radiation. Eur Phys J Spec Top (2022) 231(6):1195–204. doi:10.1140/EPJS/S11734-022-00529-2
16. Khan U, Zaib A, Ishak A, Waini I, Raizah Z, Prasannakumara B, et al. Dynamics of bio-convection agrawal axisymmetric flow of water-based Cu-TiO2 hybrid nanoparticles through a porous moving disk with zero mass flux. Chem Phys (2022) 561:111599. doi:10.1016/J.CHEMPHYS.2022.111599
17. Khan N, Ali F, Arif M, Ahmad Z, Aamina A, Khan I. Maxwell nanofluid flow over an infinite vertical plate with ramped and isothermal wall temperature and concentration. Math Probl Eng (2021) 2021:1–19. doi:10.1155/2021/3536773
18. Ali F, Haq F, Khan N, Alqahtani H, Imtiaz A, Khan I. A report of generalized blood flow model with heat conduction between blood and particles. J Magnetics (2022) 27(2):186–200. doi:10.4283/JMAG.2022.27.2.186
19. Ali F, Haq F, Khan N, Imtiaz A, Khan I. A time fractional model of hemodynamic two-phase flow with heat conduction between blood and particles: Applications in health science. Waves in Random and Complex Media (2022) 1–28. doi:10.1080/17455030.2022.2100002
20. Kao TT. Laminar free convective heat transfer response along a vertical flat plate with step jump in surface temperature. Lett Heat Mass Transfer (1975) 2(5):419–28. doi:10.1016/0094-4548(75)90008-9
21. Gong Z-X, Mujumdar AS, Itaya Y, Mori S, Hasatani M. Drying technology drying of clay and nonclay media. Heat Mass Transfer Quality Aspects (2007). doi:10.1080/07373939808917457
22. Ali F, Gohar M, Khan I. MHD flow of water-based Brinkman type nanofluid over a vertical plate embedded in a porous medium with variable surface velocity, temperature and concentration. J Mol Liquids (2016) 223:412–9. doi:10.1016/J.MOLLIQ.2016.08.068
23. Kataria HR, Patel HR. Radiation and chemical reaction effects on MHD Casson fluid flow past an oscillating vertical plate embedded in porous medium. Alexandria Eng J (2016) 55(1):583–95. doi:10.1016/j.aej.2016.01.019
25. Khan MIH, Welsh Z, Gu Y, Karim MA, Bhandari B. Modelling of simultaneous heat and mass transfer considering the spatial distribution of air velocity during intermittent microwave convective drying. Int J Heat Mass Transfer (2020) 153:119668. doi:10.1016/j.ijheatmasstransfer.2020.119668
26. Benazir AJ, Sivaraj R, Rashidi MM. Comparison between Casson fluid flow in the presence of heat and mass transfer from a vertical cone and flat plate. J Heat Transfer (2016) 138. doi:10.1115/1.4033971
27. Ahmad Z, Arif M, Khan I. Dynamics of fractional order SIR model with a case study of COVID-19 in Turkey. CITY UNIVERSITY INTERNATIONAL JOURNAL COMPUTATIONAL ANALYSIS (2020) 4(01):19–37. doi:10.33959/CUIJCA.V4I01.43
28. Khan N, Ahmad Z, Ahmad H, Tchier F, Zhang X-Z, Murtaza S. Dynamics of chaotic system based on image encryption through fractal-fractional operator of non-local kernel. AIP Adv (2022) 12(5):055129. doi:10.1063/5.0085960
29. Ahmad Z, Ali F, Almuqrin MA, Murtaza S, Hasin F, Khan N, et al. Dynamics of love affair of romeo and juliet through modern mathematical tools: A critical analysis via fractal-fractional differential operator. Fractals (2022) 30:2240167. doi:10.1142/S0218348X22401673
30. Ali F, Arif M, Khan I, Sheikh NA, Saqib M. Natural convection in polyethylene glycol based molybdenum disulfide nanofluid with thermal radiation, chemical reaction and ramped wall temperature. Int J Heat Tech (2018) 36(2):619–31. doi:10.18280/IJHT.360227
31. Chandran P, Sacheti NC, Singh AK. Natural convection near a vertical plate with ramped wall temperature. Heat Mass Transfer (2004) 41(5):459–64. doi:10.1007/S00231-004-0568-7
33. Seth GS, Ansari MS, Nandkeolyar R. MHD natural convection flow with radiative heat transfer past an impulsively moving plate with ramped wall temperature. Heat Mass Transfer (2011) 47(5):551–61. doi:10.1007/S00231-010-0740-1
34. Ahmed N, Saba F, Khan U, Khan I, Alkanhal T, Faisal I, et al. Spherical Shaped ( A g − F e 3 O 4/H 2 O ) Hybrid Nanofluid Flow Squeezed between Two Riga Plates with Nonlinear Thermal Radiation and Chemical Reaction Effects. Energies (2018) 12:76. doi:10.3390/en12010076
35. Ahmad S, Ashraf M, Ali K. Simulation of thermal radiation in a micropolar fluid flow through a porous medium between channel walls. J Therm Anal Calorim (2021) 144(3):941–53. doi:10.1007/S10973-020-09542-W
36. Nasrin S, Nath Mondal R, Mahmud Alam M, Nasrin S, Mondal RN, Alam MM. Unsteady Couette flow past between two HorizontalRiga plates with Hall and ion slip current (2021). doi:10.21203/rs.3.rs-574292/v1
37. Loganathan P, Deepa K. Electromagnetic and radiative Casson fluid flow over a permeable vertical riga-plate. J Theor Appl Mech (Poland) (2019) 57(4):987–98. doi:10.15632/jtam-pl/112421
38. Pantokratoras A, Magyari E. EMHD free-convection boundary-layer flow from a Riga-plate. J Eng Math (2009) 64(3):303–15. doi:10.1007/S10665-008-9259-6
39. Ahmad A, Asghar S, Afzal S. Flow of nanofluid past a Riga plate. J Magnetism Magn Mater (2016) 402:44–8. doi:10.1016/j.jmmm.2015.11.043
40. Hakeem AA, Ragupathi P, Shekar S, Ganga B. Three dimensional non-linear radiative nanofluid flow over a Riga plate. J Appl Comput Mech (2020) 6(4):1012–29. doi:10.22055/JACM.2019.30095.1678
41. Ramesh G, Gireesha BJ. Non-linear radiative flow of nanofluid past a moving/stationary Riga plate. Front Heat Mass Transfer (2017) 9. doi:10.5098/hmt.9.3
42. Iqbal Z, Azhar E, Mehmood Z, Maraj EN. Unique outcomes of internal heat generation and thermal deposition on viscous dissipative transport of viscoplastic fluid over a Riga-plate. Commun Theor Phys (2018) 69(1):68–76. doi:10.1088/0253-6102/69/1/68
43. Zaib A, Khan U, Khan I, Seikh AH, Sherif ESM. Entropy generation and dual solutions in mixed convection stagnation point flow of micropolar Ti6Al4V nanoparticle along a riga surface. Processes (2020) 8:14. doi:10.3390/PR8010014
44. Kataria H, Mittal AS. Velocity, mass and temperature analysis of gravity-driven convection nanofluid flow past an oscillating vertical plate in the presence of magnetic field in a porous medium. Appl Therm Eng (2017) 110:864–74. doi:10.1016/j.applthermaleng.2016.08.129
45. Patil VS, Shamshuddin MD, Ramesh K, Rajput GR. Slipperation of thermal and flow speed impacts on natural convective two-phase nanofluid model across Riga surface: Computational scrutinization. Int Commun Heat Mass Transfer (2022) 135:106135. doi:10.1016/J.ICHEATMASSTRANSFER.2022.106135
46. Shamshuddin MD, Mabood F, Rajput GR, Bég OA, Badruddin IA. Thermo-solutal dual stratified convective magnetized fluid flow from an exponentially stretching Riga plate sensor surface with thermophoresis. Int Commun Heat Mass Transfer (2022) 134:105997. doi:10.1016/J.ICHEATMASSTRANSFER.2022.105997
47. Shamshuddin MD, Ibrahim W. Finite element numerical technique for magneto-micropolar nanofluid flow filled with chemically reactive casson fluid between parallel plates subjected to rotatory system with electrical and Hall currents. Int J Model Simulation (2022) 1–20. doi:10.1080/02286203.2021.2012634
48. Ahmad A. Flow control of non-Newtonain fluid using Riga plate: Reiner-Phillipoff and Powell-Eyring viscosity models. J Appl Fluid Mech (2019) 12:127–33. doi:10.29252/jafm.75.253.28897
49. Yusof NS, Soid SK, Illias MR, Abd Aziz AS, Mohd Nasir NAA. Radiative boundary layer flow of casson fluid over an exponentially permeable slippery Riga plate with viscous dissipation. J Adv Res Appl Sci Eng Tech (2020) 21(1):41–51. doi:10.37934/ARASET.21.1.4151
50. Abbas T, Bhatti MM, Ayub M. Aiding and opposing of mixed convection Casson nanofluid flow with chemical reactions through a porous Riga plate. J Process Mech Eng (2018) 232(5):519–27. doi:10.1177/0954408917719791
51. Khashi’ie N, Arifin NM, Pop I. Mixed convective stagnation point flow towards a vertical Riga plate in hybrid Cu-Al2O3/water nanofluid. Mathematics (2020) 8:912. doi:10.3390/math8060912
52. Mahdy A, Hoshoudy GA. EMHD time-dependant tangent hyperbolic nanofluid flow by a convective heated Riga plate with chemical reaction. J Process Mech Eng (2019) 233(4):776–86. doi:10.1177/0954408918805261
53. Zaib A, Haq RU, Chamkha AJ, Rashidi MM. Impact of partial slip on mixed convective flow towards a Riga plate comprising micropolar TiO2-kerosene/water nanoparticles. Int J Numer Methods Heat Fluid Flow (2019) 29(5):1647–62. doi:10.1108/hff-06-2018-0258
54. Loganathan P, Deepa K. Stratified casson fluid flow past a Riga-plate with generative/destructive heat energy. Int J Appl Comput Math (2020) 6(4):113. doi:10.1007/S40819-020-00863-W
55. Kakaç S, Pramuanjaroenkij A. Review of convective heat transfer enhancement with nanofluids. Int J Heat Mass Transfer (2009) 52(13–14):3187–96. doi:10.1016/j.ijheatmasstransfer.2009.02.006
56. Oztop H, Abu.-Nada E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int J Heat Fluid Flow (2008) 29:1326–36. doi:10.1016/j.ijheatfluidflow.2008.04.009
57. Zakian V, Littlewood RK. Numerical inversion of Laplace transforms by weighted least-squares approximation. Comp J (1973) 16(1):66–8. doi:10.1093/COMJNL/16.1.66
Keywords: concrete, based materials, clay nanoparticles, porous medium, chemical reaction, exact solution
Citation: Khan H, Ali F, Khan N, Khan I and Mohamed A (2022) Electromagnetic flow of casson nanofluid over a vertical riga plate with ramped wall conditions. Front. Phys. 10:1005447. doi: 10.3389/fphy.2022.1005447
Received: 28 July 2022; Accepted: 31 August 2022;
Published: 06 October 2022.
Edited by:
Muhammad Mubashir Bhatti, Shandong University of Science and Technology, ChinaReviewed by:
Aurang Zaib, Sciences and Technology Islamabad, PakistanCopyright © 2022 Khan, Ali, Khan, Khan and Mohamed. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Farhad Ali, ZmFyaGFkYWxpQGN1c2l0LmVkdS5waw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.