
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 04 October 2022
Sec. Cosmology
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1005333
We propose and study the new (generalized) E-type α-attractor models of inflation, in order to include formation of primordial black holes (PBHs). The inflaton potential has a near-inflection point where slow-roll conditions are violated, thus leading to large scalar perturbations collapsing to PBHs later. An ultra-slow roll (short) phase exists between two (longer) phases of slow-roll inflation. We numerically investigate the phases of inflation, derive the power spectrum of scalar perturbations and calculate the PBHs masses. For certain values of the parameters, the asteroid-size PBHs can be formed with the masses of 1017 ÷ 1019 g, beyond the Hawking evaporation limit and in agreement with current Cosmic Microwave Background observations. Those PBHs are a candidate for (part of) dark matter in the present Universe, while the gravitational waves induced by the PBHs formation may be detectable by the future space-based gravitational interferometers.
Measurements of the Cosmic Microwave Background (CMB) radiation by the Planck mission provide tight observational constraints on cosmological inflation in the early Universe [1–3]. Nevertheless, the simple Starobinsky model of inflation [4], proposed the long time ago, is still consistent with the current precision measurements of the CMB spectral tilt ns of scalar perturbations [1–3],
The Starobinsky model also gives a prediction for the value of the CMB tensor-to-scalar ratio r up to an uncertainty in the duration of inflation measured by the number of e-folds Ne as
and H(t) is the Hubble function. The current observational bound [1–3].
is already fulfilled for Ne > 20, whereas the duration of inflation is expected at Ne = 55 ± 10. This estimate for Ne comes from the predicted value of ns in the Starobinsky model via the Mukhanov-Chibisov formula [5].
Equations 2–4 for the tilts r and ns show only the leading terms with respect to the inverse e-folds number Ne. Given higher precision of the ns-measurements, the subleading terms may also be important. For example, in the case of the Starobinsky model, one finds [6].
The scalar potential of the canonical inflaton field ϕ in the Starobinsky model reads1
where we have introduced the dimensionless field
and the inflaton mass M ∼ 10−5MPl, whose value is determined by the known CMB amplitude. The scale of inflation can be estimated by the Hubble function H during slow-roll, which is related to the (unknown) tensor-to-scalar ratio r. As regards the Starobinsky inflation, the scale of inflation HS ∼ M corresponds to super-high energy physics far beyond the electro-weak scale and not far from the GUT scale.
The flatness of the inflaton potential during slow roll is guaranteed by the smallness of yS during inflation. Therefore, the inflationary observables for CMB will be essentially the same (in the leading approximation with respect to
where ζ(yS) is a function regular at yS = 0. Some generalizations of the Starobinsky model, like Eq. 8, were studied in Ref. [7]. In this paper, we take the inflaton potential to be a real function squared because it can always be minimally embedded into supergravity as a single-field inflationary model [8].
Another simple way of generalizing the Starobinsky model of inflation is given by the cosmological α − attractors [9, 10] that come in two families called E-models and T-models. The E-models have the same scalar potential V(y) as in Eq. 6 but in terms of the new variable
that depends upon the parameter α > 0. The Starobinsky model corresponds to α = 1. The E-models lead to the same Eq. 4 for the tilt ns but significantly change the tilt r as
thus making this theoretical prediction more flexible against future measurements.
An opportunity of changing the inflaton potential by arbitrary function ζ(y) can be exploited in order to generate primordial black holes (PBHs) [11, 12] at smaller values of ϕ or, equivalently, at lower energy scales. Those energy scales (below the scale of inflation) are not tightly constrained by observations yet. Technically, the PBHs production can be engineered by demanding a near-inflection point in the potential within the double inflation scenario with an ultra-slow-roll phase between two slow-roll regimes of inflation, leading to an enhancement of the power spectrum of scalar perturbations [13–15].2 The PBHs born in the very early Universe are considered as a candidate for cold dark matter in the present Universe [16–19].
A generalization of the Starobinsky model for PBHs formation was proposed and studied in Ref. [20] by using a model very different from the α-attractors. As regards the generalized T-models of α-attractors, the PBHs production was studied in Refs. [21, 22] for single-field inflation with the scalar potentials
where f is a regular function. In this paper, we propose and investigate the generalized E-models of inflation with a near-inflection point along similar lines.
Our paper is organized as follows. In Section 2 we introduce our model and investigate its scalar potential. Section 3 is devoted to the slow-roll approximation during the first stage of inflation relevant to CMB. In Section 4 we give our results for the power spectrum of scalar perturbations and its enhancement leading to PBHs formation. Our conclusion is Section 5.
Let us consider the following potential of the canonical inflaton ϕ:
with the dimensionless parameters (α, β, γ), where the function y(ϕ) is given by
Compared to Eqs 8, 9, we have Taylor-expanded the function ζ(y) up to a linear term, ζ(y) = β − γy, and have shifted the field ϕ by a constant ϕ0 in order to have a Minkowski minimum at ϕ = 0 with V (0) = 0. Hence, the ϕ0 is fixed by other parameters. We do not give here an explicit formula for ϕ0 because it is not very illuminating.
Demanding the existence of a near-inflection point in the potential with a coordinate ϕi allows us to replace the parameters (β, γ) by the new dimensionless parameters (ϕi, ξ) as follows:
The parameters (ϕi, ξ) have the clear meaning: when ξ = 0, the potential has the inflection point at ϕ = ϕi only; when 0 < ξ ≪ 1, the potential has a local minimum
Equations 14, 15 are easily derivable from considering extrema of the cubic polynomial inside the square brackets in (12), which leads to a quadratic equation (cf. Ref. [22]). The inverse relations are given by
In terms of the new parameters our scalar potential takes the form
An example of the scalar potential leading to viable inflation and PBHs formation is given in Figure 1. The potentials in the original E-models of α-attractors, arising in the case of β = γ = ϕ0 = 0, do not have a near-inflection point and thus do not lead to PBHs formation. Our potential (17) has the small bump, associated with the local maximum, and the small dip, associated with the local minimum, with both being close to the inflection point, similarly to the models of Ref. [23].
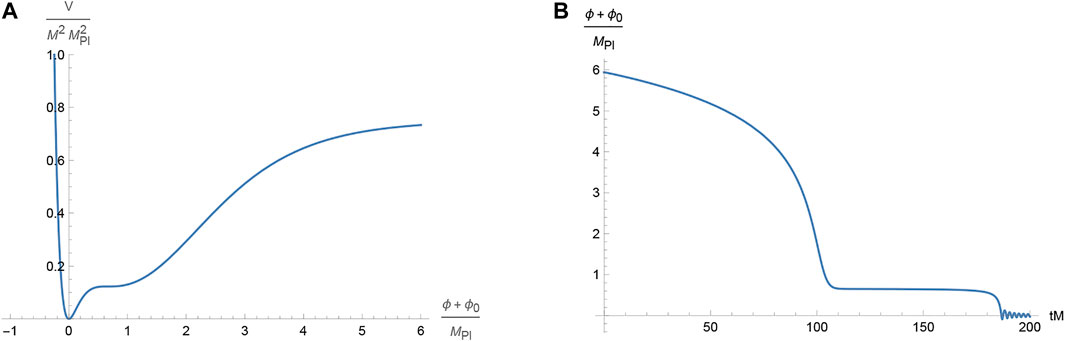
FIGURE 1. A profile of the scalar potential (A) and the inflaton dynamics (B) for the parameters α = 0.739, ϕi + ϕ0 = 0.664MPl and ξ = 0.012 with the vanishing initial velocity. The location of the inflection point is specified by the value of (ϕi + ϕ0)/MPl.
Since the flatness of the scalar potential during inflation, the standard slow-roll approximation well describes both the inflaton dynamics and the power spectrum of perturbations away from the inflection point and the end of inflation. We use the slow-roll approximation in order to calculate the observables relevant to CMB and estimate the power spectrum of scalar perturbations. It is known that the slow-roll approximation generically fails in the ultra-slow-roll (non-attractor) regime near an inflection point [21, 22]. Therefore, after having fixed our parameters in the slow-roll approximation, we numerically recalculate the power spectrum near the inflection point by using the Mukhanov-Sasaki (MS) equation [24, 25] leading to a correct answer.
The (running) number of e-folds in the slow-roll approximation is given by
where the prime denotes differentiation with respect to the given argument. The integral can be taken analytically in the case of our potential (17). We find
where N0 is an integration constant close to one. We ignore this constant for simplicity in what follows because it merely shifts counting of Ne. The standard slow-roll parameters are given by
and
It yields
whose coefficients are given by
Equation 20 reproduces Eq. 10 because r = 16ϵ. When choosing α = 1 and ϕi → −∞, Eq. 5 is also recovered up to a small correction (= 0.05) in the value of the coefficient b due to our approximation.
We numerically solve the inflaton equation of motion by using initial conditions with the vanishing initial velocities and then substitute the background solutions into the equations for perturbations. All our inflationary solutions are attractors (during slow roll) by construction. The initial inflaton field value is fixed by a desired number of e-folds, see e.g., Refs. [26, 27] for details.
A typical numerical solution to the Hubble function during double inflation is given on the left-hand-side of Figure 2. Demanding a peak in the power spectrum of scalar perturbations, required for PBHs production, we find the parameter α has to be restricted to the interval between 0.5 and 0.9, whereas the parameter ϕi also has to be fixed, as is shown on the right-hand-side of Figure 2. There is a short phase of ultra-slow-roll between the two stages of slow-roll inflation (corresponding to two plateaus), which leads to large perturbations in the power spectrum and PBHs production.
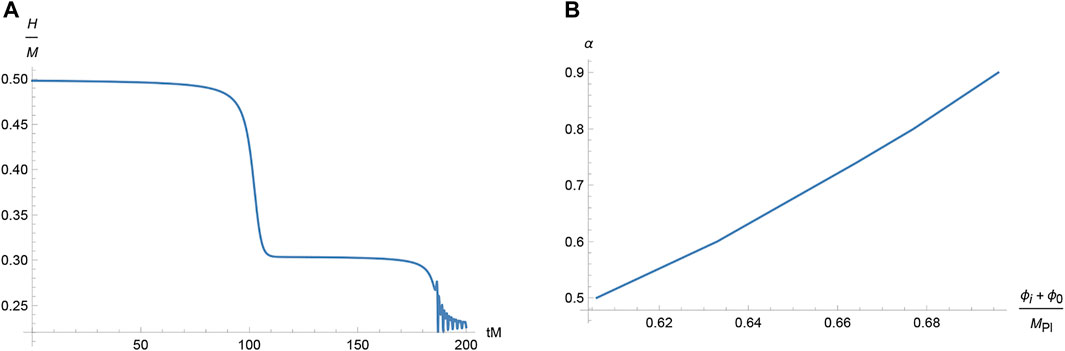
FIGURE 2. The Hubble function H (A) and the relation between the parameters ϕi and α for the power spectrum enhancement and PBHs production (B).
The standard formula for the power spectrum of scalar perturbations in the slow-roll approximation [13].
is useful for analytic studies of the power spectrum and its dependence upon the parameters. However, it cannot be used in the ultra-slow-roll phase where the slow-roll conditions are violated. Instead, one should use the MS equation [24, 25]. We used both in our calculations in order to see a difference between the two methods.
The scalar tilt ns is related to the power spectrum by a relation
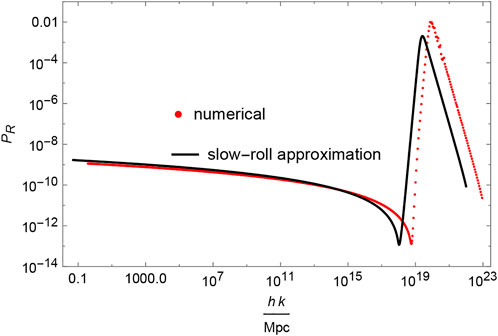
FIGURE 3. The power spectrum PR(k) of scalar perturbations from a numerical solution to the MS equation (in red) vs. an analytic derivation from Eq. 24 in the slow-roll approximation (in black), with the same parameters as in Figure 1.
As is clear from Figure 3, the exact results based on the MS equation vs. the slow-roll approximation increase the hight of the peak by one or two orders of magnitude, whereas the amplification of the peak vs. the CMB spectrum (on the very left-hand-side of the power spectrum) is given by the seven orders of magnitude.
The PBHs masses can be estimated from the peaks as follows [28]:
The right-hand-side of this equation is mainly sensitive to the value of ΔN = Ntotal − Npeak, whereas the integral gives a sub-leading correction.
Our findings are summarized in the Table below where we give the values of the CMB tilts ns and r associated with the values of the parameters α, ϕi and ξ, together with the corresponding values of ΔN and PBHs masses MPBH in our model.
The ns values below 0.9545 are certainly excluded by CMB observations, so we do not include our results for the lower values of ns, see Eq. 1. The values of ns above 0.9565 are in good agreement with CMB observations at the 95% C.L. The values of the tensor-to scalar ratio r in the Table are well inside the current observational bound (3). We also found that lowering the value of the parameter α leads to narrowing the peaks in the scalar perturbations spectrum. The PBHs masses are very sensitive to the value of ΔN.
PBHs may be part of the present dark matter when the PBH masses are beyond the Hawking evaporation limit of 1015 g, which is required for survival of those PBHs in the present Universe. However, consistency with the measured CMB value of ns restricts ΔN from above, as is clear from the Table.
Our approach is this paper is phenomenological and classical. However, it is not excluded that our deformations of the E-models of inflation proposed in this paper could appear as quantum corrections from a more fundamental theory of quantum gravity.
We modified the scalar potential of the single-field E-models of α-attractors in order to allow PBHs formation in those models at lower scales, while keeping success in the theoretical description of large-single-field inflation in agreement with CMB measurements. We found that efficient PBHs production consistent with CMB measurements restricts the α parameter to approximately 0.7 ± 0.2 and leads to the asteroid-size PBHs with masses of the order 1017 ÷ 1019 g. The masses of the PBHs formed in the very early Universe may grow further with time via accretion and mergers.
A similar approach was realized in the T-models of α-attractors [21, 22]. In terms of pole inflation [10] with a non-canonical inflaton field having just a mass term, the kinetic terms in the E-models have a pole of order two and exhibit the SL (2,R) symmetry, whereas the kinetic terms in the T-models also have a pole of order two but with the SU(1, 1) symmetry. Since those symmetries are equivalent, the main predictions of the standard E- and T-models for inflation are essentially the same. The generalized E-models of inflation proposed in this paper simultaneously describe viable inflation and PBHs formation.
The next generation of CMB measurements will probe deeper regions of parameter space, leading to a discrimination among currently viable models of inflation, which may falsify the Starobinsky model in particular. The α-attractors add more flexibility on the theoretical side, as regards the tensor-to-scalar ratio. We demonstrated that certain deformations of the scalars potentials in the E-models can also lead to efficient PBHs production capable to describe a whole (or part of) dark matter in the present Universe.
We tuned the parameters of our model in order to overcome the Hawking radiation bound 1015 g for the PBHs masses, so that those PBHs may contribute to the current dark matter. Remarkably, the PBHs with the masses between 1017 g and 1019 g belong to the current observational mass window where those PBHs may constitute the whole dark matter [18, 19]. With lower PBHs masses we found no strong constraints on the parameters, but those PBHs should all evaporate until now. Still, those PBHs may have dominated the early Universe, while their remnants could form dark matter at present.
The PBHs formation in the very early Universe should lead to a stochastic background of gravitational waves (GW) at present [29].3 The frequency of those GW can be estimated as
It was argued in the literature [30–32] that those GW may be detectable by the future space-based gravitational interferometers such as LISA [33], TAIJI [34], TianQin [35] and DECIGO [36].
Publicly available datasets were analyzed in this study. This data can be found here: https://inspirehep.net.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This work was supported by Tomsk State University under the development program Priority-2030. SK was also supported by Tokyo Metropolitan University, the Japanese Society for Promotion of Science under the grant No. 22K03624, and the World Premier International Research Center Initiative (MEXT, Japan).by the University of Tokyo.
SK thanks G. Domenech, S. Mishra and C. Unal for correspondence.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1See e.g., Refs. [7, 26, 37] for details about the Starobinsky model, various extensions and applications. We do not reproduce here the standard equations describing background dynamics, perturbations and their power spectrum in single-field inflation, because they are well known and easily can be found in the literature.
2See Ref. [27] for a current review of PBHs formation in single-field inflationary models.
3See e.g., Ref. [38] for a current review.
1. Akrami Y, Arroja F, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. X. Constraints on inflation. Astron Astrophys (2020) 641:A10. arXiv:1807.06211 [astro-ph.CO].
2. Ade PAR, Barkats D, Thakur RB, Bischoff C, Bock JJ, Boenish H, et al. Improved constraints on primordial gravitational waves using Planck, WMAP, and BICEP/keck observations through the 2018 observing season. Phys Rev Lett (2021) 127(15):151301. arXiv:2110.00483 [astro-ph.CO]. doi:10.1103/physrevlett.127.151301
3. Tristram M, Banday AJ, Górski KM, Keskitalo R, Lawrence CR, Andersen KJ, et al. (2021). Improved limits on the tensor-to-scalar ratio using BICEP and Planck. Phys. Rev. D. 8, 083524. Availabe at: http://arXiv.org/abs/2112.07961.
4. Starobinsky AA. A new type of isotropic cosmological models without singularity. Phys Lett B (1980) 91(1):99–102. doi:10.1016/0370-2693(80)90670-x
5. Mukhanov VF, Chibisov GV. Quantum fluctuations and a nonsingular universe. JETP Lett (1981) 33:532–5.
6. Kaneda S, Ketov SV, Watanabe N. Fourth-order gravity as the inflationary model revisited. Mod Phys Lett A (2010) 25:2753–62. arXiv:1001.5118 [hep-th]. doi:10.1142/s0217732310033918
7. Ivanov VR, Ketov SV, Pozdeeva EO, Vernov SY. Analytic extensions of Starobinsky model of inflation. JCAP (2022) 03:053. arXiv:2111.09058 [gr-qc]. doi:10.48550/arXiv.2111.09058
8. Ketov SV. On the equivalence of Starobinsky and Higgs inflationary models in gravity and supergravity. J Phys A: Math Theor (2020) 53(8):084001. arXiv:1911.01008 [hep-th]. doi:10.1088/1751-8121/ab6a33
9. Kallosh R, Linde A. Universality class in conformal inflation. JCAP (2013) 07:002. arXiv:1306.5220 [hep-th]. doi:10.48550/arXiv.1306.5220
10. Galante M, Kallosh R, Linde A, Roest D. Unity of cosmological inflation attractors. Phys Rev Lett (2015) 11414:141302. arXiv:1412.3797 [hep-th]. doi:10.1103/physrevlett.114.141302
11. Novikov I, Zeldovic Y. Cosmology. Ann Rev Astron Astrophys (1967) 5:627–49. doi:10.1146/annurev.aa.05.090167.003211
12. Hawking S. Gravitationally collapsed objects of very low mass. Mon Not R Astron Soc (1971) 152:75–8. doi:10.1093/mnras/152.1.75
13. Garcia-Bellido J, Ruiz Morales E. Primordial black holes from single field models of inflation. Phys Dark Universe (2017) 18:47–54. arXiv:1702.03901 [astro-ph.CO]. doi:10.1016/j.dark.2017.09.007
14. Germani C, Prokopec T. On primordial black holes from an inflection point. Phys Dark Universe (2017) 18:6–10. arXiv:1706.04226 [astro-ph.CO]. doi:10.1016/j.dark.2017.09.001
15. Germani C, Musco I. Abundance of primordial black holes depends on the shape of the inflationary power spectrum. Phys Rev Lett (2019) 12214:141302. arXiv:1805.04087 [astro-ph.CO]. doi:10.1103/physrevlett.122.141302
16. Barrow JD, Copeland EJ, Liddle AR. The Cosmology of black hole relics. Phys Rev D (1992) 46:645–57. doi:10.1103/physrevd.46.645
17. Carr BJ. Primordial black holes as a probe of cosmology and high energy physics. Lect Notes Phys (2003) 631:301–21. arXiv:astro-ph/0310838. doi:10.1007/978-3-540-45230-0_7
18. Sasaki M, Suyama T, Tanaka T, Yokoyama S. Primordial black holes—Perspectives in gravitational wave astronomy. Class Quan Gravity (2018) 35(6):063001. arXiv:1801.05235 [astro-ph.CO]. doi:10.1088/1361-6382/aaa7b4
19. Carr B, Kohri K, Sendouda Y, Yokoyama J. Constraints on primordial black holes. Rep Prog Phys (2021) 84:116902. arXiv:2002.12778 [astro-ph.CO]. doi:10.1088/1361-6633/ac1e31
20. Frolovsky D, Ketov SV, Saburov S, "Formation of primordial black holes after Starobinsky inflation". Mod Phys Lett A (2022) 37, 2250135. arXiv:2205.00603 [astro-ph.CO]. doi:10.1142/S0217732322501358
21. Dalianis I, Kehagias A, Tringas G. Primordial black holes from α-attractors. JCAP (2019) 01:037. arXiv:1805.09483 [astro-ph.CO]. doi:10.48550/arXiv.1805.09483
22. Iacconi L, Assadullahi H, Fasiello M, Wands D (2022). Revisiting small-scale fluctuations in α-attractor models of inflation. JCAP. 06, 007. Availabe at: http://arXiv.org/abs/2112.05092.
23. Mishra SS, Sahni V. Primordial Black Holes from a tiny bump/dip in the Inflaton potential. J Cosmol Astropart Phys (2020) 04:007. arXiv:1911.00057 [gr-qc]. doi:10.1088/1475-7516/2020/04/007
24. Mukhanov VF. Gravitational instability of the universe filled with a scalar field. JETP Lett (1985) 41:493–6.
25. Sasaki M. Large scale quantum fluctuations in the inflationary universe. Prog Theor Phys (1986) 76:1036–46. doi:10.1143/ptp.76.1036
26. Ketov SV. Multi-field versus single-field in the supergravity models of inflation and primordial black holes. Universe (2021) 7:115. doi:10.3390/universe7050115
27. Karam A, Koivunen N, Tomberg E, Vaskonen V, Veermäe H (2019). Anatomy of single-field inflationary models for primordial black holes. Available at https://arXiv.org/abs/2205.13540.
28. Pi S, Zhang Y-l., Huang Q-G, Sasaki M. Scalaron from R2-gravity as a heavy field. J Cosmol Astropart Phys (2018) 05:042. arXiv:1712.09896 [astro-ph.CO]. doi:10.1088/1475-7516/2018/05/042
29. Saito R, Yokoyama J. Gravitational wave background as a probe of the primordial black hole abundance. Phys Rev Lett (2009) 102:161101. arXiv:0812.4339 [astro-ph]. [Erratum. doi:10.1103/physrevlett.102.161101
30. Garcia-Bellido J, Peloso M, Unal C. Gravitational wave signatures of inflationary models from primordial black hole dark matter. J Cosmol Astropart Phys (2017) 09:013. arXiv:1707.02441 [astro-ph.CO]. doi:10.1088/1475-7516/2017/09/013
31. Cai R-G, Pi S, Sasaki M. Gravitational waves induced by non-Gaussian scalar perturbations. Phys Rev Lett (2019) 122:20. arXiv:1810.11000 [astro-ph.CO]. doi:10.1103/physrevlett.122.201101
32. Bartolo N, De Luca V, Franciolini G, Lewis A, Peloso M, Riotto A. Primordial black hole dark matter: LISA serendipity. Phys Rev Lett (2019) 122(21):211301. arXiv:1810.12218 [astro-ph.CO]. doi:10.1103/physrevlett.122.211301
33. Amaro-Seoane P, Audley H, Babak S, Baker J, Barausse E, Bender P, et al. (2022). Laser interferometer space antenna. Availabe at: http://arXiv.org/abs/1702.00786.
34. Gong X, Lau YK, Xu S, Amaro-Seoane P, Bai S, Bian X, et al. Descope of the ALIA mission. J Phys : Conf Ser (2015) 610(1):012011. arXiv:1410.7296 [gr-qc]. doi:10.1088/1742-6596/610/1/012011
35. Qin T, Luo J, Duan HZ, Gong YG, Hu S, Ji J, et al. TianQin: A space-borne gravitational wave detector. Class Quan Gravity (2016) 33(3):035010. arXiv:1512.02076 [astro-ph.IM]. doi:10.1088/0264-9381/33/3/035010
36. Kudoh H, Taruya A, Hiramatsu T, Himemoto Y. Detecting a gravitational-wave background with next-generation space interferometers. Phys Rev D (2006) 73:064006. arXiv:gr-qc/0511145. doi:10.1103/physrevd.73.064006
37. Ketov SV. On the large-field equivalence between Starobinsky and Higgs inflation in gravity and supergravity. J.Phys.A:Math.Theor (2022) 53:084001. doi:10.48550/arXiv.1911.01008
Keywords: cosmological inflation, black holes, cosmic microwave “background (CMB), dark matter, cosmology
Citation: Frolovsky D, Ketov SV and Saburov S (2022) E-models of inflation and primordial black holes. Front. Phys. 10:1005333. doi: 10.3389/fphy.2022.1005333
Received: 28 July 2022; Accepted: 31 August 2022;
Published: 04 October 2022.
Edited by:
Antonino Marciano, Fudan University, ChinaReviewed by:
Vladimir Dzhunushaliev, Al-Farabi Kazakh National University, KazakhstanCopyright © 2022 Frolovsky, Ketov and Saburov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sergei V. Ketov, a2V0b3ZAdG11LmFjLmpw
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.