Material and wave relaxation phenomena effects on the rheology of Maxwell nanofluids

This study analyzed thermal and mass transport in magnetohydrodynamic Maxwell nanofluids over a cylinder stretched along the z-direction. The Cattaneo-Christov diffusion theory and Buongiorno’s model were employed to model the problem. The influences of Joule heating, chemical reaction rate, and heat generation were also considered. Appropriate similar variables were utilized to transform the constitutive equations. A semi-analytical method, namely the homotopy analysis method (HAM) in Wolfram Mathematica, was used to compute the problem solution. The results demonstrated the inverse variation in flow behavior with increased Maxwell parameter values; however, thermal and solutal transport displays the opposite trend. Additionally, the flow field showed resistance due to the presence of the magnetic field, while Joule heating enhanced the energy and mass transport phenomena. The results regarding the coefficient of skin friction along the radial direction are consistent with values reported in the literature.

1 Introduction

Maxwell [1] proposed a rate-type model, which is well-known because of its viscoelastic conduct and the prediction of stress-relaxation. The study of stretching surfaces is also an intriguing topic for mathematicians, physicists, and engineers. The non-Newtonian Maxwell model also has significant application to problems in industrial fields, including aerodynamics, petroleum, and pharmaceutical processes. Mukhopadhyay [2] adopted the boundary layer theory to model the Maxwell MHD flow and shooting scheme. Yang et al. [3] distinguished the thermal conductivity of a two-phase medium for the Maxwell fluid. They reported decreased conduction due to insulating pores caused by stretchiness. In their heat transport study of the Maxwell model with variable conditions, Ahmad et al. [4] reported a decreased heat-flux because of additions to the stretching parameter. Ramzan et al. [5] examined convective Maxwell flow with Dufour impression, while Hsiao [6] analyzed a thermal extrusion problem with radiation and dissipation for the Maxwell model, in which they inferred that free convection is more reliable than forced convection energy transformation. Madhu et al. [7] investigated the viscoelastic behavior of the flow with thermal radiation and MHD. Irfan et al. [8] applied the HAM for Maxwell fluid with the consideration of source/sink. Aziz and Shams [9]evaluatedthe importance of thermal radiation and heat source in entropy generation for a permeable surface. Their quantitative results showed significantly decreased entropy generation with increased magnetic field strength and medium permeability.

The term nanofluid refers to nanometer-sized structured particles suspended in a base-fluid, generally water or intricate hydrocarbon compounds. Recently, due to their extensive use in applied science, biomedicine, industries, etc., nanofluids have attracted increased attention. Choi [10] pioneered the term nanofluid; since then, many studies have been conducted. The mathematical modeling of nanofluid transport has adopted the two-phased model described by Buongiorno [11]. To understand the flow pattern and heat transport capacities of nanofluids, numerous studies have been conducted in aerospace, biosciences, and industrial fields. Cattaneo [12] modified the traditional Fourier model by incorporating the thermal relaxation time property, resulting in the Maxwell-Cattaneo principle. Christov [13]modifiedCattaneo’s findings with the Oldroyd derivative to produce an invariant form. The Cattaneo-Christov model and Fourier law were compared by Han et al. [14]. Mustafa [15] deduced the viscoelastic behavior of flow through the Cattaneo-Christov theory on a stretching surface and inferred that heat transport was inversely associated with the relaxation time. Li et al. [16] analyzed the heat transfer and viscoelastic conduct of models used with a steady boundary layer and the Cattaneo-Christov theory. Khan [17] reported the numerical significance of the heat-mass transference rate on the Carreau fluid flow. Acharya et al. [18] presented a generalized model for Fourier-Fick’s law, in which they concluded the concentration distribution increased due to Fick’s law. Additional studies on heat transfer in nanofluids and the Cattaneo-Christov theory are discussed in Refs. [19–33].

Motivated by these previous studies, the present study discussed Maxwell nanofluid flow and its heat transport rate over a stretching cylinder at a steady state. This study also utilized Cattaneo-Christov’s theory to develop energy and concentration equations. The theory of double diffusion was applied to examine the characteristics of heat transfer in viscoelastic flow. The effects of magnetic field (Lorentz force and Joule heating), heat source/sink, and the chemical reaction rate on the temperature and concentration profiles were also evaluated. The practical applications of this study include deforming and stretching surfaces, particularly in application and development in industrial processes such as fiber-glass production, enhancement of electronic devices by employing microchips, plastic manufacturing, etc. We also examined the response of fluid motion, concentration, and energy distribution by altering attrition and other relevant parameters. All the graphs show exponential decay, which highlights the dependence of these profiles on the independent variable η. The homotopy analysis method (HAM) was used to develop the series of convergent solutions for the ordinary differential equations (ODEs). We applied this analytical scheme to quantitatively compare our results to those previously reported.

Section 2 of this report describes the mathematical modeling of the problem. Section 3 discusses the solution approach to solve the problem. Section 4 discusses the graphs and tables showing the results of comparisons with Refs. [22–29]. Finally, Section 5 presents the concluding remarks.

2 Mathematical formulation

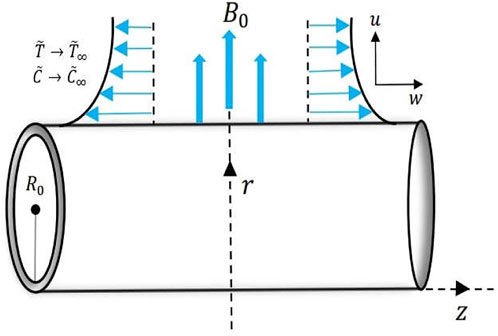
Consider a steady laminar two-dimensional incompressible flow over a cylinder of radius R₀ stretched along the z-direction with velocity ${\tilde{u}}_w\left(z\right)=Az$, (where $A=\frac{U_0}{l}>0$ is the ratio of the reference velocity to a specific length), drenched into the Maxwell nanofluid. The geometry of the flow is shown in Figure 1. The magnetic field $\mathbf{B}=\left[B_0,\mathrm{0,0}\right]$ is applied normal to the axis of the cylinder; i.e., the z-axis. Moreover, the Cattaneo-Christov diffusion causes thermal and solutal transportation in the flow. At the cylinder surface, the temperature and concentration of the Maxwell nanofluid are constant; i.e., $\tilde{T}={\tilde{T}}_w$ and $\tilde{C}={\tilde{C}}_w$, respectively. At the free-stream, their values are $\tilde{T}={\tilde{T}}_{\infty }$ and $\tilde{C}={\tilde{C}}_{\infty }$, respectively. The extra stress tensor S for the Maxwell fluid is:

$\left(1+{\lambda }_1\frac{D}{Dt}\right)\mathbf{S}=\mu {\mathbf{A}}_1,(1)$

where ${\mathbf{A}}_1=\left(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathbf{V}\right)+{\left(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathbf{V}\right)}^T$ is the first Rivlin–Ericksen tensor, μ is the dynamic viscosity, $\frac{D}{Dt}$ is the upper convective time derivative (Oldroyd derivative), and λ₁ is the relaxation time.

FIGURE 1

FIGURE 1. Flow configuration.

The Cattaneo-Christov model is utilized in preference to the classical Fourier’s law of heat conduction and Fick’s law of diffusion, with the heat flux q and the mass flux J given as:

$\mathbf{q}+{\lambda }_t\left(\frac{\partial \mathbf{q}}{\partial t}+\mathbf{V}\cdot \nabla \mathbf{q}+(\nabla \cdot \mathbf{V})\mathbf{q}-\mathbf{q}\cdot \nabla \mathbf{V}\right)=-k\nabla \tilde{T},(2)$

$\mathbf{J}+{\lambda }_c\left(\frac{\partial \mathbf{J}}{\partial t}+\mathbf{V}\cdot \nabla \mathbf{J}+(\nabla \cdot \mathbf{V})\mathbf{J}-\mathbf{J}\cdot \nabla \mathbf{V}\right)=-D_b\nabla \tilde{C},(3)$

where λ_t, λ_c, k, and D_b are the thermal time relaxation, the mass time relaxation, the thermal conductivity of the fluid, and the Brownian diffusion coefficient, respectively. Eqs 2 and 3 are reduced to the classical Fourier’s law of heat conduction and Fick’s law of diffusion when λ_t = λ_c = 0. For incompressible flow $\left(\nabla \cdot \mathbf{V}=0\right)$, Eqs 2, 3 reduce to:

$\mathbf{q}+{\lambda }_t\left(\frac{\partial \mathbf{q}}{\partial t}+\mathbf{V}\cdot \nabla \mathbf{q}-\mathbf{q}\cdot \nabla \mathbf{V}\right)=-k\nabla \tilde{T},(4)$

$\mathbf{J}+{\lambda }_c\left(\frac{\partial \mathbf{J}}{\partial t}+\mathbf{V}\cdot \nabla \mathbf{J}-\mathbf{J}\cdot \nabla \mathbf{V}\right)=-D_b\nabla \tilde{C}.(5)$

Given the above assumptions, and eliminating S, q, and J, the governing equations for the Maxwell nanofluid flow are:

$\frac{\partial \tilde{u}}{\partial r}+\frac{\tilde{u}}{r}+\frac{\partial \tilde{w}}{\partial z}=0,(6)$

$\begin{array}{ll}\hfill \tilde{u}\frac{\partial \tilde{w}}{\partial r}+\tilde{w}\frac{\partial \tilde{w}}{\partial z}+{\lambda }_1\left[{\tilde{w}}^2\frac{{\partial }^2\tilde{w}}{\partial z^2}+{\tilde{u}}^2\frac{{\partial }^2\tilde{w}}{\partial r^2}+2\tilde{u}\tilde{w}\frac{{\partial }^2\tilde{w}}{\partial r\partial z}\right]& =\nu \left[\frac{{\partial }^2\tilde{w}}{\partial r^2}+\frac{1}{r}\frac{\partial \tilde{w}}{\partial r}\right]\hfill \\ \hfill & -\frac{\sigma B_0^2}{{\rho }_f}\left[\tilde{w}+{\lambda }_1\tilde{u}\frac{\partial \tilde{w}}{\partial r}\right],\hfill \end{array}(7)$

$\begin{array}{ll}\hfill & \tilde{u}\frac{\partial \tilde{T}}{\partial r}+\tilde{w}\frac{\partial \tilde{T}}{\partial z}+{\lambda }_t\left[{\tilde{u}}^2\frac{{\partial }^2\tilde{T}}{\partial r^2}+{\tilde{w}}^2\frac{{\partial }^2\tilde{T}}{\partial z^2}+2\tilde{u}\tilde{w}\frac{{\partial }^2\tilde{T}}{\partial r\partial z}+\tilde{u}\frac{\partial \tilde{u}}{\partial r}\frac{\partial \tilde{T}}{\partial r}+\tilde{u}\frac{\partial \tilde{w}}{\partial r}\frac{\partial \tilde{T}}{\partial z}\right.\hfill \\ \hfill & \left.+\tilde{w}\frac{\partial \tilde{u}}{\partial z}\frac{\partial \tilde{T}}{\partial r}+\tilde{w}\frac{\partial \tilde{w}}{\partial z}\frac{\partial \tilde{T}}{\partial z}\right]=\tau \frac{D_t}{{\tilde{T}}_{\infty }}\left[{\left(\frac{\partial \tilde{T}}{\partial r}\right)}^2+2{\lambda }_t\left(\tilde{u}\frac{\partial \tilde{T}}{\partial r}\frac{{\partial }^2\tilde{T}}{\partial r^2}+\tilde{w}\frac{\partial \tilde{T}}{\partial z}\frac{{\partial }^2\tilde{T}}{\partial z^2}\right)\right]\hfill \\ \hfill & +\tau D_b\left[\frac{\partial \tilde{C}}{\partial r}\frac{\partial \tilde{T}}{\partial r}-{\lambda }_t\left(\tilde{u}\frac{{\partial }^2\tilde{T}}{\partial r^2}\frac{\partial \tilde{C}}{\partial z}+\tilde{u}\frac{{\partial }^2\tilde{C}}{\partial r^2}\frac{\partial \tilde{T}}{\partial r}+\tilde{w}\frac{{\partial }^2\tilde{T}}{\partial r\partial z}\frac{\partial \tilde{C}}{\partial r}+\tilde{w}\frac{{\partial }^2\tilde{C}}{\partial r\partial z}\frac{\partial \tilde{T}}{\partial r}\right)\right]\hfill \\ \hfill & +{\alpha }_1\left[\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \tilde{T}}{\partial r}\right)\right]+\frac{Q_0}{\rho c_p}\left[\left(\tilde{T}-{\tilde{T}}_{\infty }\right)+{\lambda }_t\left(\tilde{u}\frac{\partial \tilde{T}}{\partial r}+\tilde{w}\frac{\partial \tilde{T}}{\partial z}\right)\right]\hfill \\ \hfill & +\frac{\sigma B_0^2}{\rho c_p}\left[{\tilde{w}}^2+2{\lambda }_t\left({\tilde{w}}^2\frac{\partial \tilde{w}}{\partial z}+\tilde{u}\tilde{w}\frac{\partial \tilde{u}}{\partial r}\right)\right],\hfill \end{array}(8)$

$\begin{array}{ll}\hfill & \tilde{u}\frac{\partial \tilde{C}}{\partial r}+\tilde{w}\frac{\partial \tilde{C}}{\partial z}+{\lambda }_c\left[{\tilde{u}}^2\frac{{\partial }^2\tilde{C}}{\partial r^2}+{\tilde{w}}^2\frac{{\partial }^2\tilde{C}}{\partial z^2}+2\tilde{u}\tilde{w}\frac{{\partial }^2\tilde{C}}{\partial r\partial z}+\tilde{u}\frac{\partial \tilde{u}}{\partial r}\frac{\partial \tilde{C}}{\partial r}+\tilde{u}\frac{\partial \tilde{w}}{\partial r}\frac{\partial \tilde{C}}{\partial z}\right.\hfill \\ \hfill & \left.+\tilde{w}\frac{\partial \tilde{u}}{\partial z}\frac{\partial \tilde{C}}{\partial r}+\tilde{w}\frac{\partial \tilde{w}}{\partial z}\frac{\partial \tilde{C}}{\partial z}\right]=D_b\left[\frac{{\partial }^2\tilde{C}}{\partial r^2}+\frac{1}{r}\frac{\partial \tilde{C}}{\partial r}\right]+\frac{D_t}{{\tilde{T}}_{\infty }}\left[\left(\frac{{\partial }^2\tilde{T}}{\partial r^2}+\frac{1}{r}\frac{\partial \tilde{T}}{\partial r}\right)\right.\hfill \\ \hfill & \left.+{\lambda }_c\left(\tilde{u}\frac{{\partial }^3\tilde{T}}{\partial r^3}+\frac{\tilde{u}}{r^2}\frac{\partial \tilde{T}}{\partial r}+\frac{\tilde{u}}{r}\frac{{\partial }^2\tilde{T}}{\partial r^2}+\tilde{w}\frac{{\partial }^3\tilde{T}}{\partial r^2\partial z}+\frac{\tilde{w}}{r^2}\frac{{\partial }^2\tilde{T}}{\partial r\partial z}\right)\right]\hfill \\ \hfill & -K_0\left[\left(\tilde{C}-{\tilde{C}}_{\infty }\right)+{\lambda }_c\left(\tilde{u}\frac{\partial \tilde{C}}{\partial r}+\tilde{w}\frac{\partial \tilde{C}}{\partial z}\right)\right].\hfill \end{array}(9)$

In the above equations, ρ_f, σ, B₀, τ, c_p, α₁, D_t, Q₀, and K₀ are the density of the fluid, the electric conductivity of the fluid, the intensity of the magnetic field, the effective heat capacity of the nanoparticles in the base fluid, the heat capacity, the thermal diffusivity of the nanofluid, the thermophoresis coefficient, the volumetric rate of heat absorption/generation source, and the chemical reaction rate, respectively.

The corresponding boundary conditions are:

$\tilde{u}\left(z,r\right)=0,\tilde{w}\left(z,r\right)=Az,\tilde{T}={\tilde{T}}_w,\tilde{C}={\tilde{C}}_w\text{\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}}r=R_0,(10)$

$\tilde{u}\to 0,\tilde{T}\to {\tilde{T}}_{\infty },\tilde{C}\to {\tilde{C}}_{\infty }\text{\hspace{0.17em}as\hspace{0.17em}\hspace{0.17em}}r\to \infty .(11)$

The conversion ansatz for the flow, thermal, and mass transport are:

$\begin{array}{ll}\hfill \tilde{u}& =-\frac{R_0}{r}\sqrt{A\nu }\tilde{f}\left(\eta \right),\tilde{w}=Az{\tilde{f}}^{\prime }\left(\eta \right),\theta \left(\eta \right)=\frac{\tilde{T}-{\tilde{T}}_{\infty }}{{\tilde{T}}_w-{\tilde{T}}_{\infty }},\hfill \\ \hfill \varphi \left(\eta \right)& =\frac{\tilde{C}-{\tilde{C}}_{\infty }}{{\tilde{C}}_w-{\tilde{C}}_{\infty }},\text{\hspace{0.17em}with\hspace{0.17em}}\eta =\sqrt{\frac{A}{\nu }}\left(\frac{r^2}{2R_0}-\frac{R_0}{2}\right).\hfill \end{array}(12)$

Note that Eq. 6 is satisfied and Eqs 7–9 yield the following dimensionless ODEs.

$\begin{array}{ll}\hfill & \left(1+2\eta \alpha \right){\tilde{f}}^{\prime \prime \prime }-{\tilde{f}}^{\prime 2}+\tilde{f}{\tilde{f}}^{\prime \prime }+2\alpha {\tilde{f}}^{\prime \prime }+2{\beta }_1\tilde{f}{\tilde{f}}^{\prime }{\tilde{f}}^{\prime \prime }-{\beta }_1{\tilde{f}}^2{\tilde{f}}^{\prime \prime \prime }\hfill \\ \hfill & -\frac{\alpha {\beta }_1}{\left(1+2\eta \alpha \right)}{\tilde{f}}^2{\tilde{f}}^{\prime \prime }-M\left({\tilde{f}}^{\prime }-{\beta }_1\tilde{f}{\tilde{f}}^{\prime \prime }\right)=0,\hfill \end{array}(13)$

$\begin{array}{ll}\hfill & \left(1+2\eta \alpha \right){\theta }^{\prime \prime }+2\alpha {\theta }^{\prime }+\mathrm{Pr}\left[\tilde{f}{\theta }^{\prime }-{\beta }_t\left(\tilde{f}{\tilde{f}}^{\prime }{\theta }^{\prime }+{\tilde{f}}^2{\theta }^{\prime \prime }\right)\right]+\mathrm{Pr}{N}_b\left[\left(1+2\eta \alpha \right){\theta }^{\prime }{\varphi }^{\prime }\right.\hfill \\ \hfill & \left.-{\beta }_t\left\{2\alpha \tilde{f}{\theta }^{\prime }{\varphi }^{\prime }+\left(1+2\eta \alpha \right)\left(\tilde{f}{\theta }^{\prime \prime }{\varphi }^{\prime }+\tilde{f}{\theta }^{\prime }{\varphi }^{\prime \prime }\right)\right\}\right]+\mathrm{Pr}{N}_t\left[\left(1+2\eta \alpha \right){\theta }^{\prime 2}\right.\hfill \\ \hfill & \left.-2{\beta }_t\left\{\left(1+2\eta \alpha \right)\tilde{f}{\theta }^{\prime }{\theta }^{\prime \prime }+\alpha \tilde{f}{\theta }^{\prime 2}\right\}\right]+2\mathrm{Pr}M\mathrm{E}\mathrm{c}\left[{\tilde{f}}^{\prime 2}+{\beta }_t\left({\tilde{f}}^{\prime 3}-\tilde{f}{\tilde{f}}^{\prime }{\tilde{f}}^{\prime \prime }\right)\right]\hfill \\ \hfill & +\mathrm{Pr}{Q}^{*}\left[\theta +{\beta }_t\left(\tilde{f}{\theta }^{\prime }\right)\right]=0,\hfill \end{array}(14)$

$\begin{array}{ll}\hfill & \left(1+2\eta \alpha \right){\varphi }^{\prime \prime }+2\alpha {\varphi }^{\prime }+\mathrm{S}\mathrm{c}\left[\tilde{f}{\varphi }^{\prime }-{\beta }_c\left(\tilde{f}{\tilde{f}}^{\prime }{\varphi }^{\prime }+{\tilde{f}}^2{\varphi }^{\prime \prime }\right)\right]\hfill \\ \hfill & +\frac{N_t}{N_b}\left[\left(1+2\eta \alpha \right){\theta }^{\prime \prime }-{\beta }_c\left(\tilde{f}{\theta }^{\prime \prime \prime }-4\alpha \tilde{f}{\theta }^{\prime \prime }\right)\right]-\mathrm{S}\mathrm{c}{K}^{*}\left[\varphi +{\beta }_c\left(\tilde{f}{\varphi }^{\prime }\right)\right]=0.\hfill \end{array}(15)$

with boundary conditions:

$\tilde{f}\left(\eta \right)=0,{\tilde{f}}^{\prime }\left(\eta \right)=1,\theta \left(\eta \right)=1,\varphi \left(\eta \right)=1,\text{\hspace{0.17em}\hspace{0.17em}as\hspace{0.17em}}\eta =0,(16)$

${\tilde{f}}^{\prime }\left(\eta \right)=0,\theta \left(\eta \right)=0,\varphi \left(\eta \right)=0\text{\hspace{0.17em}\hspace{0.17em}as\hspace{0.17em}\hspace{0.17em}}\eta \to \infty .(17)$

The dimensionless parameters involve the fluid relaxation time parameter β₁, the curvature parameter α, the magnetic field parameter M, the Prandtl number Pr, the Schmidt number Sc, the Brownian diffusion parameter N_b, the thermophoresis parameter N_t, the thermal relaxation time parameter β_t, the solutal relaxation time parameter β_c, the Eckert number Ec due to the stretching of the cylinder in the z-direction, the heat generation parameter Q*, and the chemical reaction parameter K*, respectively.

$\left.\begin{array}{c}\hfill {\beta }_1=A{\lambda }_1,\alpha =\frac{1}{R_0}\sqrt{\frac{\nu }{A}},M=\frac{\sigma B_0^2}{\rho A},\mathrm{Pr}=\frac{\nu }{{\alpha }_1},\mathrm{S}\mathrm{c}=\frac{\nu }{D_b},\hfill \\ \hfill N_b=\frac{D_b\left({\tilde{C}}_w-{\tilde{C}}_{\infty }\right)\tau }{\nu },N_t=\frac{D_t\left({\tilde{T}}_w-{\tilde{T}}_{\infty }\right)\tau }{\nu {\tilde{T}}_{\infty }},{\beta }_t=A{\lambda }_t,{\beta }_c=A{\lambda }_c,\hfill \\ \hfill \mathrm{E}\mathrm{c}=\frac{{\tilde{u}}_w^2}{c_p\left({\tilde{T}}_w-{\tilde{T}}_{\infty }\right)},Q^{\ast }=\frac{Q_0}{A\left(\rho c_p\right)},K^{\ast }=A{K}_0.\hfill \end{array}\right\}(18)$

3 Solution approach

The resulting ODEs were highly non-linear; therefore, to obtain a numerical solution, we used a semi-analytical scheme, namely the HAM in Wolfram Mathematica. The advantages of this technique include its utility if the equations under consideration include any large or small parameters. Furthermore, it can be applied to achieve a non-linear approximate problem by selecting distinct sets of base functions. The detail of this technique can be seen in [30]. Eqs 13–15 for the flow, temperature, and concentration fields are solved analytically by implementing the principles of homotopy. In this technique, the corresponding auxiliary linear operators $\left({\mathcal{L}}_{\tilde{f}},{\mathcal{L}}_{\theta },{\mathcal{L}}_{\varphi }\right)$ and initial guesses $\left({\tilde{f}}_0,{\theta }_0,{\varphi }_0\right)$ are selected to obtain a convergent series solution. Thus, the non-linear problem is converted into an infinite series of linear ones. The selected linear operators with initial guesses for this problem are:

${\tilde{f}}_0\left(\eta \right)=1-e^{-\eta },{\theta }_0\left(\eta \right)=e^{-\eta },{\varphi }_0\left(\eta \right)=e^{-\eta },(19)$

${\mathcal{L}}_{\tilde{f}}\left[\tilde{f}\left(\eta \right)\right]={\tilde{f}}^{\prime \prime \prime }-{\tilde{f}}^{\prime },{\mathcal{L}}_{\theta }\left[\theta \left(\eta \right)\right]={\theta }^{\prime \prime }-\theta ,{\mathcal{L}}_{\varphi }\left[\varphi \left(\eta \right)\right]={\varphi }^{\prime \prime }-\varphi .(20)$

4 Solution convergence

The parameters ℏ_f, ℏ_θ, and ℏ_ϕ for the velocity field, temperature, and concentration distribution, respectively, ensure the convergence of the homotopic series solutions. The values of these parameters are found by applying the following least-square error formula:

$F_{f,m}=\frac{1}{N+1}\sum _{j=0}^N{\left[N_f\sum _{i=0}^m{F}_j\left(i\mathrm{\Delta }\eta \right)\right]}^2.(21)$

The velocity, temperature, and concentration field solutions converge at the sixth order of estimate.

5 Discussion of results

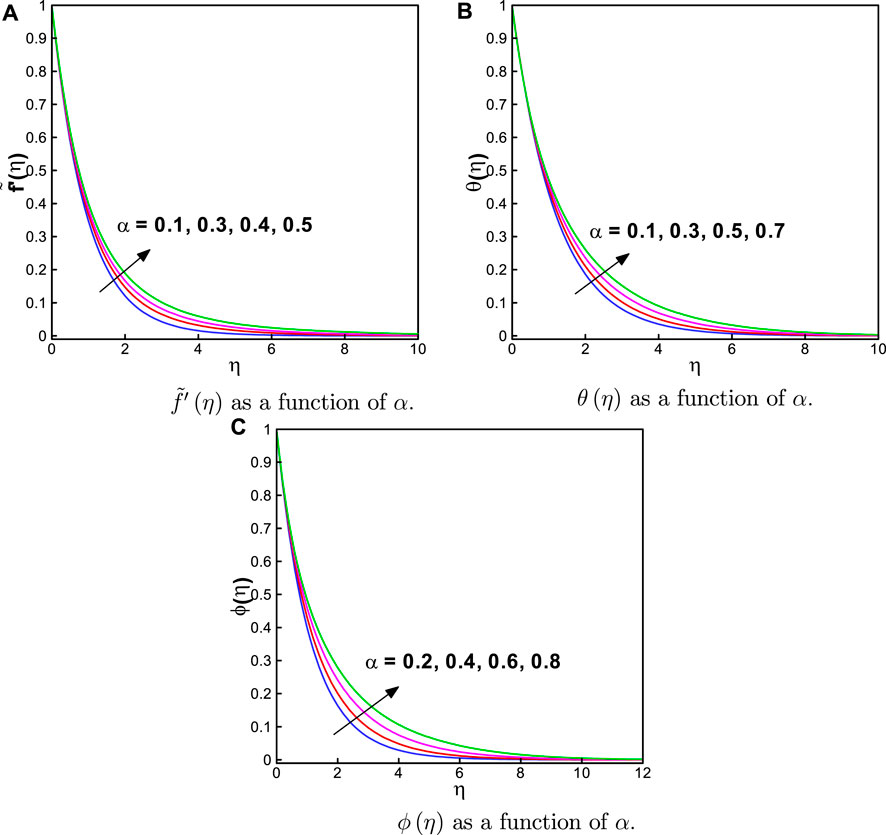
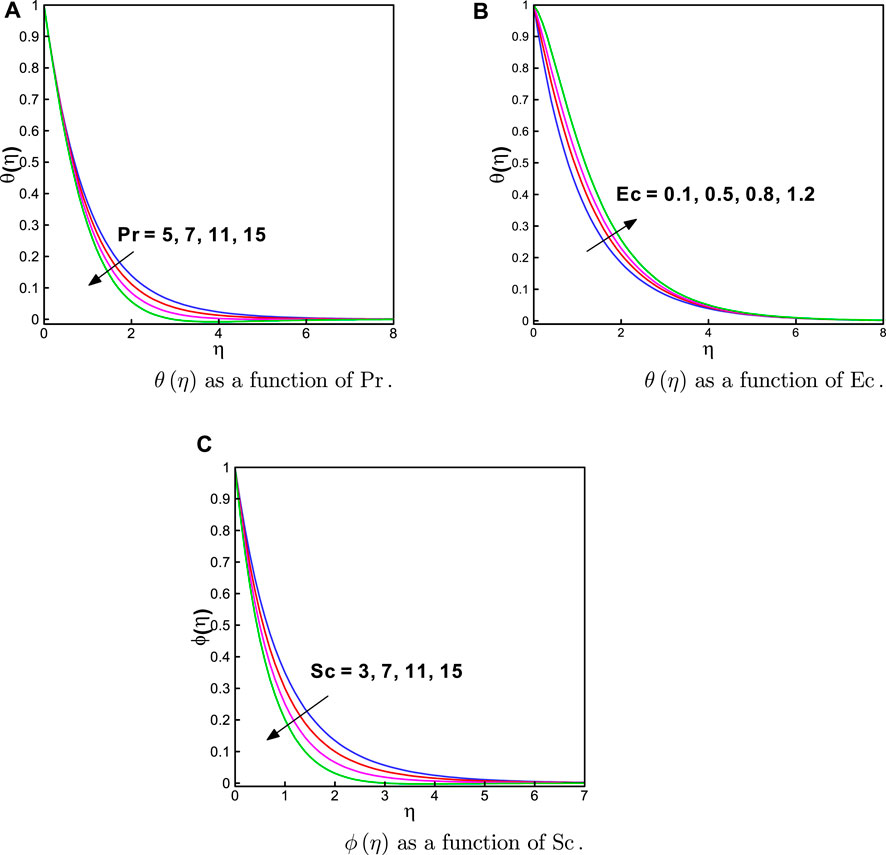
This section discusses the impact of the factors affecting the flow, thermal, and mass transportation. The behavior of the Maxwell parameter β₁, the curvature parameter α, the magnetic field parameter M, the thermophoresis parameter N_t, the Brownian parameter N_b, the heat source/sink parameter Q*, the thermal relaxation time parameter β_t, the solutal relaxation time parameter β_c, the Prandtl number Pr, the Eckert number Ec, and the Schmidt number Sc are scrutinized for the velocity ${\tilde{f}}^{\prime }\left(\eta \right)$, temperature $\theta \left(\eta \right)$ and concentration $\varphi \left(\eta \right)$ fields.

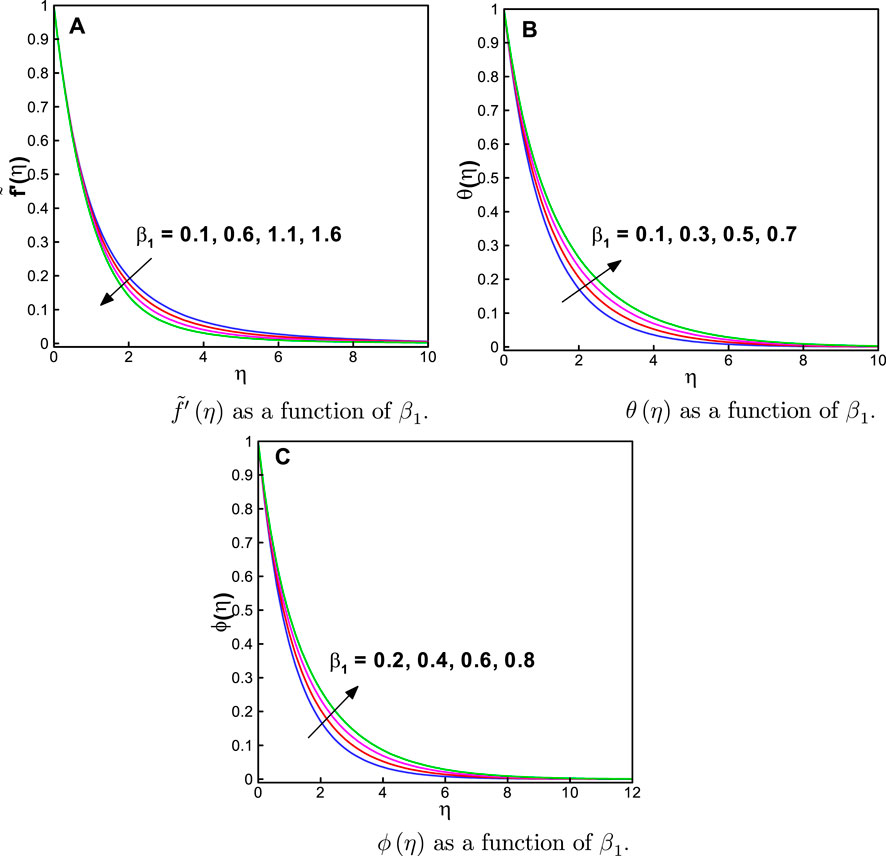
Since the behaviors of fluid motion, thermal, and mass distributions are dependent on η (on the x-axis), fluid is closer to the boundary, i.e., at η = 0; thus, we noted the maximum values of velocity, temperature, and concentration profiles, as shown in the graphs. Physically, the stretching effect is most prominent for fluid near the boundary; however, as the value of η increases, the stretching effect starts to decrease. This behavior is strictly/continuously decreasing and can be defined as a monotonic decreasing behavior. Furthermore, the motion near the surface is signified when a graph converges more easily. To achieve a better solution convergence, we fixed the values of the relevant parameters, as follows: β₁ = α = 0.8, M = 1.0, N_t = 0.4, N_b = 0.1, Q* = K* = 0.6, and β_t = β_c = 0.5.

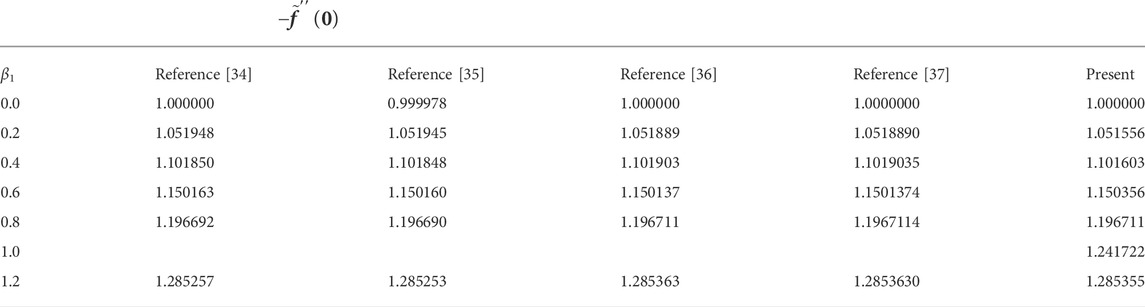
Tables 1 and 2 compare our findings to those reported previously. The numerical outcomes attained here are in best agreement with these studies. Table 3 shows that the values of the skin friction coefficient along the radial direction $-{\tilde{f}}^{\prime \prime }\left(0\right)$ increased for β₁ ≥ 0. Table 1 shows that by incrementing the values of the magnetic parameter M ≥ 0, the coefficient of skin friction $-{\tilde{f}}^{\prime \prime }\left(0\right)$ also increased.

TABLE 1

TABLE 1. Comparison values of$-{\tilde{f}}^{\prime \prime }\left(0\right)$ for β₁ ≥ 0 when α = M = 0.

TABLE 2

TABLE 2. Comparison values of $-{\tilde{f}}^{\prime \prime }\left(0\right)$ for M ≥ 0 when α = β₁ = 0.

TABLE 3

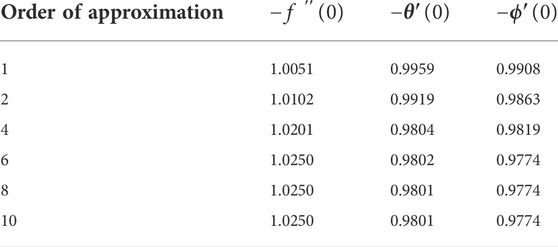
TABLE 3. Convergence of homotopic solutions for fixed β₁ = N_b = N_t = Le = M = S = 0.1, β_t = β_c = 0.5, and Pr = 2.0.

Figures 2A–C illustrate the influence of the Maxwell parameter β₁ on ${\tilde{f}}^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$. Figure 2A shows that by increasing the value of β₁ from 0.1, 0.6, 1.1, to 1.6, the velocity field decreases because β₁ causes friction against the flow field. However, the opposite behavior is shown for thermal and mass transport in Figures 2B,C. The energy of the system increases with increasing Maxwell parameter values. Physically, β₁ corresponds to the deformation of viscoelastic fluids. The stress relaxation phenomenon increases with increased β₁values, which hardens the material under observation; i.e., it behaves as solid, with the distance between fluid particles decreasing. This requires more time to sustain deformation and lowers the velocity profile. Furthermore, the thermal conductivity of the fluid improves simultaneously, which eventually boosts the heat and mass transport phenomenon. Figures 3A–C show the influence of the curvature parameter α on ${\tilde{f}}^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$. The graphs demonstrate the increased flow field and energy of the system due to increased α values; i.e., their behavior varies linearly for α. The radius of curvature reduces, which decreases the surface-liquid interface constituency and boosts the velocity profile. The root cause of this behavior is an increment in the collision rate among the particles, which decays the heat transfer rate and raises the temperature and concentration distribution as illustrated in Figures 3A–C. In Figures 4A–C influence of magnetic parameter M is seen on ${\tilde{f}}^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$. The higher values of M strengthen the Lorentz/electromagnetic force due to the external magnetic field, which produces resistance against the fluid flow. Thus, the velocity field decreases with increasing M value from 1.0 to 3.0, 5.0, and 7.0. However, this force induces more collisions among the fluid particles, which significantly increases the temperature and mass distribution. This effect is shiwn in Figures 4B,C.

FIGURE 2

FIGURE 2. (A) ${\tilde{f}}^{\prime }\left(\eta \right)$ as a function of β₁. (B) $\theta \left(\eta \right)$ as a function of β₁. (C) $\varphi \left(\eta \right)$ as a function of β₁.

FIGURE 3

FIGURE 3. (A) ${\tilde{f}}^{\prime }\left(\eta \right)$ as a function of α. (B) $\theta \left(\eta \right)$ as a function of α. (C) $\varphi \left(\eta \right)$ as a function of α.

FIGURE 4

FIGURE 4. (A) ${\tilde{f}}^{\prime }\left(\eta \right)$ as a function of M. (B) $\theta \left(\eta \right)$ as a function of M. (C) $\varphi \left(\eta \right)$ as a function of M.

Figures 5A,B illustrate the effect of the thermal relaxation time parameter β_t and the solutal relaxation time parameter β_c on $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$, respectively. The thermal and concentration fields are compressed by magnifying the thermal and the solutal relaxation time parameters. In a physical sense, the particles require additional time to conduct heat towards the adjacent particles, which results in a deterioration of the fluid temperature. However, due to an accretion of β_c, particles require extra time to diffuse mass, resulting in a reduced concentration distribution. Figures 5C,D show the consequences of the heat source/sink parameter Q* and the chemical reaction parameter K* on $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$, respectively. The mass distribution decreases with increasing chemical reaction rate K*, as illustrated in Figure 5D. The species transfer in chemical reactions results in a decreased mass distribution. However, Figure 5C shows the increased energy of the system due to the random motion of the particles, which ultimately increases the fluid temperature for Q* > 0. Figures 6A–D highlight the significance of the thermophoresis parameter N_t and the Brownian diffusion parameter N_b on $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$. The effects of N_b on the thermal and mass transport are shown in Figures 6C,D, respectively. Due to Brownian motion, the particles exhibit erratic movements, which magnifies their rapidity and, hence, increases the average kinetic energy of the system. This immediate boost in kinetic energy provokes more tumultuous collisions among particles by directly increasing the temperature field; however, the concentration distribution decreases, as shown in Figure 6D. However, as demonstrated in Figure 6B, the rate of mass transport is amplified and drives the particles to relocate into areas of low concentration by inducing the thermophoresis phenomenon. The massive particles quickly experience the positive Soret effect, in which they proceed from warmer to lower temperature zones. These effects lead to increased fluid temperature and concentration fields, as shown in Figures 6A,C. In Figures 7A,B the effect of Prandtl number Pr and Eckert number Ec is determined on $\theta \left(\eta \right)$. The thermal diffusivity of the fluid decreases due to increased Pr as Pr enhances the specific heat capacity of the liquid, whereas heat transmission delays fluid flow. Thus, the heat transfer rate and temperature field decrease. Figure 7B shows the dissipation of energy due to increased Ec values owing to the stretching of the sheet, which causes changes in thermal transportation, for Ec = 0.1, 0.5, 0.8, 1.2. Physically, fluid friction is generated due to increased Ec values, which causes the transformation of mechanical energy into heat energy. Therefore, $\theta \left(\eta \right)$ rises. Figure 7C illustrates the impact of Schmidt number Sc on $\varphi \left(\eta \right)$. Since Sc corresponds to the momentum and mass diffusivity, with increases in the diffusion ratio to 3, 7, 11, and 15, the momentum diffusion predominates over the mass diffusion. Thus, the mass transport decreases.

FIGURE 5

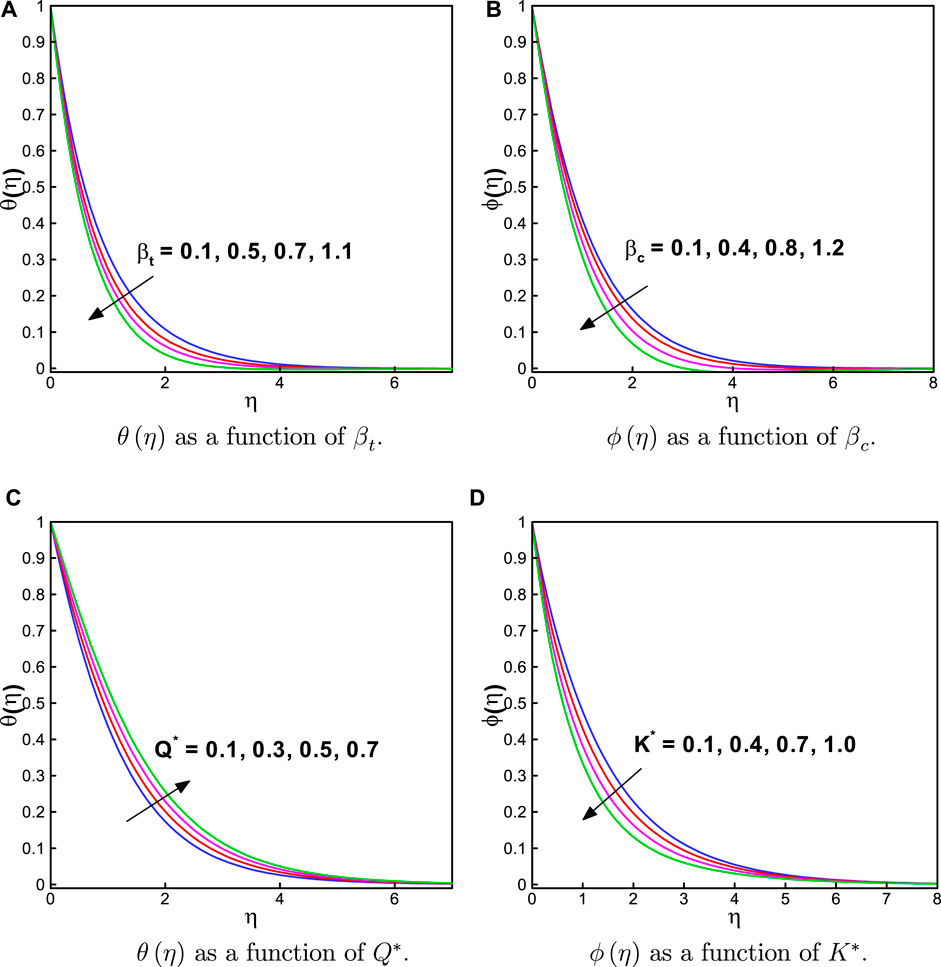
FIGURE 5. (A) $\theta \left(\eta \right)$ as a function of β_t. (B) $\varphi \left(\eta \right)$ as a function of β_c. (C) $\theta \left(\eta \right)$ as a function of Q*. (D) $\varphi \left(\eta \right)$ as a function of K*.

FIGURE 6

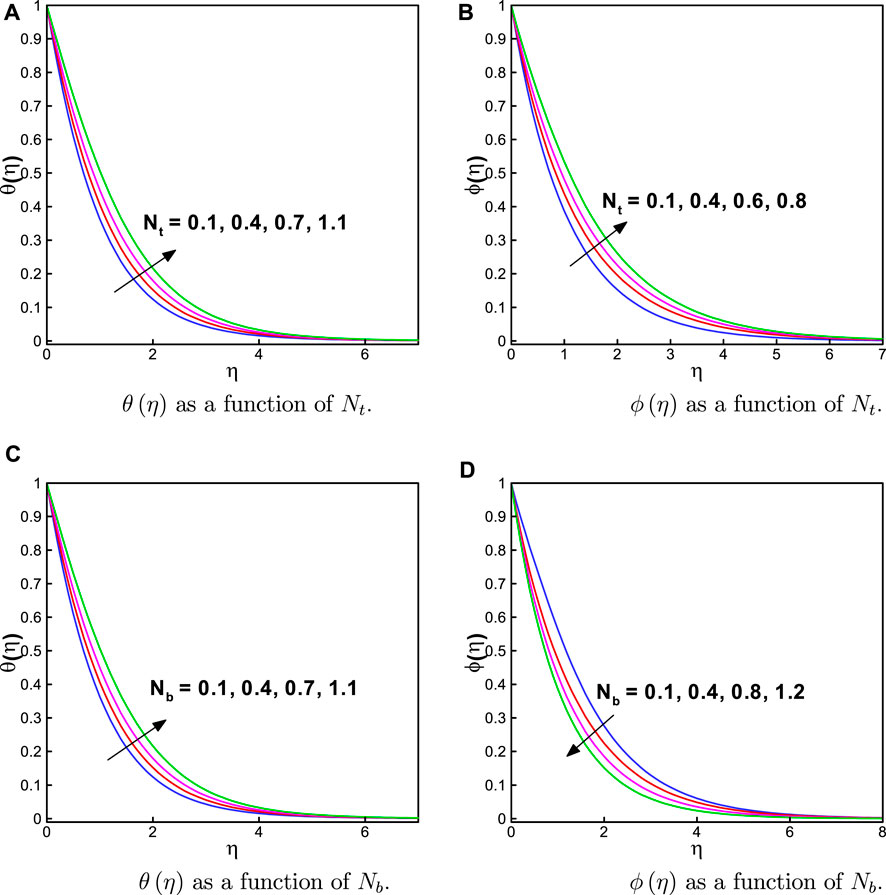
FIGURE 6. (A) $\theta \left(\eta \right)$ as a function of N_t. (B) $\varphi \left(\eta \right)$ as a function of N_t. (C) $\theta \left(\eta \right)$ as a function of N_b. (D) $\varphi \left(\eta \right)$ as a function of N_b.

FIGURE 7

FIGURE 7. (A) $\theta \left(\eta \right)$ as a function of Pr. (B) $\theta \left(\eta \right)$ as a function of Ec. (C) $\varphi \left(\eta \right)$ as a function of Sc.

6 Conclusion

This study assessed 2D Maxwell nanofluid flow over a stretched cylinder along the z-direction with the thermal and solutal transportation in flow induced by Cattaneo-Christov diffusion. The effects of the chemical reaction, heat generation source/sink, and Joule heating were also considered in the heat and mass transport analysis. A semi-analytical method, the homotopy analysis method (HAM) in Wolfram Mathematica, was used to compute the convergent series solution. The main outcomes were:

• The coefficient of skin friction along the radial direction $-{\tilde{f}}^{\prime \prime }\left(0\right)$ was enhanced for non-negative values of Maxwell and magnetic parameters.

• The Maxwell parameter decreased the behavior of the flow field. However, improving the thermal conductivity strengthened the temperature and concentration profiles.

• The Lorentz force induced by the magnetic field produced resistance and reduced the flow field; however, the thermal and mass transport increased due to the Joule heating effect.

• Due to Brownian motion and thermophoresis, the thermal transport escalated. However, the concentration field was decayed by the former and augmented by the latter.

• The temperature distribution increased due to the effects of the heat source/sink. However, the chemical reaction rate reduced the concentration profile.

• The thermal and mass relaxation parameters reduced the heat and mass transfer rates, respectively.

• The fluid friction generated as a result of Ec converted the mechanical energy into thermal energy, which increased the temperature field.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author contributions

AA: modeled the problem and solved the governing equation. MS: discussed the outcomes of the problem. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through the Research Group Program (grant no. RGP.2/12/43).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Maxwell JC. A treatise on electricity and magnetism, (Vol. 1). Clarendon Press (1881).

Google Scholar

2. Mukhopadhyay S. Heat transfer analysis of the unsteady flow of a Maxwell fluid over a stretching surface in the presence of a heat source/sink. Chin Phys Lett (2012) 29:054703. doi:10.1088/0256-307x/29/5/054703

CrossRef Full Text | Google Scholar

3. Yang X, Lu T, Kim T. Thermal stretching in two-phase porous media: Physical basis for Maxwell model. Theor Appl Mech Lett (2013) 3:021011. doi:10.1063/2.1302111

CrossRef Full Text | Google Scholar

4. Ahmad M, Ahmad I, Sajid M. Magnetohydrodynamic time-dependent three-dimensional flow of Maxwell fluid over a stretching surface through porous space with variable thermal conditions. J Braz Soc Mech Sci Eng (2016) 38:1767–78. doi:10.1007/s40430-016-0501-2

CrossRef Full Text | Google Scholar

5. Ramzan M, Bilal M, Chung JD, Farooq U. Mixed convective flow of Maxwell nanofluid past a porous vertical stretched surface–An optimal solution. Results Phys (2016) 6:1072–9. doi:10.1016/j.rinp.2016.11.036

CrossRef Full Text | Google Scholar

6. Hsiao KL. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl Therm Eng (2017) 112:1281–8. doi:10.1016/j.applthermaleng.2016.08.208

CrossRef Full Text | Google Scholar

7. Madhu M, Kishan N, Chamkha AJ. Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propulsion Power Res (2017) 6:31–40. doi:10.1016/j.jppr.2017.01.002

CrossRef Full Text | Google Scholar

8. Irfan M, Khan M, Khan WA, Ayaz M. Modern development on the features of magnetic field and heat sink/source in Maxwell nanofluid subject to convective heat transport. Phys Lett A (2018) 382:1992–2002. doi:10.1016/j.physleta.2018.05.008

CrossRef Full Text | Google Scholar

9. Aziz A, Shams M. Entropy generation in MHD Maxwell nanofluid flow with variable thermal conductivity, thermal radiation, slip conditions, and heat source. AIP Adv (2020) 10:015038. doi:10.1063/1.5129569

CrossRef Full Text | Google Scholar

10. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. In: 1995 International mechanical engineering congress and exhibition. San Francisco, CA (United States): Argonne National Lab (1995). p. 99–105.

Google Scholar

11. Buongiorno J. Convective transport in nanofluids. J Heat Transfer (2006) 128:240–50. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

12. Cattaneo C. Sulla conduzione del calore. Atti Sem Mat Fis Univ Modena (1948) 3:83–101.

Google Scholar

13. Christov CI. On frame indifferent formulation of the Maxwell-Cattaneo model of finite speed heat conduction. Mech Res Commun (2009) 36:481–6. doi:10.1016/j.mechrescom.2008.11.003

CrossRef Full Text | Google Scholar

14. Han S, Zheng L, Li C, Zhang X. Coupled flow and heat transfer in viscoelastic fluid with Cattaneo-Christov heat flux model. Appl Math Lett (2014) 38:87–93. doi:10.1016/j.aml.2014.07.013

CrossRef Full Text | Google Scholar

15. Mustafa M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Adv (2015) 5:047109. doi:10.1063/1.4917306

CrossRef Full Text | Google Scholar

16. Li J, Zheng L, Liu L. MHD viscoelastic flow and heat transfer over a vertical stretching sheet with Cattaneo-Christov heat flux effects. J Mol Liq (2016) 221:19–25. doi:10.1016/j.molliq.2016.05.051

CrossRef Full Text | Google Scholar

17. Khan M. On Cattaneo-Christov heat flux model for Carreau fluid flow over a slendering sheet. Results Phys (2017) 7:310–9. doi:10.1016/j.rinp.2016.12.031

CrossRef Full Text | Google Scholar

18. Acharya N, Das K, Kundu PK. Cattaneo-christov intensity of magnetised upper-convected Maxwell nanofluid flow over an inclined stretching sheet: A generalised fourier and Fick’s perspective. Int J Mech Sci (2017) 130:167–73. doi:10.1016/j.ijmecsci.2017.05.043

CrossRef Full Text | Google Scholar

19. Loganathan K, Alessa N, Kayikci S. Heat transfer analysis of 3-D viscoelastic nanofluid flow over a convectively heated porous riga plate with cattaneo-christov double flux. Front Phys (2021) 379:1. doi:10.3389/fphy.2021.641645

CrossRef Full Text | Google Scholar

20. Loganathan K, Alessa N, NamgyelKarthik NTS. MHD flow of thermally radiative Maxwell fluid past a heated stretching sheet with Cattaneo–Christov dual diffusion. J Math (2021) 2021:1–10. doi:10.1155/2021/5562667

CrossRef Full Text | Google Scholar

21. Loganathan K, Mohana K, Mohanraj M, Sakthivel P, Rajan S. Impact of third-grade nanofluid flow across a convective surface in the presence of inclined Lorentz force: An approach to entropy optimization. J Therm Anal Calorim (2021) 144(5):1935–47. doi:10.1007/s10973-020-09751-3

CrossRef Full Text | Google Scholar

22. Venkata Ramana K, Gangadhar K, Kannan T, Chamkha AJ. Cattaneo–Christov heat flux theory on transverse MHD Oldroyd-B liquid over nonlinear stretched flow. J Therm Anal Calorim (2022) 147(3):2749–59. doi:10.1007/s10973-021-10568-x

CrossRef Full Text | Google Scholar

23. Gangadhar K, Kumari MA, Chamkha AJ. EMHD flow of radiative second-grade nanofluid over a Riga Plate due to convective heating: Revised Buongiorno’s nanofluid model. Arab J Sci Eng (2022) 47(7):8093–103. doi:10.1007/s13369-021-06092-7

CrossRef Full Text | Google Scholar

24. Gangadhar K, Kumari MA, Subba Rao MV, Alnefaie K, Khan I, Andualem M. Magnetization for burgers’ fluid subject to convective heating and heterogeneous-homogeneous reactions. Math Probl Eng (2022) 2022:1–15. doi:10.1155/2022/2747676

CrossRef Full Text | Google Scholar

25. Turkyilmazoglu M. Heat transfer enhancement feature of the Non-Fourier Cattaneo–Christov heat flux model. J Heat Transfer (2021) 143(9):1. doi:10.1115/1.4051671

CrossRef Full Text | Google Scholar

26. Turkyilmazoglu M. Flow and heat over a rotating disk subject to a uniform horizontal magnetic field. Z für Naturforschung A (2022) 77(4):329–37. doi:10.1515/zna-2021-0350

CrossRef Full Text | Google Scholar

27. Turkyilmazoglu M. Exact solutions concerning momentum and thermal fields induced by a long circular cylinder. Eur Phys J Plus (2021) 136(5):483–10. doi:10.1140/epjp/s13360-021-01500-1

CrossRef Full Text | Google Scholar

28. Yaseen M, Rawat SK, Kumar M. Hybrid nanofluid (MoS2–SiO2/water) flow with viscous dissipation and Ohmic heating on an irregular variably thick convex/concave-shaped sheet in a porous medium. Heat Trans (2022) 51(1):789–817. doi:10.1002/htj.22330

CrossRef Full Text | Google Scholar

29. Yaseen M, Kumar M, Rawat SK. Assisting and opposing flow of a MHD hybrid nanofluid flow past a permeable moving surface with heat source/sink and thermal radiation. Partial Differ Equ Appl Math (2021) 4:100168. doi:10.1016/j.padiff.2021.100168

CrossRef Full Text | Google Scholar

30. Gumber P, Yaseen M, Rawat SK, Kumar M. Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. Partial Differ Equ Appl Math (2022) 5:100240. doi:10.1016/j.padiff.2021.100240

CrossRef Full Text | Google Scholar

31. Yaseen M, Rawat SK, Kumar M. Cattaneo–Christov heat flux model in Darcy–Forchheimer radiative flow of MoS2–SiO2/kerosene oil between two parallel rotating disks. J Therm Anal Calori (2022) 6:1–23.

Google Scholar

32. Iqbal MS, Ghaffari A, Riaz A, Mustafa I, Raza M. Nanofluid transport through a complex wavy geometry with magnetic and permeability effects. Inventions (2021) 7(1):7. doi:10.3390/inventions7010007

CrossRef Full Text | Google Scholar

33. Abdelmalek Z, Khan SU, Waqas H, Riaz A, Khan IA, Tlili I. A mathematical model for bioconvection flow of Williamson nanofluid over a stretching cylinder featuring variable thermal conductivity, activation energy and second-order slip. J Therm Anal Calorim (2021) 144(1):205–17. doi:10.1007/s10973-020-09450-z

CrossRef Full Text | Google Scholar

34. Abel MS, Tawade JV, Nandeppanavar MM. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica (2012) 47:385–93. doi:10.1007/s11012-011-9448-7

CrossRef Full Text | Google Scholar

35. Megahed AM. Variable fluid properties and variable heat flux effects on the flow and heat transfer in a non-Newtonian Maxwell fluid over an unsteady stretching sheet with slip velocity. Chin Phys B (2013) 2013:094701. doi:10.1088/1674-1056/22/9/094701

CrossRef Full Text | Google Scholar

36. Waqas M, Khan MI, Hayat T, Alsaedi A. Stratified flow of an Oldroyd-B nanofluid with heat generation. Results Phys (2017) 7:2489–96.

CrossRef Full Text | Google Scholar

37. Irfan M, Khan M, Khan WA. Impact of homogeneous–heterogeneous reactions and non-Fourier heat flux theory in Oldroyd-B fluid with variable conductivity. J Braz Soc Mech Sci Eng (2019) 41:135. doi:10.1007/s40430-019-1619-9

CrossRef Full Text | Google Scholar

38. Fang T, Zhang J, Yao S. Slip MHD viscous flow over a stretching sheet – an exact solution. Commun Nonlinear Sci Numer Simul (2009) 14:3731–7. doi:10.1016/j.cnsns.2009.02.012

CrossRef Full Text | Google Scholar

39. Fathizadeh M, Madani M, Khan Y, Faraz N, Yıldırım A, Tutkun S. An effective modification of the homotopy perturbation method for MHD viscous flow over a stretching sheet. J King Saud Univ - Sci (2013) 25:107–13. doi:10.1016/j.jksus.2011.08.003

CrossRef Full Text | Google Scholar

40. Hayat T, Shafiq A, Alsaedi A. MHD axisymmetric flow of third grade fluid by a stretching cylinder. Alexandria Eng J (2015) 54:205–12. doi:10.1016/j.aej.2015.03.013

CrossRef Full Text | Google Scholar

41. Ahmed A, Khan M, Irfan M, Ahmed J. Transient MHD flow of Maxwell nanofluid subject to nonlinear thermal radiation and convective heat transport. Appl Nanoscience (2020) 10:5361–73. doi:10.1007/s13204-020-01375-1

CrossRef Full Text | Google Scholar