PA_CasualLSTM: A new time series prediction network with the physical constraint and adjusted Fourier neural operator for the time-dependent partial differential equation

In this work, a new time series prediction network is proposed in the framework of CasualLSTM with physical constraints and an adjusted Fourier neural operator (FNO) for the solution of the time-dependent partial differential equation. The framework of CasualLSTM is employed to learn the time evolution of spatial features which strengthens the extrapolation capability. With the help of adjusted Fourier layers (AFLs), residual connection, and the adaptive time-marching strategy, the network can quickly converge and extrapolate without labeled data by encoding PDE constraints into loss functions. Two examples, namely, Burger’s equation and two-dimensional Navier–Stokes (N-S) equation are used to evaluate the proposed method. Numerical results show that the proposed method has a good performance in solution accuracy and extrapolability.

1 Introduction

In most complex spatiotemporal systems, a partial differential equation is indispensable as a means of simulating systems and explaining corresponding phenomena. Many physical phenomena and engineering technologies (such as convection and diffusion, fluid motion, and communication technology) are modeled and analyzed using a partial differential equation, but the analytical solutions of these governing equations are mostly unavailable. The numerical solution of the partial differential equation is the core foundation of scientific computing. In recent decades, the explosive development of computing power has provided the basis for traditional numerical methods (such as finite difference method, finite element method, and finite volume method [1,2]) to solve the partial differential equation. Although the traditional numerical methods have achieved very high accuracy in forward analysis, it is still a challenge to balance computational cost and solution accuracy in most real application scenarios and the requirements of arbitrary resolution. Therefore, it is a direction to achieve an ideal balance between computational efficiency and prediction accuracy. Also, in many cases, there are modeling errors when using the partial differential equation to model the system, so there will be irreconcilable errors between the numerical solution of the partial differential equation and the real phenomenon.

Furthermore, researchers attempt to model nonlinear systems by other approaches, which are divided into forward and inverse problems. Hornik et al. [3] proposed the universal approximation theorem and theoretically proved that deep neural networks can simulate arbitrarily complex functions. At the same time, due to the rapid development of backpropagation algorithms and GPU-based computing systems, deep learning can avoid repeated modeling in forward analysis and provide a new research direction for data assimilation and inverse problem-solving. As a mathematical method for modeling nonlinear systems, the partial differential equation has always been a concern of researchers in deep learning. In fact, in the last century, Lagaris [4,5] used artificial neural networks to solve the initial and boundary condition problems of the partial differential equation. The pioneering work of using a neural network as an approximator to solve the equation is proposed. The network consists of two parts, one for satisfying the initial and boundary conditions and the other for meeting the equation with a feed-forward neural network with tunable parameters. In the past decade, with the breakthrough development of machine learning and deep learning, the application of deep learning models in many fields has achieved widespread success, such as image recognition [6], natural language processing [7], and fault detection [8]. Therefore, many researchers once again introduced deep learning into the solution of partial differential equations and achieved a series of developments [9–16]. Similar to the modeling of nonlinear systems, the latest research is divided into two directions: forward-solving partial differential equation and data-driven discovery of the partial differential equation. The most representative work is the physical information neural network (PINN), a fully connected neural network proposed by Raissi et al. [13], which takes into account the solution of the aforementioned problems. The innovative work of the network is to integrate the PDE residual into the loss function, which only requires the labeled data about the initial value and boundary conditions [17,18] or no labeled data [19–21] during the training process. PINN achieves good results in PDE and has a wide range of applications in other disciplines, including temperature modeling [22,23], traffic flow evaluation [24], and partial differential equation mining [25,26]. Despite the great success and wide application, there are still some problems in the application of the deep leaning method in the solution of PDE. 1) PDE residual as a physical soft constraint is limited by the application environment [27,28]. 2) Compared with traditional numerical solvers, it is difficult to extrapolate information to future times only from initial values or boundary conditions [29,30]. Therefore, in many cases, PINN is still not comparable to traditional numerical solvers.

For the time-dependent partial differential equation, some studies treat it as a problem of time series prediction [31–35]. As with the traditional solution method, discrete integration is performed in the time domain to solve the extrapolation problems. These methods can achieve a good extrapolation effect and high solution accuracy. However, there are still some challenges: as the resolution increases, the required computational time increases dramatically. Limited by mesh and different filters, the network is not as flexible as the pseudo-spectral method for solving PDE using the inverse Laplace transform.

Recently, neural operators are not negligible for solving PDE, that is, the neural network is used to find the mapping relationship between input and output in a finite dimension. The method improves the computational efficiency and suits the PDE models by replacing the traditional neural network [36–42]. The biggest advantage of this network is its high computational efficiency and great success in highly nonlinear problems [43]. The Fourier operator proposed by Li et al. [38] trains the network parameters in the Fourier space, which makes the solution of partial differential equations more efficient. The spatial resolution is not affected by the size of the grid spacing, and the calculation speed becomes fast. However, there are still challenges in two aspects: 1) label data are still needed during training, which are obtained through traditional solvers or empirical data; 2) information cannot be extrapolated accurately to future time periods.

In order to address the challenges of the aforementioned networks, we propose a new time series prediction network with physical constraints and an adjusted Fourier neural operator (PA_CasualLSTM) which quickly solves time-dependent PDE using only the initial and boundary conditions. In this work, the network combines the soft constraints of PDE residuals, the adjusted Fourier layers, and the adaptive time-marching strategy to optimize the extrapolation solution accuracy. We do not intend to replace the traditional numerical solver with PA_CasualLSTM, but it provides new ideas for the solution of PDE and possibly a new research method for subsequent data assimilation and inverse problems. Our contributions can be summarized as follows:

1) We propose a new time series prediction network with physical constraints and an adjusted Fourier neural operator (PA_CasualLSTM), which combines physical information as a soft constraint, the adjusted neural operator as a spatial derivative optimizer, and the global residual connection.

2) By using the CasualLSTM module to learn the time evolution of spatial features, PA_CasualLSTM alleviates the issue of low extrapolation accuracy in PINN and neural operators.

3) Compared with other neural operator networks, PA_CasualLSTM with the PDE constraints does not require any label data in the training process. Starting from the initial conditions, the proposed method trains the network with physical information as a loss function.

The remainder of the article is structured as follows: Section 2 states the PDE system and introduces the idea of a deep learning solution, while Section 3 provides the construction and implementation of the PA_CasualLSTM. In Section 4, the performance of PA_CasualLSTM, especially the extrapolation ability for solving PDE is verified by Burger’s equation and the two-dimensional incompressible Navier–Stokes equation. Section 5 discusses the network and the prospect of future works. Finally, a conclusion is presented.

2 Problem setting

Here, we consider the general form of a multidimensional, nonlinear, time-dependent parametric PDE:

$u_t+\text{R}\left[u,\nabla u,∆u,u\nabla u,\dots ;\lambda \right]=0,inD\times \left[0,T\right],$

$\mathit{u}={\mathit{u}}_{\mathit{b}},\mathit{i}\mathit{n}\partial \mathit{D}\times \left[\mathbf{0},\mathit{T}\right],(1)$

$u=u_0,inD\times \left\{0\right\},$

where $u\left(x,t\right)$ denotes the solution in the space interval $D$ and the time area $t\in \left[0,\mathrm{T}\right]$. $\mathcal{R}$ stands for a nonlinear spatial operator with parameter λ. $u_0$ and $u_b$ are the initial and boundary conditions, respectively, where $\partial D$ represents the boundary of the spatial region.

In this article, we set up a neural network for Eq. 1 to solve time-dependent PDE. More accurately, a neural network is used to fit the nonlinear spatial operator $\mathcal{R}$. The entire training only needs the initial conditions, and Eq. 1 is used as a constraint to design the loss function without label data.

First, after discretizing the PDE in space and time, the network pre-trains the initial state to achieve the solution at the first K moments. Then, the pre-trained results are fed into the next PA_CasualLSTM cell to fit the spatial derivatives with the adjusted Fourier layer and learn the spatiotemporal evolution with residual connections and CasualLSTM. In this article, we focus on the regular physical space region and the periodic boundary. In the network implementation, these constraints are encoded into the loss function like PINN. Finally, $u\left(x,t;\theta \right)$ is obtained by minimizing the loss function for satisfying the PDE constraints. The specific network construction and training skills are described in Section 3.

3 Methodology

This section introduces an operator-based time series prediction network to solve time-dependent PDE. The network focuses on learning nonlinear spatial operators and propagating information. Regarding the application of neural networks for information propagation, Geneva and Zabaras [32] elaborated on recurrent neural networks and proved that they have powerful capabilities for time series prediction. We first introduce a time series prediction network CasualLSTM.

3.1 CasualLSTM

CasualLSTM proposed by Wang et al. [44] is a spatiotemporal recurrent neural network framework and one of the variants of the long short-term memory neural (LSTM [45]) network, which has certain advantages in modeling PDE systems evolving over time [31]. As a spatiotemporal memory unit, it is the greatest innovation that nonlinear operations have been added in CasualLSTM, which enlarges the spatial features. It is more conducive to capturing short-term dynamic changes and updating them in time during temporal evolution. At the same time, as a spatiotemporal sequence-to-sequence learning framework, CasualLSTM alleviates the vanishing gradient problem in RNN with the help of the characteristics of LSTM. In addition, inheriting the basic framework of LSTM, CasualLSTM adds the nonlinear layer to realize the cascade, which strengthens the network depth and improves the mutation prediction ability in the short term compared with LSTM. For more detailed work on CasualLSTM, refer to the work [44].

3.2 The adjusted Fourier layers

The neural operator is proposed by Li et al. [37] to find the mapping relationship between input and output after neural network training. In other words, the neural operator is used as an iterative format to calculate z₀$\Rightarrow$z₁$\Rightarrow$z₂ … $\Rightarrow$z_T, and its specific expression is defined as Eq 2.1, where z_i (i = 0, 1, … , T) is a series of functions obtained through a fully connected network (FCN) and takes the following form Eq. 2.2:

$z_{t+1}\left(x\right)≔\sigma \left(W{z}_t\left(x\right)+\left(K_{\theta }{z}_t\right)\left(x\right)\right),\forall x\in D,$(2.1)

$z_t\left(x\right)=P\left(u_t;x_{1,}{x}_{2,}{x}_{3,}\dots ,x_n\right)\forall x_{1\sim n}\in D,$(2.2)

where $\sigma \left(\cdot \right)$ represents the nonlinear activation function, $W\left(\cdot \right)$ is a linear transformation, $x_{1\sim n}$ is the location point in the spatial region $D$, and $n$ represents the number of spatial dimensions. $K_{\theta }$ is a linear operator represented by a neural network with the parameter $\theta$. $P\left(\cdot \right)$ is a fully connected network, and $u_t$ is the solution at time $t$. From Eq. 2.2, $z_t\left(x\right)$ is related to the position $x$.

While applying $\left(K_{\theta }{z}_t\right)\left(x\right)$ and the convolution theorem to the Fourier space, the Fourier neural operator (FNO) [38] is formed, which is used for the solution of PDE and other fields, such as weather forecast [46] and numerical simulation [47]. Li et al. defined it as the Fourier integral operator Eq. 3.1, and the Fourier layer is expressed as Eq. 3.2:

$\left(K_{\theta }{z}_t\right)\left(x\right)={\mathcal{F}}^{-1}\left(R_{\theta }\cdot \left(\mathcal{F}{z}_t\right)\left(x\right)\right),\forall x\in D,$(3.1)

$z_{t+1}\left(x\right)≔\sigma \left(W{z}_t\left(x\right)+{\mathcal{F}}^{-1}\left(R_{\theta }\cdot \left(\mathcal{F}{z}_t\right)\left(x\right)\right)\right),\forall x\in D,$(3.2)

where $\mathcal{F}\left(\cdot \right)$ is the discrete Fourier transform (DFT) and ${\mathcal{F}}^{-1}$ is the inverse Fourier transform (IDFT). $R_{\theta }$ represents the Fourier transform of a periodic function. After passing through a $P\left(\cdot \right)$-like fully connected network (FCN), $Q\left(\cdot \right)$ is converted to the desired $u_t$. The FNO model is shown in Figure 1A.

FIGURE 1

FIGURE 1. (A) Structure of FNO. (B) Neural network structure of the adjusted Fourier layer (AFL).

Comparing Eq. 1 and Eq. 2.1, $\mathcal{R}\left(\cdot \right)$ can be similarly constructed by a neural network of $\left(K_{\theta }{z}_t\right)\left(x\right)$. In this work, we construct $z_{t+1}^{\prime }\left(x\right)$ by applying $W{z}_t\left(x\right)$ in Eq. 3.2 to connect with CasualLSTM and residual connection. Eq. 4 gives the expression of the adjusted Fourier layer, and the graphic illustration is shown in Figure 1B:

$z_{t+1}^{\prime }\left(x\right)≔\sigma {\mathcal{F}}^{-1}\left(R_{\theta }\cdot \left(\mathcal{F}{z}_t\right)\left(x\right)\right),\forall x\in D.(4)$

3.3 Network architecture: PA_CasualLSTM

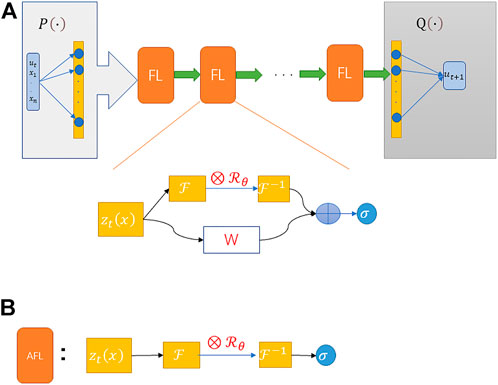
This section introduces the construction of PA_CasualLSTM, which is an adaptive time-marching strategy, as shown in Figure 2A. The time series prediction is formed by combining the operator with AFL and CasualLSTM as shown in Figure 2B. The PA_CasualLSTM cell consists of an operator module, an autoregressive (AR) process, and a Fourier transform-based filter. The operator module first performs a full connection operation ($P\left(\cdot \right)$) on the input of the state value $u_{k\sim 2k}$, where k represents the number of time steps. Then, the tensor processed by AFL enters into the next fully connected layer, and the results are fed into the autoregressive (AR) process for time propagation processing and finally pass through a fully connected layer.

FIGURE 2

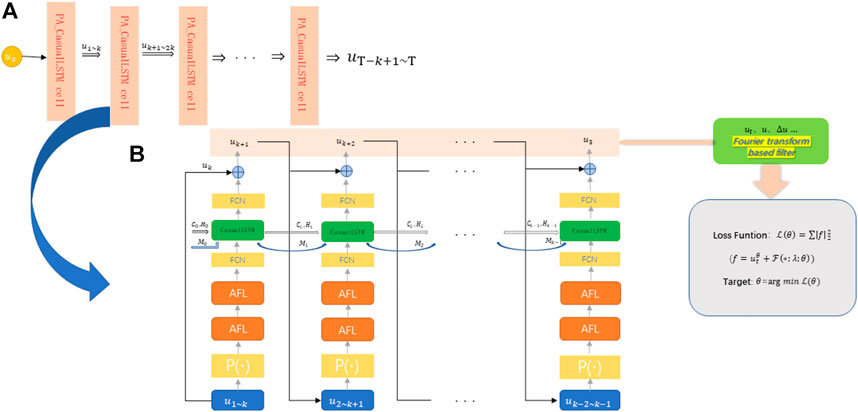
FIGURE 2. (A) The network structure of PA_CasualLSTM. It is an adaptive time marching strategy composed of the PA_CasualLSTM cell. After the current group is trained, some training results are taken as the input of the next stage; (B) The network structure of PA_CasualLSTM cell. H, C, and M are the hidden state, temporal memory, and spatial memory of CasualLSTM. $\theta$ needs to be acquired by training the network.

We apply ReLU as the activation function of the fully connected layer. Unlike the first two fully connected layers, there is no activation function behind the last layer. The CasualLSTM layer acts as a time propagator for propagating information, so that $C_k,H_k{,M}_k$ are used as the unit of information propagator. Inspired by the traditional integral method, the forward Euler scheme in the connection module is adopted. To the last $u_{k+i}$ of the input value and the output $u_{k+i+1}$, we add a global connection, and the expression is $u_{k+i+1}=u_{k+i}+\delta t\cdot G\left[u_{i\sim k+i};\theta \right]$, where $G\left[\cdot \right]$ represents the combined network with AFL and CasualLSTM, $\delta t$ is the time interval, and input is rolling backward update. This way of connecting the input and output is regarded as an autoregressive (AR) process.

The discrete outputs are encoded into the loss function by means of Fourier transform-based filters and finite difference methods. The time derivative is calculated by convolving the outputs with a finite difference filter, which is the fourth-order central difference method like Eq. 5. For the spatial derivative, because of only considering the periodic boundary conditions, the solution can be solved by the discrete Fourier transform method. So, the PDE constraints are achieved and the loss function is constructed, which will be explained in detail in Section 3.4.

$D_t=\left[1,-\mathrm{8,0,8},-1\right]\times \frac{1}{12\delta t}.(5)$

Finally, it is about the skills of network training. Since the network has only one initial condition, after getting the value of the subsequent $k$ moments through pre-training, the value of $1\sim k$ is regarded as the input of the next PA_CasualLSTM cell. After the training, the value of $k+1\sim 2k$ is achieved. In this way, the iterative training is repeated until the value of the entire training period is derived.

3.4 Physical information loss function

With the initial conditions as the only input, we choose the time-dependent PDE with periodic boundary conditions as the solution. The boundary conditions are incorporated into the constraints of the PDE. We define $f\left(t;x;\theta \right)$ on the left side of Eq. 1, which is represented by the following formula:

$f\left(t;x;\theta \right):=u_t^{\theta }+\mathcal{R}\left[u_t^{\theta },\nabla u_t^{\theta },∆u_t^{\theta },\dots ;\lambda \right].(6)$

The shared network parameter $\theta$ is achieved by training the network to minimize the loss function $\mathcal{L}\left(\theta \right)$. In other words, $f\left(t;x;\theta \right)$ and $u\left(t;x\right)$ can be obtained by minimizing the loss function $\mathcal{L}\left(\theta \right)$, which is defined as the mean-squared error obtained, namely,

$\mathcal{L}\left(\theta \right)={\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{k=1}^T{\left|f\left(t_k;x_i;\theta \right)\right|}^2,(7)$

$Target:\theta =argmin\mathcal{L}\left(\theta \right),(8)$

where $N$ and $T$ represent the number of points in space and the total number of time steps, respectively.

Fourier transform, a section of the pseudo-spectral method, is often used to solve PDE. In deep learning, the application of the Fourier transform can accelerate convolutional neural networks [48]. In this article, the Fourier transform is used for the PDE constraint construction of loss function. The Fourier-transformed function has an obvious advantage in which it has a wider range of applications. When solving the spatial derivatives, the related operations (such as the inverse Laplace transforms) are a challenge for finite differences. The function is very easy to calculate in the frequency domain using the discrete Fourier transform (DFT) [49,50].

4 Numerical experiments

In this section, we evaluate the proposed method by two nonlinear time-dependent PDE systems. By solving Burger’s equation and the two-dimensional incompressible Navier–Stokes (N-S) equation, we demonstrate the solution accuracy and extrapolation ability of PA_CasualLSTM compared with those of FNO. The following section introduces the parameters and prediction evaluation indicators of each part of the network construction and then conducts experiments on the two PDEs. All numerical experiments and constructed networks in this article are coded using PyTorch [51], and PyCharm is used as the development environment for the experiments, and an NVIDIA GeForce GTX 3090 (24G) is used to train the network.

4.1 Network settings

We consider the same network architecture setting for the two examples in this article. The PA_CasualLSTM cell consists of three FCNs with 20, 64, and 64 neurons, respectively, the two layers of AFL, and a CasualLSTM cell. All networks are trained by the stochastic gradient descent Adam optimizer [52].

4.1.1 Baseline

As an important part of evaluating the architecture and performance of the neural network, we choose the FNO as the baseline to demonstrate the capability of the proposed method. After hyperparameter optimization, we choose the following model as the solution baseline:

FNO: the four-layer Fourier neural operator with three FCNs with 20, 64, and 64 neurons, respectively, is chosen. The first FCN lifts the dynamics from Dⁱⁿ to D²⁰, and the third FCN projects the dynamics from D⁶⁴ to D¹. Also, each Fourier layer is parameterized with 13 truncated modes.

4.1.2 Evaluation metrics

To evaluate the pros and cons of the proposed network, our error evaluation is divided into two parts: training and extrapolation. The root-mean-square error (RMSE) is reported which is defined as follows:

${RMSE}_{\tau }=\sqrt{\frac{1}{N_{\tau }m}{\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_k^{N_{\tau }}{\left|u\left(x_i,t_k\right)-u\left(x_i,t_k;\theta \right)\right|}^2,}(9)$

where $N_{\tau }$ represents the whole number of time steps in [0, τ] and τ represents the moment of this time step. $m$ is the number of all spatial points in the area. $u\left(x_i,t_{\tau }\right)$ and $u\left(x_i,t_{\tau };\theta \right)$ are the reference solution and the network solution, respectively.

4.2 Burger’s equation

Considering a hydrodynamic problem, the two-dimensional viscous Burger’s equation has the following form:

$u_t+u\left(x,y,t\right)\left(u_x\left(x,y,t\right)+u_y\left(x,y,t\right)\right)=\nu \left(u_{xx}\left(x,y,t\right)+u_{yy}\left(x,y,t\right)\right)x,y\in \Omega ,t\in (0,T],$

$u_0\left(x,y,0\right)=\sin \left(2\pi x\right)\sin \left(2\pi y\right)x,y\in \text{Ω},(10)$

where $u$ represents the velocity of the fluid; ν is the viscosity coefficient; $u_x$, $u_y$, $u_{xx}$, and $u_{yy}$ are the partial derivatives; and $u_0\left(x,y,0\right)$ is the initial condition.

As a nonlinear partial differential equation describing the phenomenon of wave diffusion, Burger’s equation is widely applied in many physical problems such as sound waves and vibrations. Although its equation form is simple, it contains nonlinear derivatives, partial derivatives, and other terms, so it is widely used to verify the effectiveness of numerical methods. Here, we take $\nu =0.005$, and the spatial region takes $\Omega \in {\left[\mathrm{0,1}\right]}^2$ with a grid resolution of [64$\times 64$].

In addition, the reference solution is solved using a pseudo-spectral method with a fourth-order Runge–Kutta time integration scheme ($\delta t=1\times {10}^{-4}$), while for the baseline and PA_CasualLSTM, we use a larger time interval ($\delta t=5\times {10}^{-2}$). PA_CasualLSTM is trained from 5, 10, and 20 to 40 time steps, with each training epoch being 3,000, the learning rate being 0.001, and the learning rate being reduced by 2% every 100 epochs. In the training phase, the number of time steps is 40, and the time range is [0,2]. Based on the trained model, we predict its solution with a number of time steps of 40 and a time range of [2, 4] to verify its extrapolation ability.

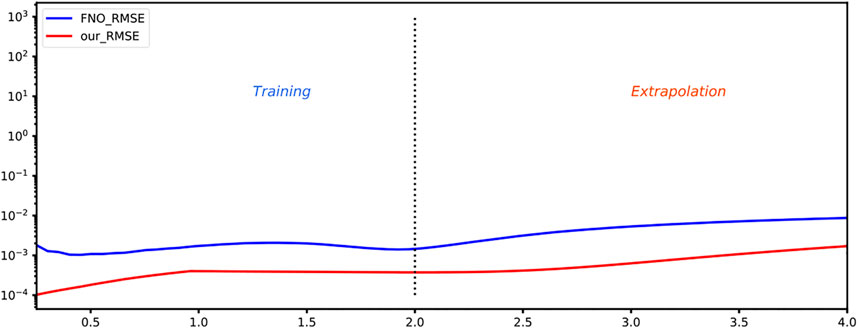
Figure 3 depicts four snapshots of $u$ taken from the training phase ($t$ = 0.75, 1.5s) and the extrapolation phase ($t$ = 2.5, 3.5s), respectively. Each snapshot from top to bottom is reference solutions, predictions by FNO and PA_CasualLSTM, and errors of FNO and PA_CasualLSTM, respectively. First, both the trained and extrapolated results of PA_CasualLSTM are excellently consistent with the overall change of the reference solution, while the baseline prediction fails to match the truth, especially it is obvious that the whole error of PA_CasualLSTM is close to zero, whereas the solution from FNO maintaining the same trend presents a much larger error. Second, the numerical results of PA_CasualLSTM are shown in Table 1, and two points ($x$ = 16/64, $y$ = 16/64; $x$ = 16/64, $y$ = 48/64) at four time are selected to verify the proposed method. It can be found that the error of FNO is larger than that of PA_CasualLSTM, especially in the extrapolation proceedings. Also, for the error propagation shown in Figure 4, it is validated that PA_CasualLSTM possesses superior solution accuracy to FNO. The RMSE of PA_CasualLSTM surpasses that of FNO during the entire time period. The reason for this phenomenon is that the loss function designing of FNO only relies on the MSE constructed with the truth, which is limited by the grid sizes. In addition, due to CasualLSTM and the residual connection on the input and output, PA_CasualLSTM remains an outstanding performance effect on extrapolation.

FIGURE 3

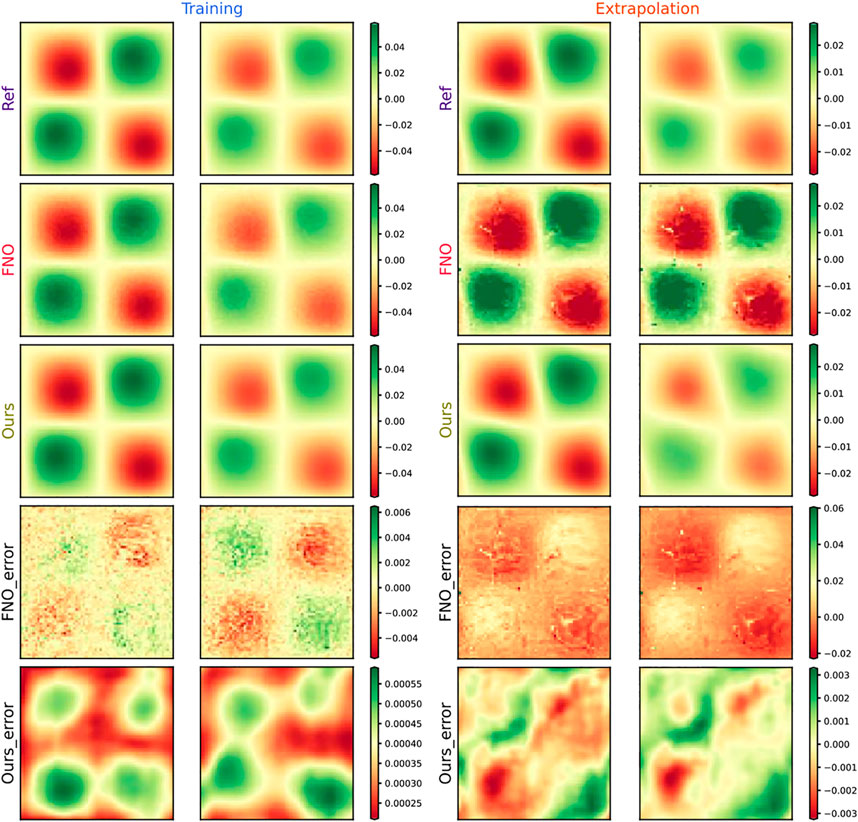
FIGURE 3. Result of PA_CasualLSTM solving Burger’s equation. Four representative moments are selected for comparison, namely, training ($t$ = 0.75, 1.5s) and extrapolation ($t$ = 2.5, 3.5s), and the entire interval error is compared. The subfigures from top to bottom are reference solutions, predictions by FNO and PA_CasualLSTM, and errors of FNO and PA_CasualLSTM, respectively.

TABLE 1

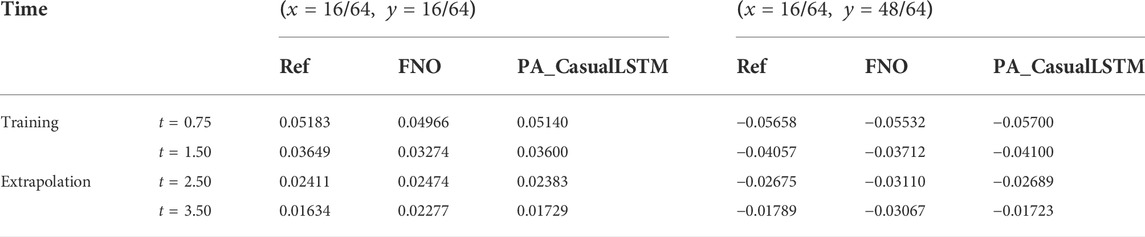
TABLE 1. Numerical result of the classical numerical method, FNO, and PA_CasualLSTM for Burger’s equation.

FIGURE 4

FIGURE 4. RMSE of PA_CasualLSTM and FNO for Burger’s equation.

4.3 Two-dimensional Navier–Stokes equation

We consider the two-dimensional Navier–Stokes equation for viscous incompressible fluids [38]:

${\partial }_t\zeta \left(x,y,t\right)+u\left(x,y,t\right)\cdot \nabla \zeta \left(x,y,t\right)=\nu \Delta \zeta \left(x,y,t\right)+f\left(x,y\right)x,y\in \left[\mathrm{0,1}\right],t\in (0,T],$

$\nabla \cdot u\left(x,y,t\right)=0x,y\in \left[\mathrm{0,1}\right],t\in (0,T],$

${\zeta }_0\left(x,y,0\right)=\sin \left(2\pi y\right)x,y\in \left[\mathrm{0,1}\right],(11)$

where $u\left(x,y,t\right)$ is the velocity field containing ($u,v$), $\zeta =\nabla \times u$ is the vorticity, and ${\zeta }_0\left(x,y,0\right)$ is the initial condition with periodic boundary properties. The viscosity coefficient $\nu =1e-3$ and the forcing $f\left(x,y\right)=0.1\left(\sin \left(2\pi \right(x+y)\right)+\cos \left(2\pi \right(x+y))$. The reference solution is generated using the pseudo-spectral method. First, the velocity field is calculated in Fourier space by the flow function. Second, the nonlinear term of the geometric space and the Laplace operator of the vorticity are computed, respectively. Finally, in the time domain, the Crank–Nicolson formula is used for forward integration and the time step is $\delta t=1\times {10}^{-4}$. We train the model for 20-time steps with a time duration of [0,2] and extrapolate the inference for [2,4] with a time interval of 0.1, where the resolution is 64 × 64. The learning rate is set at 5 × 10^–4 and decays by 2% every 100 epochs.

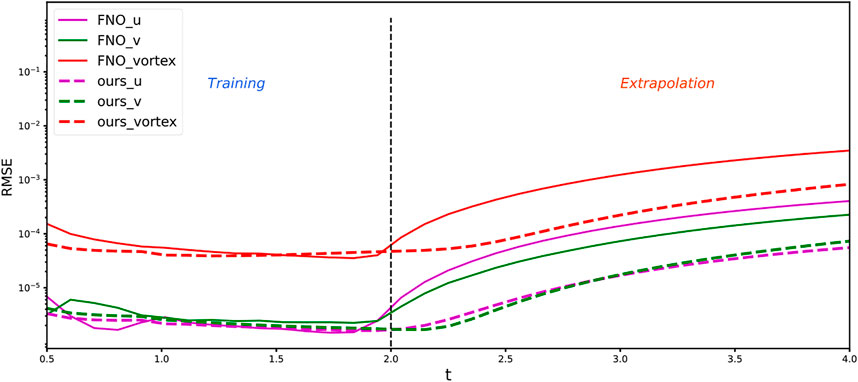
The solution snapshots of vorticity and velocity predicted by PA_CasualLSTM and FNO are shown in Figures 5, 6, along with the ground truth reference and error maps. In general, the vorticity and velocity solution of both PA_CasualLSTM and FNO are in good agreement with the reference truth. However, the error distribution of PA_CasualLSTM is much smaller, especially in the extrapolation phase. Tables 2–Tables 4 show the numerical results of vorticity and velocity $u$ and $v$ by PA_CasualLSTM, respectively, and two points ($x$ = 16/64, $y$ = 16/64; $x$ = 16/64, $y$ = 48/64) are selected for comparison. According to Figures 5, 6, the overall trends of all physical quantities are nearly the same, and the numerical solutions of PA_CasualLSTM are closer to the reference solutions during extrapolation. The changes in error magnitude in Figures 5, 6 are further verified by the results in Table 2–Table 3, especially the extrapolation error. Moreover, the error propagation in Figure 7 further validates the superior solution accuracy. The vorticity or velocity RMSE of PA_CasualLSTM increases along with time, keeping at a low level (10⁻³ and 10⁻⁴, respectively), but the proposed method prevails FNO in extrapolation by one order of magnitude. The extrapolated error levels show the great potential of PA_CasualLSTM for generalization.

FIGURE 5

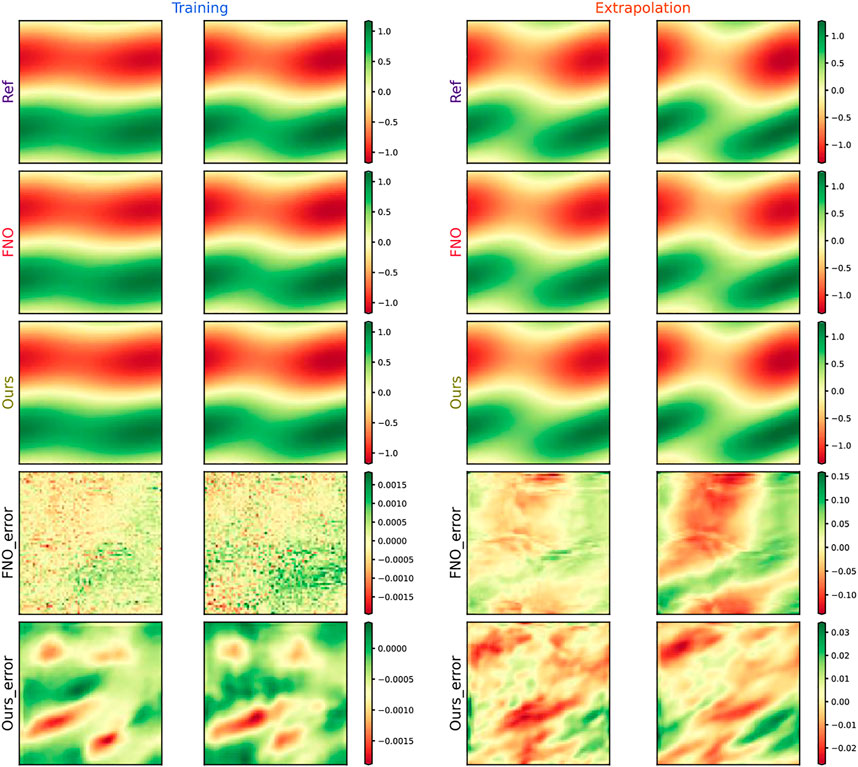
FIGURE 5. Vorticity results of PA_CasualLSTM-solved 2D Navier–Stokes equation, and four representative moments are selected for comparison, namely, training ($t$ = 1, 1.7s) and extrapolation ($t$ = 2.5, 3.5s), and the errors across the entire interval are compared. The subfigures from top to bottom are reference solutions, predictions by FNO and PA_CasualLSTM, and errors of FNO and PA_CasualLSTM, respectively.

FIGURE 6

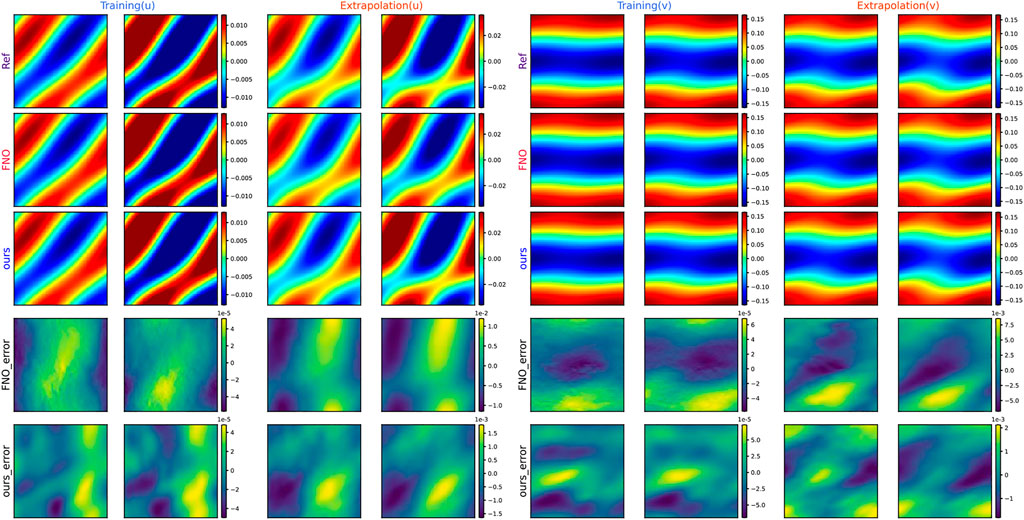
FIGURE 6. Velocity results of PA_CasualLSTM-solved 2D Navier–Stokes equation, four representative moments are selected as comparisons, namely, training ($t$ = 1, 1.7s) and extrapolation ($t$ = 2.5, 3.5s), and one-by-one errors over the entire interval are compared. The subfigures from top to bottom are reference solutions, predictions by FNO and PA_CasualLSTM, and errors of FNO and PA_CasualLSTM, respectively.

TABLE 2

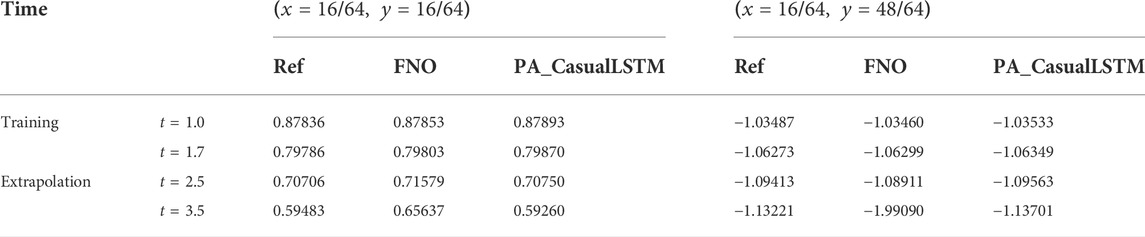
TABLE 2. Numerical results of vorticity for 2D Navier–Stokes equations solved by the classical numerical method, FNO, and PA_CasualLSTM.

TABLE 3

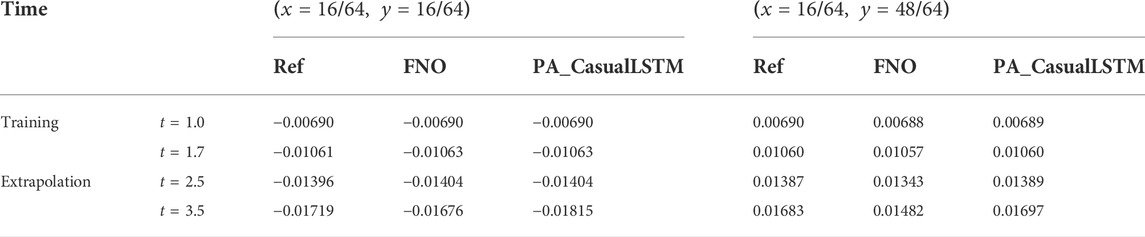
TABLE 3. Numerical results of velocity ($u$) for 2D Navier–Stokes equations solved by the classical numerical method, FNO, and PA_CasualLSTM.

TABLE 4

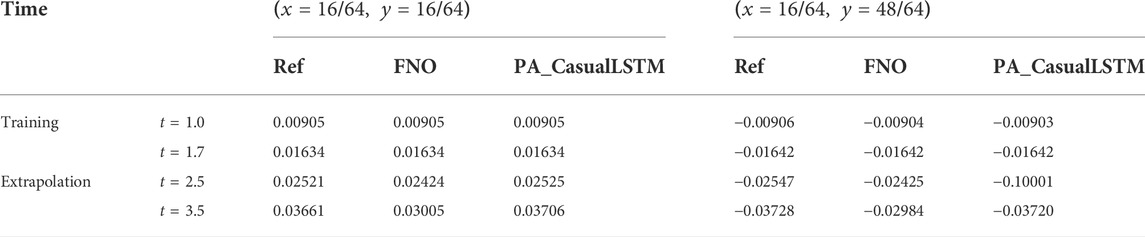
TABLE 4. Numerical results of velocity ($v$) for 2D Navier–Stokes equations solved by the classical numerical method, FNO, and PA_CasualLSTM.

FIGURE 7

FIGURE 7. RMSE of PA_CasualLSTM- and FNO-solved 2D Navier–Stokes equations.

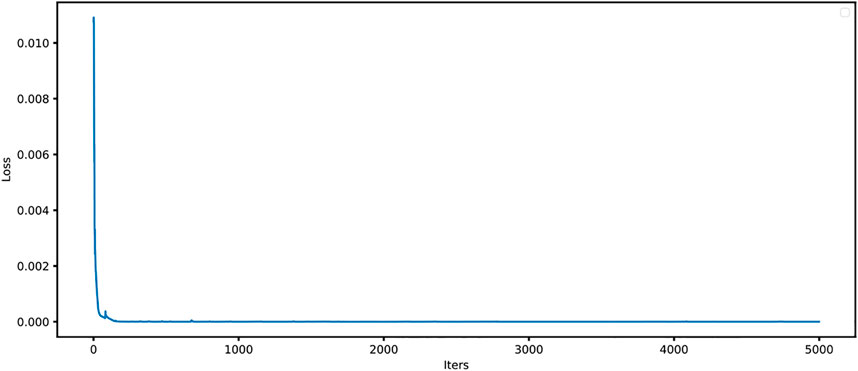
In this section, the loss history of PA_CasualLSTM for the 2D Navier–Stokes equation is shown in Figure 8. It is obvious that the loss value decreases very quickly after a few iterations. As the number of iteration steps increases, the change of the loss value becomes flat. From the change of loss history, it can be found that the network reaches convergence after training. Another example has a similar conclusion.

FIGURE 8

FIGURE 8. Convergence history of PA_CasualLSTM.

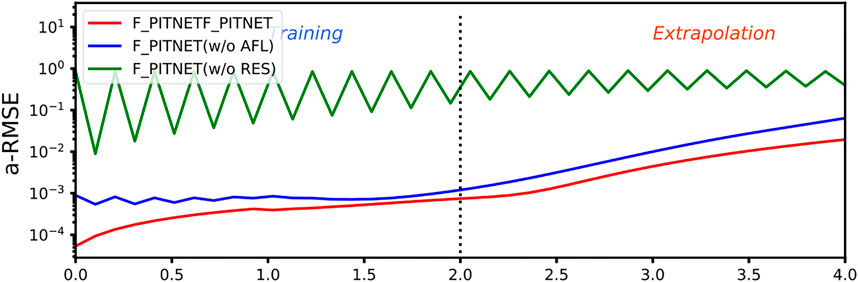
4.4 Ablation experiment

To verify the effectiveness of the proposed network, we implement an ablation study on PA_CasualLSTM by solving the 2D Navier–Stokes equation. The AFL is added to the time series prediction, and the residual connection method is adopted between the input and output. Here, we study the contributions of these two parts. The experimental setting composes three architectures: full PA_CasualLSTM, PA_CasualLSTM without AFL, and PA_CasualLSTM without residual connections. Other works are consistent with 4.3, and the results are used for performance evaluation. The comparison result is described in Figure 9. The structure of PA_CasualLSTM without residual connections scheme works the worst. PA_CasualLSTM has the best performance in both training and extrapolation. Therefore, both ablation experiments fully verify that AFL and residual connections play a vital role in the network architecture.

FIGURE 9

FIGURE 9. Ablation experiment.

5 Discussion

The work [38] has demonstrated the great potential of FNO for the solution of PDE. However, there is still a lack of research on networks with unlabeled data and extrapolating information into the future. Through two numerical experiments (Burger’s equation and 2D N-S equation), we have verified the capability of PA_CasualLSTM in the solution of time-dependent PDE. In this section, we provide a comprehensive discussion about the proposed network.

1) The training process without labeled data. As an operator learning method, FNO needs label data from traditional numerical solvers to construct the network, while our PA_CasualLSTM frameworks only rely on the initial conditions and PDE law incorporated into the loss function as soft constraints. PA_CasualLSTM, which belongs to a self-supervised method, enhances interpretability by encoding physical law and does not require label data obtained by traditional numerical methods in the training process.

2) The more accurate results of extrapolation. The proposed network architecture involves two related temporal processes. Unlike the Fourier layer in FNO, because of the adjusted Fourier layer learning the spatial derivative, the global residual connection establishes a temporal relationship between input and output in PA_CasualLSTM. The addition of the CasualLSTM module strengthens the temporal evolution. So, the network holds a more accurate extrapolation solution due to the embedding of the aforementioned modules.

3) The construction of loss function. The loss function of traditional supervised deep learning is always based on MSE between output and labeled data. Different from the implementation of physical constraint in PINN, encoding PDE laws is realized by the Fourier filter to calculate the spatial derivative, which speeds up convergence and improves solution accuracy. The network is currently limited by a uniform grid, and we can extend the network into the irregular grid to strengthen the generalization of the network by using graph neural network learning [53,54].

4) The adaptive time-marching strategy. It adopts a timely update approach to adapt time-marching strategies, thus improving the solution accuracy. This adaptive process continuously updates the input to optimize the network parameters, but it also leads to a sharp increase in the amount of computation over time. Therefore, it is of great practical significance to strike a balance between accuracy and efficiency.

6 Conclusion

In this article, we propose a new time series prediction network with physical constraints and an adjusted Fourier neural operator (PA_CasualLSTM) to solve time-dependent PDE. Compared with previous deep learning methods, PA_CasualLSTM can avoid the high-quality requirements of training data and the rapid propagation of errors. By taking the advantage of the physical constrained network, AFL and CasualLSTM, PA_CasualLSTM, a self-supervised learning method, can quickly converge without labeled data and extrapolate the information to the future by the adaptive time-marching strategy. The excellent performance of solution accuracy and extrapolability is verified by solving Burger’s and N-S equations. In the future, we will extend the network to irregular networks with other boundary conditions and adopt a more accurate forward scheme to improve the solution accuracy and prolong the time interval.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CX, XZ, FY, XC, JN, and FH contributed to the writing of the manuscript and to the interpretation of the results. CX contributed to conceptualization and writing—original draft preparation. CX and FY contributed to software and validation. XZ, XC, JN, and FH contributed to writing—reviewing and editing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Quarteroni A, Valli A. Numerical approximation of partial differential equations. Berlin, Germany: Springer Science & Business Media (2008).

Google Scholar

2. Ames WF. Numerical methods for partial differential equations. Cambridge, MA, USA: Academic Press (2014).

Google Scholar

3. Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. nature (1986) 323(6088):533–6. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

4. Lagaris IE, Likas A, Fotiadis DI. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans Neural Netw (1998) 9(5):987–1000. doi:10.1109/72.712178

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Lagaris IE, Likas AC, Papageorgiou DG. Neural-network methods for boundary value problems with irregular boundaries. IEEE Trans Neural Netw (2000) 11(5):1041–9. doi:10.1109/72.870037

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Li S, Song W, Fang L, Chen Y, Ghamisi P, Benediktsson JA. Deep learning for hyperspectral image classification: An overview. IEEE Trans Geosci Remote Sens (2019) 57(9):6690–709. doi:10.1109/tgrs.2019.2907932

CrossRef Full Text | Google Scholar

7. Goldberg Y. A primer on neural network models for natural language processing. J Artif Intell Res (2016) 57:345–420. doi:10.1613/jair.4992

CrossRef Full Text | Google Scholar

8. Helbing G, Ritter M. Deep Learning for fault detection in wind turbines. Renew Sustain Energ Rev (2018) 98:189–98. doi:10.1016/j.rser.2018.09.012

CrossRef Full Text | Google Scholar

9. Han J, Jentzen A, Weinan E. Solving high-dimensional partial differential equations using deep learning. Proc Natl Acad Sci U S A (2018) 115(34):8505–10. doi:10.1073/pnas.1718942115

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Raissi M. Deep hidden physics models: Deep learning of nonlinear partial differential equations. J Machine Learn Res (2018) 19(1):932–55.

Google Scholar

11. Zhang J, Shields MD. The effect of prior probabilities on quantification and propagation of imprecise probabilities resulting from small datasets. Comput Methods Appl Mech Eng (2018) 334:483–506. doi:10.1016/j.cma.2018.01.045

CrossRef Full Text | Google Scholar

12. Bar-Sinai Y, Hoyer S, Hickey J, Brenner MP. Learning data-driven discretizations for partial differential equations. Proc Natl Acad Sci U S A (2019) 116(31):15344–9. doi:10.1073/pnas.1814058116

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys (2019) 378:686–707. doi:10.1016/j.jcp.2018.10.045

CrossRef Full Text | Google Scholar

14. Gorodetsky AA, Jakeman JD, Geraci G, Eldred MS. MFNets: Multi-fidelity data-driven networks for Bayesian learning and prediction. Int J Uncertain Quantif (2020) 10(6):595–622. doi:10.1615/int.j.uncertaintyquantification.2020032978

CrossRef Full Text | Google Scholar

15. Guo Y, Cao X, Liu B, Gao M. Solving partial differential equations using deep learning and physical constraints. Appl Sci (2020) 10(17):5917. doi:10.3390/app10175917

CrossRef Full Text | Google Scholar

16. Lu L, Meng X, Mao Z, Karniadakis GE. DeepXDE: A deep learning library for solving differential equations. SIAM Rev Soc Ind Appl Math (2021) 63(1):208–28. doi:10.1137/19m1274067

CrossRef Full Text | Google Scholar

17. Meng X, Li Z, Zhang D, Karniadakis GE. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput Methods Appl Mech Eng (2020) 370:113250. doi:10.1016/j.cma.2020.113250

CrossRef Full Text | Google Scholar

18. Wight CL, Zhao J. Solving allen-Cahn and Cahn-Hilliard equations using the adaptive physics informed neural networks (2020). arXiv preprint arXiv:2007.04542.

Google Scholar

19. Zhu Y, Zabaras N, Koutsourelakis P-S, Perdikaris P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J Comput Phys (2019) 394:56–81. doi:10.1016/j.jcp.2019.05.024

CrossRef Full Text | Google Scholar

20. Sun L, Gao H, Pan S, Wang J-X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput Methods Appl Mech Eng (2020) 361:112732. doi:10.1016/j.cma.2019.112732

CrossRef Full Text | Google Scholar

21. Rao C, Sun H, Liu Y. Physics-informed deep learning for computational elastodynamics without labeled data. J Eng Mech (2021) 147(8):04021043. doi:10.1061/(asce)em.1943-7889.0001947

CrossRef Full Text | Google Scholar

22. Daw A, Karpatne A, Watkins W, Read J, Kumar V. Physics-guided neural networks (pgnn): An application in lake temperature modeling (2017). arXiv preprint arXiv:1710.11431.

Google Scholar

23. Jia X, Willard J, Karpatne A, Read J, Zwart J, Steinbach M, et al. Physics guided RNNs for modeling dynamical systems: A case study in simulating lake temperature profiles. In: Proceedings of the 2019 SIAM International Conference on Data Mining: SIAM (2019). p. 558–66.

CrossRef Full Text | Google Scholar

24. Barreau M, Aguiar M, Liu J, Johansson KH. Physics-informed learning for identification and state reconstruction of traffic density (2021). arXiv preprint arXiv:2103.13852.

Google Scholar

25. Chen Z, Liu Y, Sun H. Physics-informed learning of governing equations from scarce data. Nat Commun (2021) 12(1):6136–13. doi:10.1038/s41467-021-26434-1

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Rao C, Ren P, Liu Y, Sun H. Discovering nonlinear PDEs from scarce data with physics-encoded learning (2022). arXiv preprint arXiv:2201.12354.

Google Scholar

27. Krishnapriyan A, Gholami A, Zhe S, Kirby R, Mahoney MW. Characterizing possible failure modes in physics-informed neural networks. Adv Neural Inf Process Syst (2021) 34.

Google Scholar

28. Wang S, Teng Y, Perdikaris P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J Sci Comput (2021) 43(5):A3055–81. doi:10.1137/20m1318043

CrossRef Full Text | Google Scholar

29. Dwivedi V, Srinivasan B. Physics informed extreme learning machine (pielm)–a rapid method for the numerical solution of partial differential equations. Neurocomputing (2020) 391:96–118. doi:10.1016/j.neucom.2019.12.099

CrossRef Full Text | Google Scholar

30. Schiassi E, Furfaro R, Leake C, De Florio M, Johnston H, Mortari D. Extreme theory of functional connections: A fast physics-informed neural network method for solving ordinary and partial differential equations. Neurocomputing (2021) 457:334–56. doi:10.1016/j.neucom.2021.06.015

CrossRef Full Text | Google Scholar

31. Fotiadis S, Pignatelli E, Valencia ML, Cantwell C, Storkey A, Bharath AA. Comparing recurrent and convolutional neural networks for predicting wave propagation (2020). arXiv preprint arXiv:2002.08981.

Google Scholar

32. Geneva N, Zabaras N. Modeling the dynamics of PDE systems with physics-constrained deep auto-regressive networks. J Comput Phys (2020) 403:109056. doi:10.1016/j.jcp.2019.109056

CrossRef Full Text | Google Scholar

33. Hu Y, Zhao T, Xu Z, Lin L. Neural time-dependent partial differential equation (2020).

Google Scholar

34. Zhang R, Liu Y, Sun H. Physics-informed multi-LSTM networks for metamodeling of nonlinear structures. Comput Methods Appl Mech Eng (2020) 369:113226. doi:10.1016/j.cma.2020.113226

CrossRef Full Text | Google Scholar

35. Saha P, Dash S, Mukhopadhyay S. Physics-incorporated convolutional recurrent neural networks for source identification and forecasting of dynamical systems. Neural Networks (2021) 144:359–71. doi:10.1016/j.neunet.2021.08.033

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Lu L, Jin P, Karniadakis GE. Deeponet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators (2019). arXiv preprint arXiv:1910.03193.

Google Scholar

37. Li Z, Kovachki N, Azizzadenesheli K, Liu B, Bhattacharya K, Stuart A, et al. Neural operator: Graph kernel network for partial differential equations (2020). arXiv preprint arXiv:2003.03485.

Google Scholar

38. Li Z, Kovachki N, Azizzadenesheli K, Liu B, Bhattacharya K, Stuart A, et al. Fourier neural operator for parametric partial differential equations (2020). arXiv preprint arXiv:2010.08895.

Google Scholar

39. Duvall J, Duraisamy K, Pan S. Non-linear independent dual system (NIDS) for discretization-independent surrogate modeling over complex geometries (2021). arXiv preprint arXiv:2109.07018.

Google Scholar

40. Kovachki N, Li Z, Liu B, Azizzadenesheli K, Bhattacharya K, Stuart A, et al. Neural operator: Learning maps between function spaces (2021). arXiv preprint arXiv:2108.08481.

Google Scholar

41. Li Z, Kovachki N, Azizzadenesheli K, Liu B, Bhattacharya K, Stuart A, et al. Markov neural operators for learning chaotic systems (2021). arXiv preprint arXiv:2106.06898.

Google Scholar

42. Patel RG, Trask NA, Wood MA, Cyr EC. A physics-informed operator regression framework for extracting data-driven continuum models. Comput Methods Appl Mech Eng (2021) 373:113500. doi:10.1016/j.cma.2020.113500

CrossRef Full Text | Google Scholar

43. Li Z, Kovachki N, Azizzadenesheli K, Liu B, Stuart A, Bhattacharya K, et al. Multipole graph neural operator for parametric partial differential equations. Adv Neural Inf Process Syst (2020) 33:6755–66.

Google Scholar

44. Wang Y, Gao Z, Long M, Wang J, Philip SY. Predrnn++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In: International Conference on Machine Learning: PMLR (2018). p. 5123–32.

Google Scholar

45. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput (1997) 9(8):1735–80. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Pathak J, Subramanian S, Harrington P, Raja S, Chattopadhyay A, Mardani M, et al. Fourcastnet: A global data-driven high-resolution weather model using adaptive fourier neural operators (2022). arXiv preprint arXiv:2202.11214.

Google Scholar

47. Wen G, Li Z, Azizzadenesheli K, Anandkumar A, Benson SM. U-FNO–An enhanced Fourier neural operator-based deep-learning model for multiphase flow. Adv Water Resour (2022) 163:104180. doi:10.1016/j.advwatres.2022.104180

CrossRef Full Text | Google Scholar

48. Mathieu M, Henaff M, LeCun Y. Fast training of convolutional networks through ffts (2013). arXiv preprint arXiv:1312.5851.

Google Scholar

49. Winograd S. On computing the discrete Fourier transform. Math Comput (1978) 32(141):175–99. doi:10.1090/s0025-5718-1978-0468306-4

CrossRef Full Text | Google Scholar

50. Anand AV. A brief study of discrete and fast fourier transforms. Chicago, IL, USA: University of Chicago VIGRE REU (2010).

Google Scholar

51. Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, et al. Automatic differentiation in pytorch (2017).

Google Scholar

52. Kingma DP, Ba J. Adam: A method for stochastic optimization (2014). arXiv preprint arXiv:1412.6980.

Google Scholar

53. Battaglia PW, Hamrick JB, Bapst V, Sanchez-Gonzalez A, Zambaldi V, Malinowski M, et al. Relational inductive biases, deep learning, and graph networks (2018). arXiv preprint arXiv:1806.01261.

Google Scholar

54. Zhou J, Cui G, Hu S, Zhang Z, Yang C, Liu Z, et al. Graph neural networks: A review of methods and applications. AI Open (2020) 1:57–81. doi:10.1016/j.aiopen.2021.01.001

CrossRef Full Text | Google Scholar