Controlling electron recollision with combined linear and circular polarization

We theoretically investigate the non-sequential double ionization of Ar atoms in the combined fields of linearly polarized laser and circularly polarized laser through 3D semiclassical simulations. By partially overlapping the two time-delayed multicycle laser pulses, we construct an optical waveform whose polarization ellipticity increase slowly for consecutive optical cycles. This composite laser pulses with the time-dependent ellipticity can tunnel-ionize atoms and steer the first tunneling electron to recollision with the second bound electron through different trajectories, in which the recollision occurs with different return times of the first ionized electron. Through tuning delay time between the two laser pulses, the double ionization yields and recollision trajectories with different return times can be controlled. The time-dependent ellipticity with different delay time can enhance or suppress the probability of different return times. This work provides a scheme exploring electron dynamics in few optical cycle or even subcycle time scale in a multicycle laser field without having to be limited to near-single-cycle laser pulses.

1 Introduction

The research on the interaction of atoms and molecules with intense laser pulses plays a key role in a comprehensive understanding of the nonlinear physics. Plenty of ultrafast processes are directly related to photoionization, which is the foundation of many strong field phenomena such as high harmonic generation (HHG), attosecond pulse synthetization [1–5], above threshold ionization (ATI) [6], and non-sequential double ionization (NSDI) [7]. NSDI has drawn much attention because of containing extensive information about collision dynamics and electron-electron correlation [8]. Researchers widely hold the idea that NSDI is described by a three-step model [9]. In this model, one electron tunnel ionizes when the laser field is strong enough and then is driven back to the parent ion as the oscillating electric field reverses its direction. It recollides with the parent ion and transfers a part of energy to it, which enables the second NSDI event. This model is a semiclassical perspective.

In order to achieve deep insight into the collision dynamics in strong field physics, various ionization channels in recollision process have been explored in details, such as electron multiple rescattering processes. The rescattering or recollision with multiple return times is considered to play an important role in the laser-atom interactions, especially driven by the midinfrared laser fields. For example, the finite tunnel distance inherent in strong-field ionization can be extracted from an experimental observable through studying laser-driven electron multiple scattering [10]. The low energy structure of strong field ionization by mid-IR laser pulses is considered to be related to the multiple rescattering [11,12]. Multiple rescattering processes also play an important role in HHG in an intense laser field [13–15]. In addition, multiple-return-collision (MRC) trajectories have been explored in NSDI with linearly [16,17] or elliptically [18–20], polarized laser field in recent years, in which sub-cycle dynamics was investigated and Coulomb-potential effects was considered to play an indispensable role.

In another aspect, it is expected that various recollision channels could be artificially controlled. With the development of the laser technology, more complex combined laser pulses have been employed to investigate the strong field physics, which makes many ultrafast dynamics controllable. For example, controlling the dynamics of double electron emission in non-sequential double ionization by tuning the subcycle shape of the orthogonal laser field [21]. Photoelectron intracycle interference can be controlled by polarization-gated laser pulses [22]. The ionization by two-color counter-rotating and co-rotating circularly polarized fields has been studied experimentally and theoretically [23,24]. Controlling of NSDI dynamics was also explored through this kind of bicircular fields [25–28]. Recently, a new phenomenon of electron vortices has attracted much attention. The vortex structures in the momentum distributions of photoelectron wave packets comes from the photoionization of atoms with sequences of two time-delayed counter-rotating circularly polarized laser pulses [29–35]. The local enhancement of the laser pulse is achieved by superimposing the terahertz field, thereby realizing the control of the electron dynamics [36].

Based on the above analysis, it is believed that the MRC channel should be controlled by shaping the laser pulses. In this paper, we propose and numerically demonstrate a scheme to control return times before recollision in NSDI by the complex field with combining linearly and circularly polarized pulses. This kind of combined laser field has the characteristics of time-dependent ellipticity, in which the polarization gradually transitions from linear polarization to circular polarization. By changing the time delay between the two laser beams, the transition property of the time-dependent ellipticity in the superposition region can be adjusted, and different degrees of lateral effect can be exerted on the first ionized electron for different return times. Therefore, the control mechanism of recollision trajectories with different return times can be realized. Atomic units are used throughout the paper unless stated otherwise.

2 Theoretical method

In this work, the semiclassical model [37,38] is used to describe the NSDI process of Ar. One electron (recolliding) tunnel ionizes through the Coulomb barrier. The initial state of the tunnelling electron is defined according to Ammosov-Delone-Krainov theory [39]. The initial exit point is along the laser-field direction and near the barrier. The initial electron momentum is taken to be equal to zero along the laser field while the transverse one is given by a Gaussian distribution. The initially bound electron is described by a microcanonical distribution [40]. The weight of each classical trajectory that we propagate in time is given by

$\omega \left(t_0,v_0\right)\propto \exp \left[-\frac{2{\left(2I_p\right)}^{3/2}}{3E\left(t_0\right)}\right]\exp \left[-\frac{{\left(2I_p\right)}^{1/2}{v}_0^2}{E\left(t_0\right)}\right],(1)$

Where t₀ is tunnel-ionization time, v₀ is initial transverse momentum and I_p is the first ionization potential. Then, the subsequent evolution of the two electrons is governed by classical equations of motion. Hamilton canonical equation is

${\dot{q}}_i=\frac{\partial H}{\partial p_i},{\dot{p}}_i=-\frac{\partial H}{\partial q_i},\left(i=\mathrm{1,2}\right),(2)$

with the Hamiltonian function

$H=\frac{{\mathbf{p}}_1^2}{2}+\frac{{\mathbf{p}}_2^2}{2}-\frac{2}{|{\mathbf{r}}_1|}-\frac{2}{|{\mathbf{r}}_2|}+\frac{1}{|{\mathbf{r}}_1-{\mathbf{r}}_2|}+\left({\mathbf{r}}_1+{\mathbf{r}}_2\right)\cdot \mathbf{E}\left(t\right),(3)$

where q_i and p_i are the canonical coordinates and canonical momentum of the electron.The form of the composite laser field can be written as

$\mathbf{E}\left(t\right)={\mathbf{E}}_1\left(t\right)+{\mathbf{E}}_2\left(t\right),(4)$

${\mathbf{E}}_1\left(t\right)=E_{0}f\left(t\right)\cos \left({\omega }_{1}t\right)\widehat{\mathbf{x}},(5)$

${\mathbf{E}}_2\left(t\right)=\frac{E_{0}f\left(t-\mathrm{\Delta }T\right)}{\sqrt{2}}\left\{\cos \left[{\omega }_2\left(t-\mathrm{\Delta }T\right)\right]\widehat{\mathbf{x}}+\sin \left[{\omega }_2\left(t-\mathrm{\Delta }T\right)\right]\widehat{\mathbf{y}}\right\},(6)$

where ω₁ = ω₂ = 0.0583 (λ₁ = λ₂ = 780 nm) is the frequency (wavelength) of the two laser pulses, and E₀ is the electric field strength of linearly polarized laser field. The pulse envelope is f(t) = exp[ − 4 ln 2(t²/τ²)], and τ = 18 fs indicates full width at half-maximum (FWHM). The delay time of the circularly polarized laser relative to the linearly polarized laser is expressed as ΔT.

In our model calculation 10⁸ initial points are generated, and the tunnel-ionization time t₀ is selected randomly in the time interval [ − τ, τ + ΔT]. The Hamilton canonical equation is solved by using the Runge-Kutta algorithm.

Figure 1 shows the schematic diagram of the composite laser electric field with the time delay ΔT = 8 o.c. The superimposed part makes the polarization of the laser electric field transition from linear polarization to circular polarization. With different delay time, the time-dependent ellipticity has different variation tendency, which provides a controlling mechanism of electron dynamics.

FIGURE 1

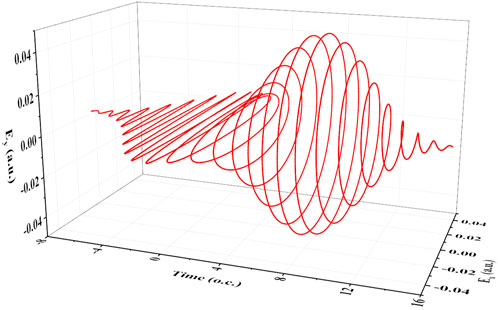
FIGURE 1. The electric field form of the laser field pulse combined with linearly polarized and circularly polarized laser of the time delay ΔT = 8 o.c.

3 Results and discussion

After determining the laser form, we appropriately select three different delay times ΔT = 2 o.c., ΔT = 5 o.c., and ΔT = 8 o.c. (corresponds to 0.3τ, 0.7τ and 1.1τ) to calculate the curve of the double ionization yield with the linearly polarized laser intensity, as shown in Figure 2. It can be seen from the figure that for all the delay times, the area where the field strength is lower than 0.7 PW/cm² presents a “knee” structure, indicating that the main mechanism of double ionization is NSDI. In the “knee” structure area, the longer the time delay of the two laser pulses, the higher the double ionization yield. This is because the longer time delay makes the two laser pulses farther away from each other, and the respective characteristics of linearly polarized and circularly polarized lasers are prominent. It is can also been seen by blue line in Figure 6. For ΔT = 8 o.c., very small time-dependent ellipticity covers large range of LP, while large time-dependent ellipticity covers most range of CP. The probability of collision of ionized electrons increases under the action of linearly polarized laser pulses. No collision process under circularly polarized laser pulses.

FIGURE 2

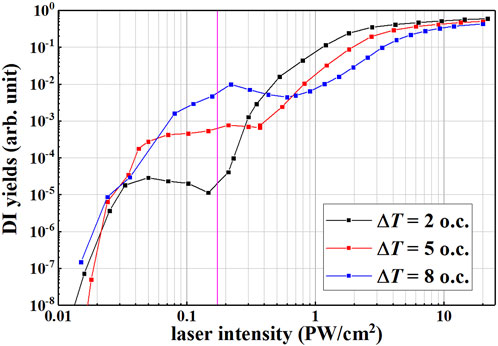
FIGURE 2. Variation curve of double ionization yield with linearly polarized laser intensity for three different delay times under compound laser field. The vertical pink lines indicate the non-sequential double ionization of Ar atoms in a compound laser field with a field strength of 0.16 PW/cm².

When the time delay is small, the superposition degree of the linearly polarized laser pulse and the circularly polarized laser pulse is large, the ellipticity of the recombination field is large as well. As shown by the red line in Figure 6, the time-dependent ellipticity with ΔT = 2 o.c. offers a larger lateral effect for almost all of the peak region of laser pulse. Therefore the collision process of ionized electrons is reduced. The NSDI process is suppressed.

In addition, the position of “knee” structures tends to be shifted to the left as decrease of the delay time. Please note that the horizontal axis in Figure 2 is the intensity of linearly polarized laser pulse, which is smaller than the compound laser intensity. As a result, the position of “knee” structures should be shifted to the left relative to the original situation (composed laser intensities) in a way, and the greater the degree of overlap (smaller delay time), the greater the shift to the left.

However, in the high field strength region, that is, the sequential double ionization (SDI) mechanism region, a longer time delay corresponds to a lower double ionization yield. Considering the pulse envelope shape, a longer delay time means a lesser degree of superposition, which in turn leads to a smaller peak field strength of the composite field. The law of smaller time delays is the opposite. In the SDI mechanism, double ionization does not have to undergo a collision process, and the ionization efficiency of two electrons only depends on the magnitude of the field strength.

For different delay times ΔT, the curves of double ionization yield with laser intensity all show the feature of “knee” structure. We calculated the effect of time delay on double ionization yield at the electric field strength of 0.16 PW/cm². As shown by the pink vertical line in Figure 2.

Overall, the double ionization yield increases with the increase of the time delay ΔT (as shown in Figure 3), which is consistent with the result of the curve of double ionization yield versus laser intensity. In addition, the double ionization yield will stabilize as ΔT tends to increase, because the two laser pulses have been separated, and only the linearly polarized laser pulse influences the NSDI. On the other hand, the double ionization yield is minimal with the time delay ΔT = 0, because the two laser pulses are completely coincident and the combined laser transform into elliptical polarization. NSDI is suppressed to the greatest extent.

FIGURE 3

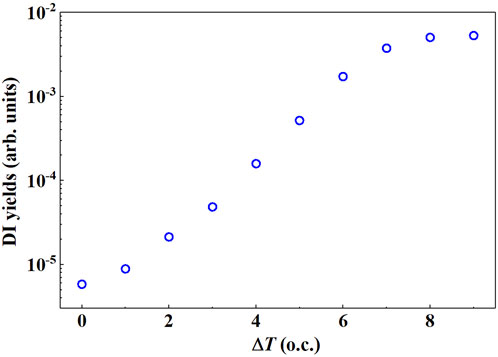
FIGURE 3. Relationship between double ionization yield and time-delay of compound laser field. The electric field strength is 0.16 PW/cm².

To account for the existence of fixed-form ionization channels in the recombined fields, we calculate the time distributions of ionized electron drift with time delays of 2 o.c. (pink line), 5 o.c. (blue line), and 8 o.c. (green line). As shown in Figure 4, the overall drift time distribution presents a multi-peak structure. The intensity of each peak is different under different delay times, but the peak position does not change much. This shows that there are various fixed forms of collision under the action of the laser field, and at the same time, they change with the change of the superposition degree of the two lasers.

FIGURE 4

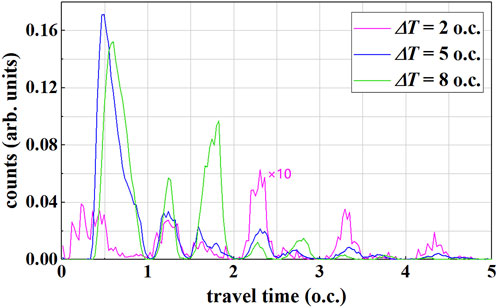
FIGURE 4. The drift time distribution of ionized electrons with the time delay 2 o.c. (pink line, multiply by 10), 5 o.c. (blue line), and 8 o.c. (green line). The results are calculated with 2 × 10⁸ initial points.

According to the Simpleman theory, driven by the linearly polarized laser field, the electron ionization returns to the origin for the first time at 0.75T (where T is an optical period). However, due to the periodic characteristics of laser oscillation, the time of returning to the origin for the following different times is 0.75T + nT(n = 0, 1, 2, …). According to the symmetry characteristics during the half optical cycle, the return time also satisfies 0.25T + nT(n = 0, 1, 2, …). Different peaks justly correspond to recollision trajectories with different return times.

In order to more intuitively show that different peaks in the drift time distribution correspond to different return times, we plot the collision trajectories of the ionized electrons for the first, second, third, and multiple returns. The first peak in the time distribution (Figure 4) corresponds to the situation where the electrons return to collide for the first time after ionization, and we draw its recollision trajectory, as shown in Figure 5A. The black line in Figure 5A represents the recollision trajectory of the first ionized electron. After the electron is ionized, it returns to the nuclear region for the first time and recollides with the bound state electron. The red line shows the trajectory of bound electrons. This kind of trajectory is the general ionization channel under the first peak if the delay time is large enough (green and blue lines in Figure 4), while it is relatively suppressed at a short time delay (pink line in Figure 4).

FIGURE 5

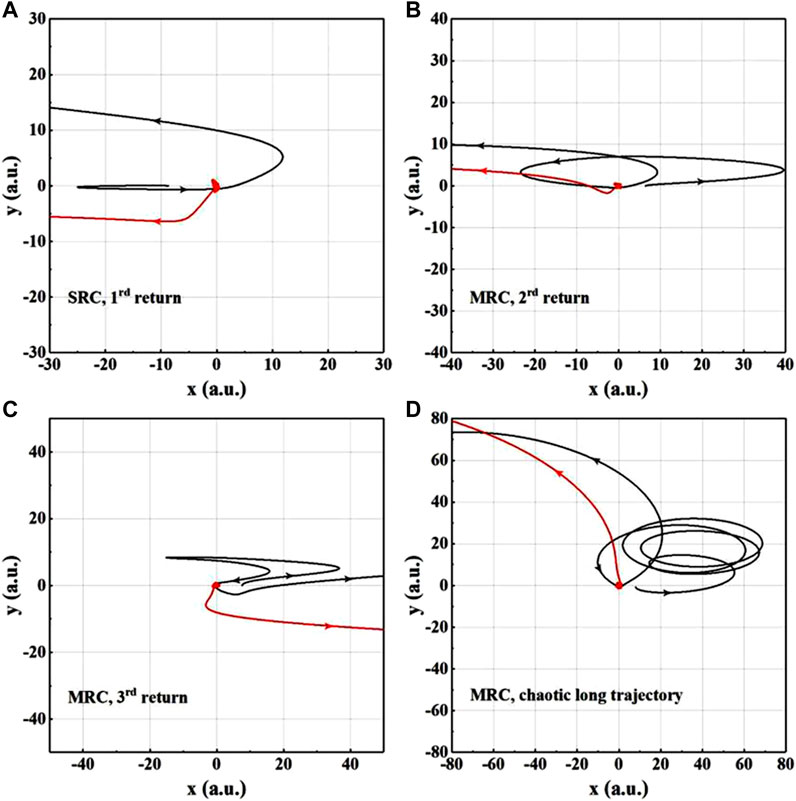
FIGURE 5. Ionized electrons return to collision trajectory for the first time (A), second times (B), third times (C) and many times (D), respectively.

As shown in Figure 5B, the recolliding electron is ionized first, and reaches the vicinity of 40 a.u. in the polarization direction, and then reverses for the first time under the action of the oscillating laser field, and pass by the nuclear region for the first time during the reverse motion. The second reversal occurs near −24 a.u., and finally collides with the second bound state electron with it returns to the nuclear region for the second time, resulting in non-sequential double ionization. The electron trajectory in this process is a typical second-return collision trajectory.

Figure 5C shows the trajectory of the third return collision. The ionized electrons are driven by the laser to pass by the nuclear region two times, and finally recollides with the bound electron at the third return, resulting in double ionization. The influence of these two MRC trajectories (Figures 5B,C) cannot be neglected when the delay time is large (the green line in Figure 4).

The complex trajectories of the ionized electrons with more return times are shown in Figure 5D. This NSDI channel is prominent when delay time is small due to the larger lateral influence of combined laser with near-elliptical polarization [41]. The collision trajectories of this multi-period motion are highly chaotic, and the electron wave packet dispersion effect is obvious. Therefore, diverse MRC trajectories all work but the ionization yields are lower (the pink line in Figure 4).

In the MRC trajectories, the ionized electrons pass through the nuclear region, at a distance from the ion nucleus in the y-direction. This lateral distance shrinks again with the electrons return to the nuclear region a certain number of times. This electron lateral drift process is closely related to the initial lateral velocity of electrons under the action of linearly polarized laser and is influenced by the Coulomb attraction of ion nuclei. This Coulomb attraction causes the electron wave packet to shrink laterally to a certain extent with passing near the nuclear region, which is the Coulomb focusing effect [42–46].

The ellipticity of the composite laser field changes with time. The effect of the laser electric field in the lateral direction and the Coulomb focusing effect will occur to different degrees from the lateral drift caused by the initial lateral velocity of the electrons. The electrons return to the parent nucleus ions after different drift times and undergo a collision process, and their flight trajectories show collision trajectories with multiple returns. In our simulations, the superposition of the two laser beams to different degrees makes the ellipticity change with time to different degrees, which in turn controls the electrons to recollide with trajectories with different return times in a higher degree of freedom to generate the NSDI process.

From Eqs. 5, 6, the time-dependent ellipticity can be expressed as

$ϵ\left(t\right)\approx \frac{\frac{1}{\sqrt{2}}f\left(t-\mathrm{\Delta }T\right)}{f\left(t\right)-\frac{1}{\sqrt{2}}f\left(t-\mathrm{\Delta }T\right)},(7)$

Taking the peak position of the linearly polarized laser as time zero, the variation of ϵ(t) represents the correction of the electric field properties of the linearly polarized laser. Therefore, we compare the time curve of the electric field of the linearly polarized laser along the x-direction with the curve ϵ(t). The lines are drawn in the same figure as the solid black line in Figure 6. The delay time is selected as ΔT = 2 o.c., 5 o.c., and 8 o.c. are shown by the red, green, and blue lines in Figure 6. The three curves reflect the change of the composite laser field from linear polarization to circular polarization with time. The longer the delay time, the faster ϵ(t) increases, and the more lag the area swept over.

FIGURE 6

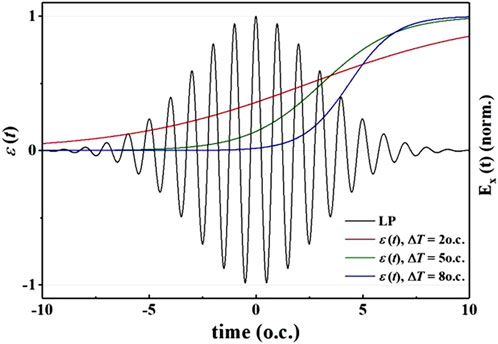
FIGURE 6. Variation of ellipsometry in laser field with different time delays. The solid black line shows the time-dependent electric field of the linearly polarized laser in the x-direction. The red, green, and blue lines show the ellipticity versus time curves for delay times ΔT = 2 o.c., 5 o.c., and 8 o.c., respectively.

The rising transition region of the red line covers the region of several larger peaks of the linearly polarized laser in a relatively larger range with ΔT = 2 o.c. Most of the electrons ionized near the laser peak are driven by the recombination field with higher ellipticity, which causes the lateral drift of the ionized electrons due to the lateral laser drive to be stronger than that caused by the initial lateral velocity. The first ionized electron prefers to stay away from the nuclear region. Therefore, most of the electrons will return to the parent nucleus in multi-period chaotic trajectories with longer drift times to collide with ions to induce NSDI [as shown in Figure 5D]. This is the reason why the ionized electron drift time is distributed over a larger range (the pink line in Figure 4).

The rising region of the blue line representing the time-dependent ellipticity overlaps the electric field of the linearly polarized laser to a small extent with ΔT = 8 o.c., which means that the changing ellipticity has less influence on the linearly polarized laser. The collision is mainly determined by several electric field peaks in the linearly polarized laser platform region. The number of electron returns is greatly affected by the initial lateral velocity and Coulomb focusing effect. The subsequent circularly polarized laser is ineffective. Therefore, as shown by the green line in Figure 4, the peak intensity of the drift time corresponding to the collision trajectories of the first three returns is stronger, and the peaks corresponding to the trajectories of other drift times are relatively suppressed.

The time-dependent ellipticity curve is shown by the green dotted line with ΔT = 5 o.c. in Figure 6. The control effect of electrons is between the above two cases. Compared with the case of ΔT = 8 o.c., the rising region of ϵ(t) only affects part of the region of the linearly polarized laser platform. The effect of the laser electric field in the lateral direction excludes the MRC trajectories. Therefore, compared with green line in Figure 4, more peaks corresponding to long drift times are suppressed, making the first peak relatively prominent (blue line in Figure 4). On the other hand, the enhancement of the first isolated peak indicates that the first return to the collision trajectory reaches the maximum. This is because compared to the case of ΔT = 2 o.c., the lateral effect of the laser electric field compensates the initial lateral velocity of the ionized electrons with the electrons return for the first time so that this channel reaches the maximum enhancement.

4 Conclusion

In summary, the NSDI of Ar in a superimposed linearly and circularly polarized compound field is investigated. The waveform change of the composite laser field is controlled by adjusting the time delay. The double ionization yield increases with the electric field strength in the electric field with different time delays. The electric field strength is chosen as 0.16 PW/cm² according to the relationship between time delay and double ionization yield. We plot the drift time distribution of ionized electrons for different delay times. By analyzing the drift time distribution of ionized electrons and electron ionization trajectories, the movement of ionized electrons in the electric field has different collision trajectories. The shape of the electric field determines the dominant trajectories of electron double ionization. the regulation of the NSDI ionization recollision trajectory form can be achieved by adjusting the delay time of the composite laser field. The MRC controlling mechanism is expected to shed more light on laser-induced electron diffraction (LIED) [47–49] or laser-induced inelastic diffraction (LIID) [50], in which electrons with different return times are considered to play different and key role in laser-induced ultrafast imaging. Our study shows that the electron dynamics in one or few optical cycle can be controlled in a multicycle laser fields, which do not have to be limited to few-cycle laser pulses.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Key Research and Development Program of China (Grant No. 2019YFA0307700), National Natural Science Foundation of China (Grant Nos. 91950101, 12074240, 11874246, 11604131, 12204136, 12204135, and 12264013), Hainan Provincial Natural Science Foundation of China (Grant Nos. 122CXTD504 and 122QN217), Natural Science Foundation of Liaoning Province of China (Grant No. LQ2020022), Sino-German Mobility Programme (Grant No. M-0031).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Krausz F, Ivanov M. Attosecond physics. Attosecond Physics Rev Mod Phys (2009) 81:163–234. doi:10.1103/RevModPhys.81.163

CrossRef Full Text | Google Scholar

2. Chang Z, Corkum P. Attosecond photon sources: The first decade and beyond [invited]. J Opt Soc Am B (2010) 27:B9. doi:10.1364/JOSAB.27.0000B9

CrossRef Full Text | Google Scholar

3. Xue B, Tamaru Y, Fu Y, Yuan H, Lan P, Mücke OD, et al. A custom-tailored multi-tw optical electric field for gigawatt soft-x-ray isolated attosecond pulses. Ultrafast Sci (2021) 2021:1. doi:10.34133/2021/9828026

CrossRef Full Text | Google Scholar

4. Hoflund M, Peschel J, Plach M, Dacasa H, Veyrinas K, Constant E, et al. Focusing properties of high-order harmonics. Ultrafast Sci (2021) 2021:1. doi:10.34133/2021/9797453

CrossRef Full Text | Google Scholar

5. Zuo R, Trautmann A, Wang G, Hannes W, Yang S, Song X, et al. Neighboring atom collisions in solid-state high harmonic generation. Ultrafast Sci (2021) 2021:1. doi:10.34133/2021/9861923

CrossRef Full Text | Google Scholar

6. Becker W, Grasbon F, Kopold R, Milošević D, Paulus G, Walther HAbove-threshold ionization: From classical features to quantum effects. Adv Mol Opt Phys (2002) 48:35–98. doi:10.1016/S1049-250X(02)80006-4

CrossRef Full Text | Google Scholar

7. Becker W, Liu XJ, Ho PJ, Eberly JHTheories of photoelectron correlation in laser-driven multiple atomic ionization. Rev Mod Phys (2012) 84:1011–43. doi:10.1103/RevModPhys.84.1011

CrossRef Full Text | Google Scholar

8. Corkum PB. Recollision physics. Phys Today (2011) 64:36–41. doi:10.1063/1.3563818

CrossRef Full Text | Google Scholar

9. Corkum PB. Plasma perspective on strong-field multiphoton ionization. Phys Rev Lett (1993) 71:1994–7. doi:10.1103/PhysRevLett.71.1994

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hickstein DD, Ranitovic P, Witte S, Tong XM, Huismans Y, Arpin P, et al. Direct visualization of laser-driven electron multiple scattering and tunneling distance in strong-field ionization. Phys Rev Lett (2012) 109:073004. doi:10.1103/PhysRevLett.109.073004

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Tong XM, Ranitovic P, Hickstein DD, Murnane MM, Kapteyn HC, Toshima N. Enhanced multiple-scattering and intra-half-cycle interferences in the photoelectron angular distributions of atoms ionized in midinfrared laser fields. Phys Rev A (Coll Park) (2013) 88:013410. doi:10.1103/PhysRevA.88.013410

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wolter B, Lemell C, Baudisch M, Pullen MG, Tong XM, Hemmer M, et al. Formation of very-low-energy states crossing the ionization threshold of argon atoms in strong mid-infrared fields. Phys Rev A (Coll Park) (2014) 90:063424. doi:10.1103/PhysRevA.90.063424

CrossRef Full Text | Google Scholar

13. Hernández-García C, Pérez-Hernández JA, Popmintchev T, Murnane MM, Kapteyn HC, Jaron-Becker A, et al. Zeptosecond high harmonic kev x-ray waveforms driven by midinfrared laser pulses. Phys Rev Lett (2013) 111:033002. doi:10.1103/PhysRevLett.111.033002

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Li PC, Sheu YL, Laughlin C, Chu SI. Dynamical origin of near- and below-threshold harmonic generation of cs in an intense mid-infrared laser field. Nat Commun (2015) 6:7178. doi:10.1038/ncomms8178

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Li PC, Sheu YL, Jooya HZ, Zhou XX, Chu SI. Exploration of laser-driven electron-multirescattering dynamics in high-order harmonic generation. Sci Rep (2016) 6:32763. doi:10.1038/srep32763

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Jia X, Hao X, Fan D, Li W, Chen J. S-matrix and semiclassical study of electron-electron correlation in strong-field nonsequential double ionization of Ne. Phys Rev A (Coll Park) (2013) 88:033402. doi:10.1103/PhysRevA.88.033402

CrossRef Full Text | Google Scholar

17. Hao X, Bai Y, Li C, Zhang J, Li W, Yang W, et al. Recollision of excited electron in below-threshold nonsequential double ionization. Commun Phys (2022) 5:31. doi:10.1038/s42005-022-00809-2

CrossRef Full Text | Google Scholar

18. Wu M, Wang Y, Liu X, Li W, Hao X, Chen J. Coulomb-potential effects in nonsequential double ionization under elliptical polarization. Phys Rev A (Coll Park) (2013) 87:013431. doi:10.1103/PhysRevA.87.013431

CrossRef Full Text | Google Scholar

19. Kang H, Henrichs K, Kunitski M, Wang Y, Hao X, Fehre K, et al. Timing recollision in nonsequential double ionization by intense elliptically polarized laser pulses. Phys Rev Lett (2018) 120:223204. doi:10.1103/PhysRevLett.120.223204

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kang H, Henrichs K, Wang Y, Hao X, Eckart S, Kunitski M, et al. Double ionization of neon in elliptically polarized femtosecond laser fields. Phys Rev A (Coll Park) (2018) 97:063403. doi:10.1103/PhysRevA.97.063403

CrossRef Full Text | Google Scholar

21. Zhang L, Xie X, Roither S, Zhou Y, Lu P, Kartashov D, et al. Subcycle control of electron-electron correlation in double ionization. Phys Rev Lett (2014) 112:193002. doi:10.1103/PhysRevLett.112.193002

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wang Y, Yu S, Lai X, Kang H, Xu S, Sun R, et al. Separating intracycle interferences in photoelectron momentum distributions by a polarization-gated pulse. Phys Rev A (Coll Park) (2018) 98:043422. doi:10.1103/PhysRevA.98.043422

CrossRef Full Text | Google Scholar

23. Mancuso CA, Hickstein DD, Grychtol P, Knut R, Kfir O, Tong X, et al. Strong-field ionization with two-color circularly polarized laser fields. Phys Rev A (Coll Park) (2015) 91:031402. doi:10.1103/PhysRevA.91.031402

CrossRef Full Text | Google Scholar

24. Mancuso CA, Dorney KM, Hickstein DD, Chaloupka JL, Tong X, Ellis JL, et al. Observation of ionization enhancement in two-color circularly polarized laser fields. Phys Rev A (Coll Park) (2017) 96:023402. doi:10.1103/PhysRevA.96.023402

CrossRef Full Text | Google Scholar

25. Chaloupka JL, Hickstein DD. Dynamics of strong-field double ionization in two-color counterrotating fields. Phys Rev Lett (2016) 116:143005. doi:10.1103/PhysRevLett.116.143005

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Mancuso CA, Dorney KM, Hickstein DD, Chaloupka JL, Ellis JL, Dollar FJ, et al. Controlling nonsequential double ionization in two-color circularly polarized femtosecond laser fields. Phys Rev Lett (2016) 117:133201. doi:10.1103/PhysRevLett.117.133201

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Eckart S, Richter M, Kunitski M, Hartung A, Rist J, Henrichs K, et al. Nonsequential double ionization by counterrotating circularly polarized two-color laser fields. Phys Rev Lett (2016) 117:133202. doi:10.1103/PhysRevLett.117.133202

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Chen Z, Su J, Zeng X, Huang X, Li Y, Huang C. Electron angular correlation in nonsequential double ionization of molecules by counter-rotating two-color circularly polarized fields. Opt Express (2021) 29:29576. doi:10.1364/OE.439864

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Djiokap JMN, Hu SX, Madsen LB, Manakov NL, Meremianin AV, Starace AF. Electron vortices in photoionization by circularly polarized attosecond pulses. Phys Rev Lett (2015) 115:113004. doi:10.1103/PhysRevLett.115.113004

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yuan KJ, Chelkowski S, Bandrauk AD. Photoelectron momentum distributions of molecules in bichromatic circularly polarized attosecond uv laser fields. Phys Rev A (Coll Park) (2016) 93:053425. doi:10.1103/PhysRevA.93.053425

CrossRef Full Text | Google Scholar

31. Pengel D, Kerbstadt S, Johannmeyer D, Englert L, Bayer T, Wollenhaupt M. Electron vortices in femtosecond multiphoton ionization. Phys Rev Lett (2017) 118:053003. doi:10.1103/PhysRevLett.118.053003

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Xiao XR, Wang MX, Liang H, Gong Q, Peng LY. Proposal for measuring electron displacement induced by a short laser pulse. Phys Rev Lett (2019) 122:053201. doi:10.1103/PhysRevLett.122.053201

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Li M, Zhang G, Ding X, Yao J. Carrier envelope phase description for an isolated attosecond pulse by momentum vortices. Chin Phys Lett (2019) 36:063201. doi:10.1088/0256-307X/36/6/063201

CrossRef Full Text | Google Scholar

34. Ben S, Chen S, Bi CR, Chen J, Liu XS. Investigation of electron vortices in time-delayed circularly polarized laser pulses with a semiclassical perspective. Opt Express (2020) 28:29442. doi:10.1364/OE.400846

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Bayer T, Wollenhaupt M. Molecular free electron vortices in photoionization by polarization-tailored ultrashort laser pulses. Front Chem (2022) 10:899461. doi:10.3389/fchem.2022.899461

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Balogh E, Kovacs K, Dombi P, Fulop JA, Farkas G, Hebling J, et al. Single attosecond pulse from terahertz-assisted high-order harmonic generation. Phys Rev A (Coll Park) (2011) 84:023806. doi:10.1103/PhysRevA.84.023806

CrossRef Full Text | Google Scholar

37. Chen J, Liu J, Fu LB, Zheng WM. Interpretation of momentum distribution of recoil ions from laser-induced nonsequential double ionization by semiclassical rescattering model. Phys Rev A (Coll Park) (2000) 63:011404. doi:10.1103/PhysRevA.63.011404

CrossRef Full Text | Google Scholar

38. Ye DF, Liu X, Liu J. Classical trajectory diagnosis of a fingerlike pattern in the correlated electron momentum distribution in strong field double ionization of helium. Phys Rev Lett (2008) 101:233003. doi:10.1103/PhysRevLett.101.233003

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Ammosov MV, Delone NB, Krainov VP. Tunnel ionization of complex atoms and atomic ions in electromagnetic field. High Intensity Laser Process (1986) 91:2008. doi:10.1117/12.938695

CrossRef Full Text | Google Scholar

40. Delone NB, Krainov VP. Energy and angular electron spectra for the tunnel ionization of atoms by strong low-frequency radiation. J Opt Soc Am B (1991) 8:1207. doi:10.1364/JOSAB.8.001207

CrossRef Full Text | Google Scholar

41. Wang X, Eberly JH. Elliptical trajectories in nonsequential double ionization. New J Phys (2010) 12:093047. doi:10.1088/1367-2630/12/9/093047

CrossRef Full Text | Google Scholar

42. Rudenko A, Zrost K, Ergler T, Voitkiv AB, Najjari B, Jesus V, et al. Coulomb singularity in the transverse momentum distribution for strong-field single ionization. J Phys B: Mol Opt Phys (2005) 38:L191–8. doi:10.1088/0953-4075/38/11/L01

CrossRef Full Text | Google Scholar

43. Shafir D, Soifer H, Vozzi C, Johnson AS, Hartung A, Dube Z, et al. Trajectory-resolved coulomb focusing in tunnel ionization of atoms with intense, elliptically polarized laser pulses. Phys Rev Lett (2013) 111:023005. doi:10.1103/PhysRevLett.111.023005

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kelvich SA, Becker W, Goreslavski SP. Coulomb focusing and defocusing in above-threshold-ionization spectra produced by strong mid-ir laser pulses. Phys Rev A (Coll Park) (2016) 93:033411. doi:10.1103/PhysRevA.93.033411

CrossRef Full Text | Google Scholar

45. Richter M, Kunitski M, Schöffler M, Jahnke T, Schmidt L, Dörner R. Ionization in orthogonal two-color laser fields: Origin and phase dependences of trajectory-resolved coulomb effects. Phys Rev A (Coll Park) (2016) 94:033416. doi:10.1103/PhysRevA.94.033416

CrossRef Full Text | Google Scholar

46. Song X, Xu J, Lin C, Sheng Z, Liu P, Yu X, et al. Attosecond interference induced by coulomb-field-driven transverse backward-scattering electron wave packets. Phys Rev A (Coll Park) (2017) 95:033426. doi:10.1103/PhysRevA.95.033426

CrossRef Full Text | Google Scholar

47. Blaga CI, Xu J, DiChiara AD, Sistrunk E, Zhang K, Agostini P, et al. Imaging ultrafast molecular dynamics with laser-induced electron diffraction. Nature (2012) 483:194–7. doi:10.1038/nature10820

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Wolter B, Pullen MG, Le AT, Baudisch M, Doblhoff-Dier K, Senftleben A, et al. Ultrafast electron diffraction imaging of bond breaking in di-ionized acetylene. Science (2016) 354:308–12. doi:10.1126/science.aah3429

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Hao X, Bai Y, Zhao X, Li C, Zhang J, Wang J, et al. Effect of coulomb field on laser-induced ultrafast imaging methods. Phys Rev A (Coll Park) (2020) 101:051401. doi:10.1103/PhysRevA.101.051401

CrossRef Full Text | Google Scholar

50. Quan W, Hao X, Hu X, Sun R, Wang Y, Chen Y, et al. Laser-induced inelastic diffraction from strong-field double ionization. Phys Rev Lett (2017) 119:243203. doi:10.1103/PhysRevLett.119.243203

PubMed Abstract | CrossRef Full Text | Google Scholar