Inefficient intramolecular vibrational energy redistribution for the H + HO2 reaction and negative internal energy dependence for its rate constant

Quasiclassical trajectories (QCT) and newly constructed global potential energy surfaces are used to compute thermal and nonthermal rate constants for the H + HO₂ reaction. The thermal QCTs rate constants are up to 50% smaller than transition state theory (TST) rate constants based on the same level of electronic structure theory. This reduction is demonstrated to result from inefficient intramolecular vibrational energy redistribution (IVR) in the transient H₂O₂ well, with a significant fraction of trajectories that reach the H₂O₂ well promptly dissociating back to reactants instead of via the heavily statistically favored 2OH channel. The nonstatistical reduction factor, κ_IVR, that quantifies this effect is shown to increase in importance with temperature, with κ_IVR = 0.81 at 300 K and 0.47 at 2500 K. Finally, we show that inefficient IVR causes H + HO₂ rate constants mediated by H₂O₂ to depend inversely on the initial vibrational excitation of HO₂.

Introduction

Transition state theory (TST) is foundational to modern chemical physics [1–3]. For more than 80 years TST has informed chemical intuition by connecting transition state structures with mechanistic insights, and more recently the high fidelity of rate constant predictions obtained by combining TST with ab initio energetics and molecular properties has been reliably demonstrated [4–7]. Over the decades, various assumptions central to TST have been tested, and here we consider the accuracy of the so-called “local equilibrium” assumption, which is the assumption of a statistically populated transition state that results from fast intramolecular vibrational energy redistribution (IVR).

Practical TST calculations involve defining a transition state dividing surface and counting the number of “forward” states N_DS on the surface, which is half the number of total states[8]. Forward states count reactive events, as per the fundamental assumption of TST[9], and the rate constant for a given candidate dividing surface k_DS is readily determined from N_DS. Importantly, approximations to the true transition state dividing surface are known to give an upper bound to the true rate constant such that a variational principle can be applied to test and optimize candidate transition state dividing surfaces via minimizations of N_DS. The optimized value of N_DS is labeled N^‡, and the resulting variational TST (VTST) rate constant k_VTST ≤ k_DS.

It can be challenging to fully minimize N^‡ with respect to all important geometric parameters defining the transition state dividing surface. So-called “recrossing” corrections κ_rc are sometimes then applied to correct for residual variational effects not fully accounted for in the variational optimizations. These correction factors are less than but typically close to 1, such that κ_rc k_VTST ≤ k_VTST ≤ k_DS. Here we are interested in characterizing a different physical effect, a dynamical or inefficient IVR correction κ_IVR ≤ 1 that can further reduce the rate constant [10–16].

Rate constants are defined relative to the equilibrating condition governing the internal and translational state distributions of the reactants, e.g., thermal rate constants describe the reactivity of thermally populated reactants, and microcanonical rate constants describe the reactivity of microcanonically populated reactants. Unlike in a global dynamics calculation, such as a classical trajectory that proceeds from reactants to products, evaluating a TST rate constant requires an additional assumption that describes the internal state population distribution at the transition state dividing surface when counting states and computing N^‡. In typical calculations, this distribution is assumed to be governed by the same equilibrating condition as the reactants. This assumption, sometimes called local equilibrium assumption, is typically but not always valid.

Here we consider the reaction H + HO₂, which can proceed on both the singlet and triplet surfaces. On the singlet surface, the major product is 2OH, which is significantly exothermic and formed via an indirect process mediated by a deep H₂O₂ well. One might expect that because the deep H₂O₂ well is the direct product of the initial capture transition state ([H + HO₂ = H₂O₂]^‡) the local equilibrium assumption would be suitable. Specifically, reactive events passing through the capture transition state might be expected to forget their history in such a deep and presumably long-lived well and would then proceed nearly exclusively via the lower energy 2OH product channel.

Instead, we show here using newly parameterized global ab initio potential energy surfaces and quasiclassical trajectories (QCTs) that an appreciable fraction of captured trajectories promptly dissociates back to reactants. This nonstatistical violation of the local equilibrium assumption for the capture rate constant has a noticeable effect on the thermal rate constant for the 2OH channel, lowering it by ∼50% relative to statistical TST predictions. Physically, this effect arises from inefficient IVR in the H₂O₂ well and an incomplete sharing of energy between the internal modes of HO₂ and the relative motion of H + HO₂. Inefficient IVR is also shown here to have an even more noticeable impact on nonthermal rate constants for H + HO₂* in which HO₂ is initially excited near its threshold energy.

Nonthermal reactions arise in energetic gas phase environments, such as in the atmosphere, shockwaves, plasmas, engines, and flames [17–26]. In these environments, HO₂ can be formed hot, and a nonnegligible fraction of HO₂* can react with abundant radicals like H atoms before it is collisionally cooled via inert “third-body” collisions. As a prototypical fast radical–atomic radical reaction, H + HO₂ has been thought to provide a significant depletion mechanism for HO₂ in the mesosphere [27], and its product branching is known to be central to controlling the second explosion limit in hydrogen oxidation [28]. This reaction has also been implicated as an initiation reaction for excited species such as ¹O₂ that are highly reactive, with noticeable impacts in hydrogen flame simulations [29]. Lastly, recent studies suggest that H + HO₂ may be a significant source for the important reactive species OH during the interaction of nonthermal atmospheric pressure plasmas with biological matter [30]. In general, while this reaction is fast under both thermal and nonthermal conditions, branching between direct and indirect products can be significantly different under nonthermal conditions thus altering the available radical pool. Here we quantify the effect that inefficient IVR has on indirect pathways both thermally and nonthermally.

This paper is organized as follows: First, we describe the construction and validation of global potential energy surfaces for the lowest-energy singlet and lowest-energy triplet states of H₂O₂. Next, the standard QCT approach used here is briefly summarized. Then, thermal rate constants are presented, and a detailed comparison of the QCT and statistical transition state theory (TST) results is made. Finally, nonthermal rate constants are discussed, and the inefficient IVR rate reduction factor κ_IVR is quantified.

Theory

Singlet and triplet potential energy surfaces

Global analytic potential energy surfaces (PESs) were generated for the lowest-energy singlet and lowest-energy triplet states of H₂O₂ using permutationally invariant polynomial (PIP) expansions [31] and the computer code PIPPy [32]. PIP expansions were trained against data sets of Molpro’s Davidson-corrected full valence MRCI + Q/CBS energies [33, 34], where the complete basis set (CBS) limit was estimated from a two-point formula using the aug'-cc-pVDZ and aug'-cc-pVTZ basis sets, and aug’ indicates the usual augmented Dunning basis sets but with diffuse functions removed for H atoms.

The MRCI + Q/CBS level of theory was benchmarked against ANL1 calculations [35] in Table 1 for the singlet and triplet stationary points illustrated in Figure 1. The ANL1 method is a composite approach employing CCSD(T)/cc-pVQZ geometries, CCSD(T) energies with complete basis set extrapolations based on quintuple-ζ and sextuple-ζ basis sets, an electron correlation correction that includes up to perturbative pentuples, a zero-point-energy anharmonicity correction, and other high-level corrections for terms commonly neglected from the electronic Hamiltonian. For small systems like H₂O₂, the expected accuracy of this approach is 0.2 kcal/mol, as demonstrated in Ref. 35. Despite its high accuracy in general, the ANL1 method cannot be reliably applied when multireference effects are large, and indeed we encounter such a case here for the saddle point for abstraction on the singlet surface, [H + HO₂ = H₂ + ¹O₂]^‡. The energy used in Figure 1 for this structure is the MRCI + Q energy. Root mean squared deviations (RMSDs) between the MRCI + Q/CBS and ANL1 results in Table 1 are 1.2 and 0.9 kcal/mol for the singlet and triplet surfaces, respectively, which is representative of the expected accuracy of the MRCI+Q/CBS method[4]. Fortunately, some of the larger deviations are for kinetically unimportant species, such as the HOOH and H₂OO wells, while kinetically important critical points, such as the threshold energy of the major singlet product 2OH and the lowest-energy triplet saddle point to form H₂ + ³O₂, are much more accurately predicted by MRCI + Q/CBS.

TABLE 1

TABLE 1. Electronic (zero point exclusive) stationary point and channel energies, kcal/mol.

FIGURE 1

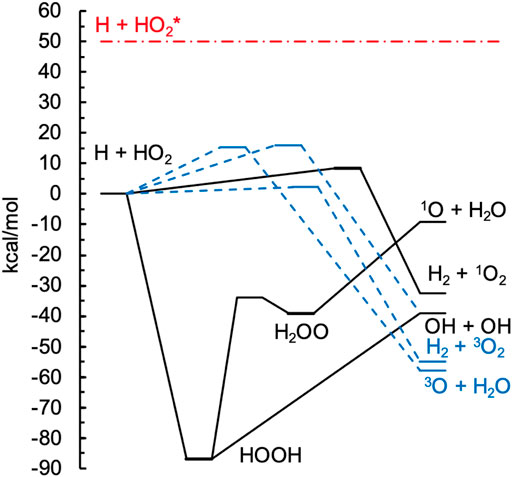
FIGURE 1. Potential energy diagram of the electronic ANL1 energies for the lowest-energy singlet (solid black lines) and triplet (dashed blue lines) surfaces for H + HO₂ → products. A typical nonthermal H + HO₂* energy is indicated by the horizontal red dash-dotted line.

Training data sets for the singlet and triplet surfaces were generated in batches, with each batch associated with a bimolecular channel or stationary point. For the unimolecular stationary points HOOH and H₂OO, geometries were generated by sampling uniformly in time from long-lived classical trajectories governed by a molecular mechanics force field [36] at total energies of 80 kcal/mol relative to H + HO₂. This procedure was also used to generate pools of sampled internal coordinates for each diatomic and polyatomic fragment appearing as a reactant or product. A batch of geometries for each bimolecular channel was then generated by sampling internal coordinates from these pools of fragment geometries and orienting the two sampled fragments at random angles with respect to each other and with a center of mass separation selected from 1 to 15 Å. Finally, batches of geometries associated with each saddle point were generated via Z-matrix displacements by up to 25% from the stationary point geometry. For the more complex singlet surface, each batch consisted of ∼36,000 geometries and MRCI + Q/CBS energies for a total of ∼288,000 training data for the singlet surface; half as many training data were generated for the simpler triplet surface.

For both the singlet and triplet electronic states, PIP expansions were generated with total expansion orders o from 7 to 11. The resulting expansions are labeled PIPo, and they are compared with the ANL1 benchmark energies and MRCI + Q/CBS training energies in Table 1. Note that the PIP expansion energies shown in Table 1 were evaluated at the MRCI + Q/CBS geometries to simplify the analysis; the magnitudes of the errors reported in Table 1 for the PIP expansions do not change significantly when optimized geometries are used.

In past work we described a strategy for weighting training data and for using out-of-sample errors to assess the quality of the PIP expansions [32, 37]. We do not report similarly detailed analyses here. Instead, we note that the weighted training errors decrease from ∼3 kcal/mol for PIP7 to ∼2 kcal/mol for PIP10, with somewhat larger errors for the triplet expansions than for the singlet expansions. The design of the weighting function leads to fitting errors that are relatively independent of energy at low energies and that have a consistent relative error at higher energies. For the PIP10 expansion for the singlet surface, for example, the weighted fitting error is 1.8 kcal/mol when averaged over the entire training set. For energies below ∼15 kcal/mol, which includes about two-thirds of the training data and the stationary points in Table 1, the weighted fitting error is 1.2 kcal/mol in good agreement with the RMS error of 1.1 kcal/mol tabulated in Table 1, as expected. For energies above ∼15 kcal/mol, the absolute errors increase with energy, such that the relative errors remain constant at about ∼8%. Errors of this magnitude are satisfactory considering that the PIP expansions are designed for nonthermal simulations with a range of relevant energies of ∼150 kcal/mol, with training data sampled at internal energies up to 80 kcal/mol above H + HO₂ while the lowest energy channels for singlet and triplet surfaces appear at –94 and –58 kcal/mol, respectively. Importantly, we demonstrate convergence with respect to the order of the PIP expansion below.

The expected quality of the PIP expansions is better quantified by the RMSDs for the stationary point energies and key stationary point thresholds reported in Table 1. Relative to the MRCI + Q/CBS training data and the ANL1 benchmark data, the PIP expansions have typical RMSDs of 1–2 kcal/mol, with notably larger errors for PIP7 than for the higher-order expansions. The RMSD for key thresholds shown in Table 1 collects errors in the saddle point energies for channels with saddle points and errors in the product energies otherwise. As shown below, trends in the RMSDs for key thresholds are found to be predictive of the QCT results, with PIP7 expansions performing poorly while the higher-order expansions are converged with respect to expansion order.

Quasiclassical trajectories

Thermal rate constants k(T) were computed using quasiclassical trajectories (QCTs) and the dynamics code DiNT [38]. Thermal ensembles are defined by the temperature T, which governs the distribution of initial rotational and vibrational state of HO₂ and the distribution of the relative translational energy. Separable harmonic oscillator and rigid rotor approximations were used to sample and randomize the phases of vibrational modes of HO₂, the initial rotational state J, and the overall orientation of HO₂ with respect to H, as usual for quasiclassical trajectories [39].

Nonthermal ensembles are defined by the parameter E_vib, the initial vibrational energy of the energized reactant HO₂*, as well as the temperature T of the other degrees of freedom. Nonthermal QCT simulations were initiated as above but with the temperature used to generate the initial vibrational coordinates and momenta for HO₂* set to E_vib/(3n–6)k_B, where n is the number of atoms in the molecule (n = 3). The vibrational momentum was then scaled such that the initial vibrational energy of HO₂* exactly equaled the desired value E_vib. The few sampled geometries where this scaling was not possible were rejected. Nonthermal rate constants are labeled k^*(E_vib,T).

Standard approaches were used for: checking convergence with respect to the maximum impact parameter, the initial and final center of mass distances, and numerical integration parameters; converting collision outcomes to rate constants; and computing two-sigma error bars representing finite-ensemble-size sampling errors [39].

Results and discussion

Thermal rate constants

We first demonstrate convergence with respect to the order of the PIP expansion. Figure 2 shows thermal QCT rate constants for H + HO₂ for both the singlet and triplet surfaces computed using several PIP expansions. Results for the three highest-order PIP expansions (PIP8, PIP9, and PIP10) differ by only a few percent from one another for the singlet surface, while the lowest-order PIP7 expansion predicts thermal rate constants that are up to 30% lower. Trends with respect to PIP order for the triplet surface are similar, although the lower rate constants and their larger statistical uncertainties lead to less definitive trends. Notably, trends in the observed QCT rate constants are predicted by trends in the RMSDs for key species reported in Table 1, where the accuracy of the PIP7 expansion is much poorer than the accuracy of the PIP8 and higher-order expansions. Throughout the rest of the article, QCT results for the PIP10 expansions are presented.

FIGURE 2

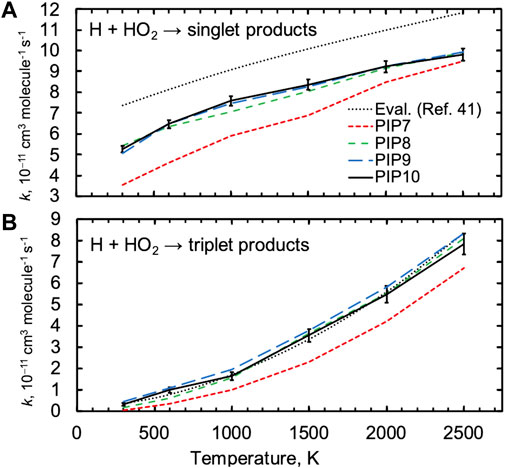
FIGURE 2. Quasiclassical trajectory thermal rate constants for H + HO₂ for the (A) singlet and (B) triplet surfaces for four PIP expansions. A set of evaluations for these rates from Ref. 41 is shown as dotted black lines. Representative two-sigma statistical error bars are shown for one set of trajectory results.

Figure 2 also shows a set of reference results for the singlet and triplet surfaces that were proposed in a recent comprehensive evaluation of H₂/O₂ chemistry based on both TST computations, modeling, and experiments [40]. The present quasiclassical trajectory results are in close agreement with the recommended rate constant for the triplet surface but are ∼25% lower than those for the singlet surface. The triplet results are discussed first.

As suggested by its lower saddle point energy in Figure 1, the major product on the triplet surface is H₂ + ³O₂, and this channel was determined to be the major triplet channel in Ref. 40. The present QCT results predict contributions from the two higher-threshold channels to be just ∼5% each at 2500 K and less than 1% at 1000 K. It is likely that the importance of these channels is overpredicted in the QCT results due to classical threshold effects, and we focus on the major triplet channel, H + HO₂ → H₂ + ³O₂.

The triplet PIP expansions accurately reproduce the benchmark energetics for the triplet saddle points, and so the good accuracy of the present QCT results for direct reaction on the triplet surface may be expected, especially at higher temperatures. The QCT method sometimes overpredicts low-probability (such as low-temperature) kinetics due to classical threshold effects, although in practice this can be compensated for by its neglect of tunneling giving rise to a fortuitous cancellation of errors. The focus of the present work is on nonstatistical effects, and so we do not explore these other effects in detail.

The QCT result for the singlet rate constant is ∼20–30% lower than the evaluation, as shown in Figure 2A, and this deviation is not a strong function of temperature in contrast to what would be expected from errors arising from threshold effects or from errors in energetics and other molecular properties. Notably, direct experimental values for the thermal rate constant H + HO₂ show significant scatter, varying from 5-7 x 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ at 300 K for example, and this range of values includes both the QCT and evaluated results [40].

Three product channels are open on the singlet surface. From Figure 1, the 2OH and ¹O+ H₂O channels can be seen to proceed indirectly via the H₂O₂ well, with the 2OH channel opening ∼30 kcal/mol lower than the ¹O+ H₂O channel, whereas the abstraction product H₂ + ¹O₂ is formed directly via a low (8 kcal/mol) barrier. As expected based on these energies, the major product channel on the singlet surface is 2OH, with the QCT method predicting up to 10% of the total singlet rate constant arising from each of the H₂ + ¹O₂ and ¹O+ H₂O channels at 2500 K and 1% and 5% for H₂ + ¹O₂ and ¹O+ H₂O at 1000 K. The evaluated rate constant shown in Figure 2A includes a contribution from the direct abstraction channel to give H₂ + ¹O₂, although this channel makes up less than 2% of the evaluated total rate constant, and the QCT rate constant for H₂ + ¹O₂ production is 2–3 times larger than the evaluated one. Again, the QCT method can overpredict small rate constants due to threshold effects, and we do not consider differences for these minor channels any further.

Comparing results for both electronic states together, we see that the dominant product at 300 K is 2OH with only minor contributions from the other product channels. At higher temperatures, direct abstraction on the triplet surface to give H₂ + ³O₂ becomes more prominent. A preliminary analysis of this channel switching between the 2OH and H₂ + ³O₂ channels and its role in combustion modeling was presented recently and is attached here as supporting information [41], and a more detailed analysis of this chemistry including a more comprehensive comparison with available experimental and theoretical work is underway [42].

Here we focus on quantifying the impact of inefficient IVR on the H + HO₂ rate constant. Figure 3 shows the PIP10 QCT singlet capture rate constant, which is the sum of the QCT rate constants for the two indirect channels 2OH and ¹O+ H₂O. Also shown is a newly computed TST capture rate constant calculated using direct variable reaction coordinate transition state theory [43, 44] (VRC-TST) and the same electronic structure theory that was used to parameterize the PIP surfaces (MRCI + Q/CBS). The present MRCI + Q/CBS-based TST capture rate constant is ∼50% larger than the QCT results, and because these two calculations are based on the same level of electronic structure theory we attribute their differences to dynamical effects, as discussed next.

FIGURE 3

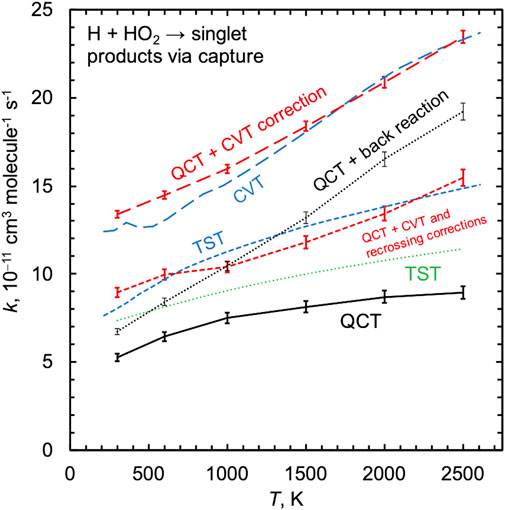
FIGURE 3. Capture rate constants for H + HO₂ on the singlet surface computed using QCT (solid black line) and TST (dashed blue line). A set of intermediate results is also shown, as discussed in Sec. 3.2. Adding nonstatistical back reaction trajectories to the QCT result is shown as a thin dotted black line. The canonical variational TST (CVT) result using atom–atom dividing surfaces (blue long dashed line) can be compared with the “QCT + CVT correction” result which counts all trajectories that access the CVT dividing surfaces (red long dashed line). The dashed red line is the result of applying a recrossing correction in addition to the CVT correction and is labeled “QCT + CVT and recrossing corrections.”

As motivated in the Introduction, the local equilibrium assumption for TST states that trajectories that encounter the transition state dividing surface do so with statistical populations, and the fundamental assumption of TST states that all of these trajectories go on to form products. The direct product of the barrierless capture process is the H₂O₂ well, which is deep enough to be expected to subsequently dissociate statistically, i.e., predominantly to the lowest-energy channel 2OH with negligible contributions to the higher-energy ¹O + H₂O channels and even smaller contributions to the higher H + HO₂ channel. Instead, we find that an appreciable fraction of trajectories that access H₂O₂ promptly turn around and reform the H + HO₂ reactants.

To demonstrate this, Figure 4 plots the probability distribution of the minimum H–OOH distance r_min along each trajectory in a thermal QCT ensemble at 1000 K. The plot shows two distinct features: a sharp feature associated with the inner turning point of the incipient OH bond around r_min = 0.7 Å and a broad feature around r_min = 2.5–3.0 Å. The sharp small-r_min feature is associated with the successful formation of a new OH bond and therefore “capture” in the deep H₂O₂ well. The broad large-r_min feature, in constrast, counts trajectories where the H atom approaches HO₂ at an unfavorable orientation and/or impact parameter for successful OH bond formation and thus avoidance of the H₂O₂ well.

FIGURE 4

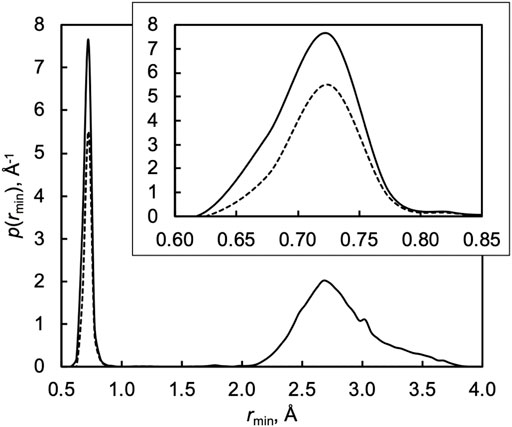
FIGURE 4. Distribution of the minimum H–OOH distance r_min along each trajectory in a QCT ensemble at 1000 K. The solid line shows the probability distribution function p for all trajectories, and the dashed line shows the probability distribution function p for reactive trajectories. The inset highlights the small-r_min region.

If energy was readily shared among all the degrees of freedom of H₂O₂, i.e., in the limit of efficient IVR, all but a negligible fraction of the trajectories associated with capture and the sharp small-r_min feature would be expected to go on to form 2OH via its low energy pathway. Instead, only two-thirds of captured trajectories are reactive at 1000 K, as highlighted in the inset of Figure 4, with the rest promptly returning to reactants and finishing the simulation as H + HO₂ instead of 2OH. Mechanistically, inefficient IVR reduces the effective dimensionality of the system. Instead of encountering a deep well with additional vibrational modes, trajectories with inefficient IVR behave as one-dimensional collisions in that they do not “see” the additional modes and instead encounter a hard wall that sends them back to the reactants.

We may quantify the deviation of the fraction of small-r_min trajectories that react from unity as the inefficient IVR reduction factor κ_IVR, which here to varies from 0.81 at 300 K to 0.67 at 1000 K to 0.47 at 2500 K. Efficient IVR is expected to be promoted when the characteristic frequencies of the two pools of energy are similar, and so we expect κ_IVR to increasingly deviate from unity with increasing temperature, as seen here.

For a given potential energy surface, one might hope to be able to interpret differences between TST and QCT rate constants as arising due to dynamical effects like inefficient IVR. We can make such a comparision here by correcting our QCT rate constant for inefficient IVR and comparing it with the TST capture rate constant. In Figure 3, the dotted line labeled “QCT + back reaction” shows the QCT rate constant for all reactive trajectories plus all nonreactive trajectories with values of r_min associated with the small-r_min sharp peak, i.e., k_QCT/κ_IVR. This quantity approximates the QCT capture rate constant and notably does not compare favorably with the TST capture rate. This is due to the unavoidable connection between IVR and variational recrossing corrections in TST; the remainder of the curves shown in Figure 3 and the discussion that follows address this issue.

The TST results include microcanonical variational optimizations, which make it difficult to produce and compare temperature-dependent information. We therefore computed another TST rate constant where simpler canonical variational optimizations were performed (i.e., where each temperature was associated with a single variationally-optimized dividing surface), and we further limited the choice of dividing surfaces to those defined by a fixed incipient O–H distance. The result of this canonical variational TST (CVT) calculation is shown in Figure 3 to be about 50% larger than the present fully variationally optimized TST results and more than a factor of two larger than the QCT results.

Using these simpler CVT dividing surfaces, we then counted the number of times they were crossed during the QCT simulations as a function of temperature. Again, we found a significant number of trajectories that accessed the CVT dividing surface and that reacted back to form H + HO₂ instead of going on to form the heavily statistically favored product 2OH. The curve labeled “QCT + CVT correction” is the result of counting all trajectories that accessed the CVT dividing surface, not just the reactive ones, and this curve indeed compares favorably to the CVT result. This demonstrates that, as expected, the QCTs are accessing the CVT transition state dividing surfaces with statistical distributions. The overprediction of the TST approach for this system arises instead because not all of these trajectories are reactive, i.e., because of the violation of the local equilibrium assumption inherent to TST caused by inefficient IVR.

The results in Figure 3 show that the ratio of the TST and QCT results depends on how the variational optimizations are carried out, as k_QCT/k_TST ≈ 0.67 is not equal to k_QCT/k_CVT ≈ 0.40, both nearly independent of temperature. More importantly, neither of these factors equals the value of κ_IVR calculated directly via the analysis in Figure 4, which instead decreases from 0.81 to 0.47 from 300 to 2500 K. This discrepancy can be explained by noting that the important variational TST dividing surfaces occur at O–H distances of 2.8 to 2.4 Å for temperatures from 300 to 2500 K. This range of O–H distances includes the shoulder of the broad large-r_min distribution of entirely nonreactive trajectories appearing in Figure 4, thus obscuring the interpretation of k_QCT/k_TST or k_QCT/k_CVT as IVR corrections distinct from recrossing/variational corrections κ_rc.

We used QCTs to compute a temperature-dependent recrossing correction, which is equal to the number of times the CVT dividing surfaces were crossed in the forward direction divided by the number of trajectories that crossed the CVT dividing surfaces at least once. This factor was found to be about 1.5 and nearly independent of temperature. When the QCT + CVT corrected rate constant is divided by this recrossing factor, the resulting rate constant is indeed found to agree with the fully variationally optimized TST result, again as expected.

This analysis demonstrates that inefficient IVR effects are inherently entangled with recrossing corrections, and simply comparing TST and QCT results, even when the same underlying electronic structure methods are used, is not sufficient to quantify the kinetic effects of inefficient IVR. In fact, the TST result in Figure 3 includes a standard VRC-TST κ_rc = 0.85 recrossing correction, which was approximated to be independent of temperature. Allowing for a temperature dependent recrossing correction might improve agreement between the TST and the “QCT + back reaction” estimate of the QCT capture rate. The present QCT results are ∼40% lower than the TST results and this difference is nearly independent of temperature. In contrast, the inefficient IVR correction κ_IVR directly computed from the QCT results is strongly temperature dependent, increasingly deviating from unity with increasing temperature (κ_IVR = 0.81 at 300 K to 0.47 at 2500 K). Indeed, the impact of inefficient IVR would be expected to increase with temperature and energy, as reflected in the behavior of κ_IVR observed here.

Nonthermal rate constants

Nonthermal rate constants k*(E_vib,T) were computed with HO₂ initially vibrationally excited up to E_vib = 53 kcal/mol above its classical minimum and for T = 1000 K for the remaining degrees of freedom. This maximum value of E_vib corresponds to a zero-point corrected internal energy of D₀ = 44 kcal/mol, which is the dissociation energy of HO₂. The average internal vibrational energy for HO₂ at 1000 K is just ∼13 kcal/mol, or 4 kcal/mol when zero-point corrected, such that the highest-energy nonthermal conditions studied here have 11× the initial internal vibrational energy as thermal conditions.

Figure 5 shows nonthermal rate constants k*(E_vib,T = 1000 K) calculated using QCTs and the PIP10 expansions for both the singlet and triplet surfaces. For all three rate constants shown, k* is in good agreement with the thermal rate constant k at 1000 K when E_vib ≈ 13 kcal/mol, the average thermal energy at 1000 K. As energy is added to HO₂ up to its dissociation threshold, the direct abstraction rate constants shown in Figure 5A increase while the indirect singlet capture rate constant shown in Figure 5B decreases. The behavior in Figure 5A is typical, as we generally expect reaction rate constants to increase with all types of energy, including vibrational energy; we indeed found this to be the case in our past studies of CH₄* + H [24] and H₂O* + H [26], both of which are direct reactions. The unusual negative vibrational energy dependence for the indirect singlet nonthermal capture rate is again attributed to inefficient IVR, as discussed next.

FIGURE 5

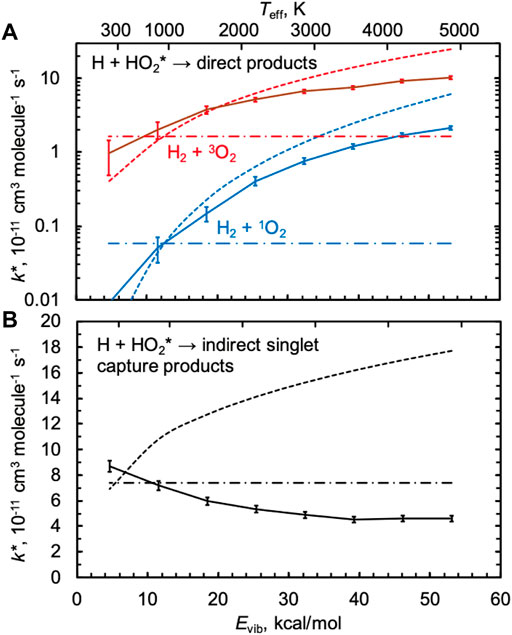
FIGURE 5. Nonthermal QCT rate constants k*(E_vib,T = 1000 (K) for several values of the classical (zero-point inclusive) initial vibrational energy E_vib of HO₂ for (A) two direct products H₂ + ¹O₂ and H₂ + ³O₂ (solid red and blue lines) and (B) the sum of the indirect singlet capture products 2OH and ¹O+ H₂O (solid black line). The associated thermal QCT rate constants at 1000 K are indicated as horizontal dash-dotted lines. The effective temperature T_eff is based on a statistical equipartition assumption and is indicated at the top of the plot, with estimates of k*≈ k(T_eff) for each rate constant shown as dotted lines.

We previously showed that one could make a statistical equipartition-of-energy assumption to approximate k*(E_vib,T) by the thermal rate constant k(T_eff), where T_eff was computed by assigning the nonthermal reactant a vibrational temperature of E_vib/k_Bln2 (3n–6), where n = 3, and then averaging the temperatures of all the modes, including rotational and translational modes equilibrated to T with each weighted half as much as each vibrational mode [24]. For HO₂* + H, T_eff varies from ∼1000 K for E_vib = 13 kcal/mol to 4900 K for the threshold energy E_vib = 53 kcal/mol for the conditions in Figure 5, as indicated at the top of the figure. The dotted lines in Figure 5 show the results of this statistical equipartition-of-energy assumption, k(T_eff), evaluated using the appropriate thermal expressions from Figures 2, 3. This is an approximate approach, such that even when statistical assumptions are favored we would not expect this model to agree quantitatively with the QCT results. Nonetheless, k(T_eff) agrees fairly well with the QCT results for the direct reactions, with differences at high energies of a factor of 3. These differences could indicate nonstatistical effects at high energies, but differences could also arise due to uncertainties in the computation of T_eff and in the extrapolation of the TST results to very high temperatures.

For the singlet capture rate in Figure 5B, the statistical equipartition-of-energy rate constant increases with energy and disagrees qualitatively with the QCT results. We calculated κ_IVR using the direct method of tracking the minimum incipient HOO–H distance r_min, as described above, and the results are shown in Figure 6. When HO₂ is vibrationally excited to its threshold energy, κ_IVR = 0.4, i.e., more than half of “captured” trajectories dissociate nonstatistically from H₂O₂ back to the reactants H + HO₂ instead of forming the heavily favored products 2OH. As E_vib decreases, κ_IVR tends toward unity. Because the indirect capture rate constant only slowly increases with E_vib, the comparatively strong negative dependence of κ_IVR on E_vib leads to a QCT capture rate constant that decreases with E_vib.

FIGURE 6

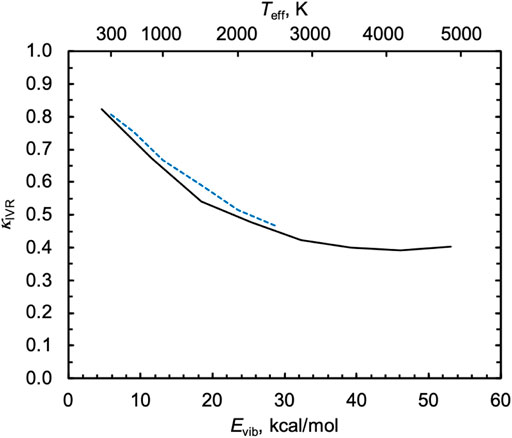
FIGURE 6. Inefficient IVR correction factors κ_IVR for the nonthermal singlet capture reaction H + HO₂* at 1000 K and as a function of the initial classical vibrational energy of HO₂, E_vib (solid black line). The calculated values of κ_IVR for the thermal singlet capture reaction is also shown (blue dashed line), where temperature was converted to E_vib using a statistical equipartition of energy model via T_eff.

Also shown in Figure 6 are the values of κ_IVR computed above for the thermal capture rate, where temperature was converted to E_vib via the statistical equipartition of energy model T_eff. The thermal values of κ_IVR are in close agreement with the nonthermal ones when plotted this way, further confirming the common origin of these effects.

Conclusion

Quasiclassical trajectories (QCTs) and newly fitted permutationally invariant polynomial (PIP) expansions were used to compute thermal and nonthermal rate constants for the H + HO₂ reaction. Inefficient sharing of intramolecular vibrational energy, i.e., inefficient IVR, was found to decrease the reaction rate for the indirect product channels (principally, 2OH), which are mediated by the H₂O₂ well. Relative to statistical TST calculations, inefficient IVR lowers the thermal rate constant by up to 50%. More dramatically, this same effect gives rise to a negative dependence of the singlet capture reaction rate on the initial vibrational energy of HO₂.

The QCT results were compared with rate constants based on statistical assumptions, including TST computations of the thermal rate constants and an ergodic energy sharing approximation for the nonthermal rate constants. This analysis demonstrated that IVR inefficiency correction factors κ_IVR calculated directly from QCTs will not necessarily agree with the ratio of QCT rates and statistical rates due to confounding recrossing corrections. Instead, κ_IVR was calculated here using QCTs and monitoring access to the H₂O₂ well and collision outcomes.

The effect of inefficient IVR on reactivity was previously characterized for reactions with HO₂, O+ OH, and H + O₂ as reactants [45–48]; these systems share features with the present system and indeed similar effects were quantified. The present nonstatistical effect is one of a variety of nonstatistical effects that have drawn notable attention as potentially limiting the accuracy of statistical approaches like TST, including inefficient thermalization of reactants [49–53], “non-RRKM” unimolecular isomerization and dissociation [54–59], and post bottleneck bifurcations [60–63]. Despite all this attention, we wish to emphasize that many reactions, including both direct and indirect ones, are often accurately treated using TST.

The nonstatistical effect quantified here––specifically, the breakdown of the local equilibrium assumption central to TST––is likely to be more prominent for small systems than for larger ones and for indirect reactions mediated by transient wells than for direct ones. An improved treatment of the quantitative effects of inefficient IVR on product branching for thermal and nonthermal reactions could impact predictive descriptions of flame modeling as well as the evolution of excited species such as ¹O₂ and ¹O in plasmas.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding author.

Author contributions

All authors contributed to design of the study. SJK calculated the ANL1 benchmark energies. AWJ and DRM constructed the PIP expansions. AWJ performed the QCT and TST computations and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the U. S. Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences through Argonne National Laboratory. Argonne is a U. S. Department of Energy laboratory managed by UChicago Argonne, LLC, under Contract Number DE-AC02-06CH11357.

Acknowledgments

We gratefully acknowledge computing resources provided by Bebop, a high-performance computing cluster operated by the Laboratory Computing Resource Center at Argonne National Laboratory. Support for DRM, YT, SJK, and RS was provided as part of the Argonne–Sandia Consortium on High-Pressure Combustion Chemistry (ANL FWP 59044).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wigner E. The transition state method. Trans Faraday Soc (1938) 34:29–41. doi:10.1039/tf9383400029

CrossRef Full Text | Google Scholar

2. Keck JC. Variational theory of chemical reaction rates applied to three-body recombinations. J Chem Phys (1960) 32:1035–50. doi:10.1063/1.1730846

CrossRef Full Text | Google Scholar

3. Pechukas P, McLafferty F. On transition-state theory and the classical mechanics of collinear collisions. J Chem Phys (1973) 58:1622–5. doi:10.1063/1.1679404

CrossRef Full Text | Google Scholar

4. Harding LB, Klippenstein SJ, Jasper AW. Ab initio methods for reactive potential surfaces. Phys Chem Chem Phys (2007) 9:4055–70. doi:10.1039/b705390h

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Klippenstein SJ, Pande VS, Truhlar DG. Chemical kinetics and mechanisms of complex systems: A perspective on recent theoretical advances. J Am Chem Soc (2014) 136:528–46. doi:10.1021/ja408723a

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Bao JL, Truhlar DG. Variational transition state theory: Theoretical framework and recent developments. Chem Soc Rev (2017) 46:7548–96. doi:10.1039/c7cs00602k

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Klippenstein SJ. From theoretical reaction dynamics to chemical modeling of combustion. Proc Combust Inst (2017) 36:77–111. doi:10.1016/j.proci.2016.07.100

CrossRef Full Text | Google Scholar

8. Miller WH. Importance of nonseparability in quantum mechanical transition-state theory. Acc Chem Res (1976) 9:306–12. doi:10.1021/ar50104a005

CrossRef Full Text | Google Scholar

9. Wigner E. Calculation of the rate of elementary association reactions. J Chem Phys (1937) 5:720–5. doi:10.1063/1.1750107

CrossRef Full Text | Google Scholar

10. Bunker DL, Hase WL. On non-RRKM unimolecular kinetics: Molecules in general and CH₃NC in particular. J Chem Phys (1973) 59:4621–32. doi:10.1063/1.1680672

CrossRef Full Text | Google Scholar

11. Bauer SH. How energy accumulation and disposal affect the rates of reactions. Chem Rev (1978) 78:147–84. doi:10.1021/cr60312a004

CrossRef Full Text | Google Scholar

12. Smally RE. Vibrational randomization measurements with supersonic beams. J Phys Chem (1982) 86:3504–12. doi:10.1021/j100215a005

CrossRef Full Text | Google Scholar

13. Uzer T, Miller WH. Theories of intramolecular vibrational energy transfer. Phys Rep (1991) 199:73–146. doi:10.1016/0370-1573(91)90140-h

CrossRef Full Text | Google Scholar

14. Nesbitt DJ, Field RW. Vibrational energy flow in highly excited molecules: Role of intramolecular vibrational redistribution. J Phys Chem (1996) 100:12735–56. doi:10.1021/jp960698w

CrossRef Full Text | Google Scholar

15. Carpenter BK. Nonstatistical dynamics in thermal reactions of polyatomic molecules. Annu Rev Phys Chem (2005) 56:57–89. doi:10.1146/annurev.physchem.56.092503.141240

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Karmakar S, Keshavamurthy S. Intramolecular vibrational energy redistribution and the quantum ergodicity transition: A phase space perspective. Phys Chem Chem Phys (2020) 22:11139–73. doi:10.1039/d0cp01413c

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Glowacki DR, Lockhart J, Blitz MA, Klippenstein SJ, Pilling MJ, Robertson SH, et al. Interception of excited vibrational quantum states by O₂ in atmospheric association reactions. Science (2012) 337:1066–9. doi:10.1126/science.1224106

PubMed Abstract | CrossRef Full Text | Google Scholar

18. da Silva G. Reaction of methacrolein with the hydroxyl radical in air: Incorporation of secondary O₂ addition into the MACR + OH master equation. J Phys Chem A (2012) 116:5317–24. doi:10.1021/jp303806w

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Pfeifle M, Olzmann M. Consecutive chemical activation steps in the OH-initiated atmospheric degradation of isoprene: An analysis with coupled master equations. Int J Chem Kinet (2014) 46:231–44. doi:10.1002/kin.20849

CrossRef Full Text | Google Scholar

20. Burke MP, Goldsmith CF, Georgievskii Y, Klippenstein SJ. Towards a quantitative understanding of the role of non-Boltzmann reactant distributions in low-temperature oxidation. Proc Combust Inst (2015) 35:205–13. doi:10.1016/j.proci.2014.05.118

CrossRef Full Text | Google Scholar

21. Goldsmith CF, Burke MP, Georgievskii Y, Klippenstein SJ. Effect of non-thermal product energy distributions on ketohydroperoxide decomposition kinetics. Proc Combust Inst (2015) 35:283–90. doi:10.1016/j.proci.2014.05.006

CrossRef Full Text | Google Scholar

22. Labbe NJ, Sivaramakrishnan R, Goldsmith CF, Georgievskii Y, Miller JA, Klippenstein SJ. Ramifications of including non-equilibrium effects for HCO in flame chemistry. Proc Combust Inst (2017) 36:525–32. doi:10.1016/j.proci.2016.06.038

CrossRef Full Text | Google Scholar

23. Burke MP, Klippenstein SJ. Ephemeral collision complexes mediate chemically termolecular transformations that affect system chemistry. Nat Chem (2017) 9:1078–82. doi:10.1038/nchem.2842

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jasper AW, Sivaramakrishnan R, Klippenstein SJ. Nonthermal rate constants for CH₄* + X → CH₃ + HX, X = H, O, OH, and O₂. J Chem Phys (2019) 150:114112. doi:10.1063/1.5090394

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Miller JA, Sivaramakrishnan R, Tao Y, Goldsmith CF, Burke MP, Jasper AW, et al. Combustion chemistry in the twenty-first century: Developing theory-informed chemical kinetics models. Prog Energ Combust Sci (2021) 83:100886. doi:10.1016/j.pecs.2020.100886

CrossRef Full Text | Google Scholar

26. Tao Y, Jasper AW, Georgievskii Y, Klippenstein SJ, Sivaramakrishnan R. Termolecular chemistry facilitated by radical-radical recombinations and its impact on flame speed predictions. Proc Combust Inst (2021) 31:515–22. doi:10.1016/j.proci.2020.06.342

CrossRef Full Text | Google Scholar

27. Prather MJ. Ozone in the upper stratosphere and mesosphere. J Geophys Res (1981) 86:5325–38. doi:10.1029/jc086ic06p05325

CrossRef Full Text | Google Scholar

28. Baldwin RR, Fuller ME, Hillman JS, Jackson D, Walker RW. Second limit of the hydrogen + oxygen mixtures: The reaction H + HO₂. J Chem Soc Faraday Trans 1 (1974) 70:635–41. doi:10.1039/f19747000635

CrossRef Full Text | Google Scholar

29. Konnov AA. On the role of excited species in hydrogen combustion. Combust Flame (2015) 162:3755–72. doi:10.1016/j.combustflame.2015.07.014

CrossRef Full Text | Google Scholar

30. Schroter S, Wijaikhum A, Gibson AR, West A, Davies HL, Minesi N, et al. Chemical kinetics in an atmospheric pressure helium plasma containing humidity. Phys Chem Chem Phys (2018) 20:24263–86. doi:10.1039/c8cp02473a

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Braams BJ, Bowman JM. Permutationally invariant potential energy surfaces in high dimensionality. Int Rev Phys Chem (2009) 28:577–606. doi:10.1080/01442350903234923

CrossRef Full Text | Google Scholar

32. Moberg DR, Jasper AW. Permutationally invariant polynomial expansions with unrestricted complexity. J Chem Theor Comput (2021) 9:5440–55. doi:10.1021/acs.jctc.1c00352

CrossRef Full Text | Google Scholar

33. Knowles PJ, Werner H-J. Chem. Phys. Lett. (1998) 145:514.

Google Scholar

34. Werner H-J, Knowles PJ. An efficient internally contracted multiconfiguration–reference configuration interaction method. J Chem Phys (1988) 89:5803–14. doi:10.1063/1.455556

CrossRef Full Text | Google Scholar

35. Klippenstein SJ, Harding LB, Ruscic B. Ab initio computations and active thermochemical tables hand in hand: Heats of formation of core combustion species. J Phys Chem A (2017) 121:6580–602. doi:10.1021/acs.jpca.7b05945

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Rackers JA, Wang Z, Lu C, Laury ML, Lagardere L, Schnieders MJ, et al. Tinker 8: Software tools for molecular design. J Chem Theor Comput (2018) 14:5273–89. doi:10.1021/acs.jctc.8b00529

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Jasper AW, Davis MJ. Parameterization strategies for intermolecular potentials for predicting trajectory-based collision parameters. J Phys Chem A (2019) 123:3464–80. doi:10.1021/acs.jpca.9b01918

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Jasper AW, Zhang RM, Truhlar DG. Direct nonadiabatic trajectories (DiNT): A code for non-born–oppenheimer molecular dynamics. Lemont, IL, United States: Argonne National Laboratory and University of Minnesota (2020).

Google Scholar

39. Truhlar DG, Muckerman JT, Bernstein RD, Raff LM, Thompson DL. In: Baer M, editor. Atom-molecule collision theory: A guide for the experimentalist. Theory of chemical reaction dynamics, 3. New YorkBoca Raton: PlenumCRC Press (1979). p. 5051–566121.

Google Scholar

40. Burke MP, Chaos M, Ju Y, Dryer FL, Klippenstein SJ. Comprehensive H₂/O₂ kinetic model for high-pressure combustion. Int J Chem Kinet (2012) 44:444–74. doi:10.1002/kin.20603

CrossRef Full Text | Google Scholar

41. Tao Y, Klippenstein SJ, Georgievskii Y, Miller JA, Lei L, Burke MP, et al. Nonthermal reactions: The final frontier in understanding the kinetics of hydrogen oxidation. Columbia, SC: Spring Technical Meeting of the Eastern States Section of the Combustion Institute (2020). Paper 1A04.

Google Scholar

42. Tao Y, Georgievskii Y, Miller JA, Klippenstein SJ, Jasper AW, Burke MP, et al. unpublished (2022).

43. Klippenstein SJA. A bond length reaction coordinate for unimolecular reactions. II. Microcanonical and canonical implementations with application to the dissociation of NCNO. J Chem Phys (1991) 94:6469–82. doi:10.1063/1.460276

CrossRef Full Text | Google Scholar

44. Klippenstein SJ. Variational optimizations in the rice–ramsperger–kassel–marcus theory calculations for unimolecular dissociations with No reverse barrier. J Chem Phys (1992) 96:367–71. doi:10.1063/1.462472

CrossRef Full Text | Google Scholar

45. Miller JA. Nonstatistical effects and detailed balance in quasiclassical trajectory calculations of the thermal rate coefficient for O + OH → O₂ + H. J Chem Phys (1986) 84:6170–7. doi:10.1063/1.450758

CrossRef Full Text | Google Scholar

46. Yang C-Y, Klippenstein S. J. Comparisons between statistics, dynamics, and experiment for the H + O₂ → OH + O reaction. J Chem Phys (1995) 103:7287–98. doi:10.1063/1.470303

CrossRef Full Text | Google Scholar

47. Miller JA, Garrett BC. Quantifying the non-RRKM effect in the H + O₂ → OH + O reaction. Int J Chem Kinet (1997) 29:275–87. doi:10.1002/(sici)1097-4601(1997)29:4<275:aid-kin6>3.0.co;2-r

CrossRef Full Text | Google Scholar

48. Perry JW, Dawes R, Wagner AF, Thompson DL. A classical trajectory study of the intramolecular dynamics, isomerization, and unimolecular dissociation of HO₂. J Chem Phys (2013) 139:084319. doi:10.1063/1.4818879

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Widom B. Reaction kinetics in stochastic models. J Chem Phys (1971) 55:44–52. doi:10.1063/1.1675541

CrossRef Full Text | Google Scholar

50. Clark TC, Dove JE, Finkelman M. Temperature dependence of rates of bimolecular elementary reactions. Acta Astronautica (1979) 6:961–75. doi:10.1016/0094-5765(79)90081-x

CrossRef Full Text | Google Scholar

51. Lim C, Truhlar DG. The effect of vibrational-rotational disequilibrium on the rate constant for an atom-transfer reaction. J Phys Chem (1986) 90:2616–34. doi:10.1021/j100403a014

CrossRef Full Text | Google Scholar

52. Levine RD. The dynamics of elementary processes and combustion kinetics. Combust Flame (1989) 78:5–11. doi:10.1016/0010-2180(89)90004-7

CrossRef Full Text | Google Scholar

53. Teitelbaum H. Non-equilibrium kinetics of bimolecular reactions. Effect of anharmonicity on the rate law. Chem Phys Lett (1993) 202:242–7. doi:10.1016/0009-2614(93)85273-q

CrossRef Full Text | Google Scholar

54. Katō T. Nonequilibrium unimolecular dissociation influenced by intramolecular vibrational energy redistribution. J Chem Phys (1998) 108:6611–8. doi:10.1063/1.476076

CrossRef Full Text | Google Scholar

55. Shalashilin DV, Thompson DL. Method for predicting IVR-limited unimolecular reaction rate coefficients. J Chem Phys (1997) 107:6204–12. doi:10.1063/1.474285

CrossRef Full Text | Google Scholar

56. Agbo JK, Leitner DM, Evans DA, Wales DJ. Influence of vibrational energy flow on isomerization of flexible molecules: Incorporating non-rice-ramsperger-kassel-marcus kinetics in the simulation of dipeptide isomerization. J Chem Phys (2005) 123:124304. doi:10.1063/1.2011399

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Lourderaj U, Hase WL. Theoretical and computational studies of non-RRKM unimolecular dynamics. J Phys Chem A (2009) 113:2236–53. doi:10.1021/jp806659f

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Ma X, Hase WL. Perspective: Chemical dynamics simulations of non-statistical reaction dynamics. Phil Trans R Soc A (2017) 375:20160204. doi:10.1098/rsta.2016.0204

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Matsugi A. Potential nonstatistical effects on the unimolecular decomposition of H₂O₂. J Phys Chem A (2022) 126:4482–96. doi:10.1021/acs.jpca.2c03501

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Wang ISY, Karplus M. Dyanmics of organic reactions. J Am Chem Soc (1973) 95:8160–4. doi:10.1021/ja00805a033

CrossRef Full Text | Google Scholar

61. Lourderaj U, Park K, Hase WL. Classical trajectory simulations of post-transition state dynamics. Int Rev Phys Chem (2008) 27:361–403. doi:10.1080/01442350802045446

CrossRef Full Text | Google Scholar

62. Ess DH, Wheeler SE, Iafe RG, Xu L, Çelebi-Ölçüm N, Houk KN. Bifurcations on potential energy surfaces of organic reactions. Angew Chem Int Ed (2008) 47:7592–601. doi:10.1002/anie.200800918

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Rehbein J, Carpenter BK. Do we fully understand what controls chemical selectivity? Phys Chem Chem Phys (2011) 13:20906–22. doi:10.1039/c1cp22565k

PubMed Abstract | CrossRef Full Text | Google Scholar