Insight into the dynamics of electro-magneto-hydrodynamic fluid flow past a sheet using the Galerkin finite element method: Effects of variable magnetic and electric fields

The aim of this work is to investigate the influence of Arrhenius activation energy and variable thermal conductivity with EMHD fluid flow over a nonlinearly radiating stretching sheet in a porous medium. The main objective of this research is to study the effects of variable electromagnetohydrodynamic (EMHD) on fluid flow motion. The significance of the combined effects of electric and magnetic fields is useful where one can create a strong Lorentz force for industry applications. The fundamental laws, that is, conservation of mass, momentum, and energy equations, are given in the form of partial differential equations (PDEs). The current fluid flow problem is not similar, which means that the presented solution is local. The introduction of nonsimilarity variables transforms PDEs into a set of coupled ODEs. The resultant ODEs are not only solved computationally by MATLAB built-in solver bvp4c but the solution is also obtained with other numerical schemes that include the shooting method and the finite element method (FEM). In applying FEM, we choose the Galerkin method in which the weight function is equal to the shape function. The aforementioned numerical methods are implemented and programmed in MATLAB. Graphs illustrate the effects of various parameters on the velocity, temperature, concentration, and microorganism profiles. Physical parameters measure the roughness of the sheet (skin friction coefficient), heat transfer rate at the sheet (local Nusselt number), the mass transfer rate of the concentration gradient (local Sherwood number), and transfer rate of microorganisms at the sheet (density of motile microorganism). The skin friction coefficient increases for higher values of (K_p) and magnetic parameters (M). The local Sherwood number decreases for different values of activation energy. An excellent agreement of FEM results with other numerical methods, shooting method, and bvp4c has been achieved. Moreover, for particular cases, the current results have a good agreement with the published work.

1 Introduction

Scientists and mathematicians encounter fluids everywhere. Studying fluid flow over a stretching sheet has a wide range of applications in technological devices, medical instruments, and in the manufacturing industry. The production of sheeting materials takes place in a number of industrial manufacturing procedures and involves metal and polymer sheets, for example, cooling an infinite metal plate in a cooling bath Rana et al. [1], Buongiorno [2], material handling conveyors, aerodynamic extrusion of plastic sheets Vajravelu [14], Char [15], glass blowing, paper production, drawing plastic films, and metal spinning Buongiorno [2], Vishalakshi et al. [16].

A bio-nanofluid is a fluid that contains a base fluid, nanoparticles, and living microorganisms. Algae and oxytaxis bacteria are a couple of examples of microorganisms Mahmud et al. [4]. Bioconvection is caused by microbes living in a fluid. This phenomenon stabilizes the nanoparticles and enhances the thermal and mass transport susceptibility of the fluid Kuznetsov [5]. Biomedical engineering, environmental systems, and biological technology depend on bioconvection and the suspension of nanoparticles Chan et al. [19]. Biosensors and biofuel cells are two other areas where bioconvection is also extensively used. The topic of bioconvection flow has been covered by Balla et al [6]. Shafiq et al. [7] considered second-grade bioconvective nanofluid flow. Ferdows et al. [8] investigated bioconvection flow over an exponentially stretchable surface. Recently, Sangeetha and Poulomi [9] discussed MHD bioconvection flow with gyrotactic microorganisms over a non-Darcian porous medium.

The capacity of a fluid to carry heat is measured by its thermal conductivity. The thermal conductivity of various materials is constant at standard conditions. However, if the temperature gradient is considerable, it may be a function of temperature. According to James et al. [10], the variation of physical parameters, such as thermal conductivity, has been regarded as a function of temperature during the heat and mass transfer flow over a hot sheet or a plate causing a major effect in the cooling process. In the context of the variable thickened surface, Hayat et al. [11] studied the variable thermal conductivity.

Heat flow is severely constrained by the base fluid’s poor thermal conductivity. Choi and Eastman [17] showed that the thermal conductivity of the fluid can be increased by suspending metallic nanoparticles with the base fluid. The colloids produced with base fluid and nanoparticle size ranging from 1 to 100 nm are known as nanofluids Choi and Eastman [17]. Since nanofluids have greater thermal conductivity and heat transfer rate, they are frequently used in electronic circuits Buongiorno [2], as a coolant in radiators Devendiran and Amirtham [18]. Rasouli et al. [3] mentioned that improper handling, blockage, and insufficient mixing of the material, in addition to the instability of nanoparticles, led to a decrease in the rate of heat and mass transfer.

An electric field is created by static charges, while a magnetic field is formed by the varying motion of electric charges. The study of the magnetic characteristics and behavior of electrically conducting fluids is known as magnetohydrodynamics (MHD). MHD has many applications in medical sciences, the transportation industry, and the engineering industry. For instance, a high-intensity electric field may be used to diminish or slow the growth of a tumor in the brain. MHD absorbs energy and depicts a controllable behavior that makes it useful as a cooling material in electrochemistry, chemical engineering Mjankwi et al. [13], polymer processing Hamad [20], Jusoh and Pop [22], and MHD generator Ganesh et al. [21]. An external magnetic field impacts the motion of the electrically conducting fluids. This interaction produces a Lorentz force. For flow control, the strong Lorentz force is required for industrial applications, which are obtained by the electric field Wakif et al. [23], and Sajid and Khan [12] studied the thermal radiation on boundary layer flow due to an exponentially stretching sheet. Similarly, electromagnetic effects deal with the electrically conducting fluids in a magnetic field. EMHD can be utilized to enhance the flow rates in microchannel Das et al. [24], Paul and Chakraborty [25], Si and Jian [26], and Sinha and Shit [27].

Activation energy is the minimum energy required for reactants to undergo a chemical transformation or physical transport. Arrhenius energy with mass transport phenomenon and chemical reaction has been widely analyzed owing to its numerous applications in the compound invention, geothermal artificial lake, and retrieval of thermal lubricant and simmer own of atomic reactors. Providing the activation energy through the Arrhenius equation can be difficult at times as the temperature highly fluctuates with the rate constant. It is crucial to be effective with the reaction and energy discarded as the conversions can have diverse effects from reactants. The joint enactment of the Arrhenius activation energy with the chemical reaction for radiative flow and heat transport to the vertical pipe was reported by Bestman [28] at first. Mustafa et al. [29] discussed the properties of magneto-nanofluid with activation energy and buoyancy influence. In recent times, many efforts have been made in this regard as this is an emerging phenomenon that has wide applications Khan et al. [30], Makinde and Animasaun [31], Andersson et al. [32], Ganesh et al. [33], Kalaivanan et al. [34], Zhang et al. [35] and Jama et al. [36].

The primary research questions and novelties addressed in this work are as follows:

1. how do Peclet number and Schmidt number affect the concentration profiles, as well as the density of motile microorganisms?

2. How do increasing Lorentz force and porosity of the medium affect the velocity?

3. To what extent does activation energy control the mass transfer rate?

4. How do convective boundary condition parameters affect the temperature and concentration profiles? Moreover, how do the local Nusselt number and local Sherwood number change at the surface due to the convective boundary condition parameter?

5. How accurate is the Galerkin FEM when compared to the shooting method and bvp4c?

In this paper, the main objective of the analysis is to study the impact of Arrhenius activation energy on the MHD flow of bio-nanofluid with heat and mass transfer through a porous medium over a nonlinear stretching sheet with thermal radiation, viscous dissipation, and chemical reaction. Moreover, variable thermal conductivity is also considered, which is a function of temperature. The paper is organized as follows: Section 1 is an introduction to a mathematical model. Problem formulation is given in Section 2. Physical parameters are discussed in Section 3. A numerical procedure is discussed in Section 4. Section 5 is about results and discussion. Section 6 draws the conclusion of the research work.

2 Problem formulation

Consider an EMHD two-dimensional steady laminar flow of bio-nanofluid over a nonlinearly stretching sheet with thermal radiation, variable thermal conductivity, Arrhenius activation energy, and convective heat and mass boundary conditions. The surface is placed at y = 0 and a variable magnetic field $B(x)=B_o{x}^{\frac{m-1}{2}}$ and a variable electric field $E(x)=E_o{x}^{\frac{m-1}{2}}$ have been applied in a perpendicular direction of the fluid flow. The sheet at y = 0 has been stretched with the velocity u_w = ax^m, where a, m > 0 are positive constants. The magnetic Reynolds number does not induce a magnetic field due to its low value. The two-dimensional magnetohydrodynamic (MHD) boundary layer flow equations are given as follows:

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

$\begin{array}{ll}\hfill u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}& =\nu \frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma }{{\rho }_f}\left(B^2\left(x\right)-E\left(x\right)B\left(x\right)\right)+\frac{1}{{\rho }_f}\left(\left(1-C_{\infty }\right){\rho }_{f\infty }{\beta }_T{g}^{*}\left(T-T_{\infty }\right)\right.\hfill \\ \hfill & \left.-\left({\rho }_p-{\rho }_{p\infty }\right){\beta }_c{g}^{*}\left(C-C_{\infty }\right)\right)-\frac{\nu }{K{p}^{*}}u,\hfill \end{array}(2)$

$\begin{array}{ll}\hfill u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}& =\frac{1}{{\left(\rho c_p\right)}_f}\frac{\partial }{\partial y}\left(\frac{k\partial T}{\partial y}\right)-\frac{1}{{\left(\rho c_p\right)}_f}\frac{\partial q_r}{\partial y}+\frac{Q\left(x\right)}{{\left(\rho c_p\right)}_f}\left(T-T_{\infty }\right)+\frac{\sigma }{{\left(\rho c_p\right)}_f}{\left(uB\left(x\right)-E\left(x\right)\right)}^2\hfill \\ \hfill & +\frac{\mu }{{\left(\rho c_p\right)}_f}{\left(\frac{\partial u}{\partial y}\right)}^2+\tau \left(D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right),\hfill \end{array}(3)$

$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2}-K_r^2\left(C-C_{\infty }\right){\left(\frac{T}{T_o}\right)}^n\mathit{exp}\left(\frac{-Ea}{K_{B}T}\right),(4)$

$u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}+\frac{b{w}_c}{\left(C_w-C_{\infty }\right)}N\frac{{\partial }^{2}C}{\partial y^2}+\frac{b{w}_c}{\left(C_w-C_{\infty }\right)}\frac{\partial N}{\partial y}\frac{\partial C}{\partial y}=D_n\frac{{\partial }^{2}N}{\partial y^2}.(5)$

The subjected boundary conditions are expressed as follows:

$\begin{array}{l}\hfill \begin{array}{cc}\hfill & u=u_w=a{x}^m,v=0,-k_o\frac{\partial T}{\partial y}=h_1\left(T_w-T\right),-D_B\frac{\partial C}{\partial y}=h_2\left(C_w-C\right),N=N_w,\text{at}y=0,\hfill \\ \hfill & u\to 0,T\to T_{\infty },C\to C_{\infty },N\to N_{\infty },\text{as}y\to \infty ,\hfill \end{array}\end{array}(6)$

where $\nu =\frac{\mu }{\rho }$ is the dynamic viscosity of the fluid, σ is the electrical conductivity, ρ_f is the density of the fluid, B is a uniform magnetic field applied transverse to the flow direction, and u and v are the velocity components in x − and y – directions, respectively. g*, β_t, and β_c are, respectively, gravitational acceleration, volumetric thermal, and solutal expansion coefficients. Here, T is the temperature; C is the nanoparticles concentration; N is the concentration of microorganisms; Kp* is the permeability of the porous medium; c_p is the specific heat constant; and D_B, D_T, and D_n are Brownian diffusion, thermophoretic diffusion, and diffusivity of microorganism, respectively. q_r is the radiative heat flux and Q(x) is the volumetric rate of heat generation/absorption. Kr is the chemical reaction rate, n is fitted rate constant, Ea is activation energy, and h₁ and h₂ are heat and mass transfer coefficients, respectively. w_c is the maximum cell swimming speed and b is the chemotaxis constant.The nondimensional similarity variables are defined as follows:

$\begin{array}{l}\hfill \begin{array}{cc}\hfill & \eta =\sqrt{\frac{a\left(m+1\right)}{2\nu }}{x}^{\frac{m-1}{2}}y,u=a{x}^m{f}^{\prime }\left(\eta \right),v=-\sqrt{\frac{\nu a\left(m+1\right)}{2}}{x}^{\frac{m-1}{2}}\left(f\left(\eta \right)+\eta \frac{m-1}{m+1}{f}^{\prime }\left(\eta \right)\right),\hfill \\ \hfill & \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\chi \left(\eta \right)=\frac{N-N_{\infty }}{N_w-N_{\infty }}.\hfill \end{array}\end{array}(7)$

$f^{‴}+f{f}^{″}-\frac{2m}{m+1}{f}^{\prime 2}-M\left(f^{\prime }-E_1\right)+\lambda \left(\theta -Nr\varphi \right)-Kp{f}^{\prime }=0,(8)$

$\left(1+ϵ\theta +\frac{4}{3}Rd\right){\theta }^{″}+ϵ{\theta }^{\prime 2}+P{r}_o\left(f{\theta }^{\prime }+MEc{\left(f^{\prime }-E_1\right)}^2+Ec{f}^{\prime \prime 2}+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{\theta }^{\prime 2}+s\theta \right)=0,(9)$

${\varphi }^{″}+\frac{Nt}{Nb}{\theta }^{″}+Sc\left(f{\varphi }^{\prime }-\frac{2}{m+1}{\sigma }_1\varphi {\left(1+\delta \theta \right)}^n\mathit{exp}\left(\frac{-E}{1+\delta \theta }\right)\right)=0,(10)$

${\chi }^{″}+Sbf{\chi }^{\prime }-Pe\left(\chi {\varphi }^{″}+{\chi }^{\prime }{\varphi }^{\prime }\right)=0.(11)$

Here, f is the dimensionless stream function. Following Prasad et al. [37], the thermal conductivity k is expressed as follows:

$k\left(T\right)=k_o\left(1+ϵ\theta \right),(12)$

The transformed boundary conditions corresponding to the above nondimensional variable are presented as follows:

$\begin{array}{l}\hfill \begin{array}{cc}\hfill & f\left(0\right)=0,f^{\prime }\left(0\right)=1,{\theta }^{\prime }\left(0\right)=-{\beta }_1\left(1-\theta \left(0\right)\right),{\varphi }^{\prime }\left(0\right)=-{\beta }_2\left(1-\varphi \left(0\right)\right),\chi \left(0\right)=1,\hfill \\ \hfill & f^{\prime }\left(\infty \right)=0,\theta \left(\infty \right)=0,\varphi \left(\infty \right)=0,\chi \left(\infty \right)=0,\hfill \end{array}\end{array}(13)$

where $M=\frac{2\sigma B_0^2}{(m+1)\rho a}$ is a magnetic parameter, $E_1=\frac{E_o}{u_w{B}_o}$ is an electric parameter, $Kp=\frac{2\nu L}{(m+1)aK{p}^{*}}$ is the porosity parameter, the Grashof number is $Gr=\frac{2g^{*}{\beta }_t(1-C_{\infty }){\rho }_{f\infty }(T_w-T_{\infty })x^3}{{\rho }_f{\nu }^2(m+1)}$, $Nr=\frac{({\rho }_p-{\rho }_{f\infty }){\beta }_c(C_w-C_{\infty })}{(1-C_{\infty }){\rho }_f{\beta }_t(T_w-T_{\infty })}$ represents the ratio of buoyancy parameter, mixed convection parameter is $\lambda =\frac{Gr}{R{e}_x^2}$, $P{r}_o=\frac{{\mu }_o{c}_p}{k_o}$ is the ambient Prandtl number, $Rd=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k_o{k}^{*}}$ denotes the radiation parameter, $s=\frac{2Q_{o}x}{a{(\rho C_p)}_f{u}_w(m+1)}$ is the local heat source/sink parameter, $Ec=\frac{u_w^2}{c_p(T_w-T_{\infty })}$ is Eckert number, $Nb=\frac{\tau D_B(C_w-C_{\infty })}{C_{\infty }\nu }$ is the Brownian motion parameter, $Nt=\frac{\tau D_T(T_w-T_{\infty })}{\nu T_{\infty }}$ is the thermophoresis parameter, $Sc=\frac{\nu }{D}$ is Schmidt number, $E=\frac{-Ea}{K_B{T}_{\infty }}$ is the dimensionless activation parameter, ${\sigma }_1=\frac{K{r}^2}{a{x}^{m-1}}$ is the chemical reaction parameter, $\delta =\frac{T_w-T_{\infty }}{T_{\infty }}$ is temperature difference, ${\beta }_1=\frac{h_1}{k_o}\sqrt{\frac{2\nu }{a(m+1)}}{x}^{\frac{-m+1}{2}}$ and ${\beta }_2=\frac{h_2}{D_B}\sqrt{\frac{2\nu }{a(m+1)}}{x}^{\frac{-m+1}{2}}$ are thermal and concentration Biot numbers, respectively, $Sb=\frac{\nu }{D_n}$ is bioconvection Schmidt number, and $Pe=\frac{b{w}_c}{D_n}$ is Peclet number.

3 Physical quantities

3.1 Skin friction coefficient

A key dimensionless parameter that determines the frictional drag on the surface is the skin friction coefficient C_f. It is defined as:

$C_f=\frac{{\tau }_w^{*}}{\rho u_w^2},(14)$

Here, the wall shear stress is written as ${\tau }_w^{*}=\mu {(\frac{\partial u}{\partial y})}_{y=0}$. After putting ${\tau }_w^{*}=\mu {(\frac{\partial u}{\partial y})}_{y=0}$ in Eq. 14 and using algebra we get,

$C_f\sqrt{R{e}_x}=\sqrt{\frac{m+1}{2}}{f}^{″}\left(0\right),(15)$

where $R{e}_x=\frac{u_{w}x}{\nu }$ is the local Reynolds number.

3.2 Local Nusselt number

To quantify the heat transfer rate at the wall, we measure the local Nusselt number Nu_x at the surface.

$N{u}_x=-\frac{x{q}_w}{k_o\left(T_w-T_{\infty }\right)},(16)$

Here, $q_w=k_o{(\frac{\partial T}{\partial y})}_{y=0}$ is the Fourier’s law at the wall. Thus, we get:

${\mathrm{R}\mathrm{e}}_x^{\frac{-1}{2}}N{u}_x=-\sqrt{\frac{m+1}{2}}\left(1+\frac{4Rd}{3}\right){\theta }^{\prime }\left(0\right).(17)$

3.3 Local Sherwood number

To measure the mass transfer rate at the wall, the local Sherwood number Sh_x is calculated by the following formula:

$S{h}_x=\frac{x{j}_w}{D_B\left(C_w-C_{\infty }\right)}.(18)$

Using Fick’s law $j_w=-D_B{(\frac{\partial C}{\partial y})}_{y=0}$ in Eq. 18 we get:

${\mathrm{R}\mathrm{e}}_x^{\frac{-1}{2}}S{h}_x=-\sqrt{\frac{m+1}{2}}{\varphi }^{\prime }\left(0\right).(19)$

3.4 Local density of motile microorganisms

The local density of motile microorganisms is defined as follows:

$N{n}_x=\frac{x{i}_w}{D_n{N}_w},(20)$

here i_w is:

$i_w=-D_n{\left(\frac{\partial N}{\partial y}\right)}_{y=0},(21)$

and local density of motile microorganisms Nn_x is converted to:

${\mathrm{R}\mathrm{e}}_x^{\frac{-1}{2}}N{n}_x=-\sqrt{\frac{m+1}{2}}{\chi }^{\prime }\left(0\right).(22)$

4 Numerical procedure

A numerical solution is obtained by three methods: finite element method (FEM), shooting method, and bvp4c. In the first section, the procedure to use the finite element method is presented followed by the shooting method and bvp4c.

4.1 Finite element method

The governing ODEs in Eqs. 8–11 are coupled and nonlinear. Before applying FEM, we first establish a procedure to linearize the ODEs. The linearization procedure is given as follows.

4.1.1 Linearization of ODEs

Let us define a variable F

$f^{\prime }=F,(23)$

for Eqs. 8–11. The abovementioned variable reduces the order of Eq. 8 from three to two. It is worth notingthat the order of other equations, that is, Eqs. 9–11, remains the same. We get,

$F^{″}+f{F}^{\prime }-\frac{2m}{m+1}{F}^2-M\left(F-E_1\right)+\lambda \left(\theta -N_r\varphi \right)-K_{p}F=0,(24)$

${\theta }^{″}+\frac{ϵ}{1+ϵ\theta +\frac{4}{3}Rd}{\theta }^{\prime 2}+\frac{P{r}_0}{1+ϵ\theta +\frac{4}{3}Rd}\left(f{\theta }^{\prime }+M{E}_c{\left(F-E_1\right)}^2+E_c{F}^{\prime 2}+N_b{\theta }^{\prime }{\varphi }^{\prime }+N_t{\theta }^{\prime 2}+s\theta \right)=0,(25)$

${\varphi }^{″}+\frac{N_t}{N_b}{\theta }^{″}+Sc\left(f{\varphi }^{\prime }-\frac{2}{m+1}{\sigma }_1\varphi {\left(1+\delta \theta \right)}^n{e}^{\frac{-E^{*}}{1+\delta \theta }}\right)=0,(26)$

${\chi }^{″}+S_{b}f\chi -P_e\left(\chi {\varphi }^{″}+{\chi }^{\prime }{\varphi }^{\prime }\right)=0.(27)$

The boundary conditions in Eq. 13 are written in terms of the new variable:

$f=0,F=1,{\theta }^{\prime }=-{\beta }_1\left(1-\theta \right),{\varphi }^{\prime }=-{\beta }_2\left(1-\varphi \right),\chi =1,\text{at}\eta =0,(28)$

$F=0,\theta =0,\varphi =0,\chi =0,\text{as}\eta \to \infty .(29)$

As mentioned earlier, the equations are nonlinear and coupled. We use the Taylor series to linearize these equations. We start with Eq. 24 and write higher-order derivative terms on the left-hand side, then,

$F^{″}=-f{F}^{\prime }+\frac{2m}{m+1}{F}^2+M\left(F-E_1\right)-\lambda \left(\theta -N_r\varphi \right)+K_{p}F.$

Writing the right-hand side as h (η, F, F′):

$h\left(\eta ,F,F^{\prime }\right)=-f{F}^{\prime }+\frac{2m}{m+1}{F}^2+M\left(F-E_1\right)-\lambda \left(\theta -N_r\varphi \right)+K_{p}F,$

differentiating h with respect to F′:

$A_n=-{\left(\frac{\partial h}{\partial F^{\prime }}\right)}_n=-\left[-f_n\right]=f_n,$

so writing it as:

$A_n=f_n.$

Similarly, differentiating h with respect to F

$B_n=-{\left(\frac{\partial h}{\partial F}\right)}_n=-\left[\frac{4m}{m+1}{F}_n+M+K_p\right],$

$B_n=-\frac{4m}{m+1}{F}_n-M-K_p,$

Now, writing D_n in terms of h, B_n, and A_n defined previously

$D_n=h\left(\eta ,F_n,F_n^{\prime }\right)-{\left(\frac{\partial h}{\partial F}\right)}_n{F}_n-{\left(\frac{\partial h}{\partial F^{\prime }}\right)}_n{F}_n^{\prime },$

$D_n=h\left(\eta ,F_n,F_n^{\prime }\right)+B_n{F}_n+A_n{F}_n^{\prime }.$

Finally, the linearized equation for F is given as follows:

$F_{n+1}^{″}+A_n\left(\eta ,F_n,F_n^{\prime }\right)F_{n+1}^{\prime }+B_n\left(\eta ,F_n,F_n^{\prime }\right)F_{n+1}=D_n\left(\eta ,F_n,F_n^{\prime }\right),$

Similarly, the same abovementioned procedure can be used for Eqs. 25–27 to linearize these.

4.2 Galerkin method

The system of Eqs. 23–27 is linearized first; then, using these equations, we computed numerical solutions by the FEM. The linearized equations are written as follows:

$f^{\prime }=F,(30)$

$F_{n+1}^{″}+A_n\left(\eta ,F_n,F_n^{\prime }\right)F_{n+1}^{\prime }+B_n\left(\eta ,F_n,F_n^{\prime }\right)F_{n+1}=D_n\left(\eta ,F_n,F_n^{\prime }\right),(31)$

${\theta }_{n+1}^{″}+A_n\left(\eta ,{\theta }_n,{\theta }_n^{\prime }\right){\theta }_{n+1}^{\prime }+B_n\left(\eta ,{\theta }_n,{\theta }_n^{\prime }\right){\theta }_{n+1}=D_n\left(\eta ,{\theta }_n,{\theta }_n^{\prime }\right),(32)$

${\varphi }_{n+1}^{″}+A_n\left(\eta ,{\varphi }_n,{\varphi }_n^{\prime }\right){\varphi }_{n+1}^{\prime }+B_n\left(\eta ,{\varphi }_n,{\varphi }_n^{\prime }\right){\varphi }_{n+1}=D_n\left(\eta ,{\varphi }_n,{\varphi }_n^{\prime }\right),(33)$

${\chi }_{n+1}^{″}+A_n\left(\eta ,{\chi }_n,{\chi }_n^{\prime }\right){\chi }_{n+1}^{\prime }+B_n\left(\eta ,{\chi }_n,{\chi }_n^{\prime }\right){\chi }_{n+1}=D_n\left(\eta ,{\chi }_n,{\chi }_n^{\prime }\right),(34)$

along with the boundary conditions

$f=0,F=1,{\theta }^{\prime }=-{\beta }_1\left(1-\theta \right),{\varphi }^{\prime }=-{\beta }_2\left(1-\varphi \right),\chi =1,\text{as}\eta =0,$

$F=0,\theta =0,\varphi =0,\chi =0,\text{as}\eta \to \infty .(35)$

Just to simplify the procedure, the finite element method is applied to Eq. 31. We write:

$F_{n+1}^{″}+A_n{F}_{n+1}^{\prime }+B_n{F}_{n+1}=D_n,(36)$

multiplying Eq. 36 with a weight function w(η) and integrating over the general domain [a,b], we get:

${\int }_a^b\left(\frac{{\mathrm{d}}^2{F}_{n+1}}{\mathrm{d}{\eta }^2}+A_n\frac{\mathrm{d}{F}_{n+1}}{\mathrm{d}\eta }+B_n{F}_{n+1}\text{w}\left(\eta \right)\right)d\eta ={\int }_a^b{D}_n\text{w}\left(\eta \right)d\eta ,$

${\int }_a^b\frac{{\mathrm{d}}^2{F}_{n+1}}{\mathrm{d}{\eta }^2}\text{w}\left(\eta \right)d\eta +{\int }_a^b{A}_n\frac{\mathrm{d}{F}_{n+1}}{\mathrm{d}\eta }\text{w}\left(\eta \right)d\eta +{\int }_a^b{B}_n{F}_{n+1}\text{w}\left(\eta \right)d\eta ={\int }_a^b{D}_n\text{w}\left(\eta \right)d\eta ,$

using integration by parts on the left-hand side to get a weak form. For Dirichlet boundary conditions, weight function w(η) is chosen in such a way that w(a) = w(b) = 0. The result is as follows:

$-{\int }_a^b\frac{\mathrm{d}{F}_{n+1}}{\mathrm{d}\eta }\frac{\mathrm{d}\text{w}}{\mathrm{d}\eta }d\eta +{\int }_a^b{A}_n\frac{\mathrm{d}{F}_{n+1}}{\mathrm{d}\eta }\text{w}\left(\eta \right)d\eta +{\int }_a^b{B}_n{F}_{n+1}\text{w}\left(\eta \right)d\eta ={\int }_a^b{D}_n\text{w}\left(\eta \right)d\eta ,(37)$

the abovementioned Eq. 37 is written in a weak formulation. Suppose the solution is of the form

$F_{n+1}=\sum _{i=1}^{Ne}{\varphi }_n{\left(F_{n+1}\right)}_i,$

where ϕ_i is the basis functions and Ne is the total number of nodes in an element.Here, we use the Galerkin finite element that requires the basis function to be defined same as the weight function, that is, w = ϕ above. Furthermore, choosing [η_i, η_i+1] as nodes of the randomly selected finite element, Eq. 37 becomes

$\begin{array}{cc}\hfill & -\sum _{i=1}^{Ne}\left[{\int }_{{\eta }_i}^{{\eta }_{i+1}}\frac{\mathrm{d}{\varphi }_i}{\mathrm{d}\eta }\frac{\mathrm{d}{\varphi }_j}{\mathrm{d}\eta }d\eta \right]{\left(F_{n+1}\right)}_i+\sum _{i=1}^{Ne}\left[{\int }_{{\eta }_i}^{{\eta }_{i+1}}{A}_n\frac{\mathrm{d}{\varphi }_i}{\mathrm{d}\eta }{\varphi }_{j}d\eta \right]{\left(F_{n+1}\right)}_i\hfill \\ \hfill & +\sum _{i=1}^{Ne}\left[{\int }_{{\eta }_i}^{{\eta }_{i+1}}{B}_n{\varphi }_i{\varphi }_{j}d\eta \right]{\left(F_{n+1}\right)}_i={\int }_{{\eta }_i}^{{\eta }_{i+1}}{D}_n{\varphi }_{j}d\eta ,\hfill \end{array}$

$\sum _{i=1}^{Ne}\left[-{\int }_{{\eta }_i}^{{\eta }_{i+1}}\frac{\mathrm{d}{\varphi }_i}{\mathrm{d}\eta }\frac{\mathrm{d}{\varphi }_j}{\mathrm{d}\eta }d\eta +{\int }_{{\eta }_i}^{{\eta }_{i+1}}{A}_n\frac{\mathrm{d}{\varphi }_i}{\mathrm{d}\eta }{\varphi }_{j}d\eta +{\int }_{{\eta }_i}^{{\eta }_{i+1}}{B}_n{\varphi }_i{\varphi }_{j}d\eta \right]{\left(F_{n+1}\right)}_i={\int }_{{\eta }_i}^{{\eta }_{i+1}}{D}_n{\varphi }_{j}d\eta .(38)$

Defining:

$L_{ij}=-{\int }_{{\eta }_i}^{{\eta }_{i+1}}\frac{\mathrm{d}{\varphi }_i}{\mathrm{d}\eta }\frac{\mathrm{d}{\varphi }_j}{\mathrm{d}\eta }d\eta ,$

$C_{ij}={\int }_{{\eta }_i}^{{\eta }_{i+1}}{A}_n\frac{\mathrm{d}{\varphi }_i}{\mathrm{d}\eta }{\varphi }_{j}d\eta ,$

$M_{ij}={\int }_{{\eta }_i}^{{\eta }_{i+1}}{B}_n{\varphi }_i{\varphi }_{j}d\eta ,$

$R_j={\int }_{{\eta }_i}^{{\eta }_{i+1}}{D}_n{\varphi }_{j}d\eta ,$

where

$K_{ij}=L_{ij}+C_{ij}+M_{ij},$

Thus, Eq. 38 is as follows:

$\sum _{i=1}^{Ne}{K}_{ij}{\left(F_{n+1}\right)}_i=R_j,$

For a single element, the matrix will be as follows and is called an element stiffness matrix.

$\left[\begin{array}{cc}\hfill K_{11}\hfill & \hfill K_{21}\hfill \\ \hfill K_{12}\hfill & \hfill K_{22}\hfill \end{array}\right]{\left[\begin{array}{c}\hfill F_1\hfill \\ \hfill F_2\hfill \end{array}\right]}^{n+1}=\left[\begin{array}{c}\hfill R_1\hfill \\ \hfill R_2\hfill \end{array}\right]$

The global stiffness matrix will be defined as follows:

$\left[\begin{array}{ccccc}\hfill K_{11}\hfill & \hfill K_{21}\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill K_{12}\hfill & \hfill K_{22}+K_{11}\hfill & \hfill K_{21}\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill K_{12}\hfill & \hfill K_{22}+K_{11}\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill K_{22}\hfill \end{array}\right]{\left[\begin{array}{c}\hfill F_1\hfill \\ \hfill F_2\hfill \\ \hfill F_3\hfill \\ \hfill ⋮\hfill \\ \hfill F_N\hfill \end{array}\right]}^{n+1}=\left[\begin{array}{c}\hfill R_1\hfill \\ \hfill R_2+R_3\hfill \\ \hfill R_3+R_4\hfill \\ \hfill ⋮\hfill \\ \hfill R_N\hfill \end{array}\right]$

We presented FEM for a single equation for convenience. The same procedure can be applied to other Eqs. 32–34.

4.3 Shooting method

The boundary value problem Eq. 8–13 are written as a pair of first-order equations so that one can apply the shooting method. The shooting method is a procedure in which the boundary value problem is converted into an initial value problem.

$\begin{array}{c}f=y_1,f^{\prime }=y_2,f^{″}=y_3,f^{‴}=y_3^{\prime }=-y_1{y}_3+\frac{2m}{m+1}{y}_2^2+M\left(y_2-E_1\right)-\lambda \left(\theta -N_r\varphi \right)+Kp{y}_2,\\ y_4=\theta ,y_5={\theta }^{\prime },\\ {\theta }^{″}=y_5^{\prime }=-ϵy_5^2-\frac{P{r}_0}{\left(1+ϵ\theta +\frac{4}{3}\right)Rd}(y_1{y}_5+MEc{\left(y_2-E_1\right)}^2+Ec{y}_3^2+Nb{y}_5{y}_7+Nt{y}_5^2+s{y}_4),\\ y_6=\varphi ,y_7={\varphi }^{\prime },y_{7\prime }=-\frac{Nt}{Nb}{y}_5^{\prime }-Sc\left(y_1{y}_7-\frac{2m}{m+1}{\sigma }_1\varphi {\left(1+\delta \theta \right)}^n\exp \left(\frac{-E}{1+\delta \theta }\right)\right),\\ y_8=\chi \left(\eta \right),y_9={\chi }^{\prime },{\chi }^{″}=y_9^{\prime }=-Sb{y}_1{y}_9+Pe\left(y_8{y}_7^{\prime }+y_7{y}_9\right).\end{array}$

The unknown values for the boundary conditions required for the shooting method are written as:

$y_3\left(0\right)=u_1,y_5\left(0\right)=u_2,y_7\left(0\right)=u_3,y_9\left(0\right)=u_4$

These unknowns are obtained first by a root-finding technique. For this, the Newton–Raphson method is implemented in MATLAB. The initial value problem is solved using the Runge–Kutta method of the fourth-order and fifth-order schemes (adaptive scheme).

4.4 bvp4c

Boundary value problems (BVPs) for ordinary differential equations (ODEs) can be solved using MATLAB bvp4c solver. The results obtained by the shooting method and Galerkin method are validated using MATLAB built-in solver bvp4c, which uses the collocation method in the background. It starts the solution with an initial guess supplied at initial mesh points and changes step size (hence, changes mesh) to get the specified accuracy. For more details, see Ref. [38].

5 Result and discussion

The research-related questions that were raised in Section 1 are answered in Section 5.1. Section 5.2 contains a discussion of the research questions. The results of the parameters other than Section 5.1, Section 5.2 are described in Section 5.3.

5.1 Analysis of results

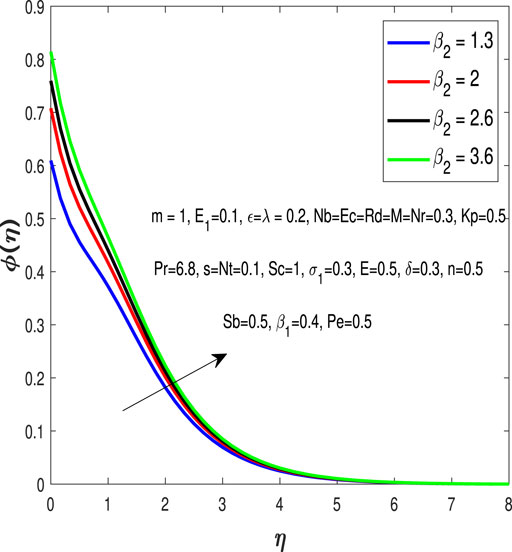
The tables and figures have been created in order to respond to the research questions posed in Section 1. For Pe = 0.6, 0.7, and 0.8 and Sc = 1.3, 1.5 and 2, and Sc= 1, 1.3 and 1.5, Table 4 and Table 5 are drawn. The concentration profiles, as well as the density of motile microorganism, is presented in tables and figures to answer research question 1. The magnetic parameter effect on the velocity profile is drawn in Figure 1 to answer research question 2. For M = 0.2, 0.5, and 0.7 and M = 0.2, 0.5, and 0.6, Table 2 and Table 3 are drawn in order to reply to research question 2. Similarly, for E =1, 1.3, and 1.5, Table 4 is drawn to answer research question 3. To answer research question 4 the value of β₂ = 1.3, 2, 2.6, 3.6 is considered in Figure 8. Finally, the accuracy of the Galerkin method is presented when compared to other numerical methods in Table 1, Table 2, Table 3, Table 4, and Table 5 to answer research question 5.

TABLE 1

TABLE 1. Comparison of − θ′(0) for different values of Pr_o.

FIGURE 1

FIGURE 1. Velocity profile f′(η) for different M.

TABLE 2

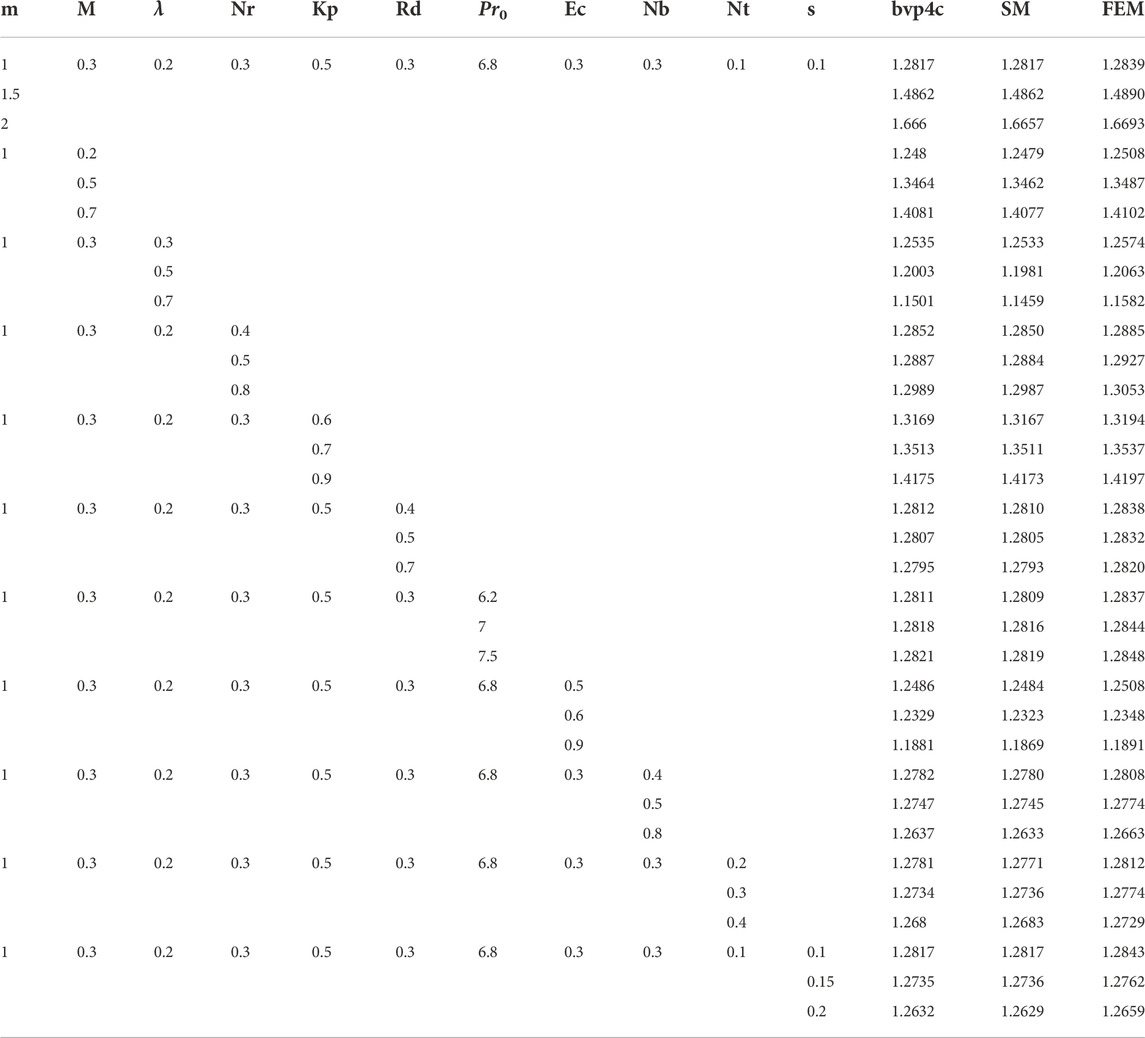
TABLE 2. Effect of different parameters on the skin friction coefficient by considering E₁=0, ϵ = 0.1, Sc = 1, E = 0.5, δ = 0.3, σ1 = 0.3, n = 0.5, Sb = 0.5, Pe = 0.5, β₁ = 0.4, and β₂ = 0.4.

TABLE 3

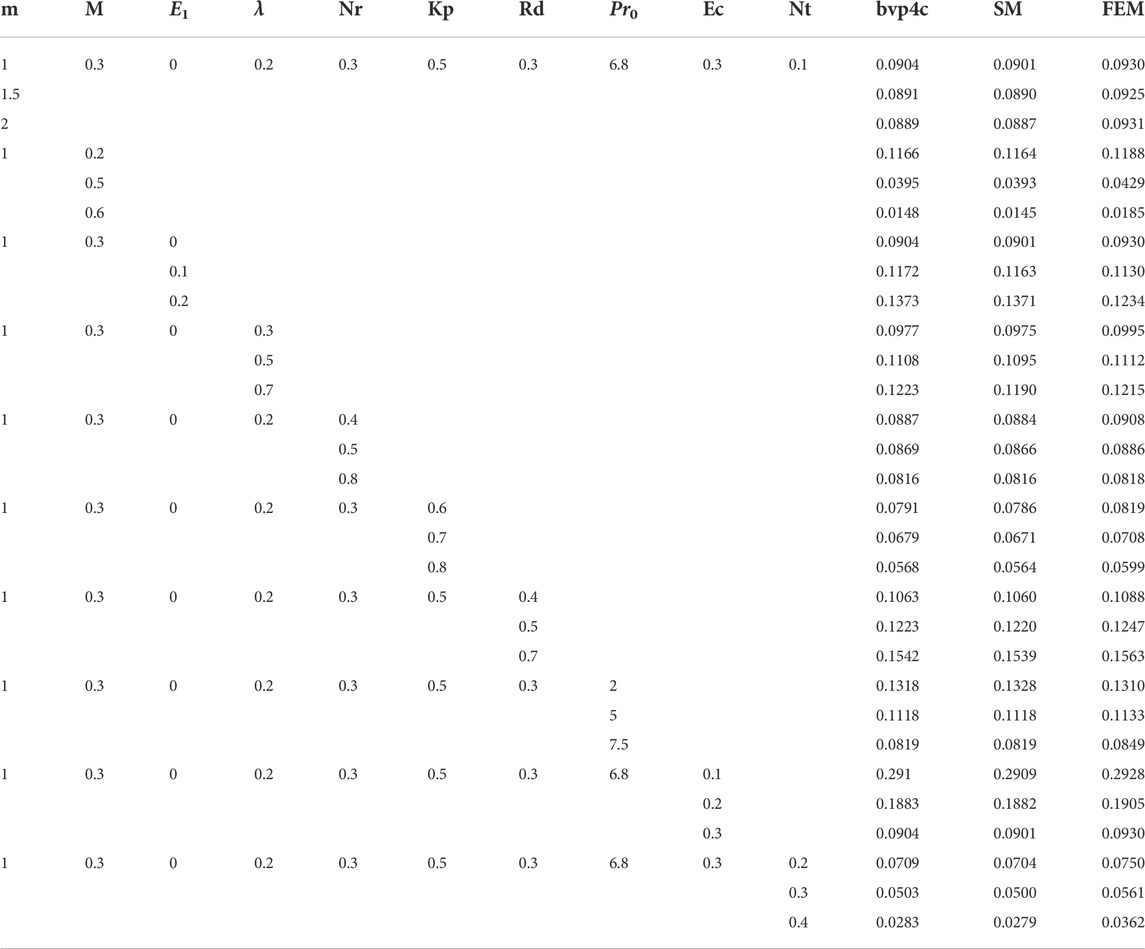
TABLE 3. Effect of different parameters on Nusselt number by considering ϵ = 0.2, s = 0.1, Sc = 1, σ1 = 0.3, E = 0.5, δ = 0.3, n = 0.5, Sb = 0.5, Pe = 0.5, Nb = 0.3, β₁ = 0.4, and β₂ = 0.4.

TABLE 4

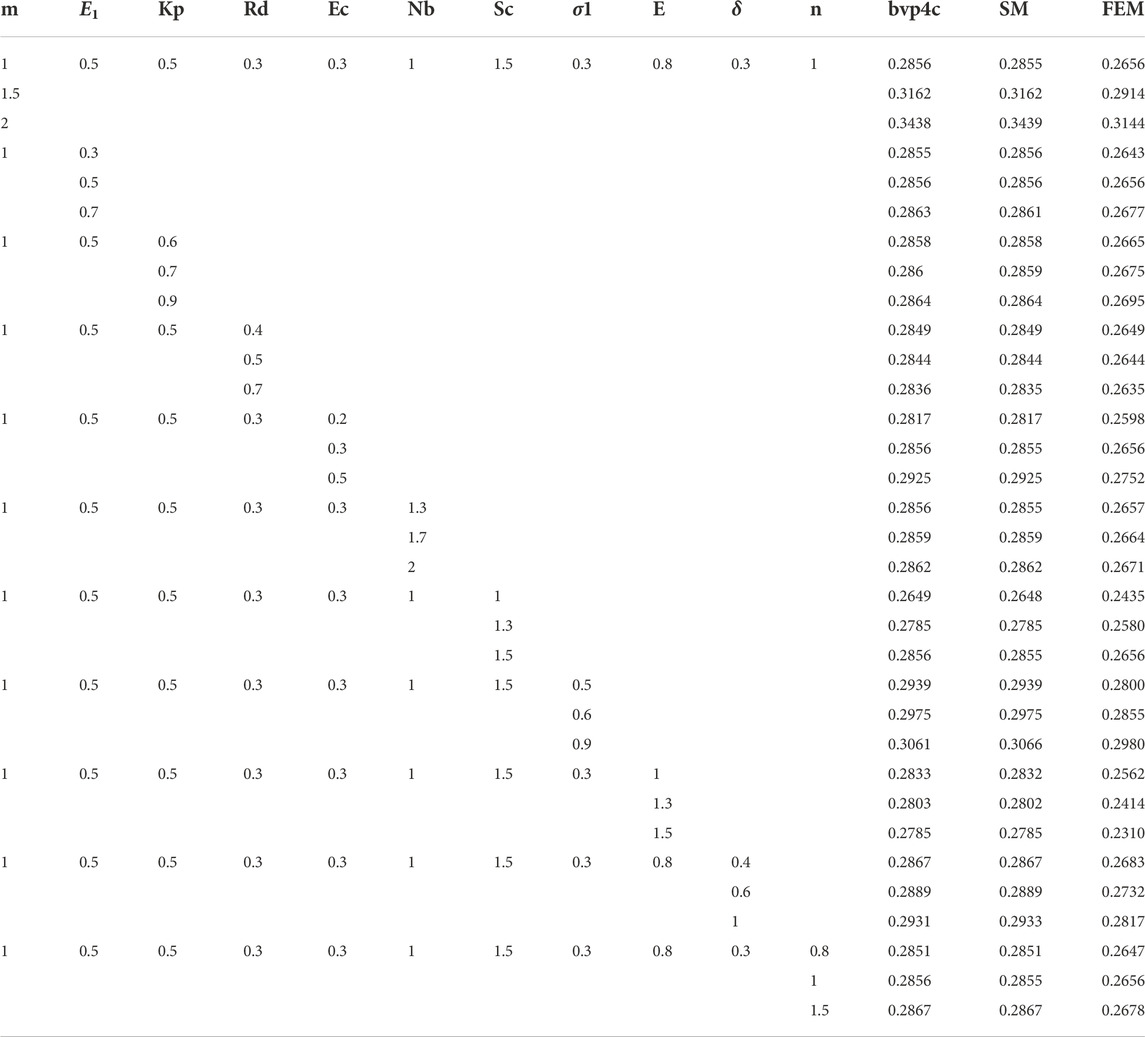
TABLE 4. Effect of different parameters on Sherwood number by considering M = 0.3, λ = 0.2, Nr = 0.3, ϵ = 0.2, Nt = 0.1, Pr₀ = 6.8, s = 0.1, Sb = 0.5, Pe = 0.5, β₁ = 0.4, and β₂ = 0.4.

TABLE 5

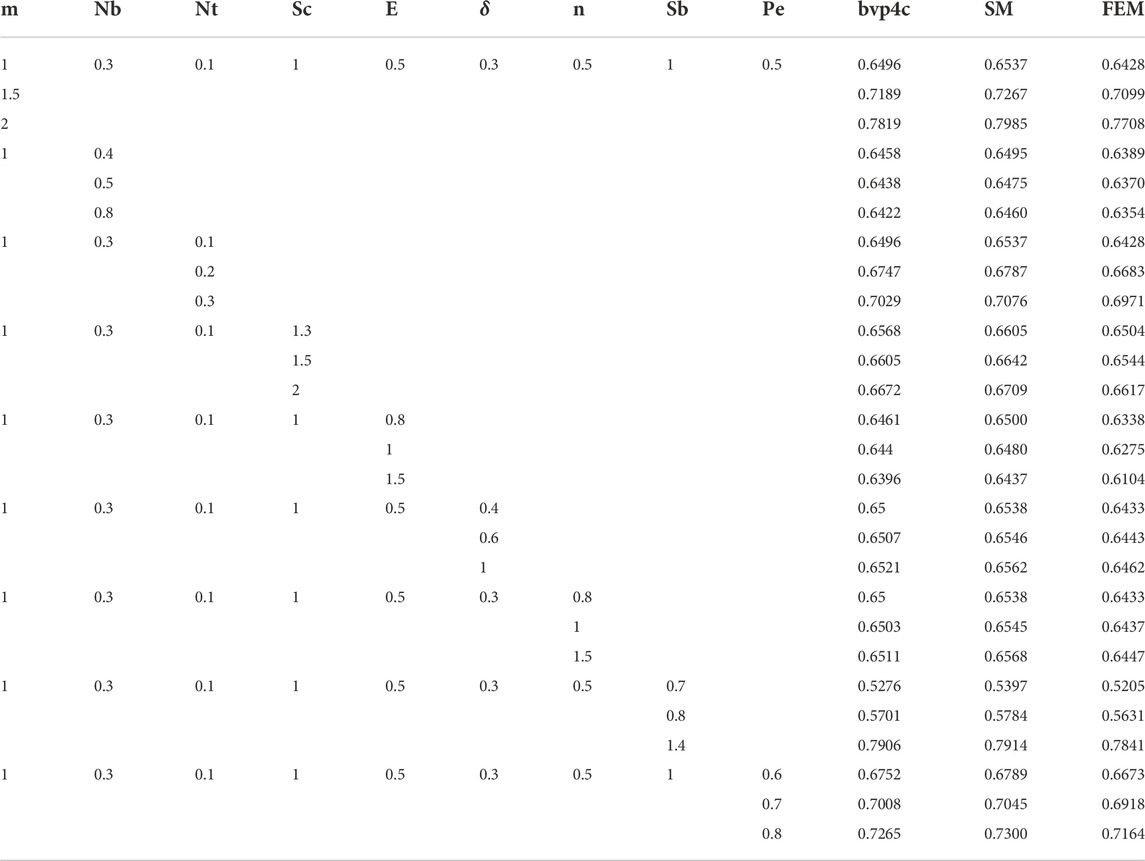
TABLE 5. Effect of different parameters for motile microorganisms by considering M =0.3, E₁=0, λ = 0.2, Nr = 0.3, Kp = 0.5, Rd = 0.3, ϵ = 0.2, Pr₀ = 6.8, σ1 = 0.3, Ec = 0.3, δ = 0.3, s = 0.1, β₁ = 0.4, and β₂ = 0.4.

5.2 Discussion of results

The results obtained to answer research questions have been discussed here. The M specifies the magnetic parameter. It represents the Lorentz force applied normally that opposes the flow of fluid. Thus, as we increase the value of M, the velocity decreases, and hence, the value of the skin friction coefficient increases.

As the velocity increases, it becomes relatively difficult for particles to transfer heat, and thus heat transfer rate decreases. The increase in the magnetic field parameter M stops the motion of the fluid and thus Brownian motion of fluid decreases, which resulted in a lowering of the heat transfer rate.

The increase in porosity parameter Kp decreases the heat transfer rate. The heat transfer rate reduces when fluid attracts to pores structured medium.

For the parameters K_p the Sherwood number has a negligible change in its values. For the Schmidt number Sc, the Sherwood number decreases.

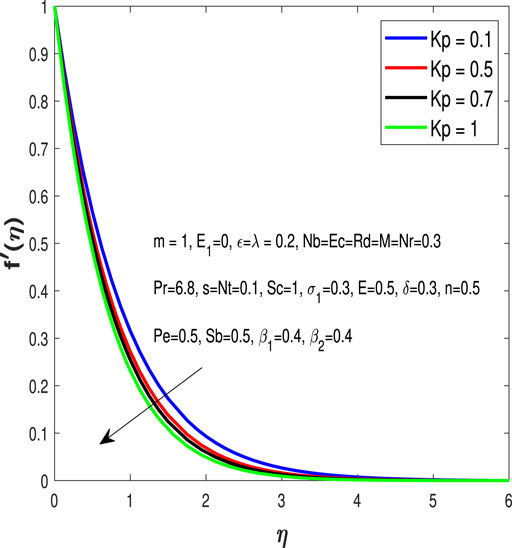
Figure 2 demonstrates the impacts of Kp on the velocity profile. It shows that increasing values of Kp decline the fluid velocity.

FIGURE 2

FIGURE 2. Velocity profile f′(η) for different Kp.

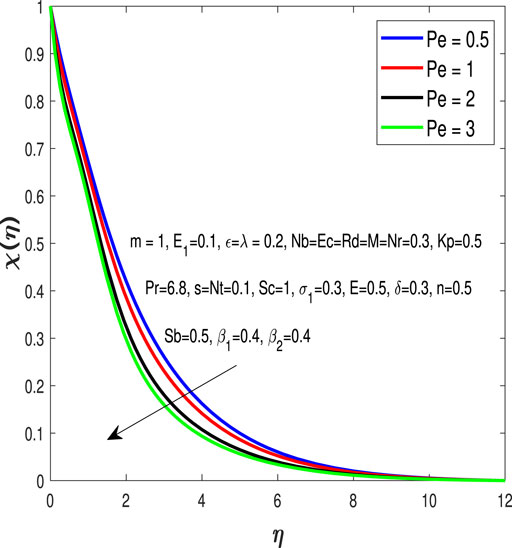
Figure 9 elucidates that the microorganism profile is decayed for greater values of Peclet number Pe.

The accuracy of the Galerkin method is shown in all tables. The results obtained from the Galerkin method have been matched with the shooting method and bvp4c. However, in some cases, the accuracy reduces, which is linked to a number of reasons. One reason is the linearization procedure in which nonlinear ODEs are first linearized. The other possible reason is the complexity of the mathematical model which contains four nonlinear coupled ODEs.

5.3 Investigation of various other parameters

Other than the research questions posed in Section 1 and discussed in Section 5, one can also see the effect of numerous other parameters on the physical parameter.

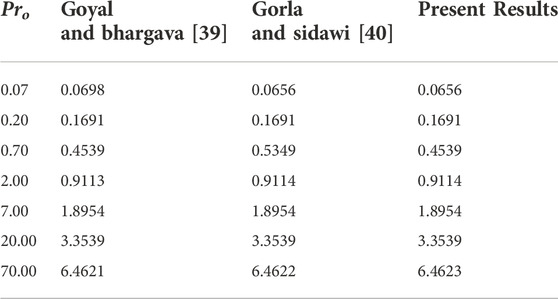
In Table 1, a comparison is drawn for the case of – θ′(0) for different values of Pr_owith published results. An excellent agreement between the published and present results is achieved.

In Table 2, the impact of different parameters on the skin friction coefficient is discussed. In Table 2, with the increased value of m, the skin friction coefficient increases. The reason for the increase is that the fluid velocity increases which affects the magnitude of the skin friction coefficient. The parameter λ is a mixed convection parameter. As we increase the value of the mixed convection parameter, the skin friction coefficient decreases. The parameter Nr represents the ratio of the buoyancy parameter. Physically, as we increase the value of Nr, the stronger buoyancy force acting normally resists the horizontal flow of the fluid. Therefore, the value of the skin friction coefficient is increased. The Kp indicates the porosity parameter. As we increase the value of Kp, the velocity of fluid decreases thus more resistance on the nanoparticles in the fluid increases the value of skin friction coefficient increases. The parameter Rd represents the radiation parameter. As we increase the radiation parameter, negligible effects are observed on the skin friction coefficient. The parameter Pr₀ represents the Prandtl number. Increasing the Prandtl number has negligible effects on the skin friction coefficients. The parameter Ec is the Eckert number. As we increase the Eckert number, the skin friction coefficient decreases. The parameter Nt represents the thermophoresis parameter. They have a negligible effect on flow velocity and thus on the skin friction coefficient. The s represents the local heat source/sink parameter. As we increase the value of s, we observe an increase in the flow velocity and thus it overcomes the resistance. Therefore, the value of the skin friction coefficient decreases.

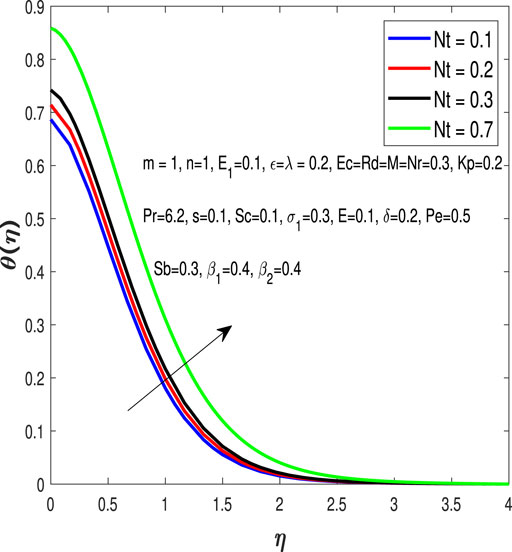
In Table 3, we discuss the effect of different parameters on the Nusselt number. m represents a positive constant. As the value of m is increased, we observe a decrease in the value of the Nusselt number. E₁ represents the electric field parameter. The increase in the electric parameter results in an increase in the Nusselt number. The temperature difference between the surface and upper layers increases and thus the rate at which heat is transferred increases. λ represents the mixed convection parameter. The increase in value of λ causes Nu to increase. Mixed convection aids the flow of fluid in order to transfer heat. The Nr represents the ratio of the buoyancy parameter. It has a negligible effect on the heat transfer rate. The radiation parameter is represented by Rd. The increase in Rd results in an increase in heat transfer rate. The radiation is absorbed by the particles of the system and thus creating a temperature difference between the surface and upper layers. Therefore, the heat is transferred at a higher rate. The increase in Pr₀ results in a decrease in the heat transfer rate. Prandtl number is the ratio of momentum diffusivity to thermal diffusivity. For a higher heat transfer rate, we have a lower value of Pr₀. The Eckert number is represented by Ec. An increase in Ec resulted in a decrease in the heat transfer rate. The Ec is the relationship between a flow’s kinetic energy and boundary layer enthalpy difference and characterizes the heat transfer dissipation. So as we increase Ec it lowers the heat transfer rate. The thermophoresis is represented by Nt. The increase in the value of Nt resulted in a decrease in the Nusselt number.

In Table 4, we discuss the effect of different parameters on the Sherwood number. As m increases, the Sherwood number increases. For the parameters E₁, Rd, Ec, Nb, and n, the Sherwood number has a negligible change in its values. For Sc, the Sherwood number decreases. For σ₁, E, and δ, there is negligible change in the Sherwood number.

In Table 5, we discuss the effect of different parameters on motile microorganisms. As the value of m increases, the motile microorganisms increases. There is no change in the values of motile microorganisms when the parameter Nb, Sc, E, δ, and n increases. With the increase of Nt, Sb, and Pe, the microorganisms increases.

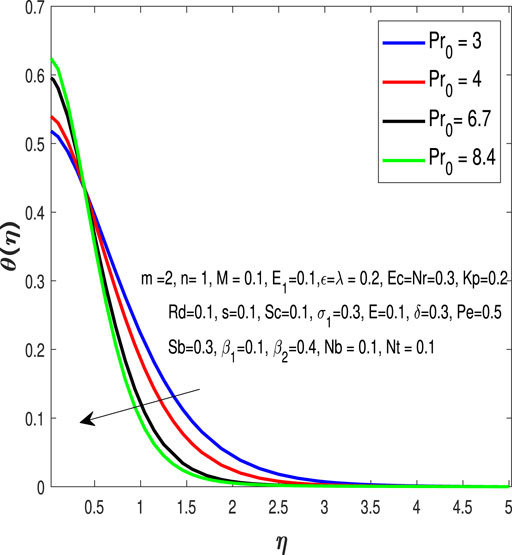
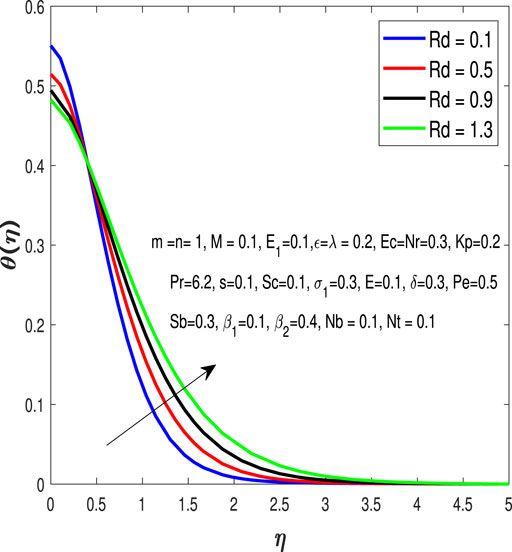
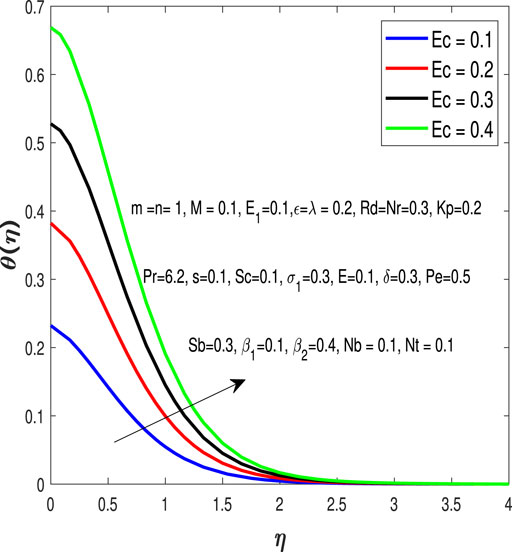
Figure 3 elaborates on the influences of the Prandtl number Pr_o on the temperature profile.Figure 4 exhibits the influence of Rd on temperature distribution. The radiation parameter heats up the fluid through radiation which increases its temperature.Figure 5 and Figure 6 are plotted to discuss the effects of Ec and Nt on the temperature profile. The Eckert number appears when the fluid motion is considered to be relatively high. The thermophoresis parameter appears due to the considered fluid.

FIGURE 3

FIGURE 3. Temperature profile θ(η) for different Pr₀.

FIGURE 4

FIGURE 4. Temperature profile θ(η) for different Rd.

FIGURE 5

FIGURE 5. Temperature profiles θ(η) for different Ec.

FIGURE 6

FIGURE 6. Temperature profile θ(η) for different Nt.

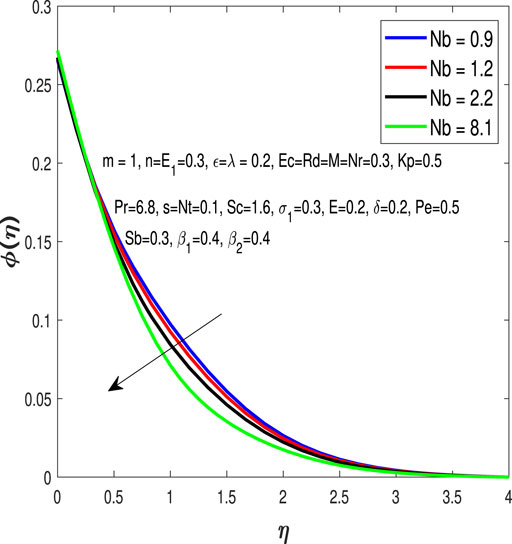
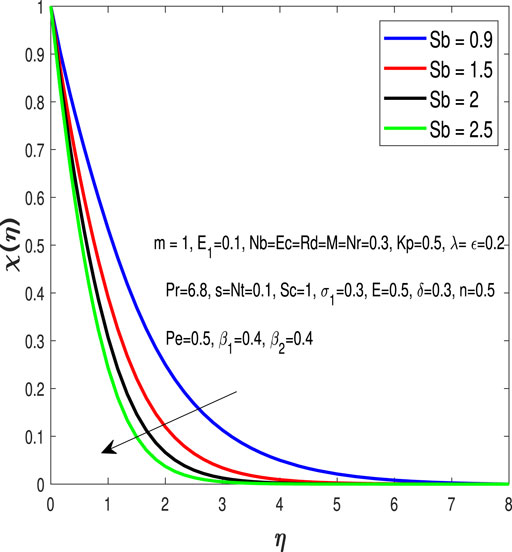
The influence of Brownian motion parameter Nb can be seen on the concentration profile in Figure 7.Figure 8 portrays the impacts of concentrated Biot number β₂ on the concentration profile.Figure 9 and Figure 10 elucidate that the microorganism profile is decayed for greater values of the bioconvection Peclet number Pe and the bio Schmidt number Sb.

FIGURE 7

FIGURE 7. Concentration profile ϕ(η) for different Nb.

FIGURE 8

FIGURE 8. Concentration profile ϕ(η) for different β₂.

FIGURE 9

FIGURE 9. Microorganisms profile χ(η) for different Pe.

FIGURE 10

FIGURE 10. Microorganisms profile χ(η) for different Sb.

6 Conclusion

This study is carried out to discuss the impacts of activation energy on EMHD mixed convection and heat transfer flow of fluid in a porous medium with radiative heat transfer while considering variable thermal conductivity over a nonlinearly stretching sheet. The significant findings based on research questions posed in Section 1 of the current study are confirmed as:

• An increasing value of magnetic parameter M and porosity parameter Kp decreases the boundary layer thickness.

• The growing values of radiation parameter Rd increase the temperature of the fluid while the boundary layer thickness decreases for growing values of Pr₀.

• The temperature is enhanced for rising values of Nt and Ec. The concentration profile increases for Biot number β₂.

• The microorganisms profile declines for higher values of bioconvection Schmidt number Sb and Peclet number Pe.

• The skin friction coefficient increases for different values of magnetic parameter M.

• The local Nusselt number increases for various values of radiation parameter Rd and decreases for Eckert number Ec.

• The density of motile microorganisms increases on increasing the value of Peclet number Pe.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

IQ, MAF, and MI wrote the manuscript and implemented numerical methods. MAF discussed the FEM. IQ and MAF contributed in results and discussion. MAF and AM discussed and reviewed the research paper and implemented changes.

Acknowledgments

The contribution and collaboration of Sabir Hussain with MF in developing FEM is highly acknowledged. AM would like to thank the Department of Mathematics, Realfag FLU, Nord University for research support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rana BMJ, Arifuzzaman SM, Islam S, Reza-E-Rabbi S, Al-Mamun A, Mazumder M, et al. Swimming of microbes in blood flow of nano-bioconvective Williamson fluid. Therm Sci Eng Prog (2021) 25(2021):101018. doi:10.1016/j.tsep.2021.101018

CrossRef Full Text | Google Scholar

2. Buongiorno J. Convective transport in nanofluids. J Heat Transfer (2006) 128(3):240–50. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

3. Rasouli MR, Abouei Mehrizi A, Lashkaripour A. Numerical study on low Reynolds mixing oft-shaped micromixers with obstacles. Transp Phenom Nano Micro Scales (2015) 3(2):68–76. doi:10.7508/TPNMS.2015.02.001

CrossRef Full Text | Google Scholar

4. Mahmud K, Rana S, Al-Zubaidi A, Mehmood R, Saleem S. Interaction of Lorentz force with cross swimming microbes in couple stress nano fluid past a porous Riga plate. Int Commun Heat Mass Transfer (2022) 138(2022):106347. doi:10.1016/j.icheatmasstransfer.2022.106347

CrossRef Full Text | Google Scholar

5. Kuznetsov AV. Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Res Lett (2011) 6(1):100. doi:10.1186/1556-276x-6-100

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Balla CS, Haritha C, Naikoti K, Rashad AM. Bioconvection in nanofluid-saturated porous square cavity containing oxytactic microorganisms. Int J Numer Methods Heat Fluid Flow (2018) 29:1448–65. doi:10.1108/hff-05-2018-0238

CrossRef Full Text | Google Scholar

7. Shafiq A, Rasool G, Khalique CM, Aslam S. Second grade bioconvective nanofluid flow with buoyancy effect and chemical reaction. Symmetry (2020) 12(4):621. doi:10.3390/sym12040621

CrossRef Full Text | Google Scholar

8. Ferdows M, Zaimi K, Rashad AM, Nabwey HA. MHD bioconvection flow and heat transfer of nanofluid through an exponentially stretchable sheet. Symmetry (2020) 12(5):692. doi:10.3390/sym12050692

CrossRef Full Text | Google Scholar

9. Sangeetha E, Poulomi D. Gyrotactic microorganisms suspended in MHD nanofluid with activation energy and binary chemical reaction over a non-Darcian porous medium. Waves in Random and Complex Media (2022) 1–17. doi:10.1080/17455030.2022.2112114

CrossRef Full Text | Google Scholar

10. James M, Mureithi EW, Kuznetsov. D. Effects of variable viscosity of nanofluid flow over a permeable wedge embedded in saturated porous medium with chemical reaction and thermal radiation. Int J Adv Appl Math Mech (2015) 2(3):101–18.

Google Scholar

11. Hayat T, Ijaz Khan M, Farooq M, Alsaedi A, Waqas M, Yasmeen. T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int J Heat mass transfer (2016) 99:702–10. doi:10.1016/j.ijheatmasstransfer.2016.04.016

CrossRef Full Text | Google Scholar

12. Sajid M, Hayat T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int Commun Heat Mass Transfer (2008) 35(3):347–56. doi:10.1016/j.icheatmasstransfer.2007.08.006

CrossRef Full Text | Google Scholar

13. Mjankwi MA, Grace Masanja V, Mureithi EW, James MN. Unsteady MHD flow of nanofluid with variable properties over a stretching sheet in the presence of thermal radiation and chemical reaction. Int J Math Math Sci (2019) 2019:1–14. doi:10.1155/2019/7392459

CrossRef Full Text | Google Scholar

14. Vajravelu K. Viscous flow over a nonlinearly stretching sheet. Appl Math Comput (2001) 124(3):281–8. doi:10.1016/s0096-3003(00)00062-x

CrossRef Full Text | Google Scholar

15. Char M-I. Heat transfer of a continuous, stretching surface with suction or blowing. J Math Anal Appl (1988) 135(2):568–80. doi:10.1016/0022-247x(88)90172-2

CrossRef Full Text | Google Scholar

16. Vishalakshi AB, Mahabaleshwar US, Sheikhnejad Y. Impact of MHD and mass transpiration on rivlin–ericksen liquid flow over a stretching sheet in a porous media with thermal communication. Transp Porous Media (2022) 142:353–81. doi:10.1007/s11242-022-01756-w

CrossRef Full Text | Google Scholar

17. Choi S, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne, IL (United States): Argonne National Lab (1995). No. ANL/MSD/CP-84938; CONF-951135-29.

Google Scholar

18. Devendiran DK, Amirtham VA. A review on preparation, characterization, properties and applications of nanofluids. Renew Sustain Energ Rev (2016) 60:21–40. doi:10.1016/j.rser.2016.01.055

CrossRef Full Text | Google Scholar

19. Chan SQ, Aman F, Mansur S. Sensitivity analysis on thermal conductivity characteristics of a water-based bionanofluid flow past a wedge surface. Math Probl Eng (2018) 2018:1–12. doi:10.1155/2018/9410167

CrossRef Full Text | Google Scholar

20. Hamad MAA. Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int Commun Heat mass transfer (2011) 38(4):487–92. doi:10.1016/j.icheatmasstransfer.2010.12.042

CrossRef Full Text | Google Scholar

21. Ganesh NV, Abdul Hakeem AK, Ganga B. Darcy–Forchheimer flow of hydromagnetic nanofluid over a stretching/shrinking sheet in a thermally stratified porous medium with second order slip, viscous and Ohmic dissipations effects. Ain Shams Eng J (2018) 9(4):939–51. doi:10.1016/j.asej.2016.04.019

CrossRef Full Text | Google Scholar

22. Jusoh R, Nazar R, Pop I. Magnetohydrodynamic boundary layer flow and heat transfer of nanofluids past a bidirectional exponential permeable stretching/shrinking sheet with viscous dissipation effect. J Heat Transfer (2019) 141:1. doi:10.1115/1.4041800

CrossRef Full Text | Google Scholar

23. Wakif A, Ali C, Animasaun IL, Zaydan M, Hassan W, Sehaqui R. Novel physical insights into the thermodynamic irreversibilities within dissipative EMHD fluid flows past over a moving horizontal riga plate in the coexistence of wall suction and joule heating effects: A comprehensive numerical investigation. Arab J Sci Eng (2020) 45(11):9423–38. doi:10.1007/s13369-020-04757-3

CrossRef Full Text | Google Scholar

24. Das S, Chakraborty S, Mitra SK. Magnetohydrodynamics in narrow fluidic channels in presence of spatially non-uniform magnetic fields: Framework for combined magnetohydrodynamic and magnetophoretic particle transport. Microfluid Nanofluidics (2012) 13(5):799–807. doi:10.1007/s10404-012-1001-z

CrossRef Full Text | Google Scholar

25. Paul D, Chakraborty S. Wall effects in microchannel-based macromolecular separation under electromagnetohydrodynamic influences. J Appl Phys (2007) 102(7):074921. doi:10.1063/1.2785004

CrossRef Full Text | Google Scholar

26. Si D, Jian Y. Electromagnetohydrodynamic (EMHD) micropump of Jeffrey fluids through two parallel microchannels with corrugated walls. J Phys D Appl Phys (2015) 48(8):085501. doi:10.1088/0022-3727/48/8/085501

CrossRef Full Text | Google Scholar

27. Sinha A, Shit GC. Electromagnetohydrodynamic flow of blood and heat transfer in a capillary with thermal radiation. J Magnetism Magn Mater (2015) 378:143–51. doi:10.1016/j.jmmm.2014.11.029

CrossRef Full Text | Google Scholar

28. Bestman AR. Radiative heat transfer to flow of a combustible mixture in a vertical pipe. Int J Energ Res (1991) 15(3):179–84. doi:10.1002/er.4440150305

CrossRef Full Text | Google Scholar

29. Mustafa M, Ahmad Khan JTH, Alsaedi A. Buoyancy effects on the MHD nanofluid flow past a vertical surface with chemical reaction and activation energy. Int J Heat Mass Transfer (2017) 108:1340–6. doi:10.1016/j.ijheatmasstransfer.2017.01.029

CrossRef Full Text | Google Scholar

30. Khan U, Zaib A, Khan I, Nisar KS. Activation energy on MHD flow of titanium alloy (Ti6Al4V) nanoparticle along with a cross flow and streamwise direction with binary chemical reaction and non-linear radiation: Dual Solutions. J Mater Res Tech (2020) 9(1):188–99. doi:10.1016/j.jmrt.2019.10.044

CrossRef Full Text | Google Scholar

31. Makinde OD, Animasaun IL. Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. Int J Therm Sci (2016) 109:159–71. doi:10.1016/j.ijthermalsci.2016.06.003

CrossRef Full Text | Google Scholar

32. Andersson HI, Hansen OR, Holmedal. B. Diffusion of a chemically reactive species from a stretching sheet. Int J Heat Mass Transfer (1994) 37(4):659–64. doi:10.1016/0017-9310(94)90137-6

CrossRef Full Text | Google Scholar

33. Ganesh NV, Al-Mdallal QM, Hirankumar G, Kalaivanan R, Chamkha AJ. Buoyancy-driven convection of MWCNT–Casson nanofluid in a wavy enclosure with a circular barrier and parallel hot/cold fins. Alexandria Eng J (2022) 61(4):3249–64. doi:10.1016/j.aej.2021.08.055

CrossRef Full Text | Google Scholar

34. Kalaivanan R, Vishnu Ganesh N, Al-Mdallal QM. Buoyancy driven flow of a second-grade nanofluid flow taking into account the Arrhenius activation energy and elastic deformation: Models and numerical results. Fluid Dyn Mater Process (2021) 17(2):319–32. doi:10.32604/fdmp.2021.012789

CrossRef Full Text | Google Scholar

35. Zhang X-H, Abidi A, El-Sayed Ahmed A, Riaz Khan M, El-Shorbagy MA, Shutaywi M, et al. MHD stagnation point flow of nanofluid over a curved stretching/shrinking surface subject to the influence of Joule heating and convective condition. Case Stud Therm Eng (2021) 26(2021):101184. doi:10.1016/j.csite.2021.101184

CrossRef Full Text | Google Scholar

36. Jama M, Singh T, Gamaleldin SM, Koc M, Samara A, Isaifan RJ, et al. Critical review on nanofluids: Preparation, characterization, and applications. J Nanomater (2016) 2016:1–22. Article ID 6717624, 22 pages. doi:10.1155/2016/6717624

CrossRef Full Text | Google Scholar

37. Prasad KV, Pal D, Umesh V, Rao NP. The effect of variable viscosity on MHD viscoelastic fluid flow and heat transfer over a stretching sheet. Commun Nonlinear Sci Numer Simulation (2010) 15(2):331–44. doi:10.1016/j.cnsns.2009.04.003

CrossRef Full Text | Google Scholar

38. Shampine LF, Kierzenka J. A BVP solver based on residual control and the Maltab PSE. ACM Trans Math Softw (2001) 27(3):299–316. doi:10.1145/502800.502801

CrossRef Full Text | Google Scholar

39. Goyal M, Bhargava R. Boundary layer flow and heat transfer of viscoelastic nanofluids past a stretching sheet with partial slip conditions. Appl Nanosci (2014) 4(6):761–7. doi:10.1007/s13204-013-0254-5

CrossRef Full Text | Google Scholar

40. Gorla R, Subba R, Sidawi I. Free convection on a vertical stretching surface with suction and blowing. Appl Sci Res (1994) 52(3):247–57. doi:10.1007/bf00853952

CrossRef Full Text | Google Scholar