Ghost crystallography

In [Opt. Lett. 38, 4023-4025 (2013)] the author predicted that the low coherent X-ray is hard to provide a high-resolution diffraction pattern from an object with a spatially periodic structure. This would severely restrict X-ray crystallography and its similar techniques. In this letter, we indicate that the Ghost diffraction technic takes advantage of the low coherence and may thus break through the bottleneck. Analytical formulae for calculating ghost diffraction patterns diffracted by the periodic structured media under any coherent state are derived.

In 1912, Laue discovered an X-ray pattern diffracted by a crystal of CuSO₄·5H₂O. His experiment pioneered X-ray spectroscopy and made the prospect of determining crystal structures promising [1]. A historic example was that in 1951 Rosalind Franklin obtained an X-ray diffraction pattern scattered by a DNA crystal [2]. Based on that, a double helix fine structure of DNA with its parameters was revealed by Watson and Crick [3]. In the past half-century, X-ray crystallography [4] has shown a tremendous impact in Nano-sciences [5], structural biology [6], and other areas [7, 8]. In recent years, many X-ray free-electron laser (FEL) facilities have been established [9], they allowed us to observe molecular structures from crystals of a few nanometers [10], and provide the possibility of visualizing macromolecular structures and complexes at high resolution even without the need for crystals [11]. From the perspective of classical diffraction, all these require a high-coherence light source [12, 13].

On the other hand, to obtain an effective diffraction pattern requires radiation sources with a wavelength much shorter than the crystal’s spatial period, or the spatial spectral information of the object remains less [14]. This can be compared to the case where the slits contain only zero-order fringes. For crystals with a spatial period close to or even below the sub-atom scale, namely 10⁻¹⁰ m, candidate sources remain few but like hard X-rays [15], gamma rays [16], and neutron rays [17]. Among them, neutron crystallography [18, 19] develops as a similar technique more than a shorter wave counterpart to sub-atomic X-ray crystallography. It is so far the only approach for the location of highly polarized H atoms and protons (H⁺), because X-rays are blind to them [20]. A further advantage of neutron crystallography is that neutron rays do much less damage to crystals than X-rays [21]. However, high-quality diffraction patterns are difficult to obtain [15–17] due to the difficulty of generating coherent radiation with these sources [22]. One may even not make a tradeoff between the quality and its coherence. The bottleneck has precisely been predicted in Ref. [12].

Ghost imaging (GI) is a technique that enables one to obtain objects’ geometrical images or diffraction patterns from the optical path that does not contain them. There have been many practicalities of GI reported during recent decades in terms of the hard X-ray sources [23], neutron ray sources [24], single-pixel detection techniques [24, 25] etc., Among former reports, issues for complete incoherent sources [22, 26] and for non-periodic objects [27] are discussed, but few partially coherent problems are addressed on periodic media, especially on the issue of crystallography. In this paper, we compare the quality of diffraction patterns and ghost diffraction patterns of the same periodic object and show that the coherence state has the opposite effect on them with respect to the quality of the patterns: An increase (decrease) of the degree of partial coherence leads to a decrease (increase) of the quality of the diffraction pattern.

We begin by writing fields in the optical path containing the object as

$\mathit{E}\left(\mathbf{r}\right)\mathrm{=}{\displaystyle \underset{\mathit{V}}{\iiint }\mathit{E}\left(\mathbf{\rho }\right){\mathit{G}}_{\mathit{obj}}\left(\mathbf{\rho }\mathrm{,}\mathbf{r}\right){\mathbf{d}}^{\mathbf{3}}\mathbf{\rho }}(1)$

and containing no object as

$\mathit{E}\left(\mathbf{r}\right)\mathrm{=}{\displaystyle \underset{\mathit{V}}{\iiint }\mathit{E}\left(\mathbf{\rho }\right)\mathit{G}\left(\mathbf{\rho }\mathrm{,}\mathbf{r}\right){\mathbf{d}}^{\mathbf{3}}\mathbf{\rho }}(2)$

Among (1)

${\mathit{G}}_{\mathit{obj}}\left(\mathbf{\rho }\mathrm{,}\mathbf{r}\right)=F\left(\mathbf{\rho }\right)\frac{{\mathit{e}}^{\mathit{jkr}}}{\mathit{r}}{\mathit{e}}^{-\mathit{jk}\mathbf{s}\mathbf{\rho }}(3)$

is the propagator in space containing the object, with scatter potential of F(ρ), and among [2].

$\mathit{G}\left(\mathbf{\rho ,r}\right)=\frac{{\mathit{e}}^{\mathit{jkr}}}{\mathit{r}}{\mathit{e}}^{-\mathit{jks}\mathbf{\rho }}(4)$

is the propagator in free space, i.e., there is no object present in the optical path. By applying Eqs 1–4, one can write, respectively, the cross-spectral density function (CSD)

$\mathit{W}\left({\mathbf{r}}_{\mathbf{1}}\mathbf{,}{\mathbf{r}}_{\mathbf{2}}\right)\equiv \langle {\mathit{E}}^{\ast }\left({\mathbf{r}}_{\mathbf{1}}\right)\mathit{E}\left({\mathbf{r}}_{\mathbf{2}}\right)\rangle (5)$

in the far zone for diffraction patterns as

${\mathit{W}}_{\mathit{D}}^{\infty }\left({\mathbf{r}}_{\mathrm{1}}\mathrm{,}{\mathbf{r}}_{\mathrm{2}}\right)\mathrm{=}{\displaystyle \underset{V}{\iiint }\mathit{W}\left({\mathbf{\rho }}_{\mathbf{1}}\mathbf{,}{\mathbf{\rho }}_{\mathbf{2}}\right){\mathit{G}}_{\mathit{obj}}^{\mathit{*}}\left({\mathbf{\rho }}_{\mathbf{1}}\mathbf{,}{\mathbf{r}}_{\mathbf{1}}\right){\mathit{G}}_{\mathit{obj}}\left({\mathbf{\rho }}_{\mathbf{2}}\mathbf{,}{\mathbf{r}}_{\mathbf{2}}\right){\mathbf{d}}^{\mathbf{3}}{\mathbf{\rho }}_{\mathbf{1}}{\mathbf{d}}^{\mathbf{3}}{\mathbf{\rho }}_{\mathbf{2}}}\mathrm{,}(6)$

and for ghost diffraction as

$W_G^{\infty }\left({\mathbf{r}}_{\mathbf{1}}\mathrm{,}{\mathbf{r}}_{\mathbf{2}}\right)={\displaystyle \underset{V}{\iiint }W\left({\mathbf{\rho }}_{\mathbf{1}}\mathrm{,}{\mathbf{\rho }}_{\mathbf{2}}\right)G^{\ast }\left({\mathbf{\rho }}_{\mathbf{1}}\mathrm{,}{\mathbf{r}}_{\mathbf{1}}\right){\mathit{G}}_{\mathit{obj}}\left({\mathbf{\rho }}_{\mathbf{2}}\mathrm{,}{\mathbf{r}}_{\mathbf{2}}\right){\mathbf{d}}^{\mathbf{3}}{\mathbf{\rho }}_{\mathbf{1}}{\mathbf{d}}^{\mathbf{3}}{\mathbf{\rho }}_{\mathbf{2}}}.(7)$

where the vector ρ = (ξ, η, ζ) represents the position in the near-field and r = (x, y, z) denotes the position in the far-field, as Figure 1 shows. Among [6, 7].

$\mathit{W}\left({\mathbf{\rho }}_{\mathbf{1}}\mathbf{,}{\mathbf{\rho }}_{\mathbf{2}}\right)\equiv \langle {\mathit{E}}^{\ast }\left({\mathbf{\rho }}_{\mathbf{1}}\right)\mathit{E}\left({\mathbf{\rho }}_{\mathbf{2}}\right)\rangle (8)$

defines the CSD for the source. We consider [8] to have a form of Gauss—Shell mode (GSM) of

$\mathit{W}\left({\mathbf{\rho }}_{\mathbf{1}}\mathbf{,}{\mathbf{\rho }}_{\mathbf{2}}\right)\mathrm{=}\mathit{A}\exp \left(\mathrm{-}\frac{{\mathit{\rho }}_{\mathrm{1}}^{\mathrm{2}}\mathrm{+}{\mathit{\rho }}_{\mathrm{2}}^{\mathrm{2}}}{{\mathit{\sigma }}^{\mathrm{2}}}\right)\exp \left[\mathrm{-}\frac{{\left({\mathbf{\rho }}_{\mathrm{2}}\mathrm{-}{\mathbf{\rho }}_{\mathrm{1}}\right)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\delta }}^{\mathrm{2}}}\right]\mathrm{,}(9)$

with σ to describe its spread size and δ to evaluate its spatial coherence length. GSM of Eq. 9. Was chosen to model CSD of Eq. 8. Because it exists most widely in nature and is easy to explain, although there are many light sources with special correlation structures [28] that are more suitable for specific occasions. It is worth noting that the physics behind Eq. 6. Was that the observable CSD W (ρ₁, ρ₂) travels like a monochromatic wave. Such an interesting physical picture derives from two-photon Helmholtz equation [29]:

${\nabla }_{\mathit{n}}^2\mathit{W}\left({\mathbf{r}}_{\mathbf{1}}\mathbf{,}{\mathbf{r}}_{\mathbf{2}}\right)+{\mathit{k}}^2\mathit{W}\left({\mathbf{r}}_{\mathbf{1}}\mathbf{,}{\mathbf{r}}_{\mathbf{2}}\right)=0,\mathit{n}=\mathrm{1,2},(10)$

one can appreciate its ghost imaging counterpart of Eq. 7. By referring to Ref. [30], which provides a unified understanding of phenomena that related to the two-photon wave packet propagation.

FIGURE 1

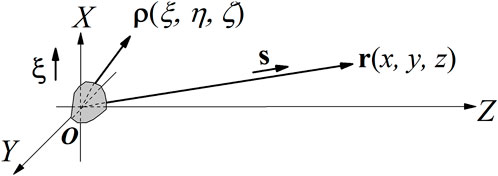
FIGURE 1. Vector ρ = (ξ, η, ζ) denotes the position in the medium, and r = rs = (x, y, z) denotes the position in the far-field. ξ is the unit vector along the X-axis, and s is the unit vector along with r.

We write the medium’s scattering potential F(ρ) with a periodic structure as [12, 31]:

$\mathit{F}\left(\mathbf{\rho }\right)={\displaystyle \sum _{\mathbf{H}}\mathrm{\Phi }\left(\mathbf{H}\right)\exp \left(\mathit{j}2\pi \mathbf{H\rho }\right)},(11)$

H is the reciprocal lattice vector. We simplify [11] by assuming it to be one-dimensional along the X direction, i.e.,

$\mathit{F}\left(\mathbf{\rho }\right)\mathit{=f}\left(\mathit{\xi }\right)\mathit{\delta }\left(\mathit{\eta }\right)\mathit{\delta }\left(\mathit{\zeta }\right)(12)$

Assuming that f (ξ) has a spatial period d, i.e., f(ξ) = f (ξ + d), one can expand f (ξ) in the form of a Fourier series as

$\mathit{f}\left(\xi \right)={\displaystyle \sum _{n=-\infty }^{+\infty }{\mathit{C}}_{\mathit{n}}\exp \left(j\frac{\mathrm{2n}\pi }{\mathit{d}}\xi \right)},(13)$

and its Fourier coefficients are given by

${\mathit{C}}_{\mathit{n}}=\frac{1}{d}{\displaystyle \underset{0}{\overset{\mathit{d}}{\int }}\mathit{f}\left(\xi \right)\exp \left(-j\frac{\mathrm{2}\mathit{n}\pi }{\mathit{d}}\xi \right)}d\xi ,\left(\mathit{n}=\pm 1,\pm 2\dots \right).(14)$

By substituting Eqs 3, 9, 12, 13, into Eq. 6, one obtains

${\mathit{W}}_{\mathit{D}}^{\infty }\left({\mathbf{r}}_{\mathbf{1}}\mathbf{,}{\mathbf{r}}_{\mathbf{2}}\right)=\frac{{\left|\mathit{A}\right|}^2{\mathit{e}}^{\mathit{jk}\left({\mathit{r}}_{\mathit{2}}\mathit{-}{\mathit{r}}_{\mathit{1}}\right)}}{{\mathit{r}}_{\mathit{1}}{\mathit{r}}_{\mathit{2}}}{\displaystyle \sum _{\mathit{m}=-\infty }^{+\infty }{\mathit{C}}_{\mathit{m}}^{\mathit{*}}{\mathit{C}}_{\mathit{n}}{\mathit{W}}_{\mathit{mn}}\left({\mathit{\theta }}_{\mathit{1}}\mathit{,}{\mathit{\theta }}_{\mathit{2}}\right)},(15)$

and by substituting Eqs. 3, 4, 9, 12, 13 into Eq. 17, one obtains

${\mathit{W}}_{\mathit{G}}^{\infty }\left({\mathbf{r}}_{\mathbf{1}}\mathbf{,}{\mathbf{r}}_{\mathbf{2}}\right)=\mathit{A}\frac{{\mathit{e}}^{\mathit{jk}\left({\mathit{r}}_{\mathit{2}}\mathit{-}{\mathit{r}}_{\mathit{1}}\right)}}{{\mathit{r}}_{\mathit{1}}{\mathit{r}}_{\mathit{2}}}\pi {\text{Δ}}^2\exp \left(-\frac{1}{4}{\mathrm{\Delta }}^2{\mathit{k}}^2\mathrm{si}{\mathrm{n}}^2{\theta }_1\right){\displaystyle \sum _{\mathit{n}=-\infty }^{+\infty }{\mathit{C}}_{\mathit{n}}{\mathit{W}}_{\mathit{n}}\left({\theta }_1,{\theta }_2\right)}(16)$

where θ is the angle between s and ξ given by

$\cos \theta =\mathbf{s}\cdot \mathbf{\xi }(17)$

In Eq. 15,

$\begin{array}{c}{\mathit{W}}_{\mathit{mn}}\left({\mathit{\theta }}_{\mathit{1}}\mathit{,}{\mathit{\theta }}_{\mathit{2}}\right)\mathit{=}{\displaystyle \underset{{\mathit{\xi }}_{\mathit{2}}}{\int }{\displaystyle \underset{{\mathit{\xi }}_{\mathit{1}}}{\int }\exp \left(\mathit{-jm2\pi }\frac{{\mathit{\xi }}_{\mathit{1}}}{\mathit{d}}\mathit{+jn2\pi }\frac{{\mathit{\xi }}_{\mathit{2}}}{\mathit{d}}\right)}}\\ \mathrm{\times exp}\left\{\mathit{-}\left[\frac{{\mathit{\xi }}_{\mathit{1}}^{\mathit{2}}\mathit{+}{\mathit{\xi }}_{\mathit{2}}^{\mathit{2}}}{{\mathit{\sigma }}^{\mathit{2}}}\mathit{+}\frac{{\left({\mathit{\xi }}_{\mathit{2}}\mathit{-}{\mathit{\xi }}_{\mathit{1}}\right)}^{\mathit{2}}}{\mathit{2}{\mathit{\delta }}^{\mathit{2}}}\right]\right\}\\ \mathrm{\times exp}\left[\mathit{-jk}\left({\mathbf{s}}_{\mathit{2}}{\mathit{\xi }}_{\mathit{2}}\mathit{-}{\mathbf{s}}_{\mathit{1}}{\mathit{\xi }}_{\mathit{1}}\right)\mathit{\xi }\right]\mathit{d}{\mathit{\xi }}_{\mathit{1}}\mathit{d}{\mathit{\xi }}_{\mathit{2}}\\ \mathit{=\pi }{\text{Δ}}_{\mathit{1}}^{\mathit{2}}\exp \{\mathit{-}\frac{{\mathrm{\Delta }}_{\mathit{1}}^{\mathit{2}}}{\mathit{8}}[\mathit{2}\frac{\mathit{n-m}}{\mathit{d}}\mathit{\pi }{\mathit{+k}\left(\cos {\mathit{\theta }}_{\mathit{1}}\mathrm{-cos}{\mathit{\theta }}_{\mathit{2}}\right)]}^{\mathit{2}}\}\\ \mathrm{\times exp}\{\mathit{-}\frac{{\mathrm{\Delta }}_{\mathit{1}}^{\mathit{2}}}{\mathit{2}}[\frac{\mathit{m+n}}{\mathit{d}}\mathit{\pi }{\mathit{-}\frac{\mathit{k}}{\mathit{2}}\left(\cos {\mathit{\theta }}_{\mathit{1}}\mathrm{+cos}{\mathit{\theta }}_{\mathit{2}}\right)]}^{\mathit{2}}\}\mathit{,}\end{array}(18)$

and in Eq. 16,

$\begin{array}{c}{\mathit{W}}_{\mathit{n}}\left({\mathit{\theta }}_{\mathit{1}}\mathit{,}{\mathit{\theta }}_{\mathit{2}}\right)\mathit{=}{\displaystyle \underset{{\mathit{\xi }}_{\mathit{2}}}{\int }{\displaystyle \underset{{\mathit{\xi }}_{\mathit{1}}}{\int }\exp \left(\mathit{jn2\pi }\frac{{\mathit{\xi }}_{\mathit{2}}}{\mathit{d}}\right)}}\exp \left[\mathit{-}\frac{{\mathit{\xi }}_{\mathit{1}}^{\mathit{2}}\mathit{+}{\mathit{\xi }}_{\mathit{2}}^{\mathit{2}}}{{\mathit{\sigma }}^{\mathit{2}}}\mathit{-}\frac{{\left({\mathit{\xi }}_{\mathit{2}}\mathit{-}{\mathit{\xi }}_{\mathit{1}}\right)}^{\mathit{2}}}{\mathit{2}{\mathit{\delta }}^{\mathit{2}}}\right]\\ \mathrm{\times exp}\left[\mathit{-jk}\left({\mathbf{s}}_{\mathit{2}}{\mathit{\xi }}_{\mathit{2}}\mathit{-}{\mathbf{s}}_{\mathit{1}}{\mathit{\xi }}_{\mathit{2}}\right)\xi \right]\mathit{d}{\mathit{\xi }}_{\mathit{1}}\mathit{d}{\mathit{\xi }}_{\mathit{2}}\\ \mathit{=\pi }{\mathrm{\Delta }}_{\mathit{1}}\mathrm{\sigma exp}\{\mathit{-}\frac{{\mathit{\sigma }}^{\mathit{2}}}{\mathit{8}}[\frac{\mathit{2n\pi }}{\mathit{d}}{\mathit{+k}\left(\cos {\mathit{\theta }}_{\mathit{1}}\mathrm{-cos}{\mathit{\theta }}_{\mathit{2}}\right)]}^{\mathit{2}}\}\\ \mathrm{\times exp}\{\mathit{-}\frac{\mathit{1}}{\mathit{2}}{\mathrm{\Delta }}_{\mathit{1}}^{\mathit{2}}[\frac{\mathit{n\pi }}{\mathit{d}}{\mathit{-}\frac{\mathit{k}}{\mathit{2}}\left(\cos {\mathit{\theta }}_{\mathit{1}}\mathrm{+cos}{\mathit{\theta }}_{\mathit{2}}\right)]}^{\mathit{2}}\}\mathit{.}\end{array}(19)$

Eqs 18, 19 are evaluated by changing the variables follows:

${\xi }_{+}=\frac{{\xi }_1+{\xi }_2}{2},{\xi }_{-}={\xi }_1-{\xi }_2;(20)$

with

$\frac{1}{{\mathrm{\Delta }}^2}=\frac{1}{2{\delta }^2}+\frac{1}{{\sigma }^2},\frac{1}{{\mathrm{\Delta }}_1^2}=\frac{1}{{\delta }^2}+\frac{1}{{\sigma }^2}.(21)$

Eqs 15, 16 together with Eqs 18, 19. are the main results of this investigation.

As a simple example, we select a one-dimensional black and white grating with period d, and slit width b to model f (ξ) as:

$\mathit{f}\left(\xi \right)={\displaystyle \sum _{\mathit{k}=-\infty }^{+\infty }\mathrm{rect}\left(\frac{\xi -\mathit{kd}}{\mathit{b}}\right)},(22)$

and by applying Eq. 14, we obtain

${\mathit{C}}_{\mathit{0}}\mathit{=}\frac{\mathit{b}}{\mathit{d}},{\mathit{C}}_{\mathit{n}}=\frac{1}{\mathit{n}\pi }\sin \frac{\mathit{n}\pi \mathit{b}}{\mathit{d}},\left(\mathit{n}=\pm 1,\pm 2\dots \right).(23)$

We use

$\mathit{I}\left(\theta \right)\equiv {\mathit{W}}_{\mathit{D}}^{\infty }\left(\mathbf{r,r}\right)(24)$

to investigate diffraction patterns. When performing ghost imaging experiments, one gets the information by applying

$\langle \mathrm{\Delta }\mathit{I}\left(\mathbf{r}\right)\mathrm{\Delta }\mathit{I}\left({\mathbf{r}}_{\mathit{0}}\right)\rangle \mathit{=}\langle \mathit{I}\left(\mathbf{r}\right)\mathit{I}\left({\mathbf{r}}_{\mathit{0}}\right)\rangle \mathit{-}\langle \mathit{I}\left(\mathbf{r}\right)\rangle \langle \mathit{I}\left({\mathbf{r}}_{\mathit{0}}\right)\rangle \mathit{,}(25)$

for GSM sources, there exists [32].

$\langle \text{Δ}\mathit{I}\left(\mathbf{r}\right)\text{Δ}\mathit{I}\left({\mathbf{r}}_{\mathrm{0}}\right)\rangle ={\left|{\mathit{W}}_{\mathit{G}}^{\infty }\left(\mathbf{r}\mathrm{,}{\mathbf{r}}_{\mathrm{0}}\right)\right|}^2(26)$

therefore, we use

$\mathit{J}\left(\theta \right)\equiv {\left|{\mathit{W}}_{\mathit{G}}^{\infty }\left(\mathbf{r}\mathrm{,}{\mathbf{r}}_{\mathrm{0}}\right)\right|}^2(27)$

to investigate ghost diffraction patterns in the far-field. In Eq. 27, r in plane XOZ denotes the position in the reference arm of GI, which contains no object, and r₀ = (0, 0, r) describes the fixed position of the detector located in the object arm containing the object.

By setting that d = 2.814 × 10⁻¹⁰ m, b = d/10, λ = 1 × 10^−10.33 m, and σ = 4 × 10⁻¹⁰ m, we plotted I(θ) in Figure 2 and J (θ) in Figure 3 with different value of δ. All of them have been normalized by their maxima. We arranged parameters as λ < d < σ. The coherence scale δ is generally larger than the wavelength λ, and might be slightly smaller than it in some places. This arrangement conforms to the diffraction experiment conditions in general. From of Figures 2A−E, one can see that as the coherent size δ of the radiation decreases, the information of the scattering object is lost gradually in the diffraction pattern I(θ). When we use these data with the same sequence to plot the ghost diffraction J(θ), one sees from Figures 3A–E that the information content of the diffraction patterns is gradually increasing if the coherence length decreases. However, reversely, a decrease in the coherence length leads to a decrease in the information content of the ordinary classical diffraction patterns.

FIGURE 2

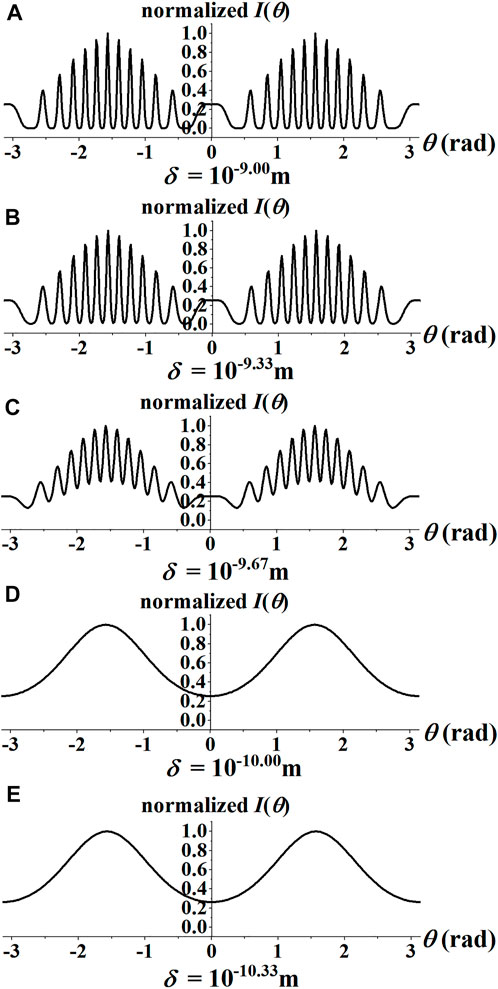
FIGURE 2. (A–E) Normalized I(θ) (with arbitrary unit) plotted against θ ≡ arccos (s·ξ) for different values of the horizontal coherent length δ. The spot size and the wavelength of the incident radiation are taken to be σ = 4 × 10⁻¹⁰ m and λ = 10^−10.33 m.

FIGURE 3

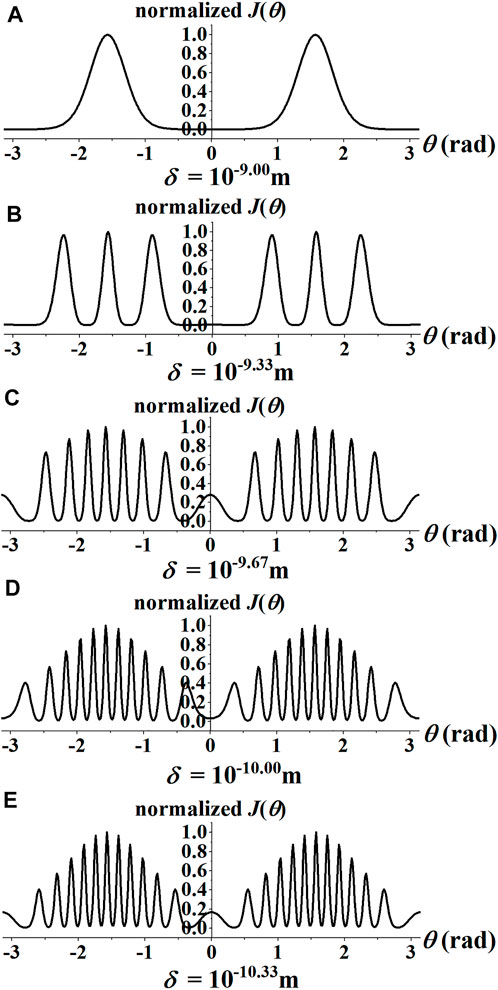
FIGURE 3. (A–E) Normalized J(θ) (with the arbitrary unit) plotted against θ ≡ arccos (s·ξ) for different values of the horizontal coherent length δ. The spot size and the wavelength of the incident radiation are taken to be σ = 4 × 10⁻¹⁰ m and λ = 10^−10.33 m.

These results clearly show that the lesser coherent the radiation source is, the more difficult it becomes to obtain high-quality classical diffraction patterns. However, the lesser the beam’s coherence, the better it will perform in the case of ghost diffraction! This suggests the superiority of ghost diffraction in crystallography, when using extremely low coherent radiation [24, 33, 34] and may thus be breaking through the bottleneck which has precisely been predicted in Ref. [12].

We address although ghost imaging provides a better resolution with a less spatially coherent field may not be unexpected, we have made a mathematical proof for the first time, not just based on experience and intuition from experiments.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

National Key Research and Development Program of China (2019YFA0705000); National Natural Science Foundation of China (11804198, 11974218, 12192254); Shandong Provincial Natural Science Foundation of China (ZR2019BA030); Innovation Group of Jinan (2018GXRC010); Local Science and Technology Development Project of the Central Government (YDZX20203700001766); China Postdoctoral Science Foundation (2018M642690). Project of Shandong Provincial Key Laboratory of Optics [K202002, K202004]; Key Lab of Advanced optical Manufacturing Technologies of Jiangsu Province, Soochow University [KJS1606].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mv L. Concerning the Detection of X-Ray Interferences. Nobel Lectures, Physics 1901-1921. Amsterdam: Elsevier Publishing Company (1967). p. 347–55.

Google Scholar

2. Britannica T. Rosalind Franklin (2021). Available from: https://www.britannica.com/biography/Rosalind-Franklin.

Google Scholar

3. Pray L. Discovery of DNA Structure and Function: Watson and Crick. Nat Educ (2008) 1(1).

Google Scholar

4. Drenth J. Sec.1.1, Principles of Protein X-Ray Crystallography. 3rd ed. USA: Springer (2006).

Google Scholar

5. Zhu X, Birringer R, Herr U, Gleiter H. X-Ray Diffraction Studies of the Structure of Nanometer-Sized Crystalline Materials. Phys Rev B (1987) 35(17):9085–90. doi:10.1103/physrevb.35.9085

CrossRef Full Text | Google Scholar

6. Shi Y. A Glimpse of Structural Biology through X-Ray Crystallography. Cell (2014) 159(5):995–1014. doi:10.1016/j.cell.2014.10.051

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ruland W. X‐Ray Studies on Preferred Orientation in Carbon Fibers. J Appl Phys (1967) 38(9):3585–9. doi:10.1063/1.1710176

CrossRef Full Text | Google Scholar

8. Das R, Eaqub Ali M. Hamid SBA. Current Applications of X-Ray Powder Diffraction - a Review. Rev Adv Mater Sci (2014) 38:15.

Google Scholar

9. Wang W, Feng K, Ke L, Yu C, Xu Y, Qi R, et al. Free-Electron Lasing at 27 Nanometres Based on a Laser Wakefield Accelerator. Nature (2021) 595(7868):516–20. doi:10.1038/s41586-021-03678-x

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chapman HN, Fromme P, Barty A, White TA, Kirian RA, Aquila A, et al. Femtosecond X-Ray Protein Nanocrystallography. Nature (2011) 470(7332):73–7. doi:10.1038/nature09750

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Stern S, Holmegaard L, Filsinger F, Rouzée A, Rudenko A, Johnsson P, et al. Toward Atomic Resolution Diffractive Imaging of Isolated Molecules with X-Ray Free-Electron Lasers. Faraday Discuss (2014) 171:393–418. doi:10.1039/c4fd00028e

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wolf E. Diffraction of Radiation of Any State of Spatial Coherence on Media with Periodic Structure. Opt Lett (2013) 38(20):4023–5. doi:10.1364/OL.38.004023

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Dušek M. Diffraction of Partially Coherent Beams on Three-Dimensional Periodic Structures and the Angular Shifts of the Diffraction Maxima. Phys Rev E (1995) 52(6):6833–40. doi:10.1103/PhysRevE.52.6833

CrossRef Full Text | Google Scholar

14. Born M, Wolf E. Sec. 8.6, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Cambridge: Cambridge University Press (2000).

Google Scholar

15. Takayama Y, Fukuda K, Kawashima M, Aoi Y, Shigematsu D, Akada T, et al. Dynamic Nanoimaging of Extended Objects via Hard X-Ray Multiple-Shot Coherent Diffraction with Projection Illumination Optics. Commun Phys (2021) 4(1):48. doi:10.1038/s42005-021-00539-x

CrossRef Full Text | Google Scholar

16. Bieberle A, Nehring H, Berger R, Arlit M, Härting H-U, Schubert M, et al. Compact High-Resolution Gamma-Ray Computed Tomography System for Multiphase Flow Studies. Rev Sci Instrum (2013) 84(3):033106. doi:10.1063/1.4795424

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Liang F, Chen L, Li F, Jin G. Data Acquisition System for the 3he Position-Sensitive Proportional Counter Based Neutron Dosimeter. Phys Proced (2012) 37:1813–8. doi:10.1016/j.phpro.2012.02.508

CrossRef Full Text | Google Scholar

18. Blakeley MP, Langan P, Niimura N, Podjarny A. Neutron Crystallography: Opportunities, Challenges, and Limitations. Curr Opin Struct Biol (2008) 18(5):593–600. doi:10.1016/j.sbi.2008.06.009

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Meilleur F. A Beginner’s Guide to Neutron Macromolecular Crystallography. Biochem (Lond) (2020) 42(6):16–20. doi:10.1042/bio20200078

CrossRef Full Text | Google Scholar

20. Matthew PB, Hasanin SS, Anonyuk SV. Sub-Atomic Resolution X-Ray Crystallography and Neutron Crystallography: Promise, Challenges and Potential. IUCrJ (2015) 2:464–74. doi:10.1107/S2052252515011239

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Keedy DA, van den Bedem H, Sivak DA, Petsko GA, Ringe D, Wilson MA, et al. Crystal Cryocooling Distorts Conformational Heterogeneity in a Model Michaelis Complex of Dhfr. Structure (2014) 22(6):899–910. doi:10.1016/j.str.2014.04.016

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhang M, Wei Q, Shen X, Liu Y, Liu H, Cheng J, et al. Lensless Fourier-Transform Ghost Imaging with Classical Incoherent Light. Phys Rev A (Coll Park) (2007) 75(2):021803. doi:10.1103/PhysRevA.75.021803

CrossRef Full Text | Google Scholar

23. Yu H, Lu R, Han S, Xie H, Du G, Xiao T, et al. Fourier-Transform Ghost Imaging with Hard X Rays. Phys Rev Lett (2016) 117(11):113901. doi:10.1103/PhysRevLett.117.113901

PubMed Abstract | CrossRef Full Text | Google Scholar

24. He Y-H, Huang Y-Y, Zeng Z-R, Li Y-F, Tan J-H, Chen L-M, et al. Single-Pixel Imaging with Neutrons. Sci Bull (Beijing) (2021) 66(2):133–8. doi:10.1016/j.scib.2020.09.030

CrossRef Full Text | Google Scholar

25. Sun B, Edgar MP, Bowman R, Vittert LE, Welsh S, Bowman A, et al. 3d Computational Imaging with Single-Pixel Detectors. Science (2013) 340(6134):844–7. doi:10.1126/science.1234454

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Cheng J, Han S. Incoherent Coincidence Imaging and its Applicability in X-Ray Diffraction. Phys Rev Lett (2004) 92(9):093903. doi:10.1103/PhysRevLett.92.093903

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Cai Y, Wang F. Lensless Imaging with Partially Coherent Light. Opt Lett (2007) 32(3):205–7. doi:10.1364/OL.32.000205

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Cai Y, Chen Y, Wang F. Generation and Propagation of Partially Coherent Beams with Nonconventional Correlation Functions: A Review [Invited]. J Opt Soc Am A (2014) 31(9):2083–96. doi:10.1364/JOSAA.31.002083

CrossRef Full Text | Google Scholar

29. Wolf E. Sec 4.1, Introduction to the Theory of Coherence and Polarization of Light. Cambridge: Cambridge University Press (2007).

Google Scholar

30. Saleh BEA, Teich MC, Sergienko AV. Wolf Equations for Two-Photon Light. Phys Rev Lett (2005) 94(22):223601. doi:10.1103/PhysRevLett.94.223601

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wang YYD, Kuebel D, Visser TD, Wolf E. Creating Von Laue Patterns in Crystal Scattering with Partially Coherent Sources. Phys Rev A (2016) 94(3):033812. doi:10.1103/PhysRevA.94.033812

CrossRef Full Text | Google Scholar

32. Goodman JW. Sec. 3.6.4, Statistical Optics. HobokenIncorporated: John Wiley & Sons (2000).

Google Scholar

33. Lane TJ, Ratner D. What Are the Advantages of Ghost Imaging? Multiplexing for X-Ray and Electron Imaging. Opt Express (2020) 28(5):5898–918. doi:10.1364/oe.379503

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Kim YY, Gelisio L, Mercurio G, Dziarzhytski S, Beye M, Bocklage L, et al. Ghost Imaging at an Xuv Free-Electron Laser. Phys Rev A (Coll Park) (2020) 101(1):013820. doi:10.1103/PhysRevA.101.013820

CrossRef Full Text | Google Scholar