Imaging Through Random Scatterer with Spatial Coherence Structure Measurement

Optical coherence is becoming an efficient degree of freedom for light field manipulations and applications. In this work, we show that the image information hidden a distance behind a random scattering medium is encoded in the complex spatial coherence structure of a partially coherent light beam that generates after the random scatterer. We validate in experiment that the image information can be well recovered with the spatial coherence measurement and the aid of the iterative phase retrieval algorithm in the Fresnel domain. We find not only the spatial shape but also the position including the lateral shift and longitudinal distances of the image hidden behind the random scatterer can be reconstructed, which indicates the potential uses in three-dimensional optical imaging through random scattering media.

1 Introduction

Spatial coherence is an important characteristic to describe the statistical properties of random light fields, and it has played a vital role in understanding interference, propagation, and light-matter interaction of both classical and quantum wave fields [1–3]. Nowadays, the spatial coherence has already been viewed as an efficient tool for light field manipulations and applications [4]. For instance, by simply adjusting the spatial coherence width, i.e., decreasing the spatial coherence of a laser beam, the generated partially (lowly) coherent beams can help reduce the turbulence-induced signal distortion in free-space optical communication [5, 6], and can restrict speckles in optical imaging [7] and beam shaping applications [8]. Since the pioneering work by Gori and his colleagues [9–11], it has been well recognized that by modulating the spatial coherence structure of light source, the partially coherent beams will display many extraordinary propagation properties [12] including self-splitting, self-focusing, self-shaping, and self-reconstruction effects. The spatial coherence structure engineering has found applications in sub-Rayleigh imaging [13], robust microscopy imaging [14], and robust far-field imaging [15].

The methods for modulating the spatial coherence structure can be divided into two types. The first type is based on the famous Wolf’s coherent-mode representation [1], in which the partially coherent beam is viewed as an incoherent superposition of a set of spatially coherent modes. By controlling the modal weight and the complex field distribution of each mode, the spatial coherence structure of the synthesized partially coherent beam can be controlled [16–21]. The second approach is based on the (generalized) van Cittert–Zernike theorem, which indicates that a partially coherent secondary source can be generated by propagating a spatially incoherent source in free space or other media [22]. In this approach, the spatial coherence structure of the secondary partially coherent source can be modulated by controlling the intensity distribution of the incoherent source and the response function of the optical system [12, 23].

In the second approach, the incoherent source is typically generated in the experiment by passing a fully coherent structured light through a dynamic random scatterer, e.g., a rotating ground glass disk [4, 23]. Based on the van Cittert–Zernike theorem, the intensity distribution p(v) of the fully coherent structured light before the random scatterer has a determinate relation with the complex spatial coherence structure μ(r₁, r₂) of the generated partially coherent secondary source. For example, when the optical system between the random scatterer and the secondary source is formed by a Fourier lens, p(v) and μ(r₁, r₂) form the Fourier transform pair. Thus, by measuring the complex spatial coherence structure of the partially coherent source, the image information encoded in the fully coherent light hidden behind the random scatterer can be well recovered. Huang and coauthors showed that both the transverse position and the spatial shape of a moving object hidden behind the rotating ground glass disk can be well reconstructed with the complex spatial coherence measurement [24]. Later, Dong and coauthors showed that the polarization properties of the hidden image can be obtained with the spatial coherence matrix measurement [25]. When the optical system is formed by a fractional Fourier transform system, it is found that the image information can be recovered by measuring the complex spatial coherence structure only when the fractional order used in recovery is correct, which indicates the potential application in coherence-based optical encryption and decryption [26].

However, in the above studies, only the image information projected on the random scatterer can be recovered by complex spatial coherence measurement since the restriction of the van Cittert–Zernike theorem. In other words, only the two-dimensional (2D) image information hidden behind the random scatterer can be extracted from the spatial coherence measurement, which limits the application in three-dimensional (3D) optical imaging through random media. To solve this limitation, a question is naturally raised: whether the information of an image (or object) at a certain distance from the random scatterer can be recovered? In this work, we show that with the help of the spatial coherence measurement and the iterative phase retrieval algorithm in the Fresnel domain, the image information hidden a distance behind the rotating ground glass disk can be well reconstructed. Further, it is demonstrated that not only the spatial shape and the lateral shift but also the longitudinal position of the hidden image can be well recovered.

We remark that the research on optical imaging through random media is a historical topic since the early study was carried out by Goodman et al. in the 1960s [27, 28]. However, this topic today is still attracting wide attention from the researchers due to the broad range of its applications from biomedical to astronomical imaging [29, 30]. Different methods have been proposed to realize the optical imaging through scattering media. The most straightforward approaches utilize ballistic photons [31–33]. However, strongly scattering media reduce the number of ballistic photons and lower the signal tremendously. Thus, these methods are used mostly for imaging static objects through a weakly scattering medium. Some methods, such as the wavefront shaping techniques [34–37] and the transmission matrix measurement methods [38, 39], require the transmission properties of the random scatterer itself before imaging. Another approach relies on the memory effect of light through scattering medium [40, 41]. Within the memory effect region, the intensity autocorrelation of the scattered light is identical to the autocorrelation of the object image hidden behind the scatterer [42–46]. Thus, the object can be reconstructed well by using the phase retrieval algorithm [47].

However, the above methods are mainly dealt with optical imaging through a static medium [48, 49]. In this work, we propose a different method for optical imaging through a dynamic scattering medium. We remark that a few of technologies for optical imaging through dynamic scattering media have been proposed recently [50, 51]. Their methods are based on the intensity correlations of the speckles. Thus, the image information can be reconstructed only when the random fluctuations of the dynamic scatterer obey Gaussian statistics [52]. For the random scattering media having non-Gaussian statistics, e.g., the turbulent atmosphere [53], the proposed method cannot be used anymore. However, our method is based on measuring the second-order field-field correlation (spatial coherence) of a partially coherent light beam. The relation between the image information and the spatial coherence is independent of the statistics of the random medium. In other words, the image information encoded in the spatial coherence structure can be recovered well for the random media with any statistical properties. Thus, our coherence-based method shows robustness in the complex environment, which we have showed in [26].

This work is organized as follows. In Section 2, we present our basic principle for encoding the image information hidden behind the random scatterer into the spatial coherence structure of a random light that generates after the random medium and we show the iterative phase retrieval algorithm used in our experiment. In Section 3, we present our experimental verification and discuss how to measure the complex spatial coherence of a random light beam with the intensity-intensity cross-correlations. The experimental results to demonstrate the feasibility of our method are presented in Section 4. We summarize our findings in Section 5.

2 Principle

The schematic diagram of the encoding system is shown in Figure 1A, in which the image is hidden a distance z in front of the scattering medium. The image is illuminated by a fully coherent light beam. Based on the Huygens-Fresnel diffraction integral formula, the optical field on the front surface of the scattering medium is expressed as

$E\left(\mathit{\rho }\right)=-\frac{\mathrm{i}}{\lambda z}\exp \left(\mathrm{i}kz\right)\iint O\left(\mathbf{v}\right)\exp \left[\frac{\mathrm{i}k}{2z}{\left(\mathit{\rho }-\mathbf{v}\right)}^2\right]{\mathrm{d}}^2\mathbf{v},(1)$

where λ denotes the wavelength, k = 2π/λ is the wavenumber, and O(v) denotes the transmission function of the image. Above, v and ρ are the spatial coordinates of the cross section where the image and the random scattering medium are located, respectively.

FIGURE 1

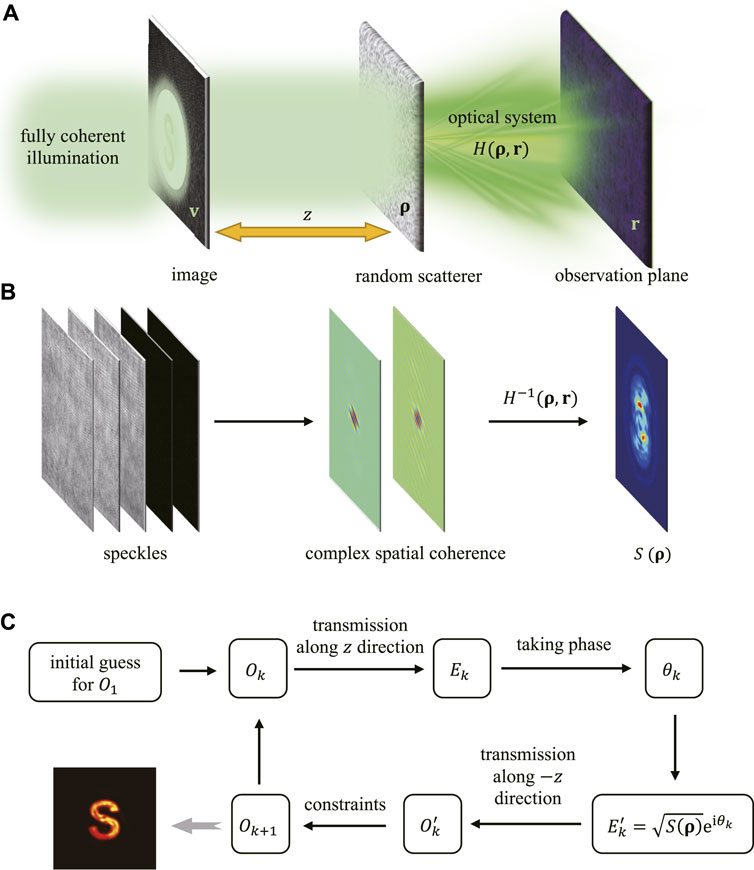
FIGURE 1. Schematic diagram of optical imaging through a random scattering medium. (A) The image hidden a distance z behind a random scatterer is illuminated by a fully coherent light. The scattered light from the random medium passes through an optical system with response function H (ρ, r). The complex spatial coherence structure is measured in the observation plane. (B) The intensity S(ρ) on the front surface of the random scatterer can be recovered through inverse transform H⁻¹ (ρ, r) of the measured complex spatial coherence. (C) The flowchart of the iterative phase retrieval algorithm.

After the beam passes through the random scattering medium, the fully coherent light becomes spatially incoherent if we assume the beam spot on the random scatterer is larger than the inhomogeneity scale of the random scatterer [52]. The statistical properties for a spatially incoherent light are characterized by the cross-spectral density function (in spatial-frequency domain) [1], i.e.

$W\left({\mathit{\rho }}_1,{\mathit{\rho }}_2\right)=\sqrt{S\left({\mathit{\rho }}_1\right)S\left({\mathit{\rho }}_2\right)}\delta \left({\mathit{\rho }}_1-{\mathit{\rho }}_2\right),(2)$

where S(ρ) = |E(ρ)|² denotes the averaged spectral density of the incoherent source and δ(ρ₁ − ρ₂) is a Dirac delta function, which indicates that the fields at two different spatial positions ρ₁ and ρ₂ are uncorrelated. Based on the pseudo-mode representation theory [54], the cross-spectral density function in Eq. 2 can be expanded as

$W\left({\mathit{\rho }}_1,{\mathit{\rho }}_2\right)=\sum _n{\alpha }_n{E}_n^{\ast }\left({\mathit{\rho }}_1\right)E_n\left({\mathit{\rho }}_2\right),(3)$

where E_n(ρ) and α_n stand for the modal function and its modal weight, respectively, for the nth mode. Such pseudo-mode representation indicates that a incoherent (or partially coherent) light can be viewed as a superposition of spatially coherent but mutually uncorrelated modes. For the spatially incoherent light, the modal distribution can be expressed as

$E_n\left(\mathit{\rho }\right)=\sqrt{S\left(\mathit{\rho }\right)}\exp \left[i{\varphi }_n\left(\mathit{\rho }\right)\right],(4)$

where ϕ_n(ρ) is a random phase. For a random scatterer obeying Gaussian statistics [52], we have ⟨ exp [iϕ_n(ρ)]⟩ = 0 and ⟨ exp [iϕ_n (ρ₁) − iϕ_n (ρ₂)]⟩ = δ(ρ₁ − ρ₂), where ⟨⋅⟩ denotes the ensemble average.

Based on the van Cittert–Zernike theorem, when the incoherent light from the random scattering medium passes through a linear optical system with an impulse response function H (ρ, r), the spatial coherence of the light will be improved. The modal function in the observation plane turns out to be

$E_n\left(\mathbf{r}\right)=\iint \sqrt{S\left(\mathit{\rho }\right)}\exp \left[i{\varphi }_n\left(\mathit{\rho }\right)\right]H\left(\mathit{\rho },\mathbf{r}\right){\mathrm{d}}^2\mathit{\rho }.(5)$

Taking all the field realizations into account, i.e., by using $W({\mathbf{r}}_1,{\mathbf{r}}_2)=⟨E_n^{*}({\mathbf{r}}_1)E_n({\mathbf{r}}_2)⟩$, we obtain the cross-spectral density of the random field in the observation plane

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=\iint \sqrt{S\left({\mathit{\rho }}_1\right)S\left({\mathit{\rho }}_2\right)}⟨\exp \left[-i{\varphi }_n\left({\mathit{\rho }}_1\right)+i{\varphi }_n\left({\mathit{\rho }}_2\right)\right]⟩H^{\ast }\left({\mathit{\rho }}_1,{\mathbf{r}}_1\right)H\left({\mathit{\rho }}_2,{\mathbf{r}}_2\right){\mathrm{d}}^2{\mathit{\rho }}_1{\mathrm{d}}^2{\mathit{\rho }}_2.(6)$

Using the Gaussian statistics condition for the random phase ϕ_n(ρ), the above integral is reduced to

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=\iint |E\left(\mathit{\rho }\right){|}^2{H}^{\ast }\left(\mathit{\rho },{\mathbf{r}}_1\right)H\left(\mathit{\rho },{\mathbf{r}}_2\right){\mathrm{d}}^2\mathit{\rho }.(7)$

It follows from Eqs. 1, 7 that the object information O(v) hidden a distance behind the random scattering medium is encoded in the spatial coherence function of a random light generated after the scattering medium, which indicates that once the complex spatial coherence structure W (r₁, r₂) is fully measured, the object information may be recovered. In the previous studies, it is showed that only the intensity S(ρ) on the front surface of the random scatterer can be measured [24–26] (see Figure 1B].

In this work, we find that the iterative phase retrieval algorithm [42–56] can be applied to recover the object information. We discuss the detail of the algorithm in this section. The algorithm will be verified experimentally in Section 3. The flowchart of the algorithm is shown in Figure 1C. The first step in the iterative phase retrieval algorithm is that we guess a initiatory amplitude for the object, e.g., $O_1(\mathbf{v})=\sqrt{S(\mathbf{v})}$. We note other functions, e.g., a random function can also be used as the initiatory amplitude. In the second step, we take O₁(v) into Eq. 1 and obtain the corresponding complex field on the front surface of the scattering medium, which can be expressed as

$E_1\left(\mathit{\rho }\right)=-\frac{\mathrm{i}}{\lambda z}\exp \left(\mathrm{i}kz\right)\iint O_1\left(\mathbf{v}\right)\exp \left[\frac{\mathrm{i}k}{2z}{\left(\mathit{\rho }-\mathbf{v}\right)}^2\right]{\mathrm{d}}^2\mathbf{v}.(8)$

The third step is extracting the phase θ₁(ρ) from E₁(ρ). We then combine θ₁(ρ) with $\sqrt{S(\mathbf{v})}$ to form a new function for the field located on the front surface of the scattering medium, i.e., $E_1^{\prime }(\mathit{\rho })=\sqrt{S(\mathbf{v})}\exp [\mathrm{i}{\theta }_1(\mathit{\rho })]$. To obtain the object information, the new field $E_1^{\prime }(\mathit{\rho })$ then transmit backwards, i.e., in − z direction. The field in the plane where the optical image located can be obtained by

$O_1^{\prime }\left(\mathbf{v}\right)=\frac{\mathrm{i}}{\lambda z}\exp \left(-\mathrm{i}kz\right)\iint E_1^{\prime }\left(\mathit{\rho }\right)\exp \left[-\frac{\mathrm{i}k}{2z}{\left(\mathit{\rho }-\mathbf{v}\right)}^2\right]{\mathrm{d}}^2\mathit{\rho }.(9)$

We assume that the original image is an amplitude image (i.e. with no phase information). Thus, O(v) is a real and positive function. With the restriction of such condition, we first take out the real part of $O_1^{\prime }(\mathbf{v})$ and then let the negative values in the real part become 0. The new obtained function is then used as the second prediction, O₂(v), for the image information hidden a distance behind the random scatterer. The function O₂(v) is then taken into the above algorithm and the third prediction image O₃(v) will be obtained. It is found in our experiment that by $\sim 70$ iterations of the above phase retrieval algorithm, the image information can be well reconstructed.

3 Experimental Verification

In this section, we carry out the experiment to verify the feasibility of the principle and the iterative algorithm. The schematic of our experimental setup is shown in Figure 2. In our experiment, the image is an English letter ‘S’, which is generated with a spatial light modulator (SLM). The random scattering medium is a rotating ground-glass disk (RGGD). The surface roughness of the RGGD used in our experiment is 400 mesh number and the rotating speed can be controlled by the controller of an optical chopper system. In the experiment, the rotating speed is fixed at 3,000 r/min. The distance between the image (SLM) and the random scatterer (RGGD) can be adjusted from 35 to 70 cm. The image is illuminated with a fully coherent beam generated by passing a He-Ne laser (with wavelength λ = 632 nm) through a linear polarizer (LP) and a beam expander (BE). The optical system between the RGGD and the observation plane is formed by a thin lens L1 of focal distance 250 mm and a thin lens L2 of focal distance 300 mm. The distances between RGGD and L1, L1 and L2, L2 and the observation plane are 250 mm, 600 mm, and 600 mm, respectively. The second thin lens L2 is used to project the optical field immediately after L1 into the observation plane. Thus, the response function of the optical system becomes

$H\left(\mathit{\rho },\mathbf{r}\right)=-\frac{\mathrm{i}}{\lambda f_1}\exp \left[\frac{\mathrm{i}\pi }{\lambda f_1}\left({\mathit{\rho }}^2-2\mathbf{r}\cdot \mathit{\rho }\right)\right],(10)$

where f₁ denotes the focal length of the thin lens L1. Taking Eq. 10 into Eq. 7, we obtain that the cross-spectral density function of the random light in the observation plane yields

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=\frac{1}{{\lambda }^2{f}^2}\iint |E\left(\mathit{\rho }\right){|}^2\exp \left[\frac{\mathrm{i}2\pi }{\lambda f}\mathit{\rho }\cdot \left({\mathbf{r}}_1-{\mathbf{r}}_2\right)\right]{\mathrm{d}}^2\mathit{\rho }.(11)$

FIGURE 2

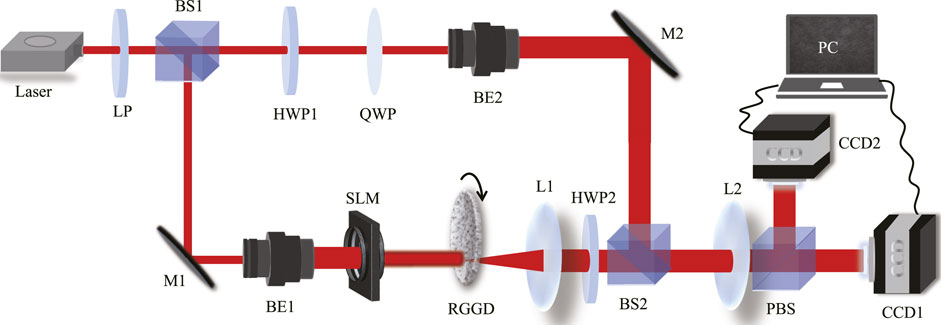
FIGURE 2. Experimental setup for optical imaging through a random scattering medium via the complex spatial coherence measurement. LP: linear polarizer; BS1 and BS2: beam splitters; HWP1 and HWP2: half-wave plates; QWP: quarter-wave plate; BE1 and BE2: beam expanders; M1 and M2: mirrors; SLM: spatial light modulator; RGGD: rotating ground-glass disk; L1 and L2, thin lenses; PBS: polarization beam splitter; CCD1 and CCD2: charge-coupled devices; PC: personal computer.

It is found from Eq. 11 that the generated partially coherent beam in the observation place is of Schell-model type, i.e., its spatial coherence distribution depends only on the position difference r₁—r₂. Moreover, we find that the spatial coherence function W (r₁, r₂) and the intensity |E(ρ)|² on the front surface of the random scatterer form a Fourier transform pair. Thus, |E(ρ)|² can be recovered by

$|E\left(\mathit{\rho }\right){|}^2=\frac{1}{{\lambda }^2{f}^2}\iint W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\exp \left[-\frac{\mathrm{i}2\pi }{\lambda f}\mathit{\rho }\cdot \left({\mathbf{r}}_1-{\mathbf{r}}_2\right)\right]{\mathrm{d}}^2{\mathbf{r}}_1{\mathrm{d}}^2{\mathbf{r}}_2.(12)$

Once |E(ρ)|² is recovery, we take the result into the iterative phase retrieval algorithm and run 66 loops.

Before discussing the experiment results, we present the details of the method for measuring the complex spatial coherence of the generated partially coherent light. The method is based on the generalized Hanbury Brown and Twiss experiment [24], in which we introduce a pair of reference waves having a constant phase difference either 0 or π/2. In our experiment, the reference waves with the stable phase difference are generated from a circularly polarized beam. In the top reference arm of Figure 2, the x-polarized light beam is transmitted through a half-wave plate (HWP) and a quarter-wave plate (QWP). The fast axis of the HWP is set to be π/8 with respect to the x-polarization direction, while the fast axis of the QWP is set to be parallel to the x-polarization direction. Therefore, a right-handed circularly polarized beam is produced immediately after the QWP. The beam expander (BE2) after QWP is used to produce a beam of the effectively uniform intensity distribution. The x- and y-components of the generated circularly polarized beam are viewed as the pair of reference waves required for our protocol.

Before combining the reference waves with the partially coherent light, we place a HWP after the thin lens L1 to transfer the x-polarized partially coherent light into π/4-linearly polarized. The x- and y-components of the field realization after the beam splitter (BS2) is then expressed as

$E_{nx}^{\text{add}}\left(\mathbf{r}\right)=E_{nx}\left(\mathbf{r}\right)+E_x^{\text{circ}}\left(\mathbf{r}\right),(13)$

$E_{ny}^{\text{add}}\left(\mathbf{r}\right)=E_{ny}\left(\mathbf{r}\right)+E_y^{\text{circ}}\left(\mathbf{r}\right),(14)$

where E_nx(r) and E_ny(r) denote the x- and y-components of one random field realization of the partially coherent light, and $E_x^{\text{circ}}(\mathbf{r})$ and $E_y^{\text{circ}}(\mathbf{r})$ are the x- and y-components of the generated circularly polarized reference wave, respectively. The x- and y-components of the composite field are then split by a polarization beam splitter (PBS) and imaged, respectively, onto CCD1 and CCD2 by a 2f imaging system formed by the thin lens L2. The direct-digital-synthesis signal generator is used as external trigger for controlling the two CCDs, to simultaneously capture the random intensities $I_{nx}^{\text{add}}(\mathbf{r})$ and $I_{ny}^{\text{add}}(\mathbf{r})$ of the x- and y-component fields.

We now calculate the cross-correlation of the two composite field intensities, i.e.,

$G_{xy}^{\text{add}}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=⟨I_{nx}^{\text{add}}\left({\mathbf{r}}_1\right)I_{ny}^{\text{add}}\left({\mathbf{r}}_2\right)⟩,(15)$

where the angle brackets denote the ensemble averaging. Taking Eqs. 13, 14 into Eq. 15, we obtain

$G_{xy}^{\text{add}}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=\langle I_{nx}^{\text{uncor}}\left({\mathbf{r}}_1\right)\rangle \langle I_{ny}^{\text{uncor}}\left({\mathbf{r}}_2\right)\rangle +|W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right){|}^2+2\sqrt{I_x^{\text{circ}}\left({\mathbf{r}}_1\right)I_y^{\text{circ}}\left({\mathbf{r}}_2\right)}\mathrm{I}\mathrm{m}\left[W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\right].(16)$

Above, $I_{nx}^{\text{uncor}}(\mathbf{r})=I_{nx}(\mathbf{r})+I_x^{\text{circ}}(\mathbf{r})$, $I_{ny}^{\text{uncor}}(\mathbf{r})=I_{ny}(\mathbf{r})+I_y^{\text{circ}}(\mathbf{r})$, I_nx(r) and I_ny(r) denote the intensities of the x- and y-components of the random field realization, and $I_x^{\text{circ}}(\mathbf{r})$ and $I_y^{\text{circ}}(\mathbf{r})$ denote the intensities of the x- and y-components of the circularly polarized light, respectively. It is found from Eq. 16 that the imaginary part of W (r₁, r₂) is encoded in the intensity cross-correlation function. The undesired background terms, i.e., $⟨I_{nx}^{\text{uncor}}({\mathbf{r}}_1)⟩⟨I_{ny}^{\text{uncor}}({\mathbf{r}}_2)⟩+|W({\mathbf{r}}_1,{\mathbf{r}}_2){|}^2$ are removed by doing the intensity cross-correlation $G_{xy}^{\text{uncor}}({\mathbf{r}}_1,{\mathbf{r}}_2)=⟨I_{nx}^{\text{uncor}}({\mathbf{r}}_1)I_{ny}^{\text{uncor}}({\mathbf{r}}_2)⟩$. Finally, the imaginary part of the spatial coherence function is obtained as

$\mathrm{I}\mathrm{m}\left[W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\right]=\frac{G_{xy}^{\text{add}}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)-G_{xy}^{\text{uncor}}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)}{2\sqrt{I_x^{\text{circ}}\left({\mathbf{r}}_1\right)I_y^{\text{circ}}\left({\mathbf{r}}_2\right)}}.(17)$

The real part of the spatial coherence function, on the other hand, can be obtained by

$\mathrm{R}\mathrm{e}\left[W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\right]=\frac{G_{xx}^{\text{add}}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)-G_{xx}^{\text{uncor}}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)}{2\sqrt{I_x^{\text{circ}}\left({\mathbf{r}}_1\right)I_x^{\text{circ}}\left({\mathbf{r}}_2\right)}},(18)$

where $G_{xx}^{\text{add}}({\mathbf{r}}_1,{\mathbf{r}}_2)=⟨I_{nx}^{\text{add}}({\mathbf{r}}_1)I_{nx}^{\text{add}}({\mathbf{r}}_2)⟩$ and $G_{xx}^{\text{uncor}}({\mathbf{r}}_1,{\mathbf{r}}_2)=⟨I_{nx}^{\text{uncor}}({\mathbf{r}}_1)I_{nx}^{\text{uncor}}({\mathbf{r}}_2)⟩$ are the intensity-intensity autocorrelation functions. In the experiment, the ensemble average in the intensity cross-correlation and autocorrelation can be replaced with the spatial average of the speckle field since the partially coherent random field is generated with the Fourier transformation optical system [57]. Thus, the real and imaginary parts of the spatial coherence function can be recovered conveniently through recording six realizations of intensity distributions, i.e., I_nx(r), I_ny(r), $I_x^{\text{circ}}(\mathbf{r})$, $I_y^{\text{circ}}(\mathbf{r})$, $I_{nx}^{\text{add}}(\mathbf{r})$, and $I_{ny}^{\text{add}}(\mathbf{r})$.

4 Results and Discussion

To show the feasibility of our method, we first place the image (SLM) 57.5 cm in front of the RGGD and record the six intensity distributions with CCD1 and CCD2, respectively. Figure 3A shows the spatial speckles of the six intensities. By using Eqs. 17, 18, the complex spatial coherence structure can be recovered. We show in Figures 3B,C the experimental results of the real and imaginary parts of the spatial coherence function of the partially coherent light in the observation plane after the random scatterer. Taking the measured W (r₁, r₂) into Eq. 12 and performing the fast Fourier transform, we obtain the intensity distribution S(ρ) on the front surface of the random scatterer, which is shown in Figure 3D. We find from Figure 3D that the image information cannot be identified from the diffraction pattern. We now apply the iterative phase retrieval algorithm introduced in Section 2 for the image information recovery. The initiatory intensity for the image is assumed to be the pattern displayed in the dotted box of Figure 3D. The algorithm is iterated 66 times. Figure 3E shows the result of the recovered image. For a better comparison, the original object loaded in the SLM is also recorded (see in Figure 3F]. We find in the experiment that the image information hidden a distance behind the random scattering medium can be well reconstructed with the help of the spatial coherence structure measurement and the iterative phase retrieval algorithm. The experimental results are consistent with our predictions.

FIGURE 3

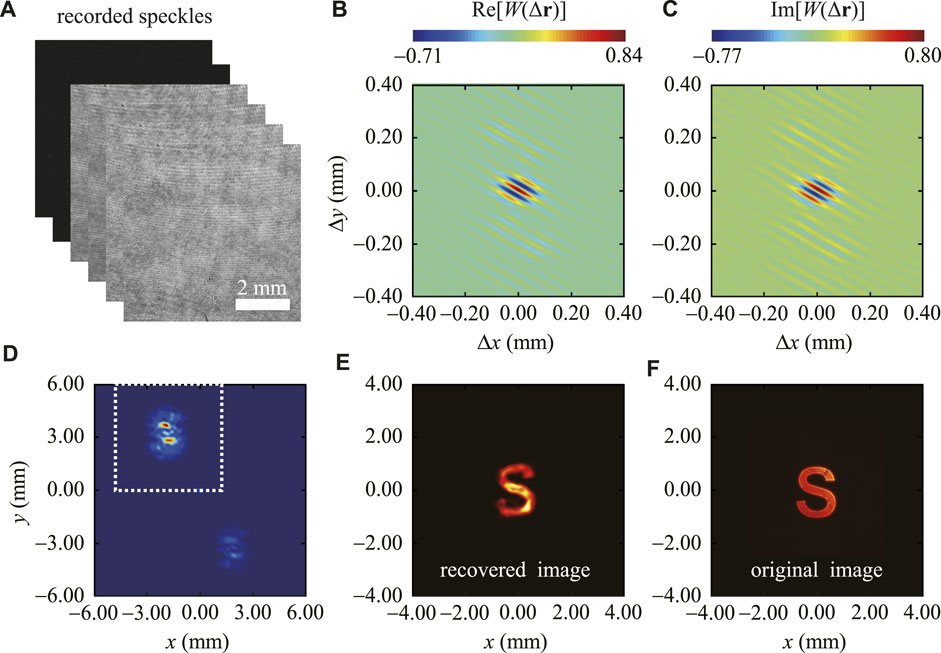
FIGURE 3. Experimental results of optical imaging through a RGGD with complex spatial coherence measurement. The optical image is placed 57.5 cm in front of the random scatterer. (A) The recorded speckles I_nx(r), I_ny(r), $I_x^{\text{circ}}(\mathbf{r})$, $I_y^{\text{circ}}(\mathbf{r})$, $I_{nx}^{\text{add}}(\mathbf{r})$, and $I_{ny}^{\text{add}}(\mathbf{r})$. (B) and (C) The recovered real and imaginary parts of the spatial coherence function from the speckles shown in (a). (D) The recovery intensity on the front surface of the RGGD. (E) The recovery image information with the iterative phase retrieval algorithm. (F) The original image displayed in the SLM.

Next, we show the ability of our method to retrieve both the lateral position and the shape of the moving object hidden behind the RGGD. The object image is created again by the SLM and placed in the plane having a distance 57.5 cm in front of the RGGD. However, the image can now move freely in the transverse plane. In the top two panels of Figure 4, the experimental results of the measured real and imaginary parts of the spatial coherence functions are presented when the image is located at different transverse positions. We find with the change of the image position, the distribution of the complex spatial coherence for the partially coherent light beam in the observation plane changes as well. The corresponding recovered intensities on the front surface of the RGGD obtained by the fast Fourier transform of measured W (r₁, r₂) are shown in the third row of Figure 4. We now assume these intensity distributions as the initiatory inputs for the iterative phase retrieval algorithm. After 66 times loops, the recovered image intensities are displayed in the bottom row of Figure 4. It is found from the experimental results that the image at different transverse positions is well recovered, which indicates that the iterative phase retrieval algorithm shown in Section 2 can preserve well the lateral position information of the image.

FIGURE 4

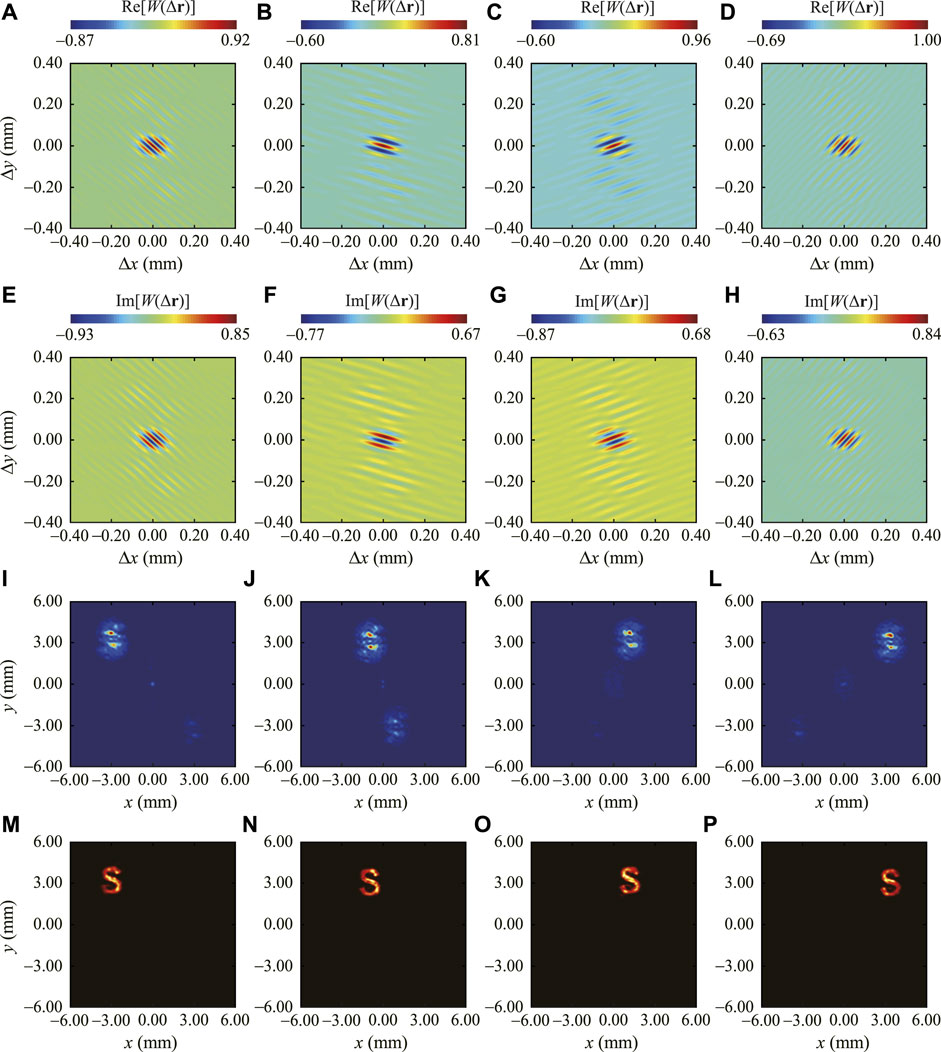
FIGURE 4. Experimental results for the recovery of a moving image hidden behind the RGGD with complex spatial coherence structure measurement. The image moves in the transverse plane where z = 57.5 cm. (A)–(D) and (E)–(H) The measured real and imaginary parts of the complex spatial coherence function for the cases when the image is located at different lateral positions. (I)–(L) The recovered intensities on the front surface of the RGGD. (M)–(P) The recovery images with the iterative phase retrieval algorithm.

Finally, we carry out the experiment to show the feasibility of our method in recovering the longitudinal position of the image hidden behind the random scattering medium. The image created by the SLM now moves freely in the longitudinal direction. In our experiment, the distance between the SLM and the RGGD can be controlled from 35 to 70 cm. Once the complex spatial coherence structure is measured in the observation plane, the intensity on the front surface of the RGGD can be recovered. After that, we take the recovery intensity as the initial input for the iterative phase retrieval algorithm and modify the value of the distance z in the algorithm. The output results for different values of input z after 66 times iterations are compared with the original image as shown in Figure 3F. When the recovered and the original images are matched, the input value of z is recorded as the longitudinal distance for the image. Figure 5 shows our experimental results of the reconstructed images at different longitudinal positions. The recovered longitudinal distances z_recover and the real longitudinal positions z are also shown in the figures. It is found from the experimental results that the image hidden behind the RGGD with different longitudinal distances can be well reconstructed with the spatial coherence measurement and the iterative phase retrieval algorithm. The experimentally recovered longitudinal distances agree well with the real distances between the image and the RGGD.

FIGURE 5

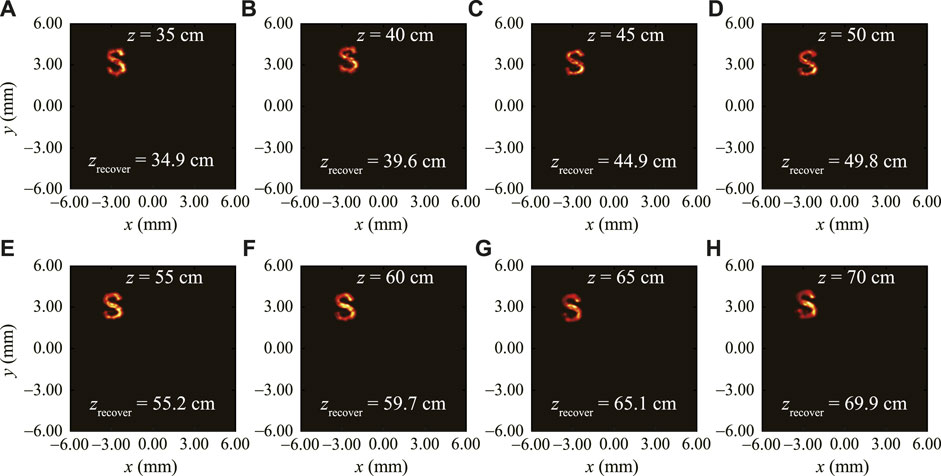
FIGURE 5. Experimental results of the recovered images with the spatial coherence measurement and the iterative phase retrieval for the case when the image moves along the longitudinal direction. The real distance z and the recovered distance z_recover from the RGGD are marked in the figures.

5 Conclusion

In this work, we studied the role of the spatial coherence structure measurement for the partially coherent scattered light on the recovery of the image information (especially the image’s longitudinal position) hidden behind a random scattering medium. We showed experimentally that the image information, including its spatial shape, lateral shift, and longitudinal position, encoded in the spatial coherence structure can be fully reconstructed with the spatial coherence measurement and the iterative phase retrieval algorithm in the Fresnel domain. Our experimental results indicate that a 2D spatial coherence measurement can find applications in the 3D optical imaging through the random scattering medium and 3D object position tracking in complex medium. We remark that the scattering from randomly inhomogeneous media (stronger than the rotating ground glass disk used here) does not completely destroy the spatial coherence of radiation [58], which indicates that the multiple-scattering media can still act as an imperfect mirror or lens for coherence-based 3D optical imaging.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

YC, FW, and YC proposed the idea. DP, XZ, YZ, YL, and YC performed the experiment. All authors analyzed the experiment. YC and DP wrote the original manuscript. YC, FW, and YC supervised the project.

Funding

National Key Research and Development Program of China (2019YFA0705000); National Natural Science Foundation of China (91 750 201, 11 874 046, 11 974 218, 11 904 247, and 12 192 254); Innovation Group of Jinan (2018GXRC010); Local Science and Technology Development Project of the Central Government (YDZX20203700001766).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mandel L, Wolf E. Optical Coherence and Quantum Optics. Cambridge: Cambridge University Press (1995).

Google Scholar

2. Friberg AT, Setälä T Electromagnetic Theory of Optical Coherence [Invited]. J Opt Soc Am A (2016) 33:2431–42. doi:10.1364/josaa.33.002431

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chen Y, Norrman A, Ponomarenko SA, Friberg AT Optical Coherence and Electromagnetic Surface Waves. Prog Opt (2020) 65:105–72. doi:10.1016/bs.po.2019.11.001

CrossRef Full Text | Google Scholar

4. Cai Y, Chen Y, Yu J, Liu X, Liu L Generation of Partially Coherent Beams. Prog Opt (2017) 62:157–223. doi:10.1016/bs.po.2016.11.001

CrossRef Full Text | Google Scholar

5. Ricklin JC, Davidson FM Atmospheric Optical Communication with a Gaussian Schell Beam. J Opt Soc Am A (2003) 20:856–66. doi:10.1364/josaa.20.000856

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gbur G Partially Coherent Beam Propagation in Atmospheric Turbulence [Invited]. J Opt Soc Am A (2014) 31:2038–45. doi:10.1364/josaa.31.002038

CrossRef Full Text | Google Scholar

7. Redding B, Choma MA, Cao H Speckle-free Laser Imaging Using Random Laser Illumination. Nat Photon (2012) 6:355–9. doi:10.1038/nphoton.2012.90

CrossRef Full Text | Google Scholar

8. Wang F, Chen Y, Liu X, Cai Y, Ponomarenko SA Self-reconstruction of Partially Coherent Light Beams Scattered by Opaque Obstacles. Opt Express (2016) 24:23735–46. doi:10.1364/oe.24.023735

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Gori F, Santarsiero M Devising Genuine Spatial Correlation Functions. Opt Lett (2007) 32:3531–3. doi:10.1364/ol.32.003531

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Martínez-Herrero R, Mejías PM, Gori F. Genuine Cross-Spectral Densities and Pseudo-modal Expansions. Opt Lett (2009) 34:1399–401.

PubMed Abstract | Google Scholar

11. Gori F, Ramírez-Sánchez V, Santarsiero M, Shirai T On Genuine Cross-Spectral Density Matrices. J Opt A: Pure Appl Opt (2009) 11:085706. doi:10.1088/1464-4258/11/8/085706

CrossRef Full Text | Google Scholar

12. Cai Y, Chen Y, Wang F Generation and Propagation of Partially Coherent Beams with Nonconventional Correlation Functions: a Review [Invited]. J Opt Soc Am A (2014) 31:2083–96. doi:10.1364/josaa.31.002083

CrossRef Full Text | Google Scholar

13. Liang C, Wu G, Wang F, Li W, Cai Y, Ponomarenko SA Overcoming the Classical Rayleigh Diffraction Limit by Controlling Two-point Correlations of Partially Coherent Light Sources. Opt Express (2017) 25:28352–62. doi:10.1364/oe.25.028352

CrossRef Full Text | Google Scholar

14. Shen Y, Sun H, Peng D, Chen Y, Cai Q, Wu D, et al. Optical Image Reconstruction in 4f Imaging System: Role of Spatial Coherence Structure Engineering. Appl Phys Lett (2021) 118:181102. doi:10.1063/5.0046288

CrossRef Full Text | Google Scholar

15. Liu Y, Chen Y, Chen Y, Wang F, Cai Y, Liang C, et al. Robust Far-Field Imaging by Spatial Coherence Engineering. Opto-Electron Adv (2021) 4:210027. doi:10.29026/oea.2021.210027

CrossRef Full Text | Google Scholar

16. Hyde MW, Basu S, Voelz DG, Xiao X Experimentally Generating Any Desired Partially Coherent Schell-Model Source Using Phase-Only Control. J Appl Phys (2015) 118:093102. doi:10.1063/1.4929811

CrossRef Full Text | Google Scholar

17. Hyde MW, Bose-Pillai SR, Wood RA Synthesis of Non-uniformly Correlated Partially Coherent Sources Using a Deformable Mirror. Appl Phys Lett (2017) 111:101106. doi:10.1063/1.4994669

CrossRef Full Text | Google Scholar

18. Chen X, Li J, Rafsanjani SMH, Korotkova O Synthesis of Im-Bessel Correlated Beams via Coherent Modes. Opt Lett (2018) 43:3590–3. doi:10.1364/ol.43.003590

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bhattacharjee A, Sahu R, Jha AK Generation of a Gaussian Schell-Model Field as a Mixture of its Coherent Modes. J Opt (2019) 21:105601. doi:10.1088/2040-8986/ab3b24

CrossRef Full Text | Google Scholar

20. Zhu X, Yu J, Chen Y, Wang F, Korotkova O, Cai Y Experimental Synthesis of Random Light Sources with Circular Coherence by Digital Micro-mirror Device. Appl Phys Lett (2020) 117:121102. doi:10.1063/5.0024283

CrossRef Full Text | Google Scholar

21. Zhu X, Yu J, Wang F, Chen Y, Cai Y, Korotkova O. Synthesis of Vector Nonuniformly Correlated Light Beams by a Single Digital Mirror Device. Opt Lett (2021) 46:2996–9. doi:10.1364/OL.428508

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wolf E. Introduction to the Theory of Coherence and Polarization of Light. Cambridge: Cambridge University Press (2007).

Google Scholar

23. Wang F, Liu X, Yuan Y, Cai Y Experimental Generation of Partially Coherent Beams with Different Complex Degrees of Coherence. Opt Lett (2013) 38:1814–6. doi:10.1364/ol.38.001814

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Huang Z, Chen Y, Wang F, Ponomarenko SA, Cai Y. Measuring Complex Degree of Coherence of Random Light fields with Generalized Hanbury Brown–Twiss experiment. Phys Rev Appl (2020) 13:044042. doi:10.1103/physrevapplied.13.044042

CrossRef Full Text | Google Scholar

25. Dong Z, Huang Z, Chen Y, Wang F, Cai Y Measuring Complex Correlation Matrix of Partially Coherent Vector Light via a Generalized Hanbury Brown-Twiss experiment. Opt Express (2020) 28:20634–44. doi:10.1364/oe.398185

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Peng D, Huang Z, Liu Y, Chen Y, Wang F, Ponomarenko SA, et al. Optical Coherence Encryption with Structured Random Light. PhotoniX (2021) 2:6–15. doi:10.1186/s43074-021-00027-z

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Goodman JW, Huntley WH, Jackson DW, Lehmann M Wavefront‐reconstruction Imaging through Random Media. Appl Phys Lett (1966) 8:311–3. doi:10.1063/1.1754453

CrossRef Full Text | Google Scholar

28. Leith EN, Upatnieks J Holographic Imagery through Diffusing media. J Opt Soc Am (1966) 56:523. doi:10.1364/josa.56.000523

CrossRef Full Text | Google Scholar

29. Rotter S, Gigan S. Light fields in Complex media: Mesoscopic Scattering Meets Wave Control. Rev Mod Phys (2017) 89:015005. doi:10.1103/revmodphys.89.015005

CrossRef Full Text | Google Scholar

30. Yoon S, Kim M, Jang M, Choi Y, Choi W, Kang S, et al. Deep Optical Imaging within Complex Scattering media. Nat Rev Phys (2020) 2:141–58. doi:10.1038/s42254-019-0143-2

CrossRef Full Text | Google Scholar

31. Denk W, Strickler JH, Webb WW Two-photon Laser Scanning Fluorescence Microscopy. Science (1990) 248:73–6. doi:10.1126/science.2321027

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, et al. Optical Coherence Tomography. Science (1991) 254:1178–81. doi:10.1126/science.1957169

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hoover EE, Squier JA Advances in Multiphoton Microscopy Technology. Nat Photon (2013) 7:93–101. doi:10.1038/nphoton.2012.361

CrossRef Full Text | Google Scholar

34. Mosk AP, Lagendijk A, Lerosey G, Fink M Controlling Waves in Space and Time for Imaging and Focusing in Complex media. Nat Photon (2012) 6:283–92. doi:10.1038/nphoton.2012.88

CrossRef Full Text | Google Scholar

35. Horstmeyer R, Ruan H, Yang C Guidestar-assisted Wavefront-Shaping Methods for Focusing Light into Biological Tissue. Nat Photon (2015) 9:563–71. doi:10.1038/nphoton.2015.140

CrossRef Full Text | Google Scholar

36. Del Hougne P, Yeo KB, Besnier P, Davy M Coherent Wave Control in Complex media with Arbitrary Wavefronts. Phys Rev Lett (2021) 126:193903. doi:10.1103/physrevlett.126.193903

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Yeminy T, Katz O. Guidestar-free Image-Guided Wavefront Shaping. Sci Adv (2021) 7:eabf5364. doi:10.1126/sciadv.abf5364

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Popoff SM, Lerosey G, Carminati R, Fink M, Boccara AC, Gigan S Measuring the Transmission Matrix in Optics: an Approach to the Study and Control of Light Propagation in Disordered media. Phys Rev Lett (2010) 104:100601. doi:10.1103/physrevlett.104.100601

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Boniface A, Dong J, Gigan S. Non-invasive Focusing and Imaging in Scattering media with a Fluorescence-Based Transmission Matrix. Nat Commun (2020) 11:6154–7. doi:10.1038/s41467-020-19696-8

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Freund I, Rosenbluh M, Feng S Memory Effects in Propagation of Optical Waves through Disordered media. Phys Rev Lett (1988) 61:2328–31. doi:10.1103/physrevlett.61.2328

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Osnabrugge G, Horstmeyer R, Papadopoulos IN, Judkewitz B, Vellekoop IM Generalized Optical Memory Effect. Optica (2017) 4:886–92. doi:10.1364/optica.4.000886

CrossRef Full Text | Google Scholar

42. Bertolotti J, Van Putten EG, Blum C, Lagendijk A, Vos WL, Mosk AP Non-invasive Imaging through Opaque Scattering Layers. Nature (2012) 491:232–4. doi:10.1038/nature11578

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Katz O, Small E, Silberberg Y Looking Around Corners and through Thin Turbid Layers in Real Time with Scattered Incoherent Light. Nat Photon (2012) 6:549–53. doi:10.1038/nphoton.2012.150

CrossRef Full Text | Google Scholar

44. Katz O, Heidmann P, Fink M, Gigan S Non-invasive Single-Shot Imaging through Scattering Layers and Around Corners via Speckle Correlations. Nat Photon (2014) 8:784–90. doi:10.1038/nphoton.2014.189

CrossRef Full Text | Google Scholar

45. Okamoto Y, Horisaki R, Tanida J Noninvasive Three-Dimensional Imaging through Scattering media by Three-Dimensional Speckle Correlation. Opt Lett (2019) 44:2526–9. doi:10.1364/ol.44.002526

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Yuan Y, Chen H Dynamic Noninvasive Imaging through Turbid media under Low Signal-Noise-Ratio. New J Phys (2020) 22:093046. doi:10.1088/1367-2630/abb16a

CrossRef Full Text | Google Scholar

47. Edrei E, Scarcelli G. Memory-effect Based Deconvolution Microscopy for Super-resolution Imaging through Scattering media. Sci Rep (2016) 6:33558–8. doi:10.1038/srep33558

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Li D, Kelly DP, Sheridan JT Three-dimensional Static Speckle fields Part I Theory and Numerical Investigation. J Opt Soc Am A (2011) 28:1896–903. doi:10.1364/josaa.28.001896

CrossRef Full Text | Google Scholar

49. Li D, Kelly DP, Sheridan JT. Three-dimensional Static Speckle fields. Part Ii. Experimental Investigation. J Opt Soc Am A (2011) 28:1904–8. doi:10.1364/josaa.28.001904

CrossRef Full Text | Google Scholar

50. Ruan H, Liu Y, Xu J, Huang Y, Yang C Fluorescence Imaging through Dynamic Scattering media with Speckle-Encoded Ultrasound-Modulated Light Correlation. Nat Photon (2020) 14:511–6. doi:10.1038/s41566-020-0630-0

CrossRef Full Text | Google Scholar

51. Wang D, Sahoo SK, Zhu X, Adamo G, Dang C. Non-invasive Super-resolution Imaging through Dynamic Scattering media. Nat Commun (2021) 12:3150–9. doi:10.1038/s41467-021-23421-4

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Goodman JW. Statistical Optics. Hoboken, NJ, USA: John Wiley & Sons (2015).

Google Scholar

53. Andrews LC, Phillips RL. Laser Beam Propagation through Tandom Media. Bellingham, Washington, USA: SPIE (2005).

Google Scholar

54. Ostrovsky AS. Coherent-mode Representations in Optics, Vol. 164. Bellingham, Washington, USA: SPIE Press (2006).

Google Scholar

55. Fienup JR Reconstruction of an Object from the Modulus of its Fourier Transform. Opt Lett (1978) 3:27–9. doi:10.1364/ol.3.000027

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Fienup JR Phase Retrieval Algorithms: a Comparison. Appl Opt (1982) 21:2758–69. doi:10.1364/ao.21.002758

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Takeda M, Wang W, Naik DN, Singh RK Spatial Statistical Optics and Spatial Correlation Holography: a Review. Opt Rev (2014) 21:849–61. doi:10.1007/s10043-014-0138-2

CrossRef Full Text | Google Scholar

58. Batarseh M, Sukhov S, Shen Z, Gemar H, Rezvani R, Dogariu A. Passive Sensing Around the Corner Using Spatial Coherence. Nat Commun (2018) 9:3629–6. doi:10.1038/s41467-018-05985-w

PubMed Abstract | CrossRef Full Text | Google Scholar