Dynamic Influence Maximization via Network Representation Learning

Influence maximization is a hot research topic in the social computing field and has gained tremendous studies motivated by its wild application scenarios. As the structures of social networks change over time, how to seek seed node sets from dynamic networks has attracted some attention. However, all of the existing studies were based on network topology structure data which have the limitations of high dimensionality and low efficiency. Aiming at this drawback, we first convert each node in the network to a low-dimensional vector representation by network representation learning and then solve the problem of dynamic influence maximization in the low-dimensional latent space. Comprehensive experiments on NetHEPT, Twitter, UCI, and Wikipedia datasets show that our method can achieve influence diffusion performance similar to state-of-the-art approaches in much less time.

1 Introduction

With the development of online social websites, information diffusion over social networks has become a new and important channel for network users to receive information. How to optimize and control the spread of information is an important problem in the field of social computing, and influence maximization is used to solve the above problem. As all kinds of information (e.g., advertisement, rumor, and political opinion) propagate in the network, therefore, the studies of influence maximization have been widely applied in viral marketing, rumor control, political campaign, and so on.

The influence maximization problem originated from “viral marketing” and “word-of-mouth effect.” In 2001, Domingos and Richardson [1, 2] first introduced the initial concept and evaluation index of the influence maximization problem. Later, Kempe et al. [3] first proposed the discrete optimization method to solve the influence maximization problem. However, the greedy algorithm with approximate accuracy guarantee proposed by them takes too much time. Leskovec et al. [4] reduced time consumption by optimizing the sub-model of the function, and the CELF they proposed was nearly 700 times faster than the traditional greedy algorithm. After that, researchers proposed other greedy algorithms [5–8]. In addition, subsequent researchers also proposed heuristic algorithms to improve operating efficiency. Chen et al. [9] developed a degree discount heuristic algorithm (DegreeDiscountIC), which has the same performance as the greedy algorithm but greatly reduces the computation time. Chen proposed the LDAG heuristic algorithm [10] based on the directed acyclic graph and MIA based on the tree structure [11]. Goyal et al. [12] proposed SIMPATH, which obtains the path of the node by backtracking and then uses the shortest path of the neighbor node to propagate the influence. Tang et al. [13] proposed TIM, which is an approximate linear solution based on reverse random sampling. Wang et al. [14] proposed CNCG considering an overlapping community structure [15, 16] and node coverage gain mechanism.

The social networks supporting information diffusion are not static but are temporal dynamic. Considering spread dynamics and structure dynamics together, exploring influence maximization in dynamic networks is an interesting and valuable problem. Zhuang et al. [17] updated the observed network by periodically detecting nodes in the real network and then selected seed nodes in the observed network as the approximate solution of the real network. Tong et al. [18] extended the static independent cascade model to the dynamic independent cascade (DIC) model and proposed two algorithms: A-greedy based on the greedy strategy and H-greedy based on the heuristic. Bao et al. [19] proposed the RSB algorithm based on multi-arm tiger machine optimization, which is suitable for dynamic non-stationary social networks. Wang [20] proposed an incremental algorithm based on the linear threshold model (DIM), which identifies top-K users in dynamic social networks based on information from the previous network. Liu et al. [21] proposed IncInf based on the independent cascade model and updated the seed set according to the topological changes of network evolution, which significantly reduces the running time of the algorithm. Chen et al. [22] extended the problem of dynamic network influence maximization and proposed the upper bound interchange (UBI) greedy algorithm to solve the problem of influence node tracking.

Although influence maximization in dynamic social networks has attracted some attention, all of the existing studies were constructed on network topology structure data which suffer from high dimensionality and low efficiency. Network representation learning aims to convert each node in the network to a low-dimensional latent representation, which has been widely applied in the tasks of visualization, clustering, classification, and link prediction. The network low-dimensional vector representation not only preserves structural feature relationships between nodes but also effectively alleviates the problem of network data sparsity. Based on the above discussions, leveraging network representation learning methods to help solve influence maximization in dynamic networks is a meaningful attempt.

In this paper, we develop dynamic influence maximization based on network representation learning, referred to as DIMNRL. First, we leverage network representation learning to obtain the low-dimensional vector representation of each node under different time steps and then construct the influence calculation method of node sets in the low-dimensional latent space. Next, aiming at the dynamic property of social networks, we propose an incremental node seed selection method to obtain the node set with maximum influence at different times. Comprehensive experimental results on NetHEPT, Twitter, UCI, and Wikipedia datasets demonstrate that compared with the state-of-the-art approaches, our method can yield similar performance in terms of influence spread but run much faster.

The rest of this paper is organized as follows: In Section 2, we introduce the definition of the problem of maximizing the influence of dynamic social networks and the design of the DIMNRL method in detail. Section 3 shows the results and analysis of our experiments. Finally, in Section 4, we put forward conclusions and discussions.

2 Materials and Methods

2.1 Problem Definition

We first define a dynamic network as $\mathcal{G}=(G^0,G^1,\dots ,G^t)$, where G^t = (V^t, E^t, W^t) is the network snapshot of the dynamic social network at time t. We assume that the network snapshot G⁰ at t = 0 is the initial network. △G^t = (△V^t, △E^t, △W^t) is the change of network topology structure of G^t at time t, so the network topology at time t + 1 can be obtained by G^t+1 = G^t ∪ △G^t. Based on the above definitions, the details of the problem we try to solve are as follows.

Influence maximization in the dynamic network. Given the topology structure G^t of a network and the network topology change △G^t at time t, the aim is to seek a seed set S^t+1 with k nodes in G^t+1 at time t + 1 such that the expected diffusion influence $\sigma \left(S^{t+1}\right)$ reaches the maximum value. For ease of description, this problem is also referred to as dynamic influence maximization.

2.2 Framework of DIMNRL

In this section, we develop dynamic influence maximization based on network representation learning, referred to as DIMNRL. The main idea of DIMNRL is to update the seed nodes by combining the information provided by the structure change of the dynamic network with seed nodes selected from the network at the previous time, so as to greatly reduce the time to obtain the seed node set with maximum influence at the current time. The DIMNRL is designed in the low-dimensional latent space gained by network representation learning, which is helpful to reduce the computational complexity and improve the computational efficiency.

Figure 1 presents the framework of our proposed DIMNRL, which is divided into three stages: dynamic network representation learning, initial seed set calculation, and seed set incremental update. The first stage is to get the low-dimensional vector representation of the dynamic network. The second stage is to obtain the initial seed set with maximum influence from the initial network. The last stage aims to incrementally update seed nodes to gain the seed sets of the networks at all times.

FIGURE 1

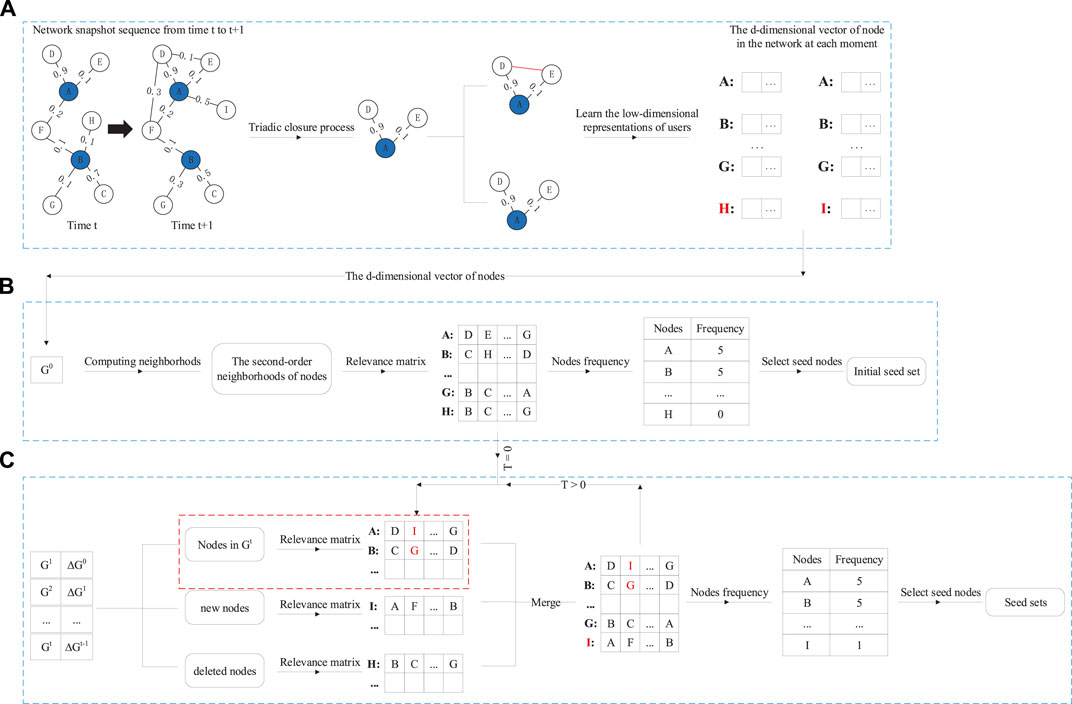
FIGURE 1. Overall framework of DIMNRL. (A) Getting the low-dimensional vector representation of the dynamic network, (B) obtaining the initial seed set with maximum influence from the initial network, and (C) incrementally updating seed nodes to gain the seed sets of the networks at all times.

2.2.1 Dynamic Network Representation Learning

The DIMNRL is to seek seed node sets from dynamic networks in the low-dimensional space. Therefore, we first need a network representation learning method to obtain low-dimensional vector representations of network snapshots at different time steps. Network representation learning is able to map large-scale and high-latitude networks to the low-dimensional space according to the relevant optimization objectives and use the vector representation of low-dimensional space to represent nodes, so as to preserve the topological structure and attribute characteristics of the original network as much as possible.

In this paper, we adopt the DynamicTriad [23] method which is suitable for dynamic social networks. DynamicTriad learns the embedding vector of each node at different time steps by quantifying the probability of an open triad evolving into a closed triad and proposes a semi-supervised learning algorithm for effective parameter estimation to optimize the model parameters. This algorithm can embed the time-varying characteristics of the network into the vector representation of nodes while maintaining the network structure properties.

2.2.2 Initial Seed Set Calculation

Keikha et al. [24] proposed the DeepIM method to solve the influence maximization problem in the static network using network representation learning. The overall idea of DeepIM is using the network representation learning algorithm to generate the vectors of nodes and then calculating the similarity of chords between nodes to select r nodes with the highest similarity as the correlation vector of each node in the network. Next, the nodes are sorted according to the number of occurrences of nodes in the correlation vectors of all nodes in the network. Finally, the top k nodes are selected as the seed sets for the network. Here, we attempt to improve the DeepIM algorithm from two aspects so that it can be applied to dynamic networks.

First, researchers have found that the influence of nodes decreases with the increase of paths in the propagation process, and the influence propagation range of nodes in the network can usually reach the range of third-order neighbors [25] or second-order neighbors [26]. However, DeepIM calculates the similarity between one node and all other nodes, and this calculation method is time-consuming and unnecessary. Aiming at this drawback, we choose a pruning strategy to limit the computation of correlation vectors for each node from the whole network to the second-order neighborhood. This pruning strategy can improve the computational efficiency of the overall solution and also ensure that r nodes most similar to the target node are achievable.

Second, DeepIM selects seed nodes from social networks according to the number of nodes appearing in the correlation vectors of all nodes, and this may cause overlapping influence in the propagation process due to the situation that the k seed nodes have many common neighbors. Therefore, it is necessary to introduce a covering mechanism to disperse seed nodes. Here, we propose a threshold rule to overcome the above limitation. We adopt the FIDD algorithm [27] to calculate the degree of common neighbors of two nodes in the network, and its formula is as follows:

$CN\left(i,j\right)=\frac{|N\left(i\right)\cap N\left(j\right)|}{|N\left(i\right)\cup N\left(j\right)|},(1)$

where CN(i, j) denotes the common neighbor degree of nodes i and j in the network and N(i) and N(j) denote the node sets in the secondary neighbors of nodes i and j, respectively. To reduce the influence overlap of seed set nodes during the propagation process, we set a threshold α to disperse the seed set nodes. If the CN values between the new selected node and the existing seed nodes are greater than the threshold α, this node will be ignored. Otherwise, if all CN values between the new selected node and the seed nodes are smaller than the threshold, this node will be added to the seed node set.

The specific algorithm is shown in Algorithm 1. In line 1, we obtain the second-order neighborhoods of each node. Lines 2–3 initialize the node’s correlation vector and seed node set. In lines 4–8, we obtain the correlation vector of the node. Lines 5–7 calculate the cosine similarity between the node and all the nodes in its secondary neighborhood by Eq 2. $u_u^t$ and $u_v^t$ represent the vector representations of nodes u and v in the network at time t. The correlation vector of each node and the minimum cosine similarity will be stored:

$\mathrm{cosine}\left(u_u^t,u_v^t\right)=\frac{u_u^t\cdot u_v^t}{|u_u^t\Vert u_v^t|}=\frac{{\sum }_{i=1}^d{u}_u^t{u}_v^t}{\sqrt{{\sum }_{i=1}^d{\left(u_u^t\right)}^2}\sqrt{{\sum }_{i=1}^d{\left(u_v^t\right)}^2}}.(2)$

In lines 9–13, after obtaining the correlation vectors of all nodes, we count the number of times each node appears in the correlation vector. In lines 14–20, we select our initial seed node set from the initial network according to our threshold mechanism.

Algorithm 1 Initial seed set selection.

2.2.3 Seed Set Incremental Update

When the network topology structure evolves slightly, the seed node set with maximum influence in this network also will not change violently. Therefore, based on network snapshots G^t at current time, seed set S^t of G^t, and network topology change △G^t at time t, designing an incremental algorithm to obtain S^t+1 for network snapshots G^t+1 quickly and accurately should be possible.

The evolution behaviors of social networks can be classified into six categories: inserting or deleting nodes, creating or deleting edges, and increasing or reducing edges’ weights. Here, we denote insertNodes, deleteNodes, addEdges, removeEdges, increaseWeight, and reduceWeight as the above six evolution behaviors. When the topology of the network changes by adding edges or nodes, some nodes may propagate influence using added new edges or nodes. When the network topology changes by reducing edges or deleting nodes, the influence propagation of some nodes may be interrupted. In the network low-dimensional representation, the information of edge change and edge weight change is retained in the vector representations of nodes. Therefore, our incremental algorithm mainly considers the impact of node change behaviors (i.e., insertNodes and deleteNodes) on seed node selection.

Algorithm 2 presents the details of updating seed nodes. Lines 1–2 initialize variables such as the correlation vector of the node model. In line 3, the change of the second-order neighborhood of each node in the network G^t+1 at time t + 1 is obtained and divided into three categories: nodes existing in G^t, new nodes, and deleted nodes. In lines 4–12, the correlation vectors of the network nodes at the previous moment are updated. For each added node, we calculate the cosine similarities between this node and its second-order neighborhoods and compare them with min_cosine. When the cosine similarity is greater than min_cosine, the node is added to the correlation vector. Otherwise, it is deleted. Lines 13–15 are to obtain the correlation vector of the new added node. This calculation process is the same as that of obtaining the initial seed set. Lines 16–18 are for the deleted nodes, and we directly delete the relevant vector of these nodes. Line 20 calculates the number of nodes in the correlation vector. In lines 21–27, we finally get the seed node set at time t + 1 according to the threshold mechanism.

Algorithm 2 Seed set incremental update.

3 Results

3.1 Datasets and Baselines

We select four real social network datasets (NetHEPT, Twitter, UCI, and Wikipedia) to validate our method. Supplementary Table S1 summarizes the details of the four datasets. As these four datasets do not provide the information of edge weights, here we adopt the uniformly model [28] to generate edge weights. Specifically, the weight of each edge is assigned to be 0.1 in the experiments.

• NetHEPT: It is a citation network of “High Energy Physics-Theory” from arXiv [29]. The dataset contains all the papers from January 1992 to April 2003. The edge between two nodes represents one paper citing another paper. We take the citation networks of 1992 and 1993 as the initial networks, and the network snapshot interval is 1 year. We use all the data from 1992 to 1998.

• Twitter: These data are extracted from Twitter, which records forwarded tweets between users from September 2010 to November 2010 [30]. Each edge indicates that one user has forwarded tweets from another. We set 10 days as the network snapshot interval.

• UCI: These data come from a Facebook-like online community at the University of California, Irvine, which records the data from April to October 2004 [31]. Each edge indicates that two users have communicated at least one piece of information. The network snapshot is set to be 1 month.

• Wikipedia: These data are from Wikipedia, which records historical data on all Wikipedia administrator elections and votes from 2004 to 2008 [32]. We record network snapshots every 1 year.

We adopt LDAG [10] and DeepIM [24] as the baseline methods and compare them with our DIMNRL solution in terms of influence diffusion range and running time. LDAG is a static network influence maximization algorithm based on the directed cyclic graph. The threshold parameter θ of LDAG in the experiment is set to 1/320, which is consistent with that in the original paper. DeepIM is an influence maximization algorithm based on deep learning. The correlation vector size r of DeepIM is set to 50 in the experiment.

To compare different methods under unified standards, we run the simulations using the independent cascade (IC) model and linear threshold (LT) model to obtain the influence of these seed node sets selected by LDAG, DeepIM, and DIMNRL. The propagation probability of the IC model and LT model is set to 0.1. All our experiments were carried out on the laptop of Inter(R) Core(TM) i7-10750H CPU @ 2.60Ghz and 16 GB RAM.

3.2 Effectiveness Evaluation

Figure 2A shows the influence spread ranges achieved by three methods on four datasets at different time steps, under the IC model. Each subfigure is corresponding to the result of a dataset, where red, blue, and brown curves represent DIMNRL, DeepIM, and LDAG methods, respectively. The x-axis represents the time step, and the y-axis represents the influence spread ranges of seed nodes selected by different methods. Similarly, Figure 2B shows the influence spread ranges achieved by three methods on four datasets at different time steps, under the LT model.

FIGURE 2

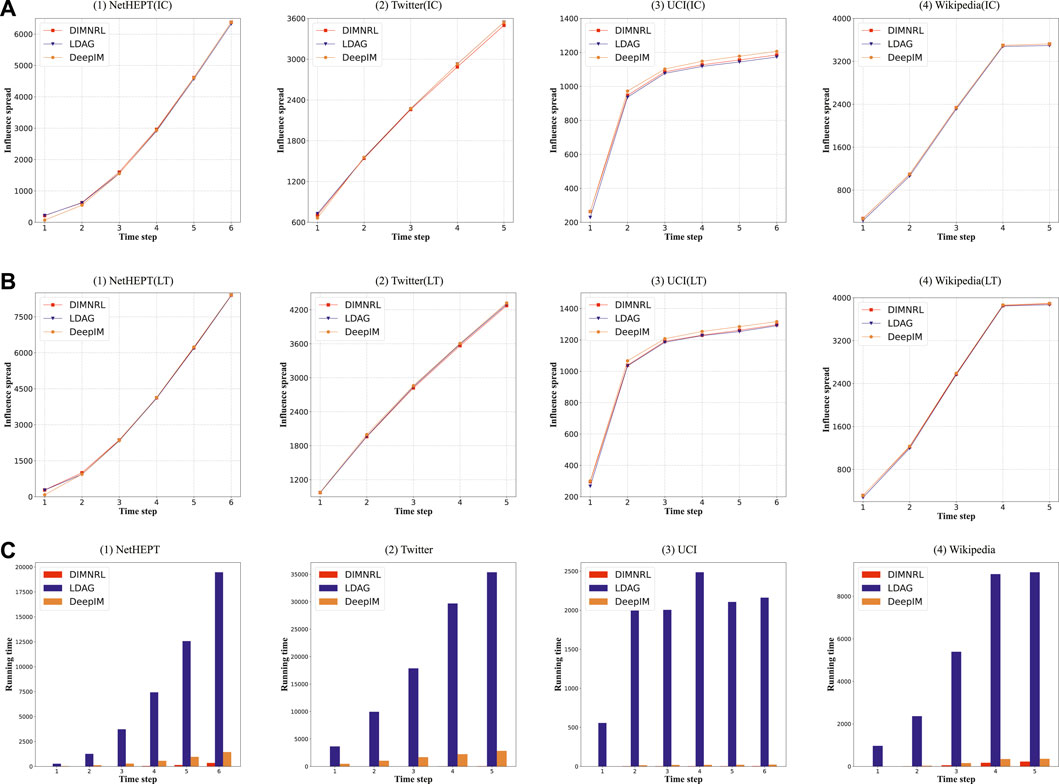
FIGURE 2. Results of our experiments. (A) Influence coverage of different algorithms on four datasets under the IC model, (B) influence coverage of different algorithms on four datasets under the LT model, and (C) running time of three algorithms on four social network datasets.

It can be seen from Figures 2A,B that, in UCI and Wikipedia datasets, LDAG has the worst performance compared with the other two methods (DIMNRL, DeepIM). On NetHEPT and Twitter datasets, LDAG has a bit of advantage over other methods in starting a few time steps and then achieves similar performance. DIMNRL and DeepIM achieve similar performance on different datasets at different time steps; DIMNRL improves DeepIM from the aspect of similar node selection, and the above experimental results validate the rationality of our improvement that only focuses on the second-order neighborhood.

3.3 Efficiency Evaluation

Figure 2C presents the running time of different methods for selecting 50 seed nodes from four datasets. Red, blue, and brown columns represent running time consumed by DIMNRL, DeepIM, and LDAG, respectively. It can be seen from Figure 2C that the running time of our DIMNRL method in each network snapshot is much shorter than that of the other two baseline methods. The LDAG method takes the most time, and the running time is especially longer in the Twitter dataset. The DeepIM algorithm finds seed nodes by traversing all nodes of the entire network, and the running time is still very terrible in a large-scale network with a large number of nodes. On NetHEPT and Twitter datasets, the running time of the DeepIM method is 2–3 orders of magnitude higher than our solution on each network snapshot. The above results fully demonstrate the high efficiency of our DIMNRL method.

In Figure 2C, we observe that the time consumption of the DIMNRL method at different times is not monotonous on the UCI dataset. The time consumption of DIMNRL in time step 2 is 3.64 s, while the time consumption in time steps 3 and 4 is 3.47 and 3.5 s, respectively. This is because our incremental seed selection method is closely related to the severity of network evolution. When the topology of the network snapshot changes greatly, the update algorithm takes a long time. When the topology of the network snapshot changes slightly, the running time of the update algorithm is short.

Based on the results shown in Figure 2, our DIMNRL method can achieve a similar or better influence performance than baseline methods, but the running time is much less. This means that the DIMNRL has the potential to effectively solve the influence maximization problem in large-scale dynamic social networks.

4 Conclusion

How to find seed node sets from temporal dynamic networks is an important extension direction in the research of influence maximization. In this paper, we combine network representation learning and influence maximization together and try to solve the influence maximization problem in dynamic networks via network low-dimensional vector representations. Extensive experiments on NetHEPT, Twitter, UCI, and Wikipedia datasets show that our method is able to achieve influence spread performance similar to existing methods but run much faster. These results fully illustrate the necessity and effectiveness of using network representation learning to maximize influence propagation over dynamic networks.

Network representation learning represents nodes as low-dimensional dense vectors and retains all information in the network as much as possible. It is possible to use network representation learning to obtain special information in social networks. Recently, network representation learning has made progress in signed networks [33], location-based networks [34], and hypernetworks [35]. Our solution in the low-dimensional latent space is not limited to dynamic influence maximization but applicable to polarity influence maximization, location-related influence maximization, and influence maximization in hypernetworks.

In addition to structural dynamics considered in this paper, relationship polarity, user preference, and geographic location also affect the effect of information/influence diffusion. How to integrate these factors into influence maximization research at the same time as much as possible is our next research direction. In today’s society, traditional media still play an important role in information dissemination. Information diffusion driven by traditional media and information spread over social networks are not isolated. How to leverage both traditional and online media together to maximize information propagation will be an interesting problem.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

DL conceptualized the research idea. WS analyzed the data and ran the software. WS and DL performed the methodology and wrote the original draft. WS, FY, DL, and YZ reviewed the paper, and WS, FY, and YZ edited the paper.

Funding

This work was funded by the National Natural Science Foundation of China (Nos. 62076149, 61702138, 61602128, 61672322, and 61672185), the Shandong Province Natural Science Foundation of China (Nos. ZR2019MF011 and ZR2016FQ13), the China Postdoctoral Science Foundation (Nos. 2020T130368, 2019M662360, 2017M621275, and 2018T110301), the Young Scholars Program of Shandong University, China, Weihai (No. 1050501318006), and the Science and Technology Development Plan of Weihai City, China (No. 1050413421912).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.827468/full#supplementary-material

References

1. Richardson M, Domingos P. Mining Knowledge-Sharing Sites for Viral Marketing. In: Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining, Edmonton, AB, July 23–26, 2002 (2002). p. 61–70. doi:10.1145/775047.775057

CrossRef Full Text | Google Scholar

2. Domingos P, Richardson M. Mining the Network Value of Customers. In: Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining, California, San Francisco, August 26–29, 2001 (2001). p. 57–66. doi:10.1145/502512.502525

CrossRef Full Text | Google Scholar

3. Kempe D, Kleinberg J, Tardos É. Maximizing the Spread of Influence through a Social Network. In: Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining, Washington, DC, August 24–27, 2003 (2003). p. 137–46. doi:10.1145/956750.956769

CrossRef Full Text | Google Scholar

4. Leskovec J, Krause A, Guestrin C, Faloutsos C, VanBriesen J, Glance N. Cost-effective Outbreak Detection in Networks. In: Proceedings of the 13th ACM SIGKDD international conference on Knowledge discovery and data mining, San Jose, CA, August 12–15, 2007 (2007). p. 420–9.

CrossRef Full Text | Google Scholar

5. Goyal A, Lu W, Lakshmanan LV. Celf++ Optimizing the Greedy Algorithm for Influence Maximization in Social Networks. In: Proceedings of the 20th international conference companion on World wide web, Hyderabad, India, March 28–April 1, 2011 (2011). p. 47–8.

CrossRef Full Text | Google Scholar

6. Cheng S, Shen H, Huang J, Zhang G, Cheng X. Staticgreedy: Solving the Scalability-Accuracy Dilemma in Influence Maximization. In: Proceedings of the 22nd ACM international conference on Information & Knowledge Management, Atlanta, GA, October 17–21, 2012 (2013). p. 509–18.

Google Scholar

7. Heidari M, Asadpour M, Faili H. Smg: Fast Scalable Greedy Algorithm for Influence Maximization in Social Networks. Physica A: Stat Mech its Appl (2015) 420:124–33. doi:10.1016/j.physa.2014.10.088

CrossRef Full Text | Google Scholar

8. Kundu S, Pal SK. Deprecation Based Greedy Strategy for Target Set Selection in Large Scale Social Networks. Inf Sci (2015) 316:107–22. doi:10.1016/j.ins.2015.04.024

CrossRef Full Text | Google Scholar

9. Chen W, Wang Y, Yang S. Efficient Influence Maximization in Social Networks. In: Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining, Paris, France, June 28–July 1, 2009 (2009). p. 199–208. doi:10.1145/1557019.1557047

CrossRef Full Text | Google Scholar

10. Chen W, Wang C, Wang Y. Scalable Influence Maximization for Prevalent Viral Marketing in Large-Scale Social Networks. In: Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining; 25-28, 2010; Washington, DC, USA (2010). p. 1029–38. doi:10.1145/1835804.1835934

CrossRef Full Text | Google Scholar

11. Chen W, Yuan Y, Zhang L. Scalable Influence Maximization in Social Networks under the Linear Threshold Model. In: Proceeding of the 2010 IEEE international conference on data mining; 13-17 Dec. 2010; Sydney, NSW, Australia. IEEE (2010). p. 88–97. doi:10.1109/ICDM.2010.118

CrossRef Full Text | Google Scholar

12. Goyal A, Lu W, Lakshmanan LVS. SIMPATH: An Efficient Algorithm for Influence Maximization under the Linear Threshold Model. In: Proceeding of the 2011 IEEE 11th international conference on data mining; 11-14 Dec. 2011; Vancouver, BC, Canada. IEEE (2011). p. 211–20. doi:10.1109/ICDM.2011.132

CrossRef Full Text | Google Scholar

13. Tang Y, Xiao X, Shi Y. Influence Maximization: Near-Optimal Time Complexity Meets Practical Efficiency. In: Proceedings of the 2014 ACM SIGMOD international conference on Management of data, Snowbird, UT, June 22–27, 2014 (2014). p. 75–86.

Google Scholar

14. Wang Z, Sun C, Xi J, Li X. Influence Maximization in Social Graphs Based on Community Structure and Node Coverage Gain. Future Generation Comput Syst (2021) 118:327–38. doi:10.1016/j.future.2021.01.025

CrossRef Full Text | Google Scholar

15. Zhang F, Liu H, Leung Y-W, Chu X, Jin B. Cbs: Community-Based Bus System as Routing Backbone for Vehicular Ad Hoc Networks. IEEE Trans Mobile Comput (2016) 16(8):2132–46. doi:10.1109/TMC.2016.2613869

CrossRef Full Text | Google Scholar

16. Zhang F, Zhang D, Xiong J, Wang H, Niu K, Jin B, et al. From Fresnel Diffraction Model to fine-grained Human Respiration Sensing with Commodity Wi-Fi Devices. Proc ACM Interact Mob Wearable Ubiquitous Technol (2018) 2(1):1–23. doi:10.1145/3191785

CrossRef Full Text | Google Scholar

17. Zhuang H, Sun Y, Tang J, Zhang J, Sun X. Influence Maximization in Dynamic Social Networks. In: Proceeding of the 2013 IEEE 13th International Conference on Data Mining; 7-10 Dec. 2013; Dallas, TX, USA. IEEE (2013). p. 1313–8. doi:10.1109/ICDM.2013.145

CrossRef Full Text | Google Scholar

18. Tong G, Wu W, Tang S, Du DZ. Adaptive Influence Maximization in Dynamic Social Networks. IEEE/ACM Trans Networking (2016) 25(1):112–25. doi:10.1109/TNET.2016.2563397

CrossRef Full Text | Google Scholar

19. Bao Y, Wang X, Wang Z, Wu C, Lau FC. Online Influence Maximization in Non-stationary Social Networks. In: 2016 IEEE/ACM 24th International Symposium on Quality of Service (IWQoS), Changsha, China, June 20–21, 2016. IEEE (2016). p. 1–6. doi:10.1109/iwqos.2016.7590438

CrossRef Full Text | Google Scholar

20. Wang Y, Zhu J, Ming Q. Incremental Influence Maximization for Dynamic Social Networks. In: International Conference of Pioneering Computer Scientists, Engineers and Educators, Harbin, China, September 22–24, 2017. Springer (2017). p. 13–27. doi:10.1007/978-981-10-6388-6_2

CrossRef Full Text | Google Scholar

21. Liu X, Liao X, Li S, Zheng S, Lin B, Zhang J, et al. On the Shoulders of Giants: Incremental Influence Maximization in Evolving Social Networks. Complexity (2017) 2017 p. 1–14. doi:10.1155/2017/5049836

CrossRef Full Text | Google Scholar

22. Chen X, Song G, He X, Xie K. On Influential Nodes Tracking in Dynamic Social Networks. In: Proceedings of the 2015 SIAM International Conference on Data Mining, Vancouver, BC, April 30–May 2, 2015. SIAM (2015). p. 613–21. doi:10.1137/1.9781611974010.69

CrossRef Full Text | Google Scholar

23. Zhou L, Yang Y, Ren X, Wu F, Zhuang Y. Dynamic Network Embedding by Modeling Triadic Closure Process. Proc AAAI Conf Artif Intelligence (2018) 32. p. 571–8.

Google Scholar

24. Keikha MM, Rahgozar M, Asadpour M, Abdollahi MF. Influence Maximization across Heterogeneous Interconnected Networks Based on Deep Learning. Expert Syst Appl (2020) 140:112905. doi:10.1016/j.eswa.2019.112905

CrossRef Full Text | Google Scholar

25. Christakis NA, Fowler JH. Connected: The Surprising Power of Our Social Networks and How They Shape Our Lives. New York, NY: Little, Brown Spark (2009).

Google Scholar

26. Pei S, Muchnik L, Andrade JS, Zheng Z, Makse HA. Searching for Superspreaders of Information in Real-World Social media. Sci Rep (2014) 4(1):5547–12. doi:10.1038/srep05547

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Sheikhahmadi A, Nematbakhsh MA, Shokrollahi A. Improving Detection of Influential Nodes in Complex Networks. Physica A: Stat Mech its Appl (2015) 436:833–45. doi:10.1016/j.physa.2015.04.035

CrossRef Full Text | Google Scholar

28. Li D, Xu Z-M, Chakraborty N, Gupta A, Sycara K, Li S. Polarity Related Influence Maximization in Signed Social Networks. PloS one (2014) 9(7):e102199. doi:10.1371/journal.pone.0102199

PubMed Abstract | CrossRef Full Text | Google Scholar

29.Cornell. arxiv nethept dataset (2003). Available from: http://www.cs.cornell.edu/projects/kddcup/datasets.html (Accessed on: September 19, 2021).

Google Scholar

30. Conover MD, Ratkiewicz J, Francisco M, Gonçalves B, Menczer F, Flammini A. Political Polarization on Twitter. In: Proceeding of the Fifth international AAAI conference on weblogs and social media; July 17-21, 2011; Barcelona, Catalonia, Spain (2011).

Google Scholar

31. Opsahl T, Panzarasa P. Clustering in Weighted Networks. Social networks (2009) 31(2):155–63. doi:10.1016/j.socnet.2009.02.002

CrossRef Full Text | Google Scholar

32. Leskovec J, Huttenlocher D, Kleinberg J. Signed Networks in Social media. In: Proceedings of the SIGCHI conference on human factors in computing systems, Atlanta, GA, April 10–15, 2010 (2010). p. 1361–70. doi:10.1145/1753326.1753532

CrossRef Full Text | Google Scholar

33. Shen X, Chung FL. Deep Network Embedding for Graph Representation Learning in Signed Networks. IEEE Trans Cybern (2020) 50(4):1556–68. doi:10.1109/TCYB.2018.2871503

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Qiao Y, Luo X, Li C, Tian H, Ma J. Heterogeneous Graph-Based Joint Representation Learning for Users and Pois in Location-Based Social Network. Inf Process Manage (2020) 57(2):102151. doi:10.1016/j.ipm.2019.102151

CrossRef Full Text | Google Scholar

35. Baytas IM, Xiao C, Wang F, Jain AK, Zhou J. Heterogeneous Hyper-Network Embedding. In: Proceeding of the 2018 IEEE International Conference on Data Mining (ICDM); 17-20 Nov. 2018; Singapore. IEEE (2018). p. 875–80. doi:10.1109/ICDM.2018.00104

CrossRef Full Text | Google Scholar