Topological One-Way Edge States in an Air-Hole Honeycomb Gyromagnetic Photonic Crystal

Topological one-way edge states have attracted increasing attention because of their intriguing fundamental physics and potential applications, particularly in the realm of photonics. In this paper, we present a theoretical and numerical demonstration of topological one-way edge states in an air-hole honeycomb gyromagnetic photonic crystal biased by an external magnetic field. Localized horizontally to the edge and confined in vertical direction by two parallel metallic plates, these unique states possess robust one-way propagation characteristics. They are strongly robust against various types of defects, imperfections and sharp corners on the path, and even can unidirectionally transport along the irregular edges of arbitrary geometries. We further utilize the one-way property of edge states to overcome entirely the issue of back-reflections and show the design of topological leaky wave antennas. Our results open a new door towards the observation of nontrivial edge states in air-hole topological photonic crystal systems, and offer useful prototype of robust topological photonic devices, such as geometry-independent topological energy flux loops and topological leaky wave antennas.

Introduction

Topological physics is flourishing as an active field, which has drawn extensive attention in both fundamental research and applied science [1]. Topological insulator commonly features the striking phenomenon of topologically protected one-way transport, exhibiting edge states or surface states that are strongly robust against defects, disorders, obstacles, sharp corners and so on [2, 3]. Inspired from the discovery of condensed quantum Hall effect, many studies have shown that topological states show essentially single-particle behavior of electrons and one can establish an analogy relationship with photon behaviors called topological photonic state (or topological one-way edge state) [4–7]. Topological one-way edge state provides a powerful platform for novel photonic devices with nontrivial functionalities and excellent performances, such as one-way waveguide [8–12], topological laser [13–17], rainbow trapping phenomenon [18–21], dispersionless slow light [22–24], topological fibre [25–27].

One feasible way to produce topological one-way edge states is to immerse a gyromagnetic photonic crystal (GPC) in an external static magnetic field to break the time-reversal symmetry [28–34]. When this symmetry is broken, truly one-wave edge states emerge, allowing the electromagnetic (EM) wave and light propagate forward smoothly when impinging on defects or propagating in disordered media, or even tanking sharp turns at arbitrary angles. To date, plenty of topological one-way edge states are focused on the two-dimensional cylinder-type GPC systems, which are consisted of an array of gyromagnetic cylinders immersed in air [30–34]. In contrast, little of them touch the air-hole-type GPC formed by an array of air holes in a gyromagnetic slab [35]. Yet, previous works in dielectric photonic crystals have shown that usually the transport behaviors of EM wave and light in cylinder-type photonic crystals are very different from that in air-hole-type photonic crystals [36–38]. So, it is interesting to examine the transport property of EM wave and light in an air-hole GPC, and it is also very worthwhile to explore the potential applications and devices of air-hole topological photonic system.

In this paper, we investigate, theoretically and numerically, topological one-way edge states in an air-hole GPC of a honeycomb lattice of air holes drilled in a gyromagnetic slab surrounded by two parallel metallic plates in vertical direction. We systematically study the projected band structures of edge states at both zigzag and armchair edges and analyze their eigenmodal fields. We demonstrate the one-way property of these special edge states, and also verify their transport robustness against various types of defects, imperfections, sharp corners, and even the irregular edges of arbitrary geometries. We further utilize the one-way property of edge states to overcome entirely the issue of back-reflections and show the design of topological leaky wave antennas. Our results open a new door towards the observation of nontrivial edge states in air-hole topological photonic systems, and show the prototype of robustly topological photonic devices.

Topological One-Way Edge States at Zigzag and Armchair Edges

We first design a rectangular air-hole GPC with 140 honeycomb lattices, where the lengths along the x and y directions are seven and twenty lattices respectively, as illustrated in Figure 1. The lattice constants of honeycomb lattice along the zigzag edge (x direction) and armchair edge (y direction) are a = 3.0 cm and $\sqrt{3}a$ respectively. Each air hole has a radius r = 0.8 cm and a height of h = 0.1a. In our simulations, this air-hole GPC is sandwiched between two parallel metallic layers with a thickness of d = 0.15 cm in vertical direction (z direction), as illustrated in Figure 1. The relative permittivity and permeability of the air are ε₁ = 1 and μ₁ = 1 respectively. The gyromagnetic slab is composed of the commercial available yttrium-iron-garnet (YIG). In the absence of external static magnetic field, the relative permittivity and permeability of YIG is ε₂ = 15.26 and μ₂ = 1 respectively. When an external static magnetic field is applied along + z direction, strong gyromagnetic anisotropy will be induced in YIG material, and its permeability can be given by [39–41].

${\widehat{\mu }}_2=\left(\begin{array}{ccc}0.78& -0.93i& 0\\ 0.93i& 0.78& 0\\ 0& 0& 1\end{array}\right).(1)$

FIGURE 1

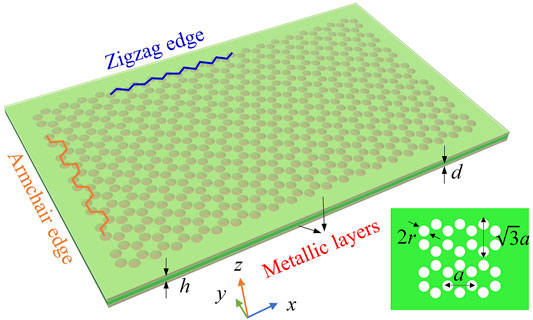
FIGURE 1. Oblique-view of a rectangular air-hole honeycomb gyromagnetic photonic crystal. There exist two zigzag edges (blue) and two armchair edges (orange) along the x and y directions, respectively. The lattice constant along the zigzag edge is a, but that along the armchair edge is $\sqrt{3}a$. The thickness of this air-hole GPC is h = 0.1a = 0.3 cm, and the radius of air-hole is r = 0.8 cm. The lower right panel is a partial schematic diagram.

These constitutive parameters correspond to those of YIG at 6.0 GHz with an external magnetic field of 500 Oe and a saturation magnetization of 1884 Gauss [39–41]. All the simulations are calculated by using the commercial software COMSOL MULTIPHYSICS with RF module in frequency domain, and only E polarization (where the electric field E is parallel to z-axis direction) is considered.

Next, we calculate the projected band structure of air-hole GPC along the zigzag edge, by adopting a supercell consisting of seven honeycomb lattices in one column, and the lattice constant is a = 3.0 cm. The projected band structures of the zigzag edges displayed in Figure 2A show that two dispersion curves (colored in red and blue respectively) appear inside the bandgap (green region) ranging from 5.52 to 6.21 GHz. The eigenmodal fields of points 1 and 2 at a frequency of f_s = 5.90 GHz depicted in Figure 2B reveal that there exist two edge states at two parallel zigzag edges. This phenomenon indicates that the YIG material shows the bandgap property that forbids the transport of EM waves in the YIG material, as a result, the one-way energy fluxes can be strongly localized at the zigzag interfaces between the air-hole GPC and the YIG material. As the slope signs of the red and blue dispersion curves are positive and negative respectively, the lower and upper zigzag edges will support right-propagating (red arrow) and left-propagating (blue arrow) one-way edge states respectively, as shown in Figure 2B. To exhibit the transport behaviors of one-way edge states, we use a configuration illustrated in Figure 2C. Two line sources (white stars) oscillating at a frequency of f_s = 5.90 GHz are placed at the center of upper and lower zigzag edges. The energy of line sources are confined at the upper and lower zigzag edges and unidirectionally propagate leftwards and rightwards respectively, in exactly agreement with the calculated results of Figures 2A,B.

FIGURE 2

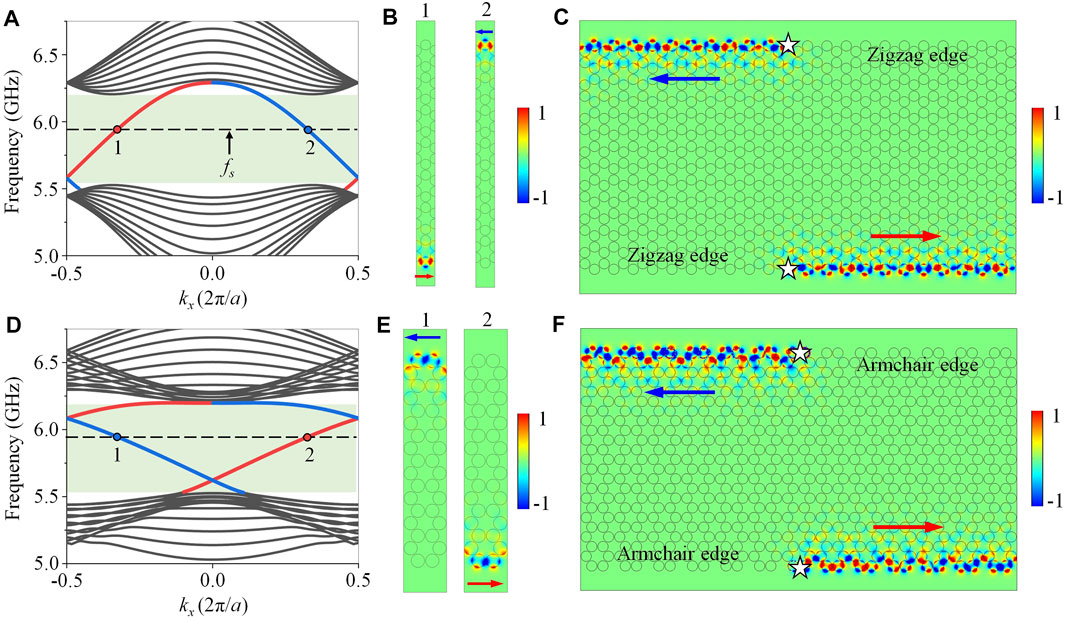
FIGURE 2. Topological one-way edge states at zigzag and armchair edges of a rectangular air-hole honeycomb GPC. (A–C) Zigzag edges. (D–F) Armchair edges. (A, D) Projected band structures. (B, E) Eigenmodal fields. (C, F) Electric field distributions. Blue and red arrows indicate the left- and right-propagating one-way edge states respectively, and white stars represent the line sources oscillating at a frequency of f_s = 5.90 GHz. The frequency at the black dotted lines is f_s = 5.90 GHz, and the bandgap are marked as the greed region with a frequency range of 5.52 ∼ 6.21 GHz.

Then, we calculate the projected band structure of air-hole GPC along the armchair edges, whose lattice constant is $\sqrt{3}a$. Their dispersions are calculated by adopting a supercell consisting of eight honeycomb lattices in one column, as plotted in Figure 2E. On the one hand, the calculated results illustrated in Figure 2D show that there exist two red and blue dispersion curves dwelling the bandgap (green region) with a frequency range of 5.52∼6.21 GHz, and their slopes are opposite. On the other hand, Figure 2E exhibits that the electric fields of eigenmodes 1 and 2 are concentrated at the armchair edges. Thus, there also exist two counter-propagating one-way edge states at the two parallel armchair edges. When two line sources oscillating at f_s = 5.90 GHz are placed at the upper and lower armchair interfaces, the left- and right-propagating one-way edge states can be excited respectively, as seen in Figure 2F. Consequently, these numerical simulations exhibit that both zigzag and armchair edges of air-hole honeycomb GPC support the one-way edge states in the green region with a frequency range of 5.52 ∼ 6.21 GHz (their bandwidth is about 11.8%).

Topological Energy Flux Loops of Arbitrary Geometries

We have demonstrated the one-way transmission property of edge states existing at both zigzag and armchair edges. Now, we proceed to show the transport robustness of these one-way edge states in the presence of various types of defects, imperfections and sharp corners on the path. We must note that in our simulations, there exist two parallel perfect electric conductors clamping the air-hole GPC along the vertical direction (z direction) to avoid energy fluxes radiating into air. The line source (white star) oscillating at f_s = 5.90 GHz is placed at the lower zigzag interface. Figure 3A shows the simulated result of one-way edge states in a perfect rectangular air-hole honeycomb GPC without any imperfections. The one-way edge states propagate along the zigzag and armchair interfaces to form a counterclockwise energy flux loop. Then, an imperfection interface can be created by moving a line of five air holes at the lower zigzag edge along the y direction with a distance of 0.55a, and the original positions of the moved air-holes are marked as five dotted circles, as plotted in Figure 3B. The electric field distribution shown in Figure 3B reveals that this imperfect interface still allows the EM wave propagating in one direction and forbidding backscattering. Figure 3C exhibits another common defected interface that can be constructed by replacing a honeycomb lattice of six air holes with six YIG cylinders of same size. As illustrated in Figure 3C, a new one-way interface between the air-hole GPC and the YIG material can be created, so that the edge states can turn around the defects without any back-reflection. We proceed to consider a regular right-angled trapezoid air-hole GPC including three types of sharp corners (60°−turn, 90°−turn and 120°−turn) and two types of edges (zigzag and armchair edges), as illustrated in Figure 3D. The schematic diagram of the partial structure (black dotted rectangle) is shown on the right panel of Figure 3D. It is a very common configuration in the previous works to be usually used to verify the transport robustness of topological edge states against the sharp corners. The simulated electric field distribution shows that the energy fluxes are strongly confined in the zigzag and armchair interfaces of trapezoid air-hole GPC. They can transport along the lower zigzag edge, climb over the 120° sharp corner, continue to transport along the tilt zigzag edge, pass through the 60°−turn to the upper zigzag edge, bypass the left armchair edge, turn around the 90°−turn at the bottom left, and finally go back to the source to form a counterclockwise energy flux loop.

FIGURE 3

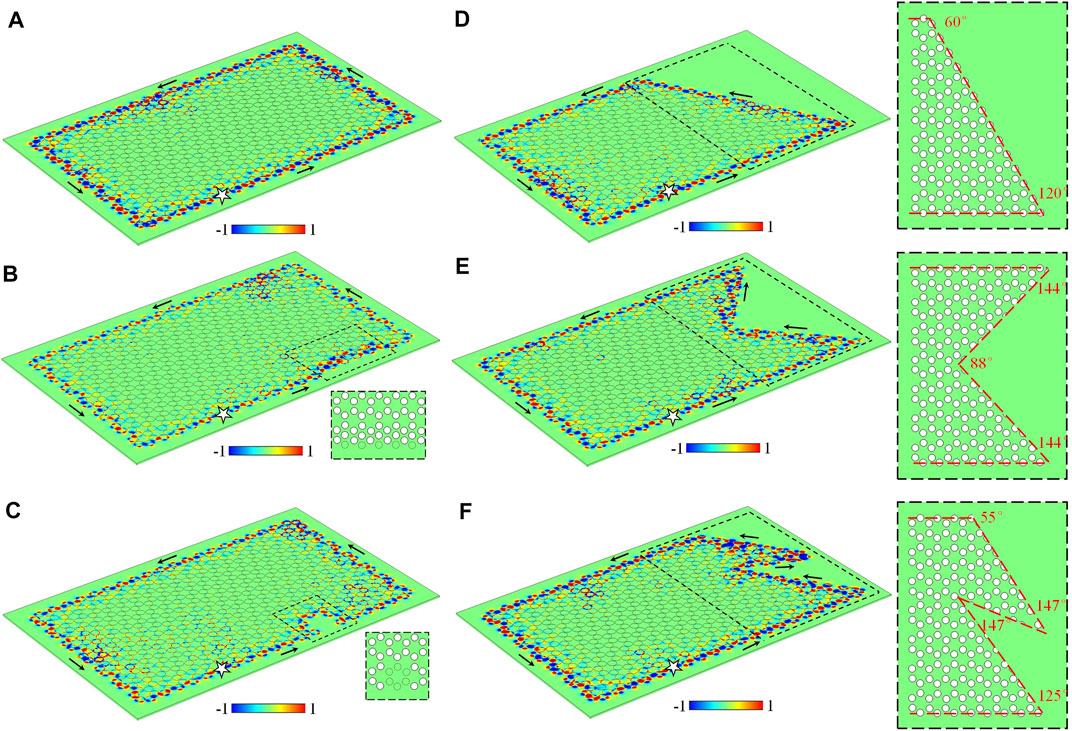
FIGURE 3. Topological one-way edge states in air-hole GPCs of various geometries. (A) A perfect rectangular honeycomb GPC. (B) An imperfect zigzag interface is created by moving a line of five air holes at the lower zigzag edge along the y direction with a distance of 0.55a. (C) A defected zigzag interface is constructed by replacing a honeycomb lattice of six air holes with six YIG cylinders of same size. (D–F) Three irregular air-hole GPCs of various geometries. The angle of sharp corner is marked near the corner and the transport interfaces are marked as the red dotted lines.

In addition to creating the common defects, imperfections and sharp corners to demonstrate the transport robustness of one-way edge states, we proceed to calculate the electric field distributions in two configurations of irregular interfaces and unusual sharp corners. Notably, a configurable, controllable and efficient way to construct these special structures is to fill the YIG material into the air holes as required. It can be seen that the EM waves can robustly transport along the atypical zigzag and armchair edges, and smoothly bypass a 88°−turn and two 144°−turns in a reflection-free way, as shown in Figure 3E. More intriguingly, the simulated electric field distributions shown in Figure 3F exhibit that the energy fluxes can almost perfectly transmit from the lower zigzag edge to the upper edge although there exist the irregular edges (not the zigzag and armchair edges) and unusual sharp corners (such as 55°−turn, 125°−turn, and 147°−turn).

We have verified that the topological one-way edge states are extremely robust against the backscattering from the defects, imperfections and unusual sharp corners at both regular and irregular edges outside the air-hole GPCs. Beyond the robust transport, these results also imply the possibility of implementing deformed topological energy flux loop of arbitrary geometries. So we further investigate the transport behaviors of EM waves in the energy flux loops of arbitrary geometries inside the air-hole GPCs, including E-shaped, Heart-shaped and Lightning-shaped energy flux loops, as illustrated in Figures 4A1–C1. The excitation frequency of line source (white star) is f_s = 5.90 GHz. The electric field distribution shown in Figure 4A2 shows that the energy fluxes are strongly confined at the interface of E-shaped loop and travel unidirectionally along the inside contour of air-hole GPC to form a counterclockwise energy flux loop. Again, both the contours of Heart-shaped and Lightning shaped energy flux loop also can be lighted by the line source due to the excitation of one-way edge states, as seen in Figures 4B2,C2. These simulated results exhibit that the geometry-independent topological energy flux loops can be created in the air-hole GPCs, which may provide the great opportunity to develop complex topological circuitry of arbitrary geometries for the robust transport of photons in classical wave regimes.

FIGURE 4

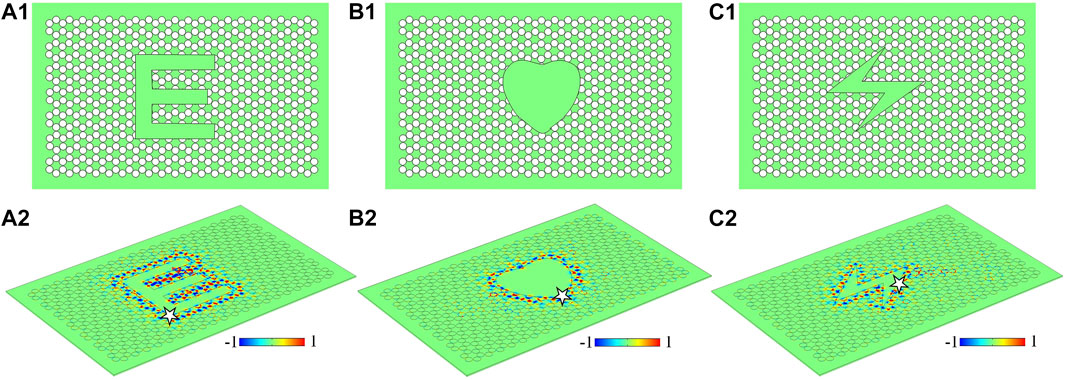
FIGURE 4. Geometry-independent topological energy flux loop. (A) E-shaped loop. (B) Heart-shaped loop. (C) Lightning-shaped loop. (A1–C1) Schematic diagrams. (A2–C2) Electric field distributions.

Topological Leaky Wave Antenna

We have mentioned above that when the metallic plates of air-hole GPC in vertical direction are removed, EM waves will leak into air. When the propagating wave is leaked out in air through a opened port, a leaky wave antenna will be formed [42, 43]. Utilizing this peculiar property, we can introduce small holes (or ports) in metallic plates (yellow) to allow EM waves to radiate outwards, thus, to achieve topological leaky wave antenna. It should be noted that one-way edge state in the rectangular air-hole GPC system shown in Figure 3A is a closed energy flux loop surrounding entire system. To suppress one-way energy fluxes making a full round trip to affect the energy of line source, holes or ports we introduced should be guaranteed that all electric field amplitudes are released before making a full round trip.

We first consider a topological leaky wave antenna with a simple configuration. Only one antenna port (Port 1) of a size of 9.0 × 6.3 cm above the upper zigzag edge is opened, and its schematic diagrams are illustrated in Figure 5A1. The simulated results displayed in Figure 5A2 show that when the one-way energy fluxes reach Port 1, all of them directly leak into the air. As a result, no energy fluxes continue to propagate forwards to form a closed energy flux loop. The electric field amplitude distributions along the upper zigzag edge shown in Figure 5A3 also exhibit that when EM wave meets Port 1, the amplitude of its electric field sharply drops to zero, exactly in agreement with our expectations. It should be noted that attributed to the one-way nature of edge states, the output port does not backscatter any EM wave to affect the radiation property of line source. In contrast, in the conventional trivial leaky wave antennas, the energy fluxes backscattered from the output port will reflect back to the previous transport channel and even transmit back to the line source, thereby affecting the energy transmission and radiation efficiency in the whole antenna system. Therefore, the one-way property of edge states can overcome entirely the issue of back-reflections and simplify the design of the leaky wave antenna.

FIGURE 5

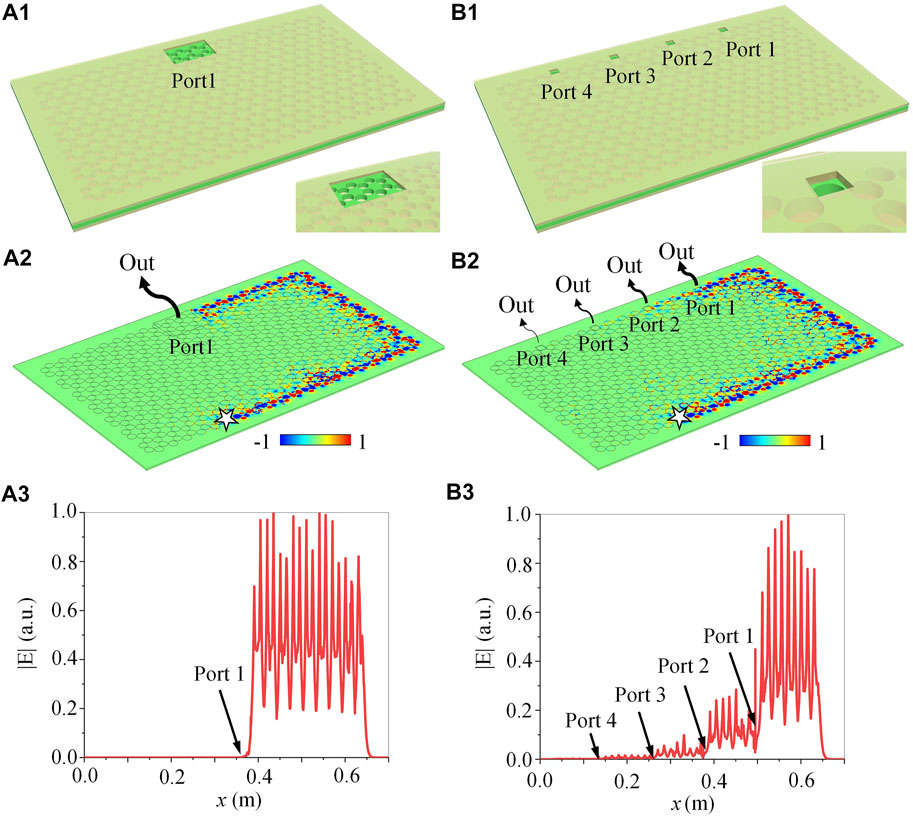
FIGURE 5. Topological leaky wave antennas. (A) Single port antenna. (B) Four ports antenna. (A1, B1) Oblique-view. (A2, B2) Electric field distribution. (A3, B3) Amplitude of electric field along the upper zigzag interface.

On the other hand, we proceed to investigate the design of a topological leaky wave antenna array, made by cascading four antenna ports in the top metallic plate one after the other, as plotted in Figure 5B1. The size of these antenna ports is 1.6 × 1.6 cm, and the distance between the neighboring ports is 12.0 cm. As seen in Figure 5B2, when the energy fluxes reach Port 1, about 75% of them are released into air, and the rest continues to propagate forwards along the upper zigzag edge. All of energy fluxes will be completely leaked into air until they reach Port 4, as shown in Figure 5B3. Certainly, one can change the energy radiation ratio by modifying the size of each port and the distance between the neighboring ports. Similarly, because the backscattering of the topological one-way edge states is forbidden, the antenna ports do not scatter back any EM waves, so that the second port with further downstream will not affect the output properties of the first port. However, for the conventional trivial leaky wave antennas, the energy fluxes will be scattered back from the second port and transmitted backward through the first port, so that the backscattering of output port has a significant influence on the energy transmission and radiation efficiency in the whole antenna system. Notably, this backscattering has also significant consequences in many other systems, specifically those systems seeded by a master oscillator whose performance may be strongly affected by reflected signals. It should be emphasized that by introducing the irregular edges of arbitrary geometries into the air-hole GPCs, the geometry-independent topological leaky wave antenna can also be realized.

Conclusion

In summary, we have demonstrated that the topological one-way edge states could exist in a rectangular air-hole honeycomb GPC biased by an external magnetic field. We have studied the projected band structures of zigzag and armchair edges and they both exhibited the transport behaviors of the topological one-way edge states. Besides, we have demonstrated that these unique states are not only strongly robust against various types of defects, imperfections and sharp corners, but also can unidirectionally transport along irregular edges of arbitrary geometries. Moreover, we have utilized the one-way property of edge states to overcome entirely the issue of back-reflections and provided the design of topological leaky wave antennas. Our findings open a new door towards the observation of nontrivial edge states in the air-hole topological photonic systems, and show the prototype of robustly topological photonic devices, such as geometry-independent topological energy flux loops and topological leaky wave antennas.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors contributed extensively to this work. CP, JC, and QQ performed the simulation. CP and JC drew the figures. JC, CP, and Z-YL wrote the manuscript. Z-YL supervised the project. All authors participated in discussions and reviewed the manuscript.

Funding

The authors are grateful for the financial support from the National Natural Science Foundation of China (11974119), Science and Technology Project of Guangdong (2020B010190001), Guangdong Innovative and Entrepreneurial Research Team Program (2016ZT06C594), National Key R&D Program of China (2018YFA 0306200).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, orclaim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hasan MZ, Kane CL, Tse WK. Colloquium: Topological Insulators. Rev Mod Phys (2010) 82(4):3045–67. doi:10.1103/revmodphys.82.3045

CrossRef Full Text | Google Scholar

2. Nadeem M, Hamilton AR, Fuhrer MS, Wang X. Quantum Anomalous Hall Effect in Magnetic Doped Topological Insulators and Ferromagnetic Spin-Gapless Semiconductors—A Perspective Review. Small (2020) 16(42):1904322. doi:10.1002/smll.201904322

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Cayssol J, Fuchs JN. Topological and Geometrical Aspects of Band Theory. J Phys Mater (2021) 4(3):034007. doi:10.1088/2515-7639/abf0b5

CrossRef Full Text | Google Scholar

4. Xie BY, Wang HF, Zhu XY, Lu MH, Wang ZD, Chen YF. Photonics Meets Topology. Opt Express (2018) 26(19):24531–50. doi:10.1364/oe.26.024531

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ozawa T, Price HM, Amo A. Topological Photonics. Rev Mod Phys (2019) 91(1):015006. doi:10.1103/revmodphys.91.015006

CrossRef Full Text | Google Scholar

6. Liu JW, Shi FL, He XT, Tang GJ, Chen WJ, Chen XD, et al. Valley Photonic Crystals. Adv Phys X (2021) 6(1):1905546. doi:10.1080/23746149.2021.1905546

CrossRef Full Text | Google Scholar

7. Chen J, Liang W, Li ZY. Progress of Topological Photonic State in Magneto-Optical Photonic Crystal. Acta Optic (2021) 41(8):0823015. doi:10.3788/aos202141.0823015

CrossRef Full Text | Google Scholar

8. Chen J, Liang W, Li ZY. Antichiral One-Way Edge States in a Gyromagnetic Photonic Crystal. Phys Rev B (2020) 101(21):214102. doi:10.1103/physrevb.101.214102

CrossRef Full Text | Google Scholar

9. Zhuang S, Chen J, Liang W, Li ZY. Zero GVD Slow-Light Originating from a Strong Coupling of One-Way Modes in Double-Channel Magneto-Optical Photonic Crystal Waveguides. Opt Express (2021) 29(2):2478–87. doi:10.1364/oe.412460

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Tasolamprou AC, Kafesaki M, Soukoulis CM, Economou EN, Koschny T. Chiral Topological Surface States on a Finite Square Photonic Crystal Bounded by Air. Phys Rev Appl (2021) 16(4):044011. doi:10.1103/physrevapplied.16.044011

CrossRef Full Text | Google Scholar

11. Mann SA, Alù A. Broadband Topological Slow Light through Brillouin Zone Winding. Phys Rev Lett (2021) 127(12):123601. doi:10.1103/physrevlett.127.123601

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang M, Zhang RY, Zhang L, Wang D, Guo Q, Zhang ZQ, et al. Topological One-Way Large-Area Waveguide States in Magnetic Photonic Crystals. Phys Rev Lett (2021) 126(6):067401. doi:10.1103/PhysRevLett.126.067401

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Bahari B, Ndao A, Vallini F, El Amili A, Fainman Y, Kanté B. Nonreciprocal Lasing in Topological Cavities of Arbitrary Geometries. Science (2017) 358(6363):636–40. doi:10.1126/science.aao4551

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bandres MA, Wittek S, Harari G, Parto M, Ren J, Segev M, et al. Topological Insulator Laser: Experiments. Science (2018) 359(6381):eaar4005. doi:10.1126/science.aar4005

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Shao ZK, Chen HZ, Wang S, Mao XR, Yang ZQ, Wang SL, et al. A High-Performance Topological Bulk Laser Based on Band-Inversion-Induced Reflection. Nat Nanotechnol (2020) 15(1):67–72. doi:10.1038/s41565-019-0584-x

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zeng Y, Chattopadhyay U, Zhu B, Qiang B, Li J, Jin Y, et al. Electrically Pumped Topological Laser with Valley Edge Modes. Nature (2020) 578(7794):246–50. doi:10.1038/s41586-020-1981-x

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Dikopoltsev A, Harder TH, Lustig E, Egorov OA, Beierlein J, Wolf A, et al. Topological Insulator Vertical-Cavity Laser Array. Science (2021) 373(6562):1514–7. doi:10.1126/science.abj2232

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chen J, Liang W, Li ZY. Switchable Slow Light Rainbow Trapping and Releasing in Strongly Coupling Topological Photonic Systems. Photon Res (2019) 19(9):091075. doi:10.1364/prj.7.001075

CrossRef Full Text | Google Scholar

19. Chen J, Qin Q, Peng C, Liang W, Li ZY. Slow Light Rainbow Trapping in a Uniformly Magnetized Gyromagnetic Photonic crystal Waveguide. Front Mater (2021) 8:728991. doi:10.3389/fmats.2021.728991

CrossRef Full Text | Google Scholar

20. Zhang H, Qian L, Wang C, Ji CY, Liu Y, Chen J, et al. Topological Rainbow Based on Graded Topological Photonic Crystals. Opt Lett (2021) 46(6):1237–40. doi:10.1364/ol.419271

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lu C, Wang C, Xiao M, Zhang ZQ, Chan CT. Topological Rainbow Concentrator Based on Synthetic Dimension. Phys Rev Lett (2021) 126(11):113902. doi:10.1103/physrevlett.126.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen J, Liang W, Li ZY. Strong Coupling of Topological Edge States Enabling Group-Dispersionless Slow Light in Magneto-Optical Photonic Crystals. Phys Rev B (2019) 99(1):014103. doi:10.1103/physrevb.99.014103

CrossRef Full Text | Google Scholar

23. Chen J, Liang W, Li ZY. Broadband Dispersionless Topological Slow Light. Opt Lett (2020) 45(18):4964–7. doi:10.1364/ol.401650

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Shi FL, Cao Y, Chen XD, Liu JW, Chen WJ, Chen M, et al. Distortionless Pulse Transmission in Valley Photonic Crystal Slab Waveguide. Phys Rev Appl (2021) 15(2):024002. doi:10.1103/physrevapplied.15.024002

CrossRef Full Text | Google Scholar

25. Lu L, Gao H, Wang Z. Topological One-Way Fiber of Second Chern Number. Nat Commun (2018) 9(1):5384. doi:10.1038/s41467-018-07817-3

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Lin H, Lu L. Dirac-Vortex Topological Photonic Crystal Fibre. Light Sci Appl (2020) 9(1):202–7. doi:10.1038/s41377-020-00432-2

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhang Z, Lu J, Liu T, Gan J, Heng X, Wu M, et al. Azimuthally and Radially Polarized Orbital Angular Momentum Modes in valley Topological Photonic crystal Fiber. Nanophotonics (2021) 10(16):4067–74. doi:10.1515/nanoph-2021-0395

CrossRef Full Text | Google Scholar

28. Raghu S, Haldane FDM. Analogs of Quantum-Hall-Effect Edge States in Photonic Crystals. Phys Rev A (2008) 78(3):033834. doi:10.1103/physreva.78.033834

CrossRef Full Text | Google Scholar

29. Haldane FD, Raghu S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys Rev Lett (2008) 100(1):013904. doi:10.1103/PhysRevLett.100.013904

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wang Z, Chong YD, Joannopoulos JD, Soljacić M. Reflection-Free One-Way Edge Modes in a Gyromagnetic Photonic Crystal. Phys Rev Lett (2008) 100(1):013905. doi:10.1103/PhysRevLett.100.013905

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wang Z, Chong Y, Joannopoulos JD, Soljačić M. Observation of Unidirectional Backscattering-Immune Topological Electromagnetic States. Nature (2009) 461(7265):772–5. doi:10.1038/nature08293

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Ao X, Lin Z, Chan CT. One-Way Edge Mode in a Magneto-Optical Honeycomb Photonic Crystal. Phys Rev B (2009) 80(3):033105. doi:10.1103/physrevb.80.033105

CrossRef Full Text | Google Scholar

33. Fu JX, Liu RJ, Li ZY. Robust One-Way Modes in Gyromagnetic Photonic Crystal Waveguides with Different Interfaces. Appl Phys Lett (2010) 97(4):041112. doi:10.1063/1.3470873

CrossRef Full Text | Google Scholar

34. Poo Y, Wu RX, Lin Z, Yang Y, Chan CT. Experimental Realization of Self-Guiding Unidirectional Electromagnetic Edge States. Phys Rev Lett (2011) 106(9):093903. doi:10.1103/PhysRevLett.106.093903

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Liu K, Shen L, He S. One-Way Edge Mode in a Gyromagnetic Photonic Crystal Slab. Opt Lett (2012) 37(19):4110–2. doi:10.1364/ol.37.004110

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wu LH, Hu X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys Rev Lett (2015) 114(22):223901. doi:10.1103/physrevlett.114.223901

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Anderson PD, Subramania G. Unidirectional Edge States in Topological Honeycomb-Lattice Membrane Photonic Crystals. Opt Express (2017) 25(19):23293–301. doi:10.1364/oe.25.023293

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zhu X, Wang HX, Xu C, Lai Y, Jiang JH, John S. Topological Transitions in Continuously Deformed Photonic Crystals. Phys Rev B (2018) 97(8):085148. doi:10.1103/physrevb.97.085148

CrossRef Full Text | Google Scholar

39. Lu J-C, Chen X-D, Deng W-M, Chen M, Dong J-W. One-Way Propagation of Bulk States and Robust Edge States in Photonic Crystals with Broken Inversion and Time-Reversal Symmetries. J Opt (2018) 20(7):075103. doi:10.1088/2040-8986/aac3a1

CrossRef Full Text | Google Scholar

40. Pozar DM. Microwave Engineering. New York: Wiley (1998). p. 497–517.

Google Scholar

41. Wohlfarth E. Handbook of Magnetic Materials. New York: Elsevier (1980). p. 293.

Google Scholar

42. Lumer Y, Engheta N. Topological Insulator Antenna Arrays. ACS Photon (2020) 7(8):2244–51. doi:10.1021/acsphotonics.0c00797

CrossRef Full Text | Google Scholar

43. Shen Q, You Y, Xu J, Shen Y, Deng X, Wang Z, et al. Mechanically Scanned Leaky-Wave Antenna Based on a Topological One-Way Waveguide. Front Phys (2020) 15(3):33601. doi:10.1007/s11467-020-0953-9

CrossRef Full Text | Google Scholar