An In Silico Study of Electrophysiological Parameters That Affect the Spiral-Wave Frequency in Mathematical Models for Cardiac Tissue

Spiral waves of excitation in cardiac tissue are associated with life-threatening cardiac arrhythmias. It is, therefore, important to study the electrophysiological factors that affect the dynamics of these spiral waves. By using an electrophysiologically detailed mathematical model of a myocyte (cardiac cell), we study the effects of cellular parameters, such as membrane-ion-channel conductances, on the properties of the action-potential (AP) of a myocyte. We then investigate how changes in these properties, specifically the upstroke velocity and the AP duration (APD), affect the frequency ω of a spiral wave in the mathematical model that we use for human-ventricular tissue. We find that an increase (decrease) in this upstroke-velocity or a decrease (increase) in the AP duration increases (decreases) ω. We also study how other intercellular factors, such as the fibroblast-myocyte coupling, diffusive coupling strength, and the effective number of neighboring myocytes and fibroblasts, modulate ω. Finally, we demonstrate how a spiral wave can drift to a region with a high density of fibroblasts. Our results provide a natural explanation for the anchoring of spiral waves in highly fibrotic regions in fibrotic hearts.

1 Introduction

Nonlinear waves in the form of rotating spirals are ubiquitous spatiotemporal patterns that occur in a variety of biological or physical systems; these include chemical-reaction waves in the Belousov-Zhabotansky system [1–5], oxidation waves of carbon monoxide on the surface of platinum [6–8], calcium-signalling waves in Xenopus oocytes [9], cyclic-AMP signalling waves in the aggregration process of Dictyostelium discoideum [10, 11], and, notably, action-potential (AP) waves that mediate muscle contraction in cardiac tissue. The organization of these AP waves in the form of spirals or scrolls in cardiac tissue is associated with abnormal and life-threatening heart rhythms known as arrhythmias. In particular, ventricular arrhythmias can lead to sudden cardiac death; therefore, it is important to understand the dynamics of such waves.

The rhythm of a normal heart is maintained by the trains of waves that are generated by its pacemaker, the sino-atrial node (SAN). This normal rhythm in a heart can be disturbed by the formation of a spiral wave, which can override the function of the SAN as the primary source of waves and entrain the heart to follow the spiral-rotation frequency. There are multiple mechanisms through which spiral waves can occur in cardiac tissue [12–18].

Ex vivo and in vitro studies [19–27] show that VT is associated with functional reentry that leads to the formation of a spiral wave. A multiple-spiral state is linked to ventricular fibrillation (VF) that results in a chaotic heart rate [13–15, 23, 28–30], and a quivering of the left ventricle, which renders it incapable of pumping oxygenated blood to the body; and, in the absence of medical intervention, this leads to death in a few minutes. It is crucial, therefore, to develop a detailed understanding of how spiral waves in cardiac tissue can get destabilized and form multiple spiral waves. Some studies have shown that heterogeneity-induced spatial gradients in the frequency ω of a spiral wave can lead to such an instability [31, 32] or to the drifting of this spiral wave [28, 33–35]. We build on the results of these studies to investigate which physiological factors affect ω and how they modulate it. In mammalian hearts, cardiac tissue is heterogeneous: there can be cellular heterogeneity, e.g., cardiac fibroblasts in addition to myocytes, or a spatial variation of electrophysiological properties, e.g., along the apico-basal direction in a heart, or between intermural layers [36] of the heart, or because of conduction inhomogeneities [37].

We investigate the effects of various intracellular (ion-channel conductances) and intercellular (gap-junctional factors) parameters on the spiral-wave frequency. At the single-cell level, we show how changes in ion-channel conductances modulate action-potential (AP) properties, such as its upstroke velocity ${\frac{dV}{dt}}_{max}$ and duration (APD). We then examine how these changes in AP properties affect the spiral-wave frequency ω at the tissue level. We find that an increase (decrease) in ${\frac{dV}{dt}}_{max}$ (APD) increases (decreases) ω. We then investigate the effects of intercellular coupling strength on ω by changing the coupling strength in the following two ways: a) by modifying the diffusion constant D of the medium; b) by interspersing inexcitable point obstacles in the medium, thereby reducing the effective number of neighboring myocytes. We find that ω is unaffected by a change in D, but, with point obstacles, ω decreases with an increase in the density of these obstacles. We examine two models for fibrosis, which occurs in diseased hearts and is usually accompanied by a proliferation of fibroblasts [38–42]. These models allow us to study how various fibroblast parameters, e.g., the fibroblast-myocyte coupling and the AP of the coupled myocyte, affect ω and spiral-wave dynamics; the fibroblast parameters include its resting potential and the number of fibroblasts coupled to a myocyte. Moreover, we show that a spiral in a medium with a heterogeneous distribution of fibroblasts, drifts towards the region with a high density of fibrolasts.

The paper is organized as follows. The Materials and Methods Section 2 contains (a) the details of the myocyte and tissue models that we use in our simulations and (b) the numerical techniques we use to solve the governing equations. We then provide the findings of our study in Section 3 on Results. Finally, in the Discussion, Section 4, we discuss our results in the light of other past studies and mention some of the limitations in our study.

2 Materials and Methods

2.1 Model

For myocytes we use the TP06 human-ventricular-cell model [43], in which the transmembrane potential V_m of an isolated myocyte is governed by the following ordinary differential equation (ODE):

$\begin{array}{ccc}\hfill \frac{d{V}_m}{dt}& =\hfill & -\frac{I_{ion}}{C_m};\hfill \\ \hfill I_{ion}& =\hfill & \sum _i{I}_i;\hfill \end{array}(1)$

I_ion is the sum of all the ion-channel currents with I_i the ith ion-channel current, and C_m the normalized transmembrane capacitance. In Table 1 we list the currents in the TP06 model; their dependence on V_m is given, e.g., in Ref. 43.

TABLE 1

TABLE 1. The various ionic currents in the TP06 model [43].The details of the ion-channel and ion-pump equations for the currents and the parameter values that we use for the TP06 model are given in the Supplementary Material.

The spatiotemporal evolution of V_m in mathematical models for cardiac tissue is governed by the following reaction-diffusion partial differential equation (PDE):

$\frac{\partial V_m}{\partial t}=D{\nabla }^{2}V-\frac{I_{ion}}{C_m};(2)$

D is the diffusion coefficient; we restrict ourselves to a scalar D for simplicity; the TP06 case is described in detail in Ref. 43. It is convenient to use the following non-dimensionalised ion-channel conductances and diffusion coefficients:

$S_G=\frac{G}{G_c};S_D=\frac{D}{D_0},(3)$

where G stands for a typical conductance, G_c is the control value of the conductance, and the control diffusion constant D₀ = 0.001 54 cm²/ms; for the conductances we consider, G_c = 14.838, 0.000 039 8, 0.153 nS/pF for G_Na, G_CaL, and G_Kr, respectively.

We use the following two models for the fibroblast cells:

• Model-I: We model the fibroblast cells as inexcitable obstacles and we replace the myocytes at random with these inexcitable obstacles throughout our simulation domain such that the percentage of sites with obstacles is p_o. The gap-junctional current between the myocyte and inexcitable obstacles in this model is zero (see Refs. 37, 44).

• Model-II: We model the fibroblasts in our study as an electrically passive cells, as in Ref. 45. Each myocyte is coupled to N_f fibroblasts; and the myocyte and fibroblast transmembrane potentials V_m and V_f, respectively, obey the following coupled ODEs:

$\begin{array}{ccc}\hfill \frac{d{V}_m}{dt}& =\hfill & -\left(\frac{I_{ion}}{C_m}+N_f\times \frac{I_{gap}}{C_m}\right);\hfill \\ \hfill \frac{d{V}_f}{dt}& =\hfill & \frac{\left(I_{gap}-I_f\right)}{C_f};\hfill \\ \hfill I_f& =\hfill & G_f\left(V_f-E_f\right);\hfill \\ \hfill I_{gap}& =\hfill & G_{gap}\left(V_m-V_f\right).\hfill \end{array}(4)$

C_f, E_f, and G_gap are the membrane capacitance of a fibroblast, the fibroblast resting potential, and the fibroblast-myocyte gap-junctional coupling, respectively. We use a bilayer model for fibroblast-myocyte couplings: fibroblasts, in the top layer, are coupled to myocytes in the bottom layer, as in Ref. 16, which contains a schematic diagram of this bilayer and the PDEs that describe the spatiotemporal evolution of waves of activation in this model; we do not include fibroblast-fibroblast couplings. Moreover, when we consider a heterogeneous distribution of fibroblasts in Section 3.4, we first consider a homogeneous region in which each myocyte is coupled to N_f fibrloblasts, which are in a layer above the myocyte cell layer as described in detail in Ref. 16. Now we introduce heterogeneity, which results in a gradient in the density of fibroblasts, we removing all the N_f fibroblasts that are coupled to a myocyte at a site, so that the percentage of myocyte cells, at which we retain the myocyte-fiboblast coupling, is p_f. To study gradients in the density of fibroblasts, we use a space-dependent density that varies linearly as we move away from chosen central site:

$p_f\left(r_i\right)=p_f\left(r_0\right)-\frac{\left[p_f\left(r_0\right)-p_f\left(r_{max}\right)\right]}{\left[r_{max}-r_0\right]}\times r_i,(5)$

where r_i is the distance from the centre, r₀ is the position of the centre, and r_max is maximum radial distance from the centre.

2.2 Numerical Methods

We update the ODEs via the forward-Euler method for Eqs 1, 4. For our two-dimensional (2D) tissue simulations as in Eq. 2 we use a square domain with N × N grid points with N = 512, the forward-Euler scheme for time marching, and a central-difference scheme with a five-point stencil for the Laplacian, with the time and space steps Δt = 0.02 ms and Δx = 0.025 cm, respectively. The control value of the diffusion coefficient D = D₀, with D₀ = 0.001 54 cm²/ms, which gives us a conduction velocity CV ≃ 70 cm/s, as has been reported for human-ventricular-tissue models [43, 46].

2.3 Data Aquisition

• We generate a spiral wave by the cross-field protocol; we pass a traveling plane wave (S1) from one end of the domain; and when the wave back of S1 reaches the middle of the domain, we pass another plane wave (S2) perpendicular to S1; when the wavefront of S2 meets the wave back of S1, a phase singularity is created at the junction; this creates a spiral wave [see Supplementary Figure S1].

• We calculate the frequency ω by recording the time-series of the transmembrane potential V_m at four representative positions in the simulation domain. From the principal peak in the Fourier transforms of these time series, we obtain ω (we take the average of the values at the four representative positions). [We show in Supplementary Table S1] that this frequency is within error bars of the frequency ω_tip of rotation of the tip of the spiral wave.]

• For the radius of the tip trajectory of rigidly rotating spiral waves, which is, on average, circular, we fit the average trajectory to a circle with radius r and center (x_c, y_c), by using a nonlinear regression model, to obtain the mean radius and the mean values of the coordinates of the center of the circle; we also calculate the standard deviation of the fluctuations in r by using the mean position of the center (x_c, y_c) and the coordinates (x, y) of the points that lie on the unaveraged tip trajectory that we compute.

• We calculate CV by pacing the simulation domain at one end with a pacing cycle length of 1 Hz; we use 20 pulses. We record the time series of V_m at two designated grid points A and B, which are separated by a distance l_AB. These grid points are chosen such that the line between the two grid points is normal to the wavefront. We obtain the times t_A and t_B at which the wavefront hits the grid points A and B, respectively; the difference t_B − t_A gives the time taken by the wavefront to propagate A to B; therefore, CV $=\frac{l_{AB}}{(t_B-t_A)}$. In the disordered case, with inexcitable obstacles distributed at random in the simulation domain, we record the time series of V_m at multiple points and repeat the above procedure; we then take the mean of the CVs obtained from these points; we also compute the standard deviation of the CVs (see Supplementary Table S2).

3 Results

We present the results of our in-silico studies as follows: In Section 3.1 we examine the dependence of the AP and of ω on various ion-channel conductances. Section 3.2 is devoted to the effects of the gap-junctional coupling on ω. In Section 3.3 we investigate the effects of the fibroblast-myocyte coupling on the myocyte AP and ω. We elucidate the drift of spiral waves in domains with an inhomogeneous distribution of fibroblasts in Section 3.4.

3.1 Effects of Conductances on the AP and the Spiral-Wave Frequency ω

The cell membrane of a myocyte is embedded with various ion channels, which we list in Table 1; V_m depends on the currents through these ion channels (Eq. 1), so, if we vary the conductances of these channels, we can modulate the AP of the myocyte. To study the effects of these ion channels on the AP, we choose three representative major ionic currents for our study: I_Na, I_CaL, and I_Kr. Figure 1A shows the APs of a myocyte for control values (magenta) and for the cases where the conductances G_Na (black), G_CaL (blue), and G_Kr (red) are increased three-fold. We find that increasing G_CaL (G_Kr) increases (decreases) the APD, whereas G_Na has no significant effect on the APD (Figure 1B). This is because the inward current I_CaL augments depolarization, and I_Kr, being an outward current, enhances repolarization; although I_Na is an inward current, it is active only during the early upstroke phase of the AP, therefore, it cannot affect the APD siginificantly. Futhermore, we find that increasing G_Na increases the upstroke velocity ${\frac{dV}{dt}}_{max}$, but G_CaL and G_Kr do not affect on ${\frac{dV}{dt}}_{max}$ (Figure 1). We have also checked the effects of other ion-channel conductances and ion-pump parameters on the AP. The results are consistent with our findings above, namely, increasing (decreasing) the conductances of inward (outward) currents increases (increases) the APD of the myocyte; and I_Na is the only current that can change the value of ${\frac{dV}{dt}}_{max}$. We give details in Supplementary Figure S1.

FIGURE 1

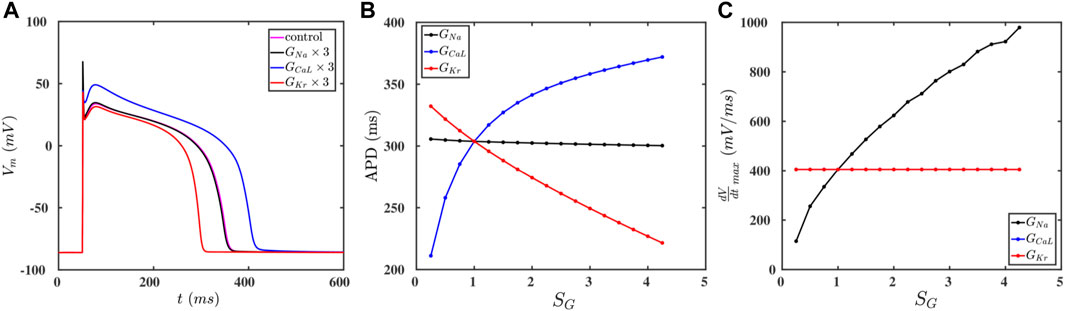
FIGURE 1. (A) Action-potential plots for the control paramater set (magenta) and the cases when the conductances G_Na (black), G_CaL (blue), and G_Kr (red) are increased by a factor of three relative to their control values. (B,C): Plots of the APD and ${\frac{dV}{dt}}_{max}$, respectively, versus S_G, the non-dimensionalized conductance (Eq. 3).

We now study how these changes in ${\frac{dV}{dt}}_{max}$ and the APD affect the dynamics of a spiral wave. In Figure 2A we show spiral-tip trajectories and how the radius r, of the averaged circular trajectory, varies with the three conductances G_CaL (blue), G_Na (black), and G_Kr (red); the columns are labelled by the values of S_G (Eq. 3), which multiply only the conductance that labels a row (all other conductances are held at their control values as we move along a row in Figure 2A). In Figures 2B–D we give plots versus S_G of, respectively, r, CV, and ω, for all these three conductances. In particular, we find that ω increases if we increase the values of G_Na and G_Kr; by contrast, ω decreases as we increase G_CaL. This is consistent with the variation of r and of CV with S_G (Figures 2B,C), for ω is related to r and CV as in Eq. 6.

$\omega \propto \frac{\text{CV}}{2\pi r}(6)$

FIGURE 2

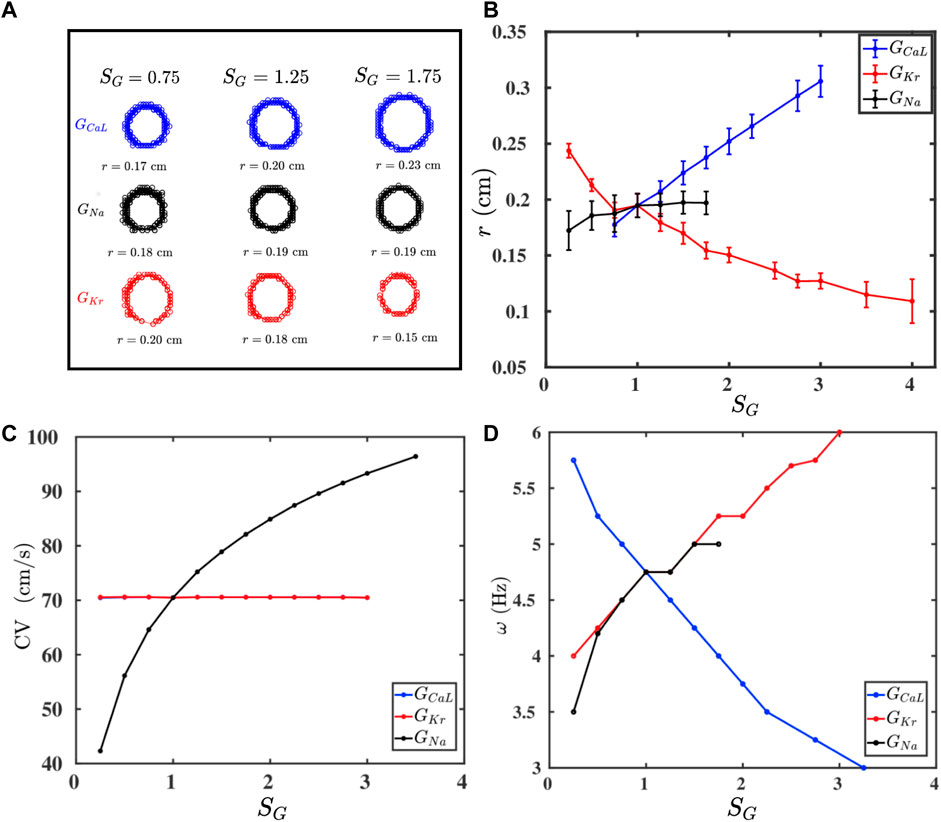
FIGURE 2. (A) Traces of the tip trajectories of a spiral for different values of conductances of three ion channels: G_CaL (blue), G_Na (black), and G_Kr (red); the columns indicate S_G (Eq. 3), which multiplies only the conductance that labels a row (all other conductances are held at their control values as we move along a row). (B–D): Plots versus S_G of, respectively, r, CV, and ω (see text), for all these three conductances; one-standard-deviation error bars are shown for r.

If we raise the values of G_CaL and G_Kr, then we find an increase and decrease the spiral core radius r, respectively, whereas G_Na has no significant effect on the value of r (Figure 2B). Furthermore, Figure 2C shows that CV increases with G_Na, whereas G_CaL and G_Kr do not affect CV; this is because only G_Na affects the value of ${\frac{dV}{dt}}_{max}$ (Figure 1C), which determines how fast a myocyte is excited and, therefore, how rapidly a wave of excitation propagates through our cardiac-tissue model. This result, along with Figure 1B, implies that the change in the APD is associated with the change in the value of r; a large (small) value of the APD is associated with a large (small) value of r; and conductances such as G_Na have no significant effect on the APD because they do not affect r substantially. We have also checked this correlation between the APD and r for other conductances (see Supplementary Figure S2) and have found similar results. In summary, the rise of ω with the increase of G_Na is primarily because of the increase in CV, and the decline (rise) of ω, with the increase of G_CaL (G_Kr), can be attributed principally because to the increase (decrease) in r.

3.2 Effect of the Gap-Junctional Coupling on ω

The strength of the gap-junctional coupling between the cells in cardiac tissue can change in diseased conditions, e.g., in the wake of a myocardial infarction [47–49]. It is, therefore, instructive to investigate the role of the diffusive coupling betwen the cells on spiral-wave dynamics. To study the effect of D on ω, we first plot, in Figure 3A, r (blue curve) and CV (red curve) versus S_D, the non-dimensionalised diffusion constant in Eq. 3; this shows that both r and CV increase with S_D, because a high diffusive coupling enhances the propagation of waves. The increase in CV is offset by the increase in r, so ω (see Eq. 6) does not depend on S_D significantly, as we show in Figure 3B.

FIGURE 3

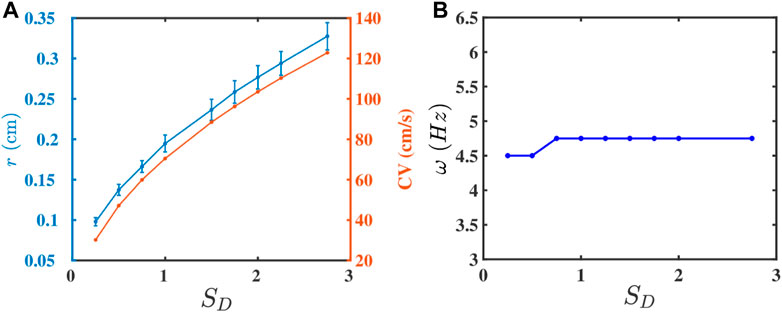
FIGURE 3. Plots versus S_D (Eq. 3) of (A) r (blue curve) and CV (red curve) and (B) ω.

We can also reduce the effective coupling strength between the cells in the medium by interspersing the medium with inexcitable point obstacles. These obstacles mimic collagen deposits in fibrotic tissue [38, 50]. The random distribution of these obstacles disrupts the propagation of a wave, as we show by the pseudocolor plots of V_m in Figure 4A; and it reduces the velocity of the wave [37, 44, 47]. In Figure 4B we plot CV versus p_o; clearly, CV decreases as the obstacle density p_o increases; and beyond p_o ≃ 38%, we observe conduction block with CV = 0. This result is consistent with the earlier study in Ref. 51. This reduction in CV, with the increase of p_o, contributes to the decline of ω with increasing p_o, which we depict by the plot in Figure 4C. Futhermore, because of the disorder-induced corrugated wavefront (Figure 4A), it becomes difficult to track the spiral-tip trajectory for p_o > 10%; for p_o < 10%, the value of r remains unaltered (see Supplementary Figure S3). Nonetheless, the simultaneous decrease of ω and CV, as we increase p_o, tells us that the change in CV is responsible principally for the variation of ω.

FIGURE 4

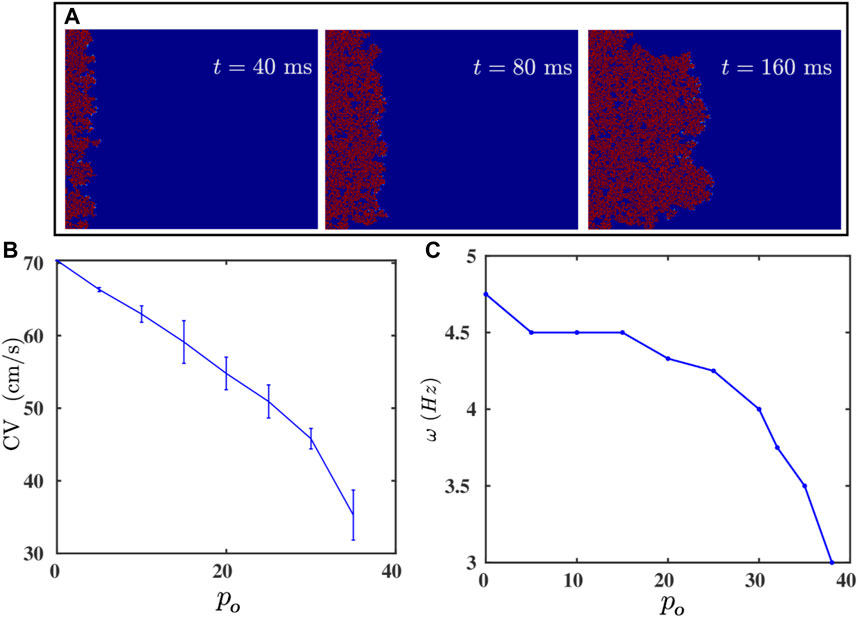
FIGURE 4. (A) Pseudocolor plots of V_m illustrating the propagation of a plane wave through the simulation domain with randomly distributed inexcitable obstacles (Model-I); the obstacle density p_o = 35%. (B,C): Plots versus p_o of the plane-wave conduction velocity CV and the spiral-wave frequency ω. CV vanishes after p_o ≥ 38%; i.e., there is conduction block.

3.3 Effect of the Fibroblast-Myocyte Coupling on AP Properties and ω

Fibroblast cells, which maintain the structural integrity of a heart, are known to (a) proliferate in diseased conditions [38, 39] and (b) form gap-junctional couplings with myocytes. Such couplings can modulate the electrophysiological properties, e.g., of the AP, of the myocytes [45, 52, 53]. We show in Figures 5A,B, how the fibroblast-myocyte coupling affects the AP morphology, APD, and ${\frac{dV}{dt}}_{max}$ for different values of fibroblast resting potential E_f and the number N_f of fibroblasts coupled to a myocyte in Model-II. We see that the APD and ${\frac{dV}{dt}}_{max}$ increase and decrease, respectively, as we increase E_f. For a fixed value of E_f, increasing N_f decreases both APD and ${\frac{dV}{dt}}_{max}$. This is because fibroblasts act as current sinks when coupled to myocytes. These changes in the properties of the AP, because of the fibroblast-myocyte coupling, affect the dynamics of wave at the tissue level. We show in Figure 5C that the rise in the APD and the decline in ${\frac{dV}{dt}}_{max}$ (Figure 5B) increases and decreases the values of r and CV, respectively, as we increase E_f. In Figure 5D we show how the combination of these effects on CV and r affect the variation of ω with E_f and N_f.

FIGURE 5

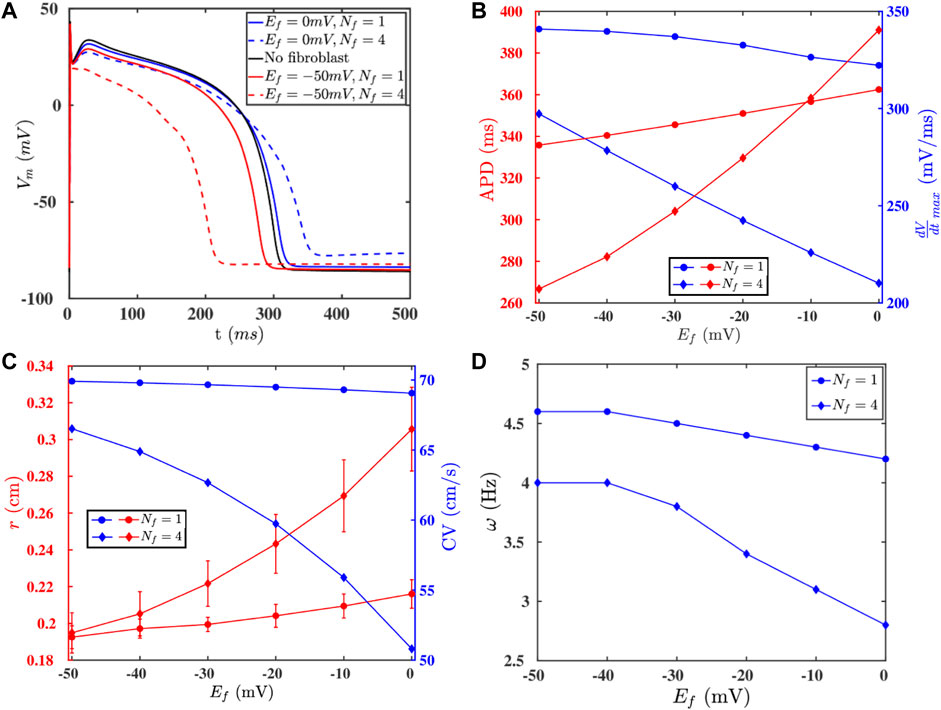
FIGURE 5. (A) APs of an isolated myocyte (black -) and a myocyte coupled to fibroblasts with various paramters: E_f = 0 mV, N_f = 1 (blue -); E_f = 0 mV, N_f = 4 (blue - -); E_f = −50 mV, N_f = 1 (red -); E_f = −50 mV, N_f = 4 (red - -). (B) The values of the APD and ${\frac{dV}{dt}}_{max}$ for different values of E_f and two different values of N_f. (C) The values of r and CV for different values of E_f and two different values of N_f. (D) The varition of ω with changes in E_f for two different values of N_f.

3.4 Drift of Spiral Waves in Domains With an Inhomogeneous Distribution of Fibroblasts

Fibrosis is a natural wound-healing process that occurs in the heart after a patient suffers from a condition such as infarction or heart attack [40–42], and such fibrotic tissue can affect the propagation of excitation waves [14, 37, 47, 48, 54, 55], which can promote arrhythmias. We now show how a heterogeneous density of fibroblasts in the medium (Model-II) can affect the dynamics of a spiral wave. Figure 6A shows the heterogeneous distribution of fibroblasts in the medium; here, yellow indicates fibroblast-myocyte composites and blue indicates myocytes. The density of fibroblasts decreases radially outwards from the centre that is marked by a red octagram in Figure 6A (Section 2; Eq. 5). Figure 6B shows the spatial variation of the APD in the medium because of the heterogeneous fibroblast density. Figures 6C,D show the spatiotemporal evolution of a spiral in this case. It shows that a spiral, initiated at the left side of the domain in the region with a low density of fibroblasts, drifts towards the region with a high density of fibroblasts; and the spiral remains anchored to the central region, where the fibroblast density is maximum. The trajectory of the spiral tip is shown in white in Figure 6D (see also the Supplementary Movie M1). In Figure 6D, we have shown the drift data up until a simulation duration of t = 60 s. The spiral indeed goes near to the red star (highest fibrotic density region shown in Figure 6A), anchors to it, and becomes stable (at t = 114 s); and the spiral does not meander after anchoring. This can be observed in the Supplementary Movie M1 provided in the Supplementary Material. This drifting of a spiral towards the region with a high density of fibroblasts is associated with the tendency of the spiral wave to drift towards the region with the highest value of the APD [33, 34, 56–58]. Such anchoring of a spiral wave to a region with a high density of fibrosis has been seen in experiments on real hearts [23, 28, 59–61]. Our study illustrates how a region with a high density of fibroblasts can behave like an attractor and an anchoring point for spiral waves in fibrotic tissue. Such drifting of a spiral wave, in a medium with heterogeneity, has also been reported in other studies in contexts other than fibrosis [33, 34, 56–58].

FIGURE 6

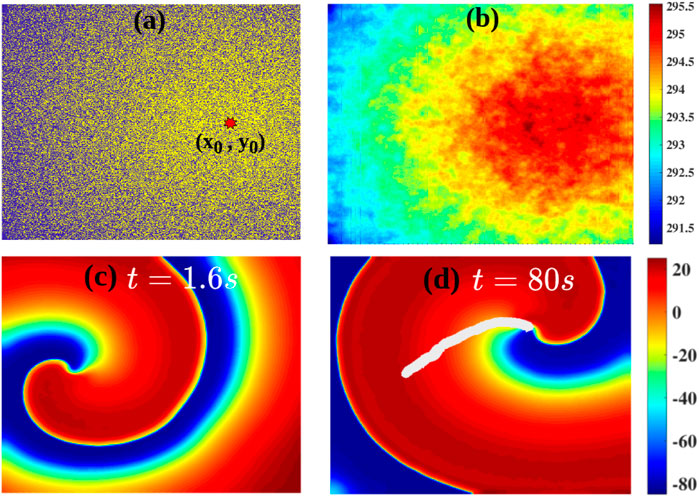
FIGURE 6. (A) The radially decreasing distribution of the fibroblast density (Model-II Eq. 5) away from a center, marked by a red octagram; yellow indicates fibroblast-myocyte composites and blue denoted myocytes. (B) The distribution of the APD because of the gradient in fibroblast density. (C,D): Pseudocolor plots of V_m showing a spiral wave in the simulation domain: a spiral initiated in the small-APD region, proximal to the left boudary, drifts towards the large-APD (low-ω) region. The tip trajectory of the spiral is marked by the white line.

4 Discussion

We have used in silico simulations of detailed mathematical models for cardiac tissue to examine the effects of various electrophysiological parameters of a cardiac cell and cardiac tissue on the AP properties and on electrical-wave dynamics. Our work is of relevance when spiral waves are formed in real hearts where their are gradients in electrophysiological parameters along the transmural [36, 62, 63] and the apico-basal [64, 65] directions. Moreover, heterogeneities can be also be induced in the heart because of diseases [64, 66–68]. In this context, we have shown how changes in various ion-channel conductances of a myocyte or the fibroblast-myocyte coupling can modulate the AP of a myocyte. We have then checked how these changes affect the spiral-wave frequency ω. We find that an increase (decrease) in ${\frac{dV}{dt}}_{max}$ or decrease (increase) in the APD increases (decreases) ω: large values of ${\frac{dV}{dt}}_{max}$ increase CV; and a low APD is associated with low values of the mean spiral-tip-trajectory radius r; these are related to ω through Eq. 6. Our study has provided a natural understanding of how changes in the AP, at the single-myocyte level, can be related to changes in ω at the cardiac-tissue level. Moreover, we have investigated how changes in the gap-junctional coupling between the cells and S_D affect ω. We have also reduced the effective coupling between the cells by interspersing the medium with inexcitable obstacles; ω changes with the density of the obstacles. It is of interest to investigate such effects on ω, because they provide insights into spiral-wave dynamics in excitable media with heterogeneities [68]. We illustrate this in detail in Figure 6 for a simulation domain with a heterogeneous distribution of fibroblast; here, we demonstrate the drift of a spiral wave towards the region with a high density of fibroblasts; such a drift has been seen in real hearts [23, 59–61].

We have explored the validity of the frequency relation Eq. 6 (Ref. 15) for a wide range of electrophysiological parameters in the models that we use. We show in Supplementary Figure S1 that our measurements of ω and $\frac{\text{CV}}{r}$ are consistent with a linear relation (see the fit that is indicated by a black line); at very low values of CV, e.g., near conduction block in Model-I which accounts for fibrosis-induced disorder, this linear relation breaks down. The randomness in these models introduces errors in the determination of r of the spiral wave, especially for large randomness; e.g., as we increase p_f, we observe, in Supplementary Figure S6 that the tip trajectory of the spiral wave becomes very noisy. Note also that the CV of a plane wave is distinct from CV_tip the velocity of the tip of the spiral wave as it goes around its trajectory (on average a circle with radius r); clearly, ω_tip = CV_tip/(2πr) (see Supplementary Table S1).

Some earlier studies have investigated the properties of spiral waves in two-variable mathematical models for cardiac [69–75]. However, such studies have been conducted in the weak- or strong-excitability limits; real cardiac tissue exhibits various degrees of excitability depending on different electrophysiological parameters. Our study, which employs electrophysiologically detailed mathematical models for cardiac tissue, has allowed us to study spiral-wave dynamics with greater realism than is possible with two-variable models for cardiac tissue. The drifting of a spiral wave towards regions with a large APD has been reported in contexts other than fibrosis [33, 34, 56–58]. Moreover, anomalous drift of a spiral towards a region with a small APD, which has been observed in generic models [34], is not seen in our study; and it is yet to be reported in any of the electrophysiologically-detailed mathematical models for the cardiac tissue. It is also observed in the two-variable models that the radius of the spiral tip trajectory is very large, in the weakly excitable limit, compared to what is observed in the strongly excitable limit [72, 76].

In our realistic models, if we consider two parameters that control excitability, e.g., G_Na and D, then we observe that r does not increase with a decrease in the value of G_Na (Figure 2); but we observe an increase in r, as we increase the value of D (see Supplementary Figure S5. Hence, our systematic study, which uses a detailed human-ventricular-tissue mathematical model, provides an important point of reference for future in silico and experimental studies of such spiral waves in cardiac tissue.

For the study of spiral-wave dynamics in the fibrosis, we have considered two types of models for fibrosis: (a) Model-I and (b) Model-II (Section 2). With these models we have investigated the following: The change of ω in (i) Model-I and (ii) Model-II as we change fibrosis parameters such as p_o (in Model-I) and N_f and E_f (in Model-II). (iii) In Model-II we show that ω decreases with an increase in N_f in homogeneous fibrotic tissue. Furthermore, we consider a heterogeneous model, based on Model-II, in which the fibroblast density P_f (number density of myocyte cells coupled to N_f fibroblast cells at a site) is highest at a central site and decreases outwards from this center. We find that a spiral wave, initiated far away from the center where P_f is low, drifts towards the region with the highest fibroblast density, i.e., the center, which has the lowest ω. There are earlier studies in this direction such as in Refs. 77, 78 that uses Model-I type fibrosis. The study of Ref. 77, induces spiral waves by a bursting or pacing mechanism and investigates the dependence of ω on the fibrosis density (Model of type I). This study shows that ω is dependent on the maximal local fibrosis density. The study in Ref. 78, considers a local fibrotic region (Model-I type) and studies the anchoring of a spiral wave initiated far from this region. The mechanism of anchoring here involves the breaking up of the spiral waves around the fibrotic tissue and a consequent alteration of the initial spiral wave; this is eventually driven near to the fibrotic tissue and is then anchored around it. However, our study investigates the drift of the spiral wave in Model-II and shows the experimentally observed drift of spiral waves towards the region of highest fibroblast density. Also, our gradient in the fibroblast density based on Model-II, in contrast to that of Refs. 77, 78, uses a continuous gradient in the fibroblast density and, in addition, with fibroblasts that are treated as passive, but electrically active, cells. We note that, multiple studies have shown that fibroblast cells are electrically active, especially in the context of infarction (see, e.g., Refs. 14, 49, 53, 79, 80). Such fibroblasts are used in our Model-II but not in the studies mentioned in Refs. 77, 78. Thus, our work extends considerably these earlier studies.

4.1 Limitations of Our Study

We end our discussion with some limitations in our study. We have used a monodomain model for cardiac tissue. Bidomain models of cardiac tissue account for the extracellular matrix. However, monodomain models have been proved to be good approximations of cardiac tissue for wave propagation [81] for the types of excitations we consider. Furthermore, our tissue model does not incorporate the effects of mechanical deformations, stretch-activated channels, and stress-dependent diffusion tensors [82–84]. Such deformations can affect the dynamics of spiral waves [85] and the drift of spirals in a heterogeneous medium; we defer an investigation of the interplay between deformation and drift for future work.

Data Availability Statement

The equations of the ionic currents, ion-dynamics and the parameter values used in the TP06 model required to reproduce our simulations are been provided in the data sheet 2 file.

Author Contributions

MKM and SZ designed the problem; MKM performed the numerical simulations; MKM together with SZ and RP, did the analysis; MKM, SZ and RP wrote the manuscript.

Funding

We thank SERB (India) JC Bose fellowship grant no: SR/S2/JCB-17/2007 and the National Supercomputing Mission (NSM-India) grant no: DST/NSM/HPC_Applications/2021-1500, and CSIR (India) for the financial support and the Supercomputer Education and Research Centre (SERC, IISc) for computational resources.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.819873/full#supplementary-material

Data Sheet 1 | We provide the additional details of our simulations in this file.

Data Sheet 2 | The normal parameter values and the equations for the 12 currents and ion-dynamics of the TP06 model is provided in this file.

Movie-M1 | This movie shows the drift of the spiral waves in the gradient of the fibroblast density.

References

1. Zaikin AN, Zhabotinsky AM. Concentration Wave Propagation in Two-Dimensional Liquid-phase Self-Oscillating System. Nature (1970) 225(5232):535–7. doi:10.1038/225535b0

CrossRef Full Text | Google Scholar

2. Winfree AT. Spiral Waves of Chemical Activity. Science (1972) 175(4022):634–6. doi:10.1126/science.175.4022.634

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Field RJ. Chaos in Chemistry and Biochemistry. Singapore: World Scientific (1993).

Google Scholar

4. Ott E. Chaos in Dynamical Systems. Cambridge, United Kingdom: Cambridge University Press (2002).

Google Scholar

5. Strogatz SH. Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering. Boca Raton, FL: CRC Press (2018).

Google Scholar

6. Falcke M, Bär M, Engel H, Eiswirth M. Traveling Waves in the CO Oxidation on Pt(110): Theory. J Chem Phys (1992) 97(6):4555–63. doi:10.1063/1.463900

CrossRef Full Text | Google Scholar

7. Imbihl R, Ertl G. Oscillatory Kinetics in Heterogeneous Catalysis. Chem Rev (1995) 95(3):697–733. doi:10.1021/cr00035a012

CrossRef Full Text | Google Scholar

8. Pande A, Pandit R. Spatiotemporal Chaos in a Model for Co Oxidation on Pt (110). In: 4th Meeting of the Royal-Society-Unilever-Indo-UK Forum in Materials Science and Engineering (1999).

Google Scholar

9. Lechleiter J, Girard S, Peralta E, Clapham D. Spiral Calcium Wave Propagation and Annihilation in xenopus Laevis Oocytes. Science (1991) 252(5002):123–6. doi:10.1126/science.2011747

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Tyson JJ, Murray JD. Cyclic Amp Waves During Aggregation of Dictyostelium Amoebae. Development (1989) 106(3):421–6. doi:10.1242/dev.106.3.421

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Rietdorf J, Siegert F, Weijer CJ. Analysis of Optical Density Wave Propagation and Cell Movement During Mound Formation in Dictyostelium discoideum. Developmental Biol (1996) 177(2):427–38. doi:10.1006/dbio.1996.0175

CrossRef Full Text | Google Scholar

12. Panfilov AV, Vasiev BN. Vortex Initiation in a Heterogeneous Excitable Medium. Physica D: Nonlinear Phenomena (1991) 49(1-2):107. doi:10.1016/0167-2789(91)90200-s

CrossRef Full Text | Google Scholar

13. Lim ZY, Maskara B, Aguel F, Emokpae R, Tung L. Spiral Wave Attachment to Millimeter-Sized Obstacles. Circulation (2006) 114(20):2113–21. doi:10.1161/circulationaha.105.598631

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Xie Y, Garfinkel A, Camelliti P, Kohl P, Weiss JN, Qu Z. Effects of Fibroblast-Myocyte Coupling on Cardiac Conduction and Vulnerability to Reentry: a Computational Study. Heart Rhythm (2009) 6(11):1641–9. doi:10.1016/j.hrthm.2009.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Qu Z, Hu G, Garfinkel A, Weiss JN. Nonlinear and Stochastic Dynamics in the Heart. Phys Rep (2014) 543(2):61–162. doi:10.1016/j.physrep.2014.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nayak AR, Shajahan TK, Panfilov AV, Pandit R. Spiral-wave Dynamics in a Mathematical Model of Human Ventricular Tissue with Myocytes and Fibroblasts. PloS one (2013) 8(9):e72950. doi:10.1371/journal.pone.0072950

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Nayak AR, Pandit R. Turbulent States and Their Transitions in Mathematical Models for Ventricular Tissue: The Effects of Random Interstitial Fibroblasts. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92(3):032720. doi:10.1103/PhysRevE.92.032720

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zimik S, Pandit R. Reentry via High-Frequency Pacing in a Mathematical Model for Human-Ventricular Cardiac Tissue With a Localized Fibrotic Region. Sci Rep (2017) 7(1):15350. doi:10.1038/s41598-017-15735-5

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Allessie MA, Bonke FI, Schopman FJ. Circus Movement in Rabbit Atrial Muscle as a Mechanism of Tachycardia. III. The "Leading Circle" Concept: a New Model of circus Movement in Cardiac Tissue Without the Involvement of an Anatomical Obstacle. Circ Res (1977) 41(1):9–18. doi:10.1161/01.res.41.1.9

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Gray RA, PertsovPertsov AM, Jalife J. Spatial and Temporal Organization During Cardiac Fibrillation. Nature (1998) 392(6671):75–8. doi:10.1038/32164

PubMed Abstract | CrossRef Full Text | Google Scholar

21. PertsovPertsov AM, Davidenko JM, Salomonsz R, Baxter WT, Jalife J. Spiral Waves of Excitation Underlie Reentrant Activity in Isolated Cardiac Muscle. Circ Res (1993) 72(3):631–50. doi:10.1161/01.res.72.3.631

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Davidenko JM, Kent PF, Chialvo DR, Michaels DC, Jalife J. Sustained Vortex-Like Waves in Normal Isolated Ventricular Muscle. Proc Natl Acad Sci (1990) 87(22):8785–9. doi:10.1073/pnas.87.22.8785

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Davidenko JM, PertsovPertsov AV, Salomonsz R, Baxter W, Jalife J. Stationary and Drifting Spiral Waves of Excitation in Isolated Cardiac Muscle. Nature (1992) 355(6358):349–51. doi:10.1038/355349a0

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Gray RA, Jalife J, Panfilov A, Baxter WT, Cabo C, Davidenko JM, et al. Nonstationary Vortexlike Reentrant Activity as a Mechanism of Polymorphic Ventricular Tachycardia in the Isolated Rabbit Heart. Circulation (1995) 91(9):2454–69. doi:10.1161/01.cir.91.9.2454

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bray M-A, Lin S-F, Wikswo J. Three-Dimensional Visualization of Phase Singularities on the Isolated Rabbit Heart. J Cardiovasc Electrophysiol (2002) 13(12):1311. doi:10.1046/j.1540-8167.2002.01311.x

CrossRef Full Text | Google Scholar

26. Valderrábano M, Chen PS, Lin SF. Spatial Distribution of Phase Singularities in Ventricular Fibrillation. Circulation (2003) 108(3):354–9. doi:10.1161/01.CIR.0000080322.67408.B4

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pandit SV, Jalife J. Rotors and the Dynamics of Cardiac Fibrillation. Circ Res (2013) 112(5):849–62. doi:10.1161/CIRCRESAHA.111.300158

PubMed Abstract | CrossRef Full Text | Google Scholar

28. ten Tusscher KH, Panfilov AV. Reentry in Heterogeneous Cardiac Tissue Described by the Luo-Rudy Ventricular Action Potential Model. Am J Physiol Heart Circ Physiol (2003) 284(2):H542–8. doi:10.1152/ajpheart.00608.2002

CrossRef Full Text | Google Scholar

29. Clayton RH, Bernus O, Cherry EM, Dierckx H, Fenton FH, Mirabella L, et al. Models of Cardiac Tissue Electrophysiology: Progress, Challenges and Open Questions. Prog Biophys Mol Biol (2011) 104(1):22–48. doi:10.1016/j.pbiomolbio.2010.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Alonso S, dos Santos RW, Bär M. Reentry and Ectopic Pacemakers Emerge in a Three-Dimensional Model for a Slab of Cardiac Tissue With Diffuse Microfibrosis Near the Percolation Threshold. PloS one (2016) 11(11):e0166972. doi:10.1371/journal.pone.0166972

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zimik S, Pandit R. Instability of Spiral and Scroll Waves in the Presence of a Gradient in the Fibroblast Density: the Effects of Fibroblast-Myocyte Coupling. New J Phys (2016) 18(12):123014. doi:10.1088/1367-2630/18/12/123014

CrossRef Full Text | Google Scholar

32. Zimik S, Pandit R, Majumder R. Anisotropic Shortening in the Wavelength of Electrical Waves Promotes Onset of Electrical Turbulence in Cardiac Tissue: An In Silico Study. Plos one (2020) 15(3):e0230214. doi:10.1371/journal.pone.0230214

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Krinsky V, Hamm E, Voignier V. Dense and Sparse Vortices in Excitable media Drift in Opposite Directions in Electric Field. Phys Rev Lett (1996) 76(20):3854–7. doi:10.1103/physrevlett.76.3854

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Sridhar S, Sinha S, PanfilovPanfilov AV. Anomalous Drift of Spiral Waves in Heterogeneous Excitable media. Phys Rev E Stat Nonlin Soft Matter Phys (2010) 82(5):051908. doi:10.1103/PhysRevE.82.051908

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Biktashev VN, BiktashevaBiktasheva IV, Sarvazyan NA. Evolution of Spiral and Scroll Waves of Excitation in a Mathematical Model of Ischaemic Border Zone. PLoS One (2011) 6(9):e24388. doi:10.1371/journal.pone.0024388

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wolk R, Cobbe SM, Hicks MN, Kane KA. Functional, Structural, and Dynamic Basis of Electrical Heterogeneity in Healthy and Diseased Cardiac Muscle Implications for Arrhythmogenesis and Anti-arrhythmic Drug Therapy. Pharmacol Ther (1999) 84(2):207–31. doi:10.1016/s0163-7258(99)00033-9

PubMed Abstract | CrossRef Full Text | Google Scholar

37. ten Tusscher KH, Alexander V. Wave Propagation in Excitable media with Randomly Distributed Obstacles. Multiscale Model Simulation (2005) 3(2):265–82. doi:10.1137/030602654

CrossRef Full Text | Google Scholar

38. Weber KT, Sun Y, Tyagi SC, Cleutjens JPM. Collagen Network of the Myocardium: Function, Structural Remodeling and Regulatory Mechanisms. J Mol Cell Cardiol (1994) 26(3):279–92. doi:10.1006/jmcc.1994.1036

CrossRef Full Text | Google Scholar

39. Manabe I, Shindo T, Nagai R. Gene Expression in Fibroblasts and Fibrosis. Circ Res (2002) 91(12):1103–13. doi:10.1161/01.res.0000046452.67724.b8

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gurtner GC, Werner S, Barrandon Y, Longaker MT. Wound Repair and Regeneration. Nature (2008) 453:314–21. doi:10.1038/nature07039

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Biernacka A, Frangogiannis NG. Aging and Cardiac Fibrosis. Aging Dis (2011) 2(2):158–73.

PubMed Abstract | Google Scholar

42. Hinderer S, Schenke-Layland K. Cardiac Fibrosis - A Short Review of Causes and Therapeutic Strategies. Adv Drug Deliv Rev (2019) 146:77–82. doi:10.1016/j.addr.2019.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

43. ten Tusscher KH, Panfilov AV. Alternans and Spiral Breakup in a Human Ventricular Tissue Model. Am J Physiol Heart Circ Physiol (2006) 291(3):H1088–100. doi:10.1152/ajpheart.00109.2006

CrossRef Full Text | Google Scholar

44. Majumder R, Nayak AR, Pandit R. Nonequilibrium Arrhythmic States and Transitions in a Mathematical Model for Diffuse Fibrosis in Human Cardiac Tissue. PLoS one (2012) 7(10):e45040. doi:10.1371/journal.pone.0045040

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Andrew MacCannell K, Bazzazi H, Chilton L, Shibukawa Y, Clark RB, Giles WR. A Mathematical Model of Electrotonic Interactions between Ventricular Myocytes and Fibroblasts. Biophysical J (2007) 92(11):4121–32. doi:10.1529/biophysj.106.101410

CrossRef Full Text | Google Scholar

46. ten Tusscher KH, Noble D, Noble PJ, Panfilov AV. A Model for Human Ventricular Tissue. Am J Physiol Heart Circ Physiol (2004) 286(4):H1573–89. doi:10.1152/ajpheart.00794.2003

CrossRef Full Text | Google Scholar

47. de Bakker JM, van Capelle FJ, Janse MJ, TasseronVermeulen S, Vermeulen JT, de JongeLahpor N, et al. Slow Conduction in the Infarcted Human Heart. 'Zigzag' Course of Activation. Circulation (1993) 88(3):915–26. doi:10.1161/01.cir.88.3.915

PubMed Abstract | CrossRef Full Text | Google Scholar

48. King JH, Huang CL, Fraser JA. Determinants of Myocardial Conduction Velocity: Implications for Arrhythmogenesis. Front Physiol (2013) 4:154. doi:10.3389/fphys.2013.00154

PubMed Abstract | CrossRef Full Text | Google Scholar

49. McDowell KS, Arevalo HJ, Maleckar MM, Trayanova NA. Susceptibility to Arrhythmia in the Infarcted Heart Depends on Myofibroblast Density. Biophysical J (2011) 101(6):1307–15. doi:10.1016/j.bpj.2011.08.009

CrossRef Full Text | Google Scholar

50. Spach MS, Boineau JP. Microfibrosis Produces Electrical Load Variations Due to Loss of Side-To-Side Cell Connections; a Major Mechanism of Structural Heart Disease Arrhythmias. Pacing Clin Electro (1997) 20(2):397–413. doi:10.1111/j.1540-8159.1997.tb06199.x

CrossRef Full Text | Google Scholar

51. Vigmond E, Pashaei A, Amraoui S, Cochet H, Hassaguerre M. Percolation as a Mechanism to Explain Atrial Fractionated Electrograms and Reentry in a Fibrosis Model Based on Imaging Data. Heart rhythm (2016) 13(7):1536–43. doi:10.1016/j.hrthm.2016.03.019

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Jacquemet V, Henriquez CS. Modelling Cardiac Fibroblasts: Interactions with Myocytes and Their Impact on Impulse Propagation. Europace (2007) 9 Suppl 6(Suppl. l_6):vi29–37. doi:10.1093/europace/eum207

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Zlochiver S, Muñoz V, Vikstrom KL, Taffet SM, Berenfeld O, Jalife J. Electrotonic Myofibroblast-To-Myocyte Coupling Increases Propensity to Reentrant Arrhythmias in Two-Dimensional Cardiac Monolayers. Biophysical J (2008) 95(9):4469–80. doi:10.1529/biophysj.108.136473

CrossRef Full Text | Google Scholar

54. Kawara T, Derksen R, de GrootGroot JR, Coronel R, Tasseron S, Linnenbank AC, et al. Activation Delay after Premature Stimulation in Chronically Diseased Human Myocardium Relates to the Architecture of Interstitial Fibrosis. Circulation (2001) 104(25):3069–75. doi:10.1161/hc5001.100833

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Morgan R, Colman MA, Chubb H, Seemann G, AslanidiAslanidi OV. Slow Conduction in the Border Zones of Patchy Fibrosis Stabilizes the Drivers for Atrial Fibrillation: Insights From Multi-Scale Human Atrial Modeling. Front Physiol (2016) 7:474. doi:10.3389/fphys.2016.00474

PubMed Abstract | CrossRef Full Text | Google Scholar

56. An R, Alexander P. Drift and Interaction of Vortices in Two-Dimensional Heterogeneous Active Medium. Studia Biophys (1983) 98(3):183–8.

Google Scholar

57. Qu Z, Weiss JN. Effects of Na+ and K+ Channel Blockade on Vulnerability to and Termination of Fibrillation in Simulated Normal Cardiac Tissue. Am J Physiology-Heart Circulatory Physiol (2005) 289(4):H1692–H1701. doi:10.1152/ajpheart.00241.2005

CrossRef Full Text | Google Scholar

58. Berenfeld O. The Major Role of Ik1 in Mechanisms of Rotor Drift in the Atria: A Computational Study. Clin Med Insights Cardiol (2016) 10:71–9. doi:10.4137/CMC.S39773

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Fast VG, Pertsov AM. Drift of Vortex in the Myocardium. Biofizika (1990) 35(3):478–82.

PubMed Abstract | Google Scholar

60. Jalife J, Gray R. Drifting Vortices of Electrical Waves Underlie Ventricular Fibrillation in the Rabbit Heart. Acta Physiol Scand (1996) 157(2):123–32. doi:10.1046/j.1365-201x.1996.505249000.x

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Roney CH, BayerBayer JD, Zahid S, Meo M, Boyle PMJ, Trayanova NA, et al. Modelling Methodology of Atrial Fibrosis Affects Rotor Dynamics and Electrograms. EP Europace (2016) 18(Suppl. l_4):iv146–iv155. doi:10.1093/europace/euw365

CrossRef Full Text | Google Scholar

62. Antzelevitch C, Fish J. Electrical Heterogeneity Within the Ventricular wall. Basic Res Cardiol (2001) 96(6):517–27. doi:10.1007/s003950170002

PubMed Abstract | CrossRef Full Text | Google Scholar

63. McCrossan ZA, illeter R, White E. Transmural Changes in Size, Contractile and Electrical Properties of Shr Left Ventricular Myocytes During Compensated Hypertrophy. Cardiovasc Res (2004) 63(2):283–92. doi:10.1016/j.cardiores.2004.04.013

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Burton F, Cobbe SM. Dispersion of Ventricular Repolarization and Refractory Period. Cardiovasc Res (2001) 50(1):10–23. doi:10.1016/s0008-6363(01)00197-3

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Szentadrassy N, Banyasz T, Biro T, Szabo G, Toth B, Magyar J, et al. Apico?basal Inhomogeneity in Distribution of Ion Channels in Canine and Human Ventricular Myocardium. Cardiovasc Res (2005) 65(4):851–60. doi:10.1016/j.cardiores.2004.11.022

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Viswanathan PC, Rudy Y. Cellular Arrhythmogenic Effects of Congenital and Acquired Long-Qt Syndrome in the Heterogeneous Myocardium. Circulation (2000) 101(10):1192–8. doi:10.1161/01.cir.101.10.1192

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Schmidt A, Azevedo CF, Cheng A, Gupta SN, Bluemke DA, FooFoo TK, et al. Infarct Tissue Heterogeneity by Magnetic Resonance Imaging Identifies Enhanced Cardiac Arrhythmia Susceptibility in Patients with Left Ventricular Dysfunction. Circulation (2006) 115(15):2006–14. doi:10.1161/CIRCULATIONAHA.106.653568

CrossRef Full Text | Google Scholar

68. Antzelevitch C. Heterogeneity and Cardiac Arrhythmias: an Overview. Heart Rhythm (2007) 4:964. doi:10.1016/j.hrthm.2007.03.036

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Mikhailov AS, Krinsky VI. Rotating Spiral Waves in Excitable media: the Analytical Results. Physica D: Nonlinear Phenomena (1983) 9(3):346–71. doi:10.1016/0167-2789(83)90277-4

CrossRef Full Text | Google Scholar

70. Winfree AT. Varieties of Spiral Wave Behavior: An Experimentalist's Approach to the Theory of Excitable media. Chaos (1991) 1(3):303–34. doi:10.1063/1.165844

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Mikhailov AS, Davydov VA, Zykov VS. Complex Dynamics of Spiral Waves and Motion of Curves. Physica D: Nonlinear Phenomena (1994) 70(1-2):1–39. doi:10.1016/0167-2789(94)90054-x

CrossRef Full Text | Google Scholar

72. Hakim V, Karma A. Theory of Spiral Wave Dynamics in Weakly Excitable media: Asymptotic Reduction to a Kinematic Model and Applications. Phys Rev E (1999) 60(5):5073–105. doi:10.1103/physreve.60.5073

CrossRef Full Text | Google Scholar

73. Margerit D, Barkley D. Cookbook Asymptotics for Spiral and Scroll Waves in Excitable media. Chaos (2002) 12(3):636–49. doi:10.1063/1.1494875

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Zykov VS. Kinematics of Rigidly Rotating Spiral Waves. Physica D: Nonlinear Phenomena (2009) 238(11-12):931–40. doi:10.1016/j.physd.2008.06.009

CrossRef Full Text | Google Scholar

75. Löber J, Engel H. Analytical Approximations for Spiral Waves. Chaos (2013) 23(4):043135. doi:10.1063/1.4848576

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Barkley D. Euclidean Symmetry and the Dynamics of Rotating Spiral Waves. Phys Rev Lett (1994) 72(1):164–7. doi:10.1103/physrevlett.72.164

PubMed Abstract | CrossRef Full Text | Google Scholar

77. KazbanovKazbanov IV, ten Tusscher KH, Panfilov AV. Effects of Heterogeneous Diffuse Fibrosis on Arrhythmia Dynamics and Mechanism. Sci Rep (2016) 6:20835. doi:10.1038/srep20835

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Vandersickel N, Watanabe M, Tao Q, Fostier J, Zeppenfeld K, PanfilovPanfilov AV. Dynamical Anchoring of Distant Arrhythmia Sources by Fibrotic Regions via Restructuring of the Activation Pattern. Plos Comput Biol (2018) 14(12):e1006637. doi:10.1371/journal.pcbi.1006637

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Camelliti P, Green CR, Kohl P. Structural and Functional Coupling of Cardiac Myocytes and Fibroblasts. Cardiovasc Gap Junctions (2006) 42:132–49. doi:10.1159/000092566

CrossRef Full Text | Google Scholar

80. Gaudesius G, Miragoli M, Thomas SP, Rohr S. Coupling of Cardiac Electrical Activity over Extended Distances by Fibroblasts of Cardiac Origin. Circ Res (2003) 93(5):421–8. doi:10.1161/01.res.0000089258.40661.0c

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Potse M, Dube B, Richer J, Vinet A, Gulrajani RM. A Comparison of Monodomain and Bidomain Reaction-Diffusion Models for Action Potential Propagation in the Human Heart. IEEE Trans Biomed Eng (2006) 53(12):2425–35. doi:10.1109/tbme.2006.880875

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Zeng T, Bett GCL, Sachs F. Stretch-Activated Whole Cell Currents in Adult Rat Cardiac Myocytes. Am J Physiology-Heart Circulatory Physiol (2000) 278(2):H548–H557. doi:10.1152/ajpheart.2000.278.2.h548

CrossRef Full Text | Google Scholar

83. Kamkin A, Kiseleva I, Isenberg G. Stretch-activated Currents in Ventricular Myocytes: Amplitude and Arrhythmogenic Effects Increase with Hypertrophy. Cardiovasc Res (2000) 48(3):409–20. doi:10.1016/s0008-6363(00)00208-x

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Thompson SA, Copeland CR, Reich DH, Tung L. Mechanical Coupling between Myofibroblasts and Cardiomyocytes Slows Electric Conduction in Fibrotic Cell Monolayers. Circulation (2011) 123(19):2083–93. doi:10.1161/circulationaha.110.015057

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Panfilov AV, Keldermann RH, Nash MP. Drift and Breakup of Spiral Waves in Reaction Diffusion Mechanics Systems. Proc Natl Acad Sci (2007) 104(19):7922–6. doi:10.1073/pnas.0701895104

PubMed Abstract | CrossRef Full Text | Google Scholar