Direct Observation of Axial Dynamics of Particle Manipulation With Weber Self-Accelerating Beams

Optical manipulation of micro-particles with nondiffracting and self-accelerating beams has been successfully applied in many research fields such as chemicophysics, material sciences and biomedicine. Such operation mainly focuses on the particle transport and control in the beam propagation direction. However, the conventional optical microscopy is specifically designed for obtaining the sample information located in the lateral plane, which is perpendicular to the optical axis of the detecting objective lens, making the real-time observation of particle dynamics in axial plane a challenge. In this work, we propose and demonstrate a technique which integrates a special beam optical tweezer with a direct axial plane imaging system. Here, particles are transported in aqueous solution along a parabolic trajectory by a designed nonparaxial Weber self-accelerating beam, and the particle motion dynamics both in lateral and axial plane are monitored in real-time by the axial plane imaging technique.

1 Introduction

Self-accelerating beams have attracted great interest since the first demonstration in 2007 [1, 2]. As exact solutions of the paraxial wave equation, Airy beams propagate along parabolic trajectories and remain invariant intensity profiles. By virtue of the remarkable features of non-diffracting, self-accelerating, and self-healing [3, 4], applications of Airy beams have been developed in many research fields, such as particle manipulation [5–8], optical microscopy [9–11], plasmons [12–14] and material processing [15, 16]. However, Airy beams are destructive when bending to large angles due to the paraxial limit. Against this drawback, nonparaxial self-accelerating beams, such as Mathieu beams and Weber beams, have been proposed and demonstrated theoretically and experimentally [17–22]. Such novel beams are found as exact solutions of the Helmholtz equation in different coordinate systems without the paraxial approximation. Therefore, compared to Airy beams, they can bend to larger angles and maintain the non-diffracting and self-healing capabilities as well.

With the development of optical field modulation technique, introducing novel beams into optical tweezers is convenient to achieve. For example, Baumgartl J et al. used Airy beam to guide particles vertically along a parabolic trajectory [5]. Zhang Z et al. experimentally demonstrated stable trapping of multiple particles using an array of optical bottle beams by employing multiple Airy beams [23]. Schley R et al. steered particles to much steeper angles in absorbing media with loss-proof accelerating beams [24]. However, there are challenges in observing the axial dynamics of trapping behavior in the light propagation direction. Most the conventional optical microscopes equipped for optical tweezers can only observe the particle motion occurred in the lateral plane (perpendicular to the optical axis) [25, 26]. The acquisition of axial plane (parallel to the optical axis) information usually relies on setting another objective orthogonally [24] or axial scanning [27, 28]. The former restricts the sample mounting strategy and the numerical aperture (NA) of objectives. The latter needs to extract a certain axial plane from the three-dimensional (3D) bulk reconstructed by stacking a series of lateral frames, limiting the image speed and resulting in data redundancy. It’s worth mentioning that a novel technique termed axial plane optical microscopy (APOM) has been developed to directly image the axial cross-section of samples without scanning [29]. This technique employed a 45°-tilted mirror to convert the axial plane information into a lateral plane and then re-image onto a camera. This innovative approach has been successfully applied in single-molecule super-resolution microscopy [30, 31].

In this work, we introduce the nonparaxial Weber beam into the optical tweezer system for particle manipulation. To observe the trapping dynamics, the APOM technique is assembled in the special beam optical tweezer system, directly observing both the particle motion along the parabolic trajectory in axial plane and the “focus/defocus” status in lateral plane. The proposed system integrates the special beam generation module based on spatial light modulator (SLM) and the APOM technique together. It allows real-time observation of trapping behavior in lateral and axial planes simultaneously. Due to the large field of view and real-time capability in nature, this technique is suitable for investigating special beams with axial particularities such as non-diffracting and self-accelerating, and has potential applications in biomedicine and biophysics.

2 Methods

2.1 Optical Setup

The optical setup of the Weber beam optical tweezer system equipped with APOM was shown in Figure 1A. In the optical tweezer part, a laser beam with the wavelength of 532 nm (MW-GL-532A/3000 mW-16020122, Changchun Laser Optoelectronics Technology Co., Ltd., China) was expanded and collimated by a pair of achromatic lenses L1 (f = 50 mm) and L2 (f = 100 mm). After matching the polarization by a polarizer P, the horizontal polarized light beam was guided by a 96°-triangle reflector (96°-TR) onto a SLM (PLUTO-VIS-016, HoloEye Inc., Germany, 1920 pixels × 1080 pixels, pixel size: 8.0 µm, frame rate: 60 Hz) and then back to the original optical path. Instead of normal incidence, the 96°-TR allowed the small angle (= 6°) incidence modality of SLM to be used for enhancing the light efficiency while maintaining the compact experimental configuration. Here, the SLM was located in the focal plane of L3 (f = 200 mm). The pre-designed masks (Figure 1C) were loaded on the SLM for beam modulation. After focusing by L3, the SLM-modulated special beam was generated in the focal region of L3. Then, a tube lens (L4, f = 200 mm) and an objective (Obj1, 100×, NA = 1.4, oil immersion, Nikon Corp., Japan) were used to shrink the special beam in the focal region of Obj1 for particle trapping and transporting.

FIGURE 1

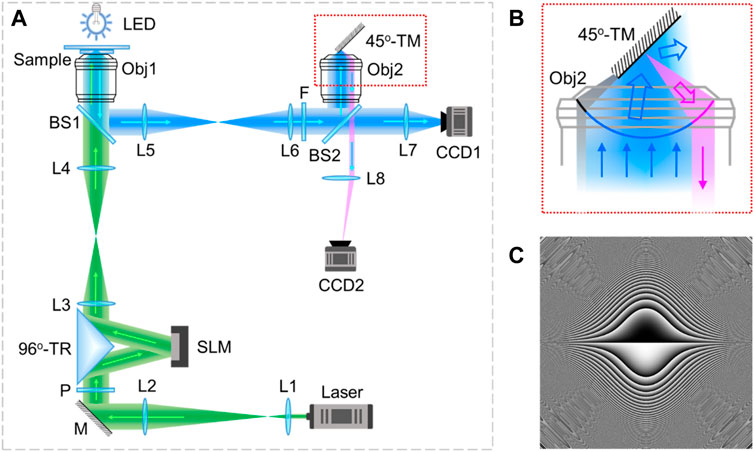
FIGURE 1. Schematic diagram of the Weber beam optical tweezer system equipped with APOM. (A) Optical setup; (B) enlarged view of the area marked with red dotted rectangle in (A); (C) phase mask loaded on the SLM. L: lens, M: mirror, P: polarizer, 96°-TR: 96°-triangle reflector, BS: beam splitter, Obj: objective, LED: light emitting diode, F: filter, CCD: Charge coupled device, 45°-TM: 45°-tilted mirror.

In the optical microscopy part, a light emitting diode (LED) with a central wavelength of 488 nm was used for wide-field illumination. The signal with sample information was collected by Obj1 and reflected by a beam splitter (BS1, 50:50), then relayed to another beam splitter (BS2, 50:50) by a 4f-system consisting of L5 (f = 200 mm) and L6 (f = 200 mm). Before BS2, a short-pass optical filter F with a cut-off wavelength of 500 nm was used to distinguish the trapping laser and imaging light. With BS2, the signal was split into two parts of transmission and reflection. The transmitted part directly formed a lateral plane image on a charge-coupled device (CCD1, DMK23G445, The Imaging Source Inc., Germany, 1280 pixels × 960 pixels, pixel size: 3.75 µm, frame rate: 30 fps) through a condenser (L7, f = 75 mm). The reflected part went through an identical objective lens Obj2 and then formed an intermediate image of the sample in the focal region of Obj2. A custom-made 45°-tilted mirror (45°-TM) was placed in front of Obj2 for converting the axial plane image into the lateral plane, and then a part of the signal light was re-collected by Obj2. After transmitting through BS2, the returned light finally formed an axial plane image of the sample on another CCD camera (CCD2, DMK23U445, The Imaging Source Inc., Germany, 1280 pixels × 960 pixels, pixel size: 3.75 µm, frame rate: 30 fps) through a condenser (L8, f = 75 mm).

The 45°-TM was made by coating a thin layer of silver on the surface of a right-angle prism with a straight and sharp edge. According to the principle of reflection, a ray can be rotated 90° when it comes to a mirror at an incident angle of 45°. Likewise, the 45°-TM can rotate an axial plane image to lateral plane. The reflection details of the 45°-TM were shown in Figure 1B. After reflecting, the light rays were divided into three parts, marked with different colors of gray, blue and magenta respectively. The gray part represented rays blocked by the 45°-TM. The blue part was reflected by the 45°-TM to directions which cannot be collected by Obj2. Whereas rays indicated in magenta were reflected back by the 45°-TM and collected by Obj2 to perform axial plane imaging.

2.2 Generation of Weber Self-Accelerating Beams

Comparing with the Airy beam, Weber beam is an exact solution of the Helmholtz equation in parabolic coordinates without the paraxial approximation, so it can travel longer distance and bend to larger angle while preserving all the unique characteristics of the Airy beam. Therefore, in this paper, we designed and selected the proper Weber beam for particle transporting along parabolic trajectory in axial space.

To investigate the propagation characteristics of Weber beams, we followed the similar procedures as our previous work [32], loading the predesigned masks on an SLM. The Fourier spectrum ${\phi }_W$ associated with Weber beams can be expressed as:

${\phi }_W\left(f_x,f_y\right)=\frac{\text{exp}\left[i\gamma \left(\frac{f_x}{k}+\frac{f_y}{k}\right)+i\gamma \text{ln}\left(\tan \left(\text{arccos}\left(\frac{f_x}{k}\right)/2\right)\right)+i\gamma \text{ln}\left(\tan \left(\text{arccos}\left(\frac{f_y}{k}\right)/2\right)\right)\right]}{\sqrt{k^2-f_x^2-f_y^2}}(1)$

where, $f_x$ and $f_y$ are the spatial frequencies in x and y directions, respectively. λ is the wavelength in the medium. $k=2\pi /\lambda$ is the wave number. γ is related to the separation constant. Considering the paraxial approximation, we assumed $f_x/k\ll 1$ and $f_y/k\ll 1$, so the Eq. 1 can be derived as:

${\phi }_A\left(f_x,f_y\right)=\text{exp}\left(-i\gamma \frac{f_x^3}{3k^3}-i\gamma \frac{f_y^3}{3k^3}\right)/k(2)$

which is the typical Fourier spectrum of Airy beams, indicating that Airy beams are the paraxial approximation of Weber beams.

In simulation, the Fourier spectrum was produced according to Eq. 1. The lateral light fields were calculated by the angular spectrum theory of diffraction [33], and the axial cross-sections of Weber beams were formed by reconstruction. In experiment, the pre-designed mask according to Eq. 1 was loaded on the SLM. A flat mirror was placed in the sample position, and it was controlled by a one-dimensional translation stage to acquire a series of lateral plane images of the generated Weber beam on CCD1 by axial scanning. Then, the axial cross-section of the beam was extracted from the 3D light field rendered by stacking up these lateral plane images.

3 Results and Analysis

3.1 Simulated and Experimental Results of Weber Self-Accelerating Beams

To investigate the propagation characteristics of Weber beams, simulations and the counterpart experiments were carried out. The corresponding results were shown in Figure 2. In simulation, the size of Weber beams can be adjusted flexibly by changing the value of γ in Eq. 1. Given λ = 532 nm, the central lateral and axial cross-sections of Weber beams were calculated by the beam propagation method based on the angular spectrum theory of diffraction [33]. The simulated results were shown in Figures 2C,D and Figures 2E,F when the value of γ was taken as 300 and 800, respectively, suggesting that a larger γ resulted in a larger main lobe size, longer propagation distance and smaller curvature.

FIGURE 2

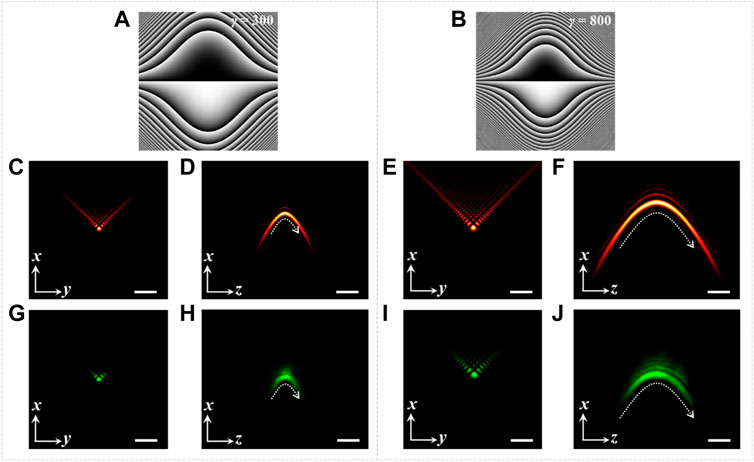
FIGURE 2. Modulation of Weber beams. (A,B) Phase masks of Weber beams with γ = 300 and 800, respectively; (C–F) simulated results of the lateral and axial cross-sections of Weber beams, (C) and (D) correspond to γ = 300, (E) and (F) correspond to γ = 800; (G–J) experimental results of the lateral and axial cross-sections of Weber beams corresponding to (C–F), respectively. Scale bar: 2 µm.

The use of SLM also made the beam size modulation easy to implement in experiment. The phase patterns of masks loaded on SLM were shown in Figures 2A,B with the value of γ as 300 and 800, respectively. After sending a Gaussian beam to the SLM with these pre-designed masks, Weber beams were generated by the Fourier transformation of a convex lens L3, and then presented in the focal region of Obj1 with a strong focusing form suitable for particle trapping. When a flat mirror was set in the focal plane of Obj1, the central lateral cross-sections of Weber beams were imaged by CCD1, as shown in Figure 2G (γ = 300) and Figure 2I (γ = 800). The corresponding axial cross-sections were obtained from 300 lateral frames captured by scanning the flat mirror along axial direction. The experimental results were shown in Figure 2H (γ = 300) and Figure 2J (γ = 800), indicating the effect of γ on the characteristic of Weber beams was that the larger γ is, the larger main lobe size is, and the longer propagation distance is, but the smaller curvature of the parabolic trajectory is. It was consistent with the conclusion suggested by the simulated results.

Moreover, taking γ = 300 as an example to compare the experimental and simulated results, the side lobes in experiment (Figure 2G) were less than in simulation (Figure 2C), and the propagation distance in experiment (Figure 2H) was shorter than in simulation (Figure 2D). This was caused by the aperture limitation of experimental elements and the very low initial incident laser intensity of about 2 µW we set for beam measurement. Nevertheless, as the white dashed curves shown in Figures 2D,H the experimental and simulated beams still shared the same parabolic trajectory. And the case of γ = 800 gave the same phenomenon.

3.2 Experimental Results of Particle Transporting and Imaging

Based on the above investigation of Weber beams both in simulation and experiment, it is expected to transport particle in the axial space along a curved trajectory with Weber beams, and the dynamics can be monitored in real-time by the presented system shown in Figure 1A. This system has intrinsic large field of view in axial plane, which is greater than 70 µm × 70 µm in this work. In order to get a long transporting distance in optical manipulation experiment, we set a large value of γ = 3600 to produce a mask pattern according to Eq. 1 and then loaded it on the SLM. Comparing to the beam measurement mentioned above, the beam intensity for particle trapping was set to a much higher value of about 20 mW to guarantee the stability of optical trap.

The experimental observation results of transporting a polystyrene bead of 5 µm in diameter along a parabolic trajectory of the Weber beam were shown in Figure 3. The lateral (x-y) plane and the corresponding axial (x-z) plane information of the transporting dynamics were captured by CCD1 and CCD2 simultaneously, displayed as screenshots at different time in Figures 3A–E and Figures 3F–J, respectively. As can be seen from Figures 3A–E, the trapped particle underwent a process of “defocus-focus-defocus” accompanied by the displacement up and down along x direction. Obviously, these lateral images obtained by CCD1 were not enough to give an intuitive description of the particle motion. However, as shown in Figures 3F–J, the axial plane images obtained by CCD2 visually displayed that the trapped particle moved along a curved trajectory in x-z plane and stayed in focus throughout the whole journey of about 35 µm.

FIGURE 3

FIGURE 3. Experimental observation results of particle transporting dynamics along the Weber beam trajectory. (A–E) The lateral (x-y) plane images of a trapped particle at different time; (F–J) the axial (x-z) plane images corresponding to (A–E). Particles: polystyrene beads of 5 µm in diameter. Scale bar: 10 µm.

The whole experimental system was set in horizontal alignment; the used sample was aqueous solution containing polystyrene beads; there was enough axial space for implementing the particle transportation; the target bead was stably trapped in lateral dimension and transported along parabolic trajectory of the designed Weber beam. In view of above conditions, the primary forces acting on the target bead were shown in Figure 4A, including the gravity, floatage, scattering force, lateral gradient force and axial gradient force. Among them, the lateral gradient force and scattering force played dominant roles in the particle manipulation. The former performed a 2D trap in lateral dimension and bounded the particle to the main lobe area of the Weber beam, and the latter pushed the particle moving along the beam propagation trajectory.

FIGURE 4

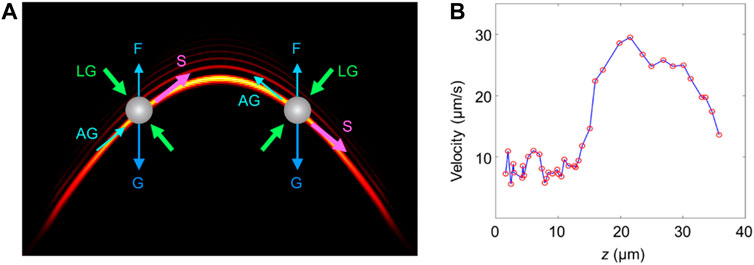
FIGURE 4. Quantification of the particle motion. (A) Schematic diagram of the primary forces acting on the particle. G: gravity, F: floatage, LG: lateral gradient force, AG: axial gradient force, S: scattering force; (B) velocities of the particle at different axial positions.

From the axial plane real-time monitoring results directly captured by CCD2, the motion of the trapped particle can be quantified conveniently. We measured the velocities of the particle at different z positions. As shown in Figure 4B, the results indicated that the particle moved faster in the middle region of the transporting path than on either side. It was because the maximum scattering force and quite small axial gradient force of the Weber beam occurred in this region. Moreover, the particle moved faster in the latter half of its motion path than in the first half. This difference was mainly caused by the gravity. As shown in Figure 4A, the gravity component along beam trajectory was in opposite direction of the scattering force in the first half, so as to impede the particle movement. The case of the latter half was on the contrary.

4 Conclusion

In this work, we proposed an integrated system which combined the SLM-based special beam generation module, optical manipulation technique and axial plane optical microscopy together, achieving particle transporting along parabolic trajectory of the designed Weber self-accelerating beam with the real-time observation in lateral and axial planes, simultaneously. This method solves the problem that the axial capture dynamics cannot be directly observed in traditional optical tweezers. Because there is only a single objective for both beam generation and signal detection, this system has no particular geometric requirement for sample preparation, and the objectives with high NA are allowed to be used for improving the resolution. In addition, this technique can be further developed to perform particle tracking, because arbitrary plane information of samples can be acquired by translating and rotating the tilted mirror. In a word, by virtue of the flexible light modulation based on the use of SLM, the direct axial plane imaging with the intrinsic large field of view, and good compatibility with other technologies, we believe the proposed technique will become a useful tool for studying a variety of novel beams, and find applications in fields of chemicophysics and biomedicine.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

SA, TP, BY, and PZ conceived the project. BY and PZ supervised the study. SA and TP performed the experiments. SA and SY analyzed the data. SA wrote the draft of the manuscript. All the authors edited the manuscript.

Funding

This work is supported by National Natural Science Foundation of China (NSFC 11974417).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Siviloglou GA, Christodoulides DN. Accelerating Finite Energy Airy Beams. Opt Lett (2007) 32:979–81. doi:10.1364/OL.32.000979

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Siviloglou GA, Broky J, Dogariu A, Christodoulides DN. Observation of Accelerating Airy Beams. Phys Rev Lett (2007) 99:213901. doi:10.1103/PHYSREVLETT.99.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Broky J, Siviloglou GA, Dogariu A, Christodoulides DN. Self-healing Properties of Optical Airy Beams. Opt Express (2008) 16:12880–91. doi:10.1364/OE.16.012880

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Chu X. Evolution of an Airy Beam in Turbulence. Opt Lett (2011) 36:2701–3. doi:10.1364/OL.36.002701

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Baumgartl J, Mazilu M, Dholakia K. Optically Mediated Particle Clearing Using Airy Wavepackets. Nat Photon (2008) 2:675–8. doi:10.1038/NPHOTON.2008.201

CrossRef Full Text | Google Scholar

6. Cheng H, Zang W, Zhou W, Tian J. Analysis of Optical Trapping and Propulsion of Rayleigh Particles Using Airy Beam. Opt Express (2010) 18:20384–94. doi:10.1364/OE.18.020384

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhang P, Prakash J, Zhang Z, Mills MS, Efremidis NK, Christodoulides DN. Trapping and Guiding Microparticles with Morphing Autofocusing Airy Beams. Opt Lett (2011) 36:2883–5. doi:10.1364/OL.36.002883

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zheng Z, Zhang B-F, Chen H, Ding J, Wang H-T. Optical Trapping with Focused Airy Beams. Appl Opt (2011) 50:43–9. doi:10.1364/AO.50.000043

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Jia S, Vaughan JC, Zhuang X. Isotropic Three-Dimensional Super-resolution Imaging with a Self-Bending point Spread Function. Nat Photon (2014) 8:302–6. doi:10.1038/nphoton.2014.13

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Vettenburg T, Dalgarno HIC, Nylk J, Coll-Lladó C, Ferrier DEK, Čižmár T. Light-sheet Microscopy Using an Airy Beam. Nat Methods (2014) 11:541–4. doi:10.1038/NMETH.2922

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kafian H, Lalenejad M, Moradi-Mehr S, Birgani SA, Abdollahpour D. Light-sheet Fluorescence Microscopy with Scanning Non-diffracting Beams. Sci Rep (2020) 10:8501. doi:10.1038/S41598-020-63847-2

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Polynkin P, Kolesik M, Moloney JV, Siviloglou GA, Christodoulides DN. Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science (2009) 324:229–32. doi:10.1126/science.1169544

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Salandrino A, Christodoulides DN. Airy Plasmon: a Nondiffracting Surface Wave. Opt Lett (2010) 35:2082–4. doi:10.1364/OL.35.002082

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Li L, Li T, Wang SM, Zhang C, Zhu SN. Plasmonic Airy Beam Generated by In-Plane Diffraction. Phys Rev Lett (2011) 107:126804. doi:10.1103/PHYSREVLETT.107.126804

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mathis A, Courvoisier F, Froehly L, Furfaro L, Jacquot M, Lacourt PA. Micromachining along a Curve: Femtosecond Laser Micromachining of Curved Profiles in diamond and Silicon Using Accelerating Beams. Appl Phys Lett (2012) 101:071110. doi:10.1063/1.4745925

CrossRef Full Text | Google Scholar

16. Götte N, Winkler T, Meinl T, Kusserow T, Zielinski B, Sarpe C. Temporal Airy Pulses for Controlled High Aspect Ratio Nanomachining of Dielectrics. Optica (2016) 3:389–95. doi:10.1364/OPTICA.3.000389

CrossRef Full Text | Google Scholar

17. Novitsky AV, Novitsky DV. Nonparaxial Airy Beams: Role of Evanescent Waves. Opt Lett (2009) 34:3430–2. doi:10.1364/OL.34.003430

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kaminer I, Bekenstein R, Nemirovsky J, Segev M. Nondiffracting Accelerating Wave Packets of Maxwell's Equations. Phys Rev Lett (2012) 108:163901. doi:10.1103/PHYSREVLETT.108.163901

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Courvoisier F, Mathis A, Froehly L, Giust R, Furfaro L, Lacourt PA. Sending Femtosecond Pulses in Circles: Highly Nonparaxial Accelerating Beams. Opt Lett (2012) 37:1736–8. doi:10.1364/OL.37.001736

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zhang P, Hu Y, Cannan D, Salandrino A, Li T, Morandotti R. Generation of Linear and Nonlinear Nonparaxial Accelerating Beams. Opt Lett (2012) 37:2820–2. doi:10.1364/OL.37.002820

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhang P, Hu Y, Li T, Cannan D, Yin X, Morandotti R. Nonparaxial Mathieu and Weber Accelerating Beams. Phys Rev Lett (2012) 109:193901. doi:10.1103/PHYSREVLETT.109.193901

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Bandres MA, Rodríguez-Lara BM. Nondiffracting Accelerating Waves: Weber Waves and Parabolic Momentum. New J Phys (2013) 15:013054. doi:10.1088/1367-2630/15/1/013054

CrossRef Full Text | Google Scholar

23. Zhang Z, Zhang P, Mills M, Chen Z, Christodoulides DN, Liu J. Trapping Aerosols with Optical Bottle Arrays Generated through a Superposition of Multiple Airy Beams. Chin Opt Lett (2013) 11:033502. doi:10.3788/col201311.033502

CrossRef Full Text | Google Scholar

24. Schley R, Kaminer I, Greenfield E, Bekenstein R, Lumer Y, Segev M. Loss-proof Self-Accelerating Beams and Their Use in Non-paraxial Manipulation of Particles' Trajectories. Nat Commun (2014) 5:5189. doi:10.1038/NCOMMS6189

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Maragò OM, Jones PH, Gucciardi PG, Volpe G, Ferrari AC. Optical Trapping and Manipulation of Nanostructures. Nat Nanotech (2013) 8:807–19. doi:10.1038/nnano.2013.208

CrossRef Full Text | Google Scholar

26. Xin H, Xu R, Li B. Optical Trapping, Driving and Arrangement of Particles Using a Tapered Fibre Probe. Sci Rep (2012) 2:818. doi:10.1038/srep00818

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Vossen DLJ, van der Horst A, Dogterom M, van Blaaderen A. Optical Tweezers and Confocal Microscopy for Simultaneous Three-Dimensional Manipulation and Imaging in Concentrated Colloidal Dispersions. Rev Scientific Instr (2004) 75:2960–70. doi:10.1063/1.1784559

CrossRef Full Text | Google Scholar

28. Curran A, Tuohy S, Aarts DGAL, Booth MJ, Wilson T, Dullens RPA. Decoupled and Simultaneous Three-Dimensional Imaging and Optical Manipulation through a Single Objective. Optica (2014) 1:223–6. doi:10.1364/OPTICA.1.000223

CrossRef Full Text | Google Scholar

29. Li T, Ota S, Kim J, Wong ZJ, Wang Y, Yin X. Axial Plane Optical Microscopy. Sci Rep (2015) 4:7253. doi:10.1038/SREP07253

CrossRef Full Text | Google Scholar

30. Kim J, Wojcik M, Wang Y, Moon S, Zin EA, Marnani N. Oblique-plane Single-Molecule Localization Microscopy for Tissues and Small Intact Animals. Nat Methods (2019) 16:853–7. doi:10.1038/S41592-019-0510-Z

PubMed Abstract | CrossRef Full Text | Google Scholar

31. An S, Ziegler KF, Zhang P, Wang Y, Kwok T, Xu F. Axial Plane Single-Molecule Super-resolution Microscopy of Whole Cells. Biomed Opt Express (2020) 11:461–79. doi:10.1364/BOE.377890

PubMed Abstract | CrossRef Full Text | Google Scholar

32. An S, Peng T, Yan S, Zhang P, Li M, Yao B. Direct Axial Plane Imaging of Particle Manipulation with Nondiffracting Bessel Beams. Appl Opt (2021) 60:2974–80. doi:10.1364/AO.417854

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Poon T-C, Banerjee PP. Single and Double Lens Image Processing Systems. In: Contemporary Optical Image Processing with MATLAB. Oxford, United Kingdom: Elsevier (2001). p. 133–67. doi:10.1016/b978-008043788-0/50005-6

CrossRef Full Text | Google Scholar