Polarization-Based Histopathology Classification of Ex Vivo Colon Samples Supported by Machine Learning

In biophotonics, novel techniques and approaches are being constantly sought to assist medical doctors and to increase both sensitivity and specificity of the existing diagnostic methods. In such context, tissue polarimetry holds promise to become a valuable optical diagnostic technique as it is sensitive to tissue alterations caused by different benign and malignant formations. In our studies, multiple Mueller matrices were recorded for formalin-fixed, human, ex vivo colon specimens containing healthy and tumor zones. The available data were pre-processed to filter noise and experimental errors, and then all Mueller matrices were decomposed to derive polarimetric quantities sensitive to malignant formations in tissues. In addition, the Poincaré sphere representation of the experimental results was implemented. We also used the canonical and natural indices of polarimetric purity depolarization spaces for plotting our experimental data. A feature selection was used to perform a statistical analysis and normalization procedure on the available data, in order to create a polarimetric model for colon cancer assessment with strong predictors. Both unsupervised (principal component analysis) and supervised (logistic regression, random forest, and support vector machines) machine learning algorithms were used to extract particular features from the model and for classification purposes. The results from logistic regression allowed to evaluate the best polarimetric quantities for tumor detection, while the use of random forest yielded the highest accuracy values. Attention was paid to the correlation between the predictors in the model as well as both losses and relative risk of misclassification. Apart from the mathematical interpretation of the polarimetric quantities, the presented polarimetric model was able to support the physical interpretation of the results from previous studies and relate the latter to the samples’ health condition, respectively.

1 Introduction

Ellipsometry and polarimetry have established their duly and justified realm for material characterization [1–6]. Yet, in the purview of biomedical optics, tissue polarimetry strives toward a novel domain for non-invasive, supplementary assistance in histopathology [7–13]. Unlike skin cancer, whose origins could be detected at an earlier stage of development due to its presence predominantly in the areas of the human body available for direct visual inspection, colon cancer is localized and diagnosed out of straight sight of notice often at a later stage of development [14]. Such an inevitable obstacle could be overcome by adopting various multimodal optical techniques for providing adequate support to clinicians [15–19]. It was shown earlier that tissue polarimetry techniques could be effectively combined to juxtapose polarization and depolarization parameters from different health conditions after scanning, embrace the Poincaré sphere visualization for qualitative differentiation, and construct various depolarization spaces [20–28]. Ample diagnostic information related to the morphology of the tissue specimens under study is encoded in their Mueller matrices [26, 29–32]. Nevertheless, the intertwined relation between the samples’ polarization and depolarization properties and their matrix elements is accessible only after the application of pertinent decomposition algorithms [33–38]. For instance, Cloude’s physical realizability is able to filter out experimental errors and/or data noise [39, 40], while logarithmic [37, 41, 42], Lu–Chipman [35, 43–45], or symmetric [36, 46] decompositions were found capable of extracting the embedded diagnostic information for the samples under study. With the increasing size and amount of the experimental data, apt post-processing algorithms are required, alongside the inclusion of statistical analyses and implementation of the artificial intelligence (AI) framework. The latter could be utilized to mimic human-like intellect when handling large and complex datasets, images, etc. Being part of AI, the vastly expanding field of machine learning (ML) covers a wide spectrum of applications for solving multiple scientific problems [47–53] as well as for cancer classification [54–62]. Since conventional programming processes an input data by means of particular syntax and semantics to produce a desired output, such a method is prone to multiple errors repetition. To overcome this issue, ML uses both the input and output data to train an algorithm for an a priori defined purpose. Depending on the purpose desired, ML algorithms can be grouped into three distinct classes [63, 64], namely, supervised, unsupervised, and reinforcement. The scope of the current study is focused on an application with both supervised and unsupervised ML algorithms for colon cancer assessment. In this study, the data used were obtained from tissue polarimetric experiments with various formalin-fixed, human ex vivo colon samples, containing healthy and malignant zones. For all specimens and health conditions a spatial x-y scan was conducted, where for each of the measured locations a Mueller matrix (MM) was obtained. Every MM was filtered for data noise and measurements errors before applying a decomposition algorithm and depolarization metrics calculus. Afterward, a selection of a subset from all polarimetric quantities was carried out, in order to form tissue polarimetric model with predictors, which non-redundantly summarizes all polarization and depolarization properties of both colon’s healthy and cancerous tissue zones. In order to avoid multicollinearity and overfitting, the main model was split into two submodels, and consequently, all unsupervised and supervised ML algorithms were applied for both submodels independently. Finally, the performance of each ML algorithm with each of the submodels was evaluated by means of computing the corresponding confusion matrix, areas under the curves (AUC), and loss and relative risk calculations related to misclassifications.

2 Theory

When dealing with light propagation in a turbid medium, it is feasible to adopt the Stokes–Mueller calculus and operate with real and measurable quantities. Hence, the full Stokes vector S = (S₀,S₁,S₂,S₃)^T is able to provide description for all polarization states even if time dependence S(t) is on avail. Knowledge of both the total degree of light polarization ρ ∈ [0, 1] and light intensity I facilitate the adoption of more explicit definitive convention [33, 39]as follows:

$\mathbf{S}=I{\left(1,\mathbf{p}\right)}^T,\mathbf{p}=\rho \mathbf{u},\mathbf{u}={\left[\mathit{cos}\left(2\theta \right)\mathit{cos}\left(2ϵ\right),\mathit{sin}\left(2\theta \right)\mathit{cos}\left(2ϵ\right),\mathit{sin}\left(2ϵ\right)\right]}^T,(1)$

where p and u are the polarization and Poincaré vectors, respectively. The latter translates the conversion from Cartesian to spherical coordinate system, thus making possible to visualize and utilize the Poincaré sphere representation with the available polarimetric data, where θ ∈ [ − π/2, π/2] and ϵ ∈ [ − π/4, π/4] are the azimuth and the angle of ellipticity, respectively. The individual polarization fingerprint of a turbid medium under study is encoded in its Mueller matrix (M) from which one could read all polarization and depolarization properties related to both the surface and structural sample properties/characteristics. Every output Stokes vector (S^o) is linearly dependent on the input one (Sⁱ) and also on M, obeying the relation S^o = M_ij⋅Sⁱ. A minimum of four input and four output polarization co-variations are required to obtain a full Mueller matrix by solving a system of four linear equations for each i [65]:

$\begin{array}{c}\hfill {\mathbf{S}}_{\mathbf{Q}/-\mathbf{Q}}^{\mathbf{o}}={\mathbf{M}}_{\mathbf{i1}}\pm {\mathbf{M}}_{\mathbf{i1∕2}}\hfill \\ \hfill {\mathbf{S}}_{\mathbf{U∕V}}^{\mathbf{o}}={\mathbf{M}}_{\mathbf{i1}}+{\mathbf{M}}_{\mathbf{i3∕4}},\hfill \end{array}(2)$

where Q/-Q denote horizontal/vertical and U/V denote +45°/right circular polarization states, while i,j = ∈ [1, 4]. Physically realizable, depolarizing M must be represented as weighted averages of non-depolarizing M. By this way each Mueller matrix is to preserve the value of ρ parameter for totally polarized input light beam. Imprecise calibration, data noise, and experimental errors may lead to the violation of the Cloude’s condition for physical realizability [34, 66], and a filtration procedure is required. In such a case, one needs to solve the eigenvalue-eigenvector problem for the Hermitian covariance matrix H [33]:

$\mathbf{H}=\frac{1}{4}\sum _{i,j=1}^4{\mathbf{M}}_{\mathit{ij}}\left(\sigma \mathit{i}\otimes \sigma \mathit{j}\right),(3)$

where σ_i are the four Pauli spin matrices and the symbol ⊗ denotes the Kronecker product. If all eigenvalues (λ_i) of H are positive, then the corresponding M is in compliance to the Cloude’s condition. On the contrary, if the aforementioned condition is not met, then all negative λ_i are assigned to zero, and the filtered covariance (H^f) and Mueller M^f matrices are obtained likewise [33]:

${\mathrm{H}}^{\mathit{f}}=\mathbf{V}\mathbf{\Lambda }{\mathbf{V}}^{-\mathbf{1}},m_{ij}^f=\text{tr}\left[\left(\sigma \mathit{i}\otimes \sigma \mathit{j}\right){\mathbf{H}}_{\mathit{i}\mathit{j}}^{\mathit{f}}\right].(4)$

Here, the matrix V is constructed from the eigenvectors of H, while Λ = diag (λ_i) and contains only positive eigenvalues, while small $m_{ij}^f$ indicates an element of the filtered Mueller matrix. If one is interested only in the polarimetric properties, by setting tr (H^f) = 1 or simply normalizing the eigenvalues sum to unit, both processes of transmissivity and reflectivity can be disregarded. Next, additional depolarization information can be extracted from H^f, which will be correspondingly related to the depolarization properties of the underlying medium and M^f, respectively. Three depolarization indicators could be plainly derived from λ_i (H^f), whereas the following set of equations is valid when tr (H^f) = 1 and λ₁ ≥ λ₂ ≥ λ₃ ≥ λ₄ [33]:

$P_1={\lambda }_1-{\lambda }_2,P_2={\lambda }_1+{\lambda }_2-2{\lambda }_3,P_3={\lambda }_1+{\lambda }_2+{\lambda }_3-3{\lambda }_4.(5)$

The overall depolarization ability P_Δ and polarization purity PI could be summarized explicitly as [33]:

$P_{\mathrm{\Delta }}=\sqrt{\frac{1}{3}\left(2P_1^2+\frac{2}{3}{P}_2^2+\frac{1}{3}{P}_3^2\right)},PI=\sqrt{\frac{1}{3}\left(P_1^2+P_2^2+P_3^2\right)}.(6)$

From Eq. 5 and Eq. 6, two limiting cases could be identified: pure non-depolarizing media, when P_i = P_Δ = PI = 1, and pure depolarizing media, when P_i = P_Δ = PI = 0. In some cases it may become useful to form and visualize three-dimensional depolarization space(s) as natural ${\mathrm{\Sigma }}_{{\lambda }_i}$ and indices of polarimetric purity Σ_IPP, in order to evaluate the (de)polarization properties of an arbitrary Mueller matrix, instead of using the scalar quantities in Eq. 6. Yet, even more information is encoded in H^f via the Cloude’s entropy S, which is related to the spatial heterogeneity of a given sample of interest [33]:

$S=-\sum _{i=1}^4{\lambda }_i{\mathit{log}}_4\left({\lambda }_i\right).(7)$

Unlike P_i, P_Δ, and PI, S = 1 would lead to an assumption of heterogeneous inner structure, responsible for a complete randomization of the input light polarization state(s). On the contrary, S = 0 would presume homogeneous inner structure, indicative for a complete preservation of ρ for fully polarized light.

Currently, the concepts for physical modeling and physical interpretation of a measured Mueller matrix are of growing importance for both theoreticians and experimentalists. However, such tasks are out of the triviality scope, especially for highly anisotropic and heterogeneous structures such as bio-tissues. Once M^f is obtained, on a straightforward manner, it could be useful and even computationally efficient for large number of measurements to acquire another two polarimetric quantities such as the net diattenuation D and net polarizance P [39]:

$D=\frac{1}{m_{11}}\sqrt{\sum _j{m}_{1j}^2},P=\frac{1}{m_{11}}\sqrt{\sum _i{m}_{i1}^2},i,j=\mathrm{2,3,4},0\le D,P\le 1.(8)$

From a phenomenological point of view, each M^f can undergo certain decomposition algorithm(s), in order to extract particular polarimetric characteristics. The interpretation of depolarizing systems and samples has been extensively studied either with Lu–Chipman [35, 43] or logarithmic decompositions [37, 41]. The former may exhibit forward and reverse forms, thus yielding two asymmetric depolarizers containing either polarizance or diattenuation. On the other hand, the latter assumes a transversally homogeneous and longitudinally inhomogeneous anisotropic medium with continuous distribution of all optical features throughout the sample volume. Such a condition might not be met due to macroscopic variations of the refractive index and, additionally, the high anisotropic structure of bio-tissues. Furthermore, a variety of samples require implementation of angular-resolved measurements and also assumption for pure depolarizer with non-polarizance and diattenuation. Hence, an arbitrary M^f can be decomposed into the so called symmetric factorization in such a way so that the canonical depolarizer is placed between pairs of diattenuators and retarders [36, 46]:

${\mathbf{M}}^{\mathit{f}}={\mathbf{M}}_{{\mathbf{D}}_{\mathbf{2}}}{\mathbf{M}}_{{\mathbf{R}}_{\mathbf{2}}}{\mathbf{M}}_{\mathbf{\Delta }}{\mathbf{M}}_{{\mathbf{R}}_{\mathbf{1}}}^{\mathbf{T}}{\mathbf{M}}_{{\mathbf{D}}_{\mathbf{1}}}.(9)$

For better clarity, it is convenient to adopt a partitioned form for all product matrices in Eq. 9, that is, their general form reads as follows:

${\mathbf{M}}_{\mathbf{D}}=\left[\begin{array}{cc}\hfill 1\hfill & \hfill {\vec{\mathbf{D}}}^{\mathbf{T}}\hfill \\ \hfill \vec{\mathbf{D}}\hfill & \hfill {\mathbf{m}}_{\mathbf{D}}\hfill \end{array}\right],{\mathbf{M}}_{\mathbf{R}=}\left[\begin{array}{cc}\hfill 1\hfill & \hfill {\vec{\mathbf{0}}}^{\mathbf{T}}\hfill \\ \hfill \vec{\mathbf{0}}\hfill & \hfill {\mathbf{m}}_{\mathbf{R}}\hfill \end{array}\right],{\mathbf{M}}_{\mathbf{\Delta }=}\mathit{diag}\left(1,d_1,d_2,d_3\right),(10)$

where the 3 × 3 sub-matrices m_D and m_R are constructed from the diattenuation vector $\vec{\mathbf{D}}$ and the retardance value φ, respectively. All d_i are termed as the principal depolarization factors and could be utilized to form another three-dimensional depolarization space—the canonical one Σ_Δ. By this way, additional polarimetric information can be extracted from M^f after finding each product matrices from Eq. 9 (from here on, the M^f entering the symmetric decomposition will be used interchangeably with M_f). To achieve this, first, one needs to find the diattenuation matrices by solving the eigenvector–eigenvalue problem of [36]:

$\left({\mathbf{M}}_{\mathit{f}}^{\mathbf{T}}{\mathbf{G}\mathbf{M}}_{\mathit{f}}\mathbf{G}\right){\mathit{\xi }}_{\mathbf{1}}={\beta }^2{\mathit{\xi }}_{\mathbf{1}},\left({\mathbf{M}}_{\mathit{f}}{\mathbf{G}\mathbf{M}}_{\mathit{f}}^{\mathbf{T}}\mathbf{G}\right){\mathit{\xi }}_{\mathbf{2}}={\beta }^2{\mathit{\xi }}_{\mathbf{2}},(11)$

where G = diag (1,-1,-1,-1) is the Minkowski metric tensor and β² is a common eigenvalue. When the eigenvectors ${\xi }_{\mathbf{1,2}}={(1,{\vec{\mathbf{D}}}_{\mathbf{1,2}})}^{\mathbf{T}}$ are found, then the diattenuation vectors can be used to obtain m_Di and M_Di:

${\mathbf{m}}_{\mathbf{D}}=\sqrt{1-{\mathbf{D}}^2}\mathbf{I}+\left(1-\sqrt{1-{\mathbf{D}}^2}\right)\widehat{\mathbf{D}}{\widehat{\mathbf{D}}}^{\mathbf{T}},(12)$

where I is 3 × 3 identity matrix and $\widehat{\mathbf{D}}$ is the unit vector along $\vec{\mathbf{D}}$. Once the diattenuation matrices are determined, one can put and calculate:

${\mathbf{M}}_{{\mathbf{D}}_{\mathbf{2}}}^{-\mathbf{1}}{\mathbf{M}}^{\mathit{f}}{\mathbf{M}}_{{\mathbf{D}}_{\mathbf{1}}}^{-\mathbf{1}}={\mathbf{M}}_{{\mathbf{R}}_{\mathbf{2}}}{\mathbf{M}}_{\mathbf{\Delta }}{\mathbf{M}}_{{\mathbf{R}}_{\mathbf{1}}}^{\mathbf{T}}={\mathbf{M}}^{\prime }=\left[\begin{array}{cc}\hfill \beta \hfill & \hfill {\vec{\mathbf{0}}}^{\mathbf{T}}\hfill \\ \hfill \vec{\mathbf{0}}\hfill & \hfill {\mathbf{m}}^{\prime }\hfill \end{array}\right].(13)$

Since M′ and M_Δ contain no diattenuation and polarizance, by virtue of SVD the 3 × 3 sub-matrix m′ can be reckoned, which will be sufficient to construct the retarder matrices M_R1,2 and the canonical depolarizer matrix M_Δ, thus completing the symmetric decomposition algorithm. After this step, it becomes possible to calculate the retardance and the net depolarization values from the following:

$\phi ={\cos }^{-1}\left[\frac{tr\left({\mathbf{m}}_{\mathbf{R}}\right)-1}{2}\right],\mathit{\Delta }=1-\frac{\left|d_1\right|+\left|d_2\right|+\left|d_3\right|}{3},0\le \mathit{\Delta }\le 1.(14)$

3 Materials and Methods

3.1 Ex vivo Colon Samples

A cooperation framework for optical examination of cancerous tissues (approval #286/2012 of the local Ethical Committee) between the Institute of Electronics—Bulgarian Academy of Sciences and the Surgical Department of University Hospital “Tsaritsa Yoanna—ISUL,” Sofia was initially formed. As a result, multiple tissue samples for optical measurements were provided, initially diagnosed by the physicians. The tissue samples included in this study were excised during standard surgical procedure for tumor removal. Part of the excised tumors underwent standard pathology evaluation and the other part of the tumors with the adjacent healthy tissue sections were transported to the optical laboratory. No additional contrast agents were used. The samples’ safe-keeping was done via modified Kreb’s solution under isothermal conditions. First, at the Biophotonics Laboratory, Institute of Electronics, their fluorescence spectra were evaluated with different modalities [67–69]. Although the fluorescence measurements and inelastic scattering are not the subject of this study, we planned to apply the ML approach to the obtained fluorescence spectra for future studies. Afterward, a fixation in 10% formaline solution of the tissue samples was done. For this study in elastic scattering mode, in total five samples were selected for polarimetric measurements in the optoelectronics laboratory, Oulu University. The investigated samples include colon and gastric adenocarcinoma, G2: moderately differentiated (intermediate grade) and G3: poorly differentiated (high grade). The thickness range for both healthy and tumor tissue zones is of several millimeters and, therefore, the polarimetric measurements were performed in reflection geometry with angular configuration of the experimental setup shown in side view for better clarity in Figure 1.

FIGURE 1

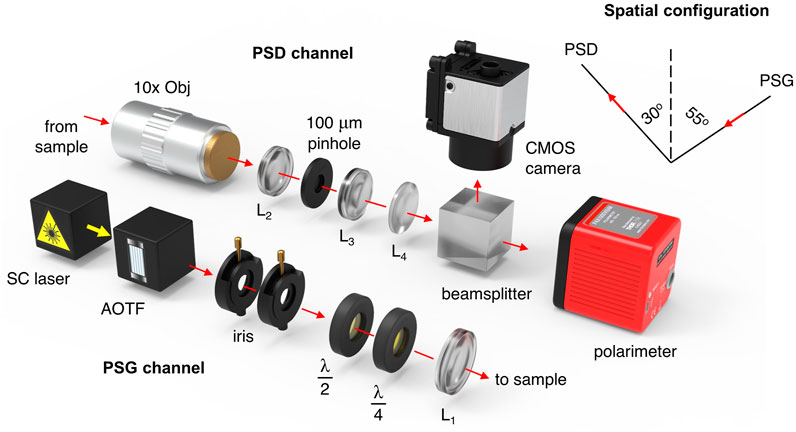
FIGURE 1. Schematic representation of the experimental setup. Reprinted with permission from [26]^© The Optical Society (Optica Publishing Group).

3.2 Polarimetric Set-Up

For the current study, the angles of incidence and detection were fixed at 55° and 30°, respectively. Schematically, the optical system is shown in Figure 1, where the presented optical configuration allowed us to measure a full Mueller matrix of an arbitrary sample with Stokes polarimeter by performing only four sequential measurements.

For each of the input polarization states (H,V,P,R), a continuous modulation was performed with commercially available polarimetric device (Thorlabs Ltd., United States), utilizing a rotating quarter-wave plate and a fixed linear polarizer. The polarimetric device has been initially calibrated by the manufacturer, while the whole optical system was tested in reflection geometry to measure a mirror Mueller matrix, whose theoretical form is diag (1,1,1,1). As a results, for each matrix element a RMSE value of 0.02 was calculated (i.e., see [26]). Tube systems were used to protect all measurements of undesired stray light, while for reproducibility, a motorized x-y translation stage was employed. All samples and their corresponding healthy and cancerous zones were scanned two-dimensionally with each of the abovementioned input polarization states. The whole region of interest was selected to be 1 mm², while the step size in both x-y directions—0.2 mm, respectively. The combination of a supercontinuum fiber laser—SC (Leukos Ltd., France) and an acousto-optic tunable filter—AOTF (Leukos Ltd., France) was used to produce a probing wavelength of 635 nm (FWHM 8 nm) and output power—2 mW. The beam was collimated with the help of two sequentially placed irises. To rotate the azimuth of the linearly polarized laser beam, a half-wave plate was used. For acquisition of input circularly polarized light, an electrically-driven liquid crystal variable quarter-wave plate was employed. Objective lenses (10×), lens L₂, 100 μm pinhole, and lens L₃ were adopted to collect the scattered light and factor out any out-of-focus photons. Finally, the 90–10 beam splitter and the CMOS camera provided more precise focus adjustments. All Mueller matrix elements were obtained following the approach presented in [26]. In total, 330 healthy and 340 tumor Mueller matrices were measured and filtered with Cloude’s physical realizability method. Afterward, the filtered matrices were decomposed using the symmetric decomposition and the depolarization metric calculus, as described in Section 2.

4 Results and Discussion

4.1 Polarimetry

As can be seen from Figure 2, upon inclusion of all experimental data from various colon samples with tumors at different stages of development, a superimposing for the majority of the data points from both health conditions could be observed. Hence, the inter-patient variability restricts us to evaluate two separate clusters corresponding to the measurements of healthy and cancerous zones of colon specimens or to find specific trends within either Poincaré sphere or the three depolarization spaces. As a result, supplementary techniques and algorithms for data processing must be included all of which will be addressed in the following subsections.

FIGURE 2

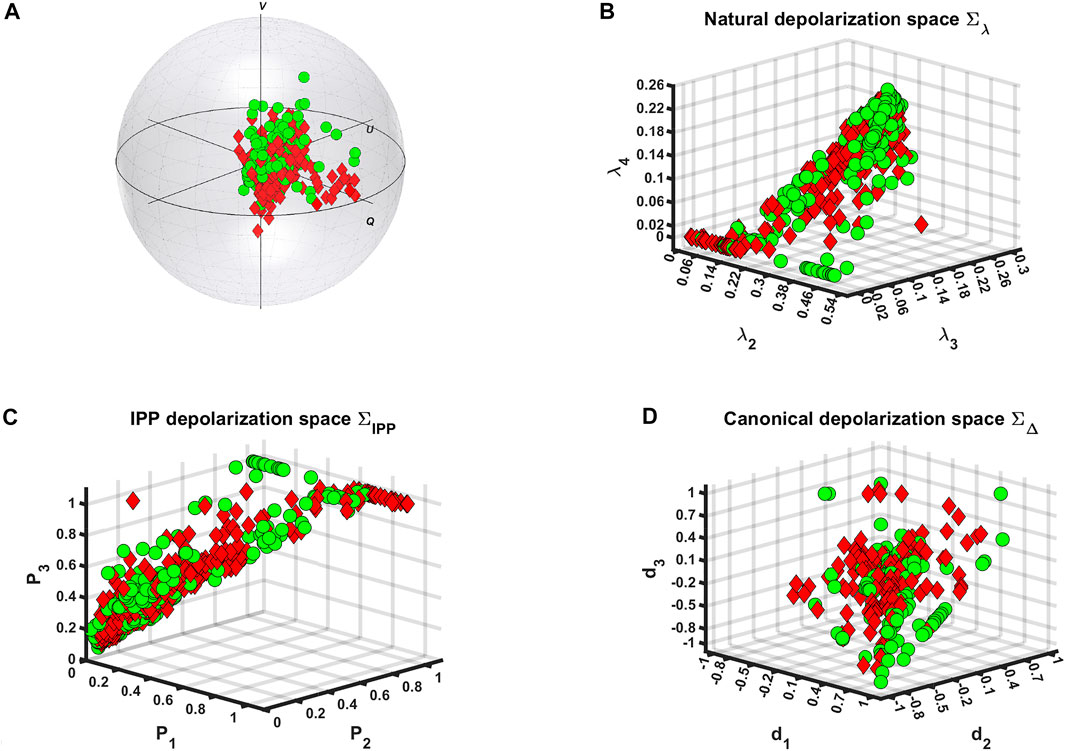
FIGURE 2. Visualization of polarimetric data at all spatial locations for both colon tissue zones measurements ◦—healthy and ⋄ —tumor via: (A) Poincaré sphere for probing (or incident) circular polarization, (B) natural, (C) IPP, and (D) canonical depolarization spaces.

4.2 Data Post-processing

After inspection of the initial data processing sequence from Eq. 1 through Eq. 14, it became possible to extract 20 polarimetric quantities that describe unambiguously the polarimetric response of the tissue samples and are to be used as predictors, namely, λ_1,2,3,4, P_1,2,3, P_Δ, PI, S, D, P, D_1,2, d_1,2,3, Δ, and φ_1,2. Initially, the mean values and their standard deviations were calculated, where for both health conditions the second statistical moment of the mean for φ₂ was found to be approximately three times higher than the second statistical moment of the mean for φ₁, thus considering φ₂ as an unreliable predictor and, consequently, it was omitted. Second, the Shapiro–Wilk normality test [70, 71] was computed on a significance level α = 0.05, where test’s results indicated non-Gaussian distribution for all polarimetric quantities. Thus, further on non-parametric statistical tests and machine learning algorithms (MLAs), which do not require data from normal distribution were used. Next, for each of the polarimetric parameters pairs grouped as healthy vs tumor, the Mann–Whitney test [70, 72] was computed for the same α, in order to find out whether the polarimetric pairs were drawn from different or similar distributions. Only for λ_1,2, P₁, D, P, and D_1,2, the test indicated that these parameters were drawn from different distributions (all tests were considered as statistically significant if the computed p-value $<\alpha$). Afterward, the dataset was reorganized with each column j being a polarimetric quantity, where the measurements from both health conditions were concatenated by rows. Then a factor/categorical variable was added to indicate the health condition as either 0–healthy or 1–tumor. Finally, with the exception of the categorical variable, all other quantities were normalized with the following function ${\mathcal{F}}_{\mathrm{n}}$ = $(x(j)-x_{\mathit{min}}(j))\cdot {(x_{\mathit{max}}(j)-x_{\mathit{min}}(j))}^{-1}$, in order to restrict them as dimensionless variables that vary within the closed interval [0,1]. Additional feature selection is necessary, in order to avoid the use of highly correlated predictors and multicollinearity, respectively. For instance, Δ, S, P_Δ, and PI were removed from the main model since they are derived from d_i, λ_i, and P_i, and according to the Mann–Whitney test, their data for both health conditions are drawn from the same distribution. Moreover, a priori high correlation is also expected for λ_i and P_i after inspection of Eq. 5, therefore two submodels were formed: one omitting all P_i—shortly denoted as—“eigenvalue model” and one omitting all λ_i referred as—“IPP model.” The remaining predictors: D, P, D_1,2, d_1,2,3, and φ₁ were included in both submodels.

4.3 Machine Learning

4.3.1 Unsupervised Machine Learning and Principal Component Analysis (PCA)

For n number of predictors, there are n(n-1)/2 scatter plots to summarize and graphically represent the available data. For large number of n, such approach would be computationally and analytically ineffective as most of the plots may be redundant, for instance 55 plots to be analyzed for each of the submodels. Therefore, we started the ML approach with the principal component analysis. For each of the submodels PCA was applied to summarize the available data, as shown in Figure 3, where from Figure 3A it was calculated that 7 principal components (PCs) retain more than 95% of the total variance for the eigenvalue model and 6 PCs—for the IPP model. By this way, PCA can be combined with classification MLAs, in order to use the non-redundant features only from both submodels, and any other collinear or highly correlated features could be avoided (i.e., all collinear features will result in a single PCA component). To project the experimental data onto the principal component space, one can compute the principal component scores (PCS). As a result, there is no correlation between all PCS of both submodels, as shown in Figures 3B,C, whereas 95% of the total variance is sustained. Such an approach would facilitate in increasing the final classification accuracy.

FIGURE 3

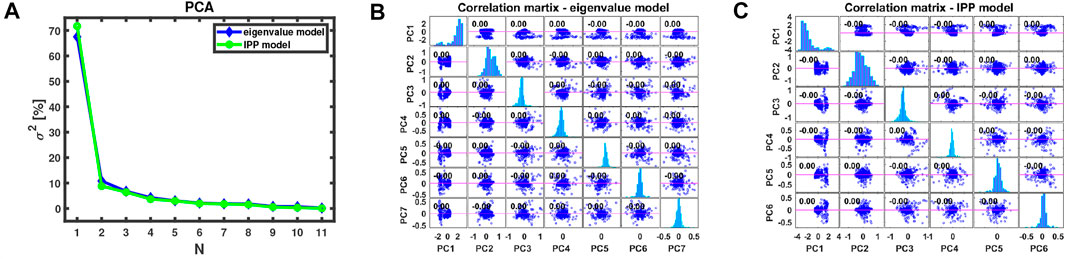
FIGURE 3. (A) PCA for N number of components, explaining the corresponding percentage of variance σ² for both submodels. Correlation matrices for (B) 7 PCs and their scores—eigenvalue model and (C) 6 PCs and their scores—IPP model.

4.3.2 Supervised Machine Learning

First, the datasets for both submodels without the PCs were randomly split to obtain two data subsets for training and testing as follows: 570 samples (85% of the total data) for training and 100 samples (15% of the total data) for testing. To evaluate the best predictors for tumor detection (see Figure 4), logistic regression (LR) was trained independently with both submodels but without using their PCS. By this way, it was found out that the inclusion of λ₁ is deteriorating for the model performance, and this parameter was consequently removed from the analysis. In Figure 4 the top and bottom axes include 1D distribution of the predictors’ normalized data, for both health conditions (0–Healthy, 1–Tumor), respectively. It could be well observed that d₁, R₁, and λ₂ show excellent detection performance for malignant formations, where the uncertainty intervals (in grey) remain close to the probability values (all blue lines). Although the probabilities for P, D₂, and P₁ parameters are lower and have higher uncertainties compared to the former triplet of polarimetric parameters, each one of the latter triplet could also be identified with sufficient probability values. Typically, malignant tumor formations cause morphological alterations in tissues and alter the collagen extracellular matrix as well as the cellular organelles by modifying their sizes and shapes. This leads to changes in tissue heterogeneity, followed by reduced number of scattering events as R₁ may indicate. Also, Rayleigh–Mie transition of light scattering regime occurs that in turn affects light (de) polarization [10, 11, 46]. Whereas the depolarization parameter d₁ can be considered as a weight coefficient for the Stokes component S₁, higher polarimetric purity would indicate less depolarizing media. Such a conclusion is consistent with previously reported results for colon tumor tissues [26, 45]. Additionally, both polarizance and diattenuation (especially D₂ from the symmetric decomposition) were also found with higher values for the tumor tissue zones of colon in [26]. By this way, this polarimetric doublet may be considered as noteworthy tumor markers for the angular-resolved measurements with wide angle acceptance or any angles of incidence and detection different from normal.

FIGURE 4

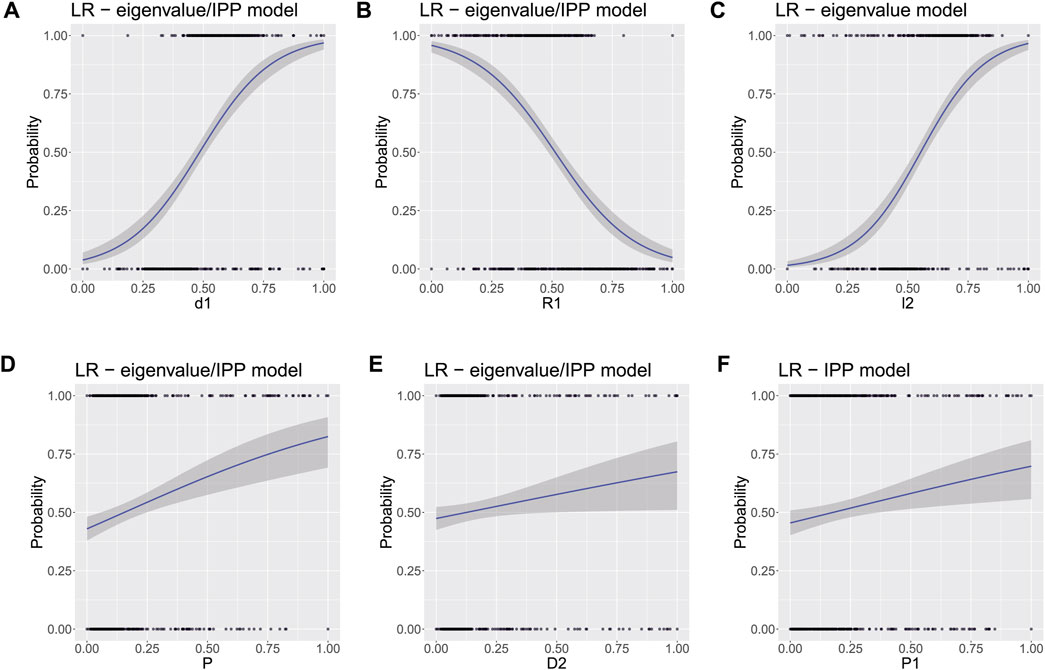
FIGURE 4. Probability for tumor detection, calculated from LR: (A) d₁, (B) R₁, (C) λ₂, (D) P, (E) D₂, and (F) D₂. For subfigures A, B, D, and E the results are comparable for both submodels, while subfigures C and F were computed from the eigenvalue and the IPP model, respectively (φ₁ ≡ R₁ and λ₁ ≡ l₁).

Next, solely for the classification purpose LR, random forest (RF), and support vector machines (SVM) algorithms were again trained with the corresponding PCS data subsets for both submodels, split again randomly with the same proportions. All MLAs models underwent initial tuning to pick up the best possible hyperparameters. In the case of RF, a randomly selected fraction of k = N^1/2 from all predictors was drawn without replications to create an ensemble of decision trees. For both submodels, having three predictors per split was found to be the most optimal choice. By setting the number of trees to 30, we reached the same classification accuracy as with 500 trees, while the training time was reduced by an order of magnitude. Without replications, there are 35 possible predictor combinations (3 randomly selected PCs and their scores from total 7) for the eigenvalue model and 20 possible predictor combinations (3 randomly selected PCs and their scores from 6) for the IPP model, calculated from $C_N^k$ = N!⋅(k!(N-k)!)⁻¹. For all decision trees in the ensemble (including replications), the possible number of predictor combinations for training is 4,960 for both submodels, calculated from $K_N^k$ =(N + k-1)!⋅(k!(N-1)!)⁻¹. By this way, RF algorithm could be considered as more reliable MLA for tumor classification, even if the dataset size is small and/or there is a presence of correlated predictors. The out-of-bag (OOB) error was found ≈5% for the eigenvalue model and ≈11% for the IPP model. In the case of SVM algorithm, after cross-validation a polynomial kernel of third degree was found to provide the best classification accuracy with both submodels. Additional regularization C [63, 64] was necessary to add a penalty for each misclassified data point. Usually, small values of C result in smaller margin, low bias, and high variance in the model and vice versa for large C values [63, 64]. After the cross-validation cycle, the optimal values of C were found to be 1 for both submodels.

After the application of the aforementioned MLAs for classification, various other metrics were used to evaluate the classifiers’ performances. For instance, their accuracy, sensitivity, specificity, relative risk of misclassification (R_r), receiver operating characteristic (ROC) curve, and the corresponding area under curve (AUC). While the sensitivity represents the portion of the correctly predicted true positive (TP) values (or in this study—the tumor class), the specificity is related to the amount of the correctly predicted true negative (TN) values (analogously—the healthy class). For the ideal classifier, the accuracy (sum of all true predicted classes normalized to the sum of all true and all false predicted classes), sensitivity, and specificity should be 100%. However, due to the presence of wrongly predicted class values such as false positive (FP—healthy tissue but detected as tumor class) and false negative (FN—tumor tissue but detected as healthy class), the models’ detection performance deteriorate. In this regard, the relative risk of misclassifications can be calculated as follows:

$R_r=\frac{FP}{FP+TN}\cdot {\left[\frac{TP}{TP+FN}\right]}^{-1}.(15)$

Ideally, lesser misclassified values will lead to closer proximity of the ROC curve to a stepwise profile. As there is no perfect model, losses introduced from wrongly predicted class values will always be a considerable factor, which can be simply calculated as 1-AUC. The results from all classification MLAs are presented in Figure 5 and in Table 1.

FIGURE 5

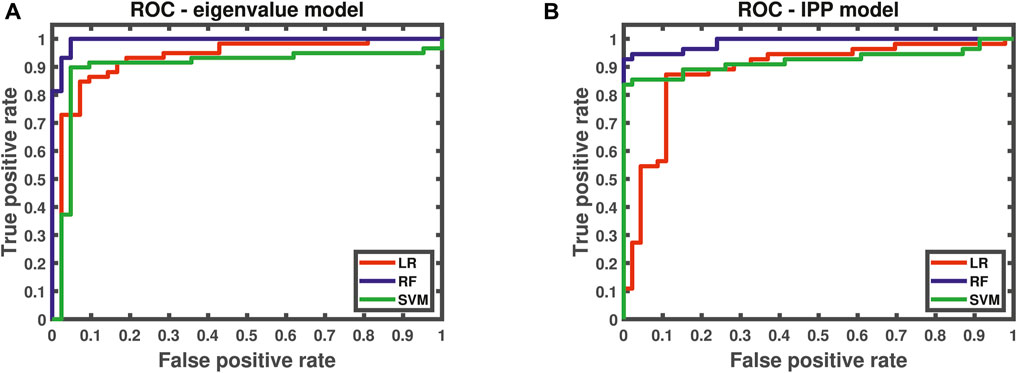
FIGURE 5. ROC curves for (A) eigenvalue model (trained with 7 PCs and their scores) and (B) IPP model (trained with 6 PCs and their scores).

TABLE 1

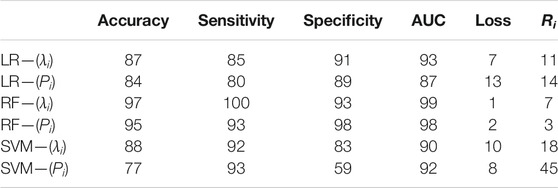
TABLE 1. Supplementary table associated with all classification MLAs performances, where all numerical values are in %. All MLAs were trained with 7 PCs and their scores for the eigenvalue model and 6 PCs and their scores for the IPP model.

From the graphical representation of the figures above and the values in Table 1, it becomes possible to outline both submodels performances for tumor tissue classification. To sum up, all MLAs trained with the corresponding PCS provide reliable accuracy and AUC values close to 1. The eignevalue submodel seems to perform better than the IPP model with lower OOB error and higher diagnostic quantities. Whereas the LR algorithm is better suited to evaluate the predictor’s probability for tumor detection and has higher specificity values than SVM, the latter MLA has higher sensitivity values than LR and is better suited to predict the healthy class. On the other hand, the RF algorithm yielded the best results for classification with negligible losses and misclassification risk. However, a parallel should be drawn between RF and SVM. The former can be computed with only two hyperparameters—the number of variables/predictors per each random split and the number of trees. On the other hand, the latter is dependent and highly sensitive to the kernel choice and degree, regularization parameter(s), and choices for support vectors and margins all of which influence the variance-bias trade-off. Additionally, the posterior probabilities for both classes were found to differ at most for RF, whereas for SVM, the difference between these values was very small, thus reducing the reliability of SVM for classification for the current study.

5 Conclusion

In this study, multiple formalin-fixed, ex vivo, human colon samples, containing healthy and malignant formations, were measured with custom-built polarimetric setup in reflection geometry. Analogously to [25, 26, 46], where a single, human colon specimen and tumor grade were considered for binary classification of all measured sites, in the current study the same experimental approach was extended for multiple colon samples and tumor grades, respectively. All experimental Mueller matrices were filtered for data noise and/or experimental errors using Cloude’s physical realizability method. Both symmetric decomposition and the depolarization metric calculus were used in order to extract the (de)polarization fingerprint of the samples under examination. By this way, the symmetric decomposition could be regarded as very well suited decomposition algorithm for angular-resolved measurements by providing a pure, canonical depolarizer Mueller matrix and matrices for the corresponding counterparts of D₁ − D₂ and R₁ − R₂. Also, the polarimetric purity calculus enriched the polarimetric dataset and provided more predictors to be used for ML. Due to the inter-patient variability and the different tumor stages, a superimposing between the dataset points was observed. With the help of statistical analysis, the most prominent polarimetric quantities were selected for inclusion in two tissue polarimetric models. Additionally, normalization and feature selection were performed in order to deal with dimensionless quantities and to avoid highly correlated predictors. Due to the small dataset size, random split of dataset with proportions 50:25:25 [%] for training:validating:testing was not feasible. Instead, a random split as 85:15 [%] for training:testing was used, thus providing more training data to feed the MLAs. Trained by this way, LR provided the predictors’ probability for tumor detection, where d₁, R₁, λ₂, P, D₂, and P₁ were found most prominent diagnostic markers. Additionally, the data of these polarimetric quantities for both health conditions, with the exception of d₁ and R₁, were found to be drawn from different distributions, according to the Mann–Whitney test on a significance level α = 0.05. The combination of training parameters was optimized after computing PCA and training all classification MLAs with the PCs and their scores describing 95% of the total variance. By this way, any collinear and/or the redundant features were eliminated from both polarimetric models, hence reducing the computational time for training. Similar approaches and methods have been applied with success very recently to other kinds of biological samples [73]. Additional hyperparameters’ optimizations and cross validation were carried out to improve the classification accuracy. To conclude, the classification with the eigenvalue model is more accurate than the classification with the IPP model, whereas RF provided the best results for that purpose. For a single sample and colon cancer grade tissue polarimetry could be utilized as a supplementary diagnostic to support the golden standard histology analysis by a pathologist as previously reported in the studies mentioned in references [25, 26, 46]. However, when more samples are used with different grades of colon cancer, the experimental data may suffer from the inter-patient variability issue and as presented in Section 4.1, Figure 2 to produce superimposing results. In combination, both unsupervised and supervised MLAs may provide an adequate solution to overcome this obstacle. The results from the current study were also found to be consistent to the previously reported results in the studies mentioned in references [25, 26, 46]. The scope of the current pilot study involved small number of samples and measurements; therefore, only a qualitative approach was adopted for the two-class classification problems: either healthy or tumor. With more samples and measurements at avail, the methods proposed in the current study could be extended for multi-class classification, that is, the prediction of the tumor grade. This will require a transition to handle and process larger data frames, use additional boosting algorithms [63, 64] to increase the classification accuracy, and delve into reinforcement and deep learning, as well as to adopt parallel computing to reduce the computational time. By this way artificial intelligence has a great potential to come into force in supporting both physicists and physicians for classification and differentiation between healthy versus tumor colon tissues or for cancer diagnostics in general.

Data Availability Statement

The datasets presented in this article are not readily available because of both ethical and confidentiality reasons, restricting the data for further redistribution. Requests to access the datasets should be directed to DI, deyan.ivanov@polytechnique.edu.

Ethics Statement

The studies involving human participants were reviewed and approved by TG, ts.genova@gmail.com. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The experimental investigations were supported by the Bulgarian National Science Fund under grant #KP06-N38/13/2019. The current research was supported by the Academy of Finland (Grants 314639 and 325097) and INFOTECH strategic funding. Prof. Igor Meglinski also acknowledges the support from the Ministry of Science and Higher Education of the Russian Federation within the framework of state support for the creation and development of world-class research centres “Digital Biodesign and Personalized Healthcare” No. 075-15-2020-926. VD kindly acknowledges for personal support from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant, agreement No. 839888.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

All authors acknowledge the anonymous patients who volunteered for this study. The current article is also intended to pay special tribute in memory of Assoc. Prof. Ekaterina Borisova, PhD. DI acknowledges the PhD fellowship funding by the Doctoral School of Institut Polytechnique de Paris. Last but not least, special acknowledgements to Milen Minev for all his valuable data science advice.

References

1. Azzam RMA, Bashra NM. Ellipsometry and Polarized Light. Amsterdam: North-Holland (1977).

Google Scholar

2. Bertrand N, Drévillon B, Bulkin P. In Situ infrared Ellipsometry Study of the Growth of Plasma Deposited Silica Thin Films. J Vacuum Sci Technol A: Vacuum, Surf Films (1998) 16(1):63–71. doi:10.1116/1.581012

CrossRef Full Text | Google Scholar

3. Fallet C, Novikova T, Foldyna M, Manhas S, Ibrahim BH, De Martino A, et al. Overlay Measurements by Mueller Polarimetry in Back Focal Plane. J Micro/nanolith MEMS MOEMS (2011) 10:033017. doi:10.1117/1.3626852

CrossRef Full Text | Google Scholar

4. Novikova T, Bulkin P, Popov V, Haj Ibrahim B, De Martino A. Mueller Polarimetry as a Tool for Detecting Asymmetry in Diffraction Grating Profiles. J Vacuum Sci Technol B, Nanotechnology Microelectronics: Mater Process Meas Phenomena (2011) 29:051804. doi:10.1116/1.3633693

CrossRef Full Text | Google Scholar

5. Gottlieb D, Arteaga O. Mueller Matrix Imaging with a Polarization Camera: Application to Microscopy. Opt Express (2021) 29(21):34723–34. doi:10.1364/oe.439529

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Manhas S, Swami MK, Buddhiwant P, Ghosh N, Gupta PK, Singh J. Mueller Matrix Approach for Determination of Optical Rotation in Chiral Turbid media in Backscattering Geometry. Opt Express (2006) 14:190–202. doi:10.1364/opex.14.000190

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Meglinski I, Trifonyk L, Bachinsky V, Vanchulyak O, Bodnar B, Sidor M, et al. Shedding the Polarized Light on Biological Tissues. Singapore: Spinger Briefs in Applied Science and Technology (2021).

Google Scholar

8. Ghosh N, Vitkin I. Tissue Polarimetry: Concepts, Challenges, Applications, and Outlook. J Biomed Opt (2011) 16:110801. doi:10.1117/1.3652896

CrossRef Full Text | Google Scholar

9. Mazumder N, Xiang L, Qiu J, Fu-Jen K. In Pixel Analysis of Molecular Structure with Stokes Vector Resolved Second Harmonic Generation Microscopy. Proc SPIE (2014) 8948:894822. doi:10.1117/12.2036651

CrossRef Full Text | Google Scholar

10. Borovkova M, Peyvasteh M, Dubolazov O, Ushenko Y, Ushenko V, Bykov A, et al. Complementary Analysis of Mueller-Matrix Images of Optically Anisotropic Highly Scattering Biological Tissues. J Eur Opt Soc.-Rapid Publ (2018) 14:20. doi:10.1186/s41476-018-0085-9

CrossRef Full Text | Google Scholar

11. Borovkova M, Bykov A, Popov A, Pierangelo A, Novikova T, Pahnke J, et al. Evaluating β-amyloidosis Progression in Alzheimer's Disease with Mueller Polarimetry. Biomed Opt Express (2020) 11:4509–19. doi:10.1364/boe.396294

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li P, Lee HR, Chandel S, Lotz C, Groeber-Becker FK, Dembski S, et al. Analysis of Tissue Microstructure with Mueller Microscopy: Logarithmic Decomposition and Monte Carlo Modeling. J Biomed Opt (2020) 25(1):1–11. doi:10.1117/1.JBO.25.1.015002

PubMed Abstract | CrossRef Full Text | Google Scholar

13. He C, He H, Chang J, Chen B, Ma H, J Booth M. Polarisation Optics for Biomedical and Clinical Applications: a Review. Nat Light: Sci Appl (1942) 10:1–20.

Google Scholar

14. Sobin L, Gospodarowicz M, Wittekind C. TNM Classification of Malignant Tumors. 7th ed. New York: John Wiley & Sons (2009). International Union Against Cancer (UICC).

Google Scholar

15. Wang TD, Van Dam J. Optical Biopsy: A New Frontier in Endoscopic Detection and Diagnosis. Clin Gastroenterol Hepatol (2004) 2:744–53. doi:10.1016/s1542-3565(04)00345-3

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Croce AC, Ferrigno A, Bottiroli G, Vairetti M. Autofluorescence-based Optical Biopsy: An Effective Diagnostic Tool in Hepatology. Liver Int (2018) 38:1160–74. doi:10.1111/liv.13753

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Georgakoudi I, Feld MS. The Combined Use of Fluorescence, Reflectance, and Light-Scattering Spectroscopy for Evaluating Dysplasia in Barrett's Esophagus. Gastrointest Endosc Clin North America (2004) 14:519–37. doi:10.1016/j.giec.2004.03.008

CrossRef Full Text | Google Scholar

18. He K, Zhao L, Chen Y, Huang X, Ding Y, Hua H, et al. Label‐free Multiphoton Microscopic Imaging as a Novel Real‐time Approach for Discriminating Colorectal Lesions: A Preliminary Study. J Gastroenterol Hepatol (2019) 34:2144–51. doi:10.1111/jgh.14772

CrossRef Full Text | Google Scholar

19. Khristoforova YA, Bratchenko IA, Myakinin OO, Artemyev DN, Moryatov AA, Orlov AE, et al. Portable Spectroscopic System for In Vivo Skin Neoplasms Diagnostics by Raman and Autofluorescence Analysis. J Biophotonics (2019) 12:e201800400. doi:10.1002/jbio.201800400

CrossRef Full Text | Google Scholar

20. Kupinski M, Boffety M, Goudail F, Ossikovski R, Pierangelo A, Rehbinder J, et al. Polarimetric Measurement Utility for Pre-cancer Detection from Uterine Cervix Specimens. Biomed Opt Express (2018) 9(11):5691–702. doi:10.1364/boe.9.005691

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kupinski M, Rehbinder J, Haddad H, Deby S, Vizét J, Teig B, et al. Tasked-based Quantification of Measurement Utility for Ex Vivo Multi-Spectral Mueller Polarimetry of the Uterine Cervix. In: SPIE Proceedings (Optical Society of America, 2017); June 2017; Munich, Germany. paper 104110N–1.

Google Scholar

22. Ushenko VA, Hogan BT, Dubolazov A, Grechina AV, Boronikhina TV, Gorsky M, et al. Embossed Topographic Depolarisation Maps of Biological Tissues with Different Morphological Structures. Sci Rep (2021) 11:3871. doi:10.1038/s41598-021-83017-2

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Hogan BT, Ushenko VA, Syvokorovskaya A-V, Dubolazov AV, Vanchulyak OY, Ushenko AG, et al. 3D Mueller Matrix Reconstruction of the Optical Anisotropy Parameters of Myocardial Histopathology Tissue Samples. Front Phys (2021) 9:737866. doi:10.3389/fphy.2021.737866

CrossRef Full Text | Google Scholar

24. Ushenko VA, Hogan BT, Dubolazov A, Piavchenko G, Kuznetsov SL, Ushenko AG, et al. 3D Mueller Matrix Mapping of Layered Distributions of Depolarisation Degree for Analysis of Prostate Adenoma and Carcinoma Diffuse Tissues. Sci Rep (2021) 11:5162. doi:10.1038/s41598-021-83986-4

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ivanov D, Dremin V, Bykov A, Borisova E, Genova T, Popov A, et al. Colon Cancer Detection by Using Poincaré Sphere and 2D Polarimetric Mapping of Ex Vivo colon Samples. J Biophotonics (2020) 13:e202000082. doi:10.1002/jbio.202000082

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Ivanov D, Dremin V, Borisova E, Bykov A, Novikova T, Meglinski I, et al. Polarization and Depolarization Metrics as Optical Markers in Support to Histopathology of Ex Vivo colon Tissue. Biomed Opt Express (2021) 12:4560–72. doi:10.1364/BOE.426713

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Dremin V, Sieryi O, Borovkova M, Näpänkangas J, Meglinski I, Bykov A. Histological Imaging of Unstained Cancer Tissue Samples by Circularly Polarized Light. In: European Conferences on Biomedical Optics 2021 (ECBO); June 2021; Munich, Germany. EM3A.3.

Google Scholar

28. Dremin V, Anin D, Sieryi O, Borovkova M, Näpänkangas J, Meglinski I, et al. Imaging of Early Stage Breast Cancer with Circularly Polarized Light. Proc SPIE (2020) 11363:1136304. doi:10.1117/12.2554166

CrossRef Full Text | Google Scholar

29. Rodríguez-Núñez O, Schucht P, Hewer E, Novikova T, Pierangelo A. Polarimetric Visualization of Healthy Brain Fiber Tracts under Adverse Conditions: Ex Vivo Studies. Biomed Opt Express (2021) 12(10):6674–85. doi:10.1364/boe.439754

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Lee HR, Saytashev I, Du Le VN, Mahendroo M, Ramella-Roman J, Novikova T. Mueller Matrix Imaging for Collagen Scoring in Mice Model of Pregnancy. Sci Rep (2021) 11(1):15621. doi:10.1038/s41598-021-95020-8

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Schucht P, Lee HR, Mezouar HM, Hewer E, Raabe A, Murek M, et al. Visualization of white Matter Fiber Tracts of Brain Tissue Sections with Wide-Field Imaging Mueller Polarimetry. IEEE Trans Med Imaging (2020) 39(12):4376–82. doi:10.1109/tmi.2020.3018439

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Novikova T, Rehbinder J, Haddad H, Deby S, Teig B, Nazac A, et al. Multi-spectral Mueller Matrix Imaging Polarimetry for Studies of Human Tissue. Clinical and Translational Biophotonics 10.1364/TRANSLATIONAL.2016.TTh3B.2. Fort Lauderdale, Florida United States: OSA Biophotonics Congress (2016). paper TTh3B.

Google Scholar

33. Gil-Perez GJ, Ossikovski R. Polarized Light and the Mueller Matrix Approach. Boca Raton, Florida: Taylor and Francis: CRC Press (2016).

Google Scholar

34. Cloude S. Conditions for the Physical Realizability of Matrix Operators in Polarimetry. Proc SPIE (1989) 1166:177–85.

Google Scholar

35. Lu S-Y, Chipman RA. Interpretation of Mueller Matrices Based on Polar Decomposition. J Opt Soc Am A (1996) 13:1106–13. doi:10.1364/josaa.13.001106

CrossRef Full Text | Google Scholar

36. Ossikovski R. Analysis of Depolarizing Mueller Matrices through a Symmetric Decomposition. J Opt Soc Am A (2009) 26:1109–18. doi:10.1364/josaa.26.001109

CrossRef Full Text | Google Scholar

37. Ossikovski R. Differential Matrix Formalism for Depolarizing Anisotropic media. Opt Lett (2011) 36:2330–2. doi:10.1364/ol.36.002330

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Gonzalez M, Ossikovski R, Novikova T, Ramella-Roman JC. Introduction of a 3 X 4 Mueller Matrix Decomposition Method. J Phys D: Appl Phys (2021) 54(42):424005. (1–9). doi:10.1088/1361-6463/ac1622

CrossRef Full Text | Google Scholar

39. Goldstein DH. Polarized Light. 3rd ed. Boca Raton, Florida: Taylor and Francis: CRC Press (2010).

Google Scholar

40. Cloude S. Conditions for the Physical Realisability of Matrix Operators in Polarimetry. Proc SPIE (1989) 1166:177–85.

Google Scholar

41. Lee HR, Li P, Yoo TSH, Lotz C, Groeber-Becker FK, Dembski S, et al. Digital Histology with Mueller Microscopy: How to Mitigate an Impact of Tissue Cut Thickness Fluctuations. J Biomed Opt (2019) 24:1–9. doi:10.1117/1.JBO.24.7.076004

CrossRef Full Text | Google Scholar

42. Trifonyuk L, Sdobnov A, Baranowski W, Ushenko V, Olar O, Dubolazov A, et al. Differential Mueller Matrix Imaging of Partially Depolarizing Optically Anisotropic Biological Tissues. Lasers Med Sci (2020) 35(4):877–91. doi:10.1007/s10103-019-02878-2

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ahmad I, Ahmad M, Khan K, Ashraf S, Ahmad S, Ikram M. Ex Vivocharacterization of normal and Adenocarcinoma colon Samples by Mueller Matrix Polarimetry. J Biomed Opt (2015) 20:056012. doi:10.1117/1.jbo.20.5.056012

CrossRef Full Text | Google Scholar

44. Rehbinder J, Haddad H, Deby S, Teig B, Nazac A, Novikova T, et al. Ex vivoMueller Polarimetric Imaging of the Uterine Cervix: a First Statistical Evaluation. J Biomed Opt (2016) 21(7):071113. doi:10.1117/1.jbo.21.7.071113

CrossRef Full Text | Google Scholar

45. Pierangelo A, Manhas S, Benali A, Antonelli MR, Novikova T, Validire P, et al. Use of Mueller Polarimetric Imaging for the Staging of Human colon Cancer. Proc SPIE (2011) 7895:78950E. doi:10.1117/12.878248

CrossRef Full Text | Google Scholar

46. Ivanov D, Dremin V, Borisova E, Bykov A, Meglinski I, Novikova T, et al. Symmetric Decomposition of Mueller Matrices Reveals a New Parametric Space for Polarimetric Assistance in colon Cancer Histopathology. Proc SPIE (2021) 11646:1164614. doi:10.1117/12.2578090

CrossRef Full Text | Google Scholar

47. Dremin V, Marcinkevics Z, Zherebtsov E, Popov A, Grabovskis A, Kronberga H, et al. Skin Complications of Diabetes Mellitus Revealed by Polarized Hyperspectral Imaging and Machine Learning. IEEE Trans Med Imaging (2021) 40:1207–16. doi:10.1109/tmi.2021.3049591

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Rodríguez C, Van Eeckhout A, Ferrer L, Garcia-Caurel E, González-Arnay E, Campos J, et al. Polarimetric Data-Based Model for Tissue Recognition. Biomed Opt Express (2021) 12:4852–72. doi:10.1364/BOE.426387

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Zhu Y, Dong Y, Yao Y, Si L, Liu Y, He H, et al. Probing Layered Structures by Multi-Color Backscattering Polarimetry and Machine Learning. Biomed Opt Express (2021) 12:4324–39. doi:10.1364/BOE.425614

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Yousaf MS, Ahmad I, Khurshid A, Ikram M. Machine Assisted Classification of Chicken, Beef and Mutton Tissues Using Optical Polarimetry and Bagging Model. Photodiagnosis Photodynamic Ther (2020) 31:101779. doi:10.1016/j.pdpdt.2020.101779

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Queau Y, Leporcq F, Lechervy A, Alfalou A. Learning to Classify Materials Using Mueller Imaging Polarimetry. Proc SPIE (2019) 11172:111720Z. doi:10.1117/12.2516351

CrossRef Full Text | Google Scholar

52. Vaughn I, Hoover B, Tyo S. Classification Using Active Polarimetry. Proc SPIE (2012) 8364:83640S. doi:10.1117/12.922623

CrossRef Full Text | Google Scholar

53. Zhu Y, Dong Y, Yao Y, Si L, Liu Y, He H, et al. Probing Layered Structures by Multi-Color Backscattering Polarimetry and Machine Learning. Biomed Opt Express (2021) 12(7):4324–39. doi:10.1364/BOE.425614

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Panigrahi S, Swarnkar T. Machine Learning Techniques Used for the Histopathological Image Analysis of Oral Cancer-A Review. Tobioij (2020) 13:106–18. doi:10.2174/1875036202013010106

CrossRef Full Text | Google Scholar

55. Luu N, Le TH, Phan QH, Pham TTH. Characterization of Mueller Matrix Elements for Classifying Human Skin Cancer Utilizing Random forest Algorithm. J Biomed Opt (2021) 26:075001. doi:10.1117/1.jbo.26.7.075001

CrossRef Full Text | Google Scholar

56. Ahmad I, Ahmad M, Khan K, Ikram M. Polarimetry Based Partial Least Square Classification of Ex Vivo Healthy and Basal Cell Carcinoma Human Skin Tissues. Photodiagnosis Photodynamic Ther (2016) 14:134–41. doi:10.1016/j.pdpdt.2016.04.004

CrossRef Full Text | Google Scholar

57. Zhou X, Ma L, Brown W, Little J, Chen A, Myers L, et al. Automatic Detection of Head and Neck Squamous Cell Carcinoma on Pathologic Slides Using Polarized Hyperspectral Imaging and Machine Learning. Proc SPIE (2021) 11603:16030Q. doi:10.1117/12.2582330

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Mukhopadhyay S, Kurmi I, Dey R, Das N, Pradhan S, Pradhan A, et al. Optical Diagnosis of colon and Cervical Cancer by Support Vector Machine. Proc SPIE (2016) 9887:98870U. doi:10.1117/12.2227316

CrossRef Full Text | Google Scholar

59. Dremin V, Potapova E, Zherebtsov E, Kandurova K, Shupletsov V, Alekseyev A, et al. Optical Percutaneous Needle Biopsy of the Liver: a Pilot Animal and Clinical Study. Sci Rep (2020) 10:14200. doi:10.1038/s41598-020-71089-5

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Zherebtsov E, Zajnulina M, Kandurova K, Potapova E, Dremin V, Mamoshin A, et al. Machine Learning Aided Photonic Diagnostic System for Minimally Invasive Optically Guided Surgery in the Hepatoduodenal Area. Diagnostics (2020) 10:873. doi:10.3390/diagnostics10110873

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Wang G, Sun Y, Jiang S, Wu G, Liao W, Chen Y, et al. Machine Learning-Based Rapid Diagnosis of Human Borderline Ovarian Cancer on Second-Harmonic Generation Images. Biomed Opt Express (2021) 12(9):5658–69. doi:10.1364/boe.429918

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Dang Y, Wan J, Si L, Meng Y, Dong Y, Liu S, et al. Deriving Polarimetry Feature Parameters to Characterize Microstructural Features in Histological Sections of Breast Tissues. IEEE T Bio-med Ing (2021) 68(3):881–92. doi:10.1109/TBME.2020.3019755

CrossRef Full Text | Google Scholar

63. James G, Witten D, Hastie T, Tibshirani R. An Introduction to Statistical Learning: With Applications in R. New York: Springer (2013).

Google Scholar

64. Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd ed. New York: Springer (2009).

Google Scholar

65. Wang LV, Hsin W. Biomedical Optics, Principles and Imaging. New Jersey: Wiley and Sons (2007).

Google Scholar

66. Cloude S. Group Theory and Polarisation Algebra. Optik (1986) 75:26–36.

Google Scholar

67. Genova T, Borisova E, Penkov N, Vladimirov B, Zhelyazkova A, Avramov L. Excitation-emission Matrices and Synchronous Fluorescence Spectroscopy for the Diagnosis of Gastrointestinal Cancers. Quan Electron. (2016) 46:510–4. doi:10.1070/qel16112

CrossRef Full Text | Google Scholar

68. Genova T, Borisova E, Zhelyazkova A, Penkov N, Vladimirov B, Terziev I, et al. Colorectal Cancer Stage Evaluation Using Synchronous Fluorescence Spectroscopy Technique. Opt Quant Electron (2016) 48:378. doi:10.1007/s11082-016-0634-7

CrossRef Full Text | Google Scholar

69. Genova T, Borisova E, Penkov N, Vladimirov B, Avramov L. Synchronous Fluorescence Spectroscopy with and without Polarization Sensitivity for Colorectal Cancer Differentiation. Proc SPIE (2018) 10685:106852L. doi:10.1117/12.2306877

CrossRef Full Text | Google Scholar

70. Mould RF. Introductory Medical Statistics. 3rd ed. Boca Raton: CRC Press (1998).

Google Scholar

71. Motulsky H, Christopoulos A. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. New York: Oxford University Press (2004).

Google Scholar

72. Motulsky H. Intuitive Biostatistics. New York: Oxford University Press (1995).

Google Scholar

73. Rodríguez C, Van Eeckhout A, Ferrer L, Garcia-Caurel E, González-Arnay E, Campos J, et al. Polarimetric Data-Based Model for Tissue Recognition. Biomed Opt Express (2021) 12(8):4852–72. doi:10.1364/boe.426387

PubMed Abstract | CrossRef Full Text | Google Scholar