Adaptive Synchronization for Hyperchaotic Liu System

In this paper, the adaptive control design is investigated for the chaos synchronization of two identical hyperchaotic Liu systems. First, an adaptive control law with two inputs is proposed based on Lyapunov stability theory. Secondly, two other control schemes are obtained based on a further analysis of the proposed adaptive control law. Finally, numerical simulations are presented to validate the effectiveness and correctness of these results.

1 Introduction

Since it was introduced by Pecora and Carroll [1] in 1990, the synchronization of chaotic systems has attracted increasing attention due to its possible applications in secure communication [2–4], biomedical Engineering [5], information science [6], chemical reactions [7, 8], etc. Then a wide variety of control methods of chaos synchronization have been studied such as the linear feedback control [9, 10], the sliding mode control [11], the adaptive control [12–16], the backstepping control [17, 18] and so on.

A hyperchaotic system is a chaotic system with at least two positive Lyapunov exponents which improves the security by generating more complex dynamics and so hyperchaotic systems have much more applications than low-dimension chaotic systems in the areas such as secure communication and image encryption, etc. Therefore in the past three decades, an increasing interest has been devoted to the study of chaos synchronization for hyperchaotic systems and plenty of research works can be found in literature [13, 19–25]. However, there are few studies about the adaptive synchronization of hyperchaotic Liu system that was introduced in [26]. A difficulty for this problem is that it is not evident to construct a suitable Lyapunov function to prove the stability of the error dynamics because of the special complex structure of hyperchaotic Liu system, since such a Lyapunov function depends on how to choose the feedback gain of controller in the slave system. Regarding those gains as unknown parameters, the use of adaptive control concept to estimate those unknown gains may be helpful to solve this problem. Therefore, this paper investigates the adaptive control design for the synchronization of hyperchaotic Liu system. First, an adaptive control law with two inputs is proposed and moreover, by introducing a suitable Lyapunov function, the main result is proved based on Lyapunov stability theory and Barbalat’s lemma. In addition, two special cases of this adaptive control scheme is further analyzed so that two other control laws are derived for the synchronization of hyperchaotic Liu system.

This paper is organized as follows. Section 2 formulates the problem. In Section 3, an adaptive control law for the synchronization of hyperchaotic Liu systems is proposed. In Section 4, two other control laws are derived based on further analysis of the proposed adaptive control law. Numerical simulations are given in Section 5. We conclude this paper in Section 6.

2 System Description and Problem Formulation

2.1 System Description

The hyperchaotic Liu system was proposed firstly in [26] and can be described by the following differential equations

$\left\{\begin{array}{c}{\dot{x}}_1=a(x_2-x_1),\hfill \\ {\dot{x}}_2=b{x}_1-x_4+x_1{x}_3,\hfill \\ {\dot{x}}_3=-c{x}_3+x_4-x_1{x}_2,\hfill \\ {\dot{x}}_4=d{x}_1+x_2,\hfill \end{array}\right.(1)$

where a, b, c, d are positive real constants and $x={(x_1,x_2,x_3,x_4)}^{\top }\in {\mathbb{R}}^4$ denotes the state vector. System (Eq. 1) was proved to exhibit hyperchaotic behavior when a = 10, b = 35, c = 1.4, d = 5. The projections of the chaotic attractor onto the (x₁, x₂, x₃) and (x₂, x₃, x₄) spaces are shown in Figure 1. Moreover, the state trajectories x₁(t), x₂(t), x₃(t), x₄(t) are globally bounded for all t ⩾ 0 and hence, there exist four positive real constants M₁, M₂, M₃, M₄ such that |x₁(t)| ⩽M₁,|x₂(t)| ⩽M₂, |x₃(t)|⩽M₃, |x₄(t)|⩽M₄ hold for all t ⩾ 0.

FIGURE 1

FIGURE 1. Chaotic attractor of hyperchaotic Liu system.

2.2 Problem Formulation

Let system (Eq. 1) be the master system and the corresponding slave system is described by the following equations:

$\left\{\begin{array}{c}{\dot{y}}_1=a(y_2-y_1)+u_1,\hfill \\ {\dot{y}}_2=b{y}_1-y_4+y_1{y}_3+u_2,\hfill \\ {\dot{y}}_3=-c{y}_3+y_4-y_1{y}_2+u_3,\hfill \\ {\dot{y}}_4=d{y}_1+y_2+u_4,\hfill \end{array}\right.(2)$

where $y={(y_1,y_2,y_3,y_4)}^{\top }\in {\mathbb{R}}^4$ denotes the state vector and $u={(u_1,u_2,u_3,u_4)}^{\top }$ is the control vector to be designed. Define the error states as e_i = y_i − x_i, for i = 1, 2, 3, 4, and thus the error dynamics can be described in the following form:

$\left\{\begin{array}{c}{\dot{e}}_1=a(e_2-e_1)+u_1,\hfill \\ {\dot{e}}_2=b{e}_1-e_4+y_1{e}_3+x_3{e}_1+u_2,\hfill \\ {\dot{e}}_3=-c{e}_3+e_4-y_1{e}_2-x_2{e}_1+u_3,\hfill \\ {\dot{e}}_4=d{e}_1+e_2+u_4.\hfill \end{array}\right.(3)$

It is evident that the synchronization between (Eqs 1, 2) can be easily achieved if we can use all measurements x_i of (Eq. 1) to active all controller u_i in (Eq. 2). But the interesting question is: can we use less information of (Eq. 1) to active only some of the controllers u_i in (Eq. 2)? The positive answer of this question will be more applausive since less sensors are needed for (Eq. 1) to measure only the necessary states, and less energy will be consumed to actuate some necessary u_i in (Eq. 2). Consequently, the purpose of this paper is, by using less measurement from (Eq. 1) and activating less actuator for (Eq. 2), to design an adaptive control scheme in order to achieve global chaos synchronization of two identical hyperchaotic Liu systems, i.e., for any initial conditions y(0) ≠ x(0), we have

$\underset{t\to \infty }{\lim }\Vert e(t)\Vert =\underset{t\to \infty }{\lim }\Vert y(t,y(0))-x(t,x(0))\Vert =0,$

where $e(t)={(e_1(t),e_2(t),e_3(t),e_4(t))}^{\top }$.

3 Adaptive Synchronization of Hyperchaotic Liu System

In the following, we will present our result by activating only two controllers (u₂ and u₄) in (Eq. 2) with only two measurements (x₂ and x₄) of (Eq. 1) to solve the global synchronization problem.

Theorem 3.1. The master system (Eq. 1) and the slave system (Eq. 2) can be global synchronized by the following controllers

$u_1=0,u_2=k_1{e}_2,u_3=0,u_4=k_2{e}_4,(4)$

where k₁ and k₂ denote the feedback gains which are updated by the following adaptive laws

${\dot{k}}_1=-{\gamma }_1{e}_2^2,{\dot{k}}_2=-{\gamma }_2{e}_4^2,(5)$

with γ₁ and γ₂ being arbitrary positive constants.

Proof. Under the adaptive control laws (Eqs 4, 5), the error dynamics (Eq. 3) reads

$\left\{\begin{array}{c}{\dot{e}}_1=a(e_2-e_1),\hfill \\ {\dot{e}}_2=b{e}_1-e_4+y_1{e}_3+x_3{e}_1+k_1{e}_2,\hfill \\ {\dot{e}}_3=-c{e}_3+e_4-y_1{e}_2-x_2{e}_1,\hfill \\ {\dot{e}}_4=d{e}_1+e_2+k_2{e}_4,\hfill \\ {\dot{k}}_1=-{\gamma }_1{e}_2^2,\hfill \\ {\dot{k}}_2=-{\gamma }_2{e}_4^2.\hfill \end{array}\right.(6)$

Consider the following Lyapunov function

$V=\frac{1}{2}(\rho e_1^2+e_2^2+e_3^2+e_4^2)+\frac{1}{2{\gamma }_1}{(k_1+L_1)}^2+\frac{1}{2{\gamma }_2}{(k_2+L_2)}^2,(7)$

where L₁, L₂ and ρ are positive constants which will be determined later. Calculating the differentiation of (Eq. 7) with respect to time t along trajectories of system (Eq. 6), we obtain

$\begin{array}{cc}\hfill \dot{V}=\hfill & \hfill \rho e_1{\dot{e}}_1+e_2{\dot{e}}_2+e_3{\dot{e}}_3+e_4{\dot{e}}_4+\frac{1}{{\gamma }_1}(k_1+L_1){\dot{k}}_1+\frac{1}{{\gamma }_2}(k_2+L_2){\dot{k}}_2\hfill \\ \hfill =\hfill & \hfill \rho a{e}_1(e_2-e_1)+e_2(b{e}_1-e_4+y_1{e}_3+x_3{e}_1-L_1{e}_2)\hfill \\ \hfill \hfill & \hfill +e_3(-c{e}_3+e_4-y_1{e}_2-x_2{e}_1)+e_4(d{e}_1+e_2-L_2{e}_4)\hfill \\ \hfill =\hfill & -\rho a{e}_1^2-L_1{e}_2^2-c{e}_3^2-L_2{e}_4^2+(\rho a+b+x_3)e_1{e}_2\hfill \\ \hfill \hfill & \hfill -x_2{e}_1{e}_3+d{e}_1{e}_4+e_3{e}_4\hfill \\ \hfill \le \hfill & \hfill -\left(\rho a-\frac{d}{2}\right)e_1^2-L_1{e}_2^2-\left(c-\frac{1}{2}\right)e_3^2-\left(L_2-\frac{d+1}{2}\right)e_4^2\hfill \\ \hfill \hfill & \hfill +(\rho a+b+M_3)|e_1{e}_2|+M_2|e_1{e}_3|\hfill \\ \hfill =\hfill & \hfill -|e{|}^{\top }{P}_1|e|,\hfill \end{array}(8)$

where $|e|={(|e_1|,|e_2|,|e_3|,|e_4|)}^{\top }$, M₂ and M₃ represent the boundedness of x₂ and x₃, and P₁ is a symmetric matrix of the following form

$P_1=\left(\begin{array}{cccc}\hfill \rho a-\frac{d}{2}\hfill & \hfill -\frac{\rho a+b+M_3}{2}\hfill & \hfill -\frac{M_2}{2}\hfill & \hfill 0\hfill \\ \hfill -\frac{\rho a+b+M_3}{2}\hfill & \hfill L_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{M_2}{2}\hfill & \hfill 0\hfill & \hfill c-\frac{1}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill L_2-\frac{d+1}{2}\hfill \end{array}\right).(9)$

Clearly, if the symmetric matrix P₁ is positive definite, then we have $\dot{V}\le 0$. Moreover, it is well known that P₁ is positive definite if and only if Δ_k > 0, for 1 ≤ k ≤ 4, where Δ_k denotes the Leading Principle Minor of order k of P₁. A straightforward calculation gives

$\begin{array}{c}\hfill {\mathrm{\Delta }}_1=\rho a-\frac{d}{2},\hfill \\ \hfill {\mathrm{\Delta }}_2=L_1{\mathrm{\Delta }}_1-\frac{{(\rho a+b+M_3)}^2}{4},\hfill \\ \hfill {\mathrm{\Delta }}_3=\left(c-\frac{1}{2}\right){\mathrm{\Delta }}_2-L_1\frac{M_2^2}{4},\hfill \\ \hfill {\mathrm{\Delta }}_4=\left(L_2-\frac{d+1}{2}\right){\mathrm{\Delta }}_3.\hfill \end{array}(10)$

From the condition Δ_k > 0, for 1 ≤ k ≤ 4, and (Eq. 10), it is easy to obtain

$\begin{array}{ccc}\hfill L_1& >\hfill & \mathrm{m}\mathrm{a}\mathrm{x}\{\frac{{(\rho a+b+M_3)}^2}{4a\rho -2d},\frac{(c-1/2){(\rho a+b+M_3)}^2}{(2c-1)(2a\rho -d)-M_2^2}\},\hfill \\ \hfill L_2& >\hfill & \frac{d+1}{2},\rho >\frac{1}{2a}(\frac{M_2^2}{2c-1}+d).\hfill \end{array}$

Therefore, there always exist positive L₁, L₂ and ρ satisfying the above conditions so that $\dot{V}\le 0$ and thus V is positive and decrescent. It follows that the equilibrium point $(e_1=0,e_2=0,e_3=0,e_4=0,k_1=k_1^{*},k_2=k_2^{*})$ of systems (Eq. 6) is uniformly stable which implies, from (Eq. 6), that ${\dot{e}}_1(t),{\dot{e}}_2(t),{\dot{e}}_3(t),{\dot{e}}_4(t)$ are also uniformly stable. Moreover, it is easy to conclude from (Eq. 8) that the error states e₁(t), e₂(t), e₃(t), e₄(t) are quadratically integrable function, i.e., e₁(t), e₂(t), e₃(t), e₄(t) ∈ L₂. Therefore, according to Barbalat’s lemma, given any initial conditions, we have always e₁(t) → 0, e₂(t) → 0, e₃(t) → 0, e₄(t) → 0 (t → ∞) and $k_1\to k_1^{*},k_2\to k_2^{*}(t\to \infty )$, which imply that the master system (Eq. 1) and slave system (Eq. 2) are globally asymptotically synchronized under the adaptive control law (Eq. 4) associated with (Eq. 5).

Remark 3.1. In the Lyapunov function (Eq. 7), a positive constant ρ has to be introduced to guarantee the positive definite of the symmetric matrix P₁.

Remark 3.2. The feedback gains k₁ and k₂ will converge to two constants $k_1^{*}$ and $k_2^{*}$, respectively, which depend on not only the initial condition k₁(0) and k₂(0), but also the value of γ₁ and γ₂.

4 Further Analysis of Theorem 3.1

In Theorem 3.1, the feedback gains k₁ and k₂ are defined to be updated by the adaptive laws (Eq. 5), i.e.,

${\dot{k}}_1=-{\gamma }_1{e}_2^2,{\dot{k}}_2=-{\gamma }_2{e}_4^2,$

where γ₁ and γ₂ are arbitrary positive constants. Two interesting questions arise:

• If γ₁ = γ₂ = 0 that implies ${\dot{k}}_1={\dot{k}}_2=0$, i.e., k₁ and k₂ are both constants equal to their initial values, then is the control law (Eq. 4) still valid?

• If the feedback gains k₁ and k₂ are equal (for the sake of implementation simplicity), i.e., k₁ = k₂, how to modify the adaptive law (Eq. 5) such that the chaos synchronization can still be achieved?

In the following, we will answer the above two questions and derive two other special control laws for the chaos synchronization of hyperchaotic Liu system.

4.1 Case 1: k₁ and k₂ Are Constants

Proposition 4.1. The master system (Eq. 1) and the slave system (Eq. 2) can be global synchronized by the following linear feedback controller

$u_1=0,u_2=k_1{e}_2,u_3=0,u_4=k_2{e}_4,(11)$

where the feedback gains k₁, k₂ satisfy

$\begin{array}{c}\hfill k_1<\mathrm{m}\mathrm{i}\mathrm{n}\left\{-\frac{{(\rho a+b+M_3)}^2}{4a\rho -2d},-\frac{(c-1/2){(\rho a+b+M_3)}^2}{(2c-1)(2a\rho -d)-M_2^2}\right\},\hfill \\ \hfill k_2<-\frac{d+1}{2},\hfill \end{array}(12)$

with

$\rho >\frac{1}{2a}(\frac{M_2^2}{2c-1}+d).(13)$

Proof. The proof of the above result is quite similar to that of Theorem 3.1. Consider the following Lyapunov function

$V=\frac{1}{2}(\rho e_1^2+e_2^2+e_3^2+e_4^2),(14)$

where ρ is a positive constant which will be determined later. Taking the differentiation of (Eq. 14) with respect to time t and following the similar procedure in the proof of Theorem 3.1, we obtain

$\begin{array}{c}\hfill \dot{V}\le -(|e_1|,|e_2|,|e_3|,|e_4|)P_2{(|e_1|,|e_2|,|e_3|,|e_4|)}^{\top },\hfill \end{array}(15)$

where

$P_2=\left(\begin{array}{cccc}\hfill \rho a-\frac{d}{2}\hfill & \hfill -\frac{\rho a+b+M_3}{2}\hfill & \hfill -\frac{M_2}{2}\hfill & \hfill 0\hfill \\ \hfill -\frac{\rho a+b+M_3}{2}\hfill & \hfill -k_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{M_2}{2}\hfill & \hfill 0\hfill & \hfill c-\frac{1}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -k_2-\frac{d+1}{2}\hfill \end{array}\right).(16)$

It is easy to see that the symmetric matrix P₂ has the same structure with P₁, given by (Eq. 9), and the only difference is that L₁ and L₂ are replaced by −k₁ and −k₂, respectively. Therefore, by a similar procedure of the proof of Theorem 3.1, we can obtain that P₂ is positive definite if and only if the following conditions are satisfied

$\begin{array}{ccc}\hfill k_1& <\hfill & \mathrm{m}\mathrm{i}\mathrm{n}\{-\frac{{(\rho a+b+M_3)}^2}{4a\rho -2d},-\frac{(c-1/2){(\rho a+b+M_3)}^2}{(2c-1)(2a\rho -d)-M_2^2}\}\hfill \\ \hfill k_2& <\hfill & -\frac{d+1}{2},\mathrm{a}\mathrm{n}\mathrm{d}\rho >\frac{1}{2a}(\frac{M_2^2}{2c-1}+d).\hfill \end{array}$

Therefore, there always exist k₁, k₂ and ρ satisfying the above conditions so that $\dot{V}\le 0$ and thus V is positive and decrescent. Clearly $\dot{V}=0$ if and only if e_i = 0, 0 ≤ i ≤ 4 which means the set $R=\{e\in {\mathbb{R}}^4:\dot{V}=0\}$ contains no other trajectories except {e₁ = 0, e₂ = 0, e₃ = 0, e₄ = 0}. Therefore, by the LaSalle invariance principle, starting with arbitrary initial values, e = 0 is asymptotically stable which implies that the chaos synchronization of hyperchaotic Liu system is achieved by the control law (Eqs 11, 12).

4.2 Case 2: k₁ and k₂ Are Equal

Proposition 4.2. The master system (Eq. 1) and the slave system (Eq. 2) can be synchronized by the following adaptive controller

$u_1=0,u_2=k{e}_2,u_3=0,u_4=k{e}_4,(17)$

where k denotes the feedback gain which is updated by the following adaptive law

$\dot{k}=-\gamma (e_2^2+e_4^2),(18)$

with γ being an arbitrary positive constant.

Proof. Following the same procedure as that in the proof of Theorem 3.1, by considering the following Lyapunov function

$V=\frac{1}{2}(\rho e_1^2+e_2^2+e_3^2+e_4^2)+\frac{1}{2\gamma }{(k+L)}^2(19)$

where ρ and L are positive constants which will be determined later, we obtain

$\begin{array}{c}\hfill \dot{V}\le -(|e_1|,|e_2|,|e_3|,|e_4|)P_3{(|e_1|,|e_2|,|e_3|,|e_4|)}^{\top },\hfill \end{array}(20)$

with

$P_3=\left(\begin{array}{cccc}\hfill \rho a-\frac{d}{2}\hfill & \hfill -\frac{\rho a+b+M_3}{2}\hfill & \hfill -\frac{M_2}{2}\hfill & \hfill 0\hfill \\ \hfill -\frac{\rho a+b+M_3}{2}\hfill & \hfill L\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{M_2}{2}\hfill & \hfill 0\hfill & \hfill c-\frac{1}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill L-\frac{d+1}{2}\hfill \end{array}\right).$

Clearly, the symmetric matrix P₃ has the same structure with P₁, given by (Eq. 9), in which L₁ = L₂ = L. Thus, by a similar procedure of the proof of Theorem 3.1, we can obtain that P₃ is positive definite if and only if the following conditions are satisfied

$\begin{array}{ccc}\hfill L& >\hfill & \mathrm{m}\mathrm{a}\mathrm{x}\{\frac{d+1}{2},\frac{{(\rho a+b+M_3)}^2}{4a\rho -2d},\frac{(c-1/2){(\rho a+b+M_3)}^2}{(2c-1)(2a\rho -d)-M_2^2}\}\hfill \\ \hfill \rho & >\hfill & \frac{1}{2a}(\frac{M_2^2}{2c-1}+d).\hfill \end{array}$

The rest of the proof is exactly the same as that in the proof of Theorem 3.1.

5 Numerical Simulations

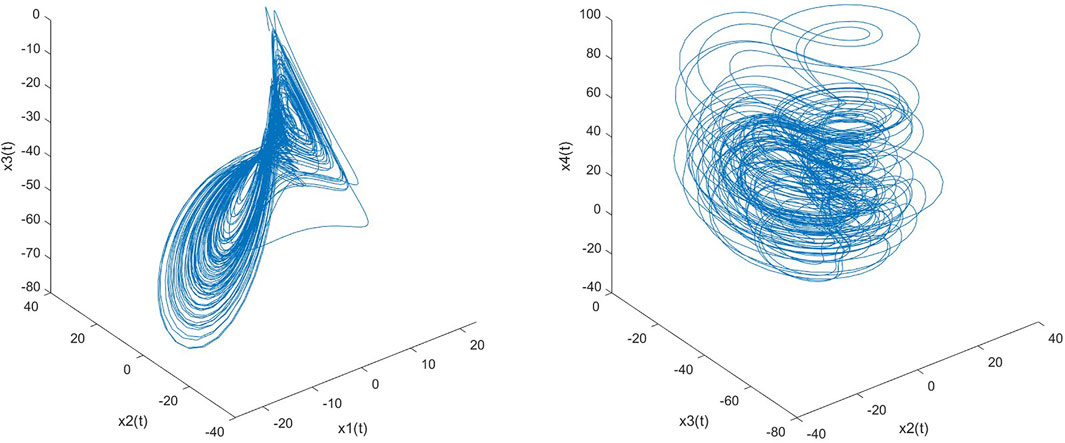
In this section, numerical simulations by MATLAB will be given to validate the correctness and effectiveness of the proposed controller designs. Fourth order Runge-Kutta method is applied to approximate the solution of differential equations with a small chosen fixed time step size. The system parameters are set to a = 10, b = 35, c = 1.4, d = 5 so that the Hyperchaotic Liu system exhibits chaotic behavior when no control is applied.

In order to compare the three control laws proposed in Theorem 3.1, Proposition 4.1 and Proposition 4.2, we will use the same initial conditions x(0) and y(0) for all the three numerical simulations. The initial conditions of the master system are chosen as x₁(0) = 15, x₂(0) = 22, x₃(0) = −46 and x₄(0) = −21 while the initial conditions of the slave system are chosen as y₁(0) = 18, y₂(0) = −13, y₃(0) = −1 and y₄(0) = 37.

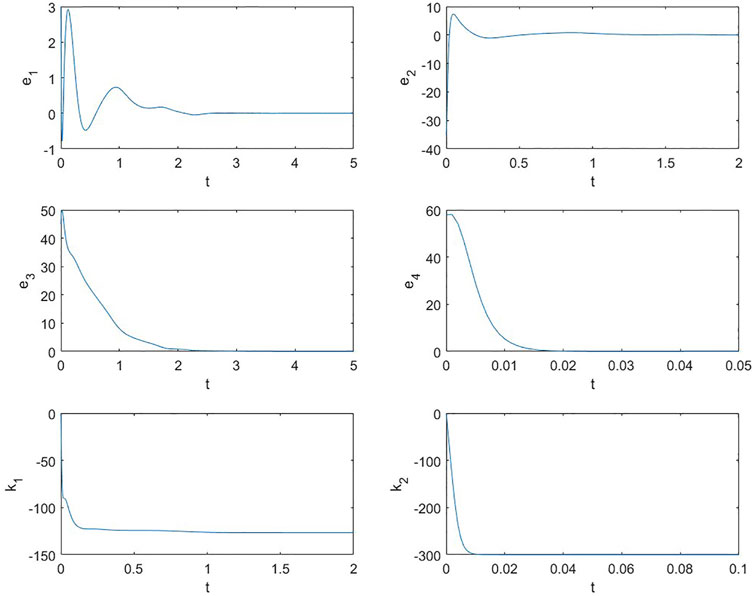
First, consider the adaptive control law (Eq. 4) associated with (Eq. 5) proposed in Theorem 3.1 and select γ₁ = 10, γ₂ = 20 and the initial conditions of the feedback gain by k₁(0) = k₂(0) = 1. Figure 2 shows that the error states are asymptotically stable to zero while the control gains k₁ and k₂ tend to two negative constants, respectively, as t tends to infinity.

FIGURE 2

FIGURE 2. Error synchronization by the control law (Eq. 4) associated with (Eq. 5).

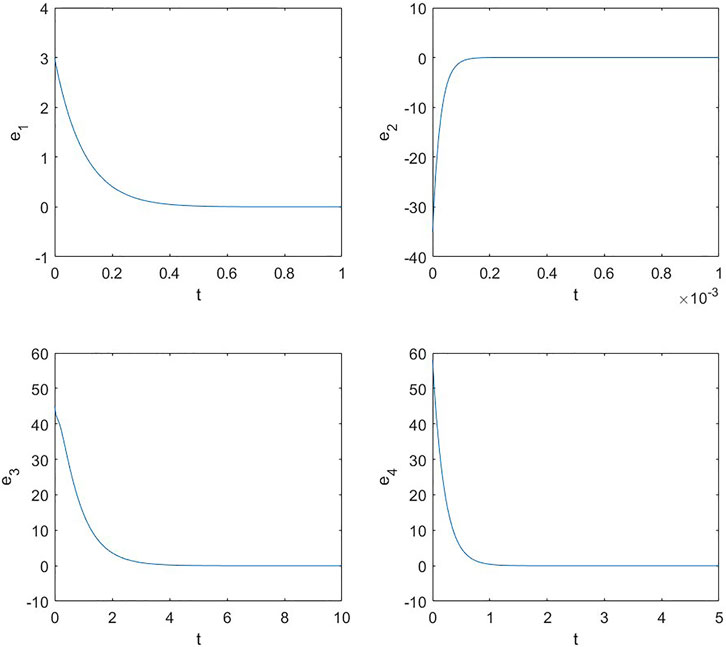
Second, consider the control law proposed in Proposition 4.2 and select upper bounds of M₂ and M₃ by M₂ = 52, M₃ = 82 (according to the bounded simulation results depicted in Figure 1). From conditions (Eqs 12, 13), a direct calculation gives that k₁ < −30 097 and k₂ < −3 and we choose k₁ = −31 000 and k₂ = −5. Figure 3 shows that the error states asymptotically converge to zero, as t tends to infinity.

FIGURE 3

FIGURE 3. Error synchronization by the control law (Eq. 11) associated with (Eqs 12, 13).

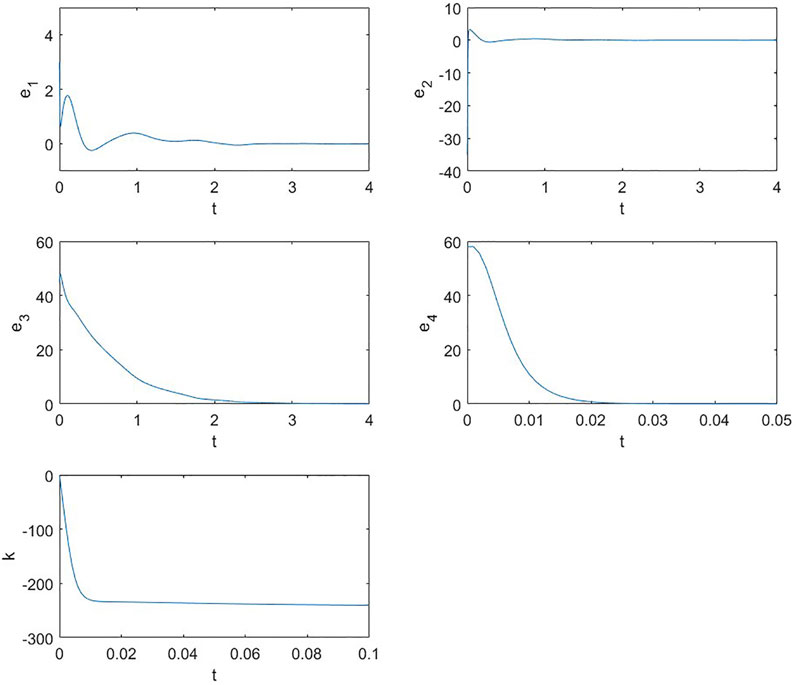
Finally, consider the adaptive control law (Eq. 17) associated with (Eq. 18) proposed in Theorem 3.1 and select γ = 10 and k(0) = 1. Figure 4 shows that the error system is asymptotically stable to zero and the control gain k tends to a negative constant as t tends to infinity.

FIGURE 4

FIGURE 4. Error synchronization by the control law (Eq. 17) associated with (Eq. 18).

6 Conclusion

This paper has addressed the adaptive synchronization problems of hyperchaotic Liu systems. An adaptive control scheme has been proposed for the asymptotically synchronization of two identical hyperchaotic Liu systems. This result was proved according to Lyapunov stability theory and Barbalat’s lemma by constructing a suitable Lyapunov function. Moreover, through further discussions of the main result, two other control schemes have been derived. The numerical simulations verify the effectiveness and correctness of the control laws proposed in this work.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SL: Conceptualization, Methodology, Project administration, Funding acquisition. YW: Validation, Investigation, Writing–Original Draft. GZ: Supervision, Writing–Review and Editing.

Funding

This work is supported by the Natural Science Foundation of China (No. 61573192).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Pecora LM, Carroll TL. Synchronization in Chaotic Systems. Controlling Chaos (1996) 6:142–5. doi:10.1016/b978-012396840-1/50040-0

CrossRef Full Text | Google Scholar

2. Liao T-L, Tsai S-H. Adaptive Synchronization of Chaotic Systems and its Application to Secure Communications. Chaos, Solitons & Fractals (2000) 11:1387–96. doi:10.1016/s0960-0779(99)00051-x

CrossRef Full Text | Google Scholar

3. Zheng G, Boutat D, Floquet T, Barbot J-P. Secure Data Transmission Based on Multi-Input Multi-Output Delayed Chaotic System. Int J Bifurcation Chaos (2008) 18:2063–72. doi:10.1142/s0218127408021567

CrossRef Full Text | Google Scholar

4. Hoang TM. A New Secure Communication Model Based on Synchronization of Coupled Multidelay Feedback Systems. Int J Electronics Commun Eng (2010) 4:491–7. doi:10.5281/zenodo.1329807

CrossRef Full Text | Google Scholar

5. Vuksanović V, Gal V. Nonlinear and Chaos Characteristics of Heart Period Time Series: Healthy Aging and Postural Change. Auton Neurosci (2005) 121:94–100. doi:10.1016/j.autneu.2005.06.004

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wang L, Dong T, Ge M-F. Finite-Time Synchronization of Memristor Chaotic Systems and its Application in Image Encryption. Appl Mathematics Comput (2019) 347:293–305. doi:10.1016/j.amc.2018.11.017

CrossRef Full Text | Google Scholar

7. Vaidyanathan S. Anti-synchronization of Brusselator Chemical Reaction Systems via Adaptive Control. Int J ChemTech Res (2015) 8:759–68.

Google Scholar

8. Li Y-N, Chen L, Cai Z-S, Zhao X-z. Experimental Study of Chaos Synchronization in the Belousov-Zhabotinsky Chemical System. Chaos, Solitons & Fractals (2004) 22:767–71. doi:10.1016/j.chaos.2004.03.023

CrossRef Full Text | Google Scholar

9. Yassen MT. Controlling Chaos and Synchronization for New Chaotic System Using Linear Feedback Control. Chaos, Solitons & Fractals (2005) 26:913–20. doi:10.1016/j.chaos.2005.01.047

CrossRef Full Text | Google Scholar

10. Huijberts H, Nijmeijer H. Nonlinear Chaos Control and Synchronization (Handbook of Chaos Control). 2nd ed. (2007) Weinheim, Germany: WILET-VCH Verlag GmbH & Co. KGaA.

Google Scholar

11. Yau H-T. Design of Adaptive Sliding Mode Controller for Chaos Synchronization with Uncertainties. Chaos, Solitons & Fractals (2004) 22:341–7. doi:10.1016/j.chaos.2004.02.004

CrossRef Full Text | Google Scholar

12. Wang Y, Guan Z-H, Wang HO. Feedback and Adaptive Control for the Synchronization of Chen System via a Single Variable. Phys Lett A (2003) 312:34–40. doi:10.1016/s0375-9601(03)00573-5

CrossRef Full Text | Google Scholar

13. Wang X, Wang Y. Adaptive Control for Synchronization of a Four-Dimensional Chaotic System via a Single Variable. Nonlinear Dyn (2011) 65:311–6. doi:10.1007/s11071-010-9893-1

CrossRef Full Text | Google Scholar

14. Rasappan S, Kumar Jothi N, Kumar Kumaravel S. Control of Colpitts-Oscillator via Adaptive Feedback Control. Malaysian J Math Sci (2016) 10:46–60.

Google Scholar

15. Wu J, Ma Rr. Robust Adaptive Finite‐Time and Fixed‐time Synchronization of Chaotic Systems With Smooth Control. Int J Robust Nonlinear Control (2021) 31:8974–88. doi:10.1002/rnc.5750

CrossRef Full Text | Google Scholar

16. Li S-J, Wu Y-W, Zheng G. Adaptive Synchronization of Chaotic Systems With Less Measurement and Actuation. Chin Phys. B (2021) 30:100503. doi:10.1088/1674-1056/abec33

CrossRef Full Text | Google Scholar

17. Wang C, Ge SS. Synchronization of Two Uncertain Chaotic Systems via Adaptive Backstepping. Int J Bifurcation Chaos (2001) 11:1743–51. doi:10.1142/s0218127401002985

CrossRef Full Text | Google Scholar

18. Bowong S, Moukam Kakmeni FM. Synchronization of Uncertain Chaotic Systems via Backstepping Approach. Chaos, Solitons & Fractals (2004) 21:999–1011. doi:10.1016/j.chaos.2003.12.084

CrossRef Full Text | Google Scholar

19. Zheng G, Boutat D. Synchronisation of Chaotic Systems via Reduced Observers. IET Control Theor Appl (2011) 5:308–14. doi:10.1049/iet-cta.2010.0078

CrossRef Full Text | Google Scholar

20. Elabbasy EM, Agiza HN, El-Dessoky MM. Adaptive Synchronization of a Hyperchaotic System With Uncertain Parameter. Chaos, Solitons & Fractals (2006) 30:1133–42. doi:10.1016/j.chaos.2005.09.047

CrossRef Full Text | Google Scholar

21. Qiang J. Adaptive Control and Synchronization of a New Hyperchaotic System With Unknown Parameters. Phys Lett A (2007) 362:424–9. doi:10.1016/j.physleta.2006.10.044

CrossRef Full Text | Google Scholar

22. Cai G, Zheng S, Tian L. Adaptive Control and Synchronization of an Uncertain New Hyperchaotic Lorenz System. Chin Phys B (2008) 17:2412–9. doi:10.1088/1674-1056/17/7/014

CrossRef Full Text | Google Scholar

23. Yu S-H, Hyun C-H, Park M-N. Backstepping Control and Synchronization for 4-d Lorenz-Stenflo Chaotic System With Single Input. Int J Fuzzy Logic Intell Syst (2011) 11:143–8. doi:10.5391/ijfis.2011.11.3.143

CrossRef Full Text | Google Scholar

24. Vaidyanathan S. Analysis, Control and Synchronization of Hyperchaotic Zhou System via Adaptive Control. (Eds) Meghanathan N., Nagamalai D., Chaki N. Advances in Computing and Information Technology. Advances in Intelligent Systems and Computing, 177. Springer Berlin Heidelberg (2013). doi:10.1007/978-3-642-31552-7_1

CrossRef Full Text | Google Scholar

25. Rasappan S, Niranjan Kumar K. Dynamics, Control, Stability, Diffusion and Synchronization of Modified Chaotic Colpitts Oscillator. Arch Control Sci (2021) 31:731–59. doi:10.24425/acs.2021.138699

CrossRef Full Text | Google Scholar

26. Liu L, Liu CX, Zhang YB. Analysis of a Novel Four-Dimensional Hyperchaotic System. Chin J Phys (2008) 46:386–93.

Google Scholar