Correspondences Between Parameters in a Reaction-Diffusion Model and Connexin Functions During Zebrafish Stripe Formation

Different diffusivities among interacting substances actualize the potential instability of a system. When these elicited instabilities manifest as forms of spatial periodicity, they are called Turing patterns. Simulations using general reaction-diffusion (RD) models demonstrate that pigment patterns on the body trunk of growing fish follow a Turing pattern. Laser ablation experiments performed on zebrafish reveal apparent interactions among pigment cells, which allow for a three-component RD model to be derived. However, the underlying molecular mechanisms responsible for Turing pattern formation in this system remain unknown. A zebrafish mutant with a spotted pattern was found to have a defect in Connexin41.8 (Cx41.8) which, together with Cx39.4, exists in pigment cells and controls pattern formation. Here, molecular-level evidence derived from connexin analyses is linked to the interactions among pigment cells described in previous RD modeling. Channels on pigment cells are generalized as “gates,” and the effects of respective gates were deduced. The model uses partial differential equations (PDEs) to enable numerical and mathematical analyses of characteristics observed in the experiments. Furthermore, the improved PDE model, including nonlinear reaction terms, enables the consideration of the behavior of components realistically.

1 Introduction

In 1952, Alan Turing postulated that two substrates interacting with each other show instability when they diffuse at different speeds. He explained this diffusion-driven instability by utilizing a linear reaction-diffusion (RD) model. This model demonstrates that spatial inhomogeneity (i.e., the Turing pattern) could be generated by such conditions. This relationship is known to generate patterns though the components remain to be explored.

More than two decades ago, [1] reported that pigment stripes on the bodies of growing marine angel fish behave as a Turing pattern. The research focus then shifted mainly to zebrafish (Danio rerio) as a model organism for pattern-formation studies [2–4]. Zebrafish have a pattern of stripes on their body and fins (Figure 1A). The pattern is generated by three types of pigment cells: complementarily distributed black melanophores and yellow xanthophores (Figure 1C) plus iridescent iridophores. Numerous zebrafish pigment-pattern mutants were artificially generated [5], and the corresponding genes were identified. One of the most important mutants is leopard, which produces a spotted pattern that is representative of Turing patterns (Figure 1B) [6] identifies connexin41.8 (cx41.8) as the gene responsible for the leopard mutation [6]. Besides Cx41.8, other connexins, such as Cx39.4, exist in pigment cells and affect pigment-pattern formation. Six connexins form a hemi-channel (or “connexon”), which connects intracellular and extracellular spaces (Figure 1D). Docking of two hemi-channels from adjacent cells give rise to a gap junction, which mediates intercellular signal transfer [7]. The minimal connexin network required to originate a striped pattern was recently revealed by regulating connexin expression in each pigment cell [8]. Therefore, these channels are important for pigment-pattern formation.

FIGURE 1

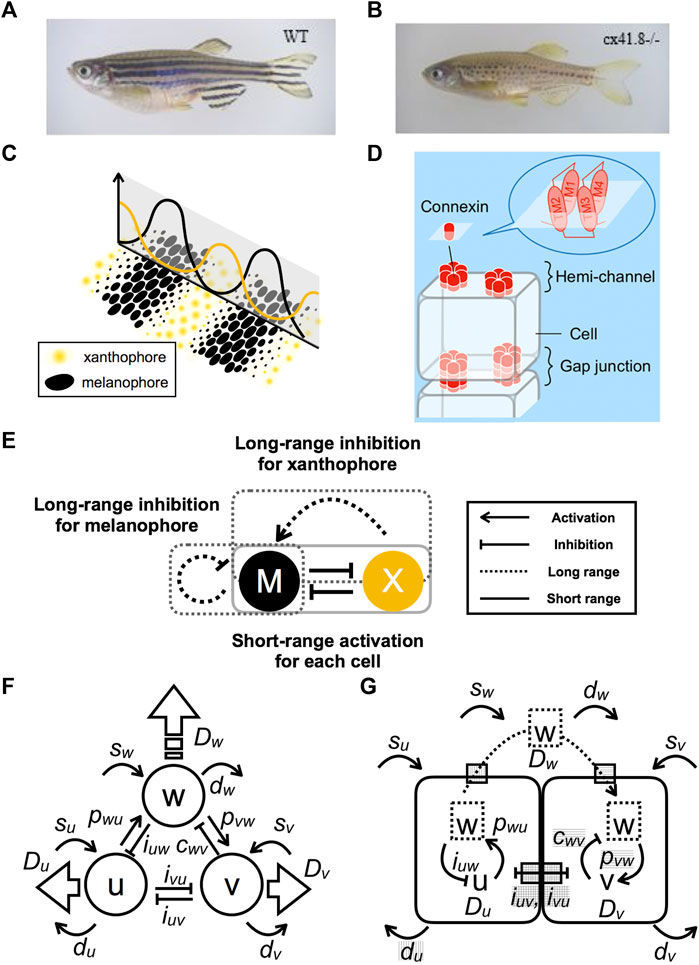
FIGURE 1. Model-based prediction of defects in channels and interactions. (A) Striped wild-type (WT) zebrafish. (B) Spotted leopard mutant zebrafish. (C) Schematic representation of the relationship between the distribution of pigment cells and the numerical result of the continuous model. (D) Schematic representation of channels composed of connexin complexes. Hemi-channels are open to the outside of a cell, whereas gap junctions form by the docking of hemi-channel connecting to adjacent cells. (E) Apparent interactions of pigment cells as revealed by laser ablation experiments. (F) Schematic diagram of a three-component PDE model composed of components $U$ or $V$, which correspond to melanophores or xanthophores, respectively, and component $w$, which represents a highly diffusible molecule. Interactions are indicated by fine arrows, diffusion coefficients (the motility of the components) are indicated by wide arrows, and corresponding parameters are indicated. (G) Schematic diagram of the effect of channels on pigment cells according to the mathematical model. Parameters related to the function of each gate are indicated by hatchings.

Interactions among pigment cells and their molecular mechanisms involved in pattern formation are summarized in [9]. However, the molecular mechanisms leading to Turing instability remain mostly unresolved. Mosaic fish experiments indicate that both leopard/cx41.8 and jaguar/obelix/kcnj13 genes are required for segregation of melanophores and xanthophores. Such segregation is proposed to involve local interactions between adjacent pigment cells [10]. Xanthophore ablation using a temperature-sensitive csf1ra allele led to the gradual death of melanophores in both the body trunk and fins of adult fish [11]. Accordingly, melanophore survival requires continuous signaling from xanthophores. Laser ablation of stripe and interstripe areas has revealed the mutual interactions between melanophores and xanthophores [12]. The interactions comply with the requirements for Turing pattern formation (Figure 1E). Specifically, both types of pigment cells activate their own types at a single-cell distance (short range) by inhibitions of other types and then inhibit their own types beyond the width of the stripe (long range). The difference in reaction distances achieves the “local activation and lateral inhibition” condition needed for pattern formations [13]. It should be noted, however, that the distinction between iridophores and xanthophores is sometimes unclear in those experiments.

To explain the opposing actions at long vs. short distance, a model that includes a highly diffusible molecule (i.e., long-range factor) and two cells (regarded as short-range factors with low diffusivity) was constructed [12]. This three-component RD model with its linear reaction terms and upper and lower limits describes the apparent interactions obtained experimentally. Then, the different diffusibilities and the interactions in the model achieved diffusion-driven instability (Turing instability).

Further investigations reveal that the interactions are mediated by cell projections [14]. The interaction mediated by gap junctions on the tip of the projection is considered to be a long-range effect observed in the previous experiments [15]. The researchers mention the possibility that the pattern formation might not require actual diffusion. Later, a Turing model based on an integral kernel was suggested [16] though the link between parameter and molecular function was ambiguous. Most other models for pigment-pattern formation are based on interactions at a cellular level. These models implement different effects depending on the distance from each pigment cell by agent-based models [17, 18] and by minimal lattice models [19, 20]. Several attempts were made to explain the observed patterns in zebrafish mutants by a general Turing model [21, 22]; however, they were not supported experimentally even though there are several paths to cause the expected pattern changes in mutants.

Here, the interactions in a three-component model, including a hypothetical highly diffusible factor, are developed to attempt to link the molecular functions of connexins in zebrafish. Channels thought to be important for pattern formation are generalized as “gates” of pigment cells. These gates enable transport of the diffusible molecule across the membrane. The parameters affected by each gate are deduced; then, the effects on pattern selection and size are analyzed. Finally, the model is improved to an analogous model with nonlinear terms. These models together enable reasonable explanations of detailed behavior of the components that relate to the pattern formation.

2 Materials and Methods

2.1 Numerical Simulations

For the linear model, $d_u$ was increased from 0 to 0.2 within limits of the reaction term along the $x$-axis (Figures 4A, D–H). It can change the distance between the equilibrium point of u and the upper limitation [23] without shifting the maximum of the limit, and the parameters $p_{vw}$ and $c_{wv}$ were decreased linearly from 1 to 0 (Figures 4B,D–H) for investigation of the effect of gates on each cell. For short-range effects, $i_{uv}$ and $i_{vu}$ were decreased linearly from 1 to 0.6 in Figure 4C. Accordingly, the arbitrary parameter set generating stripes (wild type) was placed in the right top of the phase plane (Figures 4D–I). Partial differential equations (PDEs) were calculated with 20,000 and 40,000 iterations with $dt=0.1$ and $dt=0.05$ in fields sized $xl=56.25$, $yl=225$ with $dx=0.75$, and $xl= yl=200$ with $ds=0.5$ for Figures 4A–C and Figures 4D–H, respectively. These conditions satisfy each CLF condition. In Figure 4I, to investigate the simultaneous gap-junction effects with hemi-channels $s_d\left(x,y\right)=1-0.002\max \left\{x,y\right\}$, $u_d\left(x\right)=0.0004x$, and $v_d\left(y\right)=1-0.002y$ were utilized in the field sized $x=y=300\left(dx=0.75\right)$ and $dt=0.1$ for 20,000 iterations.

For the nonlinear improved model with nonlinear terms, the parameters $d_u$, $i_{uv}$, and $i_{vu}$ were decreased linearly from 1 to 0.6. ${\mathit{c}}_{\mathit{wv}}$ and ${\mathit{p}}_{\mathit{vw}}$ were decreased linearly from 0.5 to 0.1 in Figures 5A–C and decreased by $s_d\left(x,y\right)=1-0.002\max \left\{x,y\right\}$ simultaneously in Figure 5D. Accordingly, the arbitrary parameter set generating stripes (wild type) was placed in the right top of the phase plane. PDEs were calculated in fields sized $xl=10$, $yl=40$ in Figures 5A–C and $xl=yl=50$ with $ds=0.25$ in Figure 5D. Then, after 500,000 iterations calculated with $dt=0.01$, we obtained the result.

Calculations were performed in the language Full BASIC ver. 8.1 with no-diffusion boundary conditions with difference calculus; then, results are shown as density plots of $u$. Parameters utilized in this study are summarized in Table 1.

TABLE 1

TABLE 1. Parameter set utilized in this paper.

2.2 Quantification of Simulated Color Patterns

Color pattern complexity and overall tone were quantified from binarized images using ImageJ as described in [24]. Briefly, the pattern simplicity score (PSS) is defined as the area weighted mean isoperimetric quotient of the contours extracted from each image. The overall color tone (OCT) of a pattern is defined and calculated as the ratio of white pixels in the binarized image. Analyzed images were prepared by the quaternary connection of a numerical result ($100\times 100$ individual fields with periodic boundary conditions) of $u$ in each parameter.

3 Results

3.1 Linear RD Model for Pigment-Pattern Formation

Previous laser ablation experiments reveal that the presence of mutual interactions between two types of pigment cells are necessary to generate Turing patterns (Figure 1E). Briefly, the density of melanophore existing and newly generated in a stripe decreases when the xanthophores in adjacent interstripes are ablated. On the other hand, that of xanthophore was not drastically changed. Then, two types of pigment cell inhibit each other at a one-cell distance even though the inhibition from xanthophore is inapparent until melanophores in adjacent stripes are eliminated. A mathematical model is derived from these apparent interactions in [12] although the details of the relationship between the experimental results and the model are not described. This model is based on the following set of RD equations:

$\{\begin{array}{c}\frac{\mathbf{\partial }\mathit{u}}{\partial \mathit{t}}={\mathit{D}}_{\mathit{u}}{\mathbf{\nabla }}^{\mathbf{2}}\mathit{u}+\mathit{f}\left(\mathit{v},\mathit{w}\right)-{\mathit{d}}_{\mathit{u}}\mathit{u}\\ \frac{\partial \mathit{v}}{\partial \mathit{t}}={\mathit{D}}_{\mathit{v}}{\mathbf{\nabla }}^{\mathbf{2}}\mathit{v}+\mathit{g}\left(\mathit{u},\mathit{w}\right)-{\mathit{d}}_{\mathit{v}}\mathit{v}\\ \frac{\partial \mathit{w}}{\partial \mathit{t}}={\mathit{D}}_{\mathit{w}}{\mathbf{\nabla }}^{\mathbf{2}}\mathit{w}+\mathit{h}\left(\mathit{u},\mathit{v}\right)-{\mathit{d}}_{\mathit{w}}\mathit{w}\end{array}.(1)$

Here the alternative distribution of two types of pigment cells (Figure 1C) is expressed by two factors $\left(U,V\right)$ of the three components. Then, $u$ and $v$ are each volume (viability). The numerical simulation of this model results in a Turing pattern in which $u$ and $v$ are distributed with antiphase, and a concentration of third factor $W\left(w\right)$ presents peaks synchronized with $u$ (Figure 2). It should be noted that cell divisions of differentiated melanophores contribute only minimally to the pigment-pattern formation in fish (Figure 1F). Therefore, the number of melanophores is changed by 1) the supply of new cells from randomly scattered precursor cells, 2) the death of existing pigment cells, or 3) the migration from a position close to the skin surface [25]. In the case of melanophores, it is known that cell movements and cell deaths are complementary to each other [26]. Even though they are inhibited, xanthophores are found in the stripe region, where they exist with a pale color [27–29]. Xanthophores do not move actively in vivo as may be the case for iridophores. As detailed in Figure 1F, motilities of the cells are approximated by small diffusion coefficients $\left(D\right)$. The rapidly diffusing factor $W$ is assumed to have a large diffusion coefficient 1 in the outer region of the cells based on the results of electro-physiological experiments [30–32].

FIGURE 2

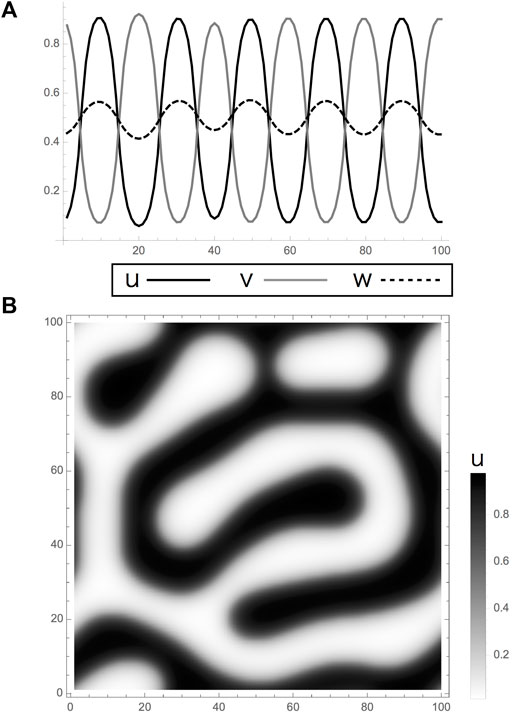
FIGURE 2. Turing pattern obtained by a reaction-diffusion model in Eqs 1, 2. (A,B). Calculation results of the model had linear terms with limits. (A) One and (B) two dimensions. Results indicate Turing patterns in which the variables $u$ and $v$ are distributed complementarily, and the highly diffusible molecule $W$ peaks at high $u$.

In the reaction, rather than it should be called an interaction, formulae, the dimension-less parameters are chosen arbitrarily from the sets that bring diffusion-driven instability. They are positive constants as shown in Table 1. Each formula is composed of a set of linear terms with upper and lower limits as utilized in the two-component system mentioned by [1] as follows:

$\{\begin{array}{c}f\left(v,w\right)=\left(\begin{array}{c}\mathbf{0};-i_{uv}v-i_{uw}w+s_u<\mathbf{0}\\ -i_{uv}v-i_{uw}w+s_u;0<-i_{uv}v-i_{uw}w+s_u<f_{\mathit{max}}\\ f_{\mathit{max}};-i_{uv}v-i_{uw}w+s_u>f_{\mathit{max}}\end{array}\right)\\ g\left(u,w\right)=\left(\begin{array}{c}\mathbf{0};-i_{vu}u+p_{vw}w+s_v<\mathbf{0}\\ -i_{vu}u+p_{vw}w+s_v;\mathbf{0}<-i_{vu}u+p_{vw}w+s_v<g_{\mathit{max}}\\ g_{\mathit{max}};-i_{vu}u+p_{vw}w+s_v>g_{\mathit{max}}\end{array}\right)\\ h\left(u,v\right)=\left(\begin{array}{c}\mathbf{0};p_{wu}u-c_{wv}v+s_w<\mathbf{0}\\ p_{wu}u-c_{wv}v+s_w;\mathbf{0}<p_{wu}u-c_{wv}v+s_w<\\ h_{\mathit{max}};p_{wu}u-c_{wv}v+s_w>h_{\mathit{max}}\end{array}{h}_{\mathit{max}}\right)\end{array}.(2)$

These equations simply indicate negative or positive interactions among two cells and molecules by the coefficients with different signs. They are derived from the interaction network obtained by the experimental results in [12]. The cells are assumed to be inhibiting mutually $\left(-i_{uv},-i_{vu}\right)$, and then $W$ is assumed to be produced by $U\left(p_{wu}\right)$ and consumed by $V\left(-c_{wv}\right)$. Accordingly, $W$ is assumed to inhibit pigment cells of the producer $\left(-i_{uw}\right)$ and produce (or preserve) the consumer $\left(p_{vw}\right)$. The self-coupling parameters $-d_u$, $-d_v$, $-d_w$ corresponded to degradation (or death) coefficients, whereas $s$’s represent constants related to the supply (also called “support sustainability”) of each component. The producer $U$ activates $V$ but then inhibits itself at long range via $W$. By consuming $W$, $V$ also indirectly inhibits itself but then is activating $U$ by double inhibition at long range. As a result, $U$ and $V$ exhibit no difference in apparent interactions, making it difficult to identify which factor corresponds to which cell type. Besides melanophores, xanthophores also show self-inhibition at long range. In laser ablation experiments, melanophore elimination in adjacent stripes causes pale-colored xanthophores in an interstripe region. Therefore, the pale color reflects xanthophore inhibition even without a change in cell number.

The three-component model in (1) is somewhat complex though it can be roughly regarded as a combination of two-component systems originally suggested by [33] as follows. For ease of mathematical analyses, I use the following two-component system that shares a component with high-diffusivity.

$\{\begin{array}{c}\frac{\partial x}{\partial t}=f_{x}x+f_{y}y+D_x{\mathbf{\nabla }}^{\mathbf{2}}x\\ \frac{\partial y}{\partial t}=g_{x}x+g_{y}y+D_y{\mathbf{\nabla }}^{\mathbf{2}}y\end{array}.(3)$

There are two different cases that bring diffusion-driven instabilities, i.e., activator–inhibitor type (Figure 3A) or activator–substrate–depletion type (Figure 3B), characterized by different signs of the parameters [34, 35]. Both conditions are included in the three-component model sharing with the high-diffusible component (Figure 3C). Therefore, each parameter in the model can be regarded as part of a two-component system. The first and second reaction Eq. 2 include mutual inhibitions $\left(-i_{uv}v,-i_{vu}u\right)$, each of which corresponds to the respective self-activation ($f_x>0$ for $x$) though it cannot be realized without each partner. Recent experiments reveal that xanthophores are generated from division of other xanthophores [29]. Therefore, at least one self-reaction parameter; $-d$ for $u$ or $v$ in Eq. 2 cannot be a degradation coefficient; i.e., it might be a nonnegative parameter.

FIGURE 3

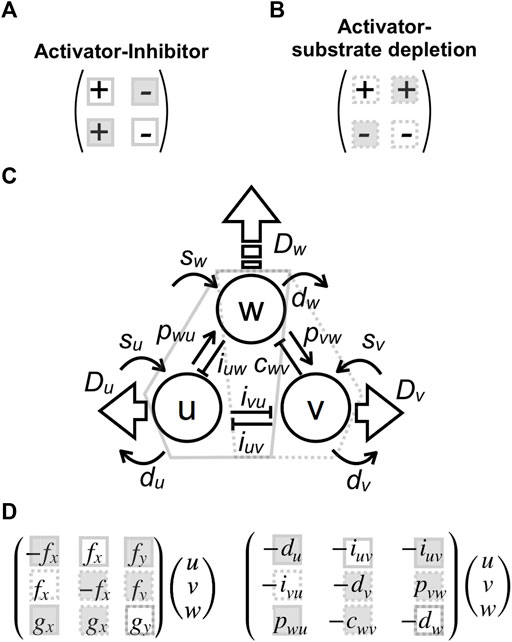
FIGURE 3. Parameter correspondences to two-component systems and effects on pattern size. (A,B) Two conditions that generate a Turing pattern: activator–inhibitor type (A) or activator–substrate–depletion type (B) with different signs of reaction parameters. (C) Correspondence between parameters in the present tree-component model and the two-component systems. Interactions included in conditions (A) and (B) are enclosed by solid and dashed polygons, respectively. (D) Matrix forms of reaction terms corresponding to the two-component system: the filled squares indicate the parameter that increases pattern size when the absolute value is decreased, and the open squares denote the opposite; the solid squares correspond to condition (A), and the dashed ones correspond to condition (B).

3.2 Effects of the Parameters on the Component Proportion and the Characteristic Wavelength of a Pattern.

Variation in patterns observed in most zebrafish mutants is explained by changes in the types and sizes of patterns. The former is defined by pattern selection [23, 36] and manifests as a general variation of the Turing pattern from spots to stripes to reverse spots. The latter is dictated by the characteristic wavelength of the pattern [37]. The following sections analytically describe the effect of parameters in the model (1)–(2) on these characteristics.

3.2.1 Effects of Parameter on Pattern Size

The characteristic wavelength of a pattern can be analytically obtained from the dispersion relation of linear stability [37]. The wavelength of a two-component RD system in (3) is given by the following equations of which derivation was mentioned in detail in [37]:

$\frac{\mathbf{2}\pi }{k_{\mathit{max}}}=\sqrt{\frac{\sqrt{D_x{D}_y}\left(D_y-D_x\right)}{\left(D_x+D_y\right)\sqrt{-f_y{g}_x}-\sqrt{D_x{D}_y}\left(f_x-g_y\right)}}.(4)$

$k_{\max }$ is a preferable wave number in a system. As mentioned, each parameter in the model can be regarded as a two-component system (Figure 3C). The mutual inhibitions $\left(-i_{uv}v, -i_{vu}u\right)$ in the three-component system correspond to self-activation though they are inversely related; i.e., the sign of the parameters is different from $f_x$ in two-component systems. The increase in the absolute values of the parameters reinforces the self-activation. At the same time, the effects of $-d_u$ and $-d_v$ are the opposite of $f_x$. The effect on pattern size when the absolute value of each parameter is decreased (i.e., the decline of each interaction) is shown in Figure 3D and indicates correspondence with two-component systems (Figures 3A,B).

3.2.2 Effects of Parameter on Pattern Selection

In zebrafish, pattern selection is determined mainly by the proportion of two types of pigment cells with complementary distribution. The relative position of the equilibrium from the limits of the reaction terms provides an index for pattern selection [23] as that is the origin of diffusion-driven instability.

Considering the differential equations, the decrease in each absolute value of parameter (i.e., the decline of each interaction) with a positive effect decreases the population volume of respective cells; then that of the parameter with a negative effect increases the population of the respective cells. Here, the component $W$ with high diffusivity represses $u$ and promotes $v$; therefore, the decrease in the positive parameter in the differential equations of $w$ increases $u$ and decreases $v$, respectively. The opposite can apply to negative parameters. From this aspect, however, it is difficult to refer about the combined effect of parameters with different signs.

3.3 Correspondence Between the Mathematical Model and Connexin Defects in Zebrafish Estimated from Molecular Function

Next, correspondence between this model and molecular functions is assumed (Figure 1G). In zebrafish, leopard mutants are known to have an aberrant pigment pattern, whereby stripes are changed to spots [6] (Figures 1A,B). The gene responsible for the leopard mutation is a connexin cx41.8, which encodes a four trans-membrane connexin protein. Additionally, mutation of connexin cx39.4 results in wavy stripes. Recent analyses of connexin activity reveal different functions associated with hemi-channels and gap junctions [30, 31]. Hemi-channels are open to the extracellular environment, whereas gap junctions form connections between cells to allow the exchange of small molecules (Figure 1D). Accordingly, connexins may be involved in both long- and short-range interactions. These channels may function as gates for the transport of molecule $W$ across the membrane (Figure 1G). Accordingly, producer $U$ produces $W$, which then diffuses outside the cell into the extracellular space via some kind of gate. Therefore, gate defects affect survival of the producer by preventing the release of harmful $W$ (i.e., $d_u$ of $-d_u$ is increased). I consider two other possibilities, i.e., the effect of the gate defect on $D_w$ and/or $i_{uw}$. If $D_w$ is changed, $W$ outside of the cells is also e affected. A $u$-dependent decrease in $D_w$ might be more appropriate for the assumption of enclosed $W$ though it gives difficulties in the analytical approach and both finally result in an increase in the death of $U$. Then, the degree of harmful effect on U by the same concentration of w does not change. Therefore, $D_w$ and $i_{uw}$ are not affected. $w$ has peaks with the peaks of producer U, and gates on cells assume passive effects on W movements. Defects of gate on a U cell will enclose W into the cell, then the production of W from U, i.e., $p_{wu}$, other than d_u will also be affected. If $p_{wu}$ is decreased, v cells will be affected to decrease. However, the supply of w from other than u cells to the system will absorb the negative effects on v, even though the s_w in Table 1 is 0.0. Then the increase in d_u itself has the effect to decrease the concentration of W. Consumer $V$ is assumed to incorporate beneficial $W$ into the cell across the gates and then to consume it, indicating that the gate defects decrease the parameters $c_{vw}$ of $-c_{vw}$ and $p_{wv}$. Both parameters are assumed to be related to intracellular events; therefore, higher $w$ is needed for the same rate of consumption and $V$ production compared with the case of intact hemi-channels. At the same time, parameters for mutual inhibitions $i_{uv}$ and $i_{vu}$ seem to be decreased by the leopard mutation [38] through gap junctions (combination of gates) at short range. They are simultaneously affected, linking with the hemi-channel defect on the corresponding cell. In Figure 1G, these parameters linked to different gates are indicated by different hatchings.

3.4 Comparisons of Results Obtained by Simulation and Experiments.

First, the independent effects of the gate on each cell were analyzed numerically. When an arbitrary stripe is set as a starting point, only gates that open to the outside on $U$ and $V$ cells were removed along the x- and y-axes. Numerical simulation of this model yielded a spot pattern of $u$ in the case in which gates on $U$ cells have defects as expected by the sign of the parameter (Figure 4A). Reversed $u$ spots are yielded in $V$ cell defects (Figure 4B) though the change is not strong because it includes opposite effects on $V$ volume. PSS increases in both cases, and then OCT are decreased and increased by respective defects. That is, the asymmetry of changes in pattern selection can be observed by the removals of gates on respective cell types.

FIGURE 4

FIGURE 4. Numerical results of gate effects and comparison with experiments. (A–I) Numerical results obtained from a model of linear reaction terms with limits. Pattern shifts were observed when the effects of gate defects on both cells were changed. Defects of gates on $U$ and $V$ cells and between the cells become larger along the $x$− , $y$−, and $z$ (or $x$, $y$)−axes, respectively. (A–C) Each defect was analyzed independently with quantification of patterns. (A) U defect, (B) $V$ defect, and (C) short-range defects. PPS and OCT were obtained quantitatively. The short-range effects by gap junctions were eliminated from arbitral wild-type condition (D) 0.05 to (E) 0.04, (F) 0.03, (G) 0.02, and (H) 0.01. (I) Numerical result of linear terms with limits in which the short-range effects were spontaneously changed along the $x$− and $y$−axes with increasing $u_d$ and decreasing $v_d$. Each small letter indicates the corresponding fish with connexin conditions. (J) Schematics of this analyses utilizing the present linear model. U defect, (B) $V$ defect, and (C) short-range defects were changed along with the axes in each panel as shown in the figures. (K) Pigmentation pattern on connexin-manipulated fish slightly changed from [8], with permission to use the figures from Dr. M. Watanabe. Gray flamed fish had correspondence to numerical results.

Defects on short-range inhibition do not have drastic effects on pattern selection though the pattern does finally disappear (Figure 4C). On the 2-D plane, the stripe region is recessive together with the defect in short-range effects by gap junctions (Figures 4D–H,J) though the tendency to shift the pattern selection is not changed. In Figure 4I, short-range effects are simultaneously decreased by respective $x$ or $y$ values that link with $U$ or $V$ defects as shown in the right panel in Figure 4J. This also keeps the same tendency to shift the pattern selection with individual cases.

The results mostly consist of the positive effects of connexin additions to WKO that increase the respective pigment cells [8]. However, experimental eliminations of the gate on each wild-type pigment cell lead to an increase in the rate of respective pigment cells; melanophore defects generate net (or rather wavy stripe) patterns of melanophores, and the xanthophore defects result in dot patterns of melanophores (i.e., net patterns of xanthophore). Therefore, the simulation results are partly inconsistent with experimental results in [8] in which the effects of connexins on each or both pigment cells are investigated in detail (Figure 4K).

From the electro-physiological experiments in [30]; each type of connexin can be considered to have different strengths of the (hemi-) channel functions on the two types of cells. Deduced patterns of respective transgenic fish are indicated by small letters on the phase plane in Figure 4I. Even though the differences in the strengths of channels are taken into account, the removal of hemi-channels on wild-type xanthophores tends to increase the proportion of xanthophores; then a faint increase of proportion in melanophore is brought in the case of connexin on melanophores (Figure 4K). If cell $U$ is a melanophore, other than that the gray-framed patterns shown in Figure 4K do not seem to correspond to Figure 4I, all of the experimentally obtained patterns exist in the simulation.

From the analyses of wavelength mentioned above, defects to the gates on cell $U$ (increasing in $d_u$ of $-d_u$) or cell $V$ (decreasing in $p_{vw}$ and $c_{wv}$) cause a decrease or an increase in pattern size, respectively. In numerical simulations, the pattern size tends to be decreased and increased by the hemi-channel defects on both $U$ and $V$ cells as expected (Figures 3A,B). The characteristic thinning of $u$ stripes and widening of $v$ interstripes are observed in the simulation of $U$-cell defects though it is not explained by the analyses. From the characteristic thinning of the $u$ stripe, each cell corresponding to one of two short-range factors may be deduced. However, the thinning is observed on melanophore stripe in the case of a defect in the xanthophore. Inconsistent with the $U$ defect, the melanophore defect tends to result in wide melanophore stripes in the experiment.

3.5 Improvements to the Model with Nonlinear Terms.

To describe the detailed behavior of the components in the system, the model is changed to a model including nonlinear terms as shown in (5).

$\{\begin{array}{c}\frac{\partial u}{\partial t}=D{\nabla }^{\mathbf{2}}u-i_{uv}uv-i_{uw}uw+d_{u}u+\frac{s_u}{\mathbf{1}+u+v}\\ \frac{\partial v}{\partial t}=D{\nabla }^{\mathbf{2}}v-i_{vu}vu+p_{vw}vw-d_{v}v+\frac{s_v}{\mathbf{1}+u+v}\\ \frac{\partial w}{\partial t}={\nabla }^{\mathbf{2}}w+p_{wu}u-c_{wv}wv-d_{w}w+s_w\end{array}.(5)$

The qualitative relationships for pattern formation shown in Figure 1F are not changed from model (1) and (2). That is, mutual inhibitions between $U$ and $V\left(-i_{uv}uv, -i_{vu}vu\right)$ are assumed; then, substance $W$ with high diffusivity is assumed to inhibit the producer $U\left(-i_{uw}uw\right)$ and to promote consumer $V\left(p_{vw}vw\right)$. Considering the interactions between different types of cells and between cells and molecules, the inhibitions were given by multiplication terms (e.g., the inhibition of $U$ by $W$ was described as $uw$ and so on). These multiple terms are based on the description of the second order reaction in the chemical kinetic equation or dimer reactions by [39]; it enables only limited reaction by the contacts between the components. $W$ is needed for maintenance of cell $V$, so this reaction is also given by a multiplication term of their volume. On the other hand, production of $W$ by $U$ only occurs $u$-dependently, and degradation (and death) is also $w$-dependent. Therefore, those terms are linearly related to each component. This model as an example of possible improvements also generated Turing patterns (Figure 5). These improvements can identify the functions on existing cells or newly differentiating cells. Then, new generations of pigment cells occur only with eliminations of existing cells [40]. Therefore, mature cells would inhibit the new generation of cells. The sign of $d_u$ seemed preferably to be positive for the starting point of pattern selection corresponding to zebrafish, i.e., the start from stripe. Even though the sign was opposite to the linear model, total $u$ change may become minus with relation to other components (i.e., $-i_{uv}v-i_{uw}w+d_u<0$ in the deformed reaction terms $\left(\left(-i_{uv}v-i_{uw}w+d_u\right) u+s_u/\left(1+u+v\right)\right)$. Therefore, the self-productivity can be small enough to agree with the low proliferation rate of melanophores. Similarly, concerns about the self-productivity of xanthophores mentioned above, $\partial v/\partial t$ in (Eq. 5) already have self-productivity by the multiplication term $vw$ regardless of the sign of $d_v$ (i.e., $-i_{vu}u+p_{vw}w-d_v>0$ in deformed reaction terms $\left(-i_{vu}u+p_{vw}w-d_v\right) v+s_v/\left(1+u+v\right)$ ). The sign of $d_v$ can be inverted though the change is not expected to substantially affect pattern characteristics.

FIGURE 5

FIGURE 5. Numerical results of gate effects by nonlinear model. (A–D) Numerical results obtained from a model with nonlinear reaction terms. Pattern shifts were observed when the effects of gate defects on both cells were changed. (A) U defect, (B) $V$ defect, and (C) short-range defects, and between the cells, became larger along the $x$−, $y$−, and $z$ (or $x$, $y$)-axes, respectively. Pattern quantification by PSS and OCT are shown on the right. Then, the short-range inhibitions were decreased along both axes, spontaneously. All results are shown as density plots of $u$.

Next, numerical calculations of the nonlinear model are performed to consider the condition in which respective gates on $U$ and $V$ cells and both-gate defects are added (Figures 5A–C). Again, numerical results consistent with the linear model can be obtained from an arbitrary parameter set generating a stripe pattern. A biased pattern shift can also be obtained by simulations, partly corresponding to connexin-mutation experiments. When gates on the $U$ cell are deleted, it results in a $u$ dot pattern (Figure 5A). Simultaneous decreases in $p_{vw}$ and $c_{wv}$ by increasing the gate defect on $V$ cells generate a net of $u$ though not so drastic (Figure 5B). A defect in the gap junction by decreasing $i_{vu}$ and $i_{uv}$ has a minimal effect though the stripe region became recessive with a combination of defects on each outer gate (Figures 5C,D). The thinning of the $u$ population is not clear because of the thin stripe at the start.

4 Discussion

In the present study, to confirm the potency of diffusion-driven instability in determining fish pigmentation patterns, channels on pigment cells are generalized as gates (Figure 1). The three-component RD model (1) is shown to be composed of two-component RD systems bringing diffusion-driven instabilities (Figures 2, 3). The proposed qualitative models help to understand the relationship between pigment cells as well as between cells and molecules even when their identity is unknown. The terms of the theoretical model are connected with the functions of each channel on different cells. Parameters affected by the gate defects were deduced (Figure 1G); then, the effects of such defects are simulated from a parameter set that generates an arbitrary stripe as a benchmark (Figures 4, 5). Then, dots and thinning of the $U$ cell population can be obtained by a defect of the gate on it in numerical simulations. The identities of melanophores and xanthophores are deduced from the change of pattern selection and the wavelengths though the identify of important substance $W$ is still missing. Then, improvements to the nonlinear model enable a description of the detailed behaviors of components that are related to pattern formation. Though the numerical analyses cannot strictly explain the pattern obtained by experimental manipulation of connexins by [8]; the present study can help to interpret the mechanism underlying the leopard mutation as a Turing system.

The determination of the signs of self-reaction terms for $U$ and $V$ is difficult. The signs of $d_u$ prefer to invert for a desirable range of pattern selection starting from the stripe in the improved model though the total changes for $U$ (= melanophore) correspond to experimental observations. The increase in existing melanophores brought by positive $d_u$ are visible by the laser ablation of adjacent xanthophores or deletion of stripes in the experiments in [12]. Each manipulation decreases $-i_{uv}vu$ or $-i_{uw}wu$ inhibitions, respectively. On the other hand, the self-productivity of xanthophores in the nonlinear model can be achieved even with the negative coefficient of self-reaction. The combination of two cases of diffusion-driven instability in the three-component model indicates the capacity to make a pattern without melanophores by the self-productivity of xanthophores if sufficient $W$ is added externally. On the other hand, if melanophores have strong self-productivity, they are also able to make a pattern without xanthophores by the removal of extra $W$.

Connexins are related to both hemi-channels and gap junctions. Hemi-channels are considered less important in physiology although it was recently revealed that the aberrant activity of hemi-channels can change the proportion of vertebrae [31] and are related to the pigment-pattern formation in zebrafish [30, 32]. Laser ablation experiments show that the interactions between xanthophores and melanophores differ depending on the distance. In the present model, the highly diffusible molecule $W$ has a positive effect on $V$. Hence, the inhibition of $V$ via gap junctions is inconsistent. Outflow of harmful $W$ from via gap junctions is also inconsistent with the inhibition. Furthermore, generation of a new gap junction between two cells takes more than 30 min [41] (Watanabe personal communication). This elicits a different signal transduction cascade as cell depolarization [42] and incorporation of functions for molecules other than connexin should be envisioned. Then, the inverted function may be derived from an observed rectified current in the gap junction. It is observed that quail melanocytes interact with each other via filopodia in vivo and in vitro [43]. Therefore, gap junctions may have functions on interactions not only between other types of cells but among the same populations though the obtained simulation results included several collisions with experimental results. Similar discords are also in experiments. The results of [8] indicate that either Cx41.8 or Cx39.4 is needed on melanophores; then, Cx41.8 is necessary and sufficient on xanthophore for (stripe) pattern formation. As plotted in Figure 6A, the proportion of pigment cells is drastically changed in the case of the manipulation of the gate on xanthophores though asymmetry of change in color tones of simulated pattern in Figures 4A–C indicate the gate on melanophores is effective. Shuffle of mutant fish further supports the numerical results shown in Figure 6B. In this case, expected “Cx41.8” manipulations show the “necessary and sufficient” trait on melanophores.

FIGURE 6

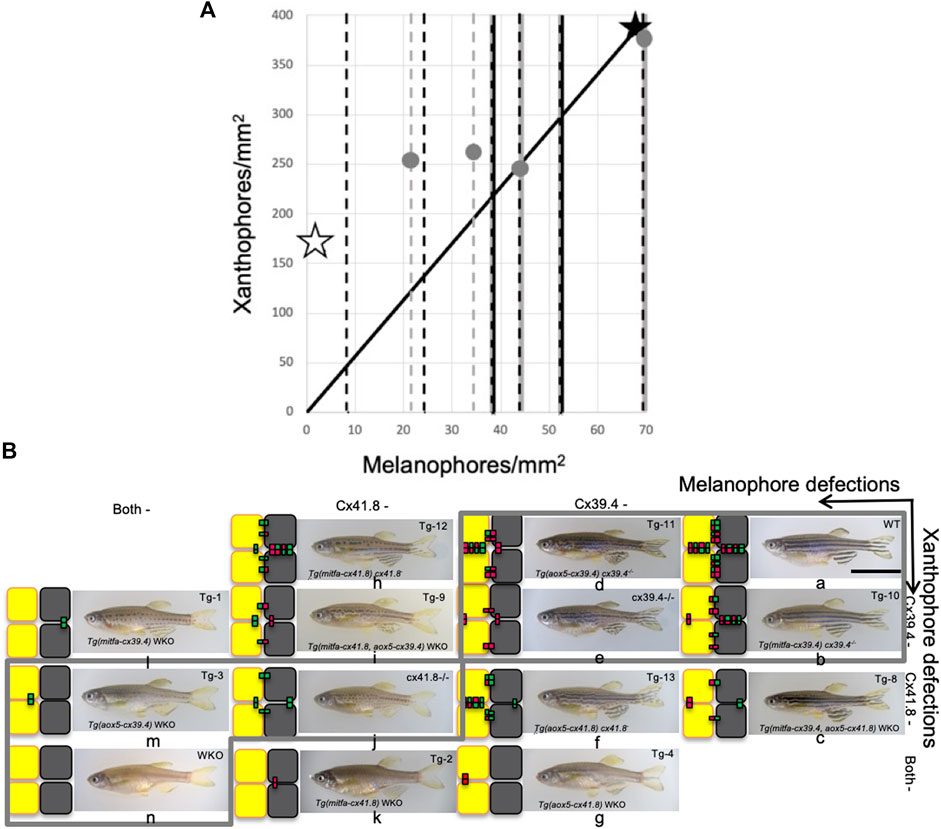
FIGURE 6. Shuffle of mutant fish that gives accordance with numerical results. (A) A scatterplot of two types of pigment cells. Stars and dots indicate shifts of proportion of pigment cells caused by experimental manipulations of connexin by [8]. However, most data can be obtained only about melanophores, so changes in melanophore number are indicated by broken lines. Simple broken lines indicate the addition of connexins to double knockout (WKO); black ones are “on melanophore,” and gray ones are “on xanthophore,” and broken lines with solid lines on the back denote deletion of connexon from WT; black dot on gray corresponds to “from melanophore” and gray dot on black “from xanthophore.” Solid lines indicate the proportion of WT. Open stars and filled ones indicate the values of WKO and WT, respectively. (B) Mutant fish are shuffled for accordance with numerical results in Figure 3I. Each small letter indicates the corresponding fish with simulation in the aspect of pattern selection.

Similar effects of connexin mutations (i.e., shift from stripe to dots) can be observed on both the body and fins. Because the fins lack iridophores, the effect on the pigment pattern formation depends on the relationship between melanophores and xanthophores. Even though pattern formation is achieved by the two types of cells, details on the role of iridophores in cellular interactions are revealed [10]. The evaluation of the iridophore function in similar modeling is also possible and should be attempted.

Using such a model with PDEs will lead to various mathematical analyses. For example, pattern size was mathematically analyzed with regard the model as combination of two-component systems here. This method cannot yet describe the independent pattern sizes of each type of pigment cell that are observed experimentally [22] and predicted numerically in this paper. Therefore, more sophisticated analyses are required in the future.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research was supported from Grant-in-Aid for Scientific Research on Innovative Areas (The Japan Society for the Promotion of Science), Periodicity and its modulation in plant No. 20H05421 and Research grant from Shimadzu Science Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author thanks Masakatsu Watanabe and Masafumi Inaba for stimulating discussions and important comments as well as members of the Higaki lab for providing a suitable environment to concentrate on this investigation. I also thank Editage (www.editage.com) for English language editing and the IROAST Proofreading/Publication Support Program. I would like to thank to S. Kondo.

References

1. Kondo S, Asai R. A Reaction-Diffusion Wave on the Skin of the marine Angelfish Pomacanthus. Nature (1995) 376:765–8. doi:10.1038/376765a0

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Johnson SL, Africa D, Horne S, Postlethwait JH. Half-tetrad Analysis in Zebrafish: Mapping the Ros Mutation and the Centromere of Linkage Group I. Genetics (1995) 139:1727–35. doi:10.1093/genetics/139.4.1727

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Johnson SL, Africa D, Walker C, Weston JA. Genetic Control of Adult Pigment Stripe Development in Zebrafish. Develop Biol (1995) 167:27–33. doi:10.1006/dbio.1995.1004

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kelsh RN. Genetics and Evolution of Pigment Patterns in Fish. Pigment Cel Res (2004) 17:326–36. doi:10.1111/j.1600-0749.2004.00174.x

CrossRef Full Text | Google Scholar

5. Haffter P, Granato M, Brand M, Mullins MC, Hammerschmidt M, Kane DA, et al. The Identification of Genes with Unique and Essential Functions in the Development of the Zebrafish, Danio rerio. Development (1996) 123:1–36. doi:10.1242/dev.123.1.1

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Watanabe M, Iwashita M, Ishii M, Kurachi Y, Kawakami A, Kondo S, et al. Spot Pattern Ofleopard Daniois Caused by Mutation in the zebrafishconnexin41.8gene. EMBO Rep (2006) 7:893–7. doi:10.1038/sj.embor.7400757

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kumar NM, Gilula NB. The gap junction Communication Channel. Cell (1996) 84:381–8. doi:10.1016/s0092-8674(00)81282-9

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Usui Y, Aramaki T, Kondo S, Watanabe M. The Minimal gap-junction Network Among Melanophores and Xanthophores Required for Stripe Pattern Formation in Zebrafish. Development (2019) 146:dev181065. doi:10.1242/dev.181065

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Volkening A. Linking Genotype, Cell Behavior, and Phenotype: Multidisciplinary Perspectives with a Basis in Zebrafish Patterns. Curr Opin Genet Develop (2020) 63:78–85. doi:10.1016/j.gde.2020.05.010

CrossRef Full Text | Google Scholar

10. Maderspacher F, Nüsslein-Volhard C. Formation of the Adult Pigment Pattern in Zebrafish Requiresleopardandobelixdependent Cell Interactions. Development (2003) 130:3447–57. doi:10.1242/dev.00519

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Parichy DM, Turner JM. Temporal and Cellular Requirements for Fms Signaling during Zebrafish Adult Pigment Pattern Development. Development (2003) 130:817–33. doi:10.1242/dev.00307

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Nakamasu A, Takahashi G, Kanbe A, Kondo S. Interactions between Zebrafish Pigment Cells Responsible for the Generation of Turing Patterns. Proc Natl Acad Sci (2009) 106:8429–34. doi:10.1073/pnas.0808622106

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Meinhardt H, Gierer A. Application of a Theory of Biological Pattern Formation Based on Lateral Inhibition. J Cel Sci. (1974) 15:132–46. doi:10.1242/jcs.15.2.321

CrossRef Full Text | Google Scholar

14. Hamada H, Watanabe M, Lau HE, Nishida T, Hasegawa T, Parichy DM, et al. Involvement of Delta/Notch Signaling in Zebrafish Adult Pigment Stripe Patterning. Development (2014) 141:318–24. doi:10.1242/dev.099804

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Watanabe M, Kondo S. Comment on "Local Reorganization of Xanthophores fine-tunes and Colors the Striped Pattern of Zebrafish". Science (2015) 348:297. doi:10.1126/science.1261947

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kondo S. An Updated Kernel-Based Turing Model for Studying the Mechanisms of Biological Pattern Formation. J Theor Biol (2017) 414:120–7. doi:10.1016/j.jtbi.2016.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Volkening A, Sandstede B. Iridophores as a Source of Robustness in Zebrafish Stripes and Variability in Danio Patterns. Nat Commun (2018) 9:3231. doi:10.1038/s41467-018-05629-z

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Owen JP, Kelsh RN, Yates CA. A Quantitative Modelling Approach to Zebrafish Pigment Pattern Formation. eLife (2020) 9:E52998. doi:10.7554/eLife.52998

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bullara D, De Decker Y. Pigment Cell Movement Is Not Required for Generation of Turing Patterns in Zebrafish Skin. Nat Commun (2015) 6:6971. doi:10.1038/ncomms7971

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Konow C, Li Z, Shepherd S, Bullara D, Epstein IR. Influence of Survival, Promotion, and Growth on Pattern Formation in Zebrafish Skin. Sci Rep (2021) 11:9864. doi:10.1038/s41598-021-89116-4

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Asai R, Taguchi E, Kume Y, Saito M, Kondo S. Zebrafish Leopard Gene as a Component of the Putative Reaction-Diffusion System. Mech Develop (1999) 89:87–92. doi:10.1016/s0925-4773(99)00211-7

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Watanabe M, Kondo S. Changing Clothes Easily: connexin41.8 Regulates Skin Pattern Variation. Pigment Cel Melanoma Res (2012) 25:326–30. doi:10.1111/j.1755-148x.2012.00984.x

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Shoji H, Iwasa Y, Kondo S. Stripes, Spots, or Reversed Spots in Two-Dimensional Turing Systems. J Theor Biol (2003) 224:339–50. doi:10.1016/s0022-5193(03)00170-x

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Miyazawa S, Okamoto M, Kondo S. Blending of Animal Colour Patterns by Hybridization. Nat Commun (2010) 1:66–6. doi:10.1038/ncomms1071

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Takahashi G, Kondo S. Melanophores in the Stripes of Adult Zebrafish Do Not Have the Nature to Gather, but Disperse when They Have the Space to Move. Pigment Cel Melanoma Res (2008) 21:677–86. doi:10.1111/j.1755-148x.2008.00504.x

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sawada R, Aramaki T, Kondo S. Flexibility of Pigment Cell Behavior Permits the Robustness of Skin Pattern Formation. Genes Cells (2018) 23:537–45. doi:10.1111/gtc.12596

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Hirata M, Nakamura K-i., Kanemaru T, Shibata Y, Kondo S. Pigment Cell Organization in the Hypodermis of Zebrafish. Dev Dyn (2003) 227:497–503. doi:10.1002/dvdy.10334

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hirata M, Nakamura K-I, Kondo S. Pigment Cell Distributions in Different Tissues of the Zebrafish, with Special Reference to the Striped Pigment Pattern. Dev Dyn (2005) 234:293–300. doi:10.1002/dvdy.20513

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Mahalwar P, Walderich B, Singh AP, Nüsslein-Volhard C. Local Reorganization of Xanthophores fine-tunes and Colors the Striped Pattern of Zebrafish. Science (2014) 345:1362–4. doi:10.1126/science.1254837

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Watanabe M, Sawada R, Aramaki T, Skerrett IM, Kondo S. The Physiological Characterization of connexin41.8 and connexin39.4, Which Are Involved in the Striped Pattern Formation of Zebrafish. J Biol Chem (2016) 291:1053–63. doi:10.1074/jbc.m115.673129

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Misu A, Yamanaka H, Aramaki T, Kondo S, Skerrett IM, Iovine MK, et al. Two Different Functions of Connexin43 Confer Two Different Bone Phenotypes in Zebrafish. J Biol Chem (2016) 291:12601–11. doi:10.1074/jbc.m116.720110

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Watanabe M. Gap junction in the Teleost Fish Lineage: Duplicated Connexins May Contribute to Skin Pattern Formation and Body Shape Determination. Front Cel Dev. Biol. (2017) 5:13. doi:10.3389/fcell.2017.00013

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Turing AM. The Chemical Basis of Morphogenesis. Philos Trans R Soc Lond B (1952) 462:27–73.

Google Scholar

34. Gierer A, Meinhardt H. A Theory of Biological Pattern Formation. Kybernetik (1972) 12:30–9. doi:10.1007/bf00289234

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Murray JD. Mathematical Biology II – Spatial Models and Biomedical Applications. Seattle, WA: University of Washington (2003).

Google Scholar

36. Ermentrout B. Stripes or Spots? Nonlinear Effects in Bifurcation of Reaction-Diffusion Equations on the Square. Proc R Soc A (1991) 434(1891). doi:10.1098/rspa.1991.0100

CrossRef Full Text | Google Scholar

37. Miura T, Maini PK. Speed of Pattern Appearance in Reaction-Diffusion Models: Implications in the Pattern Formation of Limb Bud Mesenchyme Cells. Bull Math Biol (2004) 66(4):627–49. doi:10.1016/j.bulm.2003.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Yamanaka H, Kondo S. In Vitro analysis Suggests that Difference in Cell Movement during Direct Interaction Can Generate Various Pigment Patterns In Vivo. Proc Natl Acad Sci U S A (2013) 111:1867–72. doi:10.1073/pnas.1315416111

CrossRef Full Text | Google Scholar

39. Meinhardt H. Chapter 11. Cell Determination. In: PK Maini, and HG Othmer, editors. Models of Biological Pattern Formation. London: Academic Press (1982). p. 107–17.

Google Scholar

40. Yamaguchi M, Yoshimoto E, Kondo S. Pattern Regulation in the Stripe of Zebrafish Suggests an Underlying Dynamic and Autonomous Mechanism. Proc Natl Acad Sci (2007) 104(12):4790–3. doi:10.1073/pnas.0607790104

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Usui Y, Watanabe M. Role of the Connexin C-Terminus in Skin Pattern Formation of Zebrafish. BBA Adv (2021) 1:100006. doi:10.1016/j.bbadva.2021.100006

CrossRef Full Text | Google Scholar

42. Inaba M, Yamanaka H, Kondo S. Pigment Pattern Formation by Contact-dependent Depolarization. Science (2012) 335:677. doi:10.1126/science.1212821

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Inaba M, Jiang T-X, Liang Y-C, Tsai S, Lai Y-C, Widelitz RB, et al. Instructive Role of Melanocytes during Pigment Pattern Formation of the Avian Skin. Proc Natl Acad Sci USA (2019) 116:6884–90. doi:10.1073/pnas.1816107116

PubMed Abstract | CrossRef Full Text | Google Scholar