Consensus Indices of Two-Layered Multi-Star Networks: An Application of Laplacian Spectrum

In this article, the convergence speed and robustness of the consensus for several dual-layered star-composed multi-agent networks are studied through the method of graph spectra. The consensus-related indices, which can measure the performance of the coordination systems, refer to the algebraic connectivity of the graph and the network coherence. In particular, graph operations are introduced to construct several novel two-layered networks, the methods of graph spectra are applied to derive the network coherence for the multi-agent networks, and we find that the adherence of star topologies will make the first-order coherence of the dual-layered systems increase some constants in the sense of limit computations. In the second-order case, asymptotic properties also exist when the index is divided by the number of leaf nodes. Finally, the consensus-related indices of the duplex networks with the same number of nodes but non-isomorphic structures have been compared and simulated, and it is found that both the first-order coherence and second-order coherence of the network $\mathbb{D}$ are between $\mathbb{A}$ and $\mathbb{B}$, and $\mathbb{C}$ has the best first-order robustness, but it has the worst robustness in the second-order case.

1 Introduction

Consensus is a class of distributed coordination problems of multi-agent systems, and the essence of the problem is that all agents are required to achieve a common state value under some given control strategies. In the networked system, the agents are required to communicate with each other based on the graph of the network so that they can cooperate effectively to accomplish the predetermined goals.

As a valuable interdisciplinary research field, consensus problems have received more and more attention from scholars and engineers in recent years, and there exist many potential applications in several aspects related to consensus such as sensor networks, formation control, and decision making. Researchers have done many good research works on consensus from various perspectives [1–18] and factors including the dynamics order (first/second order [1–15] or higher order), communication ways (continuous or discontinuous [4, 6], the types of topologies (fixed or switching [5]), convergence time (finite time or fixed time [16, 17]), and control methods (intermittent control [6], adaptive control [7], impulsive control, etc.).

To solve the consensus problems, the linking structure among agents is always interpreted by the communication graph of the system, and the performance indices of consensus models, such as convergence speed [1, 8] and network coherence [10–14], can be characterized by the Laplacian eigenvalues of the graph. Synchronization problems, which share similar control strategies and have the same essence as consensus problems, are always connected with the network structure [19–24] and are studied from the angle of graph theory.

There exist a great many valuable articles on coordination problems with the application of Laplacian eigenvalues [1, 5–15, 20]. This enlightening research [1] has shown that the Fiedler eigenvalue λ₂ of an undirected (or directed) graph can characterize the convergence speed of consensus problems.

In [9], the authors have investigated how the robustness depends on the properties of the Laplacian eigenvalues of graphs and give a derivation for the convergence speed and the H₂ norms of several classic graphs.

In [10, 11], the notion of network coherence has been proposed, and it had been proved that the network coherence can be quantified by nonzero Laplacian eigenvalues. Ref. [13] studies the noisy consensus dynamics on windmill-type graphs, and it is found that graph parameters and the number of leaders have a profound impact on the studied consensus algorithms. In [14], the authors found that 5-rose networks with small size have high network coherence and can be considered to be more robust to noise than networks with low coherence.

Lately, multilayer network is a frontier research branch of network science, and the multilayered structure has many examples in reality, for instance, the interactions between power grid and Internet, friendship and family relations, or transportation and aviation networks. Multiplex networks are coupled multilayer networks where each layer consists of the same node set but possibly different graph structures and layers interact with each other only via counterpart nodes of different layers [24, 25].

Considering that many real-world systems have multilayered structures, it is necessary to extend the consensus theory related to the Laplacian spectrum to multilayered graph structures. From the perspective of the application, the star graph is one of the most classic computer network structures. Star-related topologies are widely considered in many fields including coordination control problems [9, 15, 21, 22, 26, 27].

Based on the above analysis, this paper considers some dual-layered networks with certain meaningful topologies constructed by the graph operations, and each of the layers contains star subgraphs. It is familiar that the star network can be viewed as a point-to-multipoint communication system, and the dual-layered networks with star subgraphs can be comprehended as adding communication links among the counterpart nodes of different layers of the networks.

This paper makes further efforts to use the theory of graph spectra for studying the consensus indices related to robustness and convergence speed. In this research, some scale-free networks with symmetric structures and star subgraphs are considered.

Based on the chosen undirected graphs, we mainly study the network coherence of consensus to communication noise with an application of the theory of graph spectra. Specifically, the main contributions of this paper are listed as follows:

1. Several novel duplex star-composed networks with different linking structures but the same number of nodes have been constructed by graph operations, and the similar structure is the basis for comparative optimization.

2. Methods of graph spectra are applied to derive the Laplacian spectrum. Several new results on the asymptotic behavior of the consensus indices have been acquired.

3. The results that the first-order robustness will increase by a certain value depending on the number of leaf nodes have been found.

The main aim of this research is to investigate the consensus indices of the dynamical system with additive stochastic disturbances, which are described as network coherence and derived through the Laplacian spectrum.

The paper is organized as follows. In Section 2, some notations on graph theory are summarized, and the relations between performance and Laplacian eigenvalues are explained. In Section 3, the constructions of two-layered systems and main results are given. In Section 4, combined with the theorem of algebraic graph theory, the simulation results are compared and analyzed in Section 3.

2 Preliminaries

2.1 Graph Theory and Notations

A complete graph of n vertices is denoted by K_n, and a star graph with k leaves is denoted by S_k, where the leaf refers to the vertex of degree 1. ${\mathfrak{E}}_p$ is defined to be the empty graph with p vertices, where the empty graph means the graph without edges among all the nodes of the graph. Let G be a graph with vertex set V = {v₁, v₂, …, v_N}, and its edge set is defined as $\mathcal{E}=\{(i,j)|i,j=\mathrm{1,2},\dots ,N;i\ne j\}$. The adjacency matrix of G is defined as $A(G)={[a_{ij}]}_N$, where a_ij is the weight of the edge (i, j). In the undirected graph, one can see that (i, j) and (j, i) are the same edge in $\mathcal{E}$, i.e., a_ij = a_ji. All the edges in our undirected networks are 0–1 weighted; that is, $a_{ij}=\left\{\begin{array}{cc}1,\hfill & (i,j)\in \mathcal{E};\hfill \\ 0,\hfill & (i,j)\notin \mathcal{E}.\hfill \end{array}\right.$. The Laplacian matrix of G is defined as L(G) = D(G) − A(G), where D(G) is the diagonal degree matrix of G defined by D(G) = diag (d₁, d₂, …, d_N) with $d_i=\sum _{j\ne i}{a}_{ij}$. The Laplacian spectrum of G is defined as $S(L(G))=\left(\begin{array}{cccc}\hfill {\lambda }_1(G)\hfill & \hfill {\lambda }_2(G)\hfill & \hfill \dots \hfill & \hfill {\lambda }_p(G)\hfill \\ \hfill l_1\hfill & \hfill l_2\hfill & \hfill \dots \hfill & \hfill l_p\hfill \end{array}\right)$, where λ₁(G) < λ₂(G) < …, < λ_p(G) are the eigenvalues of L(G), and l₁, l₂, …, l_p are the multiplicities of the eigenvalues [28].

To construct the novel dual-layered networks, the following graph operations are needed.

Definition 1. [29] (The corona of two graphs) Let G₁ and G₂ be two graphs on disjoint sets of n and k vertices, respectively. The corona G₁◦G₂ of G₁ and G₂ is defined as the graph obtained by taking one copy of G₁ and n copies of G₂ and then joining the ith vertex of G₁ to every vertex in the ith copy of G₂.

Definition 2. [30, 31] (The Cartesian product of two graphs) For two graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂), the Cartesian product graph G = G₁ × G₂ is the graph with vertex set V₁ × V₂, and there is an edge from the vertex (x₁, y₁) to the vertex (x₂, y₂) if and only if either x₁ = x₂ and y₁, y₂ ∈ E₂ or y₁ = y₂ and x₁, x₂ ∈ E₁.

Lemma 1. [32] The eigenvalues of a circulant matrix $C=\mathfrak{C}{(c_0,c_1,c_2,\dots ,c_{n-1})}_n$ are

${\lambda }_k=c_0+c_1{w}_k+c_2{w}_k^2+\cdots +c_{n-1}{w}_k^{n-1},$

where $w_k=\exp (\frac{2k\pi i}{n})$, 0 ≤ k ≤ n − 1.

Lemma 2. [29] Let G₁ be any graph with n₁ vertices and m₁ edges and G₂ be any graph with n₂ vertices and m₂ edges. Suppose that $S(L(G_1))=({\mu }_1,{\mu }_2,\dots ,{\mu }_{n_1})$ and $S(L(G_2))=({\delta }_1,{\delta }_2,\dots ,{\delta }_{n_2})$. Then the Laplacian spectrum of G₁◦G₂ is given by

i) Two multiplicity one eigenvalues $\frac{({\mu }_i+n_2+1)\pm \sqrt{{({\mu }_i+n_2+1)}^2-4{\mu }_i}}{2}\in S(L(G_1◦G_2))$ for each eigenvalue μ_i (i = 1, 2, …, n₁) of S (L (G₁));

ii) δ_j + 1 ∈ spec (L (G₁◦G₂)) with multiplicity n₁ for every eigenvalue δ_j (j = 2, …, n₂) of S (L (G₂)).

Lemma 3. [28] Let G be a graph of order n, and let $\bar{G}$ be the graph obtained from G by deleting the edge e of G. Then $0={\lambda }_1(\bar{G})={\lambda }_1(G)\le {\lambda }_2(\bar{G})\le {\lambda }_2(G)\le {\lambda }_3(\bar{G})\le {\lambda }_3(G)\le \dots ,\le {\lambda }_{n-1}(\bar{G})\le {\lambda }_{n-1}(G)\le {\lambda }_n(\bar{G})\le {\lambda }_n(G)$.

2.2 Relations Between Consensus Index and Laplacian Spectrum

The main objective of this work is to investigate the robustness of the two-layered systems when the dynamics have external disturbances and to accurately quantify the relations between the consensus indices and Laplacian eigenvalues. The robustness of the systems with noise can be described by the network coherence; in addition, the convergence speed, which can be characterized by λ₂ (algebraic connectivity), is discussed.

i) The first-order system with noise is described by

$\dot{x}\left(t\right)=-L\left(G\right)x\left(t\right)+\xi \left(t\right)(1)$

with x ∈ R^N and where ξ(t) ∈ R^N is a vector of delta-correlated noise, and L(G) is the Laplacian matrix.

Definition 3. [10, 11] The first-order network coherence is defined as the mean steady-state variance of the deviation from the average of all node values:

$H_f=\underset{t\to \infty }{\lim }\frac{1}{N}\sum _{i=1}^N\text{Var}\left\{x_i\left(t\right)-\frac{1}{N}\sum _{j=1}^N{x}_j\left(t\right)\right\}.$

It has been proved that [10, 11] the first-order coherence H_f is completely determined by the spectrum of L. Let the eigenvalues of L be 0 = λ₁ < λ₂ ≤ …, ≤ λ_N, and then the first-order network coherence is given by

$H_f=\frac{1}{2N}\sum _{i=2}^N\frac{1}{{\lambda }_i}.(2)$

ii) In the second-order system like the vehicle formation problem, there are N vehicles, each with a position and a velocity. The states in the system have a position vector x ∈ R^N and a velocity vector v ∈ R^N. The system can be described by

$\left[\begin{array}{c}\hfill \dot{x\left(t\right)}\hfill \\ \hfill \dot{v\left(t\right)}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 0\hfill & \hfill I\hfill \\ \hfill -L\hfill & \hfill -L\hfill \end{array}\right]\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill v\left(t\right)\hfill \end{array}\right]+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill I\hfill \end{array}\right]\xi \left(t\right),(3)$

where ϱ is a 2N-vector of zero mean white noise processes. I is the identity matrix.The second-order coherence can be also determined by the eigenvalues of Laplacian matrix, that is,

$H_s=\frac{1}{2N}\sum _{i=2}^N\frac{1}{{\lambda }_i^2}.(4)$

The notion of network coherence implies the ability of maintaining its convergence trend under the effect of stochastic disturbances. The characterization of this consensus index has some similarity with the Kirhoff index [33, 34].

3 Main Results

As we mentioned in the Introduction part, the layered star-like networks of this paper are a kind of network in which all nodes have identical dynamics, and they have the topology composed by linking the center nodes among the basic star topologies. All the star-composed structures in this article are undirected and connected; therefore, the networks considered in this paper can achieve consensus. The following subsections are given to define the three classes of networks and to derive the coherence.

It should be noticed that in the case of $\mathbb{A},\mathbb{B},\mathbb{C}$, and $\mathbb{D}$, the leaf nodes in one layer is designed to be disconnected with other layers.

3.1 The consensus Indices for Network Topology $G(\mathcal{A})$ and $G(\mathbb{A})$

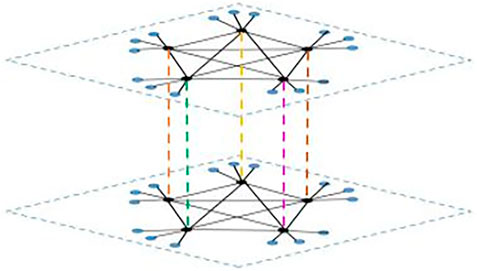
In this subsection, a sort of duplex star-like graph with symmetric structure based on $\mathbb{A}$ is considered. Set $G(\mathcal{A})≔G(K_n\times P_2)$, and $G(\mathbb{A})=G(\mathcal{A})◦{\mathfrak{E}}_k$.

As shown in Figure 1, let each node in $\mathbb{A}$ be the center nodes that stick to a star structure with k leaf nodes, and the leaf nodes with vertex degree equal to 1 are designed to have not the access to link with other layers.

FIGURE 1

FIGURE 1. An example of $\mathbb{A}$, n = 5, p = 3.

The Laplacian matrix of $G(\mathcal{A})≔G(K_n\times P_2)$ can be characterized as follows:

$L\left(G\left(\mathcal{A}\right)\right)=\left(\begin{array}{cc}\hfill n{I}_n-A\left(K_n\right)\hfill & \hfill -I_n\hfill \\ \hfill -I_n\hfill & \hfill n{I}_n-A\left(K_n\right)\hfill \end{array}\right)$

therefore, by the corresponding characteristic polynomial, one has $SL(G(\mathcal{A}))=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill n\hfill & \hfill 2\hfill & \hfill 2+n\hfill \\ \hfill 1\hfill & \hfill n-1\hfill & \hfill 1\hfill & \hfill n-1\hfill \end{array}\right)$, and since $SL({\mathfrak{E}}_k)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill k\hfill \end{array}\right)$, to network $\mathcal{A}$, we have $H^{(1)}(\mathcal{A})=\frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i}\to 0$ as n → ∞, and $H^{(2)}(\mathcal{A})\to 0$ as n → ∞. By Lemma 2, one can derive $SL[G(\mathbb{A})]$, i.e., $SL[(P_2\times K_n)◦{\mathfrak{E}}_k]$ as follows:

i) 0 and $k+1\in SL[G(\mathbb{A})]$ with multiplicity 1.

ii) $\frac{n+k+1\pm \sqrt{{(n+k+1)}^2-4n}}{2}\in SL[G(\mathbb{A})]$ with multiplicity (n − 1).

iii) $\frac{3+k\pm \sqrt{{(3+k)}^2-8}}{2}\in SL[G(\mathbb{A})]$ with multiplicity 1.

iv) $\frac{3+n+k\pm \sqrt{{(3+n+k)}^2-4(2+n)}}{2}\in SL[G(\mathbb{A})]$ with multiplicity n − 1.

v) $1\in SL[G(\mathbb{A})]$ with multiplicity 2n (k − 1).

Therefore, it can be acquired that ${\lambda }_2=\frac{3+k-\sqrt{{(3+k)}^2-8}}{2}$.The first-order coherence for $G(\mathbb{A})$ is

$\begin{array}{ll}\hfill H^{\left(1\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i}=\frac{1}{2n\left(k+1\right)}\left[\frac{1}{2\left(k+1\right)}+\left(\frac{n-1}{\left(n+k+1\right)+\sqrt{{\left(k+1+n\right)}^2-4n}}\right.\right.\hfill \\ \hfill & \left.+\frac{n-1}{\left(n+k+1\right)-\sqrt{{\left(k+1+n\right)}^2-4n}}\right)+\left(\frac{1}{\left(3+k\right)+\sqrt{{\left(3+k\right)}^2-8}}\right.+\hfill \\ \hfill & \left.\frac{1}{\left(3+k\right)-\sqrt{{\left(3+k\right)}^2-8}}\right)+\left(\frac{n-1}{\left(3+n+k\right)+\sqrt{{\left(3+n+k\right)}^2-4\left(2+n\right)}}\right.+\hfill \\ \hfill & \left.\left.\frac{n-1}{\left(3+n+k\right)-\sqrt{{\left(3+n+k\right)}^2-4\left(2+n\right)}}\right)+2n\left(k-1\right)\right]=\frac{1}{2n\left(k+1\right)}\cdot \hfill \\ \hfill & \left[\frac{1}{2\left(k+1\right)}+\frac{\left(n-1\right)\left(n+k+1\right)}{2n}+\frac{\left(3+k\right)}{4}+\frac{\left(n-1\right)\left(3+n+k\right)}{2\left(2+n\right)}+2n\left(k\right.\right.\hfill \\ \hfill & \left.\left.-1\right)\right],\hfill \end{array}$

then if the number of nodes k is fixed, let n → ∞, and then one has $H^{(1)}=\frac{2k-1}{2k+2}$; and if n is fixed, $H^{(1)}\to \frac{(n-1)}{4n^2}+\frac{1}{8n}+\frac{n-1}{4n^2+8n}+1$ as k → ∞.

The second-order coherence of the network can be calculated as follows:

$\begin{array}{ll}\hfill H^{\left(2\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i^2}=\frac{1}{2n\left(k+1\right)}\left(\frac{1}{{\left(k+1\right)}^2}+\frac{\left(n-1\right)\left\{{\left(n+k+1\right)}^2-2k\right\}}{4n^2}\right.+\hfill \\ \hfill & \left.\frac{{\left(3+k\right)}^2-4}{16}+\frac{\left(n-1\right)\left\{{\left(3+n+k\right)}^2-2\left(2+n\right)\right\}}{4{\left(2+n\right)}^2}+2n\left(k-1\right)\right),\hfill \end{array}$

when k is fixed, let n → ∞, and one has $H^{(2)}\to \frac{1}{8(k+1)}+\frac{1}{16(k+1)}+\frac{k-1}{k+1}=\frac{16k-13}{16(k+1)}$, and when k → ∞, $H^{(2)}/k\to \frac{n-1}{2n}+\frac{1}{32n}+\frac{n-1}{8n{(2+n)}^2}$.

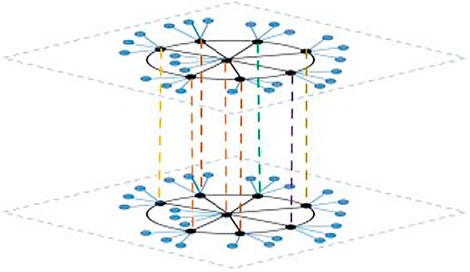
3.2 The Consensus Indices for Network Topology $G(\mathcal{B})$ and $G(\mathbb{B})$

As shown in Figure 2, let each node in $\mathcal{B}$ be the center nodes that stick to a star structure with p leaf nodes, and then $G(\mathbb{B})=G(\mathcal{B})◦{\mathfrak{E}}_p$, p ≥ 3, i.e., $[W_n\times P_2]◦{\mathfrak{E}}_p$, where W_n is the wheel graph with n circle nodes and one center node. The leaf nodes of which vertex degree equal to 1 are designed to disconnected with the other layer.

Since

$\mid L\left(G\left(\mathbb{B}\right)\right)-\lambda I\mid =\left|\begin{array}{cc}\hfill F\hfill & \hfill -I_{n+1}\hfill \\ \hfill -I_{n+1}\hfill & \hfill F\hfill \end{array}\right|=|F+I_{n+1}\Vert F-I_{n+1}|,$

where

$F=\left(\begin{array}{ccccccc}\hfill n+1-\lambda \hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill 4-\lambda \hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill 4-\lambda \hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 4-\lambda \hfill & \hfill -1\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill -1\hfill & \hfill 4-\lambda \hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 4-\lambda \hfill \end{array}\right)$

and then one has

$\begin{array}{ll}\hfill \mid L\left(G\left(\mathbb{B}\right)\right)-\lambda I\mid =& \left\{\left(n+3-\lambda \right)|\lambda I-A{|}_n+\left(-1\right)|\lambda I-B{|}_n\right\}\left\{\left(n+1-\lambda \right)\cdot \right.\hfill \\ \hfill & \left.|\lambda I-P{|}_n+\left(-1\right)|\lambda I-Q{|}_n\right\},\hfill \end{array}$

where the circulant matrices $A=\mathfrak{C}(5,-\mathrm{1,0},\dots ,0,-1)$, $B=\mathfrak{C}(\mathrm{6,0,1},\dots ,\mathrm{1,0})$, $P=\mathfrak{C}(3,-\mathrm{1,0},\dots ,0,-1)$, $Q=\mathfrak{C}(\mathrm{4,0,1},\dots ,\mathrm{1,0})$. Hence, by Lemma 1, the Laplacian spectrum of $G(\mathcal{B})$ has the following form:$SL(G(\mathcal{B}))=\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill 2\hfill & \hfill 1+n\hfill & \hfill 3+n\hfill & \hfill 1+4si{n}^2\frac{k\pi }{n}\hfill & \hfill 3+4si{n}^2\frac{k\pi }{n}\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right)$.where k = 1, 2, …, n − 1.

FIGURE 2

FIGURE 2. An example of $\mathbb{B}$, n = 7, p = 3.

Therefore, the asymptotic properties of coherence for $G(\mathcal{B})$ can be calculated as follows:

$\begin{array}{ll}\hfill \underset{n\to \infty }{\lim }{H}^{\left(1\right)}=& \frac{1}{4}{\int }_0^1\frac{1}{1+4si{n}^2\left(\pi x\right)}+\frac{1}{4}{\int }_0^1\frac{1}{3+4si{n}^2\left(\pi x\right)}\hfill \\ \hfill =& \frac{\sqrt{5}}{20}+\frac{\sqrt{21}}{84}\approx 0.166\hfill \end{array}$

$\underset{n\to \infty }{\lim }{H}^{\left(2\right)}=\frac{1}{4}{\int }_0^1\frac{1}{{\left(1+4si{n}^2\left(\pi x\right)\right)}^2}+\frac{1}{4}{\int }_0^1\frac{1}{{\left(3+4si{n}^2\left(\pi x\right)\right)}^2}\approx 0.32$

Therefore, by Lemma 2, the Laplacian spectrum of $G(\mathbb{B})$ has the following characterization:

1) p + 1 and $0\in SL[G(\mathbb{B})]$ with multiplicity 1.

2) $\frac{2+n+p\pm \sqrt{{(2+n+p)}^2-4(1+n)}}{2}\in SL[G(\mathbb{B})]$ with multiplicity 1.

3) $\frac{(2+4si{n}^2(\frac{k\pi }{n})+p)\pm \sqrt{{(2+4si{n}^2(\frac{k\pi }{n})+p)}^2-4(1+4si{n}^2(\frac{k\pi }{n}))}}{2}\in SL[G(\mathbb{B})]$ with multiplicity 1, k = 1, 2, …, n − 1.

4) $\frac{3+p\pm \sqrt{{(3+p)}^2-8}}{2}\in SL[G(\mathbb{B})]$ with multiplicity 1.

5) $\frac{4+n+p\pm \sqrt{{(4+n+p)}^2-4(3+n)}}{2}\in SL[G(\mathbb{B})]$ with multiplicity 1.

6) $\frac{(4+4si{n}^2(\frac{k\pi }{n})+p)\pm \sqrt{{(4+4si{n}^2(\frac{k\pi }{n})+p)}^2-4(3+4si{n}^2(\frac{k\pi }{n}))}}{2}\in SL[G(\mathbb{B})]$ with multiplicity 1, k = 1, 2, …, n − 1.

7) $1\in SL[G(\mathbb{B})]$ with multiplicity 2 (n + 1) (p − 1).

Therefore, the convergence speed has the description ${\lambda }_2=\frac{3+p-\sqrt{{(3+p)}^2-8}}{2}$.

Suppose that p is fixed, and then the first-order coherence of network $\mathbb{B}$ is

$\begin{array}{ll}\hfill H^{\left(1\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i}=\frac{1}{4\left(n+1\right)\left(p+1\right)}\left(\frac{1}{p+1}+\frac{2+n+p}{1+n}\right.\hfill \\ \hfill & +\sum _{k=1}^{n-1}\left(1+\frac{1+p}{1+4si{n}^2\left(\frac{k\pi }{n}\right)}\right)+\frac{3+p}{2}+\frac{4+n+p}{3+n}+\sum _{k=1}^{n-1}\left(1+\frac{1+p}{3+4si{n}^2\left(\frac{k\pi }{n}\right)}\right)\hfill \\ \hfill & +\left.2\left(n+1\right)\left(p-1\right)\right)\hfill \end{array}$

If p is fixed, then we have

$\begin{array}{ll}\hfill \underset{n\to \infty }{\lim }{H}^{\left(1\right)}=& \frac{p}{2\left(p+1\right)}+\frac{1}{4}{\int }_0^1\frac{1}{1+4si{n}^2\left(\pi x\right)}dx+\frac{1}{4}{\int }_0^1\frac{1}{3+4si{n}^2\left(\pi x\right)}dx\hfill \\ \hfill =& \frac{p}{2\left(p+1\right)}+\frac{\sqrt{5}}{20}+\frac{\sqrt{21}}{84},\hfill \end{array}$

and when n is fixed, $H^{(1)}\to \frac{1}{4{(n+1)}^2}+\frac{1}{4(n+1)}\cdot {\sum }_{k=1}^{n-1}\frac{1}{1+4si{n}^2(\frac{k\pi }{n})}+\frac{1}{8(n+1)}+\frac{1}{4(n+1)(n+3)}+\frac{1}{4(n+1)}\cdot {\sum }_{k=1}^{n-1}\frac{1}{3+4si{n}^2(\frac{k\pi }{n})}+\frac{1}{2}$;and if n → ∞, p → ∞, then

$H^{\left(1\right)}=\frac{1}{4}{\int }_0^1\frac{1}{1+4si{n}^2\left(\pi x\right)}dx+\frac{1}{4}{\int }_0^1\frac{1}{3+4si{n}^2\left(\pi x\right)}dx+\frac{1}{2}\approx 0.667$

Remark 1. From the above derivation, it can be acquired that if the layered network has been added star topologies with each node, then H⁽¹⁾ will increase $\frac{p}{2(p+1)}$ as n → ∞, which infers that if p is fixed, then the coherence will increase by a constant instead of increasing indefinitely as n → ∞.The second-order coherence of $\mathbb{B}$ can be calculated as follows:

$\begin{array}{ll}\hfill H^{\left(2\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i^2}\hfill \\ \hfill =& \frac{1}{4\left(n+1\right)\left(1+p\right)}\left(\sum _{k=1}^{n-1}\left(\frac{p^2+2p\left(2+4si{n}^2\left(\frac{k\pi }{n}\right)\right)+{\left(2+4si{n}^2\left(\frac{k\pi }{n}\right)\right)}^2}{{\left(1+4si{n}^2\left(\frac{k\pi }{n}\right)\right)}^2}\right.\right.\hfill \\ \hfill & -\left.\frac{2}{1+4si{n}^2\left(\frac{k\pi }{n}\right)}\right)+\sum _{k=1}^{n-1}\left(\frac{p^2+2p\left(4+4si{n}^2\left(\frac{k\pi }{n}\right)\right)+{\left(4+4si{n}^2\left(\frac{k\pi }{n}\right)\right)}^2}{{\left(3+4si{n}^2\left(\frac{k\pi }{n}\right)\right)}^2}\right.\hfill \\ \hfill & -\left.\frac{2}{3+4si{n}^2\left(\frac{k\pi }{n}\right)}\right)+\frac{1}{{\left(p+1\right)}^2}+{\left(1+\frac{1+p}{3+n}\right)}^2-\frac{2}{3+n}\hfill \\ \hfill & \left.+{\left(1+\frac{1+p}{1+n}\right)}^2-\frac{2}{1+n}+\frac{{\left(3+p\right)}^2-4}{4}+2\left(n+1\right)\left(p-1\right)\right)\hfill \end{array}$

If n is fixed, one has

$\begin{array}{ll}\hfill \underset{p\to \infty }{\lim }{H}^{\left(2\right)}/p=& \frac{1}{4\left(n+1\right)}\sum _{k=1}^{n-1}\frac{1}{{\left(1+4si{n}^2\left(\frac{k\pi }{n}\right)\right)}^2}+\frac{1}{4\left(n+1\right)}\sum _{k=1}^{n-1}\frac{1}{{\left(3+4si{n}^2\left(\frac{k\pi }{n}\right)\right)}^2}\hfill \\ \hfill & +\frac{1}{4\left(n+1\right){\left(n+3\right)}^2}+\frac{1}{4{\left(n+1\right)}^3}+\frac{1}{16\left(n+1\right)}.\hfill \end{array}$

If p is fixed, one has

$\begin{array}{ll}\hfill \underset{n\to \infty }{\lim }{H}^{\left(2\right)}=& \frac{p^2}{4\left(1+p\right)}{\int }_0^1\frac{1}{{\left(1+4si{n}^2\left(\pi x\right)\right)}^2}dx+\frac{p}{1+p}{\int }_0^1\frac{1+2si{n}^2\left(\pi x\right)}{{\left(1+4si{n}^2\left(\pi x\right)\right)}^2}dx\hfill \\ \hfill & +\frac{1}{1+p}{\int }_0^1\frac{{\left(1+2si{n}^2\left(\pi x\right)\right)}^2}{{\left(1+4si{n}^2\left(\pi x\right)\right)}^2}dx-\frac{1}{2\left(1+p\right)}{\int }_0^1\frac{1}{1+4si{n}^2\left(\pi x\right)}dx\hfill \\ \hfill & +\frac{p^2}{4\left(1+p\right)}{\int }_0^1\frac{1}{{\left(3+4si{n}^2\left(\pi x\right)\right)}^2}dx+\frac{2p}{1+p}{\int }_0^1\frac{1+{\sin }^2\left(\pi x\right)}{{\left(3+4si{n}^2\left(\pi x\right)\right)}^2}dx\hfill \\ \hfill & +\frac{4}{1+p}{\int }_0^1\frac{{\left(1+{\sin }^2\left(\pi x\right)\right)}^2}{{\left(3+4si{n}^2\left(\pi x\right)\right)}^2}dx-\frac{1}{2\left(1+p\right)}{\int }_0^1\frac{1}{3+4si{n}^2\left(\pi x\right)}dx\hfill \\ \hfill & +\frac{p-1}{2\left(p+1\right)}\hfill \\ \hfill =& \frac{3\sqrt{5}}{100}\frac{p^2}{\left(1+p\right)}+\frac{4\sqrt{5}}{25}\frac{p}{1+p}+\left(\frac{13\sqrt{5}}{100}+\frac{1}{4}\right)\frac{1}{1+p}-\frac{\sqrt{5}}{10}\frac{1}{\left(1+p\right)}\hfill \\ \hfill & +\frac{5\sqrt{21}}{1764}\frac{p^2}{\left(1+p\right)}+\frac{13\sqrt{21}}{441}\frac{p}{1+p}+\left(\frac{47\sqrt{21}}{1764}+\frac{1}{4}\right)\frac{1}{1+p}-\frac{\sqrt{21}}{42}\frac{1}{\left(1+p\right)}\hfill \\ \hfill & +\frac{p-1}{2\left(p+1\right)}\hfill \\ \hfill \approx & 0.801\frac{p^2}{1+p}+0.993\frac{p}{1+p}+0.079\frac{1}{1+p}.\hfill \end{array}$

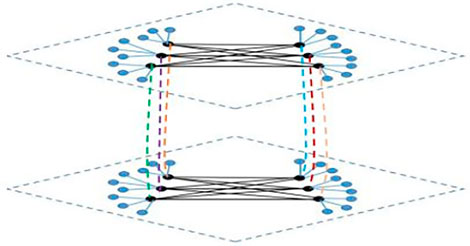
3.3 The Consensus Indices for Network Topology $G(\mathcal{C})$ and $G(\mathbb{C})$

In this subsection, based on the idea that the leaf nodes might have communications with each other, fan-graph structures are added on the original layered dual-star topology, i.e., $G(\mathbb{C})≔(S_n\times P_2)◦P_l$. As shown in Figure 3, the black nodes have a larger degree, and they compose into the topology $G(\mathcal{C})≔S_n\times P_2$, and the blue nodes form into the edges of the fan structure. The blue nodes in one layer are designed to be disconnected from the other layer.By

$\mid L\left(G\left(\mathcal{C}\right)\right)-\lambda I\mid =\left|\begin{array}{cc}\hfill J\hfill & \hfill -I_{n+1}\hfill \\ \hfill -I_{n+1}\hfill & \hfill J\hfill \end{array}\right|,$

where

$J=\left(\begin{array}{ccccc}\hfill n-\lambda \hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill \dots \hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill 2-\lambda \hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 2-\lambda \hfill & \hfill 0\hfill & \hfill \dots ,\hfill \\ \hfill ⋮\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 2-\lambda \hfill \end{array}\right)$

Then it can be derived that

$SL\left(G\left(\mathcal{C}\right)\right)=\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill 2\hfill & \hfill n+1\hfill & \hfill n+3\hfill & \hfill 1\hfill & \hfill 3\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill n-1\hfill & \hfill n-1\hfill \end{array}\right),$

therefore, to network $\mathcal{C}$, ${\lambda }_2(\mathcal{C})=1$, $H^{(1)}\to \frac{1}{3}$ and $H^{(2)}\to \frac{5}{18}$, and since $SL(P_m)=\left(\mathrm{0,4}si{n}^2(\frac{k\pi }{2m})\right),k=\mathrm{1,2},\dots ,m-1$ [35]. The Laplacian spectrum of $G(\mathbb{C})$ has the following description:

1) 0 and $m+1\in SL(G(\mathbb{C}))$ with multiplicity 1.

2) $\frac{(3+m)\pm \sqrt{{(3+m)}^2-8}}{2}\in SL(G(\mathbb{C}))$ with multiplicity 1.

3) $\frac{(n+m+2)\pm \sqrt{{(n+m+2)}^2-4(n+1)}}{2}\in SL(G(\mathbb{C}))$ with multiplicity 1.

4) $\frac{(n+m+4)\pm \sqrt{{(n+m+4)}^2-4(n+3)}}{2}\in SL(G(\mathbb{C}))$ with multiplicity 1.

5) $\frac{(m+2)\pm \sqrt{{(m+2)}^2-4}}{2}\in SL(G(\mathbb{C}))$ with multiplicity (n − 1).

6) $\frac{(m+4)\pm \sqrt{{(m+4)}^2-12}}{2}\in SL(G(\mathbb{C}))$ with multiplicity (n − 1).

7) $4si{n}^2(\frac{k\pi }{2m})+1\in SL(G(\mathbb{C}))$ with multiplicity 2 (n + 1), k = 1, 2, … , m − 1.

FIGURE 3

FIGURE 3. An example of $G(\mathbb{C})$: (S_n × P₂)◦P_m, n = 5, m = 3.

Therefore, the first-order coherence of $\mathbb{C}$ is as follows:

$\begin{array}{ll}\hfill H^{\left(1\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i}\hfill \\ \hfill =& \frac{1}{4\left(n+1\right)\left(m+1\right)}\left(\frac{1}{m+1}+\frac{3+m}{2}+\frac{n+m+2}{n+1}+\frac{n+m+4}{n+3}\right.\hfill \\ \hfill & +\left.\left(n-1\right)\left(m+2\right)+\left(n-1\right)\frac{\left(4+m\right)}{3}+2\left(n+1\right)\sum _{k=1}^{m-1}\frac{1}{4si{n}^2\frac{k\pi }{2m}+1}\right).\hfill \end{array}$

Therefore, 1) when m is fixed, n → ∞, one has $H^{(1)}\to \frac{2m+5}{6m+6}+\frac{1}{2(m+1)}{\sum }_{k=1}^{m-1}\frac{1}{4si{n}^2(\frac{k\pi }{2m})+1}$; 2) when n is fixed, m → ∞, $H^{(1)}\to \frac{1}{8(n+1)}+\frac{1}{4{(n+1)}^2}+\frac{1}{4(n+1)(n+3)}+\frac{1}{3}(\frac{n-1}{n+1})+\frac{1}{2}{\int }_0^1\frac{1}{4si{n}^2\frac{\pi x}{2}+1}dx$.

Hence, $H^{(1)}\to \frac{1}{3}+\frac{1}{2}{\int }_0^1\frac{1}{4si{n}^2\frac{\pi x}{2}+1}dx\approx 0.55$. The second-order coherence of $\mathbb{C}$ is

$\begin{array}{ll}\hfill H^{\left(2\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i^2}\hfill \\ \hfill =& \frac{1}{4\left(n+1\right)\left(m+1\right)}\left(\frac{1}{{\left(m+1\right)}^2}+\frac{{\left(m+3\right)}^2-4}{4}+\frac{{\left(m+n+2\right)}^2-2\left(n+1\right)}{{\left(n+1\right)}^2}\right.\hfill \\ \hfill & +\frac{{\left(m+n+4\right)}^2-2\left(n+3\right)}{{\left(n+3\right)}^2}+\left(n-1\right)\left[{\left(m+2\right)}^2-2\right]+\left(n-1\right)\left[{\left(m+4\right)}^2-6\right]\hfill \\ \hfill & +\left.2\left(n+1\right)\sum _{k=1}^{\mathrm{m-1}}\frac{1}{{\left(4si{n}^2\frac{k\pi }{2m}+1\right)}^2}\right)\hfill \end{array}$

Then, one has $H^{(2)}(\mathbb{C})\to \frac{m^2+6m+6}{2(m+1)}+\frac{1}{2(m+1)}{\sum }_{k=1}^{m-1}\frac{1}{{(4si{n}^2(\frac{k\pi }{2m})+1)}^2}>\frac{5}{18}=H^{(2)}(\mathcal{C})$, and it can be derived that $H^{(2)}/m\to \frac{1}{2}$, as m, n → ∞.

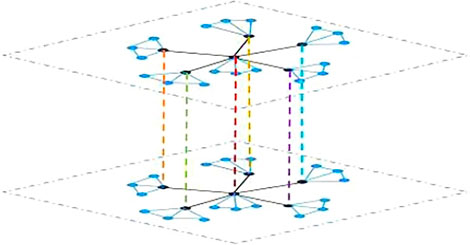
3.4 The Consensus Indices for Network Topology $G(\mathcal{D})$ and $G(\mathbb{D})$

In this subsection, the two layered star-composed multi-agent network $\mathcal{D}$ and $\mathbb{D}$ are considered, where $\mathbb{D}≔\mathcal{D}◦{\mathfrak{E}}_k$, and $\mathcal{D}$ is a duplex complete bipartite graph structure K_m,m, i.e., $\mathcal{D}=K_{m,m}\times P_2$. As shown in Figure 4, the black nodes form into a duplex structure, in which each layer is the complete bipartite graph.

FIGURE 4

FIGURE 4. An example of $\mathbb{D}$, m = 3, p = 3.

Through the similar methods of former subsection, it can be derived that

$SL\left[G\left(\mathcal{D}\right)\right]=\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill 2m\hfill & \hfill m\hfill & \hfill 2\hfill & \hfill 2m+2\hfill & \hfill m+2\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 2\left(m-1\right)\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 2\left(m-1\right)\hfill \end{array}\right),$

and then we have $H^{(1)}(\mathcal{D})=\frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i}\to 0$; $H^{(2)}(\mathcal{D})\to 0$, as m → ∞.

To the case with network structure $G(\mathbb{D}):[G(\mathcal{D})]◦{\mathfrak{E}}_k$, $SL[G(\mathbb{D})]$ has the following form:

1) 0 and $(k+1)\in SL(G(\mathbb{D}))$ with multiplicity 1.

2) $\frac{(2m+k+1)\pm \sqrt{{(2m+k+1)}^2-8m}}{2}\in SL(G(\mathbb{D}))$ with multiplicity 1.

3) $\frac{(m+k+1)\pm \sqrt{{(m+k+1)}^2-4m}}{2}\in SL(G(\mathbb{D}))$ with multiplicity 2 (m − 1).

4) $\frac{(3+k)\pm \sqrt{{(3+k)}^2-8}}{2}\in SL(G(\mathbb{D}))$ with multiplicity 1.

5) $\frac{(2m+k+3)\pm \sqrt{{(2m+k+3)}^2-8(m+1)}}{2}\in SL(G(\mathbb{D}))$ with multiplicity 1.

6) $\frac{(m+k+3)\pm \sqrt{{(m+k+3)}^2-4(m+2)}}{2}\in SL(G(\mathbb{D}))$ with multiplicity 2 (m − 1).

7) $1\in SL(G(\mathbb{D}))$ with multiplicity 4m (k − 1).

Then the coherence for $\mathbb{D}$ can be derived as follows:

$\begin{array}{ll}\hfill H^{\left(1\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i}\hfill \\ \hfill =& \frac{1}{8m\left(1+k\right)}\left(\frac{1}{\left(k+1\right)}+\frac{2m+k+1}{2m}+2\left(m-1\right)\frac{m+k+1}{m}+\frac{3+k}{2}\right.\hfill \\ \hfill & +\left.\frac{2m+3+k}{2\left(m+1\right)}+2\left(m-1\right)\frac{m+3+k}{m+2}+4m\left(k-1\right)\right),\hfill \end{array}$

when the number of leaves, i.e., k is fixed, and m → ∞, then $H^{(1)}\to \frac{k}{2k+2}$; and if m is fixed, and k → ∞, then $H^{(1)}\to \frac{5m-3}{16m^2}+\frac{1}{16m^2+16m}+\frac{m-1}{4m^2+8m}+\frac{1}{2}$.

$\begin{array}{ll}\hfill H^{\left(2\right)}=& \frac{1}{2N_a}\sum _{i=2}^N\frac{1}{{\lambda }_i^2}\hfill \\ \hfill =& \frac{1}{8m\left(1+k\right)}\left(\frac{1}{{\left(k+1\right)}^2}+\frac{{\left(2m+k+1\right)}^2-4m}{8m^2}+\frac{\left(m-1\right)\left[{\left(m+k+1\right)}^2-2m\right]}{m^2}\right.\hfill \\ \hfill & +\frac{{\left(3+k\right)}^2-4}{8}+\frac{{\left(2m+3+k\right)}^2-8\left(m+1\right)}{8{\left(m+1\right)}^2}+2\left(m-1\right)\frac{{\left(m+3+k\right)}^2-2\left(m+2\right)}{{\left(m+2\right)}^2}\hfill \\ \hfill & +\left.4m\left(k-1\right)\right).\hfill \end{array}$

If the number of leaf nodes k is fixed, then one has ${\lim }_{m\to \infty }{H}^{(2)}=\frac{4k-1}{8(k+1)}$; and if m is fixed, we have $H^{(2)}/k\to \frac{m^2+8m-7}{64m^3}+\frac{1}{64m{(m+1)}^2}+\frac{(m-1)}{4m{(m+2)}^2}$, (k → ∞).

Remark 2. To the dual-layered star-composed networks $\mathbb{A},\mathbb{B},\mathbb{C}$ and $\mathbb{D}$, if the two counterpart nodes of the leaf nodes of different layers are designed to have connections with each other, then the robustness of the acquired duplex networks is better than that does not have links between the counterpart leaf nodes. For instance, to $\mathbb{A}$ (see Figure 1), if the graph structure is changed from $(K_n\times P_2)◦{\mathfrak{E}}_k$ to $(K_n◦{\mathfrak{E}}_k)\times P_2$, then by Lemma 3, it can be derived that the coherence performance is better than before.

Remark 3. A limitation of the framework in this article is that the graph is undirected, and one may consider some reasonable directed cases in future research. In addition, another worthy research direction may be focused on extending the two-layered case into multilayered ones.

4 Simulation and Comparison

In this section, the comparisons of performance for these two-layered multi-star networks are made. One can see from Section 3 that the convergence speed of $\mathcal{A},\mathcal{B},\mathcal{D}$ has the following relation: ${\lambda }_2(\mathcal{A})={\lambda }_2(\mathcal{B})={\lambda }_2(\mathcal{D})>{\lambda }_2(\mathcal{C})=1$, and if the number of center nodes and leaf nodes are both equal, then the convergence speed of the four multi-star networks has the following relation: $((p+3)-\sqrt{{(p+3)}^2-8})/2={\lambda }_2(\mathbb{A})={\lambda }_2(\mathbb{B})={\lambda }_2(\mathbb{D})>{\lambda }_2(\mathbb{C})=((k+2)-\sqrt{{(k+2)}^2-4})/2$. Furthermore, one can get the maximum convergence speed of A, B, and D, i.e., ${\bar{\lambda }}_{2max}=3-\sqrt{7}$, and the maximum convergence speed of $\mathbb{C}$ is ${\lambda }_{2max}(\mathbb{C})=(5-\sqrt{21})/2$. One can see that the convergence speed of the two-layered multi-star network is irrelevant with the number of center nodes n.

To the network coherence for the duplex networks and the two-layered multi-star ones, two perspective comparisons are made; that is, vertically, $\mathcal{A}$ and $\mathbb{A}$, $\mathcal{B}$ and $\mathbb{B}$, etc. The following asymptotic relations can be acquired:

${\lim }_{n\to \infty }{H}^{(1)}(\mathbb{A})={\lim }_{n\to \infty }{H}^{(1)}(\mathcal{A})+(2k-1)/(2k+1)$.

${\lim }_{n\to \infty }{H}^{(2)}(\mathbb{A})={\lim }_{n\to \infty }{H}^{(2)}(\mathcal{A})+(16k-13)/(16k+16)$.

${\lim }_{n\to \infty }{H}^{(1)}(\mathbb{B})={\lim }_{n\to \infty }{H}^{(1)}(\mathcal{B})+p/(2p+2)$.

${\lim }_{n\to \infty }{H}^{(2)}(\mathbb{B})/p={\lim }_{n\to \infty }{H}^{(2)}(\mathcal{B})$, and for $\mathbb{C}$, when m is large enough.

${\lim }_{n\to \infty }{H}^{(1)}(\mathbb{C})={\lim }_{n\to \infty }{H}^{(1)}(\mathcal{C})+\sqrt{5}/10$, ${\lim }_{n\to \infty }{H}^{(2)}(\mathbb{C})\gg H^{(2)}(\mathcal{C})$ when m is a larger constant. For $\mathbb{D}$, we have ${\lim }_{n\to \infty }{H}^{(1)}(\mathbb{D})={\lim }_{n\to \infty }{H}^{(1)}(\mathcal{D})+1/(k+1)$.

${\lim }_{n\to \infty }{H}^{(2)}(\mathbb{D})={\lim }_{n\to \infty }{H}^{(2)}(\mathcal{D})+(4k-1)/(8k+8)$;

Horizontally, $\mathcal{A},\mathcal{B},\mathcal{C},\mathcal{D}$ and $\mathbb{A},\mathbb{B},\mathbb{C},\mathbb{D}$. It can be inferred that the operation of adding star topologies to $\mathcal{D}$ has less influence on both first- and second-order coherence than to $\mathcal{A}$.

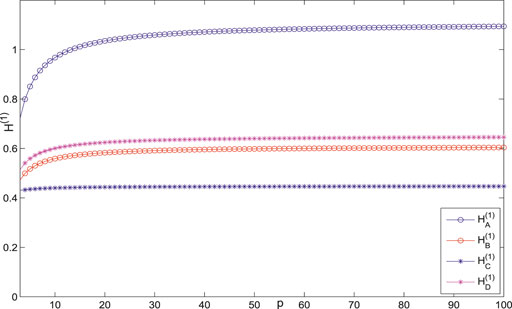
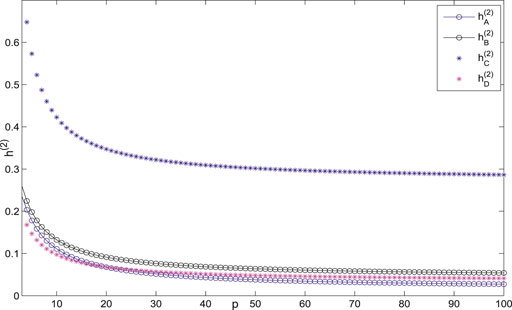
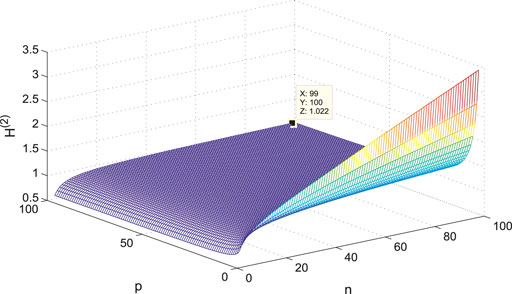
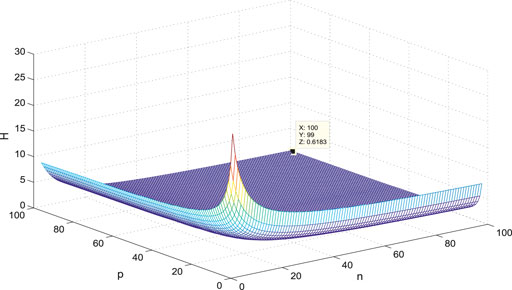
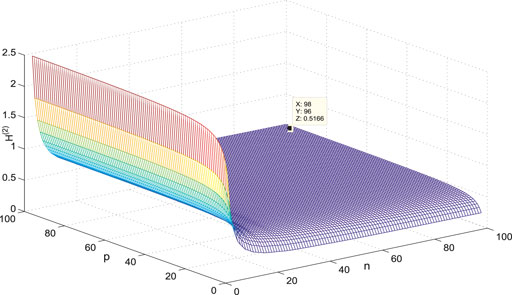
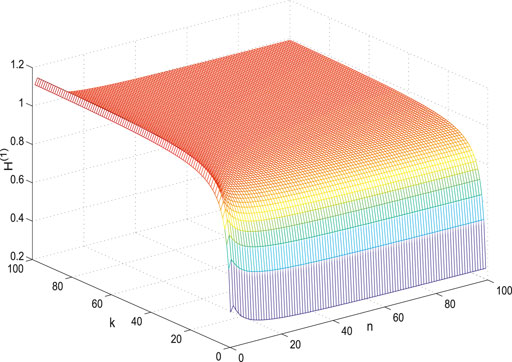
The variance of the first- and second-order coherence for $\mathbb{A},\mathbb{B},\mathbb{C},\mathbb{D}$ is shown in Figures 5–14. From the results in Section 3 and Figures 5, 6, when n is fixed, one can see that $\mathbb{C}$ has the best first-order robustness of the four networks. $\mathbb{B}$ and $\mathbb{D}$ have similar first-order robustness, and $\mathbb{B}$ is slightly better than $\mathbb{D}$, and of them, $H^{(1)}(\mathbb{A})$ has the largest value. To the second-order case, $\mathbb{C}$ has the largest value of the four; this is just the opposite of the first-order case. Around n = 20, $H^{(2)}(\mathbb{D})$ is less than that of $\mathbb{A}$ at first, and then its value is gradually between $\mathbb{A}$ and $\mathbb{B}$ (see Figure 6).

FIGURE 5

FIGURE 5. The change of H⁽¹⁾ for the four networks, n = 4.

FIGURE 6

FIGURE 6. The change of H⁽²⁾ for the four networks, n = 4.

FIGURE 8

FIGURE 8. The change of H⁽¹⁾ for $\mathbb{B}$.

FIGURE 9

FIGURE 9. The change of H⁽¹⁾ for $\mathbb{C}$.

FIGURE 10

FIGURE 10. The change of H⁽¹⁾ for $\mathbb{D}$.

FIGURE 11

FIGURE 11. The change of H⁽²⁾ for $\mathbb{A}$.

FIGURE 12

FIGURE 12. The change of H⁽²⁾ for $\mathbb{B}$.

FIGURE 13

FIGURE 13. The change of H⁽²⁾ for $\mathbb{C}$.

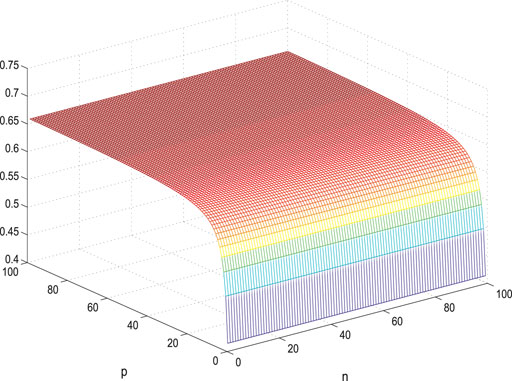
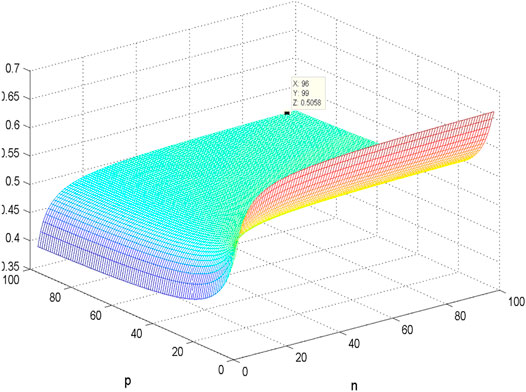
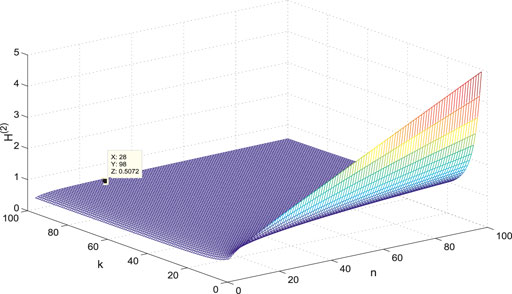
Figures 7–14 show the change of the first- and second-order coherence of the four networks with respect to the two parameters n and p (n, p ∈ [3, 100]). It can be seen that the simulation verifies the results well.

FIGURE 7

FIGURE 7. The change of H⁽¹⁾ for $\mathbb{A}$.

FIGURE 14

FIGURE 14. The change of H⁽²⁾ for $\mathbb{D}$.

Conclusion

In this research, the convergence speed and robustness of the consensus for several dual-layered multi-agent systems, which can be measured by the algebraic connectivity and the network coherence, are studied. In particular, the methods of graph spectra are applied to analyze the graph structure and derive the network coherence for the multi-agent networks, and it is found that there exist some asymptotic properties for the indices. When the number of leaf and center node p, n is large enough, the operation of adding star topologies will make the first-order coherence of $\mathcal{A}$ increase approximately at 1, and $\frac{1}{2}$ to $\mathcal{B}$ and $\mathcal{D}$, $\frac{\sqrt{5}}{10}$ to $\mathcal{C}$.

Finally, the consensus-related indices of the duplex networks with the same number of nodes but non-isomorphic structures have been compared and simulated, and it is found that $\mathbb{A}$ has the worst first-order network coherence of these networks, but it has the fastest convergence speed and the best second-order coherence; $\mathbb{C}$ has the best first-order robustness, but it has the worst robustness in the second-order case. Both the first-order coherence and second-order coherence of $\mathbb{D}$ are between $\mathbb{A}$ and $\mathbb{B}$.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

DH and HJ: methodology. ZY and DH: software. DH and JB: validation. DH and JB: formal analysis. DH: writing—original draft preparation. DH and JB: writing—review and editing. HJ and ZY: supervision. DH: project administration.

Funding

This work was supported by the Natural Science Foundation of Xinjiang (NSFXJ) (No. 2019D01B10), National Natural Science Foundation of the People’s Republic of China (NSFC) (Grant No. 62003289), and Research Fund for the Doctoral Program of Xinjiang Institute of Engineering (2020xgy012302).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We express our sincere gratitude to the people who gave us valuable comments.

References

1. Olfati-Saber R, Murray RM. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans Automat Contr (2004) 49(9):1520–33. doi:10.1109/tac.2004.834113

CrossRef Full Text | Google Scholar

2. Ren W. On Consensus Algorithms for Double-Integrator Dynamics. IEEE Trans Automat Contr (2008) 53:1503–9. doi:10.1109/tac.2008.924961

CrossRef Full Text | Google Scholar

3. Wenwu Yu W, Guanrong Chen G, Ming Cao M, Kurths J. Second-order Consensus for Multiagent Systems with Directed Topologies and Nonlinear Dynamics. IEEE Trans Syst Man Cybern B (2010) 40:881–91. doi:10.1109/tsmcb.2009.2031624

CrossRef Full Text | Google Scholar

4. Wen G, Duan Z, Yu W, Chen G. Consensus of Second-Order Multi-Agent Systems with Delayed Nonlinear Dynamics and Intermittent Communications. Int J Control (2013) 86:322–31. doi:10.1080/00207179.2012.727473

CrossRef Full Text | Google Scholar

5. Yu Z, Jiang H, Huang D, Hu C. Consensus of Nonlinear Multi-Agent Systems with Directed Switching Graphs: A Directed Spanning Tree Based Error System Approach. Nonlinear Anal Hybrid Syst (2018) 28:123–40. doi:10.1016/j.nahs.2017.12.001

CrossRef Full Text | Google Scholar

6. Huang D, Jiang H, Yu Z, Hu C, Fan X. Cluster-delay Consensus in MASs with Layered Intermittent Communication: a Multi-Tracking Approach. Nonlinear Dyn (2019) 95:1713–30. doi:10.1007/s11071-018-4604-4

CrossRef Full Text | Google Scholar

7. Yu Z, Huang D, Jiang H, Hu C. Consensus of Second-Order Multi-Agent Systems with Nonlinear Dynamics via Edge-Based Distributed Adaptive Protocols. J Franklin Inst (2016) 353:4821–44. doi:10.1016/j.jfranklin.2016.09.015

CrossRef Full Text | Google Scholar

8. Sun Y, Li W, Zhao D. Convergence Time and Speed of Multi-Agent Systems in Noisy Environments. Chaos (2012) 22:043126. doi:10.1063/1.4768663

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Young G, Scardovi L, Leonard N. Robustness of Noisy Consensus Dynamics with Directed Communication. In: Proceedings of the American Control Conference; 30 June-2 2010; Baltimore, MD (2010). p. 6312–7. doi:10.1109/acc.2010.5531506

CrossRef Full Text | Google Scholar

10. Bamieh B, Jovanovic MR, Mitra P, Patterson S. Coherence in Large-Scale Networks: Dimension-dependent Limitations of Local Feedback. IEEE Trans Automat Contr (2012) 57:2235–49. doi:10.1109/tac.2012.2202052

CrossRef Full Text | Google Scholar

11. Patterson S, Bamieh B. Consensus and Coherence in Fractal Networks. IEEE Trans Control Netw Syst (2014) 1(4):338–48. doi:10.1109/tcns.2014.2357552

CrossRef Full Text | Google Scholar

12. Yi Y, Zhang Z, Shan L, Chen G. Robustness of First-And Second-Order Consensus Algorithms for a Noisy Scale-free Small-World Koch Network. IEEE Trans Control Syst Technology (2016) 25(1):342–50.

Google Scholar

13. Sun W, Li Y, Liu S. Noisy Consensus Dynamics in Windmill-type Graphs. Chaos (2020) 30:123131. doi:10.1063/5.0020696

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang X, Xu H, Dai M. First-order Network Coherence in 5-rose Graphs. Physica A: Stat Mech its Appl (2019) 527:121129. doi:10.1016/j.physa.2019.121129

CrossRef Full Text | Google Scholar

15. Wan Y, Namuduri K, Akula S, Varanasi M. The Impact of Multi-Group Multi-Layer Network Structure on the Performance of Distributed Consensus Building Strategies. Int J Robust Nonlinear Control (2013) 23(6):653–62. doi:10.1002/rnc.2783

CrossRef Full Text | Google Scholar

16. Shang Y. Finite-time Consensus for Multi-Agent Systems with Fixed Topologies. Int J Syst Sci (2012) 43(3):499–506. doi:10.1080/00207721.2010.517857

CrossRef Full Text | Google Scholar

17. Shang Y. Fixed-time Group Consensus for Multi-Agent Systems with Nonlinear Dynamics and Uncertainties. IET Control Theor Appl (2015) 12(3):395–404.

Google Scholar

18. Shang Y. Consensus and Clustering of Expressed and Private Opinions in Dynamical Networks against Attacks. IEEE Syst J (2020) 14(2):2078–84. doi:10.1109/jsyst.2019.2956116

CrossRef Full Text | Google Scholar

19. Li H-L, Cao J, Jiang H, Alsaedi A. Graph Theory-Based Finite-Time Synchronization of Fractional-Order Complex Dynamical Networks. J Franklin Inst (2018) 355:5771–89. doi:10.1016/j.jfranklin.2018.05.039

CrossRef Full Text | Google Scholar

20. Drauschke F, Sawicki J, Berner R, Omelchenko IE, Schöll E. Effect of Topology upon Relay Synchronization in Triplex Neuronal Networks. Chaos (2020) 30:051104. doi:10.1063/5.0008341

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gu Y-Q, Shao C, Fu X-C. Complete Synchronization and Stability of star-shaped Complex Networks. Chaos, Solitons & Fractals (2006) 28:480–8. doi:10.1016/j.chaos.2005.07.002

CrossRef Full Text | Google Scholar

22. Xu Ming-Ming MM, Lu Jun-An JA, Zhou Jin J. Synchronizability and Eigenvalues of Two-Layer star Networks. Acta Physica Sinica (2016) 65:028902. doi:10.7498/aps.65.028902

CrossRef Full Text | Google Scholar

23. He W, Chen G, Han Q-L, Du W, Cao J, Qian F. Multiagent Systems on Multilayer Networks: Synchronization Analysis and Network Design. IEEE Trans Syst Man Cybern, Syst (2017) 47:1655–67. doi:10.1109/tsmc.2017.2659759

CrossRef Full Text | Google Scholar

24. Kivela M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer Networks. J Complex Networks (2014) 2:203–71. doi:10.1093/comnet/cnu016

CrossRef Full Text | Google Scholar

25. Wang Z, Xia C, Chen Z, Chen G. Epidemic Propagation with Positive and Negative Preventive Information in Multiplex Networks. IEEE Trans Cybern (2021) 51:1454–62. doi:10.1109/tcyb.2019.2960605

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kamal A. Star Local Area Networks: A Performance Study. IEEE Trans Comput (1987) C-36(4):483–99. doi:10.1109/tc.1987.1676930

CrossRef Full Text | Google Scholar

27. Rescigno AA. Optimally Balanced Spanning Tree of the star Network. IEEE Trans Comput (2001) 50(1):88–91. doi:10.1109/12.902755

CrossRef Full Text | Google Scholar

28. Cvetkovic D, Rowlinson P, Simic S. An Introduction to the Theory of Graph Spectra. New York: Cambridge University Press (2010).

Google Scholar

29. Barik S, Pati S, Sarma BK. The Spectrum of the Corona of Two Graphs. SIAM J Discrete Math (2007) 21(1):47–56. doi:10.1137/050624029

CrossRef Full Text | Google Scholar

30. Douglas B. W. Introduction to Graph Theory. 2nd ed. Hong Kong, China: Pearson Education (2004).

Google Scholar

31. Huang D, Zhang Z. On Cyclic Vertex-Connectivity of Cartesian Product Digraphs. J Comb Optim (2012) 24:379–88. doi:10.1007/s10878-011-9395-1

CrossRef Full Text | Google Scholar

32. Good IJ. On the Inversion of Circulant Matrices. Biometrika (1950) 37:185–6. doi:10.1093/biomet/37.1-2.185

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zhang H, Yang Y, Li C. Kirchhoff index of Composite Graphs. Discrete Appl Mathematics (2009) 157:2918–27. doi:10.1016/j.dam.2009.03.007

CrossRef Full Text | Google Scholar

34. Xu P, Huang Q. The Kirchhoff index of Enhanced Hypercubes. arXiv 2018, arXiv (2018) 1809:07189.

Google Scholar

35. Wang JF, Simić SK, Huang QX, Belardo F, Li Marzi EM. Laplacian Spectral Characterization of Disjoint union of Paths and Cycles. Linear and Multilinear Algebra (2011) 59(5):531–9. doi:10.1080/03081081003605777

CrossRef Full Text | Google Scholar