- 1Beijing National Laboratory for Condensed Matter Physics and Institute of Physics, Chinese Academy of Sciences, Beijing, China
- 2School of Physical Sciences, University of Chinese Academy of Sciences, Beijing, China
- 3Songshan Lake Materials Laboratory, Dongguan, China
- 4State Key Laboratory of Low-Dimensional Quantum Physics and Department of Physics, Tsinghua University, Beijing, China
- 5Frontier Science Center for Quantum Information, Beijing, China
We give a brief review of the Mott-Kondo scenario and its consequence in the recently-discovered infinite-layer nickelate superconductors. We argue that the parent state is a self-doped Mott insulator and propose an effective t- J-K model to account for its low-energy properties. At small doping, the model describes a low carrier density Kondo system with incoherent Kondo scattering at finite temperatures, in good agreement with experimental observation of the logarithmic temperature dependence of electric resistivity. Upon increasing Sr doping, the model predicts a breakdown of the Kondo effect, which provides a potential explanation of the non-Fermi liquid behavior of the electric resistivity with a power law scaling over a wide range of the temperature. Unconventional superconductivity is shown to undergo a transition from nodeless (d+is)-wave to nodal d-wave near the critical doping due to competition of the Kondo and Heisenberg superexchange interactions. The presence of different pairing symmetry may be supported by recent tunneling measurements.
1 Introduction
Recent discovery of superconductivity (SC) in infinite-layer Sr-doped NdNiO2 films [1] and subsequently in hole doped LaNiO2 and PrNiO2 films [2–5] has stimulated intensive interest in condensed matter community. Despite of many theoretical and experimental efforts, there are still debates on its electronic structures and pairing mechanism [6–21]. The study of possible Ni-based superconductivity was initially stimulated by cuprates, whose high Tc mechanism remains one of the most challenging topics in past three decades [22–25]. Many attempts have been devoted to exploring new families of high Tc superconductors. Nickelate superconductors are but one latest example of these efforts.
In undoped cuprates, Cu2+ ions contain nine electrons with partially occupied
However, there are clear evidences since the beginning suggesting that these two systems are different. Instead of a Mott insulator with AF long-range order like in cuprates, NdNiO2 displays metallic behavior at high temperatures with a resistivity upturn below about 70 K, showing no sign of any magnetic long-range order in the whole measured temperature range [41]. Similar results have previously been found in LaNiO2 [42]. Possible signatures of (short-range) antiferromagnetic order were reported only very recently in Nd0.8Sr0.2NiO2 thin films by X-ray magnetic linear dichroism measurements [43] and in bulk Nd0.85Sr0.15NiO2 by nuclear magnetic resonance (NMR) [44]. First-principles calculations have also revealed some subtle differences in their band structures. The O-2p orbitals are located at a deeper energy compared to that of cuprates. Nd-5d bands are found to hybridize with Ni-3d bands and produce small electron pockets in the Brillouin zone. As a consequence, holes are doped directly into Ni-3d orbitals rather than O-2p orbitals. Nickelates should thus be modelled as a self-doped Mott insulator, which implies a multi-band system with two types of charge carriers, the itinerant Nd-5d conduction electrons and the Ni-3
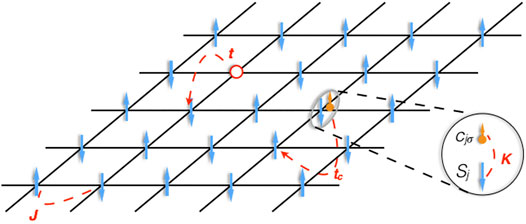
FIGURE 1. Illustration of the self-doping and Mott-Kondo scenario for NdNiO2 projected on a two-dimensional square lattice, showing one of the Ni
Interestingly, the Kondo hybridization does not appear significant at first glance in band structure calculations [32]. It was later realized that nickelates may host a special interstitial-s orbital for conduction electrons that have substantially stronger hybridization than previously thought [17]. Resonant inelastic X-ray scattering (RIXS) measurements [13, 45] confirmed the presence of hybridization between Ni
The above differences have an immediate impact on candidate pairing mechanism of the superconductivity. At critical doping, the t-J-K model predicted possible SC transition from a gapped (d + is)-wave state to a gapless d-wave pairing state due to the competition of Kondo and superexchange interactions [9]. Latest scanning tunneling experiment (STM) also revealed two different gap structures of U and V-shapes [51], supporting the possibility of above scenario. Thus, nickelates may belong to a novel class of unconventional superconductors and one may anticipate potentially more interesting properties bridging the cuprates and heavy fermions.
In this paper, we briefly summarize the consequences of the Mott-Kondo scenario based on the extended t-J-K model for nickelate superconductors [6, 9]. We propose a global phase diagram upon electron and hole doping and derive a low-energy effective Hamiltonian with doublon and holon excitations in the low doping region. We then employ the renormalized mean-field theory (RMFT) to study the possibility of superconductivity and predict a phase transition of its pairing symmetry. The latter is shown to originate from the breakdown of Kondo hybridization, accompanied with non-Fermi liquid (NFL) behavior of the resistivity ρ ∼ Tα near critical doping.
2 THEORY
2.1 Model Hamiltonian
To introduce the effective t-J-K model for describing the low-energy physics of nickelates, we start from a background lattice of Ni1+ 3
where the first term comes from the hopping of holes, the second term describes the spin lattice, and the third term gives the Kondo interaction.
For simplicity, we consider a minimal model with Ni-3d8 and Nd-5d0 as the vacuum. As in cuprates, the localized
whose ground state is a Mott insulator with AF long-range orders.
The self-doping effect is supported by first-principles band structure calculations [32], where the Nd 5d orbitals in NdNiO2 are found to hybridize with the Ni 3d orbitals and give rise to small electron pockets in the Brillouin zone. Thus, we have a small number of Nd-5d conduction electrons. This is actually supported by experiment. At high temperatures, the Hall coefficient is dominated by conduction electrons giving RH ≈ −4 × 10–3 cm3 C−1 for NdNiO2 and −3 × 10–3 cm3 C−1 for LaNiO2. By contrast, in typical heavy fermion metals such as CeMIn5 (M = Co., Rh, Ir), we have RH ≈ −3.5 × 10–4 cm3 C−1 at high temperatures [52]. The larger and negative values of the Hall coefficient implies that there are only a few percent of electron-like carriers per unit cell in NdNiO2 and LaNiO2.
The hybridization between Ni 3
where
The presence of magnetic impurities may be at first glance ascribed to the Nd 4f moments. However, the Nd3+ ion contains three f electrons forming a localized spin-3/2 moment, which acts more like a classical spin as in manganites and therefore disfavors spin-flip scattering as the quantum spin-1/2 moment. Their energy level is also far away from the Fermi energy, so it is reasonable to ignore the Nd 4f electrons. However, we should note that there exist different opinions on the importance of Nd-4f orbitals [53].
For parent compounds, self-doping also introduces an equal number of Ni
where diσ and
Quite generally, the above effective t-J-K model can be replaced by the one-band Hubbard model plus a hybridization term with additional conduction electrons:
where Ek and ϵk are the dispersion of Ni 3
2.2 Global Phase Diagram
As is in heavy fermion systems, the t-J-K model contains two competing energy scales that support different ground states. The Heisenberg superexchange J favors an antiferromagnetic long-range order, while the Kondo coupling K tends to screen the local spins and form a nonmagnetic ground state. In nickelates, due to the large charge transfer energy between O-2p and Ni-
We may propose a global phase diagram starting from an antiferromagnetic ground state. The self-doping introduces equal numbers of conduction electrons and holes. The conduction electrons tend to form Kondo singlets with local spins due to the large K. Both tend to suppress the long-range AF order and causes a paramagnetic ground state. But because of the small number of conduction electrons, local spins cannot be fully Kondo screened to become delocalized. Thus, instead of a heavy fermion metal, we are actually dealing with a low carrier density Kondo system at low temperatures. Due to insufficient Kondo screening, the resistivity exhibits insulating-like behavior (upturn) because of incoherent Kondo scattering, which is typical for low carrier density Kondo systems and has been observed previously in CeNi2−δ(As1−xPx)2 [55] and NaYbSe2 [56].
Upon Sr (hole) doping, the number of conduction electrons may be reduced, while that of holes increases. The Kondo physics may be suppressed and replaced by the usual t-J model for large hole doping, resembling the physics of cuprates. On the other hand, for electron doping, we may expect to first recover the AF long-range order with reduced hole density, and then with increasing conduction electrons and Kondo screening, the AF order will be suppressed again and the system turns into a heavy fermion metal with sufficient electron doping. SC may emerge around the quantum critical point. Whether or not the AF phase may actually exist depends on how doping changes the fraction of electron and hole carriers. But in bulk Nd1−xSrxNiO2, NMR experiment has revealed short-range glassy AF ordering, supporting the possible existence of antiferromagnetism [44]. Figure 2 summarizes possible ground states of the model on the temperature-doping plane, showing a connection between the heavy fermion and cuprate physics on two ends and the nickelates in between. However, it should be noted that current experiment on “overdoped” nickelate superconductors found a weak insulator rather than a Fermi liquid as in heavily hole-doped cuprates [50]. How exactly holes are doped in Nd1−xSrxNiO2 and whether or not multiple Ni-3d orbitals are needed remain an open question.
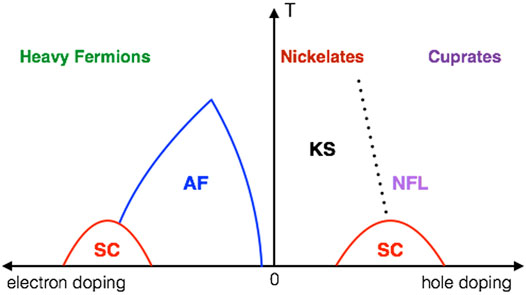
FIGURE 2. A schematic phase diagram of the t-J-K model with electron and hole doping. KS stands for incoherent Kondo scattering or Kondo semimetal. Whether or not the AF phase may exist depends on details of electron and hole densities introduced by doping.
2.3 Low Energy Excitations
As shown in the phase diagram, the paramagnetic region (KS) is responsible for undoped or low doped nickelates. In this case, we have a small number (nc) of conduction electrons per Ni-site and nc + p empty nickel sites (holons) on the NiO2 plane, where p is the hole doping ratio. In the large K limit and at zero temperature, conduction electrons form Kondo singlets or doublons with local Ni spins. We may then derive an effective low-energy Hamiltonian in terms of doublons, holons, and localized spins, to describe a doped Mott metallic state with Kondo singlets [6]. A cartoon picture is given in Figure 1.
For this, we first introduce the pseudofermion representation for the spin-1/2 local moments:
where fjσ is a fermionic operator for the spinon on site j. The Ni
The doublon operators for the on-site Kondo spin singlet and triplets may be defined as
The Kondo Term Then Becomes.
which describes the doublon formation on each site, namely, the Kondo singlet or triplet pair formed by one conduction electron with a localized spinon. We see that the triplet pair costs a higher energy of K. Similarly, there may also exist three-particle states with one localized spinon and two conduction electrons on the same site,
Following Refs. [57, 58], we first rewrite the Hamiltonian in terms of these new operators and then eliminate all high-energy terms containing bjμ (μ = 1, 2, 3) and ejσ using canonical transformation while keeping only the on-site doublon (bj0) and unpaired spinons (
where the spin operators are
which describes the doublon condensation.
This effective Hamiltonian describes the ground state of nickelates at zero or low doping. It is similar to the usual t-J model for cuprates [26], but includes two types of mobile quasiparticles: doublons (Kondo singlets) and holons. It is now clear why the self-doping can efficiently suppress the AF long-range order to yield a paramagnetic ground state in nickelates. At high temperatures, doublons become deconfined, causing incoherent Kondo scattering in transport measurements. This is confirmed by the resistivity replotted in Figure 3 as a function of temperature for both NdNiO2 and LaNiO2. Unlike cuprates, the resistivity exhibits metallic behavior at high temperature but shows an upturn below about 70 K. If we put the data on a linear-log scale, we find that the upturn follows exactly a logarithmic temperature ( ln T) dependence over a large temperature range for both compounds, which is a clear evidence for incoherent Kondo scattering typical for low carrier density Kondo systems [59]. The saturation at very low temperatures is an indication of Kondo screening. This Kondo scenario is also supported by the Hall measurement. In both compounds, the Hall coefficient RH exhibits non-monotonic temperature dependence. It approaches a negative constant at high temperatures due to the contribution of conduction electrons, but exhibits the same ln T dependence at low temperatures. The linear relation RH ∝ ρ is an indication of skew scattering by localized magnetic impurities in typical Kondo systems [60, 61].
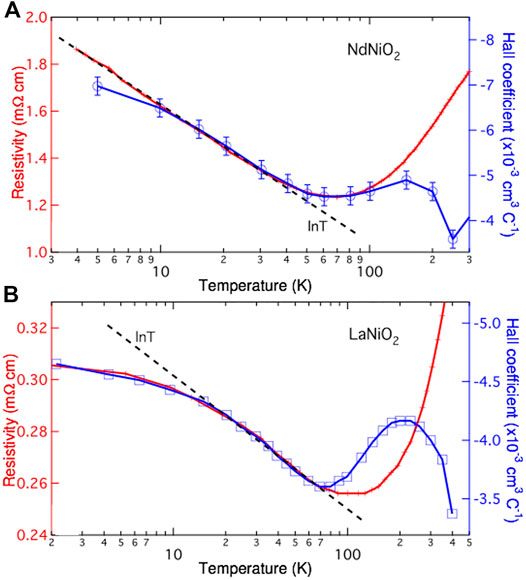
FIGURE 3. Logarithmic scaling of the resistivity (red color) and Hall coefficient (blue color) below about 70 K for (A) NdNiO2 with experimental data adopted from Ref. [1]; (B) LaNiO2 reproduced from Ref. [42]. The dashed lines are the ln T fits. Figure adapted from Ref. [6]. Copyright 2020 by the American Physical Society.
An alternative explanation for the resistivity upturn is weak localization, where disordered holes in the NiO2 plane may also give rise to a logarithmic correction. However, this explanation is not supported by the corresponding correction to the Hall coefficient and magnetoresistance.
2.4 Superconductivity
Experimentally, superconductivity was first observed to emerge and have an onset temperature of 14.9 K in 20% Sr doped NdNiO2 thin films deposited on SrTiO3 substrates [1]. From the t-J-K model, one may naively expect that sufficiently large doping may deplete conduction electrons and increase the number of holons, driving the system to an effective t-J model resembling that in cuprates. As a result, d-wave superconductivity may arise due to the superexchange interaction between Ni 3
The pairing symmetry can be studied by using the renormalized mean-field theory (RMFT) [62], which had successfully predicted the d-wave superconductivity in the t-J model for cuprates and can well describe the Fermi liquid similar to the slave-boson mean field theory. Our numerical calculations of superconductivity on the generalized t-J-K model have yielded a typical superconducting phase diagram in Figure 4 [9]. The pairing symmetry is found to depend on the hole concentration p and the effective strength of the Kondo hybridization controlled by the conduction electron hopping (tc/K). For simplicity, we have taken the Kondo coupling K as the energy unit (K = 1), and set the AF Heisenberg spin exchange J = 0.1. Both the nearest-neighbor hopping t = 0.2 and the next-nearest-neighbor hopping t′ = −0.05 are taken into consideration for Ni 3d electrons. The density of conduction electrons is taken to be nc = 0.1, while their nearest-neighbor hopping tc is chosen as a tuning parameter. Note that these parameters may in principle vary with doping in real materials. Here we fix them for simplicity in our model study and focus on the qualitative picture.
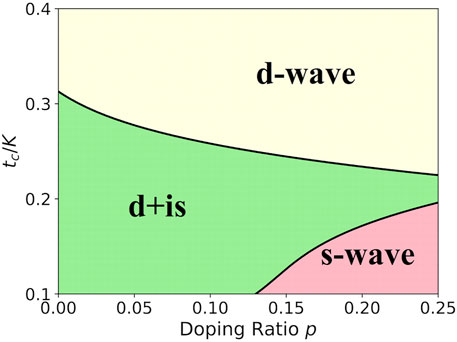
FIGURE 4. Superconducting phase diagram of the t-J-K model. At small doping p and moderate tc/K, the pairing symmetry is (d + is)-wave. At large tc/K, the pairing is d-wave. For moderate tc/K, the phase diagram predicts a superconducting transition from (d + is) to d with increasing hole doping. Figure adapted from Ref. [9]. Copyright 2020 by the American Physical Society.
For all doping, we find a dominant d-wave pairing symmetry for large tc/K or small K. But for low doping and moderate tc/K, we obtain a
Details of RMFT calculations are explained as follows [9]. We first introduce three Gutzwiller renormalization factor to approximate the operator that projects out the doubly occupied states: gt = nh/(1 + nh) for the hopping t and t′,
The resulting mean-field Hamiltonian has a simple bilinear form in the momentum space,
where we have introduced the Nambu spinors
Here α denotes the vectors of the nearest-neighbor lattice sites and δ stands for those of the next-nearest-neighbor sites. μ1 and μ2 are chemical potentials fixing the numbers of the constrained electrons diσ and conduction electrons ciσ, respectively.
The above mean-field Hamiltonian can be diagonalized using the Bogoliubov transformation,
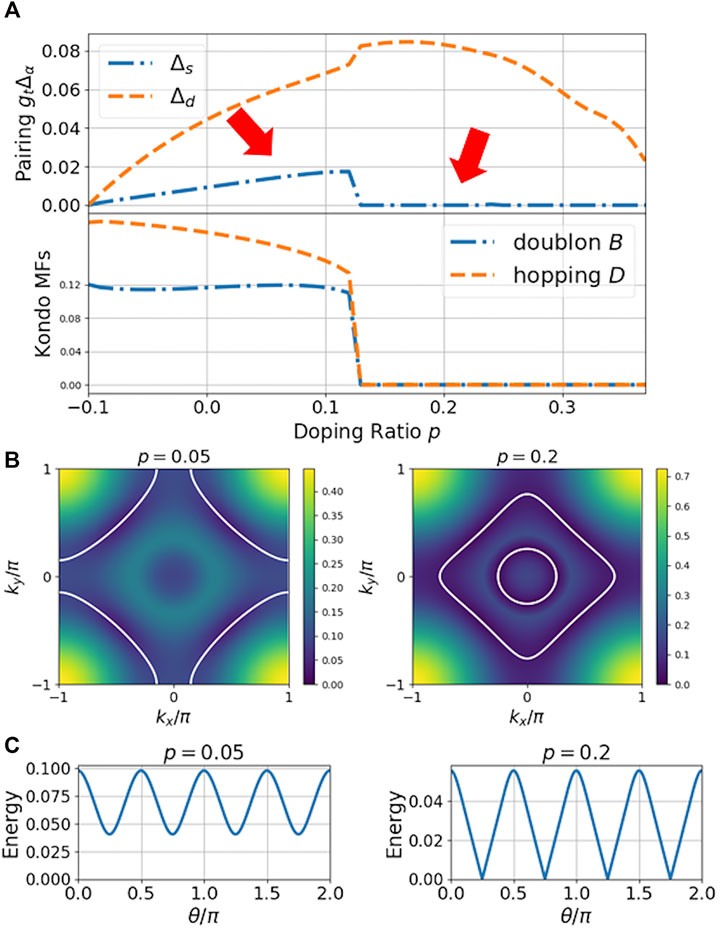
FIGURE 5. RMFT results for tc/K = 0.25. (A) Doping dependence of the mean-field parameters gtΔ (upper panel) and B and D (lower panel). Comparison of (B) the quasiparticle excitation energy (background) and the Fermi surface (white solid line) defined as the minimal excitation energy and (C) superconducting gap along the Fermi surface at p = 0.05 (d + is)-wave and p = 0.2 (d-wave) as marked by the arrows in (A). Figure adapted from Ref. [9]. Copyright 2020 by the American Physical Society.
Antiferromagnetic spin fluctuations have been observed in bulk Nd1−xSrxNiO2 by NMR [44] and may also exist and play the role of pairing glues in thin films. Hence the presence of a dominant d-wave pairing at large doping is expected from the experience in cuprates. However, our results also suggest several additional features of the nickelate superconductivity that are not present in cuprates and may be examined in experiment. First, for sufficiently large Kondo coupling K, the (d + is)-wave SC in the low doping region breaks the time reversal symmetry and as shown in Figure 5C (left panel), has a nodeless gap which is distinctly different from the usual d-wave pairing with nodes along the diagonal direction. Second, we predict a quantum phase transition between this gapped (d + is)-wave SC to the nodal d-wave superconductivity with increasing hole doping. These features can be detected by scanning tunneling, penetration depth, or μSR experiment and serve as a support for our theory. We remark that conduction electrons play an important role in our theory of nickelate superconductivity, which is not possible in the single-band Mott picture. The importance of electron pockets is in fact supported by experimental measurements of the upper critical field [65, 66].
Recent single particle tunneling experiment [51] on superconducting nickelate thin films have also observed two distinct types of spectra: a V-shape feature with a gap maximum of 3.9 meV, a U-shape feature with a gap of about 2.35 meV, and some spectra with mixed contributions of these two components. If we attribute their different observations to different hole concentrations due to possible surface effect, the two types of spectra may correspond exactly to the two pairing states in our theory. In this sense, the scanning tunneling spectra have provided a supportive evidence for our theoretical prediction of multiple superconducting phases. Of course, the (d + is)-wave pairing might not exist in real materials if the Kondo coupling K is too weak or tc/K is too large. In that case, as is seen in Figure 4, d-wave pairing may become dominant on the hole Fermi surface, but electron pockets may still have nodeless gap depending on their position in the Brillouin zone.
2.5 Quantum Criticality
As shown in Figure 5, for moderate tc/K, the SC transition from (d + is) to d-wave is accompanied with vanishing Kondo mean-field parameters B and D, which implies a breakdown of the Kondo hybridization in the large doping side. Correspondingly, the Fermi surface structures also change from a large hole-like Fermi surface around four Brillouin zone corners at low doping to two separate electron-like Fermi surfaces (from decoupled charge carriers) around the Brillouin zone center at large doping. These results may be compared with the Hall experiments in Nd1−xSrxNiO2 [49, 50], which revealed a crossover line of sign change in the temperature-doping phase diagram near the maximal Tc. The line marks a potential change in the Fermi surfaces and resembles that observed in some heavy fermion systems owing to the delocalization of localized moments [67]. It is thus attempted to link the experiment with our theoretical proposals and predict a zero-temperature quantum critical point with the SC transition and the Fermi surface change near the crossover line, although it should be cautious that they take place in different temperature region.
As a matter of fact, experiment has indeed observed quantum critical behavior in the normal state above Tc. A tentative fit of the resistivity in superconducting nickelate thin films has yielded power-law scaling with temperature, namely ρ ∼ Tα, with α = 1.1–1.3 over a wide range [6]. Figure 6 gives an example of the fit in Nd0.8Sr0.2NiO2 and we obtain α ≈ 1.13 from slightly above Tc up to the room temperature. This reminds us the strange metal above Tc in optimal-doped cuprates and the non-Fermi liquid in heavy fermion systems. Better numerical calculations are required in order to establish the exact mechanism of this scaling.
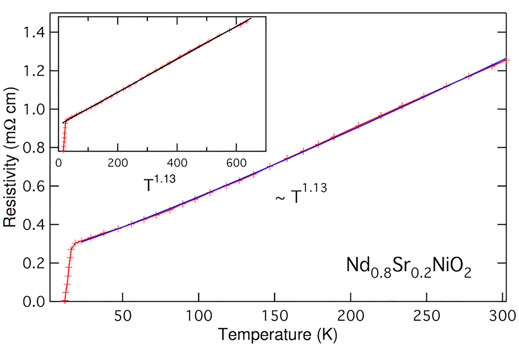
FIGURE 6. Power-law temperature dependence of the electric resistivity above Tc = 14.9K up to the room temperature for Nd0.8Sr0.2NiO2. The experimental data were reproduced from Ref. [1].
3 Future Perspective
We have introduced the picture of self-doped Mott insulator to describe the recently discovered nickelate superconductors. The self-doping effect has been generally accepted by the community and distinguishes nickelates from cuprates. We further propose a Mott-Kondo scenario and an extended t-J-K model based on transport measurements and electronic structure calculations. Our model bridges the usual Kondo lattice model for heavy fermions and the t-J model for cuprates, but shows unique features that can only be understood as an interplay of both physics. Our theory provides a natural explanation of the resistivity upturn in undoped nickelates at low temperatures, and our calculations based on the t-J-K model predict an exotic (d + is)-wave superconductivity that breaks the time reversal symmetry and a possible transition of the pairing symmetry at critical doping, around which the normal state exhibits non-Fermi liquid behavior above Tc. This implies that nickelate superconductors are a novel class of unconventional superconductors. Thus, exploration of new physics based on our theory will be an interesting direction for future investigations.
Currently there still exist different opinions on the effect of Sr doping. Some argued that holes may occupy other Ni 3d orbitals and the Hund coupling may favor a high spin state (S = 1) [8, 14, 16]. This scenario seems inconsistent with joint analyses of XAS and RIXS experiments [18] and a number of other calculations [11, 20]. Nevertheless, our model allows for a straightforward multi-orbital extension by considering a two-band Hubbard model of Ni 3d orbitals (or its projection at large U) plus hybridization with additional conduction bands. So far, bulk nickelates have not been found superconductive and many issues remain to be answered both in theory and in experiment [68]. Our proposal of the self-doping effect, the Mott-Kondo scenario, and the t-J-K model provides a promising starting basis for future investigations.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 11774401, 11974397, and 12174429), the National Key Research and Development Program of MOST of China (Nos. 2017YFA0303103 and 2017YFA0302902), and the Strategic Priority Research Program of CAS (Grand No. XDB33010100).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5
2. Osada M, Wang BY, Goodge BH, Lee K, Yoon H, Sakuma K, et al. A Superconducting Praseodymium Nickelate with Infinite Layer Structure. Nano Lett (2020) 20:5735–40. doi:10.1021/acs.nanolett.0c01392
3. Osada M, Wang BY, Lee K, Li D, Hwang HY. Phase Diagram of Infinite Layer Praseodymium Nickelate Pr1−xSrxNiO2 Thin Films. Phys Rev Mater (2020) 4:121801. doi:10.1103/physrevmaterials.4.121801
4. Zeng S, Li C, Chow L, Cao Y, Zhang Z, Tang C, et al. Superconductivity in Infinite-Layer Lanthanide Nickelates. arXiv preprint arXiv:2105.13492 (2021).
5. Osada M, Wang BY, Goodge BH, Harvey SP, Lee K, Li D, et al. Nickelate Superconductivity without Rare-Earth Magnetism: (La, Sr)NiO2. arXiv preprint arXiv:2105.13494 (2021).
6. Zhang G-M, Yang Y-f., Zhang F-C. Self-doped mott Insulator for Parent Compounds of Nickelate Superconductors. Phys Rev B (2020) 101(R):020501. doi:10.1103/PhysRevB.101.020501
7. Nomura Y, Hirayama M, Tadano T, Yoshimoto Y, Nakamura K, Arita R. Formation of a Two-Dimensional Single-Component Correlated Electron System and Band Engineering in the Nickelate Superconductor NdNiO2. Phys Rev B (2019) 100:205138. doi:10.1103/PhysRevB.100.205138
8. Hu L-H, Wu C. Two-band Model for Magnetism and Superconductivity in Nickelates. Phys Rev Res (2019) 1:032046. doi:10.1103/PhysRevResearch.1.032046
9. Wang Z, Zhang G-M, Yang Y-f., Zhang F-C. Distinct Pairing Symmetries of Superconductivity in Infinite-Layer Nickelates. Phys Rev B (2020) 102(R):220501. doi:10.1103/PhysRevB.102.220501
10. Botana AS, Norman MR. Similarities and Differences between LaNiO2 and CaCuO2 and Implications for Superconductivity. Phys Rev X (2020) 10:011024. doi:10.1103/PhysRevX.10.011024
11. Jiang M, Berciu M, Sawatzky GA. Critical Nature of the Ni Spin State in Doped NdNiO2. Phys Rev Lett (2020) 124:207004. doi:10.1103/PhysRevLett.124.207004
12. Sakakibara H, Usui H, Suzuki K, Kotani T, Aoki H, Kuroki K. Model Construction and a Possibility of Cupratelike Pairing in a New d9 Nickelate Superconductor (Nd,Sr)NiO2. Phys Rev Lett (2020) 125:077003. doi:10.1103/PhysRevLett.125.077003
13. Hepting M, Li D, Jia CJ, Lu H, Paris E, Tseng Y, et al. Electronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19:381–5. doi:10.1038/s41563-020-0761-110.1038/s41563-019-0585-z
14. Zhang Y-H, Vishwanath A. Type-II t−J Model in Superconducting Nickelate Nd1−xSrxNiO2. Phys Rev Res (2020) 2:023112. doi:10.1103/PhysRevResearch.2.023112
15. Lechermann F. Multiorbital Processes Rule the Nd1−xSrxNiO2 Normal State. Phys Rev X (2020) 10:041002. doi:10.1103/PhysRevX.10.041002
16. Werner P, Hoshino S. Nickelate Superconductors: Multiorbital Nature and Spin Freezing. Phys Rev B (2019) 101:041104. doi:10.1103/PhysRevB.101.041104
17. Gu Y, Zhu S, Wang X, Hu J, Chen H. A Substantial Hybridization between Correlated Ni-D Orbital and Itinerant Electrons in Infinite-Layer Nickelates. Commun Phys (2020) 3:1–9. doi:10.1038/s42005-020-0347-x
18. Rossi M, Lu H, Nag A, Li D, Osada M, Lee K, et al. Orbital and Spin Character of Doped Carriers in Infinite-Layer Nickelates. arXiv preprint arXiv:2011.00595 (2020).
19. Kitatani M, Si L, Janson O, Arita R, Zhong Z, Held K. Nickelate Superconductors-A Renaissance of the One-Band Hubbard Model. npj Quan Mater. (2020) 5:59. doi:10.1038/s41535-020-00260-y
20. Higashi K, Winder M, Kuneš J, Hariki A. Core-Level X-Ray Spectroscopy of Infinite-Layer Nickelate: LDA+DMFT Study. Phys Rev X (2021) 11:041009. doi:10.1103/PhysRevX.11.041009
21. Gao J, Peng S, Wang Z, Fang C, Weng H. Electronic Structures and Topological Properties in Nickelates Lnn+1NinO2n+2. Natl Sci Rev (2021) 8:nwaa218. doi:10.1093/nsr/nwaa218
22. Bednorz JG, Müller KA. Possible highT C Superconductivity in the Ba-La-Cu-O System. Z Physik B - Condensed Matter (1986) 64:189–93. doi:10.1007/BF01303701
23. Anderson PW. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science (1987) 235:1196–8. doi:10.1126/science.235.4793.1196
24. Anderson PW, Lee PA, Randeria M, Rice TM, Trivedi N, Zhang FC. The Physics behind High-Temperature Superconducting Cuprates: the plain Vanilla Version of RVB. J Phys Condens Matter (2004) 16:R755–R769. doi:10.1088/0953-8984/16/24/r02
25. Lee PA, Nagaosa N, Wen X-G. Doping a Mott Insulator: Physics of High-Temperature Superconductivity. Rev Mod Phys (2006) 78:17–85. doi:10.1103/RevModPhys.78.17
26. Zhang FC, Rice TM. Effective Hamiltonian for the Superconducting Cu Oxides. Phys Rev B (1988) 37:3759–61. doi:10.1103/PhysRevB.37.3759
27. Shen Z-X, Dessau DS, Wells BO, King DM, Spicer WE, Arko AJ, et al. Anomalously Large gap Anisotropy in the a-b Plane of Bi2Sr2CaCu2O8+δ. Phys Rev Lett (1993) 70:1553–6. doi:10.1103/physrevlett.70.1553
28. Wollman DA, Van Harlingen DJ, Lee WC, Ginsberg DM, Leggett AJ. Experimental Determination of the Superconducting Pairing State in YBCO from the Phase Coherence of YBCO-Pb dc SQUIDs. Phys Rev Lett (1993) 71:2134–7. doi:10.1103/PhysRevLett.71.2134
29. Tsuei CC, Kirtley JR, Chi CC, Yu-Jahnes LS, Gupta A, Shaw T, et al. Pairing Symmetry and Flux Quantization in a Tricrystal Superconducting Ring of YBa2Cu3O7−δ. Phys Rev Lett (1994) 73:593–6. doi:10.1103/physrevlett.73.593
30. Anisimov VI, Bukhvalov D, Rice TM. Electronic Structure of Possible Nickelate Analogs to the Cuprates. Phys Rev B (1999) 59:7901–6. doi:10.1103/PhysRevB.59.7901
31. Hayward MA, Green MA, Rosseinsky MJ, Sloan J. Sodium Hydride as a Powerful Reducing Agent for Topotactic Oxide Deintercalation: Synthesis and Characterization of the Nickel(I) Oxide LaNiO2. J Am Chem Soc (1999) 121:8843–54. doi:10.1021/ja991573i
32. Lee K-W, Pickett WE. Infinite-layer LaNiO2: Ni1+ is not Cu2+. Phys Rev B (2004) 70:165109. doi:10.1103/PhysRevB.70.165109
33. Botana AS, Pardo V, Norman MR. Electron Doped Layered Nickelates: Spanning the Phase Diagram of the Cuprates. Phys Rev Mater (2017) 1:021801. doi:10.1103/PhysRevMaterials.1.021801
34. Chaloupka J, Khaliullin G. Orbital Order and Possible Superconductivity in LaNiO3/LaMO3 Superlattices. Phys Rev Lett (2008) 100:016404. doi:10.1103/PhysRevLett.100.016404
35. Hansmann P, Yang X, Toschi A, Khaliullin G, Andersen OK, Held K. Turning a Nickelate Fermi Surface into a Cupratelike One through Heterostructuring. Phys Rev Lett (2009) 103:016401. doi:10.1103/PhysRevLett.103.016401
36. Middey S, Chakhalian J, Mahadevan P, Freeland JW, Millis AJ, Sarma DD. Physics of Ultrathin Films and Heterostructures of Rare-Earth Nickelates. Annu Rev Mater Res (2016) 46:305–34. doi:10.1146/annurev-matsci-070115-032057
37. Boris AV, Matiks Y, Benckiser E, Frano A, Popovich P, Hinkov V, et al. Dimensionality Control of Electronic Phase Transitions in Nickel-Oxide Superlattices. Science (2011) 332:937–40. doi:10.1126/science.1202647
38. Benckiser E, Haverkort MW, Brück S, Goering E, Macke S, Frañó A, et al. Orbital Reflectometry of Oxide Heterostructures. Nat Mater (2011) 10:189–93. doi:10.1038/nmat2958
39. Disa AS, Kumah DP, Malashevich A, Chen H, Arena DA, Specht ED, et al. Orbital Engineering in Symmetry-Breaking Polar Heterostructures. Phys Rev Lett (2015) 114:026801. doi:10.1103/PhysRevLett.114.026801
40. Zhang J, Botana AS, Freeland JW, Phelan D, Zheng H, Pardo V, et al. Large Orbital Polarization in a Metallic Square-Planar Nickelate. Nat Phys (2017) 13:864–9. doi:10.1038/nphys4149
41. Hayward MA, Rosseinsky MJ. Synthesis of the Infinite Layer Ni(I) Phase NdNiO2+x by Low Temperature Reduction of NdNiO3 with Sodium Hydride. Solid State Sci (2003) 5:839–50. doi:10.1016/S1293-2558(03)00111-0
42. Ikeda A, Krockenberger Y, Irie H, Naito M, Yamamoto H. Direct Observation of Infinite NiO2 Planes in LaNiO2 Films. Appl Phys Express (2016) 9:061101. doi:10.7567/APEX.9.061101
43. Zhou X, Zhang X, Yi J, Qin P, Feng Z, Jiang P, et al. Antiferromagnetism in Ni-Based Superconductors. arXiv preprint arXiv:2110.14915 (2021).
44. Cui Y, Li C, Li Q, Zhu X, Hu Z, Yang Y-f., et al. NMR Evidence of Antiferromagnetic Spin Fluctuations in Nd0.85Sr0.15NiO2. Chin Phys. Lett. (2021) 38:067401. doi:10.1088/0256-307X/38/6/067401
45. Goodge BH, Li D, Lee K, Osada M, Wang BY, Sawatzky GA, et al. Doping Evolution of the Mott-Hubbard Landscape in Infinite-Layer Nickelates. Proc Natl Acad Sci USA (2021) 118:e2007683118. doi:10.1073/pnas.2007683118
46. Fu Y, Wang L, Cheng H, Pei S, Zhou X, Chen J, et al. Core-level X-ray Photoemission and Raman Spectroscopy Studies on Electronic Structures in Mott-Hubbard Type Nickelate Oxide NdNiO2. arXiv preprint arXiv:1911.03177 (2019).
47. Lu H, Rossi M, Nag A, Osada M, Li DF, Lee K, et al. Magnetic Excitations in Infinite-Layer Nickelates. Science (2021) 373:213–6. doi:10.1126/science.abd7726
48. Been E, Lee WS, Hwang HY, Cui Y, Zaanen J, Devereaux T, et al. Electronic Structure Trends across the Rare-Earth Series in Superconducting Infinite-Layer Nickelates. Phys Rev X (2021) 11:011050. doi:10.1103/physrevx.11.011050
49. Li D, Wang BY, Lee K, Harvey SP, Osada M, Goodge BH, et al. Superconducting Dome in Nd1−xSrxNiO2 Infinite Layer Films. Phys Rev Lett (2020) 125:027001. doi:10.1103/PhysRevLett.125.027001
50. Zeng S, Tang CS, Yin X, Li C, Li M, Huang Z, et al. Phase Diagram and Superconducting Dome of Infinite-Layer Nd1−xSrxNiO2 Thin Films. Phys Rev Lett (2020) 125:147003. doi:10.1103/PhysRevLett.125.147003
51. Gu Q, Li Y, Wan S, Li H, Guo W, Yang H, et al. Single Particle Tunneling Spectrum of Superconducting Nd1-xSrxNiO2 Thin Films. Nat Commun (2020) 11:1–7. doi:10.1038/s41467-020-19908-1
52. Hundley M, Malinowski A, Pagliuso P, Sarrao J, Thompson J. Anomalous F-Electron Hall Effect in the Heavy-Fermion System CeTIn5 (T=Co, Ir, or Rh). Phys Rev B (2004) 70:035113. doi:10.1103/physrevb.70.035113
53. Jiang P, Si L, Liao Z, Zhong Z. Electronic Structure of Rare-Earth Infinite-Layer RNiO2(R=La,Nd). Phys Rev B (2019) 100:201106. doi:10.1103/PhysRevB.100.201106
54. Yang Y-f., Fisk Z, Lee H-O, Thompson JD, Pines D. Scaling the Kondo Lattice. Nature (2008) 454:611–3. doi:10.1038/nature07157
55. Chen J, Wang Z, Li Y, Feng C, Dai J, Xu Za., et al. Heavy Fermion Quantum Criticality at Dilute Carrier Limit in CeNi2−δ(As1−xPx)2. Sci Rep (2019) 9:1–10. doi:10.1038/s41598-019-48662-8
56. Xu Y, Sheng Y, Yang YF. Mechanism of the Insulator-To-Metal Transition and Superconductivity in the Spin Liquid Candidate NaYbSe2 under Pressure. arXiv preprint arXiv:2108.03218 (2021).
57. Lacroix C. Some Exact Results for the Kondo Lattice with Infinite Exchange Interaction. Solid State Commun (1985) 54:991–4. doi:10.1016/0038-1098(85)90171-1
58. Sigrist M, Ueda K, Tsunetsugu H. Ferromagnetism of the Kondo Lattice in the Low-Carrier-Concentration Limit. Phys Rev B (1992) 46:175–83. doi:10.1103/PhysRevB.46.175
60. Fert A, Levy PM. Theory of the Hall Effect in Heavy-Fermion Compounds. Phys Rev B (1987) 36:1907–16. doi:10.1103/physrevb.36.1907
61. Nagaosa N, Sinova J, Onoda S, MacDonald AH, Ong NP. Anomalous Hall Effect. Rev Mod Phys (2010) 82:1539–92. doi:10.1103/RevModPhys.82.1539
62. Zhang FC, Gros C, Rice TM, Shiba H. A Renormalised Hamiltonian Approach to a Resonant Valence Bond Wavefunction. Supercond Sci Technol (1988) 1:36–46. doi:10.1088/0953-2048/1/1/009
63. Wu X, Di Sante D, Schwemmer T, Hanke W, Hwang HY, Raghu S, Thomale R. Robust
64. Bodensiek O, Žitko R, Vojta M, Jarrell M, Pruschke T. Unconventional Superconductivity from Local Spin Fluctuations in the Kondo Lattice. Phys Rev Lett (2013) 110:146406. doi:10.1103/PhysRevLett.110.146406
65. Xiang Y, Li Q, Li Y, Yang H, Nie Y, Wen H-H. Physical Properties Revealed by Transport Measurements for Superconducting Nd0.8Sr0.2NiO2 Thin Films. Chin Phys. Lett. (2021) 38:047401. doi:10.1088/0256-307X/38/4/047401
66. Wang BY, Li D, Goodge BH, Lee K, Osada M, Harvey SP, et al. Isotropic Pauli-Limited Superconductivity in the Infinite-Layer Nickelate Nd0.775Sr0.225NiO2. Nat Phys (2021) 17:473–7. doi:10.1038/s41567-020-01128-5
67. Yang Y-f., Pines D, Lonzarich G. Quantum Critical Scaling and Fluctuations in Kondo Lattice Materials. Proc Natl Acad Sci USA (2017) 114:6250–5. doi:10.1073/pnas.1703172114
Keywords: nickelate superconductor, self-doping, Mott, Kondo, t-J-K model
Citation: Yang Y-f and Zhang G-M (2022) Self-Doping and the Mott-Kondo Scenario for Infinite-Layer Nickelate Superconductors. Front. Phys. 9:801236. doi: 10.3389/fphy.2021.801236
Received: 25 October 2021; Accepted: 02 December 2021;
Published: 10 January 2022.
Edited by:
Danfeng Li, City University of Hong Kong, Hong Kong SAR, ChinaCopyright © 2022 Yang and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yi-feng Yang, eWlmZW5nQGlwaHkuYWMuY24=; Guang-Ming Zhang, Z216aGFuZ0B0c2luZ2h1YS5lZHUuY24=
 Yi-feng Yang
Yi-feng Yang Guang-Ming Zhang4,5*
Guang-Ming Zhang4,5*