Global Mean Sea Level. Time Trends and Persistence with Long Range Dependent Data

Global mean sea level data are examined in this work by looking at the presence of time trends in the context of long memory or long range dependent processes. By looking at both seasonal signals retained and seasonal signals removed data from 1992 to 2020, the results show that the two series display significant time trend coefficients and high levels of persistence.

1 Introduction

The evidence shows that global mean sea level (GMSL) has risen during the 20th century [1], and this rise has been larger than that observed during the previous two centuries [2]. In line with this, GMSL data are examined in this work by using a long memory or long range dependent model. The idea is to estimate a linear time trend in the data under the assumption that the errors in the regression model might be fractionally integrated, which is a particular model within the long memory class. The reason for this is that this property (long memory) has been widely observed in the majority of geophysical and climatological series (see, e.g., [3–5]; etc.) and therefore it should also be expected in the sea level data (see also [6]).

The model examined in the empirical section is the following one:

$y_t={\gamma }_0+{\gamma }_1\beta t+x_t,{\left(1-B\right)}^d{x}_t=u_t,(1)$

where y_t is the sea level data; γ₀ and γ₁ are unknown parameters referring to an intercept and a (linear) time trend, and x_t is the regression error that is assumed to be integrated of order d or I (d) where d can be any real value, and thus, potentially fractional. In this context, B is the backshift operator, i.e., B^kx_t = x_t-k, and the d-differenced process u_t in (1) is supposed to be integrated of order 0, or I (0), defined as a covariance stationary process where its spectral density function is positive and bounded at all frequencies. It includes the case of a white noise process but also stationary and invertible AutoRegressive Moving Average (ARMA) models. Thus, if u_t is ARMA (p,q), x_t is said to be AutoRegressive Fractionally Integrated Moving Average (ARFIMA (p,d,q) model. In this paper, however, we will deal with the autocorrelation by using a non-parametric method [7] widely used in the context of I (d) models. In this context, evidence of significantly positive values of γ₁ in (1) will indicate that the sea level data reflect increases over time, and we do the estimation without imposing the strong assumption that the x_t in (1) are I (0) but I (d) with d freely estimated from the data.

2 Methodology

As it has been mentioned in the previous section, the methodology used in this work is based on long memory, which is a feature observed in many time series of different disciplines including among others climatological and meteorological data. Long memory processes are characterized because the spectral density function of the data (which is the Fourier transform of the autocovariances) displays values that explote at the smallest (zero) frequency, which is usually consistent with first differentiation of the data. However, in many cases, the spectral density function of the first differenced data shows values close to zero at the zero frequency, which is consistent with over-differentiation. This was the origin of fractional differentiation [8], which is a particular model satisfying the long memory property, and that is described by the second equation presented in (1).

The differencing parameter d is important from various viewpoints. Thus, if d = 0, the series is said to be short memory or I (0), unlike what happens with positive d that implies long memory or long range dependence, so-named because of the strong degree of association between the observations even if they are far distant in time; also, from a statistical viewpoint, the value 0.5 is important. Thus, if d < 0.5 the series is still covariance stationary, while d ≥ 0.5 implies nonstationarity; finally, if d < 1 the series is said to be mean reverting with the effect of the shocks disappearing in the long run, contrary to what happens with d ≥ 1 with shocks persisting forever.

We estimate the parameter d by using the Whittle function expressed in the frequency domain, employing a version of the tests of Robinson [9] widely used in empirical applications (see, e.g. [10]). Note, however, that the fractional integration approach employed in this work is merely one of the numerous formulations for long range dependence that include among others the generalized Cauchy processes, the generalized fractional Gaussian noise models and the modefied multifractional fractional Gaussian noise model (see, e.g., [11, 12]). These methods may also be considered as flexible tools to investigate long range dependence in time series, including sea level data ([13, 14], etc.).

3 Dataset

We use data which are estimates of sea level based on measurements from satellite radar altimeters. They are available for TOPEX/Poseidon (T/P), Jason-1, Jason-2, and Jason-3, which have been monitored. Only altimetry measurements between 66°S and 66°N have been processed. An inverted barometer has been applied to the time series.

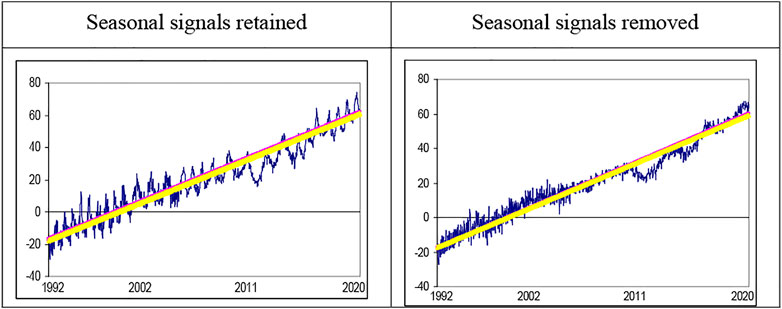
Two time series are examined (see Figure 1) referring to the global mean sea level data, with seasonal signals retained and removed.

FIGURE 1

FIGURE 1. Time series plots. Seasonal signals retained. Seasonal signals removed.

The data are provided by the NOAA Laboratory for Satellite Altimetry from the NOAA (http://www.star.nesdis.noaa.gov/sod/lsa/SeaLevelRise/) and Radar Altimeter Database System (http://www.deos.tudelft.nl/altim/rads/).

4 Results

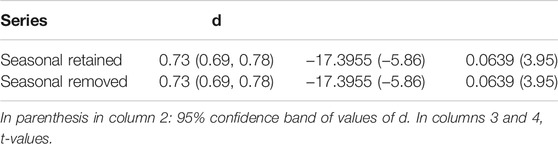
Table 1 displays the estimated coefficients of the model given by Eq. 1 under the assumption that the error term u_t is a white noise process. We observe that the estimated value of d is 0.73 for the seasonal signals retained data and 0.45 for the seasonal signals removed data, and in both cases, the confidence intervals reject the null of d = 1 in favour of d < 1, implying mean reversion in its behaviour. Thus, shocks will have a transitory effect in the series, disappearing by themselves in the long run, and faster in the case of the seasonal signals removed data. The time trend coefficient is significantly positive in the two series, being slightly higher with the seasonal signals retained data.

TABLE 1

TABLE 1. Estimated coefficients I: White noise errors.

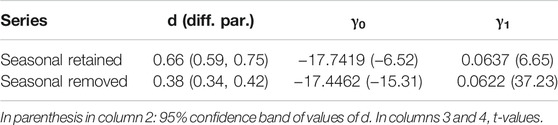
Very similar results are obtained under the assumption of autocorrelated (Bloomfield)¹ errors. The estimates of d are now slightly smaller (0.66 for the seasonal retained data and 0.38 for the seasonal removed data), and the slope coefficients are again significant, 0.0637 in the first case (seasonal retained) and 0.0622 in the seasonal signals removed data. The estimated time trends are displayed in Figure 1.

Finally, in Table 2, we display the coefficients under the assumption that x_t in Eq. 1 is I (0). Thus, the long memory feature is not taken into account. We observe that the slope coefficient, though significant, is slightly smaller than under the I (d) specification. Note, however, that this hypothesis is decisively rejected according to the results in Tables 1, 3 where d was found to be significantly positive. Thus, the fact that the long memory is not considered here produces a bias reducing the amount of the global sea level rise.

TABLE 2

TABLE 2. Estimated coefficients imposing d = 0.

TABLE 3

TABLE 3. Estimated coefficients II: Weakly autocorrelated (Bloomfield) errors.

5 Conclusion

We have examined data corresponding to the global mean sea level for the time period from 1992 to 2020, using a long range dependent model based on fractional integration and testing for the presence of time trends. Our results show first that long range dependence is a feature of these data, consistent with works such as Ercan et al. [6] and others, since the degree of differentiation is in the interval (0, 1) in the two series examined. Moreover, the slope coefficient is highly significantly positive and slightly higher than the one observed under the wrong assumption that the errors are I (0).

Further work with these series should investigate other alternative approaches for trends in the data such as LOWESS, piece-wise-linear trends, or the presence of non-linear trends, using, for example, either segmented trends based on structural breaks or, alternatively, using non-linear polynomials in time, like those based on Chebyshev polynomials [15], in both cases using still long memory and fractional integration. Data disaggregated by areas should also be examined. Finally, it would also be of interest to link the inter-annual fluctuations with ENSO as suggested by authors such as Cazenave et al. [16]. Work in these directions is now in progress.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

LG-A is the only contributor of the manuscript.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The model of Bloomfield [7] is a non-parametric approach that produces errors with the autocorrelation function decaying exponentially fast as in the ARMA case. (see [17], for its implementation in the context of fractional integration).

References

1. Oppenheimer M, Glavovic BC, Hinkel J, van de Wal R, Magnan AK, AbdElgawad A, et al. Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities. In: IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. Springer (2019). p. 321–446.

Google Scholar

2. Warrick RA, Oerlemans J. Sea Level Rise. In: JT Houghton, GJ Jenkins, and JJ Ephraum, editors. Climate Change: The IPCC Scientific Assessment. Cambridge, United Kingdom, and New York, NY, USA: Cambridge University Press (1990). p. 260–81.

Google Scholar

3. Bunde A. Long-term Memory in Climate: Detection, Extreme Events and Significance of Trends. In: CLE Franzke, and T O'Kane, editors. Chapter 11 in Nonlinear and Stochastic Climate Dynamics. Cambridge University Press (2017).

Google Scholar

4. Gil-Alana LA, Sauci L. Temperatures across Europe: Evidence of Time Trends. Climatic Change (2019) 157:355–64. doi:10.1007/s10584-019-02568-6

CrossRef Full Text | Google Scholar

5. Yuan N, Huang Y, Duan J, Zhu C, Xoplaki E, Luterbacher J. On Climate Prediction: How Much Can We Expect from Climate Memory? Clim Dyn (2019) 52:855–64. doi:10.1007/s00382-018-4168-5

CrossRef Full Text | Google Scholar

6. Ercan A, Kavvas ML, Abbasov RK. Introduction. In: Long-range Dependence and Sea Level Forecasting. Springer International Publishing. Springer Briefs in Statistics (2013). p. 1–5. doi:10.1007/978-3-319-01505-7_1

CrossRef Full Text | Google Scholar

7. Bloomfield P. An Exponential Model for the Spectrum of a Scalar Time Series. Biometrika (1973) 60:217–26. doi:10.1093/biomet/60.2.217

CrossRef Full Text | Google Scholar

8. Granger CWJ. Long Memory Relationships and the Aggregation of Dynamic Models. J Econom (1980) 14:227–38. doi:10.1016/0304-4076(80)90092-5

CrossRef Full Text | Google Scholar

9. Robinson PM. Efficient Tests of Nonstationary Hypotheses. J Am Stat Assoc (1994) 89:1420–37. doi:10.1080/01621459.1994.10476881

CrossRef Full Text | Google Scholar

10. Gil-Alaña LA, Robinson PM. Testing of Unit Root and Other Nonstationary Hypotheses in Macroeconomic Time Series. J Econom (1997) 80(2):241–68. doi:10.1016/s0304-4076(97)00038-9

CrossRef Full Text | Google Scholar

11. Beran J. Statistical Methods for Data with Long-Range Dependence. Stat Sci (1992) 7(4):404–16. doi:10.1214/ss/1177011122

CrossRef Full Text | Google Scholar

12. Li M. Generalized Fractional Gaussian Noise and its Application to Traffic Modelling. Physica A (2021) 579:123613722. doi:10.1016/j.physa.2021.126138

CrossRef Full Text | Google Scholar

13. Li M, Li J-Y. Generalized Cauchy Model of Sea Level Fluctuations with Long-Range Dependence. Physica A: Stat Mech its Appl (2017) 484:309–35. doi:10.1016/j.physa.2017.04.130

CrossRef Full Text | Google Scholar

14. Li M. Modified Multifractional Gaussian Noise and its Application. Phys Scr (2021) 96(12):12500212. doi:10.1088/1402-4896/ac1cf6

CrossRef Full Text | Google Scholar

15. Cuestas JC, Gil-Alana LA. Testing for Long Memory in the Presence of Non-linear Deterministic Trends with Chebyshev Polynomials. Stud Nonlinear Dyn Econom (2016) 20:57–74. doi:10.1515/snde-2014-0005

CrossRef Full Text | Google Scholar

16. Cazenave A, Dieng H-B, Meyssignac B, von Schuckmann K, Decharme B, Berthier E. The Rate of Sea-Level Rise. Nat Clim Change (2014) 4:358–61. doi:10.1038/nclimate2159

CrossRef Full Text | Google Scholar

17. Gil-Alana LA. The Use of the bloomfield Model as an Approximation to ARMA Processes in the Context of Fractional Integration. Math Comp Model (2004) 39:429–36. doi:10.1016/s0895-7177(04)90515-8

CrossRef Full Text | Google Scholar