Electromagnetic Field Evolution in Relativistic Heavy Ion Collision and Its Effect on Flow of Particles

We compute the electromagnetic fields generated in relativistic heavy-ion collisions using the iEBE-VISHNU framework. We calculated the incremental drift velocity from the four possible sources of electric force (coulomb, Lorentz, Faraday, and plasma-based) on the particles created. The effect of this external electromagnetic field on the flow harmonics of particles was investigated, and we found out that the flow harmonics values get suppressed and rouse in a non-uniform fashion throughout the evolution. More precisely, a maximum of close to 3% increase in elliptic flow was observed. We also found mass as the more dominant factor than charges for the change in flow harmonics due to the created electromagnetic field. On top of that, the magnetic field perpendicular to the reaction plane is found to be sizable, while the different radial electric forces were found to cancel out each other. Finally, we found out that the inclusion of electromagnetic field affects the flow of particles by suppressing or raising it in a non-uniform fashion throughout the evolution.

1 Introduction

Understanding how matter behaved at the beginning of the universe by creating and studying the quark gluon plasma (QGP) is the primary purpose of the relativistic heavy-ion collisions experiment [1]. From the many possible signatures of the quark gluon plasma, the very convincing evidences which led to the announcement in 2005 (the QGP had been discovered at RHIC [2, 3]) came from the combination of three observations: the measurements of strong anisotropic collective flow, valence quark number scaling of the elliptic flow v₂, and jet quenching [2, 4]. Elliptic flow is a measure of how the energy, momentum, and number of created particles are not uniform with direction. The fireballs produced by the little bangs at RHIC and the LHC undergo explosive collective expansion, cool down rapidly, and finally fragment into thousands of free-streaming hadrons [5]. Theoretically, relativistic hydrodynamics has established itself as an indispensable component in modeling the collective dynamics of the QGP produced in relativistic heavy-ion collisions [6–10]. The first and principal observation that has been extensively used for extracting information about the QGP from heavy-ion collisions is the collective flow of various particles, especially the elliptic flow [11]. This implies that any elliptic flow-related studies have the chance to clear the road to understand QGP well, and the answer to what affects elliptic flow is crucial.

It is obvious that there are various parameters affecting flow harmonics, such as starting time, initial energy profile, initial flow velocity with the viscous stress tensor, equation of state (EOS), specific shear viscosity, kinetic decoupling temperature, and many more [13]. However, in this research, we picked the electromagnetic field whose effect is not widely considered by many of the hydro models. In order to address this problem, our model set-up followed three basic steps. The first step is simulating the dynamical evolution of the medium produced in Pb − Pb collision at ecm = 2.76 TeV using the iEBE-VISHNU framework. The second step is computing the drift velocity from the electromagnetic field by applying Maxwell’s equation using the information that we obtained from the hydrodynamic simulator. The third step is finding out the flow harmonics by injecting the drift velocity which is deduced in the framework. As a result, the first thing that comes is exploring the sources of electric fields, and this is discussed in the following section.

2 The Electromagnetic Field

The possible origins of the created electric force are four. The first is from the positively charged spectators that fly away from the collision zone. There is an electric force on the charged plasma produced there. This is a direct coulomb source field. The second is from spectator nucleons and the charge density deposited in the plasma. We have a non-vanishing outward-pointing component of the electric field already in the lab frame.

Thirdly, there is Lorentz force that can contribute to the directional pushes that the particles experience. This is because of the perpendicular magnetic field $\vec{B}$ created in the system. Finally, there is an induced electric current because of the change in magnetic field, Faraday. A more detailed explanation is found in [14]. These four sources of electric forces—the coulomb $({\vec{E}}_C)$, Lorentz: $({\vec{E}}_L)$, Faraday: $({\vec{E}}_F)$, and plasma-based source—are illustrated in Figure 1. In order for one to compute the incremental drift velocity ${\vec{v}}_{\text{drift}}$ caused by the electromagnetic forces, the electric $(\vec{E})$ and magnetic fields $(\vec{B})$ evolved should be known from the governing Maxwell’s equation.

FIGURE 1

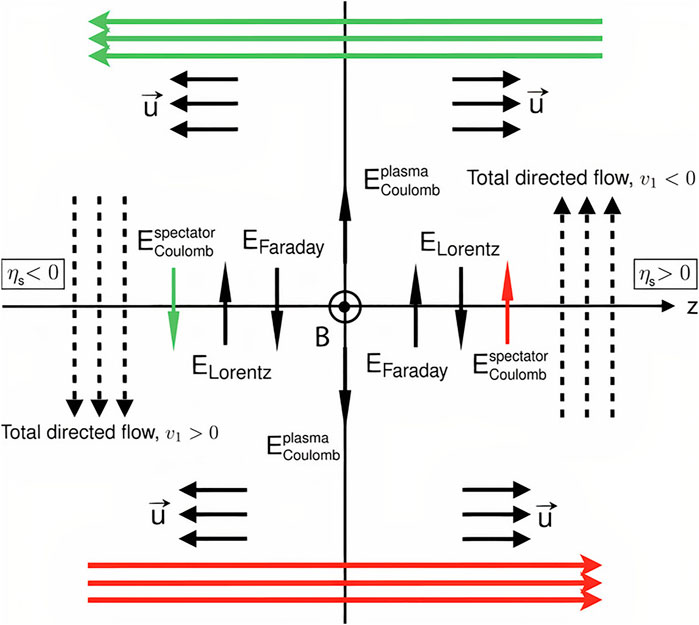
FIGURE 1. (Color online) Schematic illustration of how the electromagnetic fields in a heavy-ion collision result in a directed flow of electric charge [12].

3 Methods

As we all know, there is no unique theoretical tool to describe the whole heavy-ion collision process from the very beginning till the end, and this forces us to set up a model. We have used a similar model setup as in [15], except that we extend the drift velocity for more charge types and evaluate the effects for different particles. Following the setup, we simulate the dynamical evolution of the medium produced in Pb − Pb collision at ecm = 2.76 TeV using the iEBE-VISHNU framework and the electromagnetic field evolution which is computed alone. In general, according to the model setup, there are three basic jobs to be done. The first is simulating the dynamical evolution using the same Monte-Carlo–Glauber initialization. The second one is computing the additional velocity induced by the electromagnetic field alone and add this with the velocity from the dynamical system itself. In the last step, we injected this final velocity to the particle sampler in the framework.

3.1 The iEBE-VISHNU Framework

In this hybrid package, there are specific codes simulating each stage of the evolution and a script to link all the individual programs together. The four major components of the package are as follows:

1) superMC (the initial condition generator): This code generates fluctuating initial conditions according to Monte Carlo–Glauber and Monte Carlo–Kharzeev–Levin–Nardi (KLN) “gluon saturation” models. In this work, we have used the Monte Carlo–Glauber model initialization which assumes that the initial energy density in the transverse plane is proportional to the wounded nucleon density.

2) VISHNew (viscous hydrodynamic simulator): The Viscous Israel Stewart hydrodynamics is a (2 + 1)-d viscous hydrodynamic simulation for relativistic heavy-ion collisions. It solves the equation of motion for second-order viscous hydrodynamics Israel Stewart equations with a given EOS. VISHNew supports three versions (s95p-v0-PCE, s95p-v1, and s95p-v1-PCE) of the lattice-based equation of states by applying different implementations of partial chemical equilibrium in the hadronic phase. We have used s95p-v1-PCE for determining the pressure in the fluid by first solving for the local energy density and velocity of the fluid cell.

3) iSS (a particle sampler): iSS is an “event generator” which generates a complete collision event of emitted hadrons from Cooper–Frye freeze-out procedure similar to the events created in the experiment.

4) UrQMD (afterburner): This is a hadron cascade simulator ideally suited for the description of the dynamics of a system of hadrons both in and out of equilibrium.

4 Solving Maxwell’s Equation

The electromagnetic fields generated by a point-like charge moving in the +z-direction with velocity v is governed by the following wave equations [17]:

$\begin{array}{ccc}\hfill {\nabla }^2\vec{B}-{\partial }_t^2\vec{B}-\sigma {\partial }_t\vec{B}=-\vec{\nabla }\times {\vec{J}}_{\text{ext}}& \hfill & \hfill \end{array}$(4.1)

$\begin{array}{ccc}\hfill {\nabla }^2\vec{E}-{\sigma }_t^2\vec{E}-\sigma {\partial }_t\vec{E}=\frac{1}{ϵ}\vec{\nabla }{\rho }_{\text{ext}}+{\partial }_t{\vec{J}}_{\text{ext}}& \hfill & \hfill \end{array}$(4.2)

The electromagnetic fields are generated by both the spectators and the participant charged nucleons. The transverse distribution of the right-going (+) and left-going (−) charge density profiles ${\rho }_{\text{spectator}}^{\pm }({\vec{x}}_{\perp })$ and ${\rho }_{\text{participant}}^{\pm }({\vec{x}}_{\perp })$ is generated by averaging using the same Monte Carlo–Glauber model used to initialize the hydrodynamic calculation as in [18]. The external charge and current sources for the electromagnetic fields are functions of rapidity, which include the contraction due to relativity, and are given by:

${\rho }_{\text{ext}}\left({\vec{x}}_{\perp },{\eta }_s\right)={\rho }_{\text{ext}}^{+}\left({\vec{x}}_{\perp },{\eta }_s\right)+{\rho }_{\text{ext}}^{-}\left({\vec{x}}_{\perp },{\eta }_s\right)$(4.3)

${\vec{J}}_{\text{ext}}\left({\vec{x}}_{\perp },{\eta }_s\right)={\vec{J}}_{\text{ext}}^{+}\left({\vec{x}}_{\perp },{\eta }_s\right)+{\vec{J}}_{\text{ext}}^{-}\left({\vec{x}}_{\perp },{\eta }_s\right)$(4.4)

with

${\rho }_{\text{ext}}^{\pm }\left({\vec{x}}_{\perp },{\eta }_s\right)={\rho }_{\text{spec}}^{\pm }\left({\vec{x}}_{\perp }\right)\delta \left({\eta }_s\mp y_{\text{beam}}\right)+{\rho }_{\text{par}}^{\pm }\left({\vec{x}}_{\perp }\right)f^{\pm }\left({\eta }_s\right)$(4.5)

${\vec{J}}_{\text{ext}}^{\pm }\left({\vec{x}}_{\perp },{\eta }_s\right)={\vec{\beta }}^{\pm }\left({\eta }_s\right){\rho }_{\text{ext}}^{\pm }\left({\vec{x}}_{\perp },{\eta }_s\right)$(4.6)

$\text{with}{\vec{\beta }}^{\pm }=\left(\mathrm{0,0},\pm \tanh \left({\eta }_s\right)\right).$(4.7)

The Bjorken approximation is being made here: the space time rapidities η_s of the external charges are assumed equal to their rapidity. The spectators fly with the beam rapidity y_beam, and the participant nucleons lose some rapidity in the collisions. Solving the above-mentioned wave equations is easy since we have considered the electrical conductivity of the QGP to be constant, but making it time-varying, which in reality is because of its dependence on the temperature of the system, would make it very hard and is what we anticipate to work on next, so we took four different σ values—σ = 0.023 fm⁻¹, σ = 0.4 fm⁻¹, σ = 0.66 fm⁻¹, and σ = 1.1 fm⁻¹—to have a chance of analyzing its effect, and the numerical code for calculating the electromagnetic fields is the same as in [12] which is found at https://github.com/chunshen1987/Heavy-ion_EM_fields. For the evolution of the relativistic viscous hydro-dynamics, we chose the s95p-v1-PCE equation of state from [21]. After we knew the field evolution, we calculated the drift velocity.

4.1 The Equation of Motion

The drift velocity at each point on the freeze-out surface from the electromagnetic field evolution was calculated after solving the following force balance equation as in [12, 16]. This was done first by boosting to the local fluid rest frame at that point in space time, namely, the (primed) frame in which $\overrightarrow{u^{\prime }}=0$ at that point by a Lorentz transformation $\mathrm{\Lambda }(\vec{u})$. In the primed frame, all components of the electromagnetic field $\overrightarrow{E^{\prime }}$ and $\overrightarrow{B^{\prime }}$ are non-vanishing. We then solve the equation of motion for a charged fluid element with mass m in this frame using the Lorentz force law and requiring stationary currents:

$m\frac{d\vec{v}\prime }{dt}=q\vec{v}\prime \times \vec{B}\prime +q\vec{E}\prime -\mu m\vec{v}\prime =0$(4.8)

This gives us the local velocity due to electromagnetic effects. The last term in (4.8) describes the drag force on a fluid element with mass m on which some external (in this case, electromagnetic) force is being exerted with μ, the drag coefficient. Though the drag coefficient is still unclear, its value is precisely known only for heavy quarks in $\mathcal{N}=4$ SYM theory as stated in [16, 21].

We investigated the force balance equation from which we got the drift velocity ${\vec{v}}_{\text{drift}}^{\mathrm{l}\mathrm{r}\mathrm{f}}$ in every fluid cell along the freeze-out surface for different values of q on the equation. At the same time, we considered charges of ±1, ±2, ±1/3, and ±2/3. After having the drift velocity calculated, we added it with the usual hydrodynamic flow velocity; then after that, we fed it back to the framework in order to find out the particle velocity increment.

5 Results and Discussions

This work focused on including the electromagnetic field evolution calculation on the well-known iEBE-VISHNU code package for relativistic heavy-ion collisions [11]. We studied the percentage increase of the elliptic flow of identified particles due to the electromagnetic force evolution created in relativistic Pb + Pb collision with collision energy of $\sqrt{s}$ = 2.76 ATeV using a similar model setup as [12]. The results show that the electromagnetic force affects the flow harmonics with a different magnitude as explained below. In heavy-ion collision, the magnetic field is expected to be solenoidal fields from those flying charges. In line with this, during the beginning of the collision time, the dominant magnetic field is from the spectators, yet the participants of both incoming projectile ions contribute to the evolution of the electric and magnetic fields created. In the next two sections, we shall discuss the evolution of the electromagnetic field and its effects on observables.

5.1 The Electromagnetic Field Evolution

The first top image of Figure 2 is an illustration of the evolution of the three components of the electromagnetic field created in relativistic Pb + Pb collision with collision energy of $\sqrt{s}$ = 2.76 ATeV. The calculations were made at centrality ranging from 20 to 30% (impact parameters in the range 6.24 fm $<$ b $<$ 9.05 fm) and η_s ranging from −7.9 to 7.9. The three components of the electric fields in the local fluid rest frame at points on the freeze-out surface created are presented in Figure 2A. The created electric field seen above and below of the reaction axis is quite different, and this is expected due to the coulomb electric field created by the positively charged spectator particles at the beginning of the collision. This field created from the spectators is the reason for the current created in the plasma. The electric field in the z-direction is shown to be smaller than that of the two axes. This is presented as 2(c). The electric field evolution in the reaction plane increases as the system evolves. It is easy to notice that the transverse (x) and the longitudinal (y) components of the electric field are indistinguishable only at the very early stages of the evolution of the system, yet ${\vec{E}}_y$ and ${\vec{B}}_y$ have been found to be in the same order throughout the evolution. As can be seen in 2(a), the y-component of the electric field varies steeply, which dictates the fact that at the very beginning of the evolution a large amount of net charge stays temporally in the “almond”-shaped overlapping region as explained in [23].

FIGURE 2

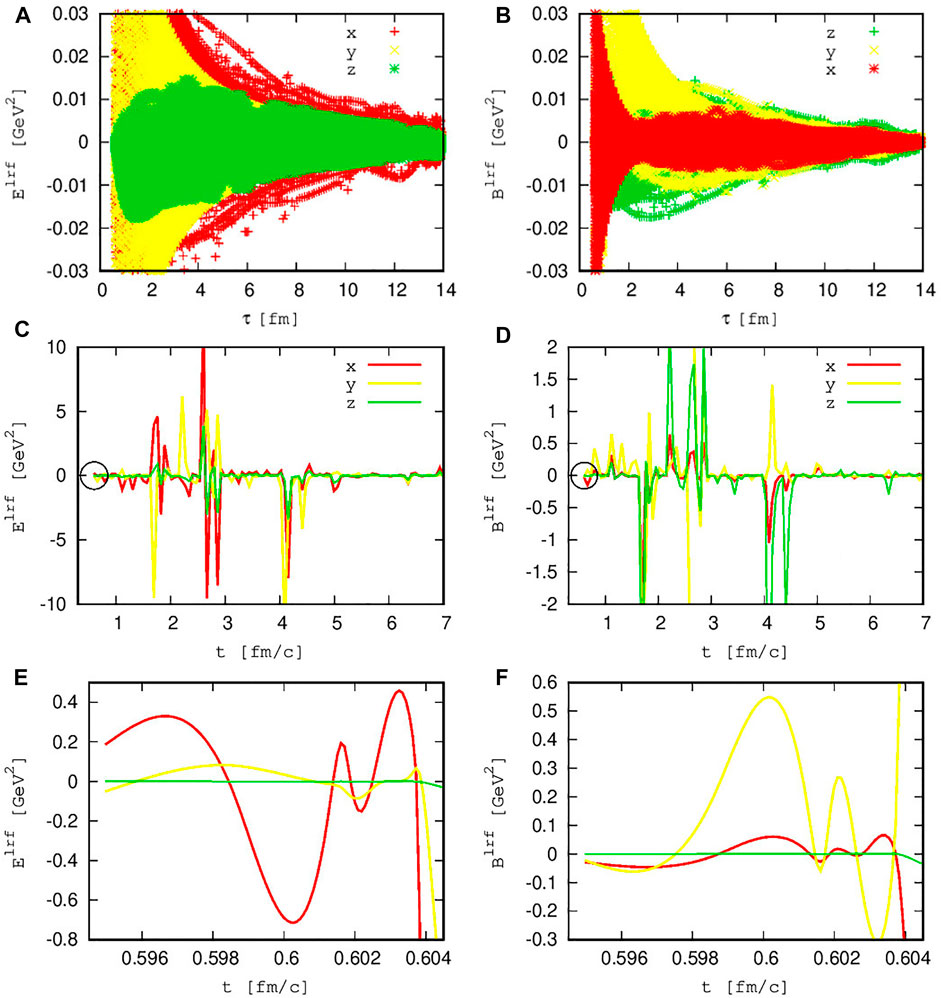
FIGURE 2. (Color online) (A) Evolution of the three components of the electric fields in the local fluid rest frame at points on the freeze-out surface created in relativistic Pb + Pb collision with collision energy of $\sqrt{s}$ = 2.76 ATeV. The calculations were made at centrality ranging from 20 to 30% (impact parameters in the range 6.24 fm $<$ b $<$ 9.05 fm) and η_s ranging from −7.9 to 7.9, where z is the reaction axis, while x and y represent the transverse and longitudinal directions, respectively. (B) Evolution of the three components of the magnetic fields in the local fluid rest frame at points on the freeze-out surface created in relativistic Pb + Pb collision with collision energy of $\sqrt{s}$ = 2.76 ATeV. The calculations were made at centrality ranging from 20 to 30% (impact parameters in the range 6.24 fm $<$ b $<$ 9.05 fm) and η_s ranging from −7.9 to 7.9. (C) The three components of the electric fields versus the local time in the fluid rest frame at a fixed space time rapidity of η_s = 0. (D) The three components of the magnetic fields versus the local time in the fluid rest frame at a fixed space time rapidity of η_s = 0. (E) The magnified version of the circled part from figure (b), showing the three components of the electric field evolution during the very early propagation time in the fluid rest frame at a fixed space time rapidity of η_s = 0. (F) The magnified version of the circled part from figure (d), showing the three components of the magnetic field evolution during the very early propagation time in the fluid rest frame at a fixed space time rapidity of η_s = 0.

We found out that By is not symmetrical and dominated Bx and Bz which can be easily seen in Figure 2B. The sudden pop-ups of By seen in Figure 2F dictates a similar conclusion. Moreover, field components Bx, Ex, and Ey, which are as large as By, are seen in a different time of the system evolution. This can be due to the fluctuations of the positions of charged particles. This inhomogeneous spatial structural distribution of the electromagnetic field has also been studied in [23], where they have utilized the HIJING model to investigate the generation and evolution of the electromagnetic fields in heavy-ion collisions.

By zooming out Figure 2A, we have noticed that the electric fields perpendicular to the reaction plane shows a larger gradient than the electric fields created parallel to this plane. As explained in [23], depending on how the electrical conductivity is, these outside electric fields can derive positively (negatively) charged particles to move outward (toward) the reaction plane and thus induce an electric quadruple moment which can lead to an elliptic flow imbalance between the same particles of different signs, and our result have confirmed this by presenting the elliptic flow variation as given in Figure 4.

To provide more complete information on the early evolution of E and B fields, we showed in 2(e) and (f) by magnifying the circled region from 2(c) and (d), respectively. As expected, E_x is shifted away from zero earlier, which dictates the dominance of the field from the positively charged spectator particles in the beginning of the hydrodynamics. The coulomb force between the particles in the plasma creates an electric field which is against the coulomb electric field. The decrease of the electric field in the reaction plane, in turn, drops the magnetic field—causing the Faraday electric field to evolve. Furthermore, as expected, Bz is smaller than Bx and By.

As explained in the previous sections, the total electric field comes from Coulomb field of the spectators plus the plasma, the Faraday, and finally the Lorentz field from the moving charges. The fluctuating electric field evolution at a fixed space time rapidity given in Figure 2C assures the non-uniformity of the created field, yet, at a later time when the spectators have already moved far away from the collision region, the contributions from the residue become important because they move much slower than the spectators. These residues can essentially slow down the decay of the transverse fields in the later time, as seen from Figure 2 and [23].

The electrical conductivity governs how fast the magnetic fields sourced initially. When it is large, the magnetic field in the plasma decays more slowly, and this gives a large magnetic field for drifting particles away. Practically, since the electrical conductivity is highly sensitive to temperature, a temperature-dependent function should have been used. However, as given by Figure 3, our analysis used four different values of conductivity to see the order of estimate of its effect on electromagnetic field evolution which potentially can be seen on the flow patterns. At the lower conductivity, it is easy to see that the evolution of the electric field is dominated by the x component of the electric field. This is to mean that the evolved electric field contributes to the side flow rather than the longitudinal flow. This occurred due to the coulomb electric field created by the positively charged spectator particles at the beginning of the collision. These spectators should have found enough time to evolve before the electromagnetic fields were built up by the wounded particles and the fluid itself.

FIGURE 3

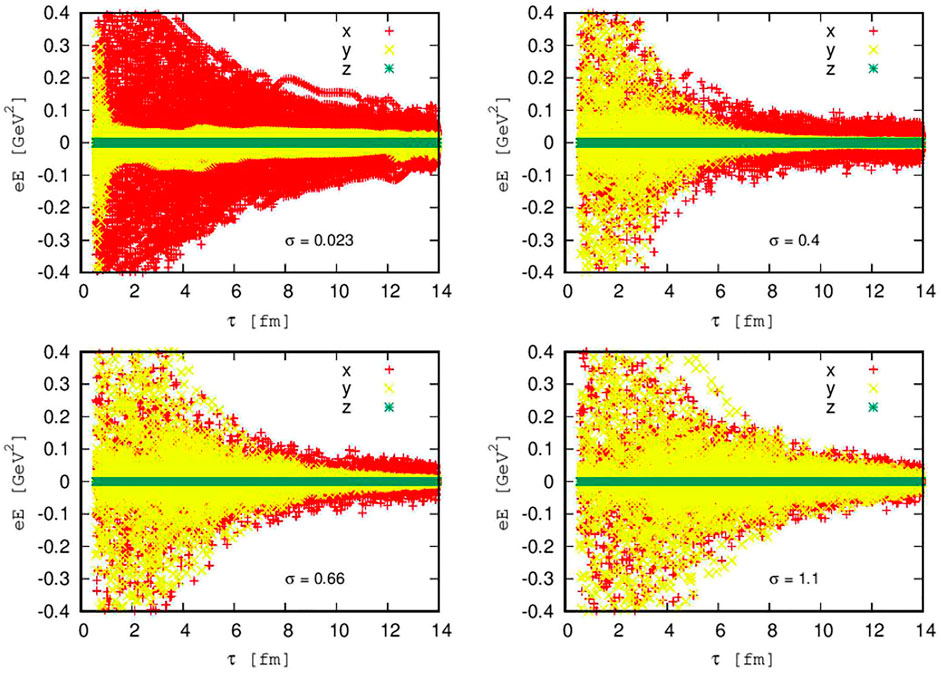
FIGURE 3. (Color online) The electric field evolution created in a system of relativistic heavy-ion collision after a Pb + Pb collision with 20–30% centrality at collision energy $\sqrt{s}$ = 2.76 ATeV on the choice of different electrical conductivity for the Maxwell equations.

As the conductivity increases, the electromagnetic field evolution in both transverse and longitudinal directions become similar. The two components of electric fields are indistinguishable at higher conductivity because the conductivity suppresses the fields.

5.2 The Electromagnetic Field on Flow Harmonics

In Tables 1–3, the momentum-dependent elliptic flow coefficients for proton-P, Pion Plus-π⁺, and Kaon Plus-K⁺ are shown. The elliptic flow for the ideal case is compared to the case with the electromagnetic field. The electromagnetic field acts on the evolution of flow that leads to the reduction of elliptic flow of these positively charged particles dominantly. The elliptic flow of protons was suppressed up to 2.37% of its initial value. At a lower momentum, they also get a percentage increase of −1.5% from its initial value. It is different for pions, and at a lower momentum, the created electromagnetic field raised their elliptic flow up to 2.7%. The effect of the electromagnetic evolution is seen to be the same for the considered three particles at higher momentum. As far as the system evolution is concerned, the flow harmonics values get suppressed or rouse in a non-uniform fashion throughout the evolution. In order to explain the effects caused by the electromagnetic evolutions better, every possible contributor like drag force, electrical conductivity, and gluon charge density shall be explained well. The electromagnetic field suppressing the elliptic flow at higher momentum is also seen in [11], with the change on the increase percentage being closer to 5%.

TABLE 1

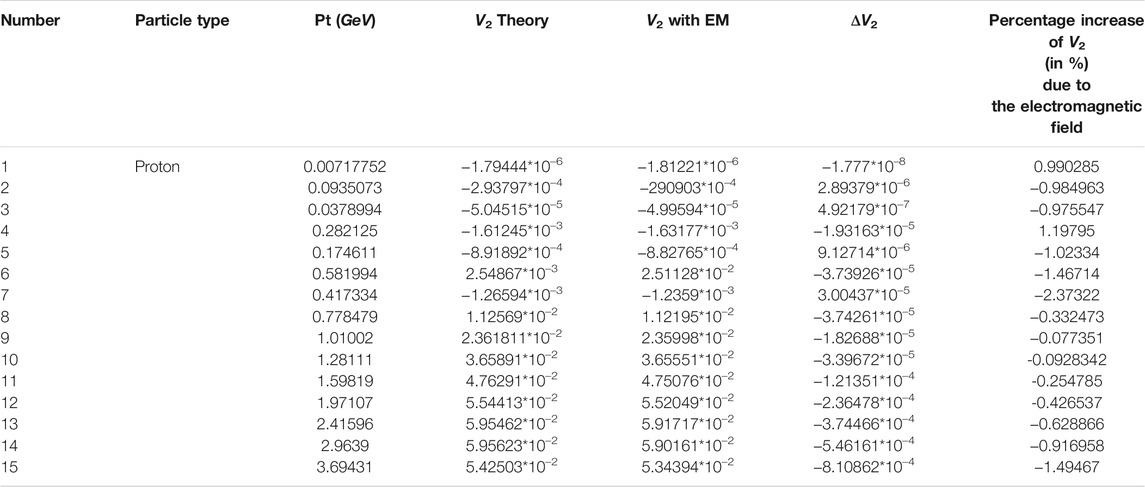
TABLE 1. The percentage increase of the elliptic flow of proton due to the electromagnetic force evolution created in relativistic Pb + Pb collision with collision energy of $\sqrt{s}$ = 2.76 A TeV at centrality ranging from 20 to 30% (impact parameters in the range 6.24 fm $<$ b $<$ 9.05 fm). The change in elliptic flow (ΔV₂) is the difference between V₂ theory and V₂ with EM.

TABLE 2

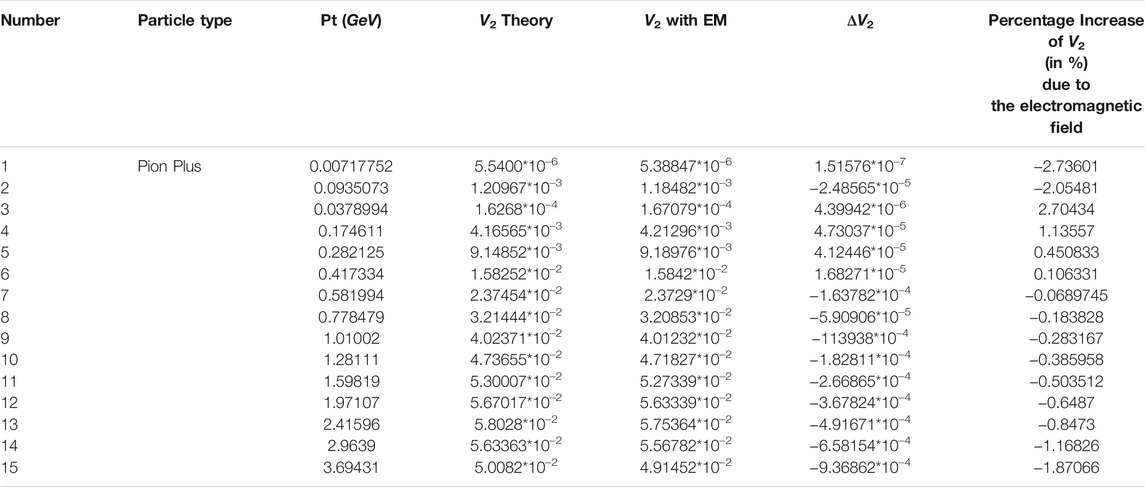
TABLE 2. The percentage increase of elliptic flow of Pion-Plus due to the electromagnetic force evolution created in relativistic Pb + Pb collision with collision energy of $\sqrt{s}$ = 2.76 A TeV at centrality ranging from 20 to 30% (impact parameters in the range 6.24 fm $<$ b $<$ 9.05 fm). The change in elliptic flow (ΔV₂) is the difference between V₂ theory and V₂ with EM.

TABLE 3

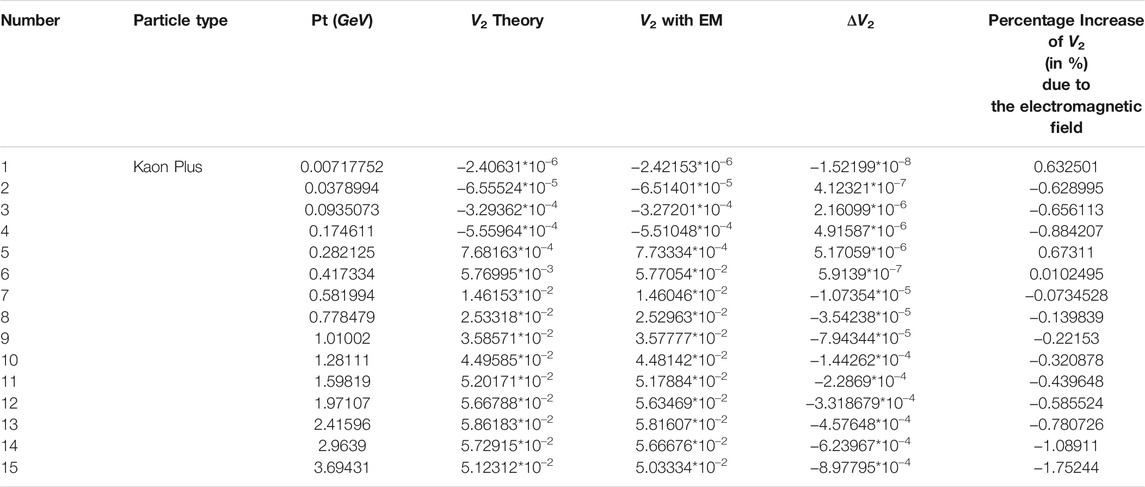
TABLE 3. The percentage increase of elliptic flow of Kaon-Plus due to the electromagnetic force evolution created in relativistic Pb + Pb collision with collision energy of $\sqrt{s}$ = 2.76 ATeV at centrality ranging from 20 to 30% (impact parameters in the range 6.24 fm $<$ b $<$ 9.05 fm). The change in elliptic flow (ΔV₂) is the difference between V₂ Theory and V₂ with EM.

As stated in Figure 4B, the electromagnetic field effect on Δv₂ and Δv₃ is small in magnitude for the positively charged and lighter particles. The change on the odd flow harmonics and the even ones is not quiet equal. The even flow harmonics get suppressed or lower in higher magnitude than the odd ones. The directed flow is influenced insignificantly. This is because the Faraday and Coulomb fields almost canceled the electric Lorentz field created in the fluid system. Nevertheless, there is still a very small contribution to the directed flow, and this is from the collision axis. Meanwhile, as presented in Figures 4C,D, the triangular flow change is in the order of 10^–4 for neutron, xsi, antiproton, lambda, and anti-kaon, yet from Figure 4A, it is easily depicted as the elliptic flow of neutron, xsi, antiproton, lambda, and anti-kaon is significantly influenced by the created electromagnetic evolution. This leads us to notice how the multi-directional side push of the created heavier particles is significantly influenced by the fields of electromagnetic evolution. The created particles are subject to have interactions with the electromagnetic field caused by the spectators, other created hadrons, and from the fluid itself. Even though the QCD dynamics of hadronization is not fully understood yet, our result of heavier particle elliptic flow being affected with larger magnitude than the lighter ones has to do with the time that they have spent passing through the field. Those light particles are expected to be created sooner and thus pass through the reaction region fast before all the electromagnetic field developed. The flow harmonics of protons change due to the developed electromagnetic field with comparable magnitude to that of the flow harmonics change of kaons and pions because of the spectators. Since the spectators are protons, the created proton flow harmonics get suppressed from the repulsion force. As a result, Lambda and Xsi get larger odd flow harmonics changes than proton as found in [22].

FIGURE 4

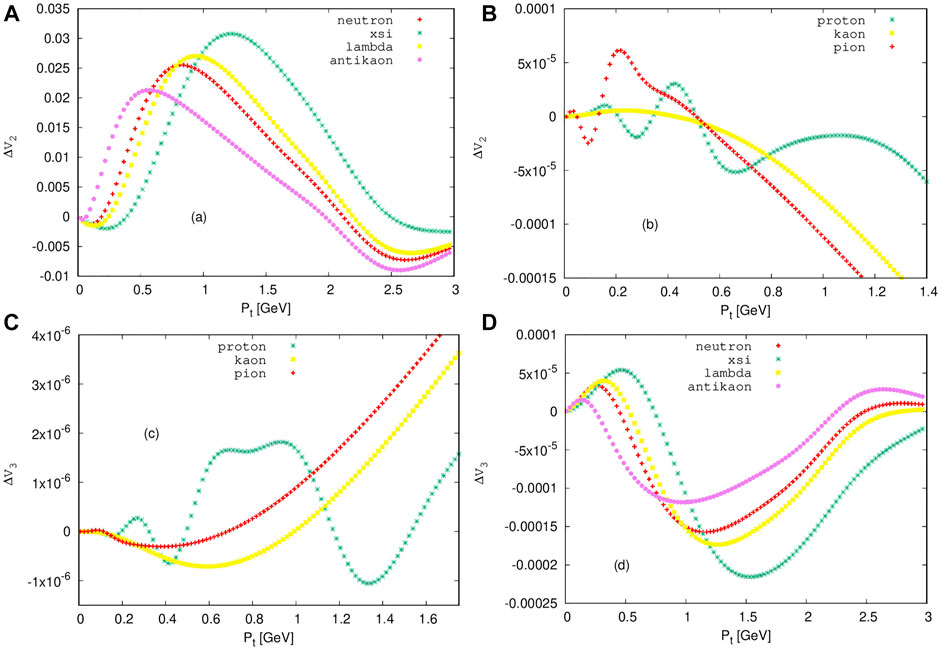
FIGURE 4. (Color online) (A) : Illustrates the effect of electromagnetic force on the change in elliptic flow ΔV2 for neutron, xsi, antiproton, lambda and anti kaon. (B) : Illustrate the effect of electromagnetic force on the change in elliptic flow ΔV2 for proton, kaon and pion. (C) : Illustrate the effect of electromagnetic force on the change in triangular flow ΔV3 for proton, kaon and pion, and (D) : Illustrate the effect of electromagnetic force on the change in triangular flow ΔV3 for neutron, xsi, antiproton, lambda and anti kaon.

A handful of other groups have studied the effect of electromagnetic field evolution on the flow of particles in relativistic heavy-ion collision. They all have used different approaches, making some crude assumptions to tackle the problem as we just did. All the studies [12, 18–20, 24–30] came up to a similar understanding, as the electromagnetic evolution has an effect on the bending of particle flow. Moreover, the result from [18] on flow harmonics changes of heavier particles agrees with ours.

6 Summary and Conclusion

We have utilized the iEBE-VISHNU framework to investigate the generation and evolution of the electromagnetic fields in relativistic heavy-ion collisions. The evolution of the electromagnetic field created after a Pb + Pb relativistic collision with 20–30 centrality and collision energy of $\sqrt{s}$ = 2.76 ATeV was explored. The spatial structure of the electromagnetic field was studied, and a very inhomogeneous distribution is found. We have also investigated the time evolution of the fields at the early stage of the evolutions. We found that the residues give considerable contribution to the fields during the early-stage evolutions. A study of the effect of this external electromagnetic field on the elliptic flow of particles was investigated. Both the ideal and the electromagnetic field cases were initialized equally, and the transverse profile was taken from a Monte Carlo–Glauber model initialization calculation.

As a result, a maximum of ±2.7% increase in elliptic flow is observed. The elliptic flow of protons was raised up to 2.37% from the initial value. At a lower momentum, the elliptic flow of proton gets suppressed to 1.5% of its initial value. For pions, the flow was raised by 2.7%. As far as the system evolution is concerned, the flow harmonics values get suppressed or rouse in a non-uniform fashion throughout the evolution. In order to explain the effects caused by the electromagnetic evolution better, every possible contributor to the change in elliptic flow should be included in functional form.

Furthermore, we found out that heavier particles like lambda and xsi get the higher flow harmonics increase. The directed flow is not that affected as the elliptic flow because the different radial electric forces cancel out each other. In here mass is the dominant factor than charges, which is observed as particles, and their anti-particles get washed aside by the field in a similar fashion. The lighter particles get slight flow harmonics increase, and they had to flow off the region before getting pushed by the fields.

To conclude, the present study shows that the inclusion of electromagnetic field affects the flow of particles by suppressing or raising it in a non-uniform fashion throughout the evolution. Lastly, further study is needed to establish a better understanding on the electromagnetic field evolution and its effects on the created system by softening many of the crude assumptions that we made and keeping the functionality of the parameters.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank Chun Shen for the brief discussion on the codes that we have used for the framework. Moreover, we would like to forward our gratitude to Scott Pratt of Michigan State University for the valuable discussions we had on the work. Finally, we want to thank Nigus Michael for proofreading our manuscript.

References

1. Nasim M, Shi S, Chatterjee S, Singha S, Roy V. Collectivity in High Energy Heavy-Ion Collisions. Adv High Energ Phys (2017) 2017:1–2. doi:10.1155/2017/1485353

CrossRef Full Text | Google Scholar

2.The DOE/NSF Nuclear Science Advisory Committee. The Frontiers of Nuclear Science, a Long Range Plan. Washington, DC: nucl-ex. (2008). p. 3137. arXiv:0809.3137, 0809.

Google Scholar

3.RHIC. Scientists Serve up Perfect Liquid. New York: Brookhaven National Laboratory (2013). p. 3137. bnl.gov/newsroom/news.php?a= 1103030809.

Google Scholar

4. Jacobs P. Phases of QCD: Summary of the Rutgers Long Range Plan Town Meeting. New Jersey: Nucl-Ex (2007). arXiv:0705.1930.

Google Scholar

5. Heinz U. Towards the Little Bang Standard Model. J Phys Conf Ser (2013) 455:012044. arXiv:1304.3634. doi:10.1088/1742-6596/455/1/012044

CrossRef Full Text | Google Scholar

6. Song H, Heinz U. Suppression of Elliptic Flow in a Minimally Viscous Quark-Gluon Plasma. Phys Lett B (2008) 658:279–83. arxiv.org/pdf/0709.0742. doi:10.1016/j.physletb.2007.11.019

CrossRef Full Text | Google Scholar

7. Song H, Bass SA, Heinz U, Hirano T, Shen C. 200AGeVAu+AuCollisions Serve a Nearly Perfect Quark-Gluon Liquid. Phys Rev Lett (2011) 106:192301. arxiv.org/pdf/1011.2783, 10.1103/physrevlett.106.192301. doi:10.1103/physrevlett.106.192301

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Luzum M. Elliptic Flow at Energies Available at the CERN Large Hadron Collider: Comparing Heavy-Ion Data to Viscous Hydrodynamic Predictions. Phys.Rev. (2011) C83:044911. arxiv.org/pdf/1011.5173, 10.1103/PhysRevC.83.044911. doi:10.1103/physrevc.83.044911

CrossRef Full Text | Google Scholar

9. Lee TD, Wick GC. Vacuum Stability and Vacuum Excitation in a Spin-0 Field Theory. Phys Rev D (1974) 9:2291–316. doi:10.1103/PhysRevD.9.2291

CrossRef Full Text | Google Scholar

10. Collins JC, Perry MJ. Superdense Matter: Neutrons or Asymptotically Free Quarks. Phys Rev Lett (1974) 34:1353–6. doi:10.1103/PhysRevLett.34.1353

CrossRef Full Text | Google Scholar

11. Bohao F, Wang Z. Effect of an Electromagnetic Field on the Spectra and Elliptic Flow of Particles. Phys.Rev C95 (2017) 5. arxiv.org/abs/0908.3656v1.

Google Scholar

12. Gursoy U, Kharzeev D, Marcus E, Rajagopal K, Shen C. Charge-dependent Flow Induced by Magnetic and Electric fields in Heavy Ion Collisions. Phys Rev (2018) D74:05288. arxiv.org/abs/1806.05288, 10.1103/PhysRevC.98.055288. doi:10.1103/physrevc.98.055201

CrossRef Full Text | Google Scholar

13. Shen C. The Standard Model for Relativistic Heavy-Ion Collisions and Electromagnetic Tomography. Columbus, Ohio: Doctoral dissertation The Ohio State University (2014).

Google Scholar

14. Shen C, Qiu Z, Song H, Bernhard J, Bass S, Heinz U. The iEBE-VISHNU Code Package for Relativistic Heavy-Ion Collisions. Columbus, Ohio: eprint (2014). arxiv.org/abs/1409.8164.

Google Scholar

15. Kharzeev D. Can Gluons Trace Baryon Number. Phys Lett (1996) B378. arxiv.org/abs/nucl-th/9602027, arXiv:nucl-th/9602027.

CrossRef Full Text | Google Scholar

16. Gursoy U, Kharzeev D, Rajagopal K. Magnetohydro-dynamics, Charged Currents and Directed Flow in Heavy Ion Collisions. Phys Rev (2014) C89(5). arxiv.org/abs/1401.3805, 10.1103/PhysRevC.89.054905. doi:10.1103/physrevc.89.054905

CrossRef Full Text | Google Scholar

17. Kharzeev DE, McLerran LD, Warringa HJ. The Effects of Topological Charge Change in Heavy Ion Collisions: "Event by Event and Violation". Nucl Phys A (2008) 803:227–53. arxiv.org/abs/0711.0950. doi:10.1016/j.nuclphysa.2008.02.298

CrossRef Full Text | Google Scholar

18. Zhong Y, Yang C-B, Cai X, Feng S-Q. A Systematic Study of Magnetic Field in Relativistic Heavy-Ion Collisions in the RHIC and LHC Energy Regions. Adv High Energ Phys (2014) 2014:1–10. Hindawi Limited. doi:10.1155/2014/193039

CrossRef Full Text | Google Scholar

19. Voronyuk V, Toneev V, Cassing W, Bratkovskaya E, Konchakovski V, Voloshin S. Electromagnetic Field Evolution in Relativistic Heavy-Ion Collisions. Phys Rev.C (2012) 62:361. arXiv:1202.3233v1. doi:10.1103/physrevc.83.054911

CrossRef Full Text | Google Scholar

20. Marcus E. Magnetohydrodynamics at Heavy Ion Collision. Maryland: Bachelor Thesis Utrecht University (2015). doi:10.1103/physrevc.83.054911

CrossRef Full Text | Google Scholar

21. Huovinen P, Petreczky P. QCD Equation of State and Hadron Resonance Gas. Nucl Phys A (2010) 837:262541–53. arXiv:0912. doi:10.1016/j.nuclphysa.2010.02.015

CrossRef Full Text | Google Scholar

22. Das SK, Plumari S, Chatterjee S, Alam J, Scardina F, Greco V. Directed Flow of Charm Quarks as a Witness of the Initial Strong Magnetic Field in Ultra-relativistic Heavy Ion Collisions. Phys Lett B (2017) 768260:260–4. arXiv:1608.02231. doi:10.1016/j.physletb.2017.02.046

CrossRef Full Text | Google Scholar

23. Deng W-T, Huang X-G. Event-by-event Generation of Electromagnetic fields in Heavy-Ion Collisions. Phys Rev C (2012) 85:044907. arxiv.org/pdf/1201.5108. doi:10.1103/physrevc.85.044907

CrossRef Full Text | Google Scholar

24. Tuchin K. Time and Space Dependence of the Electromagnetic Field in Relativistic Heavy-Ion Collisions. Phys Rev C (2013) 88:024911. arXiv:1305.5806. doi:10.1103/PhysRevC.88.024911

CrossRef Full Text | Google Scholar

25. Lombardo I, Campajola L, Dell'Aquila D, Commara ML, Ordine A, Rosato E, et al. Study of Nuclear Structure of13C and20Ne by Low Energy Nuclear Reactions. J Phys Conf Ser (2014) 569:012068. doi:10.1088/1742-6596/569/1/012068

CrossRef Full Text | Google Scholar

26. Stewart E, Tuchin K. Magnetic Field in Expanding Quark-Gluon Plasma. Phys Rev C (2018) 97:044906. arXiv:1710.08793. doi:10.1103/PhysRevC.97.044906

CrossRef Full Text | Google Scholar

27. Siddique I, Sheng X-L, Wang Q. Space-average Electromagnetic fields and Electromagnetic Anomaly Weighted by Energy Density in Heavy-Ion Collisions. Phys Rev C (2021) 104:034907. arXiv:arXiv:2106.00478. doi:10.1103/PhysRevC.104.034907

CrossRef Full Text | Google Scholar

28. Tuchin K. Electromagnetic Field and the Chiral Magnetic Effect in the Quark-Gluon Plasma. Phys Rev C (2015) 91:064902. arXiv:1411.1363. doi:10.1103/PhysRevC.91.064902

CrossRef Full Text | Google Scholar

29. Dubla A, Gürsoy U, Snellings R. Charge-dependent Flow as Evidence of strong Electromagnetic fields in Heavy-Ion Collisions. Mod Phys Lett A (2020) 35:2050324–39. doi:10.1142/S0217732320503241

CrossRef Full Text | Google Scholar

30. Pakou A, Pierroutsakou D, Mazzocco M, Acosta L, Aslanoglou X, Boiano A, et al. Total Reaction Cross Sections for 8Li + 90Zr at Near-Barrier Energies. Eur Phys J A (2015) 51(55):9. doi:10.1140/epja/i2015-15055-6

CrossRef Full Text | Google Scholar