Research on Calibration Method of Infrared Temperature Measurement System Near Room Temperature Field

The calibration accuracy of the infrared temperature measurement system near room temperature field is easily affected by the calibration environment. In this paper, an equivalent blackbody calibration method is proposed for this problem. In this method, the target radiation and ambient radiation superimposed in calibration data are separated by two calibration functions at different ambient temperatures, and an equivalent blackbody calibration function is constructed. The experimental verification of the proposed method is carried out, and the results show that the proposed method has a better calibration effect for the surface blackbody than the commonly used environmental compensation methods. This method can effectively improve the calibration accuracy of infrared temperature measurement system near room temperature field, and further improve the infrared temperature measurement theory.

1 Introduction

The spectral detection technology has the advantages of fast response, high sensitivity, and high resistance to electromagnetic noise [1], including TDLAS [2], CARS [3], QEPAS [4], QEPTS [5], THz [6], photoacoustic spectrum [7], infrared temperature measurement technology [8] and et al. Among them, infrared temperature measurement technology is widely used for non-contact temperature measurement in military, industrial, agricultural, biological, and other fields. Calibration is very important for infrared temperature measurement technology. The infrared radiation detection equipment needs to be calibrated regularly to ensure the measurement accuracy, and many scholars are constantly studying the calibration methods [9, 10]. Fluke has set up a new IR calibration laboratory with radiometric traceability for this reason [11]. For low-temperature infrared calibration, Kimball BA began the research of low-temperature infrared calibration in 1984 [13]. In 2004, NIST held calibration and intercomparison of infrared radiometers [12]. The ambient impact of some blackbodies used in the laboratory had been calibrated by the National Institute of Standards and Technology (NIST) Thermal-infrared Transfer Radiometer (TXR), and the blackbodies calibration results can be used for subsequent ambient compensation. In 2011, Barry T et al presents a self-calibration technique for the removal of measurement errors caused by thermal gradients in thermopile-based infrared thermometry [14, 15]. In 2012, Dai Y et al developed a surface blackbody for low-temperature infrared calibration, and calculated the ambient compensation value required when using this blackbody for calibration [16]. In 2020, Zhang Z Q et al explained the compensation method that takes into account the calibration error introduced by the blackbody emissivity and ambient temperature, and illustrated the difference of calibration curves before and after compensation with examples [17].

The calibration experiment of the infrared temperature measurement system is usually carried out in laboratory with a surface blackbody [18]. If the target temperature is close to the ambient temperature, or even lower than the ambient temperature, the calibration accuracy is easily affected by the ambient. For this problem, the method given in the reference [12, 17] can generally be used for compensation, but sometimes the effect is not good because the given emissivity is inaccurate or the compensation model does not match the experiment.

In this paper, this problem is studied. The ambient influence is removed by comparing two calibration functions under different ambient temperatures. And the equivalent blackbody calibration function is obtained.

2 Principle of Infrared Calibration and Temperature Measurement

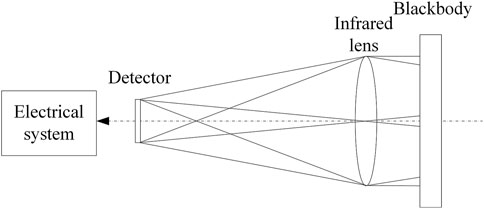
It is necessary to calibrate the infrared temperature measurement system to establish the quantitative relationship between the input radiation intensity and the output signal of the infrared detector before use. In this paper, a refrigerating photoelectric detector is used in the infrared temperature measurement system [19], and the output signal of the detector has a linear relationship with the irradiance from the infrared source [20]. When the target is a blackbody, the calibration function is shown as Eq. 1.

$V=kf\left(T\right)+b(1)$

Where V is the output voltage of detector, k system response factor, including parameters such as lens transmittance, amplifier gain, lens area, field of view area, distance between target and instrument, b system bias, f(T) is calculated according to Eq. 2 [21].

$L={\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{R}_{\lambda }{L}_{\lambda B}\left(T\right)}d\lambda ={\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{R}_{\lambda }\cdot \frac{c_1}{\pi {\lambda }^5}\cdot \frac{1}{e^{c_2/\lambda T}-1}}d\lambda =f\left(T\right)(2)$

Where λ₂ and λ₁ are the upper and lower limits of the spectral response of the detector, R_λ the wavelength function of thermometer [22], L_λB(T) the blackbody radiation exitance at T temperature, and c₁ and c₂ the first and second Plank’s radiation constants.

The calibration principle schematic diagram of the infrared temperature measurement system is shown in Figure 1 [23]. The blackbody radiation emission needs to cover the entire field of view of the calibrated infrared temperature measurement system. By changing the temperature of the blackbody, the response of the detector at the corresponding temperature can be obtained. The calibration coefficients of Eq. 1 are determined through least square fitting the band radiation response f(T) versus the detector response at different temperatures [24].

FIGURE 1

FIGURE 1. Schematic diagram of calibration principle of infrared temperature measurement system.

When calibration results are used to measure the temperature of a grey body target (with constant emissivity ε), focusing the thermometer on it, the target radiation exitance L is calculated from the output voltage with Eq. 1. And after compensating for environmental interference, the target temperature T is calculated inverting Eq. 2. So the following Eq. 3 is obtained [25]:

$T=f^{-1}\left[\frac{\frac{V-b}{k}-\left(1-\epsilon \right)f\left(T_{\text{amb}}\right)}{\epsilon }\right](3)$

Where T_amb is the ambient temperature (which behaves as a blackbody being a cavity).

3 Calibration Method Principle of Infrared Temperature Measurement System Near Room Temperature Field

For the infrared temperature measurement system which is easily affected by the environment near room temperature field, the calibration coefficients are different due to different calibration environments. Set the standard calibration function after removing ambient influence as Eq. 4.

$V=kf\left(T_{\text{obj}}\right)+b(4)$

The calibration function Eq. 5 can be obtained by calibrating with an ambient temperature of T_amb1.

$V_1=k_{1}f\left(T_{\text{obj}}\right)+b_1(5)$

The calibration function Eq. 6 can be obtained by calibrating with an ambient temperature of T_amb2.

$V_2=k_{2}f\left(T_{\text{obj}}\right)+b_2(6)$

Eq. 7 can be obtained by constructing Eq. 4 as the addition of target radiation and ambient radiation.

$V=k\left[\epsilon f\left(T_{\text{obj}}\right)+\left(1-\epsilon \right)f\left(T_{\text{amb}}\right)\right]+b(7)$

When the target temperature is the same as the ambient temperature, Eq. 7 is the same as Eq. 4. Eq. 8 can be obtained by further decomposing Eq. 7.

$V=k\epsilon f\left(T_{\text{obj}}\right)+k\left(1-\epsilon \right)f\left(T_{\text{amb}}\right)+b(8)$

It can be seen from Eq. 8 that the effects of ambient temperatures T_amb1 and T_amb2 are included in coefficients b₁ and b₂ during laboratory calibration. Eq. 9 can be obtained by combining Eq. 8 with Eq. 5.

$\{\begin{array}{l}k\epsilon =k_1\\ k\left(1-\epsilon \right)f\left(T_{\text{amb}1}\right)+b=b_1\end{array}(9)$

Eq. 10 can be obtained by combining Eq. 8 with Eq. 6.

$\{\begin{array}{l}k\epsilon =k_2\\ k\left(1-\epsilon \right)f\left(T_{\text{amb}2}\right)+b=b_2\end{array}(10)$

From Eq. 9 and Eq. 10, we can see that in theory k₁=k₂=kε. In the actual experiment, only k₁≈k₂ can be achieved, and kε≈(k₁+k₂)/2 can be used in the calculation. New calibration coefficients k and b can be obtained by substituting kε≈(k₁+k₂)/2 back to Eq. 9 and Eq. 10.

$\{\begin{array}{l}k=\frac{\frac{k_1+k_2}{2}\left[f\left(T_{\text{amb}2}\right)-f\left(T_{\text{amb}1}\right)\right]+\left(b_2-b_1\right)}{f\left(T_{\text{amb}2}\right)-f\left(T_{\text{amb}1}\right)}\\ b=b_1-kf\left(T_{\text{amb}1}\right)+\frac{k_1+k_2}{2}f\left(T_{\text{amb}1}\right)=b_2-kf\left(T_{\text{amb}2}\right)+\frac{k_1+k_2}{2}f\left(T_{\text{amb}2}\right)\end{array}(11)$

In this way, the equivalent blackbody calibration function with the target temperature equivalent blackbody radiation as a variable can be obtained.

4 Calibration Method Verification Experiment of Infrared Temperature Measurement System Near Room Temperature Field

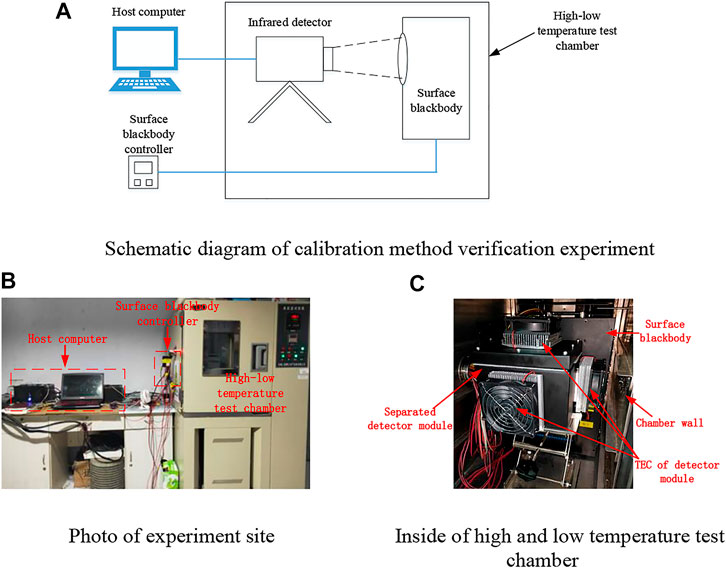
In order to verify the calibration method proposed in this paper, calibration experiments were carried out in two environments with different temperatures. The calibration functions are used to measure the target which is equal to the ambient temperature (the ambient temperature has little influence according to Eq. 7). The validity of the proposed calibration method can be verified by observing the measurement deviation. A temperature-controllable calibration environment is formed with a high and low-temperature test chamber.

4.1 Apparatus for Verification Experiment

In order to complete the verification experiment of the proposed calibration method, the infrared temperature measuring system and the small surface blackbody were disassembled to reduce their volume. They can be conveniently placed in the high and low temperature test chamber. The main experimental devices of the verification experiment include: the disassembled infrared temperature measurement system, the high and low temperature test chamber, and the disassembled small surface blackbody.

Since the minimum working temperature of the surface blackbody used in the experiment is −10°C, and the maximum working temperature of the disassembled infrared detector module is 40°C, the verification experiment is carried out in the range of −10°C–40°C. The schematic diagram and photos of calibration method verification experiment are shown in Figure 2.

FIGURE 2

FIGURE 2. Schematic diagram and photos of calibration method verification experiment.

4.2 Results of Verification Experiment

1) Calibration Function Fitting

The selected calibration ambient temperature is expected to be close to the conventional laboratory ambient temperature. The high and low temperature test chamber used in this experiment has better stability during refrigeration, so two temperatures lower than room temperature, 10°C and 15°C, are selected. After setting up the experimental environment as shown in Figure 2, set the temperature of the high and low temperature test chamber to 10°C. The calibration experiment was carried out at this ambient temperature. The blackbody temperature varied from −10°C to 40°C, and the change step was 10°C. The detector output at the corresponding temperature were recorded. Then adjust the temperature of the high and low temperature test chamber to 15°C, and perform the calibration experiment again. The summary of calibration experimental data is shown in Table 1.

TABLE 1

TABLE 1. Calibration experimental data of infrared temperature measurement system.

According to the calibration data, the calibration function at 10°C is obtained as shown in Eq. 12. The fitting correlation coefficient is 0.9981, and the linearity is good.

$V_1=\text{0}\text{.}0403f\left(T_{\text{obj}}\right)-1\text{.}5996(12)$

According to the calibration data, the calibration function at 15°C is obtained as shown in Eq. 13. The fitting correlation coefficient is 0.9982, and the linearity is good.

$V_2=\text{0}\text{.}0402f\left(T_{\text{obj}}\right)-1\text{.}5811(13)$

According to the method described in Refs. [12, 17], the calibration function obtained at a fixed ambient temperature is compensated, and the calibration function after compensation is shown as Eq. 14.

$V=0.0424f\left(T_{\text{obj}}\right)-1\text{.}6216(14)$

According to Eq. 11, Eq. 12, and Eq. 13, the coefficients of the equivalent blackbody calibration function are calculated, and the calibration function is shown as Eq. 15.

$V=\text{0}\text{.}0510f\left(T_{\text{obj}}\right)-1\text{.}7868(15)$

2) Measurement Verification

An experimental scene without ambient influence is formed by adjusting the set temperature of the high and low temperature experiment chamber and the surface blackbody simultaneously, and making the two temperatures equal. The temperature increased from −10°C to 40°C. Temperature inversion on the data collected in the experiment is carried out with Eq. 13, Eq. 14, and Eq. 15. Summarize the deviation results into a table, as shown in Table 2.

TABLE 2

TABLE 2. Verification experiment when environmental temperature equal to target temperature.

The effectiveness of the calibration method proposed in this paper can be seen from the experimental results in Table 2. The equivalent blackbody calibration function Eq. 15 has the best data inversion result, with the maximum error of ±1.8°C and the average absolute value error of 0.9°C. The maximum error of calibration function obtained by direct calibrating is ±6.6°C, and the average absolute error is 4.0°C. The maximum error of the calibration function after conventional ambient compensation is ±5.1°C, and the average absolute value error is 3.0°C.

According Table 2, the measured result is lower than the actual temperature with the conventional calibration function when the target temperature is lower than the calibration ambient temperature. This is because when calibration is carried out in this case, the total radiation received by the infrared temperature measuring equipment will be higher than the blackbody radiation at the target temperature. When the target temperature is higher than the ambient temperature, on the contrary, the experimental measurement result is higher than the actual temperature. Because the error caused by the ambient temperature is far greater than that caused by the nonlinearity and random noise of calibration data, the signs of errors obtained by the conventional calibration method show obvious regularity with the calibration ambient temperature as the dividing line. The method proposed in this paper has largely eliminated the influence of calibration ambient temperature, so the error distribution is symmetrical, which is mainly caused by the nonlinearity of calibration data.

The experimental results show that the ambient temperature has a great influence on the infrared calibration near room temperature field in the laboratory, and the maximum error can reach ±6.6°C when using the direct calibration function in the verification experiment. Conventional environmental temperature compensation methods can reduce the environmental impact, but sometimes the effect is not ideal. The maximum measurement error is reduced from ±6.6°C to ±5.1°C in the experiment. The equivalent blackbody calibration method can more effectively remove the environmental interference in the infrared calibration, and the maximum measurement error is reduced from ±6.6°C to ±1.8°C in the experiment.

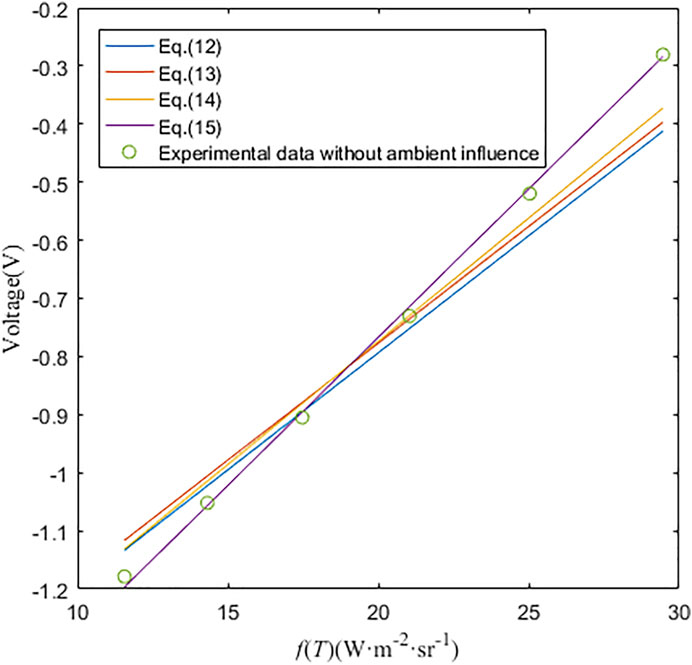
The calibration curves Eq. 12, Eq. 13, Eq. 14, Eq. 15, and the data without environmental interference measured in the verification experiment are plotted as shown in Figure 3.

FIGURE 3

FIGURE 3. Calibration functions and experimental data without environmental interference.

It can be seen from Figure 3 that the calibration functions Eq. 12 and Eq. 13 obtained by calibrating at different ambient temperatures are basically parallel, that is, the slope is basically fixed. According to Ref. [17], after environmental temperature compensation, the slope of the calibration curve increases, and calibration curve is closer to the experimental data. It is indicated that the compensation has a certain effect, but the effect is not satisfactory. The equivalent blackbody calibration function basically coincides with the experimental data without environmental interference, which shows the effectiveness of the method.

5 Conclusion

During the calibration of the infrared temperature measurement system near room temperature field, the target temperature is close to the ambient temperature, or even lower than the ambient temperature. The calibration accuracy is easily affected by the ambient. In this paper, an equivalent blackbody calibration method is proposed to solve this problem. The calibration method can be used for the calibration of large aperture infrared radiation equipment with a surface blackbody. It is studied to solve the inadaptability of the ambient compensation method in the Refs. [12, 17]. In this method, the target radiation and ambient radiation superimposed in calibration data are separated by two calibration functions at different ambient temperatures, and an equivalent blackbody calibration function is constructed. The experimental verification of the proposed method shows that the maximum measurement error is reduced from ±6.6°C to ±1.8°C. Compared with the calibration function after conventional ambient compensation, the result of the equivalent blackbody calibration function is more satisfying.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

SC: Methodology, Software, Validation, Formal analysis, Writing—Original Draft, Project administration; JX: Conceptualization, Resources, Writing—Reviewing and Editing, Supervision, Funding acquisition.

Funding

This work was supported by the National Natural Science Foundation of China (No. 61975028).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lang Z, Qiao S, He Y, Ma Y. Quartz Tuning fork-based Demodulation of an Acoustic Signal Induced by Photo-Thermo-Elastic Energy Conversion. Photoacoustics (2021) 22:100272. doi:10.1016/j.pacs.2021.100272

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Qiao S, Ma Y, He Y, Patimisco P, Sampaolo A, Spagnolo V. Ppt Level Carbon Monoxide Detection Based on Light-Induced Thermoelastic Spectroscopy Exploring Custom Quartz Tuning forks and a Mid-infrared QCL. Opt Express (2021) 29(16):25100–8. doi:10.1364/OE.434128

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Isobe K, Suda A, Tanaka M, Hashimoto H, Kannari F, Kawano H, et al. Single-pulse Coherent Anti-stokes Raman Scattering Microscopy Employing an Octave Spanning Pulse. Opt Express (2009) 17(14):11259–66. doi:10.1364/OE.17.011259

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ma Y, Lewicki R, Razeghi M, Tittel FK. QEPAS Based Ppb-Level Detection of CO and N_2O Using a High Power CW DFB-QCL. Opt Express (2013) 21(1):1008. doi:10.1364/OE.21.001008

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ma Y, He Y, Tong Y, Yu X, Tittel FK. Quartz-tuning-fork Enhanced Photothermal Spectroscopy for Ultra-high Sensitive Trace Gas Detection. Opt Express (2018) 26(24):32103–10. doi:10.1364/OE.26.032103

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Jepsen PU, Cooke DG, Koch M. Terahertz Spectroscopy and Imaging - Modern Techniques and Applications. Laser Photon Rev (2010) 5:124–66. doi:10.1002/lpor.201000011

CrossRef Full Text | Google Scholar

7. Ma Y, Hu Y, Qiao S, He Y, Tittel FK. Trace Gas Sensing Based on Multi-Quartz-Enhanced Photothermal Spectroscopy. Photoacoustics (2020) 20:100206. doi:10.1016/j.pacs.2020.100206

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhang Y-c., Chen Y-m., Luo C. A Method for Improving Temperature Measurement Precision on the Uncooled Infrared thermal Imager. Measurement (2015) 74:64–9. doi:10.1016/j.measurement.2015.07.016

CrossRef Full Text | Google Scholar

9. Choi T, Cao C, Blonski S, Wang W, Uprety S, Shao X. NOAA-20 VIIRS Reflective Solar Band Postlaunch Calibration Updates Two Years In-Orbit. IEEE Trans Geosci Remote Sensing (2020) 58(99):7633–42. doi:10.1109/TGRS.2020.2982764

CrossRef Full Text | Google Scholar

10. Chen Y, Iturbide-Sanchez F, Tremblay D, Tobin D, Strow L, Wang L, et al. Reprocessing of Suomi NPP CrIS Sensor Data Records to Improve the Radiometric and Spectral Long-Term Accuracy and Stability. IEEE Trans Geosci Remote Sensing (2021)(99) 1–14. doi:10.1109/TGRS.2021.3060639

CrossRef Full Text | Google Scholar

11. Liebmann F. Infrared Calibration Development at Fluke Corporation Hart Scientific Division. Thermosense XXX (2008) 693906. International Society for Optics and Photonics. doi:10.1117/12.781510

CrossRef Full Text | Google Scholar

12. Rice JP, Butler JJ, Johnson BC, Minnett PJ, Maillet KA, Nightingale TJ, et al. The Miami2001 Infrared Radiometer Calibration and Intercomparison. Part I: Laboratory Characterization of Blackbody Targets. J Atmos Oceanic Technol (2004) 21(2):258–67. doi:10.1175/1520-0426(2004)021<0258:tmirca>2.0.co;2

CrossRef Full Text | Google Scholar

13. Kimball BA, Mitchell ST. Low-temperature Calibration of Infrared Thermometers. J Atmos Oceanic Technol (1984) 1:379–82. doi:10.1175/1520-0426(1984)001<0379:ltcoit>2.0.co;2

CrossRef Full Text | Google Scholar

14. Barry T, Fuller G, Hayatleh K, Lidgey J. Self-Calibrating Infrared Thermometer for Low-Temperature Measurement. IEEE Trans Instrum Meas (2011) 60:2047–52. doi:10.1109/TIM.2011.2113123

CrossRef Full Text | Google Scholar

15. Barry T, Fuller G, Hayatleh K. Infrared Temperature Measurement for Remote Monitoring in Cold Climates. Meas Sci Technol (2012) 23:114001. doi:10.1088/0957-0233/23/11/114001

CrossRef Full Text | Google Scholar

16. Dai Y, Liu Z, Mao H, Zhang Y, Xiang L, Sandy T. Study on the Calibration Method for the Measurement of Low-Temperature Radiation Responsivity of IR Camera. Int Soc Opt Photon (2012) 84172F. doi:10.1117/12.977819

CrossRef Full Text | Google Scholar

17. Zhang ZQ, Wang P, Yu XD, Zhang J, Li T. Study on High Accuracy Temperature Measurement Technology of Infrared thermal Imager. Chin J Scientific Instrument (2020) 10–8. doi:10.19650/j.cnki.cjsi.J2006177

CrossRef Full Text | Google Scholar

18. Zhang H, Hui Z. Design and Experimental Test of a Novel Surface Blackbody with Honeycombs. IEEE (2010). p. 361–4.

Google Scholar

19. Vigo System SA (2017). PVMI-2TE. Available at: https://vigo.com.pl/produkty/pvmi-2te/ [Accessed December 15, 2017].

Google Scholar

20. Svensson T, Renhorn I, Broberg P. A Study of the Radiometric Calibration of Spectral Bands in the Mid-wave Infrared (MWIR) Spectral Range 1.5-5 μm. Infrared Imaging Syst Des Anal Model Test (2009) XX:73000. doi:10.1117/12.818442

CrossRef Full Text | Google Scholar

21. Yang L. Calculation and Error Analysis of Temperature Measurement Using Thermal Imager. Infrared Tech (1999) 20–4. CNKI:SUN:HWJS.0.1999-04-005.

Google Scholar

22. Coppa P, Ruffino G, Spena A. Pyrometer Wavelength Function: its Determination and Error Analysis. High temp.-High Press (1988) 20:479–90.

Google Scholar

23. Sun ZY, Wang M, Chang ST. Effect and Correction of Environmental Temperature on Infrared Radiation Measurement Precision. Laser & Infrared (2014) 522–7. CNKI:SUN:JGHW.0.2014-05-011.

Google Scholar

24. Yang CY, Zhang JP, Cao LH. Infrared Radiation Measurement Based on Real-Time Correction. J Infrared Millimeter Waves (2011) 284–8. CNKI:SUN:HWYH.0.2011-03-022.

Google Scholar

25. Cui S, Sun B, Sun X. A Method for Improving Temperature Measurement Accuracy on an Infrared Thermometer for the Ambient Temperature Field. Rev Scientific Instr (2020) 91:054903. doi:10.1063/1.5121214

CrossRef Full Text | Google Scholar