
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys., 24 December 2021
Sec. Condensed Matter Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.785801
This article is part of the Research TopicFrontiers in Physics - Rising Stars AsiaView all 10 articles
 Minnan Chen1
Minnan Chen1 Jiangtao Wu1
Jiangtao Wu1 Qing Huang2
Qing Huang2 Jinlong Jiao1
Jinlong Jiao1 Zhiling Dun3
Zhiling Dun3 Guohua Wang1
Guohua Wang1 Zhiwei Chen4
Zhiwei Chen4 Gaoting Lin1
Gaoting Lin1 Vasudevan Rathinam1
Vasudevan Rathinam1 Cangjin Li5
Cangjin Li5 Yanzhong Pei5
Yanzhong Pei5 Feng Ye6
Feng Ye6 Haidong Zhou2
Haidong Zhou2 Jie Ma1,7*
Jie Ma1,7*We have performed combined elastic neutron diffuse, electrical transport, specific heat, and thermal conductivity measurements on the quasi–one-dimensional Ba3Co2O6(CO3)0.7 single crystal to characterize its transport properties. A modulated superstructure of polyatomic CO32− is formed, which not only interferes the electronic properties of this compound, but also reduces the thermal conductivity along the c-axis. Furthermore, a large magnetic entropy is observed to be contributed to the heat conduction. Our investigations reveal the influence of both structural and magnetic effects on its transport properties and suggest a theoretical improvement on the thermoelectric materials by building up superlattice with conducting ionic group.
Thermoelectric (TE) materials can recycle waste heat into usable electricity based on the Seebeck effect and are believed to play a significant role in efficient use of energy [1]. As the energy conversion performance of TE materials is evaluated by the dimensionless figure of merit zT, zT = S2σT/(κele + κlatt), where T is operating temperature, σ is electrical conductivity, S is Seebeck coefficient, κele is electronic thermal conductivity, and κlatt is lattice thermal conductivity, the research on the TE material is usually focused on two main approaches: (1) increasing the power factor S2σ through electronic structure or energy band engineering [2–4] and (2) reducing the lattice thermal conductivity κlatt by introducing additional phonon scattering and manipulating phonon structure [5–9]. Actually, those approaches are very complex. For example, the electrical transport (σ = nμe) could be regulated by the carrier concentration n, the carrier mobility μ, and the electron charge e, whereas the acoustic phonon scattering introduces a μ ∝ T −1.5 dependence, and the ionized impurity scattering gives a μ ∝ T1.5 relationship [10]. Furthermore, the lattice thermal conductivity, κlatt, could be decreased by the grain boundary scattering, point defect scattering, disorder scattering, and Umklapp scattering [11, 12]. Therefore, if the scattering mechanisms of both the electrical and thermal transport could be well understood, the energy conversion performance of TE materials can be better optimized.
At present, alloy TE materials have been widely applied as a TE compound. Although the performance has been continuously improved, there are some unavoidable limitations on the environment, expenses, oxidization stability, and so on [13–15]. Therefore, the investigation of oxide TE materials has been proposed. Because of its special crystal structure and magnetic effect, the cobalt oxide has good electronic properties and low lattice thermal conductivity [16–21]. For example, the power factor (S2σ) of NaCo2O4 is 5 × 10–3 W · m−1 · K−2, even higher than that of Bi2Te3 [22]. Among them, NaCo2O4, Ca3Co4O9, and Bi2Sr2Co2Ox have received much attention, and their TE performance is also continuously improved and even higher than some alloys [17, 23–26].
Recently, a quasi–one-dimensional cobaltate Ba3Co2O6(CO3)0.7 has been reported as a new excellent potential TE material [27]. This compound comprised face-sharing CoO6 octahedra and carbonate CO32− molecular chains along its c-axis with the space group of P-6, a = 9.683 Å and c = 9.518 Å [28], Figures 1A, B. The average occupancy of the polyatomic CO32− molecule is 0.7. Although z of Ba3Co2O6(CO3)0.7 was reported as 5.1 × 10−5 K−1, which is comparable to NaxCoO2-y at 300 K, and it was considered as a promising cobalt oxide TE material [24], the thermal conductivity, transport properties, and the physics remain unknown.
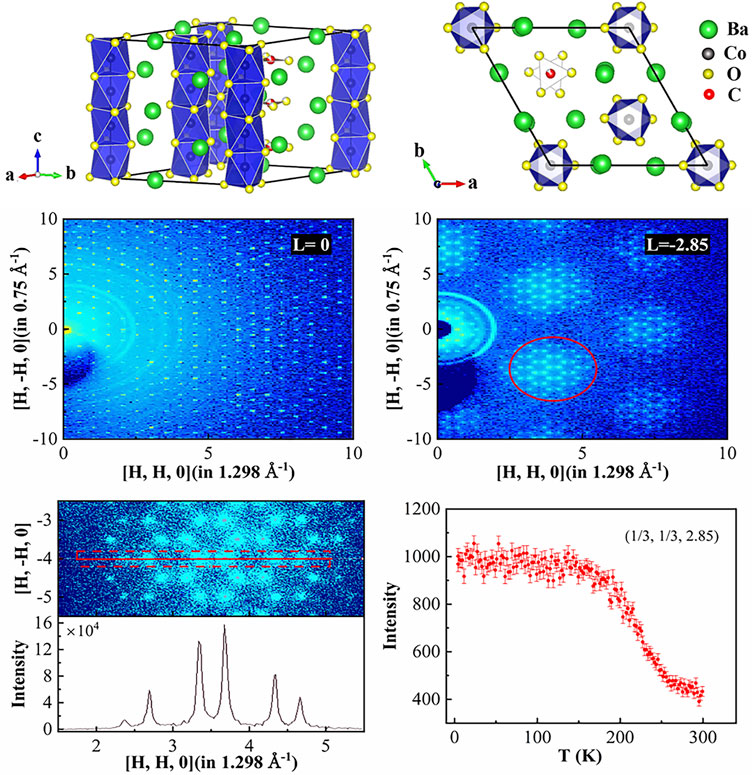
FIGURE 1. (A) Crystal structure of Ba3Co2O6(CO3)0.7 consisting of chains of CoO6 and carbonate CO3 along the c-axis in the standard orientation [space group: P-6]. (B) The c-axis projected crystal structure. 2D slice of diffuse neutron scattering patterns of Ba3Co2O6(CO3)0.7 single crystal at 50 K. (C) L = 0, (D) L = −2.85, and (E) enlarged view of a section of (D) obtained on CORELLI. (F) Cuts along the [H, H, 0] direction of the Bragg peak marked by red solid line in panel (E). (G) Temperature dependence of the peak intensity of the (1/3 1/3 2.85).
In this article, we report neutron diffuse scattering, electrical conductivity, Hall effect, specific heat, and thermal conductivity of Ba3Co2O6(CO3)0.7 single crystal. Moreover, the magnetic effect of the Co ions is discussed.
Single crystal of Ba3Co2O6(CO3)0.7 was grown by a flux method using a mixture of Co3O4, BaCO3, K2CO3, and BaCl2 [27]. These single crystals have the shape of short hexagonal rods. The c-axis was determined using the X-ray Laue method to be along the rod direction.
A single crystal with dimension of 2 × 2 × 6 mm3 was aligned in the (H, K, 0) horizontal scattering plane for the diffuse scattering studies using the elastic single crystal diffuse scattering spectrometer CORELLI at the Spallation Neutron Source (SNS), Oak Ridge Nation Laboratory [29]. Based on the Hall effect, the carrier concentration of Ba3Co2O6(CO3)0.7 in the temperature range of 80 to 300 K was measured by the van der Pauw technique at a reversible magnetic field of 2 T. And the conductivity along the c-direction was obtained by Physical Property Measurement System (PPMS, Quantum Design) with resistivity option, using the four-probe method. The specific heat measurement was applied on PPMS’s heat capacity option in two steps. First, the background specific heat was measured by an empty puck with a small amount of N-grease in the temperature range from 2 to 250 K at zero field. Then, a Ba3Co2O6 (CO3)0.7 sample (approximately 4.71 mg) was placed in the measured N-grease, and the total specific heat was measured at same conditions. Finally, we gained the specific heat of the sample by subtracting the background specific heat from the total specific heat. The thermal conductivity along the c-axis was characterized using PPMS with thermal transport options, and the four-probe lead configuration method was used. During the measurement, the matching gold-plated copper bar in PPMS was used as leads. More detail for the measurement of carrier concentration, specific heat and thermal conductivity can be find in Supplementary Material. The diffuse scattering studies, carrier concentration, electrical conductivity, and thermal conductivity, were carried out on the same crystal, and the sample for the measurement of the specific heat was cut from this crystal too.
To further understand the structural details of Ba3Co2O6(CO3)0.7, we study the elastic diffuse scattering behavior of it. Figures 1C, D show the contour plot of neutron intensity at 50 K in the (H, K, 0) plane of Ba3Co2O6(CO3)0.7 with L = 0 and L = −2.85. The sharp spots in Figure 1C demonstrate the good crystallinity of the single crystal. The signals of strong diffuse scattering are clearly observed at L = −2.85. Figure 1F, corresponding to the red solid line in Figure 1E, shows the elastic intensity along the [H, H, 0] direction and the relative diffuse intensity of each diffuse spot. Morgan et al. [30] have analyzed the short-range diffuse scattering using reverse Monte Carlo method and concluded that the diffuse scattering has short-range correlation between the disorder vibrations of polyatomic CO32−.
Figure 1G shows the temperature dependence of the superlattice (1/3, 1/3, 2.85) reflection. Upon warming, the intensity starts to decrease at 150 K and approaches a T-independent constant greater than 250 K. Thus, the vibrations of polyatomic CO32− should be affected by the thermal effect, and the localization of the CO32− cluster should be relaxed.
To obtain the electrical transport properties of Ba3Co2O6(CO3)0.7 single crystal, Hall carrier concentration nH was collected at a reversible magnetic field of 2 T, and Hall mobility μH was determined with zero-field resistivity, as shown in Figure 2. The exponential increase of carrier concentration with rising temperature indicates the thermal excitation of carriers. The charge polarity is dominated by holes in the measured temperature range, which is consistent with the positive Seebeck coefficients reported by Igarashi et al. [31]. The low carrier concentrations suggest that the further acceptor doping is required for TE applications. As marked in Figure 2A, there are two anomalies at 150 and 250 K, which agrees very well with the diffuse data and confirmed that CO32− ion is a conductor in the system.
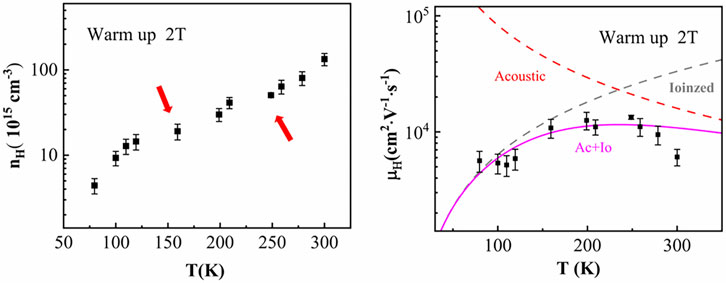
FIGURE 2. Temperature dependence of (A) carrier concentration nH and (B) Hall mobility μH along the c-axis for Ba3Co2O6(CO3)0.7. (B) Calculated carrier mobility (magenta solid line) took into account the ionized impurity scattering (gray dashed line) and acoustic phonon scattering (red dashed line) contributions.
The temperature versus μH of Ba3Co2O6(CO3)0.7 single crystal is nonmonotonic, as shown in Figure 2B. The calculated mobility involving both the ionized impurity scattering and acoustic phonon scattering can well match the experimental values over a wide temperature range. μH follows a temperature dependence closing to T1.5 at low temperature range, implying that ionized impurity scattering dominates at low temperature in Ba3Co2O6(CO3)0.7 single crystal. We believe that the ionized impurity scattering relates to polyatomic CO32−. As the temperature increases, the localized ordering of CO32− weakens, and the scattering of ionized impurity also diminishes. On the other hand, the lattice vibrations become stronger with increasing temperature. These two factors together lead to the acoustic phonon scattering, gradually overshadowing the ionized impurity scattering and becoming the dominant scattering mechanism in the material, which causes a negative temperature-dependence slope of μH greater than 250 K. The CO32− is delocalized when T > 250 K, which might introduce other scattering mechanisms affecting the carriers transports and make the carrier mobility lower than the theoretical value.
To investigate the thermal effect in Ba3Co2O6(CO3)0.7, the specific heat CP was measured in the temperature range from 2 to 250 K at zero field. As shown in Figure 3A, the profile of data is very smooth, and no obvious peak is detected, indicating the absence of structure and magnetic transitions. The inset of Figure 3A displays the data as a CP/T versus T2. According to the Debye model, the lattice term of the total specific heat CP/T is linear with T2 at low T, but the data demonstrate a deviation from the linear relationship at low temperature and a nonzero intercept (approximately 0.29 J · mol−1 · K−2) at 0 K. The nonzero intercept is an order of magnitude larger than that for NaCo2O4, which is a strongly correlated electronic cobalt system [32], and suggests Ba3Co2O6(CO3)0.7 as also a strongly correlated electronic system.
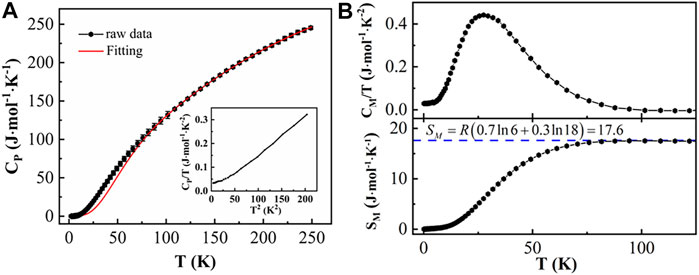
FIGURE 3. (A) The total specific heat CP of Ba3Co2O6(CO3)0.7 measured at zero field. The red line represents the lattice contribution by Eq. 1. The inset shows the CP/T vs T2 (B) The magnetic specific heat is obtained by subtracting the lattice contribution Cp from the raw data. (C) Magnetic entropy obtained by integrating CM/T over the entire measured temperature range.
In order to further study the specific heat of Ba3Co2O6(CO3)0.7, a fitting was gained by using the Debye–Einstein model, which can fit the lattice specific heat data well at both low and high temperature. The model is written as follows [33]:
where the first term is the contribution from the acoustic branch (Debye term), and the remaining terms are related to the contribution of the optical branch (Einstein terms). CD and CEi are the relative weights of the Debye and Einstein terms, respectively. R is the universal gas constant. θD and θEi represent Debye and Einstein temperatures. There are 13.8 atoms per formula in our system. The best fitting for our data results is one Debye term and three E terms with a ratio 1:6:2.8:4 for CD:CE1:CE2:CE3 and θD = 163 K, θE1 = 816 K, θE2 = 179 K, and θE3 = 290 K, respectively.
As there is no distinct phase transition in the specific heat data, and the magnetic long-range order was not observed down to 2 K [34], the deviation of the experimental data from the fitted values indicates the presence of short-range magnetic fluctuations. Figures 3B, C display the magnetic specific heat, CM, by subtracting the fitted lattice contribution from raw data, and the related magnetic entropy SM, respectively. The SM enhances with increasing temperature, and almost 100% recovered the theoretical value 17.6 J · mol−1 · K−1 at approximately 100 K. Both contributions of spin and orbital degrees of freedom are suggested to be considered [35]: Co4+ has high-spin state with S = 1/2 (3d5), and Co3+ has intermediate-spin state with S = 1 (3d6), leading to SM = R(0.7 ln 6 + 0.3 ln 18) = 17.6 J · mol−1 · K−1, as shown by the blue dotted line in Figure 3C. There may be spin-phonon scattering in the huge magnetic entropy regimen that interferes with the thermal conductivity.
Figure 4 shows the temperature dependence of the total thermal conductivity κc and the lattice thermal conductivity κc_L of Ba3Co2O6(CO3)0.7 parallel to the c-axis from 3 to 250 K κc consists of κc_L and the electronic thermal conductivity κc_e, where the electronic thermal conductivity can be determined by the Wiedemann–Franz law (κe = σLnT, where the Lorenz number Ln = 2.45 × 10–8 W · Ω · K−2) and subtracted. At low temperatures, κc and κc_L almost completely overlap due to the very small electronic thermal conductivity. As the temperature increases, κc and κc_L begin to separate because of the exponential increase in conductivity. Although κc_e is maximum at 250 K, it is only a few percent of κc_L. The contribution of phonon to κc is domain. κc_L increases rapidly at low temperature with the dominant boundary scattering, which displays a κc_L ∝ T3 dependence. A maximum with a value of 13.5 W · m−1 · K−1 appears at approximately 12 K, where the Umklapp processes with exp (θD/bT) dependence become frequent and enough to compare with boundary scattering. One notes that the peak of κc_L is an order of magnitude smaller than that of other cobalt oxides, such as Ca3Co2O6 [36]. This difference may be caused by the superlattice in Ba3Co2O6(CO3)0.7, which can enhance the scatting of κc_L. As temperature increases further, κc_L drops very quickly and reflects that the Umklapp process scattering gradually becomes the main scattering mechanism. When the temperature is higher than 60 K, the trend of the curve gets flat. At approximately 250 K, the lattice thermal conductivity of Ba3Co2O6(CO3)0.7 along the c-axis is 5.02 W · m−1 · K−1.
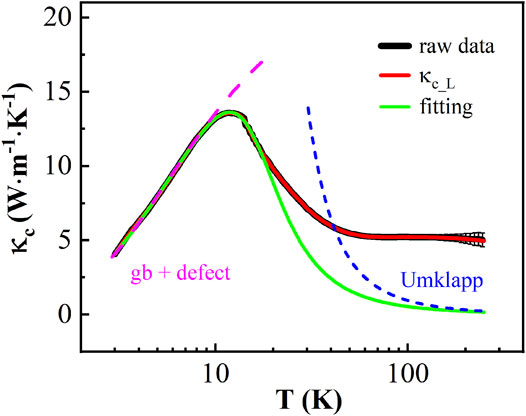
FIGURE 4. The temperature dependence of the thermal conductivity κc and the lattice thermal conductivity (κc_L) along the c-axis of Ba3Co2O6(CO3)0.7 at zero field. The black line is experimental data of the thermal conductivity; the red line is κc_L, and the green one represents the result of fitting by Eq. 2. The magenta dashed line is the contribution of the grain boundary and the point defect scattering, and the blue one is Umklapp process scattering.
The data of κc_L were fitted to the formula given by the Debye model of phonon thermal conductivity[37].
where kB is the Boltzmann’s constant, νp is the average sound velocity, ħ is the Planck constant, x = ħω/kBT, ω is frequency, and τ is the mean lifetime of phonon. The phonon relaxation is usually defined as follows:
These three items correspond with phonon boundary scattering, phonon point defect scattering, and the phonon–phonon Umklapp processes, respectively. L, A, B, and b are the fitting parameters. νp can be calculated by the Debye temperature θD = 163 K obtained by the fitting above and Eq. 4:
where N is the number of atoms in crystal, and V is the volume of crystal, and then we obtain the average sound velocity of the sample νp ≈ 1,343 m · s−1.
The best fitting is shown in Figure 4 as green solid line with L = 1.6 × 10–5 m, A = 1.7 × 10–41 s3, B = 7.4 × 10–29 K−1 s2, and b = 2.7. The lattice thermal conductivity is mainly the contribution of phonons below approximately 18 K. As the temperature increases, the fitted values gradually deviate from the raw data. An extra contribution of the thermal conductivity has also been observed in Ca3Co2O6 [38]. In combination with the heat capacity, the deviation of thermal conductivity might be due to the overestimation of the lattice thermal conductivity, because of the magnetic contribution to the total thermal conductivity: (1) The magnetic entropy increases rapidly after 18 K; in the meantime, κc_L starts to be higher than the theoretical value. (2) After the magnetic entropy reaches saturation at approximately 100 K, the κc_L also decreases slowly with growing temperature at the same rate as the theoretical one. As the electron concentration is very low, the electron–phonon scattering is not dominant in the system, and the CO32− affects grain boundary and defect.
In summary, we have studied the structural, electrical, and thermal transport properties of quasi–one-dimensional Ba3Co2O6(CO3)0.7 single crystal and the connection between the lattice structure, magnetism, and its transport properties. Neutron diffuse reveals that a modulated superstructure of CO32− is formed in Ba3Co2O6(CO3)0.7. The main hole carriers in the systems are continuously excited with increasing temperature and scattered not only by short-range ordered polyatomic CO32− at low temperature, but also by acoustic phonon and nonlocalized CO32− at high temperature. No lattice and magnetic phase transition are observed by the specific heat measurement, and the magnetic entropy is consistent with mixed Co3+ and Co4+ valence. The thermal conductivity of Ba3Co2O6(CO3)0.7 shows an enhancement at higher temperatures over classic phonon heat transfer due to the contribution of the itinerant magnetism. The unique lattice and transport properties in Ba3Co2O6(CO3)0.7 suggest a potential superlattice designs for regulating the TE properties.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
MC and JM conceived the project. QH and HZ provided single crystals used in this study. FY and ZD performed neutron scattering experiments and analyzed the data with the help from JM JW and VR. ZC, CL and YP performed carrier concentration measurement. MC performed specific heat and conductivity measurements and analyzed the data with the help with GW, GL and JJ. GW carried out the thermal property measurements. All authors discussed the results and contributed to the writing of the manuscript.
MC, JW, JJ, GW, GL, and JM thank the financial support from the National Science Foundation of China (Nos. 11774223, and U2032213), the interdisciplinary program Wuhan National High Magnetic Field Center (Grant No. WHMFC 202122), Huazhong University of Science and Technology, and the National Key Research and Development Program of China (Grant Nos. 2016YFA0300501 and 2018YFA0704300). GL thanks the project funded by China Postdoctoral Science Foundation (Grant No. 2019M661474). JM thanks a Shanghai talent program. QH and HZ thank the support from NSF-DMR- 2003117. The ND experiment was performed at CORELLI of SNS. VR thanks the project funded by Natural Science Foundation of China (Grant No. QN20200009030). A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.785801/full#supplementary-material
1. Tritt TM. Holey and Unholey Semiconductors. Science (1999) 283:804–5. doi:10.1126/science.283.5403.804
2. Pei Y, Shi X, LaLonde A, Wang H, Chen L, Snyder GJ. Convergence of Electronic Bands for High Performance Bulk Thermoelectrics. Nature (2011) 473:66–9. doi:10.1038/nature09996
3. Kim K, Kim G, Lee H, Lee KH, Lee W. Band Engineering and Tuning Thermoelectric Transport Properties of P-type Bi0.52Sb1.48Te3 by Pb Doping for Low-Temperature Power Generation. Scripta Materialia (2018) 145:41–4. doi:10.1016/j.scriptamat.2017.10.009
4. Fu C, Yao M, Chen X, Maulana LZ, Li X, Yang J, et al. Revealing the Intrinsic Electronic Structure of 3D Half‐Heusler Thermoelectric Materials by Angle‐Resolved Photoemission Spectroscopy. Adv Sci (2020) 7:1902409. doi:10.1002/advs.201902409
5. Liu Y, Xie H, Fu C, Snyder GJ, Zhao X, Zhu T. Demonstration of a Phonon-Glass Electron-crystal Strategy in (Hf,Zr)NiSn Half-Heusler Thermoelectric Materials by Alloying. J Mater Chem A (2015) 3:22716–22. doi:10.1039/c5ta04418a
6. Shen J, Fu C, Liu Y, Zhao X, Zhu T. Enhancing Thermoelectric Performance of FeNbSb Half-Heusler Compound by Hf-Ti Dual-Doping. Energ Storage Mater (2018) 10:69–74. doi:10.1016/j.ensm.2017.07.014
7. Yang Y-X, Wu Y-H, Zhang Q, Cao G-S, Zhu T-J, Zhao X-B. Enhanced Thermoelectric Performance of Bi2Se3/TiO2 Composite. Rare Met (2020) 39:887–94. doi:10.1007/s12598-020-01414-4
8. Chen X-K, Pang M, Chen T, Du D, Chen K-Q. Thermal Rectification in Asymmetric Graphene/Hexagonal Boron Nitride van der Waals Heterostructures. ACS Appl Mater Inter (2020) 12:15517–26. doi:10.1021/acsami.9b22498
9. Zeng Y-J, Feng Y-X, Tang L-M, Chen K-Q. Effect of Out-Of-Plane Strain on the Phonon Structures and Anharmonicity of Twisted Multilayer Graphene. Appl Phys Lett (2021) 118:183103. doi:10.1063/5.0047539
10. Chattopadhyay D, Queisser HJ. Electron Scattering by Ionized Impurities in Semiconductors. Rev Mod Phys (1981) 53:745–68. doi:10.1103/RevModPhys.53.745
11. Vandersande JW, Wood C. The thermal Conductivity of Insulators and Semiconductors. Contemp Phys (1986) 27:117–44. doi:10.1080/00107518608211003
12. Chen X-K, Chen K-Q. Thermal Transport of Carbon Nanomaterials. J Phys Condens Matter (2020) 32:153002. doi:10.1088/1361-648X/ab5e57
13. Perumal S, Roychowdhury S, Biswas K. High Performance Thermoelectric Materials and Devices Based on GeTe. J Mater Chem C (2016) 4:7520–36. doi:10.1039/c6tc02501c
14. Xiao Y, Zhao L-D. Charge and Phonon Transport in PbTe-Based Thermoelectric Materials. Npj Quant Mater (2018) 3:55. doi:10.1038/s41535-018-0127-y
15. Murugasami R, Vivekanandhan P, Kumaran S, Suresh Kumar R, John Tharakan T. Simultaneous Enhancement in Thermoelectric Performance and Mechanical Stability of P-type SiGe alloy Doped with Boron Prepared by Mechanical Alloying and Spark Plasma Sintering. J Alloys Compd (2019) 773:752–61. doi:10.1016/j.jallcom.2018.09.029
16. Masset AC, Michel C, Maignan A, Hervieu M, Toulemonde O, Studer F, et al. Misfit-layered Cobaltite with an Anisotropic Giant Magnetoresistance: Ca3Co4O9. Phys Rev B (2000) 62:166–75. doi:10.1103/PhysRevB.62.166
17. Yang G, Ramasse Q, Klie RF. Direct Measurement of Charge Transfer in thermoelectricCa3Co4O9. Phys Rev B (2008) 78:153109. doi:10.1103/PhysRevB.78.153109
18. Fan M, Zhang Y, Hu Q, Zhang Y, Li X-J, Song H. Enhanced Thermoelectric Properties of Bi2Sr2Co2Oy by Alkali Metal Element Doping and SiC Dispersion. Ceramics Int (2019) 45:17723–8. doi:10.1016/j.ceramint.2019.05.341
19. Sakabayashi H, Okazaki R. Crossover from Itinerant to Localized States in the Thermoelectric Oxide [Ca2CoO3 [(0.62) [CoO2]. Phys Rev B (2021) 103:125119. doi:10.1103/PhysRevB.103.125119
20. Naruse K, Kawamata T, Ohno M, Matsuoka Y, Hase M, Kuroe H, et al. Magnetic State of the Geometrically Frustrated Quasi-One-Dimensional Spin System Cu3Mo2O9 Studied by Thermal Conductivity. J Phys Soc Jpn (2015) 84:124601. doi:10.7566/jpsj.84.124601
21. Wu Z. Thermal Conductivity Anomaly in Spin-Crossover Ferropericlase under Lower Mantle Conditions and Implications for Heat Flow across the Core-Mantle Boundary. Am Mineral (2018) 103:1953–8. doi:10.2138/am-2018-6690
22. Terasaki I, Sasago Y, Uchinokura K. Large Thermoelectric Power in NaCo2O4 Single Crystals. Phys Rev B (1997) 56:R12685–R12687. doi:10.1103/PhysRevB.56.R12685
23. Kurosaki K, Muta H, Uno M, Yamanaka S. Thermoelectric Properties of NaCo2O4. J Alloys Compd (2001) 315:234–6. doi:10.1016/s0925-8388(00)01277-9
24. Fujita K., Mochida T., Nakamura K.. High-Temperature Thermoelectric Properties of NaxCoO2-Delta Single Crystals. (2001) 40:4644–47. doi:10.1143/jjap.40.4644
25. Jakubczyk EM, Mapp A, Chung CC, Sansom CL, Jones JL, Dorey RA. Enhancing Thermoelectric Properties of NaCo2O4 Ceramics through Na Pre-treatment Induced Nano-Decoration. J Alloys Compd (2019) 788:91–101. doi:10.1016/j.jallcom.2019.02.199
26. Zhang L, Liu Y, Tan TT, Liu Y, Zheng J, Yang Y, et al. Thermoelectric Performance Enhancement by Manipulation of Sr/Ti Doping in Two Sublayers of Ca3Co4O9. J Adv Ceram (2020) 9:769–81. doi:10.1007/s40145-020-0413-6
27. Iwasaki K, Yamamoto T, Yamane H, Takeda T, Arai S, Miyazaki H, et al. Thermoelectric Properties of Ba3Co2O6(CO3)0.7 Containing One-Dimensional CoO6 Octahedral Columns. J Appl Phys (2009) 106:034905. doi:10.1063/1.3174428
28. Boulahya K, Amador U, Parras M, González-Calbet JM. The Oxycarbonate Ba3Co2O6(CO3)0.60 with a 2H−ABO3-Related Structure. Chem Mater (2000) 12:966–72. doi:10.1021/cm991122x
29. Ye F, Liu Y, Whitfield R, Osborn R, Rosenkranz S. Implementation of Cross Correlation for Energy Discrimination on the Time-Of-Flight Spectrometer CORELLI. J Appl Cryst (2018) 51:315–22. doi:10.1107/S160057671800403X
30. Morgan Z, Zhou HD, Chakoumakosa B, Ye F. RMC-DISCORD. Reverse Monte Carlo Refinement of DIffuse Scattering and CORrelated Disorder from Single Crystals. J Appl Crystallogr (2021) 77:A77–A87. doi:10.1107/s0108767321099128
31. Igarashi H, Shimizu Y, Kobayashi Y, Itoh M. Spin Disorder in an Ising Honeycomb Chain Cobaltate. Phys Rev B (2014) 89:054431. doi:10.1103/PhysRevB.89.054431
32. Ando Y, Miyamoto N, Segawa K, Kawata T, Terasaki I. Specific-heat Evidence for strong Electron Correlations in the Thermoelectric material(Na,Ca)Co2O4. Phys Rev B (1999) 60:10580–3. doi:10.1103/PhysRevB.60.10580
33. Lu Z, Ge L, Wang G, Russina M, Günther G, dela Cruz CR, et al. Lattice Distortion Effects on the Frustrated Spin-1 Triangular-Antiferromagnet A3NiNb2O9 (A=Ba, Sr, and Ca). Phys Rev B (2018) 98:094412. doi:10.1103/PhysRevB.98.094412
34. Igarashi K, Shimizu Y, Satomi E, Kobayashi Y, Takami T, Itoh M. Absence of Magnetic Order in Ising Honeycomb-Lattice Ba3Co2O6(CO3)0.7. J Phys Conf Ser (2012) 400:032024. doi:10.1088/1742-6596/400/3/032024
35. Koshibae W, Tsutsui K, Maekawa S. Thermopower in Cobalt Oxides. Phys Rev B (2000) 62:6869–72. doi:10.1103/PhysRevB.62.6869
36. Che HL, Shi J, Wu JC, Rao X, Liu XG, Zhao X, et al. Thermal Conductivity of Ca3Co2O6 Single Crystals. AIP Adv (2018) 8:055811. doi:10.1063/1.5005992
37. Song JD, Wang XM, Zhao ZY, Wu JC, Zhao JY, Liu XG, et al. Low-temperature Heat Transport of CuFe1−xGaxO2 (x=0-0.12) Single Crystals. Phys Rev B (2017) 95:224419. doi:10.1103/PhysRevB.95.224419
Keywords: cobalt oxide, neutron diffuse, spin entropy, carrier mobility, thermal conductivity, scattering mechanism
Citation: Chen M, Wu J, Huang Q, Jiao J, Dun Z, Wang G, Chen Z, Lin G, Rathinam V, Li C, Pei Y, Ye F, Zhou H and Ma J (2021) The Transport Properties of Quasi–One-Dimensional Ba3Co2O6(CO3)0.7. Front. Phys. 9:785801. doi: 10.3389/fphy.2021.785801
Received: 29 September 2021; Accepted: 19 November 2021;
Published: 24 December 2021.
Edited by:
Gang Zhang, Technology and Research (A∗STAR), SingaporeReviewed by:
Ke-Qiu Chen, Hunan University, ChinaCopyright © 2021 Chen, Wu, Huang, Jiao, Dun, Wang, Chen, Lin, Rathinam, Li, Pei, Ye, Zhou and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jie Ma, am1hM0BzanR1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.