Emission of Solitons From an Obstacle Moving in the Bose-Einstein Condensate

Dark solitons dynamically generated from a potential moving in a one-dimensional Bose-Einstein condensate are displayed. Based on numerical simulations of the Gross-Pitaevskii equation, we find that the moving obstacle successively emits a series of solitons which propagate at constant speeds. The dependence of soliton emission on the system parameters is examined. The formation mechanism of solitons is interpreted as interference between a diffusing wavepacket and the condensate background, enhanced by the nonlinear interactions.

PACS numbers: 03.75.Mn, 03.75.Lm, 05.30.Jp

1 Introduction

Solitons are localized waves which move at constant velocity and stable shape [1]. They usually emerge as the nonlinear interaction counterbalance with the wave dispersion. So far, solitons are found and studied in various systems such as water waves [2], fiber optics [3], magnets [4], plasmas [5], atomic Bose-Einstein condensates (BECs) [6]. With the experiment development of ultracold atomic gases, BECs have higher degree of controllability. There have been extensively investigations about the existence [7] and dynamics of solitons [8–11], including multicomponent matter waves [12, 13] and multidimensional solitons [14] or vortices [15]. Experiment techniques like phase imprinting [16], quantum quenching [17], density engineering [18] have successfully generated dark and bright solitons. In one-dimensional (1D) BEC, manipulating the size of initial box can tune the number, size and velocity of newly generated solitons [19]. For multicomponent condensates, an increase of the initial separation or chemical potential can lead to an increase of nucleated number [20]. By inserting obstacle into the two-dimension supersonic flow of BECs, solitons are generated in numerical simulations [21] and experiments [22]. The number of solitons increases with the size and the speed of the obstacle.

In a recent paper, researchers exhibited solitonic diffusion of a hump or a notch wavepacket in a 1D BEC [23]. The travelling velocity of the generated solitons increases with the nonlinear interaction strength. In this paper, we consider a Gaussian obstacle potential moving at constant velocity in a 1D BEC of repulsively interacting atoms. We find that solitons are successively emitted from the moving obstacle. The velocity of the solitons are nearly same. Numerical simulations exhibit the dependence of soliton emission on the system parameters including the obstacle height, the nonlinear strength, and the obstacle speed as well. It shows that for higher obstacle more solitons are emitted, while fewer solitons are emitted for larger nonlinear strength. When obstacle moves faster, solitons are generated more frequently.

This paper is organized as follows. In Section 2, we introduce the model and the method of numerical simulations. In Section 3, we present the main results of our simulations, including the effects of three parameters on the dynamical generation of solitons by moving obstacle. We discuss the dynamical mechanism of the soliton emission through interference of a diffusive wave packet with the BEC background in Section 4. A brief summary is given in Section 5.

2 Model

We consider a one-dimensional uniform BEC background consisting of repulsively interacting atoms, in which a Gaussian obstacle potential moves. In the limit of zero temperature, dynamical properties of dilute atom BECs are governed by the mean-field Gross-Pitaevskii (GP) equation, which is a nonlinear Schrodinger equation (NLSE). Suppose the condensate is confined by a potential of longitudinal scale L greatly larger than the transverse scale. The energy of longitudinal excitations is much lower than that of transverse excitations. Hence the latter can be take as the ground state and is integrated out. The quasi-1D BEC which is described by a macroscopic wave function ψ (x, t) and the GP equation is written as [24].

$i\hslash \frac{\partial }{\partial t}\psi \left(x,t\right)=\left[-\frac{{\hslash }^2}{2M}\frac{{\partial }^2}{\partial x^2}+g|\psi \left(x,t\right){|}^2\right]\psi \left(x,t\right),(1)$

where g = 4πℏ²aN/M is the nonlinear strength with a the s-wave scattering length. Here, N is the total number of atoms, and M is the atomic mass. The repulsive interaction corresponds to a > 0. The atom density is ρ (x, t) = N|Φ(x, t)|². The healing length of the confined potential is $\xi ={(8\pi \bar{\rho }|a|)}^{-1/2}$. We introduce the dimensionless variables $\tilde{x}=x/{\xi }_0$, $\tilde{n}=n/n_0$, $\tilde{v}=v/c_s$, where $n_0=\sqrt{{\mu }_0/g}$ is the characteristic density with μ₀ is the characteristic energy scale. In the BEC of density n₀, the healing length is ${\xi }_0=\hslash /\sqrt{M{n}_{0}g}$, and the velocity of sound is $c_s=\sqrt{n_{0}g/m}$. For our purpose we introduce an additional moving potential V (x, t) into the uniform BEC in order to stir the dynamical process. The dimensionless GP equation is then given by [25].

$i\frac{\partial }{\partial t}\psi \left(x,t\right)=\left[-\frac{{\partial }^2}{\partial x^2}+g|\psi \left(x,t\right){|}^2+V\left(x,t\right)\right]\psi \left(x,t\right).(2)$

In the rest of this paper we always employ dimensionless variables.

Solitons are stable objects that can exist in a repulsive 1D BEC. In a uniform external potential the GP Eq. 1 has an moving dark soliton solution [26],

$\psi \left(x,t\right)=\left\{i\frac{c}{\sqrt{2g}}+\sqrt{\frac{2}{g}}k\tanh \left[k\left(x-ct\right)\right]\right\}{e}^{-i\mu t},(3)$

where the soliton transports with velocity c = 2μ − 4k² with k the width of soliton, and μ is the chemical potential of the condensate. In a non-uniform external potential it is not easy to acquire such exact solution to the GP equation. For an external moving obstacle we have recoursed to numerical simulations on the dynamical evolution of BEC. In this paper we employ a Gaussian obstacle moving in BEC with velocity v.

$V\left(x,t\right)=A{e}^{-\frac{{\left(x-vt\right)}^2}{2{\sigma }^2}},(4)$

where A is the potential height of the obstacle and σ is the width of the obstacle. Before the dynamical process, we first evolve the GP equation to the ground-state for V (x, 0) via the imaginary-time propagation. Then we take this ground-state as the initial state of the real-time evolution, using the V (x, t) in Eqs 2–4. We will observe the dynamical effects of the BEC excited by moving potential.

In BEC experiments, a moving Gaussian obstacle may be introduced by introducing a moving laser beam whose shape is $V(x,t)=A{e}^{-\frac{{(x-vt)}^2}{2{\sigma }^2}}$. Experimentally the size of the BEC is about 1um.

3 Simulation

Our simulations reveal that the moving Gaussian obstacle can constantly excite dark solitons. We explicitly examine the dependence of solition generation on the system parameters including the obstacle height, the nonlinear strength, and the obstacle velocity.

Figure 1 shows the emission of dark solitons in a BEC of nonlinear strength g = 2 which is triggered by a moving obstacle at fixed velocity v = 1. The potential height of the moving obstacle varies from 1) A = 0.7, 2) A = 1.5, 3) A = 2.5 to 4) A = 3.5, respectively. For A = 0.7, after t = 40 of real-time evolution, four dark solitons are emitted from the moving obstacle, which are the four deep blue parallel lines on the left of obstacle track. The density on the left of obstacle nearly equals to the density on the right of obstacle. The parallel blue trails indicate that the generated solitons propagate at almost the same speed. For A = 3.5, sixteen solitons are emitted with almost same speed while the density on the left of obstacle is much higher than right. Consequently, a higher potential can emit more dark solitions during the same time interval. Additionally, the speed of emitted solitons decreases as A increases. This observation result from the fact that higher obstacle may cause greater disturbance in the nonlinear system.

FIGURE 1

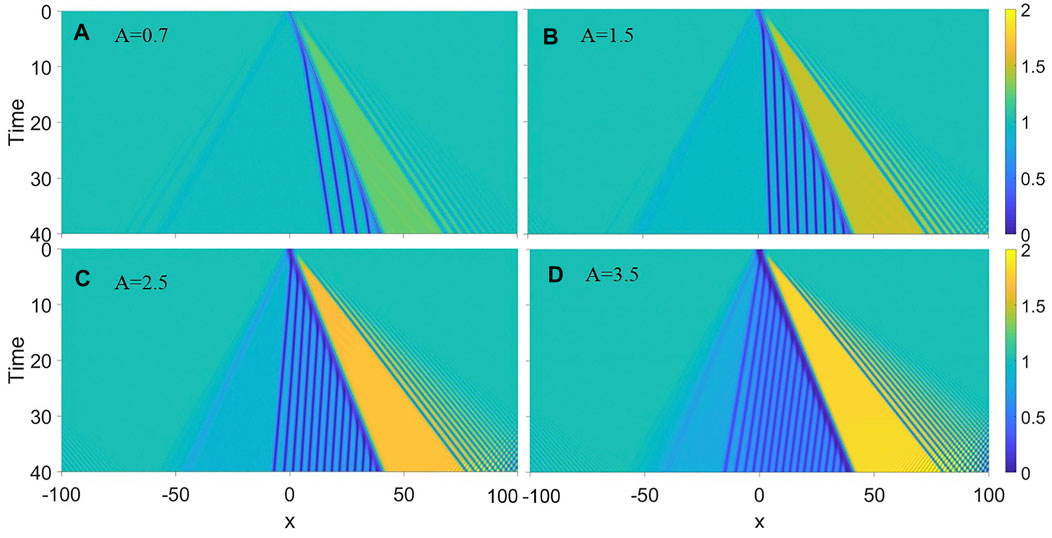
FIGURE 1. Successive emission of dark solitons from a moving Gaussian obstacle at fixed velocity v = 1 with the nonlinear strength g = 2. The obstacle height takes (A) A = 0.7, (B) A = 1.5, (C) A = 2.5, (D) A = 3.5, respectively. The color contour shows atom density. As the color is darker, the atom density is smaller. Thus, the deep blue parallel lines are dark solitonic trajectory. As the obstacle height increases, dark solitons are more frequently emitted.

Then we examine how the nonlinear strength affects the generation of solitons. For this purpose we fix the speed of the obstacle at v = 1 and the potential height A = 1. Figure 2 displays the solitonic diffusion relating to different nonlinear strength. For g = 1, seven solitons are emitted during time interval Δt = 40 and the density on right of the obstacle is much larger than on the left of obstacle. As the nonlinear strength increases, fewer and fewer dark solitons are emitted. The velocity of the emitted solitons relative to the obstacle also increases. Since the width of initial wavepacket, i.e., the ground-state under this condition, is smaller, the width of the excited solitons is also smaller.

FIGURE 2

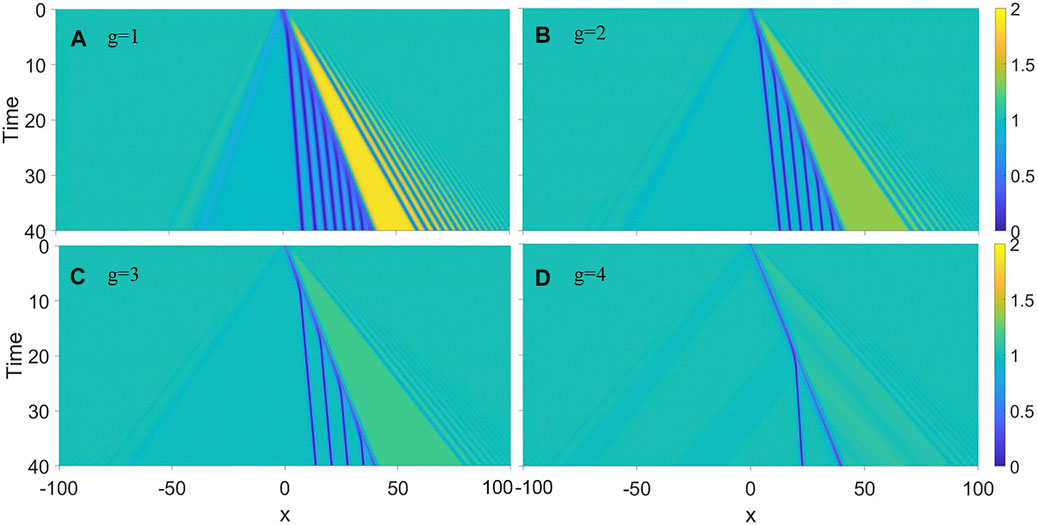
FIGURE 2. Comparison of soliton emission from a moving obstacle in a condensate of different nonlinear strength, (A) g = 1, (B) g = 2, (C) g = 3, (D) g = 4, respectively. The Gaussian obstacle with potential height A = 1 moves at fixed velocity v = 1.

We also study the dependence of soliton emission on the obstacle speed. We take the nonlinear strength g = 2 and the potential height A = 1. Figure 3 displays the emission of dark solitions from the Gaussian obstacle at different speed. More solitons are emitted as the obstacle moves faster. When v < 0.2, no solitons are emitted. As v = 0.5, the obstacle generate one soliton within time interval t = 40. We note that the solitons move leftwards instead of rightwards. As the obstacle speed increases to v = 1.2, more solitons are emitted and the solitons begin to move rightwards.

FIGURE 3

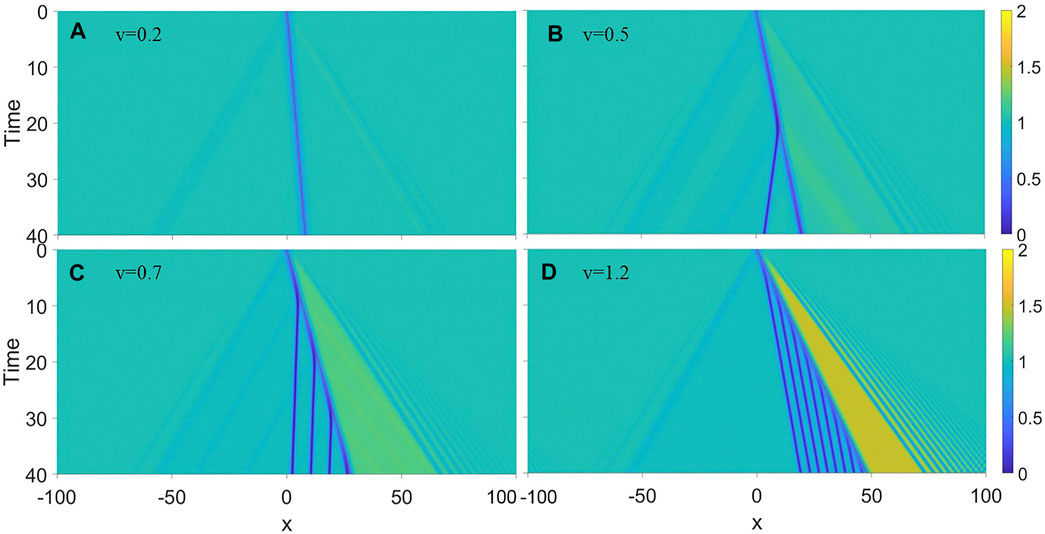
FIGURE 3. Dependence of solitonic emission on the obstacle speed v for (A) v = 0.2, (B) v = 0.5, (C) v = 0.7, (D) v = 1.2, respectively. The parameters take g = 2 and A = 1.

In Figure 4 we display the explicit relations of the soliton emission with the system parameters. For g = 2 and v = 1, the fitted curve in Figure 4A exhibits the velocity of solitons v₀ versus the height of obstacle potential A. In Figure 4B the velocity of solitons exhibits a non-monotonous dependence on the obstacle speed v under the condition of A = 1 and g = 2. Figure 4C plots the relation of soliton velocity versus the nonlinear strength g at potential height A = 1 and obstacle speed v = 1.

FIGURE 4

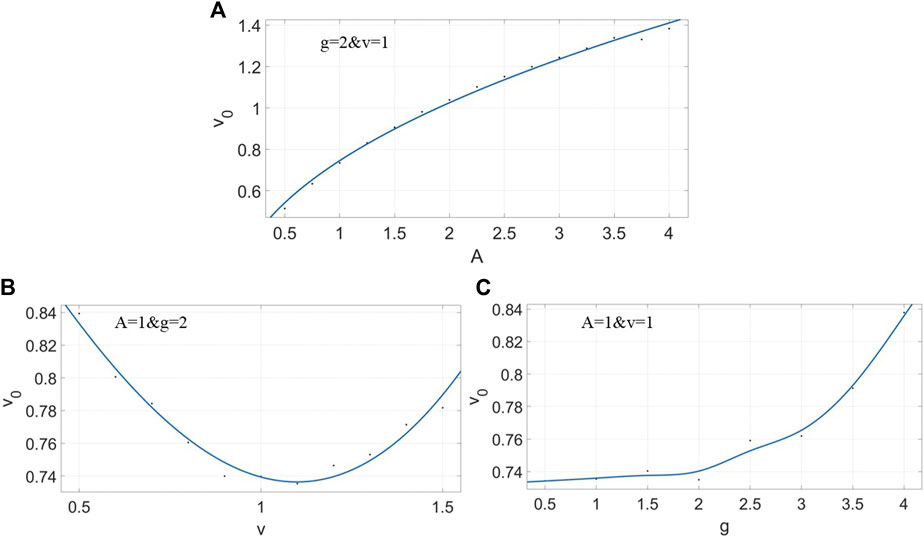
FIGURE 4. Fitting relations of soliton velocity with the system parameters. (A) Soliton velocity versus the obstacle height. (B) Soliton velocity versus the obstacle speed. (C) Soliton velocity versus the nonlinear strength.

Finally, we study a uniformly accelerated obstacle moving in the condensate from zero initial velocity. Figure 5 shows the emission of solitons from a accelerate obstacle with acceleration a = 0.05 for different nonlinear strength g. It shows that the solitons begin to emit only when the obstacle speed exceeds a critical value. The critical obstacle speed is v_c = 0.85 for g = 2 in Figure 5A and v_c = 1.3 for g = 4 in Figure 5B.

FIGURE 5

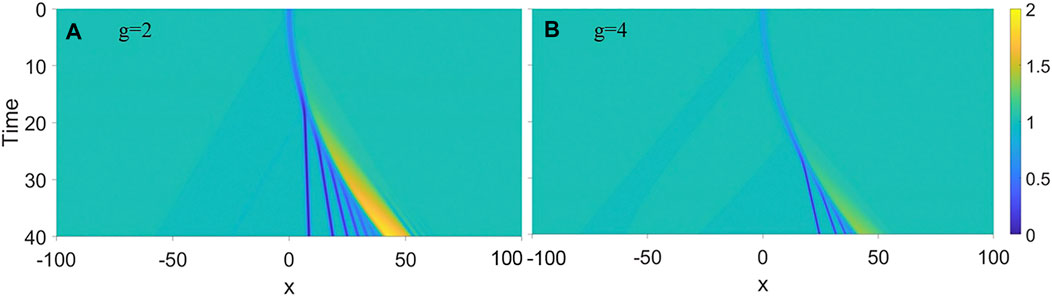
FIGURE 5. Solitonic emission from a uniformly accelerated obstacle with zero initial velocity. The acceleration is fixed at a = 0.05 and the obstacle height takes A = 1. The nonlinear strength are respectively (A) g = 2 and (B) g = 4. Dark solitons are emitted only as the obstacle velocity exceeds a critical value.

Up to this point, we have qualitatively discussed the law of solitons’ generation from moving obstacle. In short, if we want to generate more solitons during same time interval, we can take a higher obstacle moving faster and reduce the nonlinear strength. Then, if we want generate the solitons whose relative velocity is lager, we can take a higher obstacle.

4 Discussion

We try to understand the underlying mechanism of the soliton formation via a moving obstacle in the 1D condensate. In a previous publication, we have demonstrated that a hump or a defect in a uniform BEC background will exhibit solitonic diffusion [23]. The initial wavepacket splits into a series of dark solitons which travel at different velocity. The moving velocity of the soliton depends on non-linear interaction strength as well as the shape of a particular grey soliton. Soliton emission in the present paper is a phenomenon deeply related to work. In fact, the moving obstacle drills a defect in the uniform background, which thereafter diffuses like in Ref. [23]. The interference between the diffusing wavepacket and the condensate background yields a series of density fringes. These fringes are strengthened by the nonlinear interactions and finally leads to formation of dark solitons. The uniqueness comes from the diffusing source excited by the obstacle is in constant motion.

In order to explicitly show this process, we suppose that the initial wavepacket or defect is Gaussian,

$\phi \left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}},(5)$

where σ is the width of Gaussian wave-packet. The diffusion of this wavepacket in the 1D space evolves as

${\psi }_{\mathrm{d}}\left(x,t\right)=\sqrt{\frac{2\pi i}{t}}{\int }_{-\infty }^{\infty }\phi \left(x^{\prime }\right)e^{-\frac{i}{2t}{\left(x-x^{\prime }\right)}^2}d{x}^{\prime }.(6)$

Substitute Eq. 5 into Eq. 6 and perform the integral, we obtain an analytical expression for the free diffusion of wavepacket,

${\psi }_{\mathrm{d}}\left(x,t\right)=\frac{1}{\sqrt{2\pi \left({\sigma }^2+it\right)}}{e}^{-\frac{x^2}{2\left({\sigma }^2+it\right)}}.(7)$

The moving obstacle cause a moving diffusion source, hence we have the following form of diffusing wavefunction,

${\psi }_{\mathrm{d}}\left(x,t\right)=\frac{1}{\sqrt{2\pi \left({\sigma }^2+\frac{i\hslash t}{m}\right)}}{e}^{-\frac{{\left(x-vt\right)}^2}{2\left({\sigma }^2+i\hslash t/m\right)}},(8)$

where v is the obstacle speed.

On the other hand, the uniform condensate background acquire a plane wave phase relative to the moving source of diffusion. In the static frame of motion, it becomes a plane wave of the form

${\psi }_{\text{bg}}\left(x,t\right)=e^{-ip\left(x-vt\right)-\frac{i}{2}{p}^{2}t},(9)$

with the momentum of the plane wave p = v in our units. The superposition of the diffusing wavepacket ψ_d (x, t) and the uniform background ψ_bg (x, t) leads to interference described by the wavefunction

$\psi \left(x,t\right)=e^{-ip\left(x-vt\right)-\frac{i}{2}{p}^{2}t}+\frac{A}{\sqrt{2\pi \left({\sigma }^2+it\right)}}{e}^{-\frac{{\left(x-vt\right)}^2}{2\left({\sigma }^2+it\right)}},(10)$

where A is the height of Gaussian wave-packet.

Figure 6 displays the density profiles of wavefunction (10) for 1) v = 1.5 and 2) v = 2.5, respectively. The interfere fringes exhibit similar features as those in numerical simulations from the GP equation. Yet the density fringes are not solitonic, which is attributed to the effects of nonlinear interactions of the condensate. It demonstrates that the periodic emission of solitons is actually an interference effect between the diffusing defects and the BEC background. The nonlinear interactions enhance this process. The increase of obstacle speed implies increase of momentum p of the plane wave, which yields denser interference fringes. Hence, it seem more solitons are emitted in the same time interval as shown in Figure 6B.

FIGURE 6

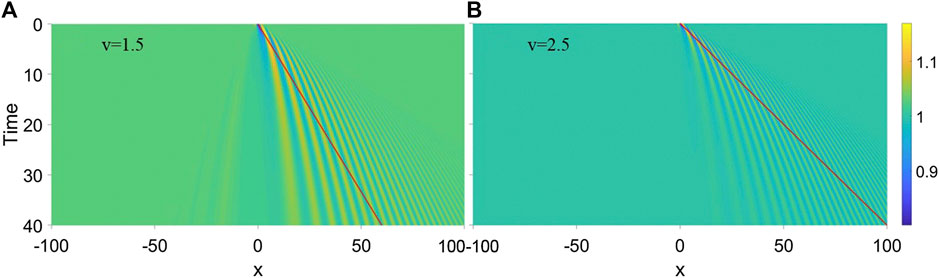
FIGURE 6. The density profiles of wavefunction (10) for (A) v = 1.5 and (B) v = 2.5, respectively. The Gaussian wavepacket takes A = 0.5 and σ = 1. The red line indicates the trail of the moving obstacle.

5 Summary

In summary, we have studied the dynamic generation of dark solitons from a moving obstacle. We find that the obstacle moving with constant velocity can periodically emit solitons. The underlying physics is explored and interpreted by interference between a diffusing wavepacket and the condensate background. Nonlinear interactions enhanced the formation of solitons during the evolution. Our prediction may be observed with the present techniques. It will help readers to get a deeper understanding of dynamical formation of solitons in nonlinear media and trigger new idea for solitonic creation for light transportation in liber.

This work is supported by the NSF of China under grant No. 11774034.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

S-JY and YS contributed to conception and design of the study. S-JY provided the ideas and directed all work. YS wrote the calculation program and organized the database. YM provided much help and many proposes about the calculation program. YS wrote the first draft of the manuscript, and S-JY revised the manuscript. Then SF revised the manuscript, and advised us to submit this paper to Frontiers in Physics.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kivshar YS, Luther-Davies B. Phys.Rep. (1998) 298:81.

CrossRef Full Text

2. Chabchoub A, Kimmoun O, Branger H, Hoffmann N, Proment D, Onorato M, et al. .Experimental Observation of Dark Solitons on the Surface of Water. Phys Rev Lett (2013) 110:124101. doi:10.1103/physrevlett.110.124101

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Weiner AM, Heritage JP, Hawkins RJ, Thurston RN, Kirschner EM, Leaird DE, et al. .Experimental Observation of the Fundamental Dark Soliton in Optical Fibers. Phys Rev Lett (1988) 61:2445–8. doi:10.1103/physrevlett.61.2445

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Baryakhtar VG, Ivanov BA, Sukstanskii AL, Melikhov EY. Soliton Relaxation in Magnets. Phys Rev B (1997) 56:619–35. doi:10.1103/physrevb.56.619

CrossRef Full Text | Google Scholar

5. Heidemann R, Zhdanov S, Sütterlin R, Thomas HM, Morfill GE. Dissipative Dark Soliton in a Complex Plasma. Phys Rev Lett (2009) 102:135002. doi:10.1103/physrevlett.102.135002

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Frantzeskakis DJ. Dark Solitons in Atomic Bose-Einstein Condensates: from Theory to Experiments. J Phys A: Math Theor (2010) 43:213001. doi:10.1088/1751-8113/43/21/213001

CrossRef Full Text | Google Scholar

7. Gisin BV. Existence of Solitons in Infinite Lattice, Phys.Rev.E (2006) 73:027601. doi:10.1103/physreve.73.027601

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Huang G, Velarde MG, Makarov VA. Phys Rev A (2001) 64:013617. doi:10.1103/physreva.64.013617

CrossRef Full Text

9. Stellmer S, Becker C, Soltan-Panahi P, Richter E-M, Dörscher S, Baumert M, et al. .Collisions of Dark Solitons in Elongated Bose-Einstein Condensates. Phys Rev Lett (2008) 101:120406. doi:10.1103/physrevlett.101.120406

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wen L, Sun Q, Wang D-S, Hu J, Chen H, Liu W-M, et al. .Motion of Solitons in One-Dimensional Spin-Orbit-Coupled Bose-Einstein Condensates. Phys Rev A (2016) 94:061602. doi:10.1103/physreva.94.061602

CrossRef Full Text | Google Scholar

11. Nguyen JHV, Dyke P, Luo D, Malomed BA, Hulet RG. Collisions of Matter-Wave Solitons. Nat Phys (2014) 10:918–22. doi:10.1038/nphys3135

CrossRef Full Text | Google Scholar

12. Yan D, Chang JJ, Hamner C, Hoefer M, Kevrekidis PG, Engels P, et al. .Beating Dark-Dark Solitons in Bose-Einstein Condensates. J Phys B: Mol Opt Phys (2012) 45:115301. doi:10.1088/0953-4075/45/11/115301

CrossRef Full Text | Google Scholar

13. Maity DK, Mukherjee K, Mistakidis SI, Das S, Kevrekidis PG, Majumder S, et al. .Parametrically Excited star-shaped Patterns at the Interface of Binary Bose-Einstein Condensates, Phys Rev A (2020) 102:033320. doi:10.1103/physreva.102.033320

CrossRef Full Text | Google Scholar

14. Parker NG, Martin AM, Cornish SL, Adams CS. Collisions of Bright Solitary Matter Waves, J Phys B: At Mol Opt Phys (2008) 41:045303. doi:10.1088/0953-4075/41/4/045303

CrossRef Full Text | Google Scholar

15. Anderson BP, Haljan PC, Regal CA, Feder DL, Collins LA, Clark CW, et al. .Watching Dark Solitons Decay into Vortex Rings in a Bose-Einstein Condensate. Phys Rev Lett (2001) 86:2926–9. doi:10.1103/physrevlett.86.2926

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wu B, Liu J, Niu Q. Controlled Generation of Dark Solitons with Phase Imprinting, Phys Rev Lett (2002) 88:034101. doi:10.1103/physrevlett.88.034101

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Polkovnikov A, Sengupta K, Silva A, Vengalattore M. Colloquium: Nonequilibrium Dynamics of Closed Interacting Quantum Systems. Rev Mod Phys (2011) 83:863–83. doi:10.1103/revmodphys.83.863

CrossRef Full Text | Google Scholar

18. Shomroni I, Lahoud E, Levy S, Steinhauer J. Evidence for an Oscillating Soliton/vortex Ring by Density Engineering of a Bose-Einstein Condensate. Nat Phys (2009) 5:193–7. doi:10.1038/nphys1177

CrossRef Full Text | Google Scholar

19. Romero-Ros A, Katsimiga GC, Kevrekidis PG, Prinari B, Biondini G, Schmelcher P. On-demand Generation of Dark Soliton Trains in Bose-Einstein Condensates, Phys Rev A (2021) 103:023329. doi:10.1103/physreva.103.023329

CrossRef Full Text | Google Scholar

20. Romero-Ros A, Katsimiga GC, Kevrekidis PG, Schmelcher P. Controlled Generation of Dark-Bright Soliton Complexes in Two-Component and Spinor Bose-Einstein Condensates, Phys Rev A (2019) 100:013626. doi:10.1103/physreva.100.013626

CrossRef Full Text | Google Scholar

21. El GA, Gammal A, Kamchatnov AM. Oblique Dark Solitons in Supersonic Flow of a Bose-Einstein Condensate. Phys Rev Lett (2006) 97. doi:10.1103/physrevlett.97.180405

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Engels P, Atherton C. Stationary and Nonstationary Fluid Flow of a Bose-Einstein Condensate through a Penetrable Barrier. Phys Rev Lett (2007) 99:160405. doi:10.1103/physrevlett.99.160405

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Mo Y, Zhang C, Feng S, Yang S-J. Chin Phys Lett (2019) 36:120301.

CrossRef Full Text

24. Pitaevskii LP, Stringari S. Bose-Einstein Condensation. Cambridge: Cambridge University Press (2003).

Google Scholar

25. Barenghi CF, Parker NG. A Primer on Quantum Fluids. Berlin: Springer (2016).

Google Scholar

26. Carr LD, Clark CW, Reinhardt WP. Stationary Solutions of the One-Dimensional Nonlinear Schrödinger Equation. I. Case of Repulsive Nonlinearity, Phys Rev A (2000) 62:063611. doi:10.1103/physreva.62.063610

CrossRef Full Text | Google Scholar