Central Density and Low-Mode Perturbation Control of Inertial Confinement Fusion Dynamic-Shell Targets

The dynamic-shell target is a new class of design for inertial confinement fusion (ICF). These targets address some of the target fabrication challenges prevalent in current ICF targets and take advantage of advances in manufacturing technologies. This study first examines how the dynamic-shell design can be used to control the density of the central region and therefore convergence ratio, thus expanding the design space for ICF. Additionally, the concern of low-mode perturbation growth is considered. A new class of high-performing beam configurations, based on icosahedral polyhedra and charged-particle simulations is proposed. These configurations achieve low levels of irradiation nonuniformity through selection of beam shapes that suppress the dominant symmetrical mode.

1 Introduction

A novel inertial confinement fusion (ICF) “dynamic-shell” target design was recently proposed by V. Goncharov et al. [1]. This new generation of target aims to address a number of challenging issues with the current cryogenic, solid DT shell capsule targets. The standard approach in ICF aims to achieve gain by igniting a small portion of low density fuel in a central hot-spot, triggering a burn wave that will propagate through a surrounding, high-density fuel shell [2]. Such targets are composed of a cryogenic, solid DT shell filled with DT gas at the equilibrium vapor pressure. These targets present a number of challenges, including the production of a uniform ice layer that can be affected by engineering features (fill tubes, stalks, characterization windows, etc.) [3–5]. By contrast, the dynamic-shell target uses a liquid DT sphere encased in a wetted-DT foam. A high-density shell is then formed dynamically in-flight via a series of laser pulses that compress the target, allow it to rebound, then decelerate the expanding plasma, forming a shock that develops into the shell. The liquid DT, foam shells are intrinsically much more uniform, do not require a gas fill tube and do not have a gas shell interface, making them an attractive choice of target for inertial fusion energy (IFE) applications [6].

Figure 1 outlines a dynamic-shell target design. The laser profile consists of a number of pickets that send a series of shocks into the target, controlling the formation of the dynamic-shell. In this case, the pulse consists of a series of pickets but it should be noted that long periods of relatively low power can be used [1]. Pickets are expected to be more robust to nonuniformity growth. Mass density profiles at key times in the dynamic-shell formation are shown in Figure 1. In the initial compression phase (0–50  ns) the target is accelerated inward and converges in the center at ∼55  ns. The target subsequently rebounds and begins to expand outward; this allows for a low-density central region to form. From then on, the pickets raise the ablation pressure in the outer regions and begin to counteract the expansion of the target. At 280 ns the ablation pressure becomes sufficient to reverse the flow, launching an inward-traveling shock and forming a high-density shell. At this point the target can be imploded and ignited in the same manner as a traditional ICF target, either through central hot-spot ignition or shock ignition [7]. For the target shown in Figure 1, 0.25 MJ of the total 1.3 MJ pulse energy was contained in the pickets.

FIGURE 1

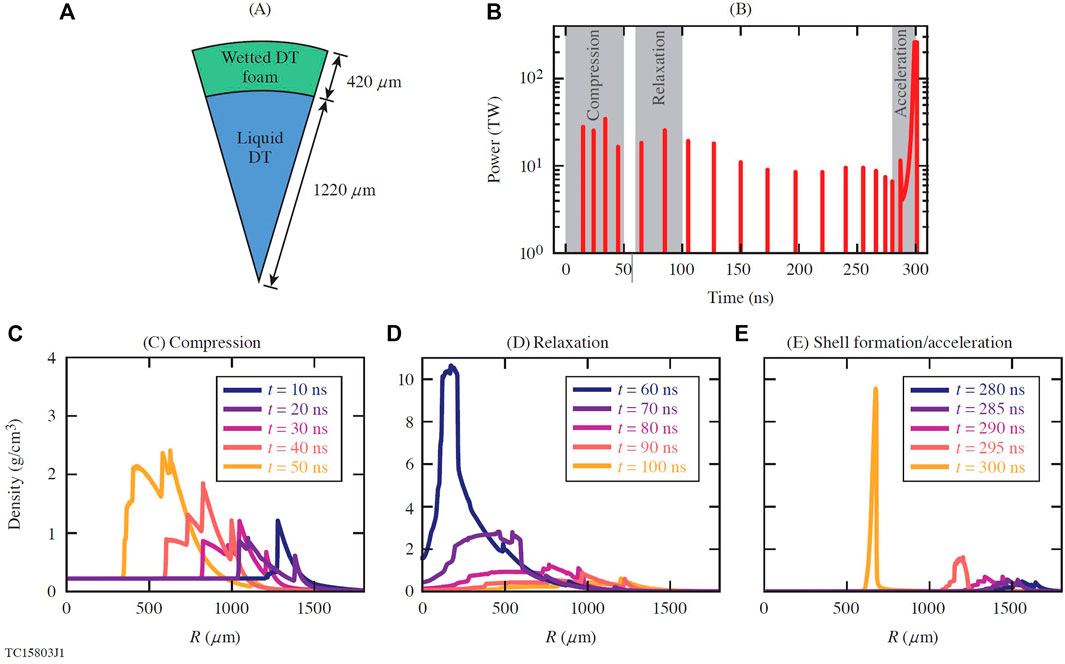
FIGURE 1. (A) A radial slice of the liquid deuterium DT-wetted foam target. (B) Time profile of the laser power, the highlighted regions correspond to the mass density profiles in the plots below. Mass density profiles taken at key times from LILAC simulations, that show (C) compression, (D) relaxation and (E) formation of the dynamic-shell.

It should be noted that the here we only consider the dynamic shell target in a direct-drive configuration [8] where the lasers are shone directly onto the capsule surface. In indirect-drive [9], the lasers are shone onto the inner surface of a high-Z casing (termed a hohlraum) creating a bath of X-rays which is then used as a drive source. Complex pulse shapes such as those employed for the dynamic shell are incredibly challenging to model in indirect-drive [10, 11], so currently we limit the scope of the dynamic shell design to direct-drive only.

The energy, power and shaping requirements of the dynamic shell pulses are all within the limits of available laser technology. However, current ICF-relevant laser systems (e.g., the National Ignition Facility [12]) only have a limited total pulse length of ≤35 ns. Ignition targets with pulses of hundreds of nanoseconds will require a new class of laser technology, such as the StarDriver™ described in Ref. [13].

In this work, it is shown how the dynamic-shell target can control the density of the central region of the target. Additionally we also summarize a study on potential laser beam configurations in order to minimize detrimental low-mode pressure perturbations.

2 Density Control of the Central Region

Shell convergence ratio (CR) in a conventional design with a cryogenic DT shell is controlled mainly by the implosion velocity V_imp and shell adiabat α defined as the ratio of shell pressure to the Fermi pressure at shell density, α = P/P_F, $\text{CR}\sim V_{\text{imp}}^{0.7}/{\alpha }^{0.3}$. Considering that the shell in-flight aspect ratio IFAR ≡ R/ΔR, scales as $\text{IFAR}\sim V_{\text{imp}}^2/(p_{\text{a}}^{2/5}{\alpha }^{3/5})$, convergence ratio mainly depends on the shell IFAR, $\text{CR}\sim {\text{IFAR}}^{0.35}{p}_{\text{a}}^{0.14}/{\alpha }^{0.1}$, and weak dependence on adiabat and ablation pressure p_a can be neglected. This shows that, to increase convergence to meet the ignition design requirement, the shell IFAR must be relatively high. This makes the shell susceptible to hydrodynamic instabilities developed during shell acceleration. This is the motivation behind recent work that has attempted to used wetted-foam [14] layers to design ICF targets with low CR [15]. There is however, one more design parameter that controls the shell convergence: initial density of the central (vapor) region. In the standard target with a cryogenic layer, density of the central region is controlled by ice temperature. At triple point of DT ice with D:T = 50:50, 19.7 K the central density is 0.7 mg/cm³. The density drops to 0.3 mg/cm³ when the ice temperature is reduced to 18 K. This reduction in the central density by more than a factor of two leads to $\sim 50\%$ increase in the shell convergence ratio (see Figure 2). A much wider range of central density can be achieved in the dynamic-shell design, where density relaxation is created by the blast wave formed as the initial shock bounces from the target center. The stronger the blast wave and the longer the relaxation time, the smaller central densities can be achieved in the dynamically formed shell.

FIGURE 2

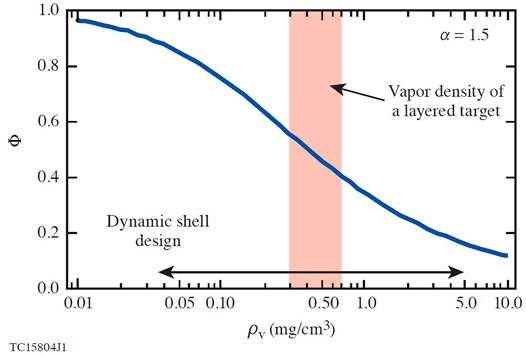
FIGURE 2. The expanded design space for the dynamic-shell compared to a standard layered target. The Φ term on the y-axis is directly proportional to the convergence ratio.

Figure 3 shows two different pulse shapes used to create a dynamic-shell. The longer pulse allows for an extended period of expansion before forming the dynamic-shell. As previously discussed, the additional expansion time should result in a lower central density. Simulations of these two laser pulses were carried out with the 1-D radiation-hydrodynamic code LILAC [16]. In each case the target was a 1220 μm-thick DT-liquid capsule with a 420 μm-thick DT-wetted foam shell. Figure 3 shows the mass density profile of the target for the long- and short-pulse designs at 208 and 295  ns, respectively. For each of the laser pulses the shell has a similar width and density profile. However, for the long-pulse, the additional expansion resulted in a central density of 0.1 mg/cm³ compared to the shorter pulse, which has a central density of 0.8 mg/cm³. Although both target designs ignite with the gain near 100, the hot-spot formation histories are quite different. The effect of reduced density in the central region of the dynamically formed shell on Rayleigh-Taylor instability during shell deceleration will be addressed in future publications.

FIGURE 3

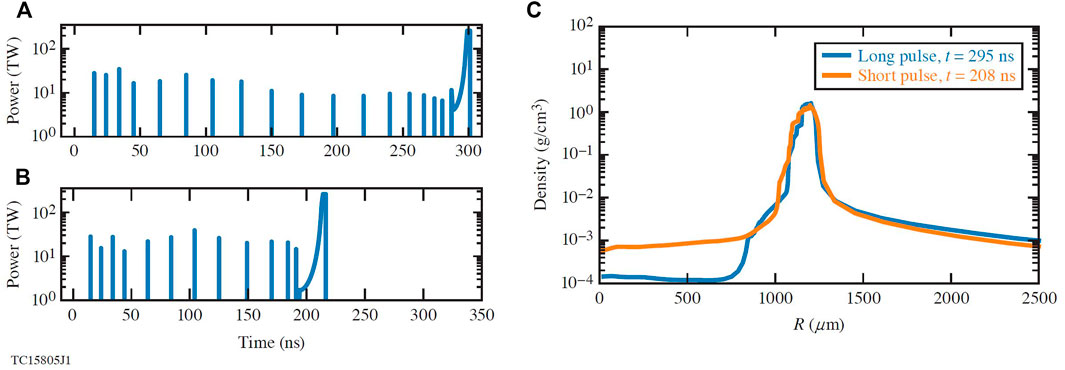
FIGURE 3. (A,B) A comparison between a short and long dynamic-shell laser pulse. (C) Mass density profiles taken from the LILAC simulations.

3 Low-Mode Perturbation Mitigation

A key concern for the dynamic-shell design is the potential growth of low-mode (ℓ⩽ 20) instabilities. The long pulse lengths involved in the dynamic-shell target give opportunity for low-mode perturbations to grow. For this reason, it is important to choose a beam configuration that minimizes any potential nonuniformity in the laser irradiation profile. Here we employ a technique developed by Murakami et al. [17–19], to investigate optimum beam configurations for the dynamic-shell design. Each beam origin is modeled as a charged-particle fixed to the surface of a sphere. In Ref. [18], the conjecture is that a configuration in which the total Coulomb potential of all particles is minimized produces the optimum beam configuration. This configuration is found via a numeric simulation where the particles are allowed to repel and move along the sphere surface. Historically, this problem is referred to as the Thomson problem, for which there exists a large body of previous work [20–22]. This study employs a method similar to that of Ref. [18]. N_B (where N_B is the number of beams) particles are distributed randomly on the surface of a sphere and allowed to repel each other through a Coulomb-like force with a friction-like term,

$F_r=A\sum _{j=1(j\ne i)}^{N_{\text{B}}}\frac{{\widehat{\mathbf{r}}}_{\mathbf{i}}-{\widehat{\mathbf{r}}}_{\mathbf{j}}}{|{\widehat{\mathbf{r}}}_{\mathbf{i}}-{\widehat{\mathbf{r}}}_{\mathbf{j}}{|}^3}-B\frac{\text{d}{\widehat{\mathbf{r}}}_{\mathbf{i}}}{\text{d}t}.(1)$

The constants A and B can be modified over the course of the simulation in order to achieve rapid convergence. Convergence was defined as the point where a time step changed the Coulomb potential E_p, by no more than 10^–11, where the potential is given by

$E_{\text{p}}=\frac{1}{2}\sum _{i=1}^{N_{\text{B}}}\sum _{j=1(j\ne i)}^{N_{\text{B}}}\frac{1}{|{\widehat{\mathbf{r}}}_{\mathbf{i}}-{\widehat{\mathbf{r}}}_{\mathbf{i}}|}.(2)$

Once a beam configuration has been determined, an analytic model is used to evaluate σ_rms, the root-mean-square (rms) nonuniformity. The analytic model was devised by Skupsky et al [23]. and extended by Murakami et al. [18]. The model is based on the following expression for the nonuniformity

${\sigma }_{\text{rms}}={\left[\sum _{n=1}^{\infty }\frac{a_n^2}{2n+1}\left(G_n^2+\frac{{\sigma }_{\text{sys}}^2}{N_{\text{B}}}\right)\right]}^{1/2},(3)$

$a_n=\frac{2n+1}{2}{\int }_{-1}^1{I}_a(\theta )P_n(\cos \theta )\text{d}(cos\theta ),(4)$

$G_n={\left[\sum _{j=1}^{N_{\text{B}}}\sum _{k=1}^{N_{\text{B}}}{P}_n({\widehat{\mathbf{\Omega }}}_{\mathbf{j}}\cdot {\widehat{\mathbf{\Omega }}}_{\mathbf{k}})\right]}^{1/2}/N_{\text{B}}.(5)$

The a_n coefficients are contributions from laser spot profile and are calculated from I_a(θ), the irradiation absorption as a function of polar angle and P_n, the Legendre polynomials. In this case, the irradiation absorption is given by [24].

$I_a(\theta )=I_0\left[1-{(1-\eta )}^{{\cos }^3\theta }\right]\exp \left[-{(\sin \theta /c)}^n\right],(6)$

where η is the absorption efficiency and c and n are super-Gaussian parameters defined by $I(r)=I_0\exp \left[-{(r/c)}^n\right]$. The model used to find Eq. 6 divides the incoming laser into a number of rays, projected through a corona with an exponential density profile; it is assumed that collisional absorption takes place along the ray trajectory [18]. Beam radius, r_beam is defined as the radius containing 95% of the beam energy. The G_n coefficients are contributions from the geometric configuration of the beams. Finally, the ${\sigma }_{\text{sys}}^2$ term accounts for any imperfections in the system (e.g., target offset, target defects, beam speckle etc.). From here on we refer to the $a_n^2/(2n+1)$ term as the “single-beam factor” and G_n as the “geometric factor”.

Configurations were found using the charged-particle technique for 6 ≤ N_B ≥ 192 (even numbers only).

With the assumption that σ_sys = 0 and η = 0.95, the σ_rms was evaluated for each configuration for a number of super-Gaussian beam parameters using Eqs 3–6; the results are displayed in Figure 4. At ∼50–70 beams the reduction in rms begins to plateau and scales as $1/\sqrt{N_{\text{B}}}$. It can be seen that at N_B = 72 there is significant drop in σ_rms. As pointed out by Murakami et al. [18, 19], this can be attributed to highly symmetric beam configurations. Here we provide a more precise reasoning for this high performance. It can be better understood by examining the single-beam factor and geometric factor for r_beam = 1.2, n = 2 and N_B = 72. Figure 5 shows the value of the single-beam factor and geometric factor at each mode number. The G_n values for N_B = 70 are also plotted to demonstrate the unique spectral mode structure of a highly symmetric configuration. For any typical configuration found with the charged-particle technique, all modes give a small contribution to the rms nonuniformity and, due to the decaying nature of the single-beam factor, the lower modes give the more significant contribution. In contrast, a symmetric configuration has specific modes where G_n peaks and all other modes are effectively negligible. This means that, in the case of N_B = 72, the ℓ = 6 mode is the only significant contributor to the rms nonuniformity. The dip in the single beam factor using r_beam = 1.2 and n = 2 suppresses the ℓ = 6 mode and results in a very low rms nonuniformity. The peak in G_n at ℓ = 6 mode is a result of the icosahedral symmetry of the N_B = 72 configuration. Working from this basis, a new class of beam configuration is found that perform better than previous designs.

FIGURE 4

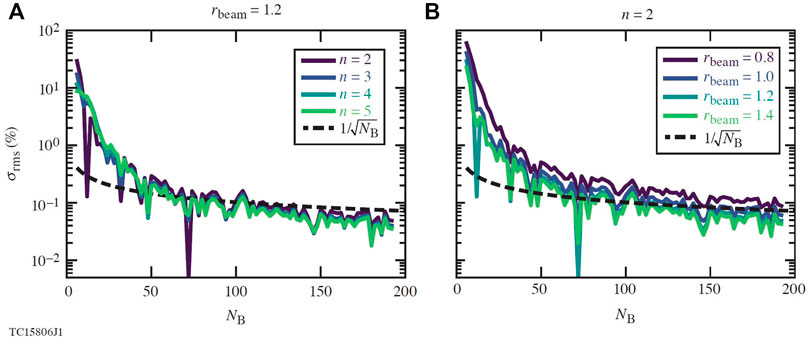
FIGURE 4. Plots of how the rms nonuniformity scales with beam number for several different Gaussian beam parameters. Note r_beam = 1.2 and n = 2 were chosen due to their high performance (see Figure 8). (A) Fixed r_beam = 1.2 with varying n. (B) Fixed n = 2 with varying r_beam.

FIGURE 5

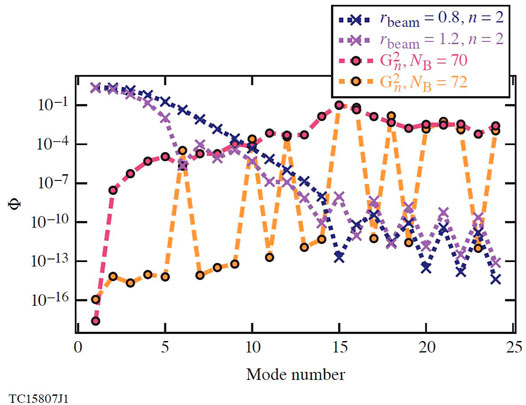
FIGURE 5. A plot of the values of G_n and $a_n^2/(2n+1)$ for mode numbers 1 to 24. Two single-beam factors are shown, the r_beam = 1.2, n = 2 beam configuration suppresses the ℓ = 6 mode. Two sets of $G_n^2$ values are shown, the N_B = 72 configuration is highly symmetric and therefore forms peaks at specific mode numbers.

Geodesic icosahedra are a class of polyhedra formed via subdivision of the faces of an icosahedron and projecting the resulting vertices onto the surface of a sphere. A list of vertex coordinates for such shapes were taken from Ref. [25] and used as angular coordinates for beam configurations. The N_B = 32, 42, 72, 92, 122, 132, 172 and 192 configurations are formed from the vertices of geometric icosahedra, whereas the N_B = 60, 80, 140 and 180 configurations used the coordinates of the face centers. The geometric factors and subsequent rms nonuniformities were calculated for these configurations using the parameters r_beam = 0.8, 1.2 and n = 2. The results are displayed in Figure 6. It can be seen that, for the beam configuration (r_beam = 1.2, n = 2) that suppresses the ℓ = 6 mode, the symmetric configurations perform better than the corresponding charged-particle configurations. Conversely it is also possible for certain beam parameters to amplify the ℓ = 6 mode resulting in a higher σ_rms; this can be seen for smaller beams with r_beam = 0.8, n = 2. It is noted that the authors suspect there is a similar class of octahedrally symmetric configurations that can be constructed from geodesic octohedra. Such configurations will have a significant ℓ = 4 mode which can similarly be suppressed with appropriate beam parameters. This is likely the origin of the high performing N_B = 48 beam configuration observed by Murakami et al. [18].

FIGURE 6

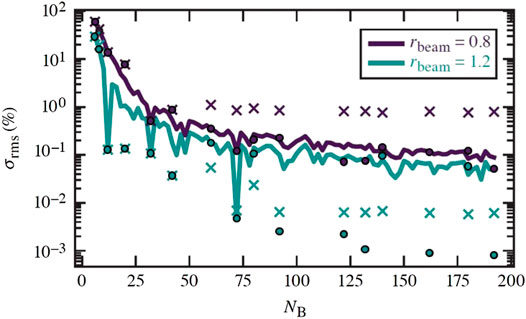
FIGURE 6. Comparison of the rms nonuniformity between symmetric and charged-particle configurations. The solid line shows the results from charged-particle configurations. The x’s are from configurations based on geometric icosahedra. The circles are from charged-particle configurations that were initialized with geometric icosahedral positions.

At $\sim N_{\text{B}}=100$ the σ_rms in the geodesic icosahedral configurations flattens (see Figure 6). An improvement was found when using the geometric configurations as a starting point for a charged-particle simulation. Figure 7 shows the difference in the icosahedral configuration and the icosahedral initialized charged-particle configuration. A small change occurs in the positioning, which results in a reduction of the ℓ = 6 mode while increasing some of the other modes. The results from those improved configurations are shown as circles on Figure 6. It is interesting to note however, that this improvement was only found in configurations with particles positioned at vertices. For face-centered particles, the charged-particle simulation reverted the configuration back to a less-optimal configuration. Consequently, it is the case that minimization of the Coulomb potential does not always result in the lowest σ_rms configuration. σ_rms also varies with the super-Gaussian parameters. Figure 8 shows contour plots of the σ_rms for the three different configurations for 92 beams. For charged-particle configurations it appears that there is a weak dependence on n and it is generally better to use large r_beam. However, for the more symmetric configurations, there is a narrow band in which high performance is achieved.

FIGURE 7

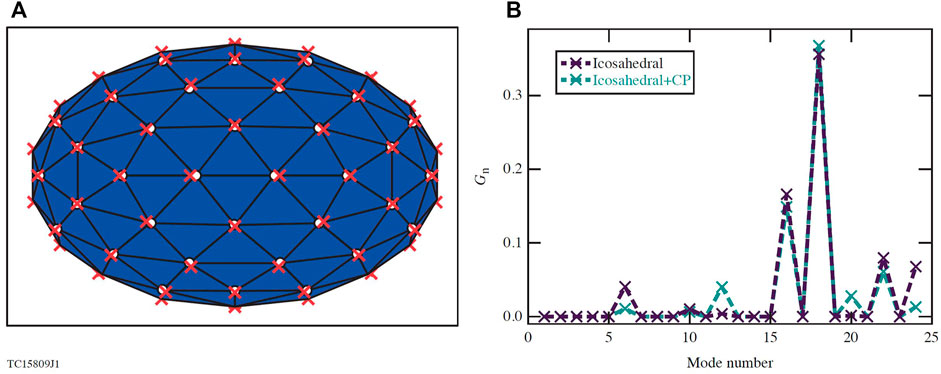
FIGURE 7. (A) 3D plot of two 92 beam configurations. The white circles and blue surface show the icosahedral configuration, the red x’s are where the points move under a charged-particle simulation initialized with the icosahedral positions. (B) The geometric factor values for the two configurations shown in (A).

FIGURE 8

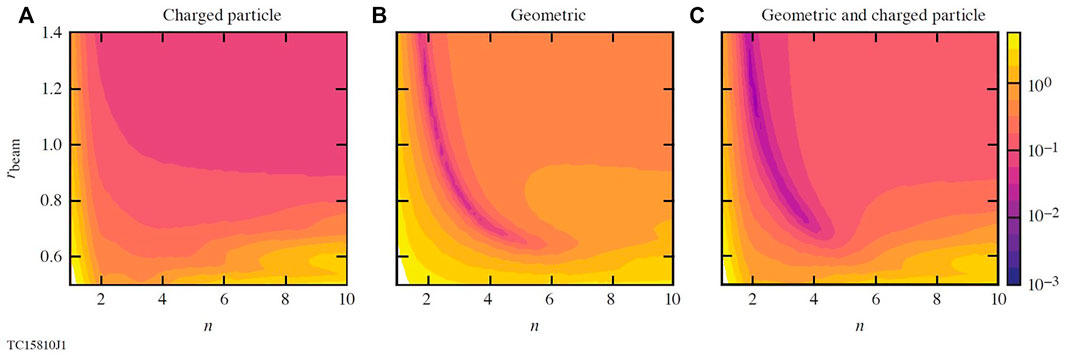
FIGURE 8. Contour plots for how σ_rms varies with the beam parameters r_beam and n. All plots are for 92 beam configurations, (A) charged-particle configuration with a random initialization (B) geodesic icosahedral configuration (C) charged-particle initialized with geodesic icosahedral configuration.

Up to this point, imperfections in the laser and target have been neglected. Such effects can be included the model via the ${\sigma }_{\text{sys}}^2$ term in Eq. 3. Figure 9 compares how the rms nonuniformity scales with σ_sys for symmetric, icosahedric configurations against charged-particle configurations. It can be seen that benefit of the geometric configurations is reduced once the system rms reaches 1–2%. From that point on, the geometric configurations perform equally as well as the charged-particle configurations. It should still be pointed out, that whilst the performance is the same, the spectral mode structure of the nonuniformity will be different. This means that for perturbations such as beam imbalance and target offset (which typically mostly contribute mode 1 and mode 2) the benefit of reduced mode 6 is still present.

FIGURE 9

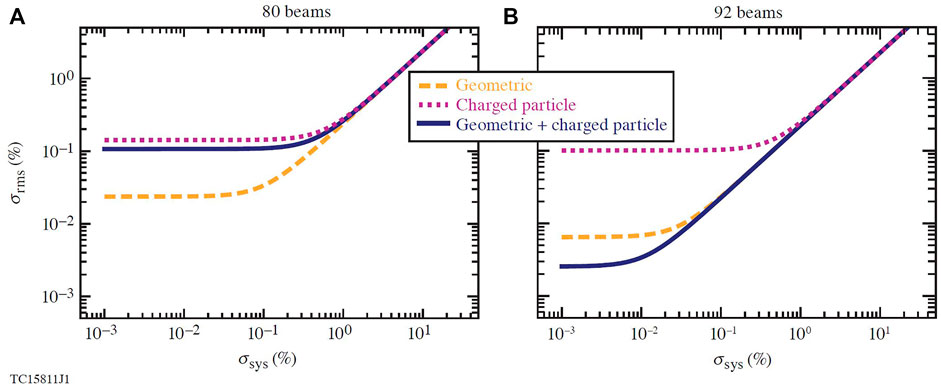
FIGURE 9. Plots that show how the rms nonuniformity scales with the system rms. In each plot the scaling is shown for charged-particle configurations (dotted line), geodesic icosahedral configurations (dashed line) and charged-particle configurations with geodesic icosahedral initial setups (solid line). The 80-beam (A) configuration is face-centered whereas the 92 beam configuration (B) is vertex-centered.

The results from this study suggest that, if system rms (e.g., target offset, beam mispointing, power imbalance etc.) can be kept below 1–2%, the optimized icosahedral configurations will perform better than the charged particle ones. This is a reasonable goal; the value of 1% is commonly used as an upper limit on acceptable nonuniformity [8]. However, it is worth noting that if nonuniformity did go above this 1% limit, a symmetric configuration would be equally as optimal as a charged-particle configuration with an equal beam number.

Current investigations have been limited to the use of an analytic physics model. Further work will be done in 2-& 3-D simulations in order to evaluate the conclusions drawn so far, also it may be interesting to consider if any further improvements can be made to beam shapes.

4 Conclusion

Dynamic-shell ICF targets represent a new class of designs that will not experience the manufacturing issues present in the standard cryogenic shell targets. In this work, an additional benefit was demonstrated in that, by controlling the central density through laser pulse shape, the convergence ratio can be modified, expanding the ICF target design space. Further to that, uniform beam irradiation was investigated in order to mitigate the low-mode perturbations to which the dynamic-shell implosion may be susceptible. A new class of beam configuration formed through charged-particle simulations of geodesic icosahedral vertices were discovered. These configurations were shown to perform better than previously proposed charged-particle configurations by more than an order of magnitude. However, to achieve high performance, specific super-Gaussian beam parameters must be used, while keeping other nonuniformities below 1%.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WT carried out all simulations and analysis directly supervised by VG. All other Authors offered support and guidance for the work.

Funding

Funding was provided by the ARPA-E BETHE Grant No. DE-FOA-0002212. This material is based upon work supported by the Department of Energy National Nuclear Security Administration under Award Number DE-NA0003856, the University of Rochester, and the New York State Energy Research and Development Authority.

Author Disclaimer

The support of DOE does not constitute an endorsement by DOE of the views expressed in this paper. This report was prepared as an account of work sponsored by an agency of the U.S. Government. Neither the U.S. Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the U.S. Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the U.S. Government or any agency thereof.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Goncharov VN, Igumenshchev IV, Harding DR, Morse SFB, Hu SX, Radha PB, et al. .Novel Hot-Spot Ignition Designs for Inertial Confinement Fusion with Liquid-Deuterium-Tritium Spheres. Phys Rev Lett (2020) 125:065001. doi:10.1103/PhysRevLett.125.065001

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Atzeni S, Meyer-ter Vehn J. The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter, Vol. 125. Oxford: OUP Oxford (2004).

Google Scholar

3. Lindl J, Landen O, Edwards J, Moses E, Adams J, Amendt PA, et al. .Review of the National Ignition Campaign 2009-2012. Phys Plasmas (2014) 21:020501. doi:10.1063/1.4865400

CrossRef Full Text | Google Scholar

4. Weber CR, Casey DT, Clark DS, Hammel BA, MacPhee A, Milovich J, et al. .Improving ICF Implosion Performance with Alternative Capsule Supports. Phys Plasmas (2017) 24:056302. doi:10.1063/1.4977536

CrossRef Full Text | Google Scholar

5. Rinderknecht HG, Casey DT, Hatarik R, Bionta RM, Macgowan BJ, Patel P, et al. .Azimuthal Drive Asymmetry in Inertial Confinement Fusion Implosions on the National Ignition Facility. Phys Rev Lett (2020) 124:145002. doi:10.1103/physrevlett.124.145002

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sacks RA, Darling DH. Direct Drive Cryogenic ICF Capsules Employing D-T Wetted Foam. Nucl Fusion (1987) 27:447–52. doi:10.1088/0029-5515/27/3/009

CrossRef Full Text | Google Scholar

7. Betti R, Zhou CD, Anderson KS, Perkins LJ, Theobald W, Solodov AA. Shock Ignition of Thermonuclear Fuel with High Areal Density. Phys Rev Lett (2007) 98(15):155001. doi:10.1103/physrevlett.98.155001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Craxton RS, Anderson KS, Boehly TR, Goncharov VN, Harding DR, Knauer JP, et al. .Direct-Drive Inertial Confinement Fusion: A review. Physics of Plasmas (2015) 22(11):110501. doi:10.1063/1.4934714

CrossRef Full Text | Google Scholar

9. Lindl J. Development of the Indirect‐drive Approach to Inertial Confinement Fusion and the Target Physics Basis for Ignition and Gain. Phys Plasmas (1995) 2:3933–4024. doi:10.1063/1.871025

CrossRef Full Text | Google Scholar

10. Kirkwood RK, Moody JD, Kline J, Dewald E, Glenzer S, Divol L, et al. .A Review of Laser-Plasma Interaction Physics of Indirect-Drive Fusion. Plasma Phys Control Fusion (2013) 55:103001. doi:10.1088/0741-3335/55/10/103001

CrossRef Full Text | Google Scholar

11. Moody JD, Callahan DA, Hinkel DE, Amendt PA, Baker KL, Bradley D, et al. .Progress in Hohlraum Physics for the National Ignition Facility. Phys Plasmas (2014) 21:056317. doi:10.1063/1.4876966

CrossRef Full Text | Google Scholar

12. Spaeth ML, Manes KR, Bowers M, Celliers P, Nicola J-MD, Nicola PD, et al. .National Ignition Facility Laser System Performance. Fusion Sci Techn (2016) 69:366–94. doi:10.13182/fst15-136

CrossRef Full Text | Google Scholar

13. Eimerl D, Campbell M, Krupke W, Zweiback J, Kruer W, Marozas J, et al. .StarDriver: A Flexible Laser Driver for Inertial Confinement Fusion and High Energy Density Physics. J Fusion Energ (2014) 33:476–488. doi:10.1007/s10894-014-9697-2

CrossRef Full Text | Google Scholar

14. Olson RE, Leeper RJ, Yi SA, Kline JL, Zylstra AB, Peterson RR, et al. .Wetted Foam Liquid Fuel ICF Target Experiments. J Phys Conf Ser (2016) 717:012042. doi:10.1088/1742-6596/717/1/012042

CrossRef Full Text | Google Scholar

15. Paddock RW, Martin H, Ruskov RT, Scott RHH, Garbett W, Haines BM, et al. .One-dimensional Hydrodynamic Simulations of Low Convergence Ratio Direct-Drive Inertial Confinement Fusion Implosions. Phil Trans R Soc A (2021) 379(2189):20200224. doi:10.1098/rsta.2020.0224

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Delettrez J, Epstein R, Richardson MC, Jaanimagi PA, Henke BL. Effect of Laser Illumination Nonuniformity on the Analysis of Time-Resolved X-ray Measurements in Uv Spherical Transport Experiments. Phys Rev A (1987) 36:3926–34. doi:10.1103/physreva.36.3926

CrossRef Full Text | Google Scholar

17. Murakami M, Nishihara K, Azechi H. Irradiation Nonuniformity Due to Imperfections of Laser Beams. J Appl Phys (1993) 74:802–8. doi:10.1063/1.354869

CrossRef Full Text | Google Scholar

18. Murakami M, Sarukura N, Azechi H, Temporal M, Schmitt AJ. Optimization of Irradiation Configuration in Laser Fusion Utilizing Self-Organizing Electrodynamic System. Phys Plasmas (2010) 17(8):082702. doi:10.1063/1.3467497

CrossRef Full Text | Google Scholar

19. Murakami M, Nishi D. Optimization of Laser Illumination Configuration for Directly Driven Inertial Confinement Fusion. Matter Radiat Extremes (2017) 2:55–68. doi:10.1016/j.mre.2016.12.002

CrossRef Full Text | Google Scholar

20. Thomson JJ. XXIV. On the Structure of the Atom: an Investigation of the Stability and Periods of Oscillation of a Number of Corpuscles Arranged at Equal Intervals Around the Circumference of a circle; with Application of the Results to the Theory of Atomic Structure. Lond Edinb Dublin Phil Mag J Sci (1904) 7(39):237–65. doi:10.1080/14786440409463107

CrossRef Full Text | Google Scholar

21. Erber T, Hockney GM. Equilibrium Configurations of N Equal Charges on a Sphere. J Phys A Math Gen (1991) 24(23):L1369–L1377. doi:10.1088/0305-4470/24/23/008

CrossRef Full Text | Google Scholar

22. Morris JR, Deaven DM, Ho KM. Genetic-algorithm Energy Minimization for point Charges on a Sphere. Phys Rev B (1996) 53:R1740–R1743. doi:10.1103/physrevb.53.r1740

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Skupsky S, Short RW, Kessler T, Craxton RS, Letzring S, Soures JM. Improved Laser‐beam Uniformity Using the Angular Dispersion of Frequency‐modulated Light. J Appl Phys (1989) 66:3456–62. doi:10.1063/1.344101

CrossRef Full Text | Google Scholar

24. Kruer WL. The Physics of Laser Plasma Interactions (2019). Boca Raton: CRC Press.

Google Scholar

25. Mccooey DI. Visual Polyhedra (2015). Available at: http://dmccooey.com/polyhedra/

Google Scholar