Critical Damage and Microstructure Characteristics of Sandstone in the Three Gorges Reservoir Area by Single Specimen Method Under Different Stress Paths

The critical damage value of rock is an important parameter of stability analysis when engineering rock mass. Based on the previous single test method, this paper, combined with the deformation characteristics of rock residual phase under different stress paths, proposed a single specimen repeated loading method to measure the critical damage value of rock based on different damage variables. The paper also proposed to modify the critical damage value based on residual constitutive energy and to improve the definition of damage variables based on constitutive energy dissipation. According to the microstructure characteristics of the rock sample, the mechanism of the single specimen method to determine the critical value of rock sample damage is revealed. The results show that: 1) Comparing the results of triaxial failure test of rock under different stress paths and single specimen repeated loading test, the residual strength of rock sample is mainly controlled by the confining pressure of loading, which is not an obvious relationship with initial confining pressure and stress path; 2) The number of repeated compressions has little effect on the internal structure, particle flatness, and particle surface smoothness of their specimens, which is reflected at the macroscopic level that the residual strength of sandstone tends to achieve a stable value; and 3) The corrected critical damage value based on residual strain energy is closer to the theoretical value. Test methods in this paper can provide useful references for determination of critical damage value.

Introduction

Conventional mechanical tests to obtain the strength, energy, and even damage values of rocks often require the measurement of multiple specimens; this method is usually called the multiple specimen method. This method not only increases the measurement cost and time consumption, but also causes the rock body to be in a continuous and discrete medium due to its complex environment and the highly nonlinear geological body that experiences different stress paths, which leads to the dispersion of the results when conducting mechanical tests. The anomalous results may even appear as the peak strength decreases while the confining pressure increases [1]. How to accurately and effectively derive the mechanical parameters of rock strength and thus quantify the degree of rock damage is a very important issue in rock engineering design [2]. In order to effectively deal with this problem, many scholars have carried out a lot of fruitful research work in improving the accuracy of the rock sample itself, with adequate screening and correction of the results afterwards [3], and these measures have reduced the dispersion of the test results to a certain extent, but the multi-test method based on the above methods cannot fundamentally solve the dispersion problem. It must be studied from a new way of thinking.

Based on this, the study of graded loading using a single specimen, and then the method of obtaining strength, usually called the single specimen multi-stage loading method, was proposed as early as 1975 [4–6]. Li Hongzhe and others [7]determined the mechanical parameters of the rock under the unloading stress path by conducting multi-stage unloading perimeter pressure damage tests on a single rock sample. Some scholars [8, 9] grafted the idea of the single specimen loading method to triaxial shear mechanics tests and carried out multi-stage direct shear tests on relevant material media. Considering that the single specimen method has a good control of test dispersion and is widely accepted by the academic community, the International Society of Rock Mechanics has included it as one of the recommended methods for rock strength testing [6]. Some studies [10, 11] have shown that the stress path of the single specimen method, loaded at each level (except the first level), causes irreversible aging damage to the rock samples, resulting in the strengths corresponding to each level with the set envelope pressure being less than those under conventional monotonic loading at the same envelope pressure. Therefore, considering the time-dependent load damage applied in graded loading, some scholars [10, 11] proposed a correction method for the strength considering the corresponding damage effect, and the obtained results were improved to some extent. And Pagoulatos, A [12] proposed a method based on the volumetric strain of 0 as the termination point of each level of loading, and the damage envelope characteristics obtained using this method showed good agreement with the single-level conventional triaxial test.

In reality, the rock mass in the project has a complex attachment environment and a complex and variable stress state, and the rock mass in many projects is often in the post-peak stage (strain softening stage and residual stage) bearing. It is also seen in field site observation that more slope and tunnel rock masses are working with a certain measure of structural surface, as shown in Figure 2.1. How to determine the damage value of the residual stage, that is, the damage value of the critical damage, so as to achieve an accurate grasp of the whole process of rock damage evolution, is particularly important, and in the evaluation of engineering rock stability analysis, the determination of the critical damage value of the rock in the process of rock damage evolution is a very important parameter. Regarding the study of damage critical value, more scholars [13, 14] carried out exploratory studies from theory and experiments, but in order to reduce the data dispersion brought by experiments, it is also necessary to conduct multiple sets of experiments. Deng Huafeng and others [15] proposed a method to determine the residual strength of a single specimen by repeated loading based on the idea of graded loading of a single specimen, and concluded that the residual strength value of a single specimen by repeated compression is not related to the amount of repeated loading, but only to the magnitude of its loading envelope, which means that the stress-strain curve of each repeatedly loaded test specimen is coincidental and its residual strength and residual strain energy are also not related to the amount of loading, but only to the loading envelope. In this paper, this idea is borrowed and further extended to the repeated loading test under unloading damage. As the natural rock body in the stress environment is complex and variable, excavation in engineering unloading stress path is one of the more common methods. Based on this, this paper proposes a new method for determining the critical damage value of rock samples under multiple stress paths by single specimen repetitive loading method based on the previous single specimen method, starting from the strength and energy perspectives, and combining the characteristics of the residual stage stress-strain curves during compression tests under triaxial monotonic loading and cross-axis compression and unloading of the rock. This is in order to lay the foundation for subsequent study of the damage evolution model and the determination of its boundary conditions, that is to say the critical damage value. The critical damage value of the rock specimens under repeated loading test are consistent with the conventional triaxial test. Most importantly, the proposed method involves relatively less dispersion and is cheap, reliable, and time-saving.

Test Scheme

Specimen Preparation

Previously, single specimen multi-stage loading has offered good applicability in determining the peak strength of rock samples in a hierarchical manner [4], but if this method is directly grafted to determine the residual strength and residual strain energy of rock samples and thus the size of their damage values in the critical damage state, it will face some technical difficulties [15].

Therefore, in this paper, based on the method of determining the residual strength index of rock samples by repeated loading of a single specimen by Deng Huafeng and others [15], the single specimen method to determine the critical damage value under different stress paths and the main experimental procedures are mainly.

The triaxial unloading envelope damage test was performed on the rock samples, and the unloading envelope pressure began when the residual phase appeared in the rock samples to obtain the rock samples at the time of unloading damage. Then the initial envelope pressure value was set for the above unloaded damaged rock samples, and then the repeated loading test was performed until the stress-strain curve entered a stable residual phase, at which point the unloading was started, and then the envelope pressure value at the time of repeated loading was increased step by step for the repeated loading test. In accordance with previous experience [15], repeated loading with 4–5 levels of enclosing pressure is generally carried out. The residual strength, shear strength, and strain energy of the residual stage of the rock sample under different confining pressures are analyzed to obtain the critical damage value of the rock sample.

The accuracy and reliability of the single specimen repeated loading method for determining the critical damage value of rock under different stress paths requires three conditions to be satisfied:

① Under the same confining pressure conditions, the stress-strain curve obtained by repeated loading of a single specimen should be basically the same as that obtained by conventional monotonic triaxial loading tests.

② For rock samples damaged by conventional triaxial compression under different initial envelope pressure conditions, the stress-strain curves obtained should be basically the same if the same envelope pressure is used for repeated loading.

③ The stress-strain curves obtained for rock samples damaged by triaxial tests using different stress paths should be basically the same as those obtained when damaged by triaxial loading if the same confining pressure is used for repeated loading.

For this purpose, the experimental steps were:

1) A conventional triaxial compression test and single specimen repeated loading test were designed. During the test, four types of confining pressures, namely 5, 10, 20, and 30MPa, were considered, and the conventional triaxial compression test was first carried out and unloaded after reaching the residual strength stage, and then single specimen repeated loading was carried out considering the above four confining pressures. In the process of repeated loading, each load was unloaded after reaching the residual strength stage, and then the confining pressure value was increased and loaded again.

2) Repeated loading tests of rock samples damaged by triaxial fixed-axis pressure-unloading confining pressure tests were carried out, and comparative analysis was performed. Considering four kinds of confining pressures (5, 10, 20, and 30 MPa), constant axial pressure was carried out to take 70% of the peak strength of triaxial loading under the corresponding confining pressure, unloading the confining pressure until destruction, and then single specimen was repeatedly loaded under the initial confining pressure was considered. In the process of repeated loading, each load is unloaded after the residual strength stage, and then the enclosing pressure value is increased and loaded again.

As is shown in Figure 1, the rock sample used in this paper is a typical sandstone from the Three Gorges reservoir area. It is a slightly weathered, sericite medium-grained quartz sandstone, 50 mm in diameter and 100 mm in height, which was strictly screened by wave velocity and density tests in order to control the discrete nature of the specimen [16]. The triaxial compression test is carried out on the RMT-150C rock mechanics test system. The degree of damage was characterized by the damage values of the corresponding physical quantities.

$V_{\text{j}}=\frac{P_0-P_j}{P_0}$(2.1)

FIGURE 1

FIGURE 1. Schematic diagram of the rock mass in the field.

V_j is the damage value of a physical quantity, P₀ is the peak value of a physical quantity of the rock sample, and P_j is the value of a physical quantity of the rock sample in the residual phase after the peak.

Triaxial Loading Test Analysis

The stress-strain curves of typical conventional triaxial compression test and single specimen repeated loading under different initial circumferential pressures are shown in Figure 2.

FIGURE 2

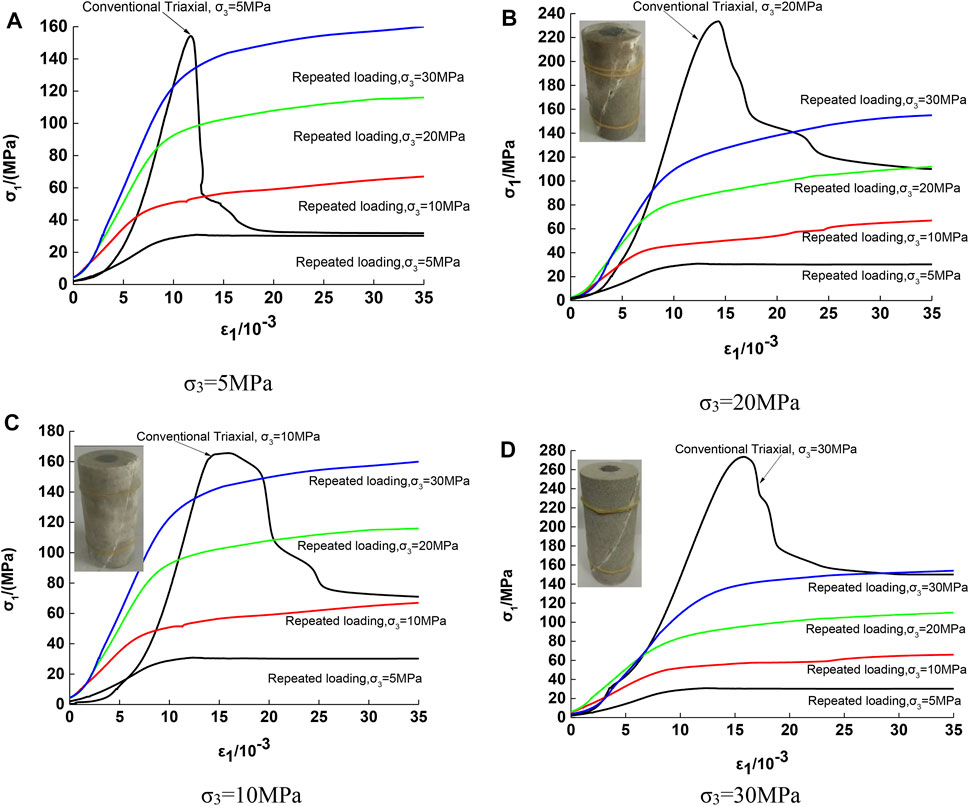
FIGURE 2. Stress-strain curves of conventional triaxial compression test and single specimen repeated loading test under different confining pressures. (A) σ₃=5MPa. (B) σ₃=10MPa. (C) σ₃=20MPa. (D) σ₃=30MPa.

Figure 2 shows that:

1) The change patterns of stress-strain curves of repeated loading tests under different repeated loading envelope pressures are also basically the same, and the first condition is satisfied. After a relatively short compression-density stage and linear elastic stage, the rock samples rapidly enter the plastic hardening stage, and neither of them has an obvious peak point, but directly enter the residual strength stage, and the strain hardening phenomenon is obvious with the increase of the confining pressure.

2) When the secondary loading envelope pressure value of the repeated loading test and the initial envelope pressure value of the initial conventional triaxial compression test are the same, the stress-strain curves of the two can coincide well after entering the residual phase, which satisfies the second condition well. It means that for the rock samples damaged by conventional triaxial monotonic loading compression, when the same loading envelope pressure is used for repeated loading, the deformation and strength characteristics of the residual stage will be basically unchanged, and the energy is the physical quantity of integrated deformation and stress, according to which the value should also be unchanged, as discussed in the latter Energy Analysis Section.

Triaxial Loading Test Analysis

The stress-strain curve of triaxial unloading test and the repeated loading test curve of single specimen under different circumferential pressures are shown in Figure 3.

FIGURE 3

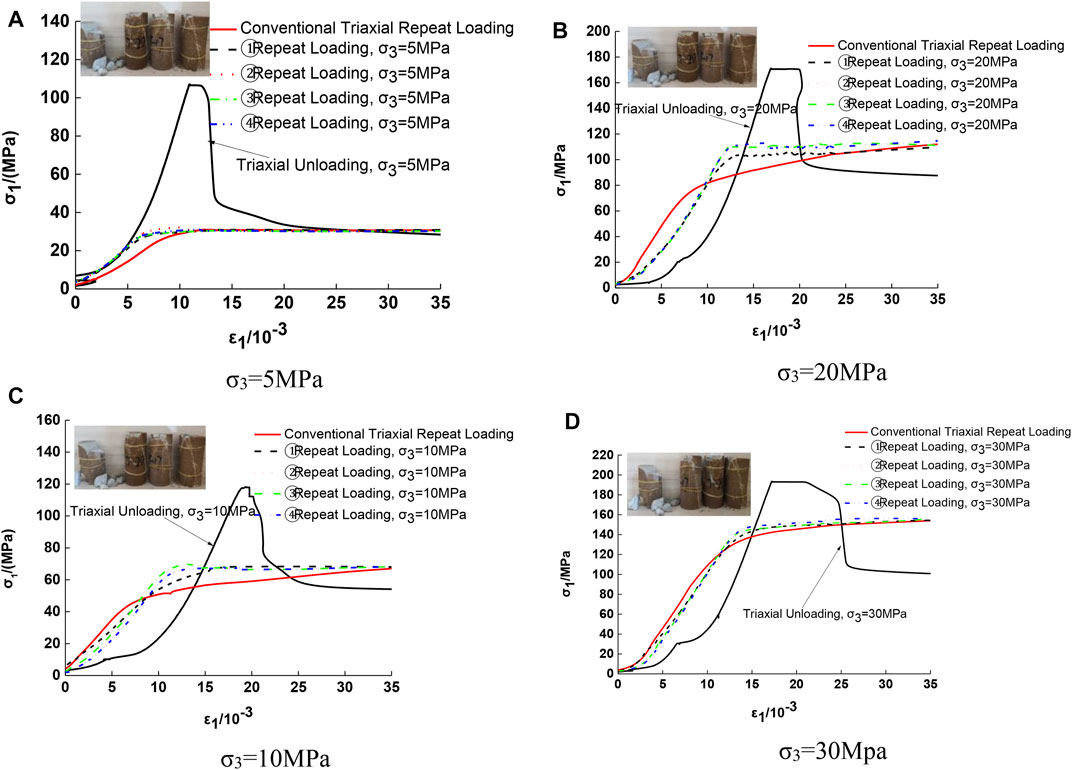
FIGURE 3. Stress-strain curves of triaxial unloading test and single specimen repetitive compression test under different confining pressures. (A) σ₃=5MPa. (B) σ₃=10MPa. (C) σ₃=20MPa. (D) σ₃=30Mpa.

From Figure 3, it can be seen that:

1) The stress-strain curves of the repetitive loading residual stage of the triaxially unloaded damaged rock samples and the repetitive loading stress-strain curves of the triaxially loaded damaged rock samples can coincide well, indicating that the residual strength of the rock mass under the same hydrostatic pressure is not highly related to its pre-peak stress path, which also satisfies the aforementioned condition 3 well and shows that the single specimen method is indeed feasible.

2) The residual strength of the triaxially unloaded damaged rock samples was significantly smaller than the residual strength value under repeated loading tests, but the stress-strain test curves basically overlapped. The reason for the analysis is that the stress path of constant axial pressure unloading circumferential pressure is used in the rock sample, and the circumferential pressure at the time of damage is obviously smaller than the initial circumferential pressure when reloading to the initial circumferential pressure, which is equivalent to the increase of the loading circumferential pressure, so the residual strength at the time of repeated loading is higher than the residual strength at the time of unloading damage.

3) Comparative analysis of the crushing degree of rock samples after repeated loading of single specimens of triaxial unloading damage under different initial envelope pressures is significantly higher than that of single specimens of triaxial loading damage after repeated loading tests, but the stress-strain curves of the residual stage basically overlap, indicating that the crushing degree of rock samples has little effect on the stress-strain curve of the residual stage, and the strength and deformation of rock samples are still generally controlled by a primary control shear structure surface.

Critical Damage Values

Compressive Strength Analysis

In order to facilitate quantitative analysis of the strength parameters of rock samples under different stress paths, the results of the conventional triaxial monotonic loading compression damage test and the single specimen repeated loading test in Figure 2 were statistically compiled, and the critical damage values based on compressive strength were obtained according to Equation 2.1, as shown in Tables 1, 2. In order to facilitate comparative analysis, the stress-strain curve tends to stabilize as its residual strength, and the residual strength in this paper is uniformly selected as the strength value corresponding to an axial strain of 3% [17].

TABLE 1

TABLE 1. Comparison of the results of conventional triaxial loading and single specimen repeated loading tests.

TABLE 2

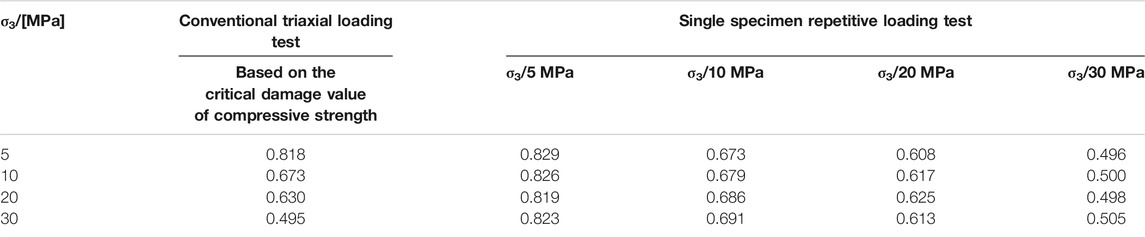
TABLE 2. Comparison of the results of conventional triaxial loading and repeated loading of single specimens based on the critical damage values of compressive strength.

From Tables 1, 2, it can be seen that:

1) In the conventional triaxial monotonic compression test, the residual strengths of the rock samples were 31.87, 60.96, 105.34, and 151.35 MPa for the four circumferential pressure cases of 5, 10, 20, and 30 MPa, respectively, and the critical damage values of their rocks based on compressive strength were 0.818, 0.673, 0.630, and The residual strength values were 30.23, 60.02, 106.57, and 149.04 MPa, respectively, with an error range of 1.15–5.14%, when the secondary envelope pressure at repeated loading was the same as the primary envelope pressure of the conventional triaxial compression test. The critical damage values obtained for their rocks based on compressive strength were 0.829, 0.679, 0.625, and 0.505, with an error range of 0.85–1.94%. Conventional triaxial loading indicates that for rock samples damaged by conventional triaxial compression, the residual strength and the critical damage values obtained based on compressive strength are basically consistent with the results of conventional triaxial rock tests when the same confining pressure is used for repeated loading.

2) The residual strengths of the rock samples damaged by the conventional triaxial monotonic compression test at 20 MPa circumferential pressure were 31.83, 58.90, 106.57, and 150.69 MPa when the rock samples were repeatedly loaded at 5, 10, 20, and 30 MPa, respectively, and the residual strengths of the rock samples based on The error range of the residual strengths obtained from the conventional triaxial compression tests was 0.13–3.38%, and the error range of the critical damage values obtained from the rock based on compressive strength was 0.03–1.97%. Moreover, the repeated loading tests of the rock samples damaged by 5, 10, and 30 MPa peritectic compression tests of conventional triaxial monotonic compression tests also obtained a consistent matching law. It indicates that the residual strengths and their damage values obtained from the repeated loading tests with different loading envelope pressures for the rock samples damaged by conventional triaxial compression are approximately equal to the values obtained from the conventional triaxial tests. It also indicates that the residual strength values of the repeated loading tests under multiple loading envelope pressures for rock samples damaged by triaxial compression are mainly controlled by the envelope pressure at the time of repeated loading, and not much related to the envelope pressure at the time of damage by primary loading.

3) The damage form of rock samples under different initial envelope pressure conditions is typical of compression-shear damage. Although each rock sample experienced the conventional triaxial monotonic compression test and four repeated loading tests under different secondary loading envelope pressures, there was only one controlled macroscopic shear damage surface in general, and no new shear damage surface was generated. It indicates that the residual strength of the rock sample during repeated loading is mainly controlled by the main shear damage surface formed during the first conventional triaxial compression.

Energy Analysis

When studying damage problems, how to accurately quantify the extent of damage directly affects the reliability of the project [18]. From the results of repeated loading tests on single specimens under different stress paths, it is clear that the residual phase repeated loading stress-strain curves can overlap well, indicating that there is indeed a critical damage value, which exists in the form of attractors in the rock damage evolution process. Therefore, this subsection will compare and analyze the magnitude of the critical damage value of the rock derived from the perspective of strength and energy, and lay the experimental foundation for subsequent research.

Xie Heping and others [19] considered that energy transformation is an essential feature of the physical process of matter as known from the laws of thermodynamics, and argued that energy dissipation causes damage to the rock, resulting in the loss of strength. The energy damage variable is defined as the ratio of unit dissipation energy to critical dissipation energy. The damage variable is considered to be 1 at critical damage, which is a discrepancy with the actual situation, and the rock still has some strength when it enters the residual phase, so the damage variable is not 1. Jin Fengnian and others [20] considered that the damage variable can be defined according to the dissipation of the material intrinsic energy, i.e., the damage variable is the ratio of dissipation energy to material energy. In the paper, the intrinsic energy is divided into elastic energy, plastic energy, rheological energy, and fracture energy, and it is considered that when the damage and fracture energy are clearly distinguished, it is possible to ignore the value of fracture energy, i.e., the dissipation energy is considered to be equal to the total deformation energy minus the elastic energy. However, fracture energy is not only consumed in the form of dissipative energy, but also released in the form of thermal energy, acoustic energy, and so on. These forms of energy in the form of damage before the value are relatively small, almost negligible, but once the residual phase after the peak is reached, the moment of rock damage will emit a violent sound and release a large amount of heat energy, then the size of the fracture energy value cannot be ignored. Then the formula for calculating the damage will produce a large damage value. Based on this, this paper proposes to use the intrinsic energy of the rock loading fracture process minus the intrinsic energy of repeated loading in the residual phase and the ratio of the intrinsic energy of the rock loading fracture process as the critical damage value to correct the definition of the damage variable in the literature [20].

$\{\begin{array}{l}D=\frac{U_d}{U},\epsilon \mathrm{<}{\epsilon }_r\\ D=1-\frac{U_r}{U},\epsilon \ge {\epsilon }_r\end{array}$(3.1)

In the equation, $U_d$ is the dissipative energy, that is the area contained in the unloading curve and stress axis; $U_r$ is the residual intrinsic energy, that is the area contained in the repeated loading stress-strain curve; $U$ is the intrinsic energy during loading fracture, that is the area of the full stress-strain curve for triaxial loading; and $D_r$ and is the critical damage value, as shown in the following table. In order to facilitate the analysis of the differences in the critical damage values obtained from different physical quantities as damage variables, the magnitude of the critical damage values of sandstone based on strength and energy as damage variables are plotted, as shown in Table 3.

TABLE 3

TABLE 3. Table of critical damage values based on different physical quantities for different confining pressures.

Table 4 shows that:

1) The residual intrinsic energy increases from 0.94 MJ/m³ to 3.21 MJ/m³, the dissipated intrinsic energy increases from 1.52 MJ/m³ to 4.63 MJ/m³, and the intrinsic energy increases from 1.54 MJ/m³ to 5.03 MJ/m³ for the circumferential pressure from 5 MPa, 10 MPa, 20 MPa, and 30 MPa. The corrected critical damage value increases from 0.395 to 0.363 and the uncorrected critical damage value decreases from 0.987 to 0.920 between the critical damage value determined by repeated compression tests, the value increases with the confining pressure, and there is no certain regularity, but seems to be in a certain oscillating nature. After analysis the following reasons are presented: 1) the existence of dispersion between the rock samples or the error brought about by the measurement accuracy; 2)in the process of system evolution, the appearance of the rise and fall is common and inevitable [21]; and 3)there is a so-called critical damage constant which needs to be studied subsequently.

2) From Table 3, the difference between the critical damage value obtained from the uncorrected formula and the corrected critical damage value is large; it is necessary to verify the rationality of the corrected data from a theoretical point of view. The damage process of rocks under stress and environmental effects has the phenomenon of overshoot, and there is also a damage threshold. The reformation group method is a very effective method to study the transmissivity threshold [22–24]. Gao Zhaoning and others [13] introduced the self-organization degree parameter to describe the stress transfer between units, and then established the corresponding reformation group, and obtained the damage threshold value in the range of [0.150,0.382]. Huang Menghong and others [14] established the reformation group in different dimensions, and obtained the critical damage value of 0.382 in two dimensions and 0.104 in three dimensions. The critical damage value is [0.104,0.382], which is closer to the critical damage value obtained by the modified formula proposed in this paper.

TABLE 4

TABLE 4. Table of energy characteristic values and critical damage values for different confining pressure.

Microstructural Characteristics and Mechanism Analysis

In order to better study the microstructural characteristics and laws of sandstone in the single specimen repetitive compression test, based on different repetitive compression times, the SEM photos with a uniform magnification of 350 times were taken for comparison, and the typical SEM photos are shown in Figure 4.

FIGURE 4

FIGURE 4. SEM microscopic morphology of rock fracture. (A) Conventional triaxial compression damage. (B) Repeated compression 1 time. (C) Repeated compression 2 times. (D) Repeated compression 3 times. (E) Repeated compression 4 times.

From Figure 4, it can be seen that during the repeated compression tests, the pattern of microstructural characteristics of the rock samples was obvious.

1) The mineral composition, particle content, internal structural composition, particle properties, and cementation strength [15], which determine the residual strength of rock samples under each repeated compression test, are almost the same, i.e., the number of repeated compressions has little effect on the internal structure, particle flatness, and particle surface smoothness of their specimens, which is reflected to the macroscopic level that the residual strength of sandstone tends to a stable value.

2) The peak and residual strengths of rock samples obtained from conventional triaxial monotonic loading compression tests under different circumferential pressures already include the effects of the differences between rock samples and the corresponding circumferential pressure values on the shear rupture surface of rock samples. The deviation between the rock samples mainly comes from the microscopic pores, fracture cracks, and other size defects in the rock samples at different scales. Once the loading stress exceeds the peak strength of the rock sample itself, the local cracks gradually penetrate to form the macroscopic shear damage surface, and the bearing capacity of the rock sample will be mainly controlled by the shear strength (friction strength) of the macroscopic shear damage surface after entering the residual stage. For the same group of rock samples, their inherent mineral composition, particle content, internal structural composition, particle properties, and cementation strength are approximately the same. Therefore, the shear strength and the residual strength of the rock samples controlled by the shear breaking surface are naturally the same between different rock samples. Therefore, the differences between rock samples mainly affect the deformation and strength characteristics of the pre-peak phase and have little effect on the residual strength phase after strain softening after damage, so that the strain energy into the residual phase and its residual strength are mainly controlled by the value of the immediate loaded confining pressure. Similar experimental results obtained in this paper can be found in the literature [5]. This further illustrates the rationality of the single specimen repeated loading method proposed in this paper to determine the critical damage value of rock samples.

Conclusion and Discussion

1) Based on the previous single specimen method, a single specimen repetitive loading method was proposed to determine the critical damage value of rock under different stress paths by combining the characteristics of the stress-strain curve of the residual phase of the rock. The validation analysis shows that the mechanical parameters of the residual stage and the critical damage value of rock samples obtained by the single-cell repeated loading method are basically consistent with the results obtained from conventional triaxial compression tests, and the test results obtained by the single-cell repeated loading method are less discrete and less expensive to measure, which indicates that the method is economical and reasonable.

2) Based on the residual strain energy obtained by the single specimen method, the residual stage mechanical parameters proposed to solve the critical damage value based on strength and energy, etc., to achieve the correction of the damage variable defined in the literature [20] to improve the validation analysis shows that the critical damage value obtained based on the residual strain energy is more consistent with the theoretical critical damage value. This shows the rationality of the single specimen repeated loading method proposed in this paper to determine the critical damage value of rock samples; it is recommended that the single specimen method to obtain the critical damage value using energy as the damage variable is more appropriate.

3) It must be pointed out that there are many kinds of rocks in nature, the environment is complex and changeable, and the stress history experienced is in various forms. In this paper, the single specimen repeated loading test determines the residual stage mechanical and damage parameters of the rock sample, namely the strength and critical damage value. The rock sample used in the test is lightly weathered, sericite medium-grained quartz sandstone. The damage test is carried out for the triaxial loading path and the triaxial constant-axis pressure unloading circumferential pressure path. Whether this method is still applicable to the tests on rocks with different lithologies and different stress paths is the work to be carried out by the author in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

HL, ZPW, and QJ contributed to conception and design of the study. LQD, LPW, and HFD, organized the database. CY JHC, and HYP performed the statistical analysis. LW modified the language of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by China Three Gorges Construction Engineering Corporation, National Nature Science foundation of China (No.51809151, No.42177132). The authors declare that this study received funding from China Three Gorges Construction Engineering Corporation. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Conflict of Interest

HL, LW, HP, LW, and QJ were employed by the company China Three Gorges Construction Engineering Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, orclaim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.775459/full#supplementary-material

References

1. Mingqing Y, Anzeng H, Yushou L. A Study of Triaxial Strength and Deformation of Flawed Specimen. Chin J Rock Mech Eng (1998) 20(2):97–101. (in Chinese).

Google Scholar

2. Vásárhelyi B, Kovács D. Empirical Methods of Calculating the Mechanical Parameters of the Rock Mass. Periodica Polytechnica Civil Eng (2017) 61(1):39–50.

Google Scholar

3. Deng H, Wang Z, Li J. Compressive Strength Correction Method of Flaw Sample in Rock Mechanics Test. Chin J Underground Space Eng (2017) 13(02):307–13. (in Chinese).

Google Scholar

4. Kovari K, Tisa A. Multiple Failure State and Strain Controlled Triaxial Tests[J]. Int J Rock Mech Mining Sci Geomechanics Abstr (1975) 7(1):17–33.

Google Scholar

5. Chengdong S, Mingqing Y. Determination Method of Strength Parameters for sandstone and marble with One Specimen. Chin J Rock Mech Eng (2004) 23(18):3055–8. (in Chinese).

Google Scholar

6. Kovarik AT, Einstein HHEA. Suggested Methods for Determining the Strength of Rock Materials in Triaxial Compression: Revised Version. Int J Rock Mech Mining Sci Geomechanics Abstr (1983) 20(6):283–90.

Google Scholar

7. Hongzhe L, Caichu X, Chongbang X. Experimental Study of Rock Unloading Strength Parameters Based on Multiple Failure Method. Chin J Rock Mech Eng (2008) 27(S1):2681–6. (in Chinese).

Google Scholar

8. Xu Y, Li Z, Ge X. Soft Rock Single Test Sample Shear experiment Methord. J Liaoning Tech Univ (2006) 25(3):367–8. (in Chinese).

Google Scholar

9. Y H TS. An Improved Method to Make the Microdroplet Single Fiber Composite Specimen for Determining the Interfacial Shear Strength. J Mater Sci (2012) 47(11):4775–8.

Google Scholar

10. Liu B, Cui S. Improvement of Single Specimen Method for Determination of Rock Strength Parameters. China Civil Eng J (2011) 44(s):162–5. (in Chinese).

Google Scholar

11. Song X. The Characteristics and Improvement Methods of Strength Parameters of Rock Are Determined by Single Test Method. Sci Tech (2016) 33–4. (in Chinese).

Google Scholar

12. Pagoulatos A. Evaluation of Multistage Triaxial Testing on Berea sandstone. The University of Oklahama (2004).

Google Scholar

13. Gao ZN, Yao LK, Xu GX. Study on Self-Organized Characteristics and Criticality Condition in the Course of Rock Failure. J SiChuan Univ (2009) 41(2):91–5.

Google Scholar

14. Menghong H. Theoretical and Experimental Research on Rock Damage Evolution Model and Damage Critical Value. China Central South University (2004).

Google Scholar

15. Deng H, Zhang H, Li J. Single Specimen Repeated Loading Method for Determination of Residual Strength Parameters of Rock. Chin J Rock Mech Eng (2019) 41(2):348–54. (in Chinese).

Google Scholar

16. Deng H, Li J, Deng C. Analysis of Sampling in Rock Mechanics Test and Compressive Strength Prediction Methods. Rock Soil Mech (2011) 32(11):3399–403. (in Chinese).

Google Scholar

17. Chen LH, Chen ZY, Li GX. Discussion of Linear Regression Method to Estimate Shear Strength Parameters from Results of Triaxial Tests. Rock and Soil Mechanic s (2005) 26(11):1785–9. (in Chinese).

Google Scholar

18. Zhang QS, Yang GS, Ren JX. New Study of Damage Variable and Constitutive Equation of Rock. Chin J Rock Mech Eng (2003) 22(1):30–4. (in Chinese).

Google Scholar

19. Xie HP, Ju Y, Li LY. Criteria for Strength An-D Structural Failure of Rocks Based on Energy Dissipation and Energy Release Principles. Chin J Rock Mech Eng (2005) 24(17):3003–10. (in Chinese).

Google Scholar

20. Jin FN, Jiang MR, Gao XL. Defining Damage Variable Based on Energy Dissipation. Chin J Rock Mech Eng (2004) 23(12):1976–80. (in Chinese).

Google Scholar

21. Zeng G. Self-organized View of Nature. Beijing: Peking University Press (1996). (in Chinese).

Google Scholar

22. de Alcantara Bonfim OF, Engelsberg M. Large-cell Monte Carlo Renormalization-Group Method for a New Type of Environmental Percolation. Phys Rev B (1986) 34(3):1977–9. doi:10.1103/physrevb.34.1977

CrossRef Full Text | Google Scholar

23. Duan LP, Lu JF, Chen J . Application of Renormalization Group Theory to Critical Behavior of Water.J Chem Industry Eng (2003) 54(1):18–23. (in Chinese). doi:10.3321/j.issn:0438-1157.2003.01.004

CrossRef Full Text | Google Scholar

24. Liang ZZ, Tang CA, Tang SB. Characteristics of Fractal and Percolation of Rocks Subjected to Uniaxial Compression during Their Failure Process. Chin J Rock Geotechnical Eng (2007) 29(9):1386–91. (in Chinese). doi:10.3321/j.issn:1000-4548.2007.09.017

CrossRef Full Text | Google Scholar